Difference between revisions of "Tugas 2 Vinia Permata Kusuma"
(→Solusi Aplikasi) |
|||
| (6 intermediate revisions by the same user not shown) | |||
| Line 8: | Line 8: | ||
== Exercise 2.2 No. 20 == | == Exercise 2.2 No. 20 == | ||
Soal yang saya pilih terdapat pada bab 2 di exercise 2.2 no. 20 mengenai aplikasi dari matriks yang berupa rangkaian pipa yang mempunyai konsentrasi yang berbeda beda untuk aliran masuk dan keluarnya yang diselesaikan dengan cara matrix dengan metode gauss | Soal yang saya pilih terdapat pada bab 2 di exercise 2.2 no. 20 mengenai aplikasi dari matriks yang berupa rangkaian pipa yang mempunyai konsentrasi yang berbeda beda untuk aliran masuk dan keluarnya yang diselesaikan dengan cara matrix dengan metode gauss | ||
| + | [[File:Vinia 2.2 20 S.jpg]] | ||
== Solusi manual == | == Solusi manual == | ||
Diselesaikan dengan eliminasi gauss dengan eselon baris tereduksi hingga membentuk segitiga bawah yang berisikan entry 0 sehingga dapat ditemukan penyelesaian untuk berbagi macam konsentrasi dengan cara substitusi | Diselesaikan dengan eliminasi gauss dengan eselon baris tereduksi hingga membentuk segitiga bawah yang berisikan entry 0 sehingga dapat ditemukan penyelesaian untuk berbagi macam konsentrasi dengan cara substitusi | ||
| − | + | [[File:Vinia 2.2 20 M.jpg|500px|thumb|center|Manual 2.2 20]] | |
== Solusi Aplikasi== | == Solusi Aplikasi== | ||
| Line 18: | Line 19: | ||
Lalu input matris B seperti matriks A lalu input n = len(A) dan masukkan range range matriks tersebut agar mendapa nilai sebenarnya | Lalu input matris B seperti matriks A lalu input n = len(A) dan masukkan range range matriks tersebut agar mendapa nilai sebenarnya | ||
| − | [[File:Vinia 2.2 20.jpg]] | + | [[File:Vinia 2.2 20.jpg|700px|thumb|center|Python 2.2 20]] |
| − | |||
== Initial Value == | == Initial Value == | ||
| Line 29: | Line 29: | ||
Lalu setelah mendapatkan percepatan dapat diselesaikan dengan Gerak Lurus Berubah Beraturan dengan menurunkan rumus ke dalam kecepatan, perpindahan, hingga menemukan ketinggian dari tebing | Lalu setelah mendapatkan percepatan dapat diselesaikan dengan Gerak Lurus Berubah Beraturan dengan menurunkan rumus ke dalam kecepatan, perpindahan, hingga menemukan ketinggian dari tebing | ||
| + | [[File:Vinia 2 initial M.jpg|500px|thumb|center|Manual Initial Value]] | ||
== Solusi Aplikasi== | == Solusi Aplikasi== | ||
Diselesaikan dengan menggunakan Python 3.7. Dengan meng-entry data yang dikathuinya terlebih dahulu seperti massa, percepatan gravitasi, hambatan udara, dan waktu sampai. Lalu masukkan algoritma python untuk memulai perhitungan percepatan menggunakan persamaan kesetimbangan gaya. Lalu dilanjutkan dengan memasukkan algoritma perhitungan h dalam gaya jatuh bebas dalam GLBB, sehingga ketinggian dapat terukur | Diselesaikan dengan menggunakan Python 3.7. Dengan meng-entry data yang dikathuinya terlebih dahulu seperti massa, percepatan gravitasi, hambatan udara, dan waktu sampai. Lalu masukkan algoritma python untuk memulai perhitungan percepatan menggunakan persamaan kesetimbangan gaya. Lalu dilanjutkan dengan memasukkan algoritma perhitungan h dalam gaya jatuh bebas dalam GLBB, sehingga ketinggian dapat terukur | ||
| − | [[File:Vinia 2 initial.jpg]] | + | [[File:Vinia 2 initial.jpg|700px|thumb|center|Python Initial Value]] |
== Komentar == | == Komentar == | ||
| Line 41: | Line 42: | ||
Dalam menghitung initial value gaya jatuh bebas dengan hambatan udara diperlukan peninjauan dari segi percepatan dengan hk. Newton ke-2 dan dilanjutkan dengan menurunkan rumus a hingga dapt rumus untuk mencari h. | Dalam menghitung initial value gaya jatuh bebas dengan hambatan udara diperlukan peninjauan dari segi percepatan dengan hk. Newton ke-2 dan dilanjutkan dengan menurunkan rumus a hingga dapt rumus untuk mencari h. | ||
| − | Namun dengan aplikasi kita | + | Namun dengan aplikasi kita dapat langsung masukkan algoritma untuk percepatan dan rumus h nya sehingga, tinggi dpt langsung muncul ketika kita play |
== Kembali Ke Profil== | == Kembali Ke Profil== | ||
| − | [http://air.eng.ui.ac.id/index.php?title=Vinia_Permata_Kusuma] | + | [http://air.eng.ui.ac.id/index.php?title=Vinia_Permata_Kusuma Vinia Permata Kusuma] |
Latest revision as of 10:38, 20 February 2020
Contents
Tugas 2 Metode Numerik
Pada Pertemuan ke-2 terdapat 2 tugas yang diberikan. 1. Memilih 1 soal yang paling menarik dari buku Numerical Method Engineering by Python 3 2. Menyelesaikan 1 soal initial value mengenai gerak jatuh bebas dengn adanya hambatan.
Exercise 2.2 No. 20
Soal yang saya pilih terdapat pada bab 2 di exercise 2.2 no. 20 mengenai aplikasi dari matriks yang berupa rangkaian pipa yang mempunyai konsentrasi yang berbeda beda untuk aliran masuk dan keluarnya yang diselesaikan dengan cara matrix dengan metode gauss
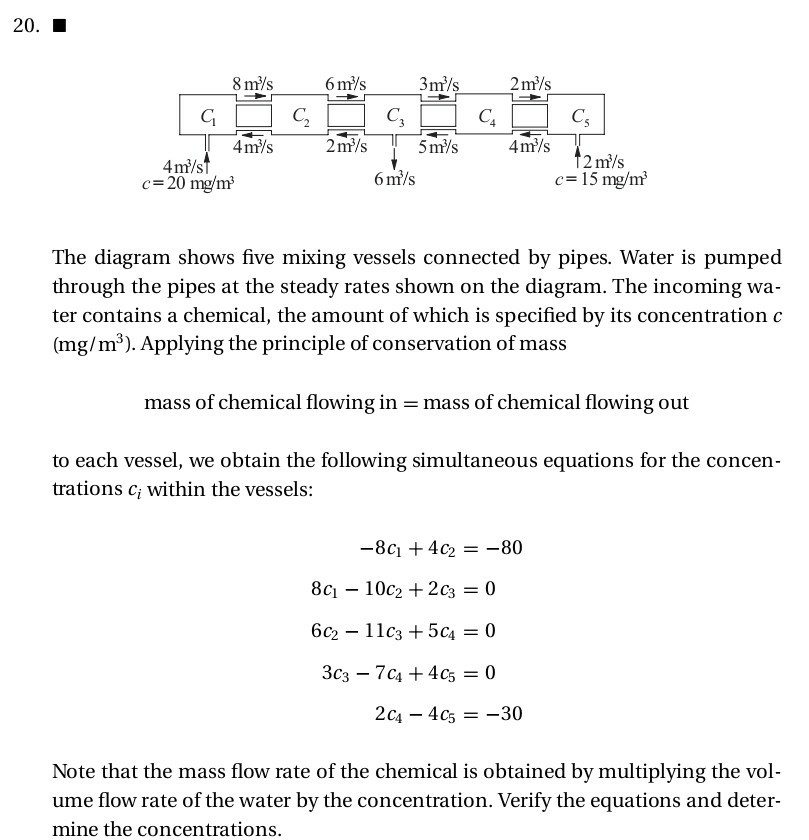
Solusi manual
Diselesaikan dengan eliminasi gauss dengan eselon baris tereduksi hingga membentuk segitiga bawah yang berisikan entry 0 sehingga dapat ditemukan penyelesaian untuk berbagi macam konsentrasi dengan cara substitusi
Solusi Aplikasi
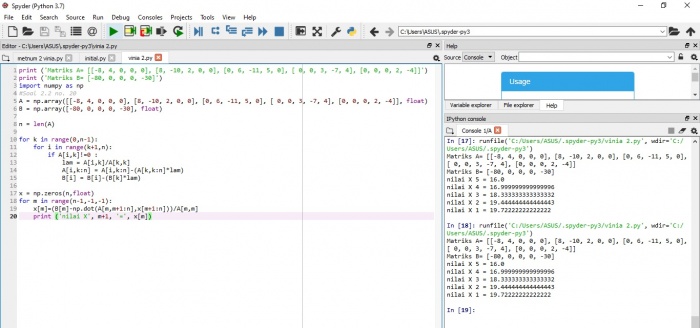
Diselesaikan dengan menggunakan Python 3.7. Dengan meng-entry algoritmanya dengan import numpy as np lalu tulis matrik yang dimaksud dengan input A = nparray([baris matriks A1,2,3])
Lalu input matris B seperti matriks A lalu input n = len(A) dan masukkan range range matriks tersebut agar mendapa nilai sebenarnya
Initial Value
Untuk soal permasalahan initial value lebih tepatnya gerak jatuh bebas dengan hambatan saya membuat kasus dimana batu dijatuhkan dari tebing yang tidak diketahui tingginya dengan massa 1.5kg hambatan udara 5m dan percepatan gravitasi 9.8m/s^2 dalam waktu 3 detik
Solusi Manual
Pada solusi secara manual diselesaikan melalui hukum Newton 2 yang menyatakan bahwa total gaya itu massa dikali dengan percepatan, di soal terdapat hambatan sehingga dapat mempengaruhi percepatan gravitasi
Lalu setelah mendapatkan percepatan dapat diselesaikan dengan Gerak Lurus Berubah Beraturan dengan menurunkan rumus ke dalam kecepatan, perpindahan, hingga menemukan ketinggian dari tebing
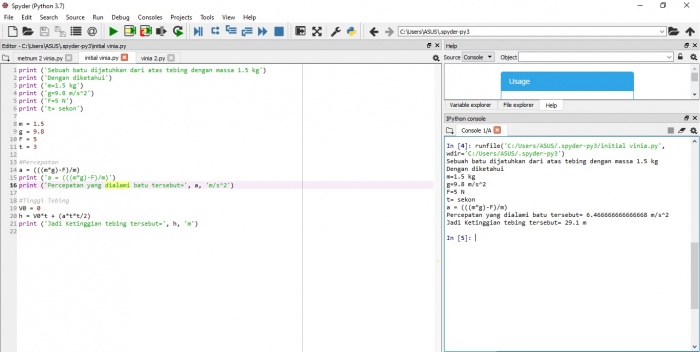
Solusi Aplikasi
Diselesaikan dengan menggunakan Python 3.7. Dengan meng-entry data yang dikathuinya terlebih dahulu seperti massa, percepatan gravitasi, hambatan udara, dan waktu sampai. Lalu masukkan algoritma python untuk memulai perhitungan percepatan menggunakan persamaan kesetimbangan gaya. Lalu dilanjutkan dengan memasukkan algoritma perhitungan h dalam gaya jatuh bebas dalam GLBB, sehingga ketinggian dapat terukur
Komentar
Dalam menghitung matriks secara manual membutuhkan kejelian yang baik dan daya pikir yang baik agar tidak terukar saat membuat eselon reduksi baris, sehingga mayoritas kesalahan terjadi karena kekurang telitian,ketidaksabaran dan keberulangan angka pada matriks sehingga nilai x dapat dicari lebih mudah dengan aplikasi.
Dalam menghitung initial value gaya jatuh bebas dengan hambatan udara diperlukan peninjauan dari segi percepatan dengan hk. Newton ke-2 dan dilanjutkan dengan menurunkan rumus a hingga dapt rumus untuk mencari h.
Namun dengan aplikasi kita dapat langsung masukkan algoritma untuk percepatan dan rumus h nya sehingga, tinggi dpt langsung muncul ketika kita play