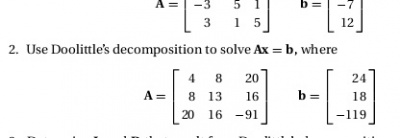Difference between revisions of "Tugas 2 Metnum Sultan Alif Zidane"
Sultan.alif (talk | contribs) (→Initial Value Problem) |
Sultan.alif (talk | contribs) (→Soal 2 Problem set 2.2) |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 18: | Line 18: | ||
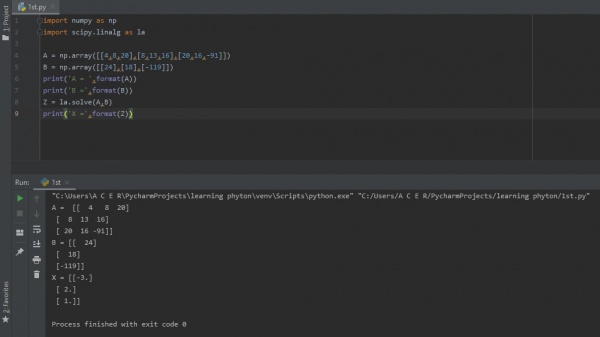
| + | Setelah melakukan percobaan kembali, dengan menggunakan aplikasi yang sudah ditambahkan module yang diperukan saya mendapat hasil yang sama seperti perhitungan manual. | ||
| + | |||
| + | |||
| + | [[File:Np array berhasil.jpg|600px|]] | ||
== Initial Value Problem == | == Initial Value Problem == | ||
| Line 75: | Line 79: | ||
[[File:Initial_Value_(Proses).png|400px|]] [[File:Initial_Value_(jawaban).png|400px|]] | [[File:Initial_Value_(Proses).png|400px|]] [[File:Initial_Value_(jawaban).png|400px|]] | ||
| + | |||
| + | |||
| + | Proses pengerjaan menggunakan aplikasi juga memakai rumus yang didapatkan dari cara manual. Dan hasil yang diperoleh pun sama, sehingga dapat disimpulkan bahwa pengerjaan initial value problem dapat diselesaikan menggunakan aplikasi. | ||
Latest revision as of 19:07, 20 February 2020
Soal 2 Problem set 2.2
Dari soal tersebut diminta untuk menyelesaikan dengan menggunakan Doolittle's Decomposition atau LUdecomposition, berikut ini merupakan penyelasaian dari tugas tersebut dengan menggunakan metode manual.
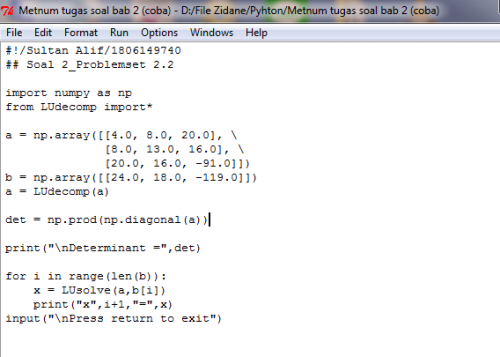
Dari perhitungan manual didapatkan hasil yang sesuai, maka dari itu saya juga akan mencoba menyelesaikan perhitungan dengan menggunakan aplikasi python. Dan berikut adalah hasil yang saya peroleh
Dari hasil yag saya peroleh masih belum mendapatkan jawaban yang tepat, karena dalam aplikasi python yang saya gunakan belum terdapat module numpy. Maka dari itu persamaan belum mendapatkan solusi yang tepat seperti perhitungan manual.
Setelah melakukan percobaan kembali, dengan menggunakan aplikasi yang sudah ditambahkan module yang diperukan saya mendapat hasil yang sama seperti perhitungan manual.
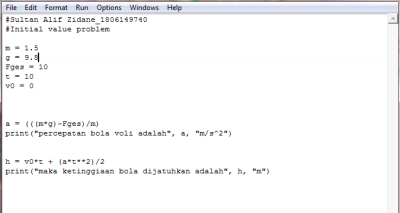
Initial Value Problem
Dalam penjelasan mengenai initial value problem, suatu gerak jatuh bebas didasarkan pada hukum newton ke 2. Yang mana F= m.a namun pada kasus kali ini akan ditambahkan sedikit faktor yang mempengaruhi yaitu gaya gesek udara. Persamaan gaya gesek udara dapat dituliskan sebagai
F = k.eta.v
dimana:
- k adalah konstanta yang bergantung bentuk benda
- eta adalah koefisien viskositas, dalam hal ini adalah udara, yang secara normal nilainya 1,8 x 10^-5 kg/ms
- v adalah kecepatan benda
Selanjutnya adalah pengembangan dari rumus mengenai hukum newton 2 adalah sebagai berikut:
ΣF = m.a
m.g - k.v = m.dv/dt
dv/(m.g - k.v) = dt/m
kemudian diintegralkan, sehingga mendapatkan
- 1/k ln (m.g - k.v) = 1/m.t + C
ln (m.g - k.v) = - k/m.t + C
m.g - k.v = e^(- k/m.t + C)
k.v = m.g - C.e^(-k/m.t)
v(t) = m.g/k - C.e^(-k/m.t)
Setelah itu karena merupakan gerak jatuh bebas maka v(0)=0. Sehingga didapatkan C = m.g/k kemudian persamaan ini disubtitusikan kembali ke v(t) = m.g/k - C.e^(-k/m.t) yang menjadi v(t) = m.g/k - m.g./k.e^(-k/m . t) Sederhanakan dan didapatkan persamaan
v(t) = mg/k . (1 - e^(-k/m . t)) yang akan menjadi persamaan yang kita gunakan.
Untuk persamaan jarak, seperti yang diketahui v(t) = dx/dt akan diubah menjadi dx/dt = mg/k . (1 - e^(-k/m . t))
lalu diintegralkan dan mendapatkan
x(t) = (m.g/k).t - (m^2.g/k^2).(1 - e^(-k/m . t)) yang akan menjadi persamaan jarak yang kita gunakan.
Penyelasaian secara manual.
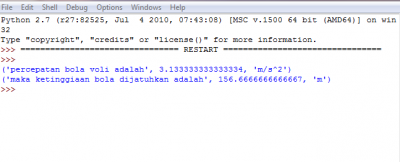
Penyeleasaian dengan aplikasi
Proses pengerjaan menggunakan aplikasi juga memakai rumus yang didapatkan dari cara manual. Dan hasil yang diperoleh pun sama, sehingga dapat disimpulkan bahwa pengerjaan initial value problem dapat diselesaikan menggunakan aplikasi.