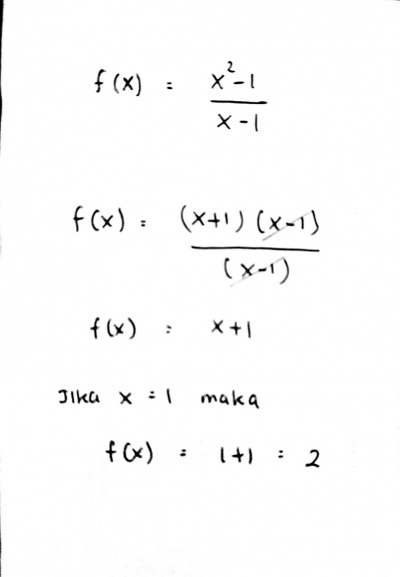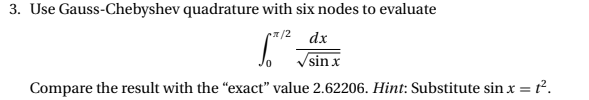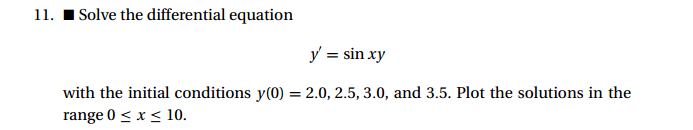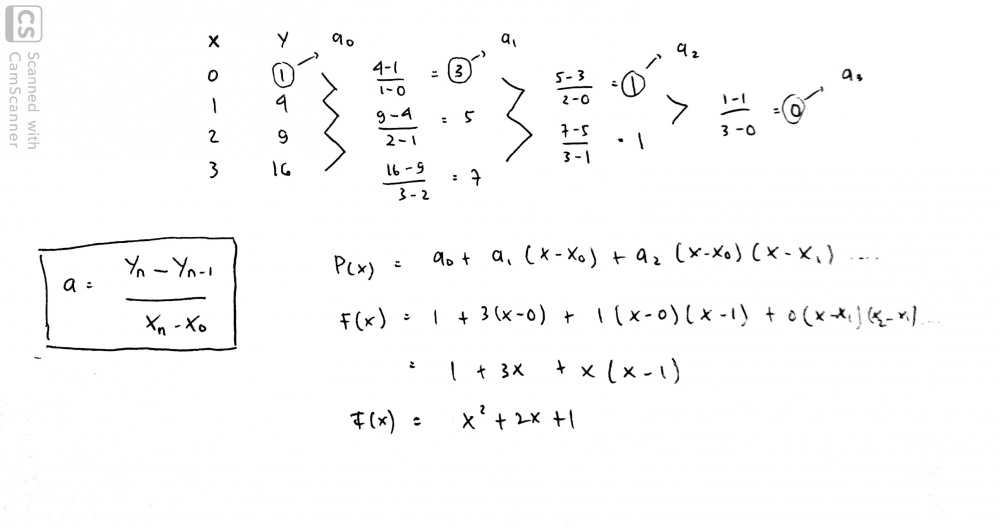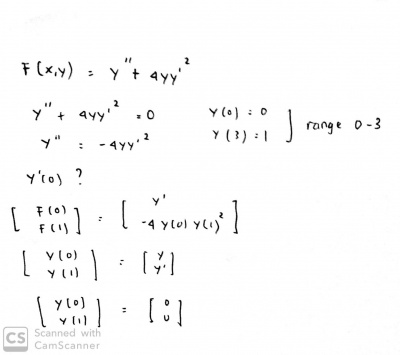Difference between revisions of "Gigin rizki novrian"
Giginrizki09 (talk | contribs) (→PERTEMUAN KEDUA (14 Februari 2020)) |
Giginrizki09 (talk | contribs) (→UTS METODE NUMERIK) |
||
| (57 intermediate revisions by the same user not shown) | |||
| Line 66: | Line 66: | ||
[[file:integralgigin2.png]] | [[file:integralgigin2.png]] | ||
| − | sumber: ''Jaan Kiusalaas-Numerical Methods in Engineering with Python 3-Cambridge University Press'' hal: | + | contoh soal: |
| + | |||
| + | [[file:soalgigin.png]] | ||
| + | |||
| + | sumber: ''Jaan Kiusalaas-Numerical Methods in Engineering with Python 3-Cambridge University Press'' | ||
| + | |||
| + | |||
| + | '''BAB 7: INITIAL VALUE PROBLEM''' | ||
| + | |||
| + | Data-> Informasi -> pengetahuan -> ilmu yang bermanfaat-> (Hikmah->Hidayah) | ||
| + | |||
| + | dilakukan analisis: - statistikal -> data diskrit (pengukuran aktual) | - Deterministik -> contoh pers.diferensial (Hk.Fisika) berdasarkan hukum-hukum teoritis | ||
| + | |||
| + | -Stokastik-> gabungan statistikal dan deterministik | ||
| + | |||
| + | ==Tugas Pertemuan Kedua== | ||
| + | '''2.1 Menyelesaikan integral dengan metode manual''' | ||
| + | |||
| + | [[file:integralgigin4.jpg|400px]] | ||
| + | [[file:integralgigin5.jpg|400px]] | ||
| + | |||
| + | Hasil metode manual menunjukkan nilai yang sama dengan jawaban di soal | ||
| + | |||
| + | '''2.2 Menyelesaikan integral tentu dengan metode numerik yaitu menggunakan pemrograman python''' | ||
| + | |||
| + | [[file:pythonintegrall.png|1080px]] | ||
| + | |||
| + | Dari hasil yang dtunjukkan oleh pemrograman python belum memberikan hasil, hal ini dikarenakan belum ada module numpy pada program python. | ||
| + | |||
| + | Setelah saya menginstall module numpy dan sympy pada program python di laptop saya, maka didapatkan hasil yang sesuai dengan hasil penghitungan manual. | ||
| + | Berikut adalah metode numeriknya, | ||
| + | |||
| + | [[file:giginintegrll.jpg|1080px]] | ||
| + | |||
| + | '''3.1 Menyelesaikan soal gerak jatuh bebas dengan metode manual''' | ||
| + | |||
| + | Soal: sebuah bola dijatuhkan dari ketinggian y=20 m dan kecepatan awal sama dengan nol. Kemudian bola jatuh hingga menyentuh lantai. Tentukan berapa kecepatan (v) dan tinggi (y) bola tersebut pada saat t=2 s ! | ||
| + | |||
| + | berikut adalah penyelesaian dengan metode manual | ||
| + | |||
| + | [[file:bolagigin.jpg|400px]] | ||
| + | |||
| + | didapatkan kecepatan (v) sebesar 19,6 m/s dan ketinggian (y) 0,4 m | ||
| + | |||
| + | '''3.2 Menyelesaikan soal gerak jatuh bebas dengan metode numerik''' | ||
| + | |||
| + | [[file:giginhasil.jpg|1080px]] | ||
| + | |||
| + | dengan pemrograman didapat hasil yang sama yaitu kecepatan (v) sebesar 19,6 m/s dan ketinggian (y) 0,4 m | ||
| + | |||
| + | '''3.3 Progres belajar Metode Numerik''' | ||
| + | |||
| + | [[file:Slidegigin2.JPG|400px]] | ||
| + | [[file:Slidegigin3.JPG|400px]] | ||
| + | [[file:Slidegigin4.JPG|400px]] | ||
| + | |||
| + | ==Tugas Asistensi== | ||
| + | |||
| + | [[file:Slide1W.JPG|400px]] | ||
| + | [[file:Slide3W.JPG|400px]] | ||
| + | [[file:Slide2W.JPG|400px]] | ||
| + | [[file:Slide4W.JPG|400px]] | ||
| + | |||
| + | ==TUGAS 3 - RUNGE-KUTTA== | ||
| + | |||
| + | [[file:Soal11gigin.PNG]] | ||
| + | |||
| + | JAWABAN: | ||
| + | |||
| + | [[file:soalggn.jpeg]] | ||
| + | [[file:soalgg.jpeg]] | ||
| + | [[file:soalgng.jpeg]] | ||
| + | |||
| + | ==RANGKUMAN ASISTENSI 2 & TUGAS== | ||
| + | |||
| + | Pada asistensi kedua bersama asisten dosen, kami membahas mengenai penggunaan aplikasi CFD dalam menghitung hambatan sebuah Submarine. Dengan mengikuti tutorial yang sudah diberikan oleh asisten dosen dalam bentuk video, kami bisa mendapatkan nilai hambatan pada submarine dengan melihat faktor kecepatan inlet. | ||
| + | |||
| + | Berikut adalah proses menghitung hambatan pada submarine menggunakan CFD | ||
| + | |||
| + | [[file:cfd.PNG|1000px]] | ||
| + | |||
| + | Seetelah mendapatkan perhitungan dan muncul grafik seperti diatas, proses penghitungan hambatan dilanjutkan dengan membuka ParaView. dan dilakukan proses kalkulasi sesuai dengan tutorial yang diberikan, maka didapatkan hambatan dilihat dari nilai Grid yang muncul seperti gambar dibawah ini | ||
| + | |||
| + | [[file:captureGrid.PNG|1000px]] | ||
| + | |||
| + | Kemudian saya melakukan pengulangan untuk mendapatkan 10 data hambatan dengan memvariasikan kecepatan inletnya, didapatkan tabel V inlet dan Grid(hambatan) seperti dibawah ini | ||
| + | |||
| + | [[file:tabelgg.PNG]] | ||
| + | |||
| + | |||
| + | Lalu dari data-data tersebut dibuatlah regresi linier dengan menggunakan pemrograman python. | ||
| + | Namun sebelum itu, asisten dosen memberikan gambaran mengenai beberapa metode regresi linier, dan salah satunya adalah metode '''Newton's Method''' | ||
| + | |||
| + | [[file:cttnewton.jpg|1000px]] | ||
| + | |||
| + | ''(Gambar diatas merupakan catatan mengenai Newton's Method dengan contoh sederhana) | ||
| + | '' | ||
| + | |||
| + | Lalu regresi linier dapat diselesaikan dengan menggunakan library pada python yang disebut dengan "Polyfit" dasar sederhana pembuatan fungsi polyfit ini dijelaskan oleh asisten sebagai berikut, | ||
| + | |||
| + | [[file:ctt2.jpg|1000px]] | ||
| + | |||
| + | Lalu saya membuat regresi linier dari data kecepatan dan hambatan diatas menggunakan pemrograman python, didapatkan hasil sebagai berikut, | ||
| + | |||
| + | [[file:regresiggn.PNG|1000px]] | ||
| + | |||
| + | didapatkan persamaan dengan 2 orde yaitu, | ||
| + | |||
| + | '''Y= 5.05963636x² - 0.49635152x + 2.23081212''' | ||
| + | |||
| + | |||
| + | ==RANGKUMAN ASISTENSI 3== | ||
| + | Berikut adalah ppt terkait hasil asistensi dengan asisten dosen minggu ini (10/03/2020) | ||
| + | |||
| + | [[file:asisg.JPG|500px]] | ||
| + | [[file:asisg1.JPG|500px]] | ||
| + | [[file:asisg2.JPG|500px]] | ||
| + | |||
| + | '''PROGRESS BELAJAR''' | ||
| + | |||
| + | Setelah mengikuti asistensi mengenai Initial Value Problem dan Boundary Value Problem, saya menjadi lebih mengerti tentang pengertian dan perbedaan keduanya, sehingga saya dapat membuat contoh kasusnya. Lalu saya juga mendapatkan pelajaran tambahan mengenai Two-Point Boundary Problem, dan mencoba menyelesaikan contoh soal yang diberikan dengan menggunakan kombinasi Ridder's Method dan Runge-Kutta. | ||
| + | |||
| + | ==TUGAS INITIAL VALUE PROBLEM & BOUNDARY VALUE PROBLEM== | ||
| + | |||
| + | Sebuah gelombang berosilasi dengan persamaan F(x, y) = y"+4yy'², dan y(0)=0 dan y(3)=1, maka y'(0) adalah | ||
| + | |||
| + | Soal diatas merupakan soal Two-point Boundary Value Problem, karena terdapat dua batas yang berbeda yaitu y(0) dan y(3), dan untuk mencari y'(0) tersebut maka kita harus menjadikan Boundary Value problem ke bentuk Initial value problem | ||
| + | |||
| + | [[file:ggnn.jpg|400px]] | ||
| + | |||
| + | kita misalkan y'(0) sebagai u dan digunakan metode ridder untuk mendapatkan nilai u | ||
| + | Kemudian memasukkan module runge-kutta | ||
| + | |||
| + | [[file:BVP1.PNG|600px]] | ||
| + | [[file:BVP2.PNG|600px]] | ||
| + | |||
| + | lalu memasukkan module ridder untuk menentukan nilai u | ||
| + | |||
| + | [[file:BVP3.PNG|600px]] | ||
| + | |||
| + | kemudian memasukkan persamaan y" ke dalam pemrograman dan menentukan batas u1 dan u2 serta menentukan interval h nya | ||
| + | |||
| + | [[file:BVP4.PNG|600px]] | ||
| + | [[file:BVP5.PNG|600px]] | ||
| + | |||
| + | kemudian dilakukan iterasi serta pendekatan matematis menggunakan python dan dilakukan plotting maka terbentuklah grafik seperti dibawah ini, | ||
| + | |||
| + | [[file:BVP6.PNG|600px]] | ||
| + | [[file:BVP7.PNG|800px]] | ||
| + | |||
| + | dan didapatkan hasil '''y'(0) = u = 0.7882062234962185''' dalam range u1= 0 - u2= 3 | ||
| + | |||
| + | '''EVALUASI BELAJAR''' | ||
| + | |||
| + | Setelah mengerjakan soal diatas saya belajar mengenai Initial Value Problem dan Boundary Value Problem serta bahasan baru mengenai Two-Point Boundary Problem yang dimana mengkombinasikan IVP dan BVP menggunakan dua metode yaitu Ridder's method dan Runge-kutta. Walaupun dalam proses pengerjaan saya mengalami beberapa kesulitan karena tidak sekedar mengimport module namun saya harus mendefinisikan secara manual module-module tersebut, dan dengan berbagai usaha dan upaya saya akhirnya tugas tersebut dapat diselesaikan dengan didapatkan hasil yang diinginkan. | ||
| + | |||
| + | ==PERTEMUAN KEENAM|OPTIMASI== | ||
| + | |||
| + | Optimasi adalah suatu proses untuk mencapai hasil yang ideal atau optimasi (nilai efektif yang dapat dicapai). Optimasi dapat diartikan sebagai suatu bentuk mengoptimalkan sesuatu hal yang sudah ada, ataupun merancang dan membuat sesusatu secara optimal.Ada beberapa istilah yang saya pelajari di kelas, beberapa istilah tersebut yaitu, | ||
| + | |||
| + | A) Fungsi Objektif yaitu fungsi yang akan kita optimasi | ||
| + | B) Constraint yaitu batasan terhadap nilai fungsi objektif | ||
| + | |||
| + | Constraint ini mirip dengan Boundary Value Problem namun perbedaannya adalah constraint ini hanya batas dari salah satu variabel saja beda dengan boundary yang merupakan batas keseluruhan atau batas suatu fungsi. | ||
| + | |||
| + | Constraint ada 2 jenis yaitu, Equality Constraint (berupa persamaan =) dan Inequality Constraint ( berupa pertidaksamaan <,>) | ||
| + | |||
| + | Contoh soal: | ||
| + | |||
| + | [[file:soalscipy.jpeg|800px]] | ||
| + | |||
| + | Jawaban: dengan bantuan module Scipy | ||
| + | |||
| + | [[file:ggnscipy.PNG|1080px]] | ||
| + | |||
| + | '''TUGAS KEENAM (asisten dosen)''' | ||
| + | |||
| + | [[file:gigin6.PNG|1080px]] | ||
| + | |||
| + | ==TUGAS VIDEO (OPTIMASI)== | ||
| + | [[file:soalq2.PNG|1080px]] | ||
| + | |||
| + | Berikut adalah link video penyelesaiannya | ||
| + | https://youtu.be/2h_tCcyU7FE | ||
| + | |||
| + | ==UTS METODE NUMERIK== | ||
| + | Berikut adalah video tutorial menghitung hambatan AUV pada CFDSOF | ||
| + | https://youtu.be/4mn48ce0dDo | ||
| + | |||
| + | Berikut adalah video tutorial membuat curve fitting dari data kecepatan dan hambatan diatas | ||
| + | https://youtu.be/mOwjxP7s9xQ | ||
Latest revision as of 22:25, 3 April 2020
Contents
- 1 BIODATA DIRI
- 2 Tugas Pertemuan Pertama (7 Februari 2020)
- 3 PERTEMUAN KEDUA (14 Februari 2020)
- 4 Tugas Pertemuan Kedua
- 5 Tugas Asistensi
- 6 TUGAS 3 - RUNGE-KUTTA
- 7 RANGKUMAN ASISTENSI 2 & TUGAS
- 8 RANGKUMAN ASISTENSI 3
- 9 TUGAS INITIAL VALUE PROBLEM & BOUNDARY VALUE PROBLEM
- 10 PERTEMUAN KEENAM|OPTIMASI
- 11 TUGAS VIDEO (OPTIMASI)
- 12 UTS METODE NUMERIK
BIODATA DIRI
Nama: Gigin Rizki Novrian Panji Handoyo Putro
NPM : 1806202235
Hobi : Futsal
Teknik Perkapalan 2018
Mata kuliah metode numerik ini cukup menarik buat saya, karena selama ini saya hanya mendengar tentang pemrogaman dll, namun belum pernah mendalami ataupun memahaminya. Saya hanya mengetahui basic/dasar menggunakan komputer dan microsoft. Software yang pernah saya pakai adalah autocad, maxsurf. Namun saya belum pernah belajar software yang khusus untuk bahasa pemrograman atau metode numerik .
Tugas Pertemuan Pertama (7 Februari 2020)
Pengajar: Dr. Ahmad Indra Siswantara (Pak DAI)
Diberikan sebuah fungsi yaitu
F(x)= (X^2-1)/(x-1) jika X=1 maka tentukan nilai F(x)
maka persamaan tersebut dapat diselesaikan dengan cara manual sebagai berikut
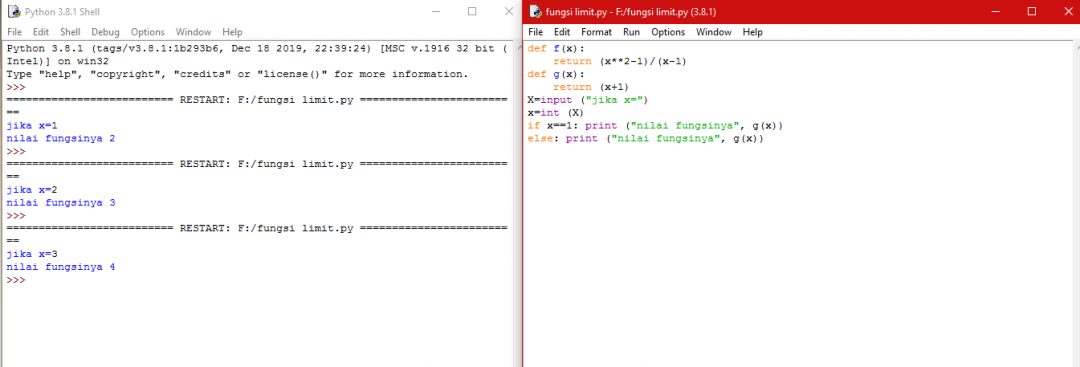
Kemudian saya menyelesaikan fungsi tersebut dengan bantuan pemrograman yaitu python sehingga didapatkan hasil sebagai berikut
Hasil yang diberikan ketika memasukkan nilai X=1 adalah F(x)=2 dan hasilnya sama dengan perhitungan menggunakan metode manual.
Ketika menyelesaikan fungsi tersebut dengan cara manual secara matematis dengan mudah saya dapat menyelesaikannya. Namun ketika mencoba dengan program python saya harus memahami terlebih dahulu bahasa-bahasa pemrogramannya agar didapatkan nilai yang ingin kita dapatkan.Bahasa tersebut saya pelajari melalui internet dan beberapa buku panduan. Dalam tugas ini saya mendapatkan banyak pengetahuan baru seperti,
- def yaitu untuk menuliskan fungsi
- return yaitu untuk memasukan variabel pada fungsi
- string yaitu tanda apit (" atau ') yang digunakan untuk menyatakan kalimat/karakter berupa huruf,angka,dll
- int atau disebut integer adalah keseluruhan angka baik positif maupun negatif tanpa ada desimal dengan panjang tak terbatas
- print untuk memunculkan hasil sesuai yang kita inginkan
Menurut saya, penyelesaian suatu fungsi yang rumit menggunakan software akan mempermudah mahasiswa untuk menyelesaikan fungsi tersebut dibanding dengan menggunakan metode manual. Untuk itu bahasa-bahasa pemrograman harus dikuasai dan dipahami secara mendalam agar dalam pengaplikasiannya dapat berjalan dengan baik.
PERTEMUAN KEDUA (14 Februari 2020)
-ilmu metode numerik itu seperti kita mencelupkan jari kelingking ke lautan yang luas, lalu kita angkat kelingking tersebut dan tetesan air itu adalah ilmu mtetode numerik yang jika dibandingkan dengan seluruh air di lautan tersebut begitu luasnya ilmu Sang Pencipta.
-kita dapat menggunakan dorongan (gaya) yang sering kita pelajari di mata kuliah untuk mendorong diri sendiri agar tidak malas.
-berjuang untuk TURN BACK KEM : yaitu melawan,
K ketidaktahuan (Kebodohan) E Egois M Malas
setelah melihat beberapa contoh kasus soal di buku Numerical Methods in Engineering with Python 3 saya tertarik dengan kasus penyelesaian integral tentu dengan menggunakan pemrograman python. Karena menurut saya dapat menyelesaikan integral dengan aplikasi akan lebih mudah dan cepat dan integral adalah langkah dasar untuk menyelesaikan berbagai macam persamaan yang rumit di mata kuliah Teknik Perkapalan.
contoh soal:
sumber: Jaan Kiusalaas-Numerical Methods in Engineering with Python 3-Cambridge University Press
BAB 7: INITIAL VALUE PROBLEM
Data-> Informasi -> pengetahuan -> ilmu yang bermanfaat-> (Hikmah->Hidayah)
dilakukan analisis: - statistikal -> data diskrit (pengukuran aktual) | - Deterministik -> contoh pers.diferensial (Hk.Fisika) berdasarkan hukum-hukum teoritis
-Stokastik-> gabungan statistikal dan deterministik
Tugas Pertemuan Kedua
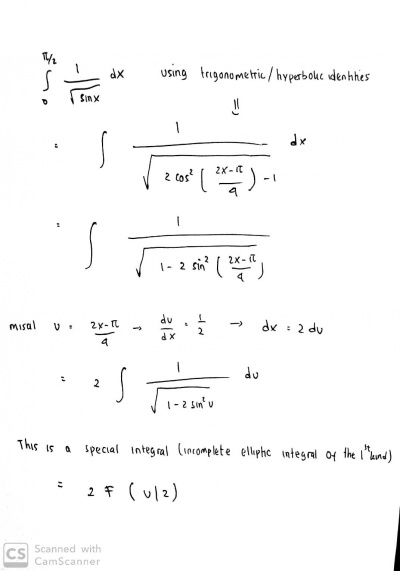
2.1 Menyelesaikan integral dengan metode manual
Hasil metode manual menunjukkan nilai yang sama dengan jawaban di soal
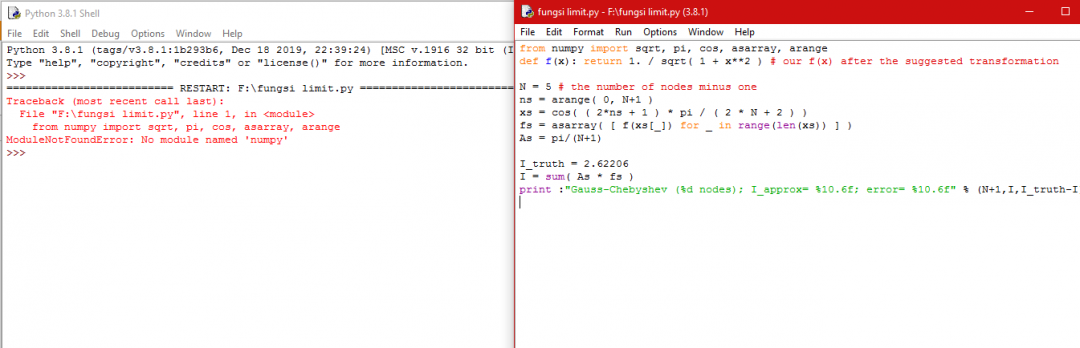
2.2 Menyelesaikan integral tentu dengan metode numerik yaitu menggunakan pemrograman python
Dari hasil yang dtunjukkan oleh pemrograman python belum memberikan hasil, hal ini dikarenakan belum ada module numpy pada program python.
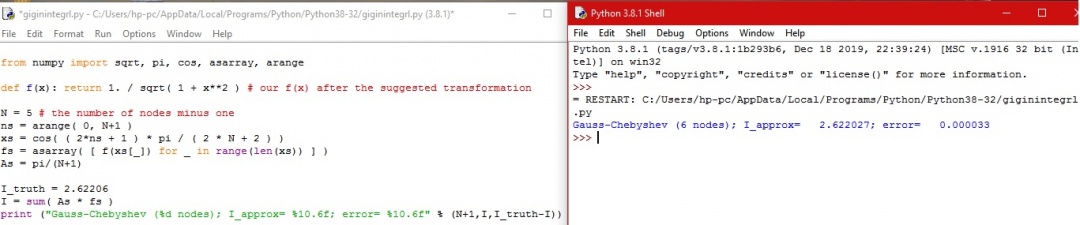
Setelah saya menginstall module numpy dan sympy pada program python di laptop saya, maka didapatkan hasil yang sesuai dengan hasil penghitungan manual. Berikut adalah metode numeriknya,
3.1 Menyelesaikan soal gerak jatuh bebas dengan metode manual
Soal: sebuah bola dijatuhkan dari ketinggian y=20 m dan kecepatan awal sama dengan nol. Kemudian bola jatuh hingga menyentuh lantai. Tentukan berapa kecepatan (v) dan tinggi (y) bola tersebut pada saat t=2 s !
berikut adalah penyelesaian dengan metode manual
didapatkan kecepatan (v) sebesar 19,6 m/s dan ketinggian (y) 0,4 m
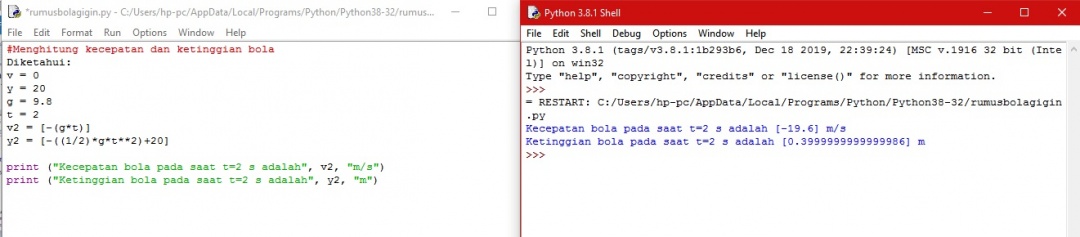
3.2 Menyelesaikan soal gerak jatuh bebas dengan metode numerik
dengan pemrograman didapat hasil yang sama yaitu kecepatan (v) sebesar 19,6 m/s dan ketinggian (y) 0,4 m
3.3 Progres belajar Metode Numerik
Tugas Asistensi
TUGAS 3 - RUNGE-KUTTA
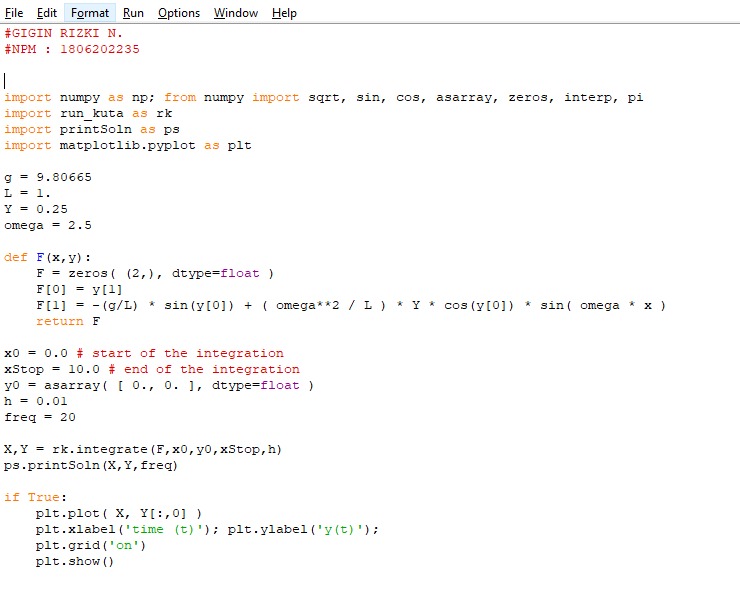
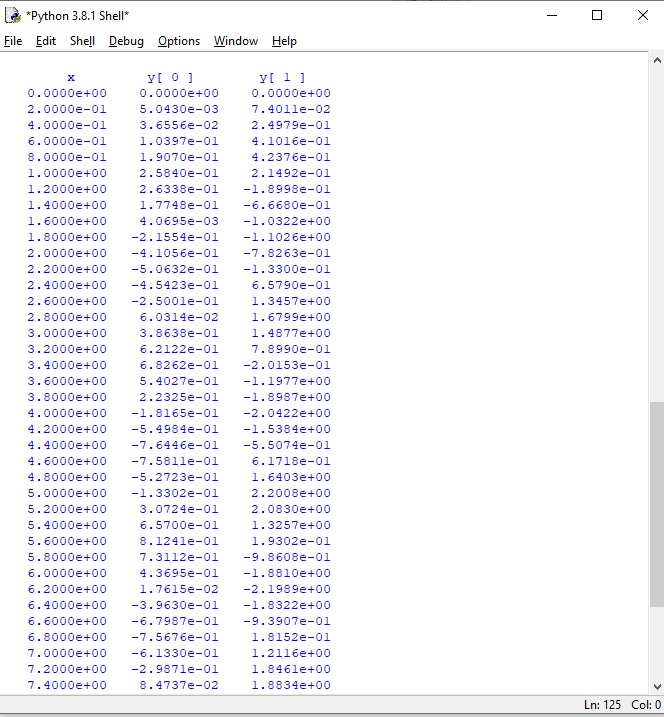
JAWABAN:
RANGKUMAN ASISTENSI 2 & TUGAS
Pada asistensi kedua bersama asisten dosen, kami membahas mengenai penggunaan aplikasi CFD dalam menghitung hambatan sebuah Submarine. Dengan mengikuti tutorial yang sudah diberikan oleh asisten dosen dalam bentuk video, kami bisa mendapatkan nilai hambatan pada submarine dengan melihat faktor kecepatan inlet.
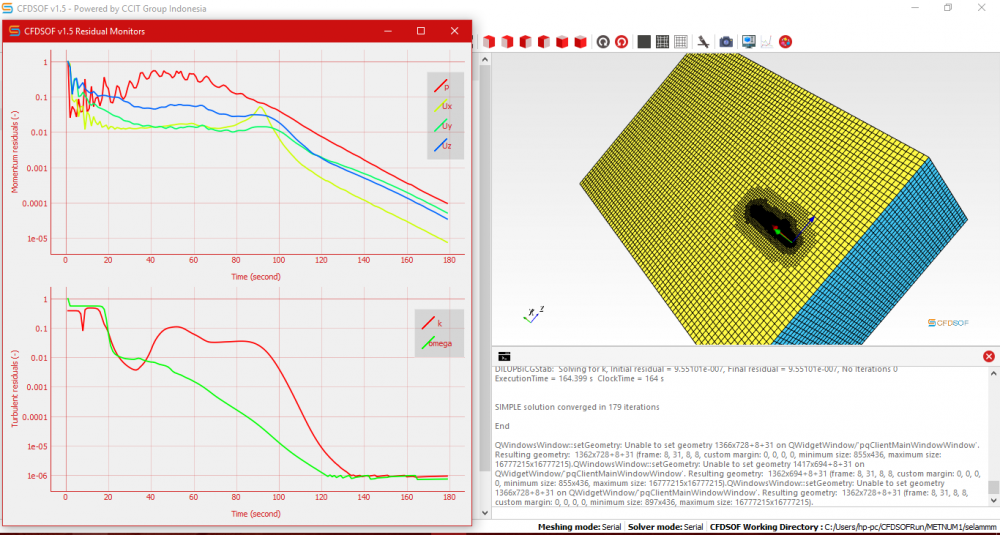
Berikut adalah proses menghitung hambatan pada submarine menggunakan CFD
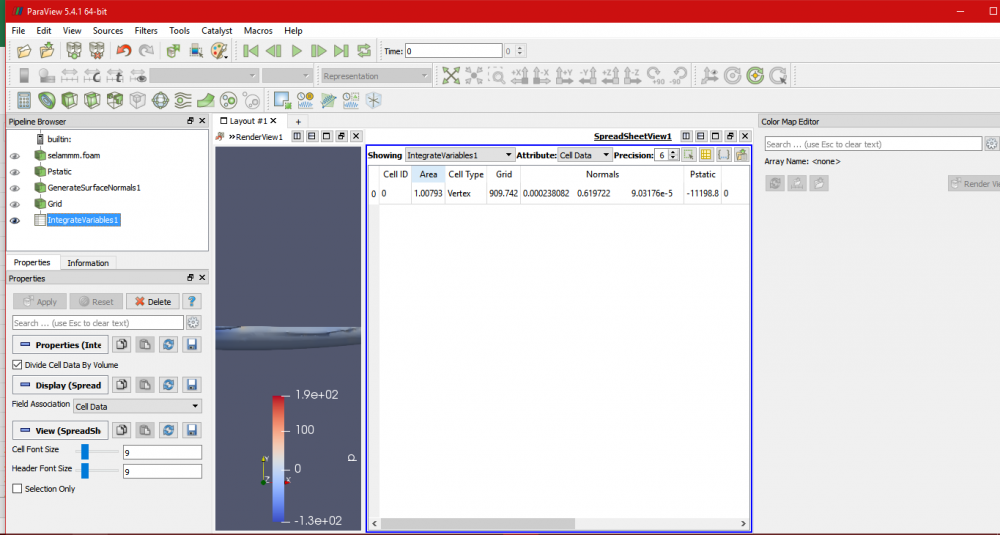
Seetelah mendapatkan perhitungan dan muncul grafik seperti diatas, proses penghitungan hambatan dilanjutkan dengan membuka ParaView. dan dilakukan proses kalkulasi sesuai dengan tutorial yang diberikan, maka didapatkan hambatan dilihat dari nilai Grid yang muncul seperti gambar dibawah ini
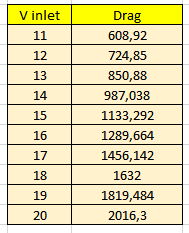
Kemudian saya melakukan pengulangan untuk mendapatkan 10 data hambatan dengan memvariasikan kecepatan inletnya, didapatkan tabel V inlet dan Grid(hambatan) seperti dibawah ini
Lalu dari data-data tersebut dibuatlah regresi linier dengan menggunakan pemrograman python.
Namun sebelum itu, asisten dosen memberikan gambaran mengenai beberapa metode regresi linier, dan salah satunya adalah metode Newton's Method
(Gambar diatas merupakan catatan mengenai Newton's Method dengan contoh sederhana)
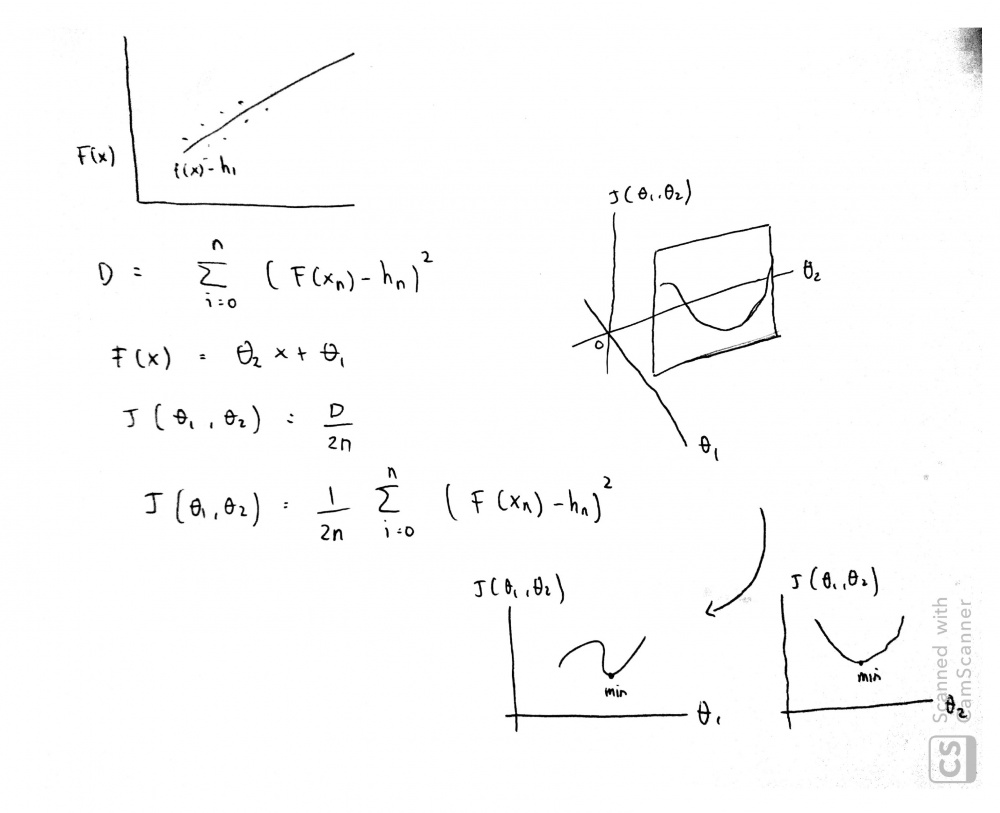
Lalu regresi linier dapat diselesaikan dengan menggunakan library pada python yang disebut dengan "Polyfit" dasar sederhana pembuatan fungsi polyfit ini dijelaskan oleh asisten sebagai berikut,
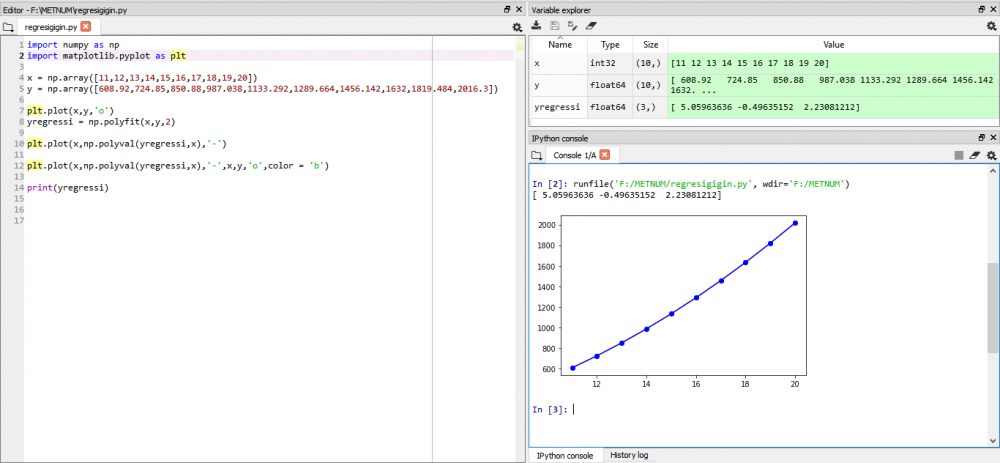
Lalu saya membuat regresi linier dari data kecepatan dan hambatan diatas menggunakan pemrograman python, didapatkan hasil sebagai berikut,
didapatkan persamaan dengan 2 orde yaitu,
Y= 5.05963636x² - 0.49635152x + 2.23081212
RANGKUMAN ASISTENSI 3
Berikut adalah ppt terkait hasil asistensi dengan asisten dosen minggu ini (10/03/2020)
PROGRESS BELAJAR
Setelah mengikuti asistensi mengenai Initial Value Problem dan Boundary Value Problem, saya menjadi lebih mengerti tentang pengertian dan perbedaan keduanya, sehingga saya dapat membuat contoh kasusnya. Lalu saya juga mendapatkan pelajaran tambahan mengenai Two-Point Boundary Problem, dan mencoba menyelesaikan contoh soal yang diberikan dengan menggunakan kombinasi Ridder's Method dan Runge-Kutta.
TUGAS INITIAL VALUE PROBLEM & BOUNDARY VALUE PROBLEM
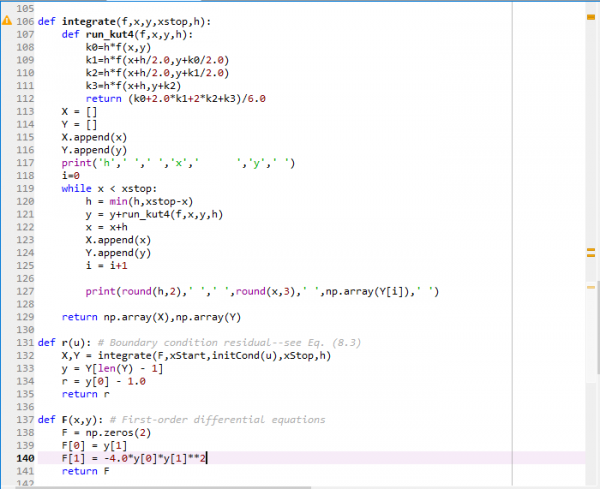
Sebuah gelombang berosilasi dengan persamaan F(x, y) = y"+4yy'², dan y(0)=0 dan y(3)=1, maka y'(0) adalah
Soal diatas merupakan soal Two-point Boundary Value Problem, karena terdapat dua batas yang berbeda yaitu y(0) dan y(3), dan untuk mencari y'(0) tersebut maka kita harus menjadikan Boundary Value problem ke bentuk Initial value problem
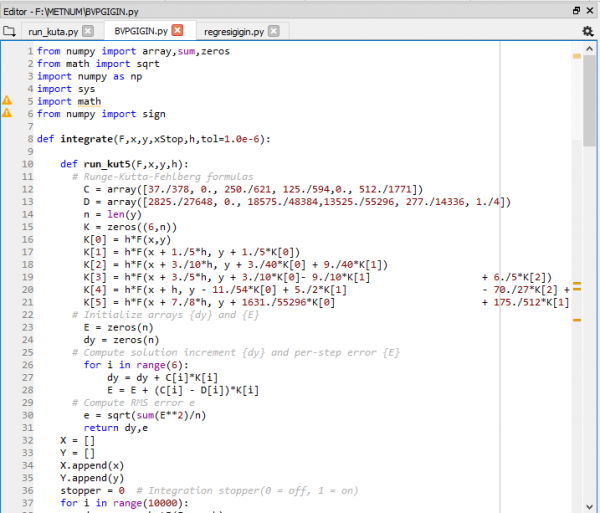
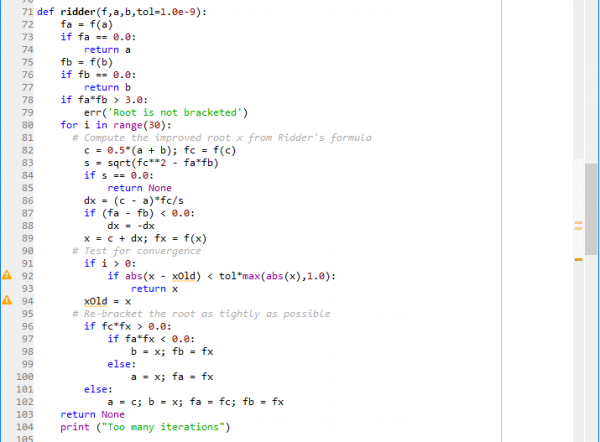
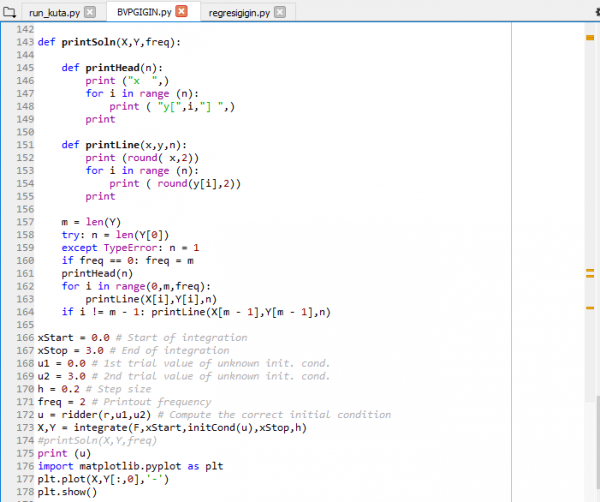
kita misalkan y'(0) sebagai u dan digunakan metode ridder untuk mendapatkan nilai u Kemudian memasukkan module runge-kutta
lalu memasukkan module ridder untuk menentukan nilai u
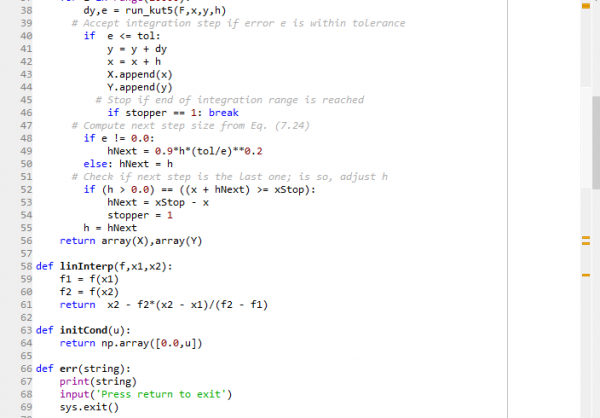
kemudian memasukkan persamaan y" ke dalam pemrograman dan menentukan batas u1 dan u2 serta menentukan interval h nya
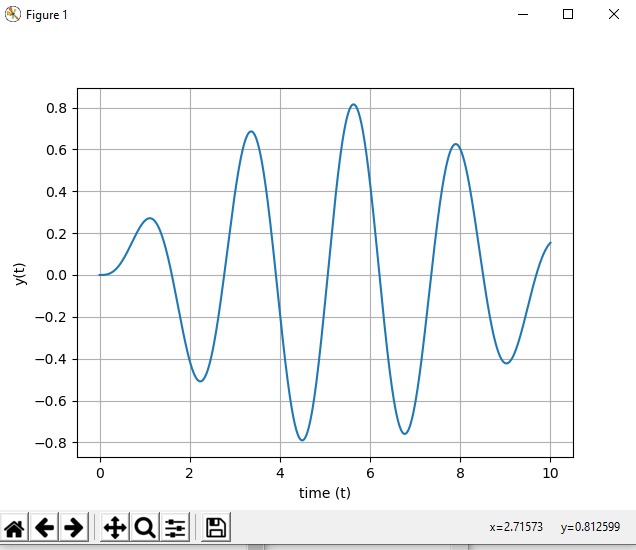
kemudian dilakukan iterasi serta pendekatan matematis menggunakan python dan dilakukan plotting maka terbentuklah grafik seperti dibawah ini,
dan didapatkan hasil y'(0) = u = 0.7882062234962185 dalam range u1= 0 - u2= 3
EVALUASI BELAJAR
Setelah mengerjakan soal diatas saya belajar mengenai Initial Value Problem dan Boundary Value Problem serta bahasan baru mengenai Two-Point Boundary Problem yang dimana mengkombinasikan IVP dan BVP menggunakan dua metode yaitu Ridder's method dan Runge-kutta. Walaupun dalam proses pengerjaan saya mengalami beberapa kesulitan karena tidak sekedar mengimport module namun saya harus mendefinisikan secara manual module-module tersebut, dan dengan berbagai usaha dan upaya saya akhirnya tugas tersebut dapat diselesaikan dengan didapatkan hasil yang diinginkan.
PERTEMUAN KEENAM|OPTIMASI
Optimasi adalah suatu proses untuk mencapai hasil yang ideal atau optimasi (nilai efektif yang dapat dicapai). Optimasi dapat diartikan sebagai suatu bentuk mengoptimalkan sesuatu hal yang sudah ada, ataupun merancang dan membuat sesusatu secara optimal.Ada beberapa istilah yang saya pelajari di kelas, beberapa istilah tersebut yaitu,
A) Fungsi Objektif yaitu fungsi yang akan kita optimasi B) Constraint yaitu batasan terhadap nilai fungsi objektif
Constraint ini mirip dengan Boundary Value Problem namun perbedaannya adalah constraint ini hanya batas dari salah satu variabel saja beda dengan boundary yang merupakan batas keseluruhan atau batas suatu fungsi.
Constraint ada 2 jenis yaitu, Equality Constraint (berupa persamaan =) dan Inequality Constraint ( berupa pertidaksamaan <,>)
Contoh soal:
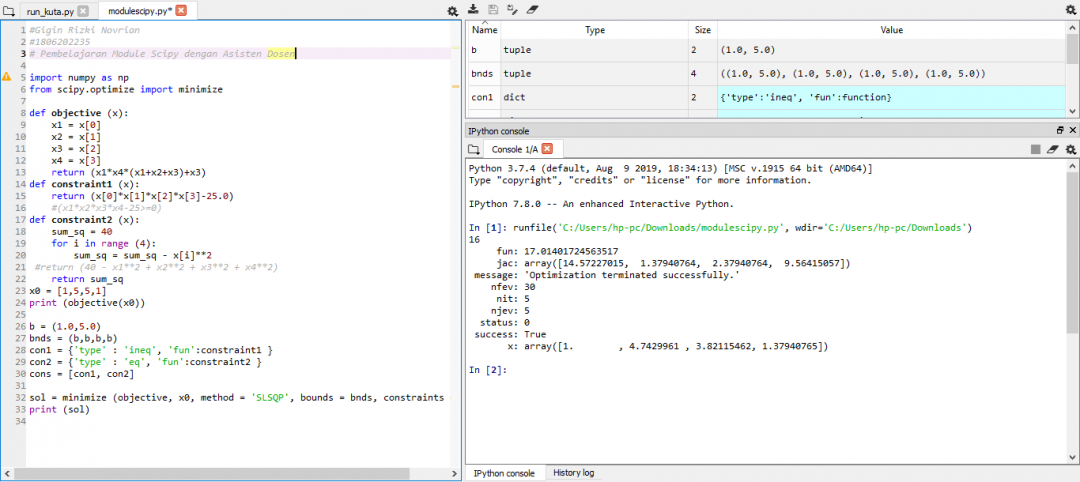
Jawaban: dengan bantuan module Scipy
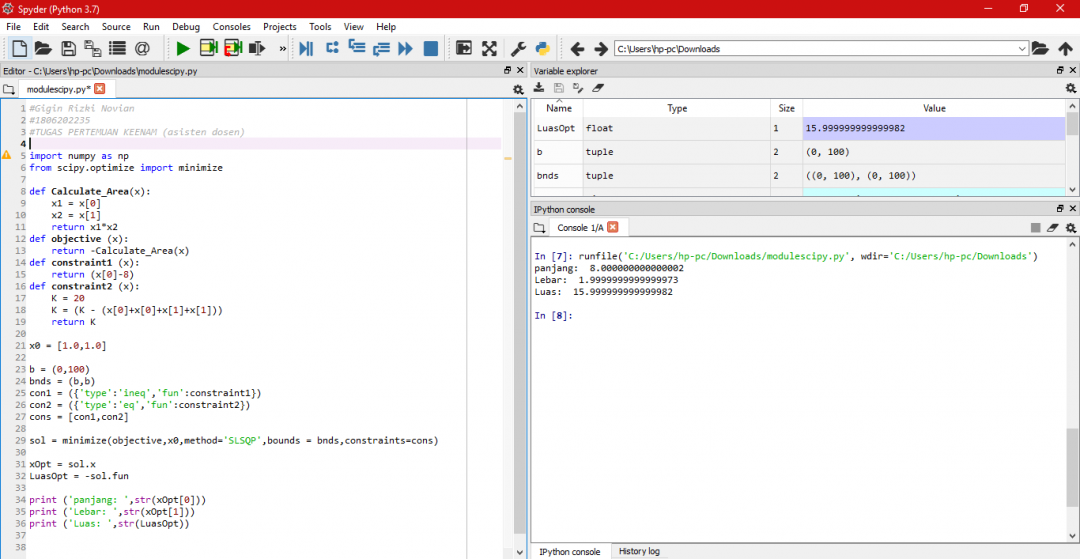
TUGAS KEENAM (asisten dosen)
TUGAS VIDEO (OPTIMASI)
Berikut adalah link video penyelesaiannya https://youtu.be/2h_tCcyU7FE
UTS METODE NUMERIK
Berikut adalah video tutorial menghitung hambatan AUV pada CFDSOF https://youtu.be/4mn48ce0dDo
Berikut adalah video tutorial membuat curve fitting dari data kecepatan dan hambatan diatas https://youtu.be/mOwjxP7s9xQ