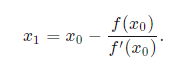Difference between revisions of "Review Materi 5"
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
'''Review Materi 1 Oktober 2019''' | '''Review Materi 1 Oktober 2019''' | ||
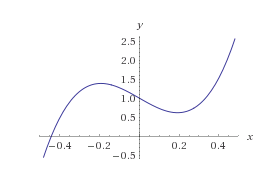
| − | + | Newton-Raphson adalah metode yang biasa yang digunakan dan metode yang tepat untuk mencari hasil yang cepat ''real-valued function''. Penyelesaian menggunakan metode ini adalah ide yang kontinu dan turunan dengan mencari nilai tangent. Selain itu, metode ini juga mempunyai kelemahan jika fungsi yang ingin diproses adalah lokal maksimum dan minimum atau puncak dan lembah. Fungsi seperti itu biasanya yang berakar 3 dan tidak lengkap. Seperti fungsi dibawah, | |
| − | + | [[File:Locmax.PNG|500px|center]] | |
| − | + | Karena kita tahu bahwa fungsi yang dapat diproses adalah fungsi kontinu atau dapat diturunkan, maka dari itu pendekatan x=xo dengan persamaan seperti berikut, | |
| − | [[File: | + | [[File:Newmet.PNG|500px|center]] |
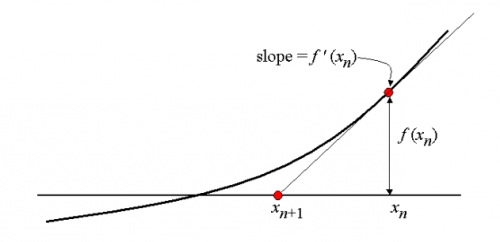
| − | + | Selain itu, penyelesaian ini dapat diselesaikan juga dengan menggunakan metode geometrik, | |
| − | + | [[File:Grafmet.PNG|500px|center]] | |
| − | + | Kita gambarkan garis tangent atau garis yang memotong garis fungsi. Dikarenakan fungsi baru (f') memotong fungsi yang kita cari, maka didapatkan penyelesaian baru, xn +1 =xn (f(xn))/(f(n+1)0 | |
| − | |||
| − | ' | ||
| − | |||
| − | |||
| − | |||
| − | |||
Latest revision as of 15:21, 17 December 2019
Review Materi 1 Oktober 2019
Newton-Raphson adalah metode yang biasa yang digunakan dan metode yang tepat untuk mencari hasil yang cepat real-valued function. Penyelesaian menggunakan metode ini adalah ide yang kontinu dan turunan dengan mencari nilai tangent. Selain itu, metode ini juga mempunyai kelemahan jika fungsi yang ingin diproses adalah lokal maksimum dan minimum atau puncak dan lembah. Fungsi seperti itu biasanya yang berakar 3 dan tidak lengkap. Seperti fungsi dibawah,
Karena kita tahu bahwa fungsi yang dapat diproses adalah fungsi kontinu atau dapat diturunkan, maka dari itu pendekatan x=xo dengan persamaan seperti berikut,
Selain itu, penyelesaian ini dapat diselesaikan juga dengan menggunakan metode geometrik,
Kita gambarkan garis tangent atau garis yang memotong garis fungsi. Dikarenakan fungsi baru (f') memotong fungsi yang kita cari, maka didapatkan penyelesaian baru, xn +1 =xn (f(xn))/(f(n+1)0