Difference between revisions of "Satria Nur Muhamad"
(→Tugas RungeKutta) |
|||
| (6 intermediate revisions by the same user not shown) | |||
| Line 271: | Line 271: | ||
[[File:Video3Satria.mp4|500px|thumb|centre|Video Muhasabah Diri]] | [[File:Video3Satria.mp4|500px|thumb|centre|Video Muhasabah Diri]] | ||
| + | |||
| + | == Tugas RungeKutta == | ||
| + | |||
| + | Pada pertemuan kali ini kami memndapat tugas mengenai metode Runge-Kutta. | ||
| + | |||
| + | menyelesaikan sebuah fenomena fisika-Gaya drag Mobil | ||
| + | |||
| + | |||
| + | m = eval(input("massa mobil : ")) | ||
| + | g = 9.81 | ||
| + | cd = eval(input("koefisien drag udara : ")) | ||
| + | ges = eval(input("koefisien gesek jalan : ")) | ||
| + | hp = eval(input("Besar Horsepower mobil : ")) | ||
| + | rpm = eval(input("Besar RPM mobil : ")) | ||
| + | sina = eval(input("Besar sina bidang miring: ")) | ||
| + | cosa = eval(input("Besar cosa bidang miring: ")) | ||
| + | v = 0 | ||
| + | t = 0 | ||
| + | dt = 1 #tinggi step atau waktu | ||
| + | error = 100 | ||
| + | |||
| + | Fmobil = (hp * 9550) / (rpm * ((2 * 3.14)/60)) | ||
| + | p = (Fmobil/m) - g*ges | ||
| + | q = cd/m | ||
| + | |||
| + | def dvdt(t, v): | ||
| + | return p-(q*(v)**(1.5))-(cosa*ges*g)-(sina*g) | ||
| + | |||
| + | while error > 0.005: | ||
| + | k1 = dvdt(t, v) | ||
| + | k2 = dvdt(t + 0.5 * h, v + 0.5 * h * k1) | ||
| + | k3 = dvdt(t + 0.5 * h, v + 0.5 * h * k2) | ||
| + | k4 = dvdt(t + h, v + h * k3) | ||
| + | v1 = v + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4) | ||
| + | t = t + h | ||
| + | error = ((v1 - v) / v1)*100 #persentase error | ||
| + | v = v1 | ||
| + | lst.append(v1) | ||
| + | |||
| + | waktu = len(lst) | ||
| + | |||
| + | print ("waktu untuk mencapai velocity maksimal adalah: ", waktu+1) | ||
| + | print ("velocity maksimal adalah: ", v1) | ||
| + | |||
| + | == Computational Fluid Dynamic Drag Analysis of a Car == | ||
| + | |||
| + | '''Tahap-Tahap Analsis Drag Mobil''' | ||
| + | Analisis Drag Force dimulai dengan menggunakan program CFDSOF. Pada program CFDSOF, dilakukan impor gambar 3D dari mobil yang akan dianalisis, pembuatan mesh, beserta input data dan boundary condition yang diinginkan. Setelah semua data telah diinput, dilakukan penjalanan solver. | ||
| + | [[File:Part_1.png|800px]] | ||
| + | |||
| + | Analisis dilanjutkan dengan menggunakan program ParaView. | ||
| + | [[File:Part_2.png|800px]] | ||
| + | |||
| + | Pada program ParaView, dilakukan penghilangan internalMesh dan dimunculkan car_body. | ||
| + | [[File:Part_3.png|800px]] | ||
| + | |||
| + | Setelah itu, dilanjutkan dengan membuat filter "Generate Surface Normal" dengan "Compute cell normal" | ||
| + | [[File:Part_3_Generate_Surface_Normal,_compute_cell_normals.png|800px]] | ||
| + | |||
| + | Setelah itu, dilakukan perhitungan menggunakan kalkulator yang ada di program dengan menggunakan Attribute Mode Cell Data, mengganti Result Array Name menjadi Drag Force, dan melakukan perhitungan p*Normal_X | ||
| + | [[File:Part_4_calculator,_cell_data,_pxnormal_x.png|200px]] | ||
| + | |||
| + | Terakhir, tambahkan filter Integrate Variables dan dapatkan nilai Drag Force | ||
| + | [[File:Part_5_integrate_variables,_cell_data.png|800px]] | ||
| + | |||
| + | Berikut Hasil yang kami dapatkan: | ||
| + | [[File:Graph.png|800px]] | ||
| + | |||
| + | == Computational Fluid Dynamic Drag and Lift Analysis of an Airfoil == | ||
| + | |||
| + | Langkah-langkah yang digunakan hampir sama seperti tugas drag force mobil, hanya saja ditambah optimasi. | ||
| + | |||
| + | Yang pertama adalah tahap desain airfoil | ||
| + | |||
| + | [[File:bagianc1.jpg]] | ||
| + | |||
| + | Yang kedua adalah tahap mesh menggunakan CFDSOF | ||
| + | |||
| + | [[File:bagianc2.jpg]] | ||
| + | |||
| + | Yang ketiga adalah tahap simulasi dan kalkulasi menggunakan paraview | ||
| + | |||
| + | [[File:bagianc3.jpg]] | ||
| + | |||
| + | Yang selanjutnya adalah memvariasikan nya terhadap sudut serang -15,15,30,45,60,75,90 derajat. | ||
| + | |||
| + | Hasilnya | ||
| + | |||
| + | [[File:bagianc4.jpg]] | ||
| + | |||
| + | [[File:bagianc5.jpg]] | ||
| + | |||
| + | [[File:bagianc6.jpg]] | ||
| + | |||
| + | [[File:bagianc7.jpg]] | ||
| + | |||
| + | Yang keempat optimasi | ||
| + | |||
| + | [[File:bagianc10.jpg]] | ||
| + | |||
| + | [[File:bagianc8.jpg]] | ||
| + | |||
| + | [[File:bagianc9.jpg]] | ||
| + | |||
| + | Hasilnya adalah sudut serang optimalnya sebesar 2.9 derajat | ||
| + | |||
| + | |||
== CFDSOF dan ANN == | == CFDSOF dan ANN == | ||
Latest revision as of 11:01, 20 December 2019
Bismillahirrahmanirrahim
Assalamualaikum warahmatullahi wabarakatuh
Selamat datang dan selamat membaca.
Contents
- 1 Perkenalan.
- 2 Kuliah Minggu Pertama
- 3 Kuliah Minggu Kedua
- 4 Kuliah Minggu Ketiga
- 5 Kuliah Minggu Keempat
- 6 Kuliah Minggu Kelima
- 7 Kuliah Minggu Keenam
- 8 Kuis / Minggu Ketujuh
- 9 UTS / Minggu Kedelapan
- 10 Tugas RungeKutta
- 11 Computational Fluid Dynamic Drag Analysis of a Car
- 12 Computational Fluid Dynamic Drag and Lift Analysis of an Airfoil
- 13 CFDSOF dan ANN
Perkenalan.
Nama saya Satria Nur Muhamad, NPM 1706036564.
Jurusan Teknik Mesin Universitas Indonesia, angkatan 2017.
Saya biasa dipanggil Satria, lahir di Kebumen, 10 April 1999.
Kuliah Minggu Pertama
Rabu, 4 September 2019
Mengapa kita mempelajari kalkulus?
Agar memudahkan dan melatih kemampuan analisis mahasiswa serta mempersiapkan mahasiswa untuk mempelajari mata kuliah selanjutnya. Mata kuliah Kalkulus juga merupakan mata kuliah wajib Fakultas Teknik. Jadi, semua mahasiswa Teknik Mesin akan mempelajari Kalkulus.
Tugas untuk minggu selanjutnya: Belajar python, bikin program untuk menyelesaikan soal (mulai dari algoritma). Kami belajar python dari buku dan dari web pembelajaran python, kami harus membuat coding untuk menyelesaikan limit(x->1) dari x^2-1/x-1. Kami juga membuat algoritma pengerjaannya yang kurang lebih saya jabarkan di bawah ini.
Tugas 1
Menyelesaikan persamaaan lim(x->1) (x^2-1)/(x-1)
Algoritma pengerjaan
1. Mulai
2. Masukkan fungsi limit, f(x) = (x^2-1)/(x-1) dan masukkan nilai x = 1. Karena jika langsung dimasukkan 1 tidak mendapatkan hasil, maka kita gunakan limit untuk mencari pendekatan nilai hasilnya
def f():
return (x**2-1)/(x-1)
for i in range(1,10):
n=0.1
a=n**i
limitkiri=f(1-a)
limitkanan=f(1+a)
print('limit kiri = ' + str(limitkiri) + 'limit kanan' + str(limitkanan)
4. Melihat hasil dengan memanggil fungsi f()
f()
2,0
5. selesai
Kuliah Minggu Kedua
Rabu, 11 September 2019
Pada pertemuan kali ini, Bapak DAI menjelaskan tentang Belajar Coding, dicontohkan seperti dalam kita bermain catur. Lalu di industri 4.0, dimana anak mesin pun diperlukan untuk mempelajari pemrograman.
Lalu Bapak Radon mengajarkan tentang python,yang kami pelajari pada pertemuan kali ini adalah Tuples dan Lists. Dimana kita memasukkan data sebagai Array. Lalu kita bisa menambahkan dan mengubah data dengan Lists.
Kuliah Minggu Ketiga
Rabu, 18 September 2019
Pada pertemuan kali ini, Bapak Radon mengadakan kuis dengan soal menyelesaikan sebuah deret fibonacci. Setelah kuis, Bapak Radon menugaskan kami untuk mengerjakan kembali soal deret fibonacci
Deretnya seperti ini, 1, 1, 2, 3, 5, 8, 13, ... , n. Untuk menentukan nilai suku ke-n?
Terdapat 2 cara untuk menyelesaikan deret fibonacci ini.
1. Menggunakan loop
a,b,c=1,1,0
N = int(input('Masukkan Batas : '))
for i in range(N):
print(a,' ', end=)
c=a+b
a=b
b=c
2. Menggunakan def function
def fibo(n):
if n<0:
print('Input Salah')
elif n==1:
return 1
elif n==2:
return 1
else:
return fibo(n-1)+fibo(n-2)
print(fibo(10))
Kuliah Minggu Keempat
Rabu, 25 September 2019
Dalam setiap penyelesaian yang kita buat, kita harus punya motivasi untuk mempelajari suatu hal.
Pemodelan Komputer
Kenapa kita harus menghitung, apakah kita mampu berhitung dengan sangat teliti dan eksak? Sesungguhnya matematik dan numerik tidak mengenal eksak atau manusia itu tidak tahu. Pancasila, di dalamnya terdapat Tuhan Yang Maha Tau. Kita harus sadar, karena suatu saat kita sampai pada suatu kondisi dimana yang bekerja adalah hati kita, otak kita hanya memorize saja. Belajar memasukkan value pada otak kita, value yang tidak dimiliki orang lain adalah hati yang mengakui bahwa Tuhan is One and the only. Modeling adalah sebuah simplifikasi sebuah objek, representasi sederhana dari sesuatu yang rumit. Contohnya arsitek, rumit nya membuat sebuah komplek perumahan.
Dalam pemodelan ada istilah Representasi dan Simplifikasi. Dua kata ini yang mampu menggambarkan apa itu Model.
Model --> Representasi - Simplifikasi - Asumsi
Manusia adalah makhluk terbaik yang diciptakan Allah. Anak Indonesia lahir langsung diperkenalkan dengan Pancasila. Kalau hati manusia seperti baja, susah buat deformasi. Kalau sebuah material susah berubah bentuk, berarti elastisitasnya rendah. Dalam elastisitas terdapat displacement.
Displacement merupakan besaran vektor
Metode Numerik tidak hanya matematikanya saja, tetapi juga fisiknya terutama engineering.
Kuliah Minggu Kelima
Pada pertemuan kali ini kami mempelajari tentang penyelesaian masalah menggunakan Python.
Kali ini Bapak Dr. Ahmad Indra dan Asisten membahas tentang metode Runge-Kutta.
Kami mendapatkan tugas untuk membaca-baca lagi mengenai metode Runge Kutta
Kuliah Minggu Keenam
Pada pertemuan pertama kali ini kami belajar mengenai metode Runge-Kutta.
Kali ini Asisten mengajarkan tentang salah satu contoh yaitu Pegas menggunakan metode Runge-Kutta.
Kuis / Minggu Ketujuh
Rabu, 16 Oktober 2019
Penyelesaian soal persamaan aljabar simultan
from numpy import linalg
import numpy as np
line1 = [0,0,2,1,2]
line2 = [0,1,0,2,-1]
line3 = [1,2,0,-2,1]
line4 = [0,0,0,-1,1]
line5 = [0,1,-1,1,-1]
ops1 = np.array ([line1,line2,line3,line4,line5])
print ("n Matrix adalah sebagai berikut:")
print (ops1)
ops2 = np.array ([1,1,-4,-2,-1])
print ("Matrix Y adalah sebagai berikut:")
print (ops2)
jawab = linalg.solve (ops1,ops2)
nilai1 = int(jawab[0])
nilai2 = int(jawab[1])
nilai3 = int(jawab[2])
nilai4 = int(jawab[3])
nilai5 = int(jawab[4])
print ("hasil X adalah :")
print ("x1= ",nilai1)
print ("x2= ",nilai2)
print ("x3= ",nilai3)
print ("x4= ",nilai4)
print ("x5= ",nilai5)
Penyelesaian soal persamaan differensial
def fungsi(x, y):
return ((x**2 - 4*y))
def RK(x0, y0, x, h):
n = (int)((x - x0)/h)
y = y0
for i in range(1, n + 1):
"Menggunakan runge-kutta untuk mendapatkan nilai y"
k1 = h * fungsi(x0, y)
k2 = h * fungsi(x0 + 0.5 * h, y + 0.5 * k1)
k3 = h * fungsi(x0 + 0.5 * h, y + 0.5 * k2)
k4 = h * fungsi(x0 + h, y + k3)
#Nilai y selanjutnya
y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
#Nilai x selanjutnya
x0 = x0 + h
return y
#misalkan :
x0 = 0
y = 1
x = 0
h = 0.1
print ('Besar nilai y pada titik x adalah:', RK(x0, y, x, h))
UTS / Minggu Kedelapan
Rabu, 23 Oktober 2019
Coding untuk penyelesaian soal 1A
from math import *
A=eval(input("masukkan m1: "))
B=eval(input("masukkan m2: "))
C=eval(input("masukkan m3: "))
D=eval(input("masukkan m4: "))
u=eval(input("masukkan koefisien gesek: "))
alfa=eval(input("masukkan sudut dalam derajat: "))
g=9.8 x=sin(alfa) y=cos(alfa) T1=A*g*(x-u*y) T2=B*g*(x-u*y) + T1 T3=C*g*(x-u*y) + T2 T4=D*g
print("Besar Tegangan Tali T4 adalah: ",T4)
Coding untuk penyelesaian soal 1B
from math import * from sympy import *
G=9.81 Roair= 1.2
Cd=eval(input("masukkan drag coefficient: "))
Luas=eval(input("masukkan area (m^2): "))
v0=eval(input("masukkan velocity awal: "))
M=eval(input("masukkan massa mobil(kg): "))
K=eval(input("masukkan koefisien gesekan: "))
A=eval(input("masukkan percepatan(m/s^2): "))
Vtop=eval(input("masukkan besar topspeed: "))
As=G*K Adrag=(Cd*Luas*Roair*v0**2)/2*M
Atot=A-(Adrag+As)
t=Vtop/Atot
print("waktu yang dibutuhkan dari diam sampai top speed: ",t)
Tugas Takehome Video
1. Presentasi Soal A
2. Presentasi Soal B
3. Video Muhasabah Diri
Tugas RungeKutta
Pada pertemuan kali ini kami memndapat tugas mengenai metode Runge-Kutta.
menyelesaikan sebuah fenomena fisika-Gaya drag Mobil
m = eval(input("massa mobil : "))
g = 9.81
cd = eval(input("koefisien drag udara : "))
ges = eval(input("koefisien gesek jalan : "))
hp = eval(input("Besar Horsepower mobil : "))
rpm = eval(input("Besar RPM mobil : "))
sina = eval(input("Besar sina bidang miring: "))
cosa = eval(input("Besar cosa bidang miring: "))
v = 0
t = 0
dt = 1 #tinggi step atau waktu
error = 100
Fmobil = (hp * 9550) / (rpm * ((2 * 3.14)/60)) p = (Fmobil/m) - g*ges q = cd/m
def dvdt(t, v):
return p-(q*(v)**(1.5))-(cosa*ges*g)-(sina*g)
while error > 0.005:
k1 = dvdt(t, v)
k2 = dvdt(t + 0.5 * h, v + 0.5 * h * k1)
k3 = dvdt(t + 0.5 * h, v + 0.5 * h * k2)
k4 = dvdt(t + h, v + h * k3)
v1 = v + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
t = t + h
error = ((v1 - v) / v1)*100 #persentase error
v = v1
lst.append(v1)
waktu = len(lst)
print ("waktu untuk mencapai velocity maksimal adalah: ", waktu+1)
print ("velocity maksimal adalah: ", v1)
Computational Fluid Dynamic Drag Analysis of a Car
Tahap-Tahap Analsis Drag Mobil Analisis Drag Force dimulai dengan menggunakan program CFDSOF. Pada program CFDSOF, dilakukan impor gambar 3D dari mobil yang akan dianalisis, pembuatan mesh, beserta input data dan boundary condition yang diinginkan. Setelah semua data telah diinput, dilakukan penjalanan solver.Analisis dilanjutkan dengan menggunakan program ParaView.
Pada program ParaView, dilakukan penghilangan internalMesh dan dimunculkan car_body.
Setelah itu, dilanjutkan dengan membuat filter "Generate Surface Normal" dengan "Compute cell normal"
Setelah itu, dilakukan perhitungan menggunakan kalkulator yang ada di program dengan menggunakan Attribute Mode Cell Data, mengganti Result Array Name menjadi Drag Force, dan melakukan perhitungan p*Normal_X
Terakhir, tambahkan filter Integrate Variables dan dapatkan nilai Drag Force
Berikut Hasil yang kami dapatkan:
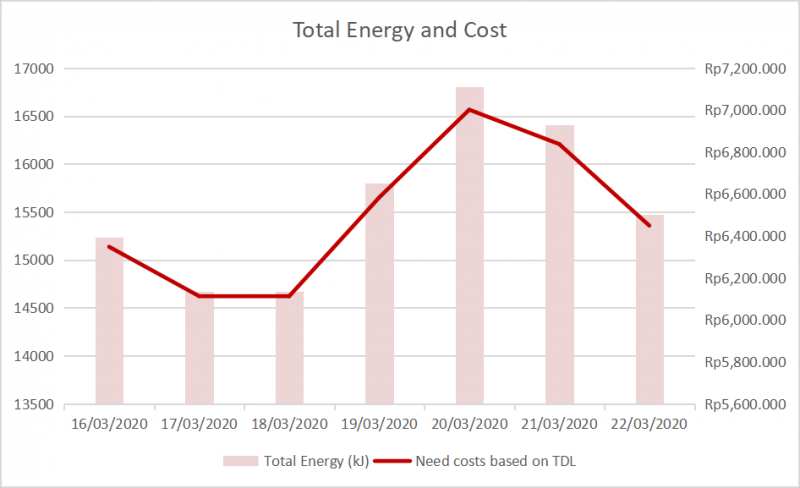
Computational Fluid Dynamic Drag and Lift Analysis of an Airfoil
Langkah-langkah yang digunakan hampir sama seperti tugas drag force mobil, hanya saja ditambah optimasi.
Yang pertama adalah tahap desain airfoil
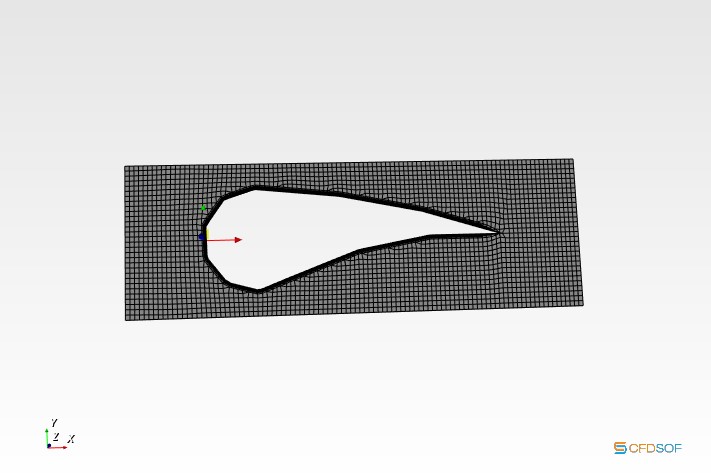
Yang kedua adalah tahap mesh menggunakan CFDSOF
Yang ketiga adalah tahap simulasi dan kalkulasi menggunakan paraview
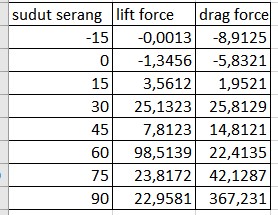
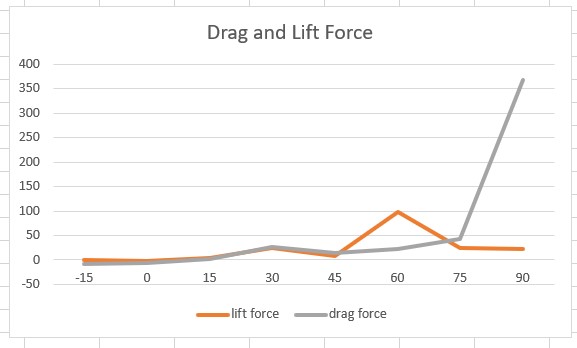
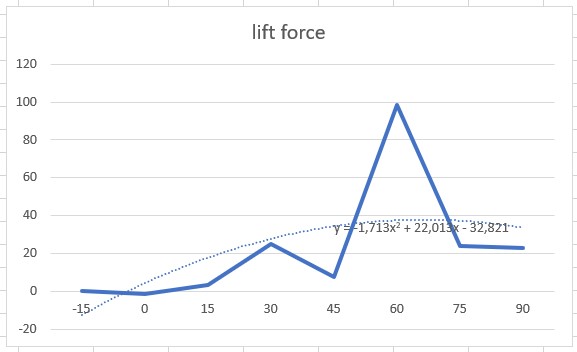
Yang selanjutnya adalah memvariasikan nya terhadap sudut serang -15,15,30,45,60,75,90 derajat.
Hasilnya
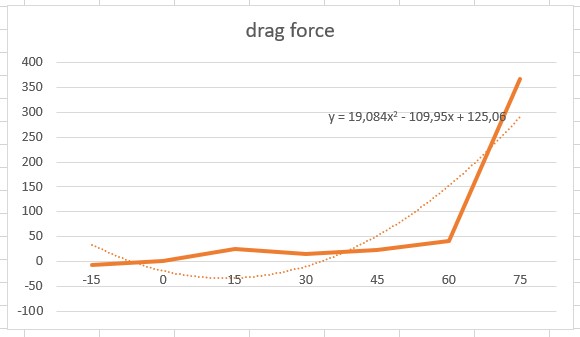
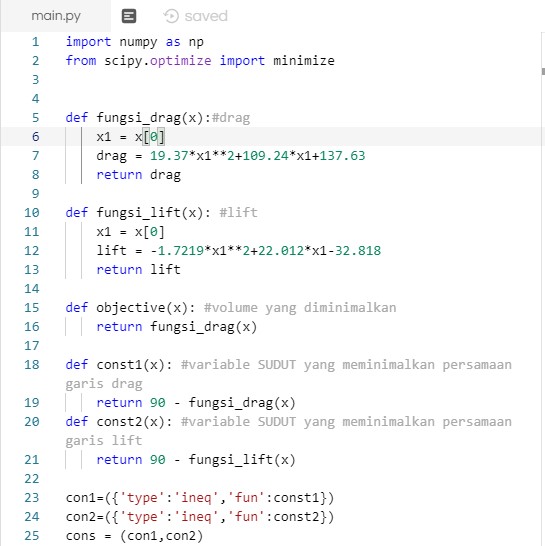
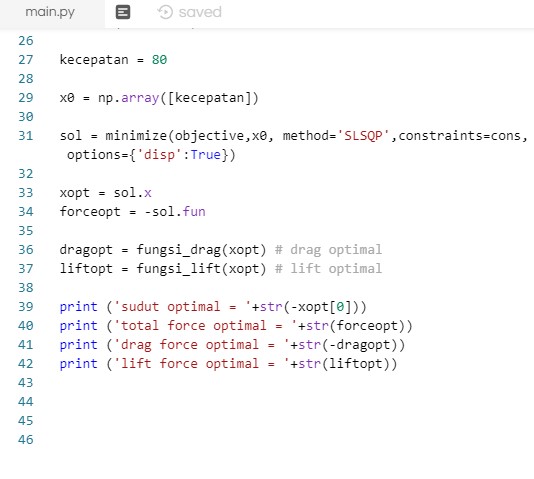
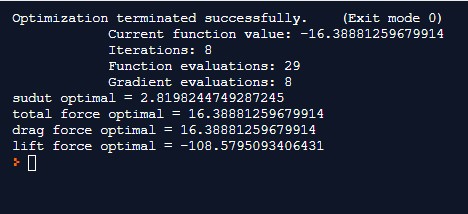
Yang keempat optimasi
Hasilnya adalah sudut serang optimalnya sebesar 2.9 derajat
CFDSOF dan ANN
CFDSOF adalah alat simulasi yang digunakan untuk menganalisis fenomena termal dan fluida yang kompleks. CFDSOF melakukan mesh geometry. Input yang dimasukkan adalah geometry dari sehuah bentuk benda seperti mobil atau airfoil. Lalu outputnya adalah sebuah hasil mesh. Lalu menggunakan sebuah aplikasi paraview untuk menemukan nilai drag and lift force.
ANN atau Artificial Neural Network adalah sistem jaringan syaraf buatan dimana berupa model komputasi yang terdiri dari beberapa elemen pemrosesan yang menerima input dan memberikan output berdasarkan fungsi aktivasi yang telah ditentukan.