Difference between revisions of "Muhammad Fadhil Zuhdi"
Fadhilmzuhdi (talk | contribs) |
(→Jawaban UAS) |
||
| (81 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | == | + | ==Profil== |
| + | [[File:crop muka.jpg|200px|thumb|right]] | ||
| − | + | Saya Muhammad Fadhil Zuhdi, akrab dipanggil Fadhil yang merupakan mahasiswa teknik mesin angkatan 2017 dengan NPM 1706036186. Di wiki ini, saya akan menulis apa saja yang sudah saya pelajari di kelas metode numerik 02 bersama Pak DAI. | |
| − | + | ==Pelajaran yang didapatkan bersama Pak Engkos== | |
| + | Sebelum UTS Metode Numerik, kami kuliah bersama Pak Engkos sebagai dosen kami. Saya mendapatkan beberapa materi yang tentang metode numerik seperti: | ||
| + | *perhitungan deret Taylor | ||
| + | *mencari akar-akar dengan metode bisection, secant, dan newton-rhapson | ||
| + | *penyelesaian masalah dengan deret Taylor | ||
| + | *interpolasi dan regresi linear dengan matriks | ||
| − | + | Hal yang belum saya pahami adalah pengaplikasiannya ke excel yang menurut saya sedikit rumit karena saya belum terlalu memahami pola maisng-masing metode | |
| − | == | + | ==Pertemuan Pertama (Rabu, 11 November 2020)== |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Pada pertemuan pertama kelas Metode Numerik, saya belajar beberapa hal bersama Pak Ahmad Indra (DAI). Pertama, saya belajar cara menggunakan wiki air dari Pak Dai. Wiki Air adalah platform untuk para mahasiswa Pak Dai untuk menulis. Dari pertemuan ini, saya mendapatkan beberapa hal, yaitu konsep metode numerik, aplikasi metode numerik, penerapan metode numerik ke ranah teknik, dan menjadi orang yang beradab. Pak DAI juga menjelaskan bahwa komputer secanggih apapun tetap memiliki batasan karena komputer merupakan karya dari manusia yang penuh keterbatasan. | |
| − | |||
| − | + | Dari kelas ini, kami juga mendiskusikan tentang apa itu belajar. Manfaat belajar sangatlah banyak. Manfaat utama belajar adalah untuk mendapatkan ilmu. Namun, belajar pelajaran kehidupan juga sama pentingnya dengan belajar pelajaran akademis. Kita juga harus sering merenungkan aapa saja yang sudah kita pelajari. Kita harus merefleksikan diri sendiri sudah bermanfaatkah yang sudah kita pelajari dan sudah berapa banyak ilmu yang sudah kita amalkan. | |
| − | + | Kami diberikan tugas oleh Pak DAI tentang Open Modellica. Kami diperintahkan untuk belajar tentang Open Modellica, merekam dan menguploadnya ke Youtube, dan memberikan tautan video dari Youtube kami di wiki masing-masing. | |
| − | |||
| − | |||
| − | + | ====Tugas OpenModelica 1==== | |
| − | + | Sebelumnya kami diberikan tugas pembelajaran metode numerik dengan OpenModelica. Di sini, saya mengangkat permasalahan gaya gesek statis dengan mencari koefisien gaya gesek statis di OpenModelica. hasil pembelajaran saya dapat ditonton di tautan berikut: | |
| − | + | <youtube width="200" height="100">https://youtu.be/JeyiRPxiixE</youtube> | |
| − | + | Terima kasih! | |
| − | |||
| − | == | + | ==Minggu ke-2 (Rabu, 18 November 2020)== |
| + | Pada hari ini, kami belajar bagaimana cara menggunakan OpenModelica. Pak Dai mereview tugas-tugas kami dan membahas apa saja kesulitan yang dialami mahasiswa dalam mengerjakan tugas kemarin bersama asisten dosen, Bang Edo. Hampir setiap anak menceritakan yang dilakukannya bersama OpenModeilca untuk menyelesaikan permasalahan yang dipilih. Dalam kelas Pak Dai juga berpesan bahwa belajar sebagai manusia itu tidak akan habisnya. Kita akan selalu melakukan hal yang bernama "belajar" dari buaian sampe ke liang lahat. Manusia harus selalu berkembang dan harus lebih baik dari hari sebelumnya agar beruntung. Bila hari ini sama saja dengan hari kemarin, manusia itu telaj merugi, apalagi bila lebih buruk. Kemudian, | ||
| − | ''' | + | Pak Dai kemudian memberikan tugas kepada kami. Untuk materi yang disampaikan berupa penggunaan open modellica dengan kelas 'class' dan 'function', yaitu dimana kita menuliskan fungsi pada kelas 'function' kemudian kita panggil melalui kelas 'class'. Kami diberikan tugas tentang materi itu. |
| − | + | ====Tugas OpenModelica 2==== | |
| + | Kami diberikan tugas oleh Pak Dai dengan menggunakan OpenModelica memecahkan permasalahan dengan sistem persamaan linear bermetode array. Inilah hasil belajar, mohon disimak secara saksama. | ||
| + | <youtube width="200" height="100">https://youtu.be/gu5krOHs3ao</youtube> | ||
| − | + | ==Minggu ke-3 (Rabu, 25 November 2020)== | |
| − | + | Pada hari ini, kami mereview tugas yang diberikan kami pada hari kemarin. Beberapa dari kami menceritakan dan berbagi apa kami dapat dan pelajari selama mengerjakan tugas kemarin melalui screen share zoom room meeting. Kami belajar bahwa permasalahan teknik dapat diselesaikan dengan metode numerik. Dalam tahapnya, terlebih dahulu hal yang dilakukan adalah analisis terhadap masalah tersebut. Kemudian, membuat model matematika dari hasil analisis tersebut. Kemudian, model matematika tersebut di-convert ke metode numerik dengan bahasa komputer yang kemudian dapat menghasilkan solusi. | |
| − | + | ===Tugas minggu ke-3=== | |
| + | Kami diberikan tugas oleh Pak Dai menyelesaikan masalah dari trusses berikut: | ||
| + | [[File:Soal Trusses 2 Jos.jpg|700px]] | ||
| − | + | 1. Membuat kelas panggil | |
| + | [[File: Screenshots (211).png|800px|center]] | ||
| + | [[File: Screenshots (212).png|800px|center]] | ||
| + | [[File: Screenshots (213).png|800px|center]] | ||
| + | [[File: Screenshots (214).png|800px|center]] | ||
| + | [[File: Screenshots (215).png|800px|center]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | 2. Membuat fungsi panggil | |
| − | * | + | *Matrice Formation |
| − | + | [[File: Screenshots (218).png|800px|center]] | |
| − | + | [[File: Screenshots (219).png|800px|center]] | |
| − | + | *Global Element Matrice | |
| + | [[File: Screenshots (220).png|800px|center]] | ||
| + | [[File: Screenshots (221).png|800px|center]] | ||
| + | *Reaction Matrice Equation | ||
| + | [[File: Screenshots (222).png|800px|center]] | ||
| − | + | ==Minggu ke-4 (Rabu, 2 Desember 2020)== | |
| + | ===Kuis=== | ||
| + | Kuis Flowchart untuk no. 4 | ||
| + | [[File: 488929.jpg|400px|center]] | ||
| + | [[File: 488930.jpg|400px|center]] | ||
| − | + | ===Tugas Minggu ke-4=== | |
| + | Diagram class dan Penyelesaian dengan OpenModellica dari soal berikut | ||
| + | [[File: Pr4tin.jpeg|600px|thumb|center|Soal Tugas ke-4]] | ||
| − | + | Saya mempelajari terlebih dahulu dari suadara Josiah Enrico dan Fashal Firdaus Amrullah. Step-step yang harus dilakukan untuk | |
| + | Pertama, terlebih dahulu membuat kelas trusses. Kelas trusses berisi matriks gaya dari trusses. Kemudian membuat fungsi matriks kekakuan. Kemudian membuat fungsi matriks global. Kemudian membuat penjumlahan kekakuan matriks global. Setelah itu membuat gauss jordan. Kemudian, membuat reaction. | ||
| + | *Kelas fungsi utama | ||
| + | [[File: 225.png|600px|center|]] | ||
| + | [[File: 226.png|600px|center|]] | ||
| + | [[File: 227.png|600px|center|]] | ||
| − | + | *matriks kekakuan elemen | |
| − | + | [[File: 228.png|600px|center|]] | |
| + | [[File: 229.png|600px|center|]] | ||
| + | [[File: 230.png|600px|center|]] | ||
| − | + | *matriks kekakuan global | |
| + | [[File: 231.png|600px|center|]] | ||
| + | [[File: 232.png|600px|center|]] | ||
| + | [[File: 233.png|600px|center|]] | ||
| − | + | *Total matriks kekauan global | |
| + | [[File: 234.png|600px|center|]] | ||
| − | + | *kondisi impelemntasi boundary | |
| − | + | [[File: 235.png|600px|center|]] | |
| + | [[File: 236.png|600px|center|]] | ||
| − | [[File: | + | *Gauss jordan |
| + | [[File: 237.png|600px|center|]] | ||
| − | + | *gaya reaksi | |
| + | [[File: 238.png|600px|center|]] | ||
| − | + | Hasil yang didapat | |
| − | + | [[File: jawaban pr 4.png|200px|center]] | |
| − | |||
| − | |||
| − | == | + | ==Minggu ke-6 (Rabu, 16 Desember 2020)== |
| − | + | "Aplikasi Metode Numerik dalam Kasus Optimasi" | |
| − | + | Dalam minggu ini, kami diajarkan bagaimana cara menggunakan metode Bracket oleh Bu Candra. Fungsi dari metode ini bisa untuk optimasi. Detilnya, kami belajar tentang one dimentional unconstrained optimization. Sembari Bu Candra mengajarkan Bracket, kami juga ikut mencoba cara membuat metode Bracket di Open Modellica mengikuti Bu Candra. Berikut hasil dari metode bracket untuk optimasi yang saya lakukan: | |
| − | + | *untuk fungsinya | |
| + | [[File: 295.png|800px|center]] | ||
| − | + | *untuk modelnya | |
| − | + | [[File: 296.png|800px|center]] | |
| − | [[File: | + | *untuk hasilnya |
| + | [[File: hasil bracket.png|800px|center]] | ||
| − | === ''' | + | ==Tugas Besar== |
| + | |||
| + | '''Pendahuluan''' | ||
| + | ---- | ||
| + | Kami diberikan tugas besar untuk melakukan optimasi dalam pemilihan bahan material dan luas penampang trusses yang akan digunakan untuk membuat konstruksi. Desain yang akan kami gunakan adalah sebagai berikut: | ||
| + | [[File:Tugas Besar Metnum Geometri Jos.jpg|center]] | ||
| − | + | '''Alur Pengerjaan''' | |
| + | ---- | ||
| + | Alur pengerjaan dibuat untuk mengurutkan prioritas pekerjaan yang harus dikerjakan. Berikut urutan pengerjaan tugas besar ini, | ||
| + | [[File:Alur Pengerjaan.png|500px|center]] | ||
| − | |||
| − | + | '''Mendifinisikan Permasalahan''' | |
| + | ---- | ||
| + | #Jenis Material adalah besi siku; | ||
| + | #Mencari optimasi dari material yang digunakan dengan optimasi elastisitas dan optimasi luas penampang; | ||
| + | #Dimensi struktur adalah (p x l x t) = 0,6 m x 0,75 m x 1,8 m; | ||
| + | #Terdapat dua gaya yang memberikan stress sebesar F1 = 2000 N dan F2 = 1000 N. | ||
| − | [[File: | + | '''Asumsi''' |
| + | ---- | ||
| + | Dalam permaslahan ini, tidak semua data yang dibutuhkan tersedia dan diketahui di soal. Maka, penulis membuat beberapa asumsi yaitu: | ||
| + | #Struktur paling bawah dianggap sebagai lantai rata dengan tanah karena tidak diketahui tinggi lantai di atas tanah (Δh = 0) | ||
| + | #Safety factor adalah 2 | ||
| + | #Beban terdistribusi dengan node karena bersifat trusses | ||
| + | #Batas displacement adalah 0,001 m sebelum buckling pada trusses paling atas | ||
| + | #Ketinggian trusses dianggap sama per lantai yaitu 0,6 m. | ||
| + | ---- | ||
| + | '''Data Material''' | ||
| + | [[File:Data material.jpg|center]] | ||
| − | + | '''Model Numerik''' | |
| + | *Untuk perhitungan displacement, reaction force, stress, dan safety factor: | ||
| + | model Trusses_3D_Tugas_Besar_Safety | ||
| + | |||
| + | //define initial variable | ||
| + | parameter Integer Points=size(P,1); //Number of Points | ||
| + | parameter Integer Trusses=size(C,1); //Number of Trusses | ||
| + | parameter Real Yield=215e6; //Yield Strength (Pa) | ||
| + | parameter Real Area=0.000224; //Area L Profile (Dimension=0.03, Thickness=0,004) (m2) | ||
| + | parameter Real Elas=193e9; //Elasticity SS 304 (Pa) | ||
| + | |||
| + | //define connection | ||
| + | parameter Integer C[:,2]=[1,5; | ||
| + | 2,6; | ||
| + | 3,7; | ||
| + | 4,8; | ||
| + | 5,6; //1st floor | ||
| + | 6,7; //1st floor | ||
| + | 7,8; //1st floor | ||
| + | 5,8; //1st floor | ||
| + | 5,9; | ||
| + | 6,10; | ||
| + | 7,11; | ||
| + | 8,12; | ||
| + | 9,10; //2nd floor | ||
| + | 10,11;//2nd floor | ||
| + | 11,12;//2nd floor | ||
| + | 9,12; //2nd floor | ||
| + | 9,13; | ||
| + | 10,14; | ||
| + | 11,15; | ||
| + | 12,16; | ||
| + | 13,14;//3rd floor | ||
| + | 14,15;//3rd floor | ||
| + | 15,16;//3rd floor | ||
| + | 13,16];//3rd floor | ||
| + | |||
| + | //define coordinates (please put orderly) | ||
| + | parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1 | ||
| + | -0.3,-0.375,0,1,1,1; //2 | ||
| + | -0.3,0.375,0,1,1,1; //3 | ||
| + | 0.3,0.375,0,1,1,1; //4 | ||
| + | |||
| + | 0.3,-0.375,0.6,0,0,0; //5 | ||
| + | -0.3,-0.375,0.6,0,0,0; //6 | ||
| + | -0.3,0.375,0.6,0,0,0; //7 | ||
| + | 0.3,0.375,0.6,0,0,0; //8 | ||
| + | |||
| + | 0.3,-0.375,1.2,0,0,0; //9 | ||
| + | -0.3,-0.375,1.2,0,0,0; //10 | ||
| + | -0.3,0.375,1.2,0,0,0; //11 | ||
| + | 0.3,0.375,1.2,0,0,0; //12 | ||
| + | |||
| + | 0.3,-0.375,1.8,0,0,0; //13 | ||
| + | -0.3,-0.375,1.8,0,0,0; //14 | ||
| + | -0.3,0.375,1.8,0,0,0; //15 | ||
| + | 0.3,0.375,1.8,0,0,0]; //16 | ||
| + | |||
| + | //define external force (please put orderly) | ||
| + | parameter Real F[Points*3]={0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,-500, | ||
| + | 0,0,-1000, | ||
| + | 0,0,-1000, | ||
| + | 0,0,-500}; | ||
| + | |||
| + | //solution | ||
| + | Real displacement[N], reaction[N]; | ||
| + | Real check[3]; | ||
| + | |||
| + | Real stress1[Trusses]; | ||
| + | Real safety[Trusses]; | ||
| + | Real dis[3]; | ||
| + | Real Str[3]; | ||
| + | |||
| + | protected | ||
| + | parameter Integer N=3*Points; | ||
| + | Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; | ||
| + | Real err=10e-10, ers=10e-4; | ||
| + | |||
| + | algorithm | ||
| + | //Creating Global Matrix | ||
| + | G:=id; | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | end for; | ||
| + | |||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | |||
| + | //Transforming to global matrix | ||
| + | g:=zeros(N,N); | ||
| + | for m,n in 1:3 loop | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n]; | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n]; | ||
| + | end for; | ||
| + | |||
| + | G_star:=G+g; | ||
| + | G:=G_star; | ||
| + | end for; | ||
| + | |||
| + | //Implementing boundary | ||
| + | for x in 1:Points loop | ||
| + | if P[x,4] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[(x*3)-2,a]:=0; | ||
| + | G[(x*3)-2,(x*3)-2]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x,5] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[(x*3)-1,a]:=0; | ||
| + | G[(x*3)-1,(x*3)-1]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x,6] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[x*3,a]:=0; | ||
| + | G[x*3,x*3]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | //Solving displacement | ||
| + | displacement:=Modelica.Math.Matrices.solve(G,F); | ||
| + | |||
| + | //Solving reaction | ||
| + | reaction:=(G_star*displacement)-F; | ||
| + | |||
| + | //Eliminating float error | ||
| + | for i in 1:N loop | ||
| + | reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; | ||
| + | displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i]; | ||
| + | end for; | ||
| + | |||
| + | //Checking Force | ||
| + | check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))}); | ||
| + | check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))}); | ||
| + | check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)}); | ||
| + | |||
| + | for i in 1:3 loop | ||
| + | check[i] := if abs(check[i])<=ers then 0 else check[i]; | ||
| + | end for; | ||
| + | |||
| + | //Calculating stress in each truss | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]); | ||
| + | end for; | ||
| + | |||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | |||
| + | Str:=(X*dis); | ||
| + | stress1[i]:=Modelica.Math.Vectors.length(Str); | ||
| + | end for; | ||
| + | |||
| + | //Safety factor | ||
| + | for i in 1:Trusses loop | ||
| + | if stress1[i]>0 then | ||
| + | safety[i]:=Yield/stress1[i]; | ||
| + | else | ||
| + | safety[i]:=0; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | end Trusses_3D_Tugas_Besar_Safety; | ||
| − | |||
| − | + | *Untuk membuat kurva curve fitting: | |
| + | function Curve_Fitting | ||
| + | |||
| + | input Real X[:]; | ||
| + | input Real Y[size(X,1)]; | ||
| + | input Integer order=2; | ||
| + | output Real Coe[order+1]; | ||
| + | |||
| + | protected | ||
| + | Real Z[size(X,1),order+1]; | ||
| + | Real ZTr[order+1,size(X,1)]; | ||
| + | Real A[order+1,order+1]; | ||
| + | Real B[order+1]; | ||
| + | |||
| + | algorithm | ||
| + | |||
| + | for i in 1:size(X,1) loop | ||
| + | for j in 1:(order+1) loop | ||
| + | Z[i,j]:=X[i]^(order+1-j); | ||
| + | end for; | ||
| + | end for; | ||
| + | ZTr:=transpose(Z); | ||
| + | |||
| + | A:=ZTr*Z; | ||
| + | B:=ZTr*Y; | ||
| + | Coe:=Modelica.Math.Matrices.solve(A,B); | ||
| + | |||
| + | end Curve_Fitting; | ||
| − | |||
| − | |||
| − | + | * Untuk golden section: | |
| + | model Opt_Gold | ||
| + | |||
| + | parameter Real xd[:]; | ||
| + | parameter Real yd[size(xd,1)]; | ||
| + | parameter Real xlo=87e-6; | ||
| + | parameter Real xhi=504e-6; | ||
| + | parameter Integer N=10; // maximum iteration | ||
| + | parameter Real es=0.0001; // maximum error | ||
| + | |||
| + | Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3]; | ||
| + | Real xopt, fx; | ||
| + | protected | ||
| + | Real d, xl, xu, xint, R=(5^(1/2)-1)/2; | ||
| + | |||
| + | algorithm | ||
| + | xl := xlo; | ||
| + | xu := xhi; | ||
| + | y := Curve_Fitting(xd,yd); | ||
| + | |||
| + | for i in 1:N loop | ||
| + | d:= R*(xu-xl); | ||
| + | x1[i]:=xl+d; | ||
| + | x2[i]:=xu-d; | ||
| + | f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3]; | ||
| + | f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3]; | ||
| + | xint:=xu-xl; | ||
| + | |||
| + | if f1[i]>f2[i] then | ||
| + | xl:=x2[i]; | ||
| + | xopt:=x1[i]; | ||
| + | fx:=f1[i]; | ||
| + | else | ||
| + | xu:=x1[i]; | ||
| + | xopt:=x2[i]; | ||
| + | fx:=f2[i]; | ||
| + | end if; | ||
| + | |||
| + | ea[i]:=(1-R)*abs((xint)/xopt); | ||
| + | if ea[i]<es then | ||
| + | break; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | end Opt_Gold; | ||
| + | |||
| + | '''Hasil Perhitungan''' | ||
| + | ---- | ||
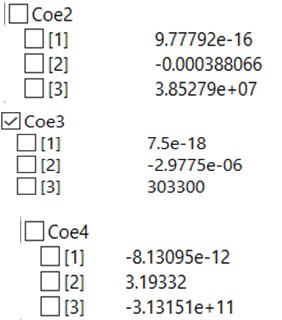
| + | Koefisien yang didapat dari data harga variasi area dan variasi material adalah sebagai berikut (coef untuk variasi area dan coef 2-4 untuk variasi material) | ||
| + | [[File:coef1.jpg|center]] | ||
| + | [[File:coef2.jpg|center]] | ||
| + | |||
| + | Kemudian, coefisien tersebut digunakan untuk mendapatkan variasi yang tidak tersedia dari sumber | ||
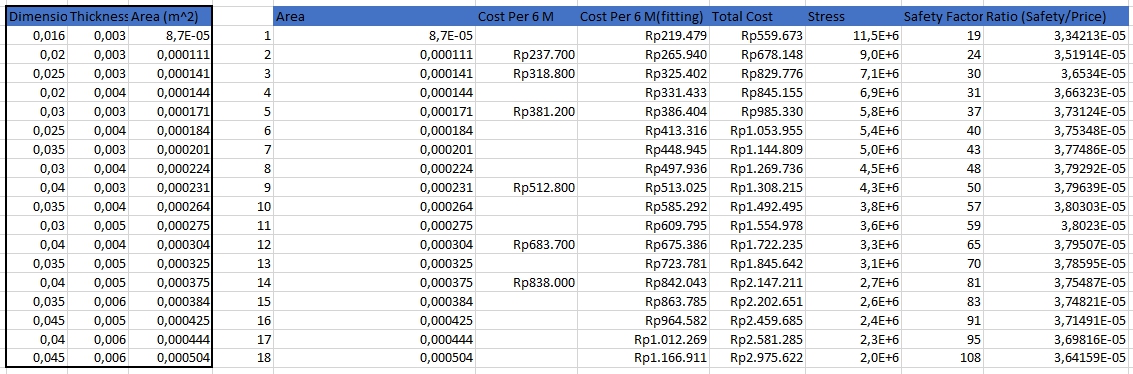
| + | [[File:Data tubes.jpg|center]] | ||
| + | |||
| + | |||
| + | =='''Jawaban UAS'''== | ||
| + | |||
| + | [[File: uas1.jpg|600px|left]] | ||
| + | |||
| + | [[File: uas2.jpg|600px|left]] | ||
| + | |||
| + | |||
| + | [[File: uas3.jpg|600px|left]] | ||
| + | |||
| + | |||
| + | [[File: uas4.jpg|600px|left]] | ||
| + | |||
| + | |||
| + | [[File: uas56.jpg|600px|left]] | ||
Latest revision as of 18:00, 13 January 2021
Contents
Profil
Saya Muhammad Fadhil Zuhdi, akrab dipanggil Fadhil yang merupakan mahasiswa teknik mesin angkatan 2017 dengan NPM 1706036186. Di wiki ini, saya akan menulis apa saja yang sudah saya pelajari di kelas metode numerik 02 bersama Pak DAI.
Pelajaran yang didapatkan bersama Pak Engkos
Sebelum UTS Metode Numerik, kami kuliah bersama Pak Engkos sebagai dosen kami. Saya mendapatkan beberapa materi yang tentang metode numerik seperti:
- perhitungan deret Taylor
- mencari akar-akar dengan metode bisection, secant, dan newton-rhapson
- penyelesaian masalah dengan deret Taylor
- interpolasi dan regresi linear dengan matriks
Hal yang belum saya pahami adalah pengaplikasiannya ke excel yang menurut saya sedikit rumit karena saya belum terlalu memahami pola maisng-masing metode
Pertemuan Pertama (Rabu, 11 November 2020)
Pada pertemuan pertama kelas Metode Numerik, saya belajar beberapa hal bersama Pak Ahmad Indra (DAI). Pertama, saya belajar cara menggunakan wiki air dari Pak Dai. Wiki Air adalah platform untuk para mahasiswa Pak Dai untuk menulis. Dari pertemuan ini, saya mendapatkan beberapa hal, yaitu konsep metode numerik, aplikasi metode numerik, penerapan metode numerik ke ranah teknik, dan menjadi orang yang beradab. Pak DAI juga menjelaskan bahwa komputer secanggih apapun tetap memiliki batasan karena komputer merupakan karya dari manusia yang penuh keterbatasan.
Dari kelas ini, kami juga mendiskusikan tentang apa itu belajar. Manfaat belajar sangatlah banyak. Manfaat utama belajar adalah untuk mendapatkan ilmu. Namun, belajar pelajaran kehidupan juga sama pentingnya dengan belajar pelajaran akademis. Kita juga harus sering merenungkan aapa saja yang sudah kita pelajari. Kita harus merefleksikan diri sendiri sudah bermanfaatkah yang sudah kita pelajari dan sudah berapa banyak ilmu yang sudah kita amalkan.
Kami diberikan tugas oleh Pak DAI tentang Open Modellica. Kami diperintahkan untuk belajar tentang Open Modellica, merekam dan menguploadnya ke Youtube, dan memberikan tautan video dari Youtube kami di wiki masing-masing.
Tugas OpenModelica 1
Sebelumnya kami diberikan tugas pembelajaran metode numerik dengan OpenModelica. Di sini, saya mengangkat permasalahan gaya gesek statis dengan mencari koefisien gaya gesek statis di OpenModelica. hasil pembelajaran saya dapat ditonton di tautan berikut:
Terima kasih!
Minggu ke-2 (Rabu, 18 November 2020)
Pada hari ini, kami belajar bagaimana cara menggunakan OpenModelica. Pak Dai mereview tugas-tugas kami dan membahas apa saja kesulitan yang dialami mahasiswa dalam mengerjakan tugas kemarin bersama asisten dosen, Bang Edo. Hampir setiap anak menceritakan yang dilakukannya bersama OpenModeilca untuk menyelesaikan permasalahan yang dipilih. Dalam kelas Pak Dai juga berpesan bahwa belajar sebagai manusia itu tidak akan habisnya. Kita akan selalu melakukan hal yang bernama "belajar" dari buaian sampe ke liang lahat. Manusia harus selalu berkembang dan harus lebih baik dari hari sebelumnya agar beruntung. Bila hari ini sama saja dengan hari kemarin, manusia itu telaj merugi, apalagi bila lebih buruk. Kemudian,
Pak Dai kemudian memberikan tugas kepada kami. Untuk materi yang disampaikan berupa penggunaan open modellica dengan kelas 'class' dan 'function', yaitu dimana kita menuliskan fungsi pada kelas 'function' kemudian kita panggil melalui kelas 'class'. Kami diberikan tugas tentang materi itu.
Tugas OpenModelica 2
Kami diberikan tugas oleh Pak Dai dengan menggunakan OpenModelica memecahkan permasalahan dengan sistem persamaan linear bermetode array. Inilah hasil belajar, mohon disimak secara saksama.
Minggu ke-3 (Rabu, 25 November 2020)
Pada hari ini, kami mereview tugas yang diberikan kami pada hari kemarin. Beberapa dari kami menceritakan dan berbagi apa kami dapat dan pelajari selama mengerjakan tugas kemarin melalui screen share zoom room meeting. Kami belajar bahwa permasalahan teknik dapat diselesaikan dengan metode numerik. Dalam tahapnya, terlebih dahulu hal yang dilakukan adalah analisis terhadap masalah tersebut. Kemudian, membuat model matematika dari hasil analisis tersebut. Kemudian, model matematika tersebut di-convert ke metode numerik dengan bahasa komputer yang kemudian dapat menghasilkan solusi.
Tugas minggu ke-3
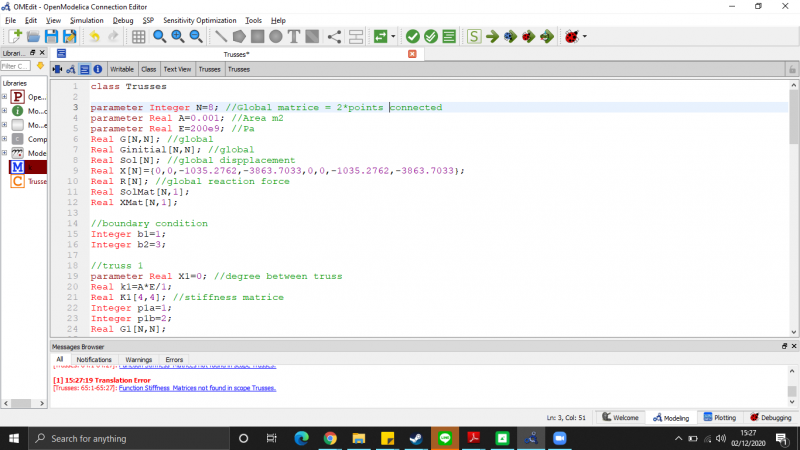
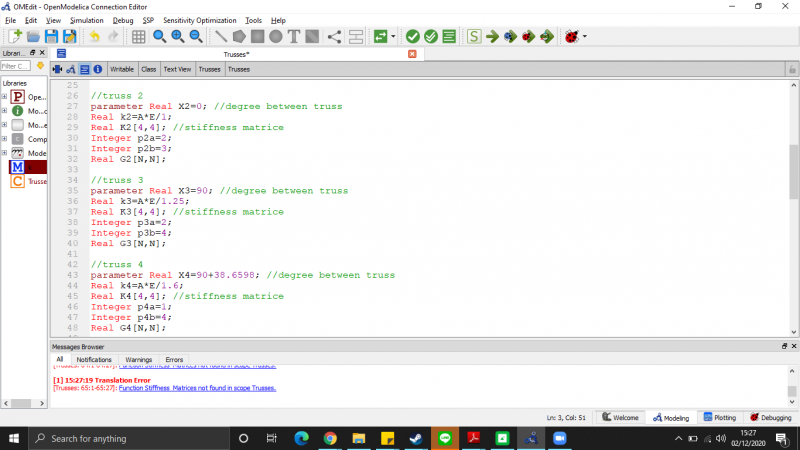
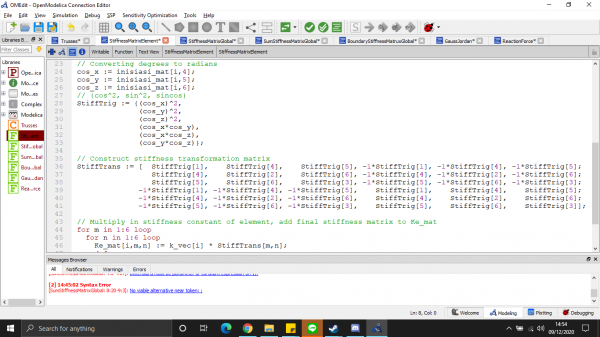
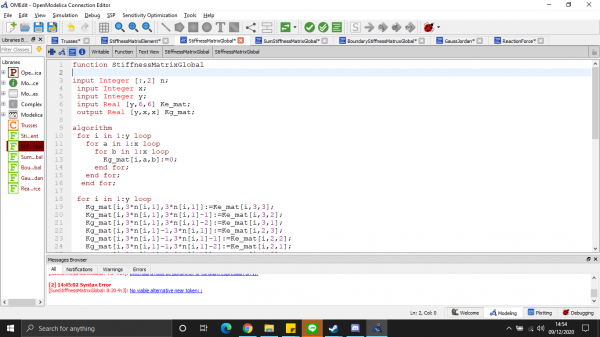
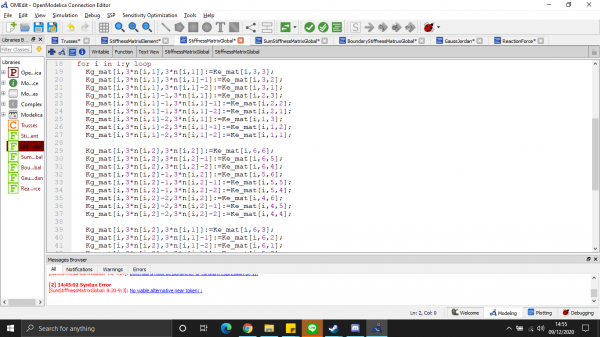
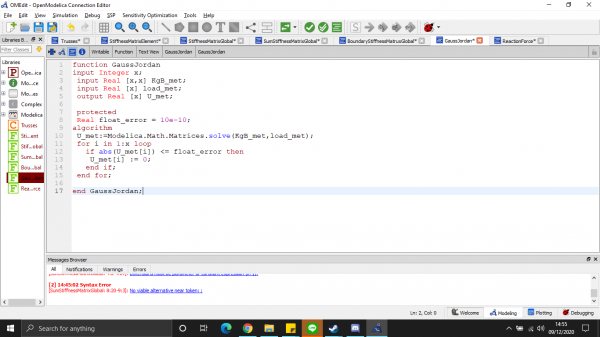
Kami diberikan tugas oleh Pak Dai menyelesaikan masalah dari trusses berikut:
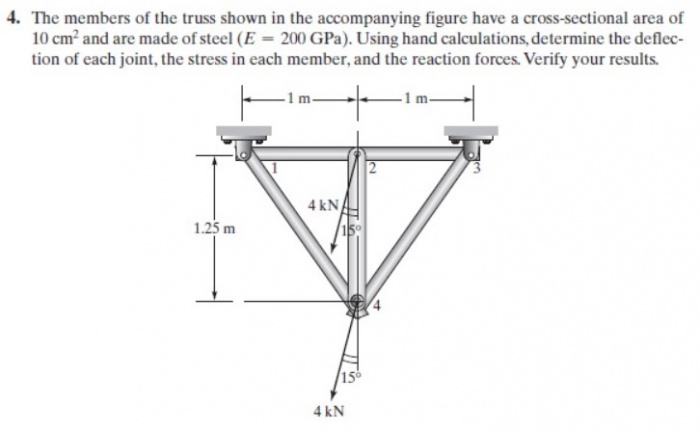
1. Membuat kelas panggil
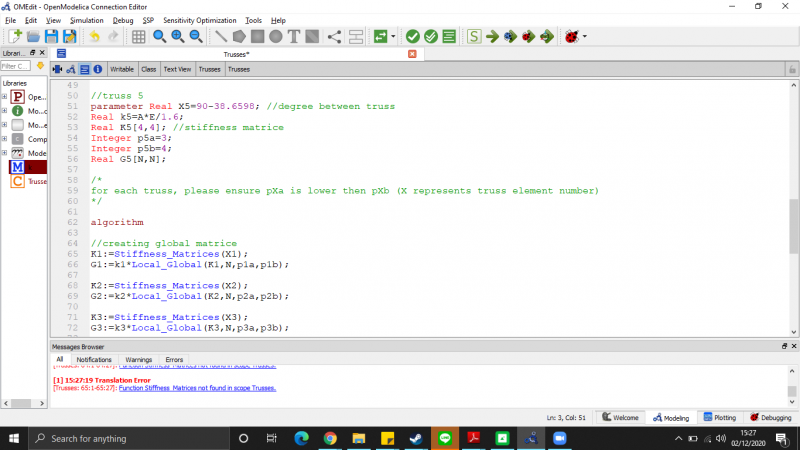
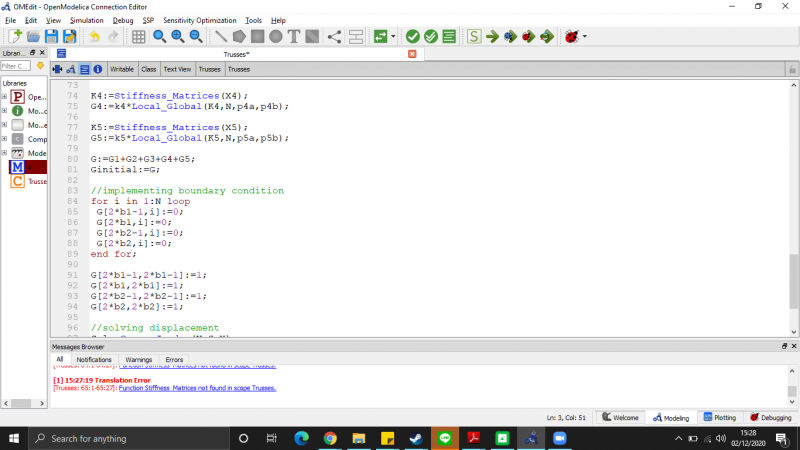
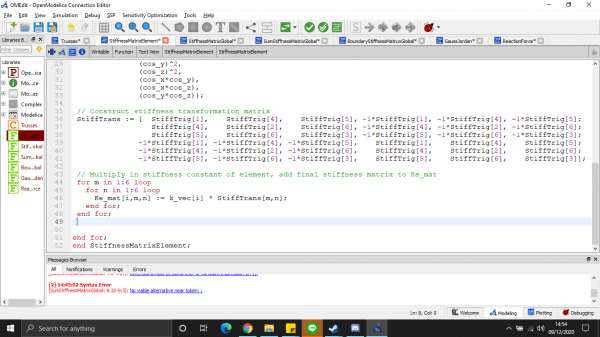
2. Membuat fungsi panggil
- Matrice Formation
- Global Element Matrice
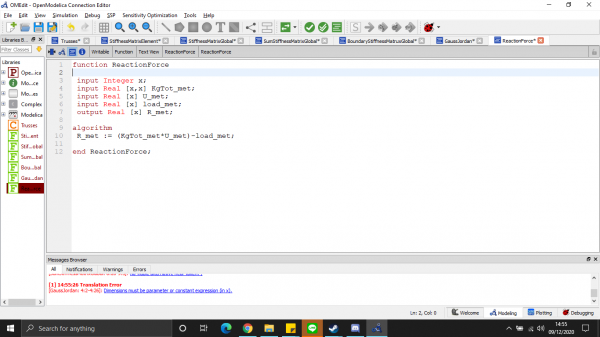
- Reaction Matrice Equation
Minggu ke-4 (Rabu, 2 Desember 2020)
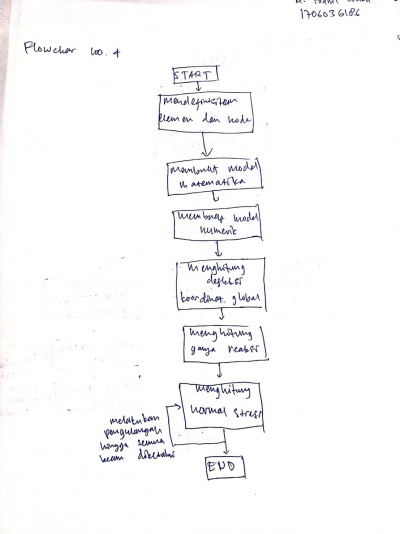
Kuis
Kuis Flowchart untuk no. 4
Tugas Minggu ke-4
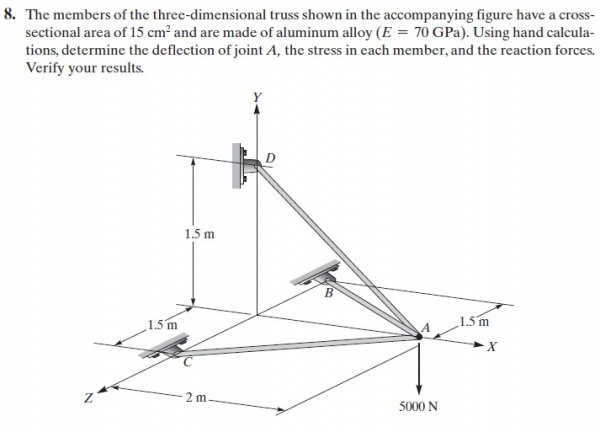
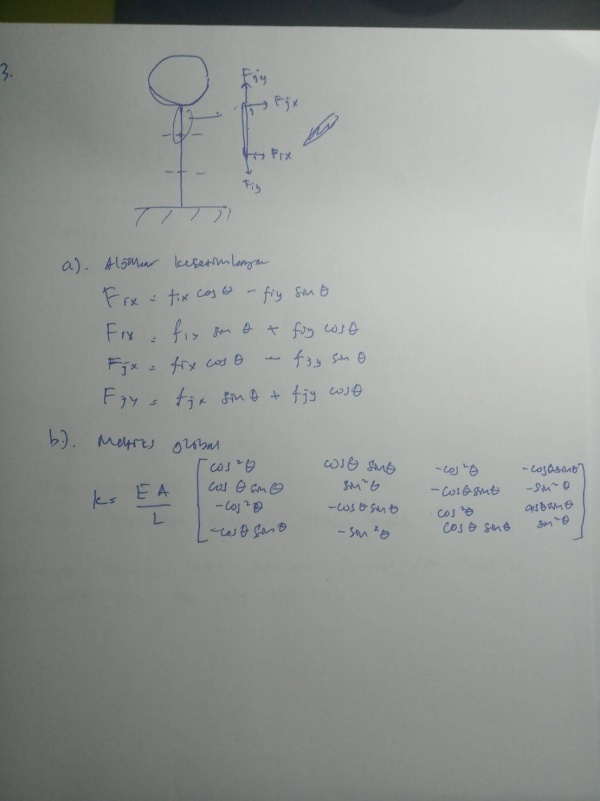
Diagram class dan Penyelesaian dengan OpenModellica dari soal berikut
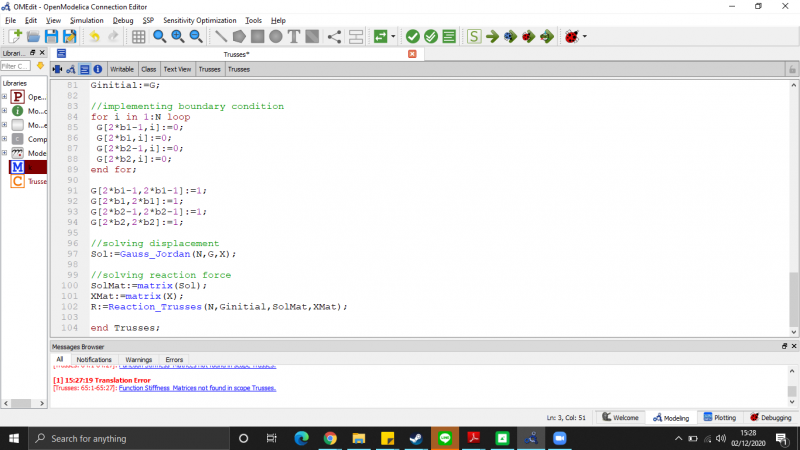
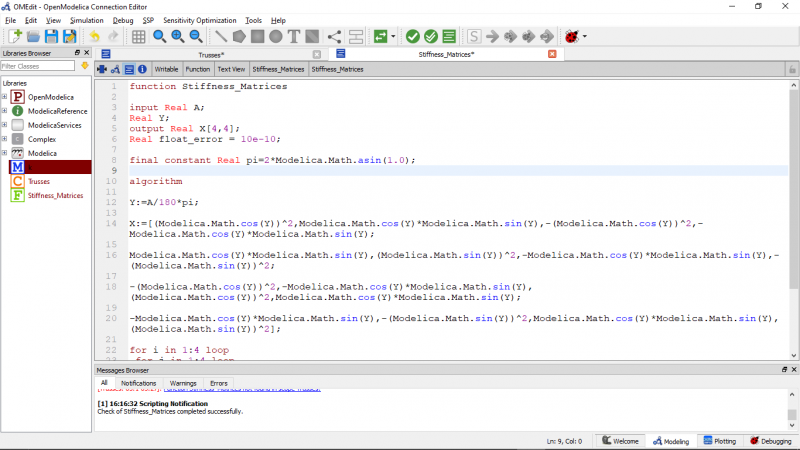
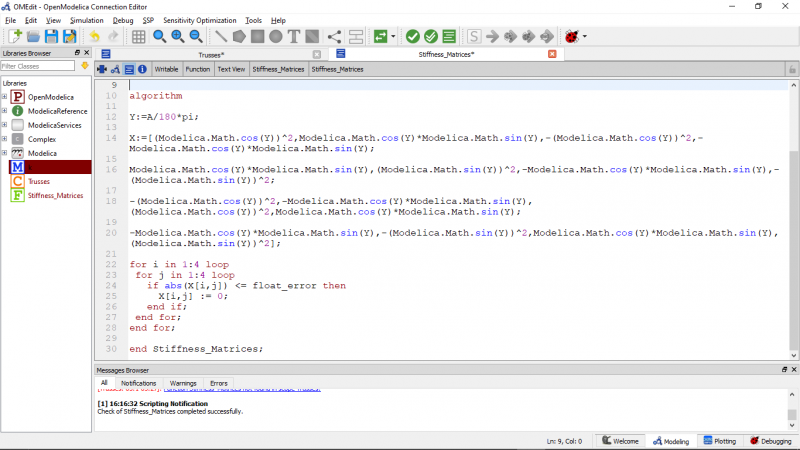
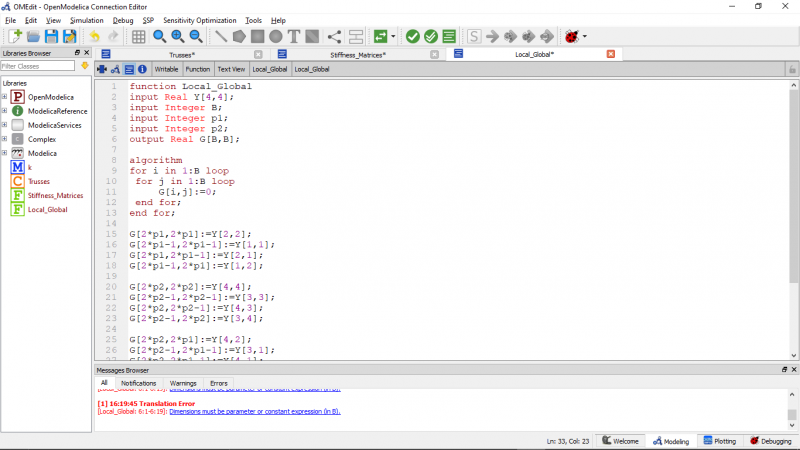
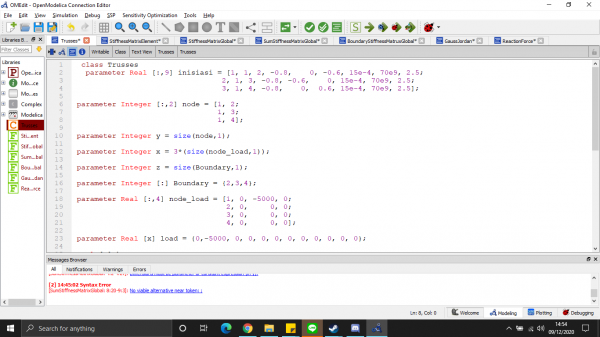
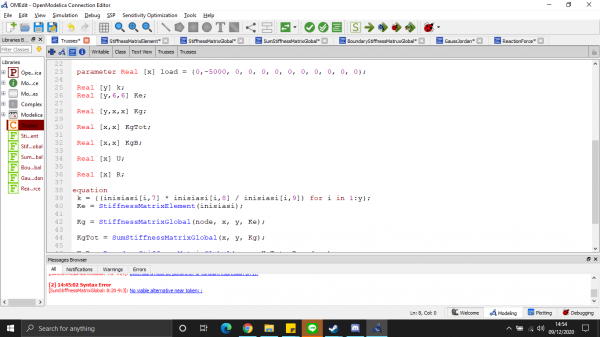
Saya mempelajari terlebih dahulu dari suadara Josiah Enrico dan Fashal Firdaus Amrullah. Step-step yang harus dilakukan untuk Pertama, terlebih dahulu membuat kelas trusses. Kelas trusses berisi matriks gaya dari trusses. Kemudian membuat fungsi matriks kekakuan. Kemudian membuat fungsi matriks global. Kemudian membuat penjumlahan kekakuan matriks global. Setelah itu membuat gauss jordan. Kemudian, membuat reaction.
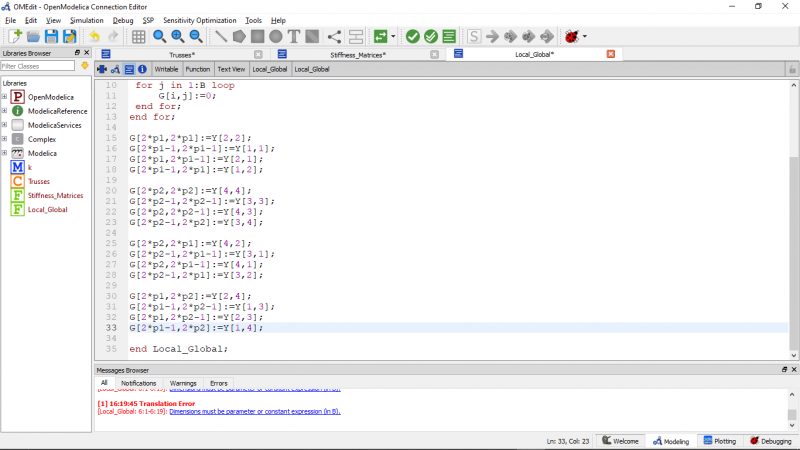
- Kelas fungsi utama
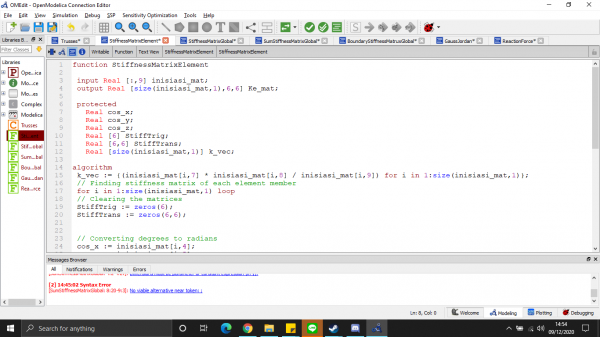
- matriks kekakuan elemen
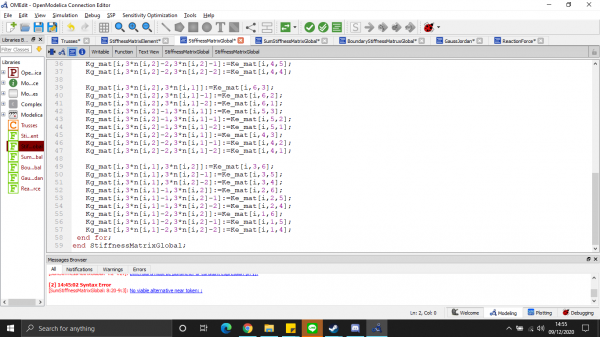
- matriks kekakuan global
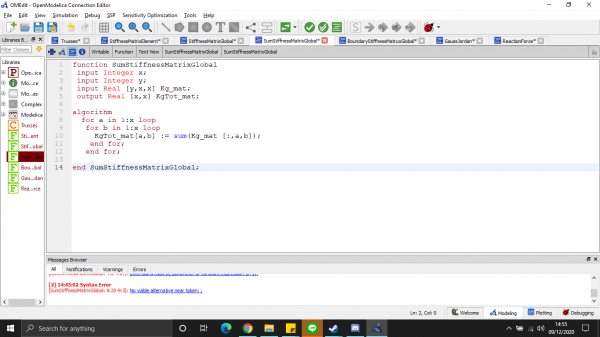
- Total matriks kekauan global
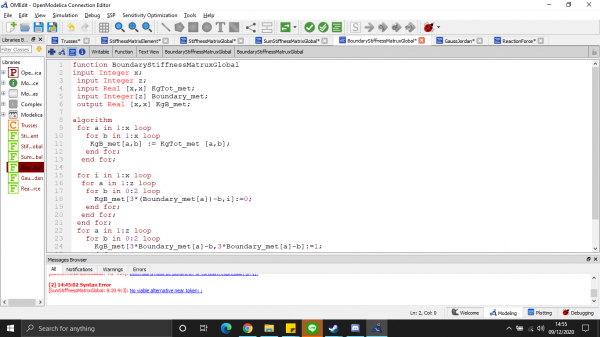
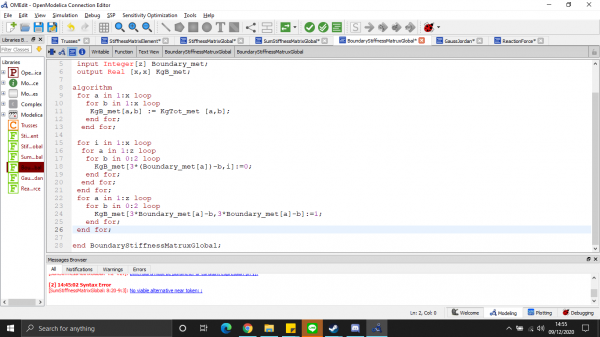
- kondisi impelemntasi boundary
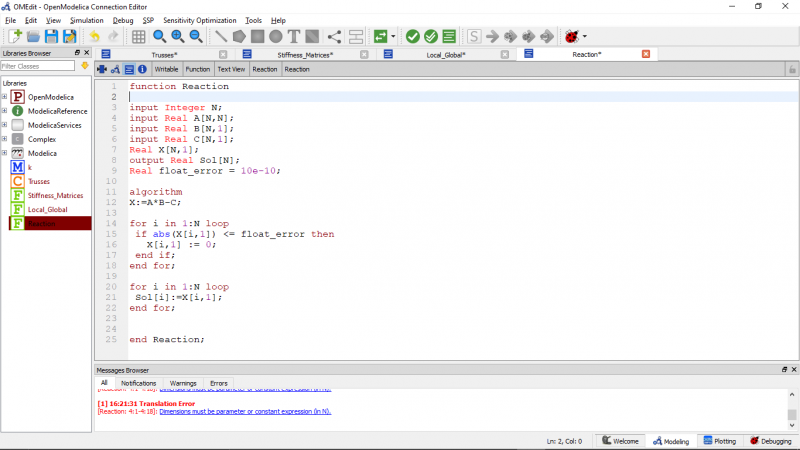
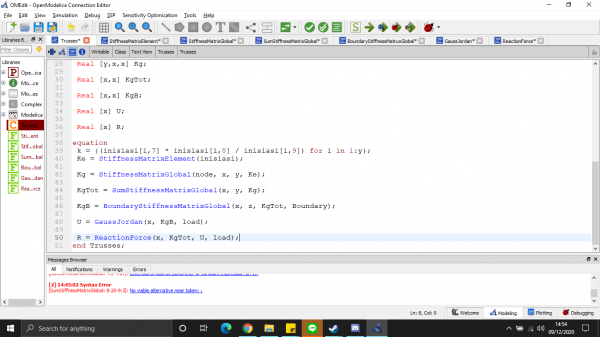
- Gauss jordan
- gaya reaksi
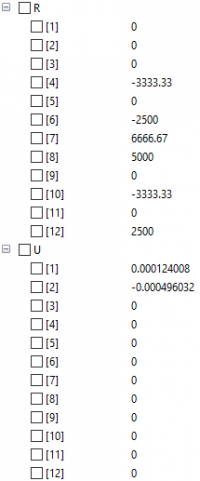
Hasil yang didapat
Minggu ke-6 (Rabu, 16 Desember 2020)
"Aplikasi Metode Numerik dalam Kasus Optimasi"
Dalam minggu ini, kami diajarkan bagaimana cara menggunakan metode Bracket oleh Bu Candra. Fungsi dari metode ini bisa untuk optimasi. Detilnya, kami belajar tentang one dimentional unconstrained optimization. Sembari Bu Candra mengajarkan Bracket, kami juga ikut mencoba cara membuat metode Bracket di Open Modellica mengikuti Bu Candra. Berikut hasil dari metode bracket untuk optimasi yang saya lakukan:
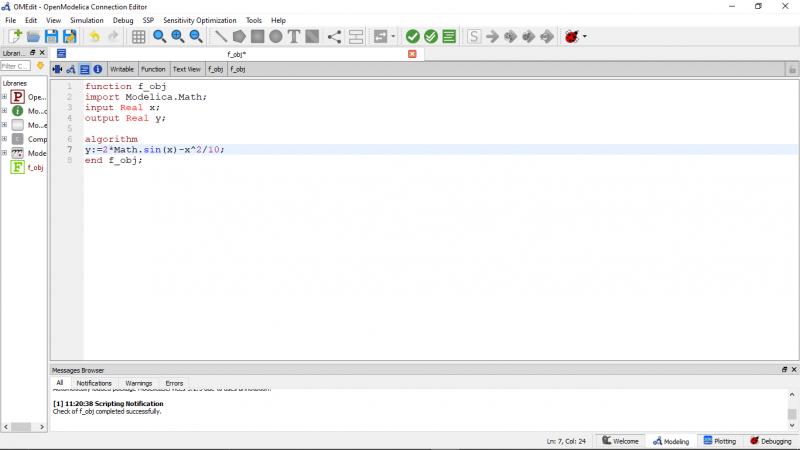
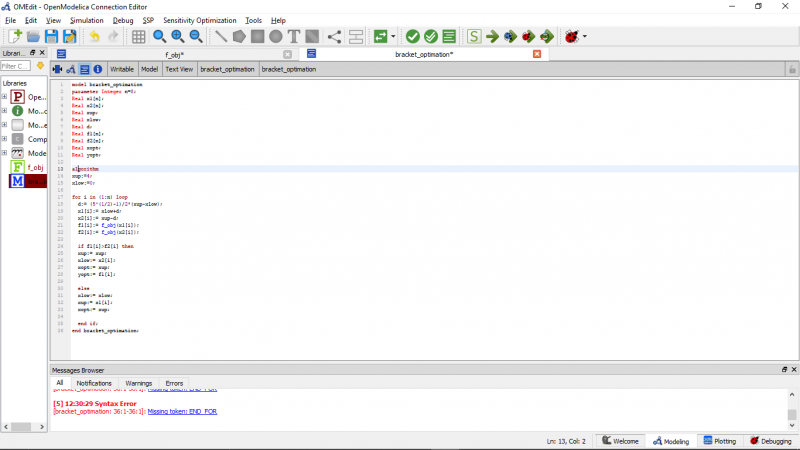
- untuk fungsinya
- untuk modelnya
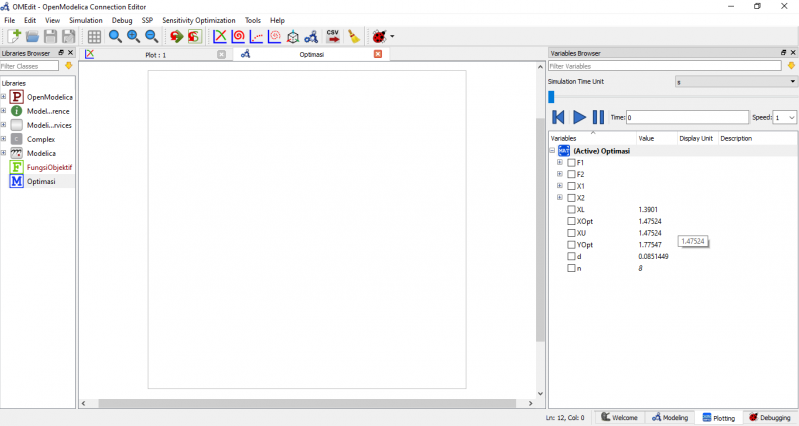
- untuk hasilnya
Tugas Besar
Pendahuluan
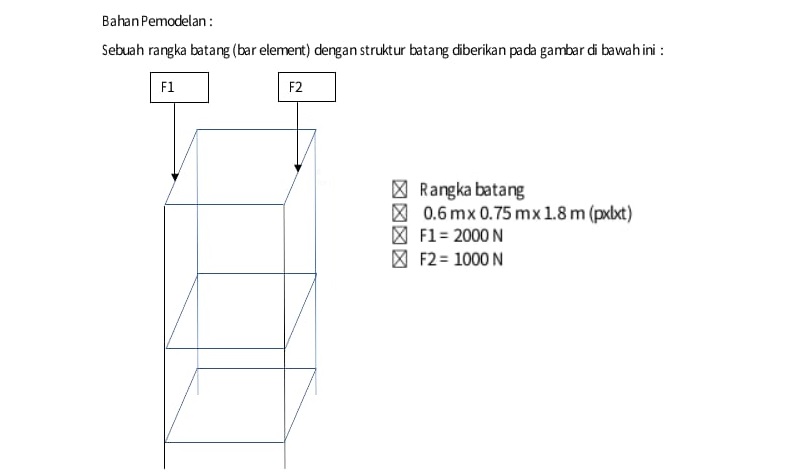
Kami diberikan tugas besar untuk melakukan optimasi dalam pemilihan bahan material dan luas penampang trusses yang akan digunakan untuk membuat konstruksi. Desain yang akan kami gunakan adalah sebagai berikut:
Alur Pengerjaan
Alur pengerjaan dibuat untuk mengurutkan prioritas pekerjaan yang harus dikerjakan. Berikut urutan pengerjaan tugas besar ini,
Mendifinisikan Permasalahan
- Jenis Material adalah besi siku;
- Mencari optimasi dari material yang digunakan dengan optimasi elastisitas dan optimasi luas penampang;
- Dimensi struktur adalah (p x l x t) = 0,6 m x 0,75 m x 1,8 m;
- Terdapat dua gaya yang memberikan stress sebesar F1 = 2000 N dan F2 = 1000 N.
Asumsi
Dalam permaslahan ini, tidak semua data yang dibutuhkan tersedia dan diketahui di soal. Maka, penulis membuat beberapa asumsi yaitu:
- Struktur paling bawah dianggap sebagai lantai rata dengan tanah karena tidak diketahui tinggi lantai di atas tanah (Δh = 0)
- Safety factor adalah 2
- Beban terdistribusi dengan node karena bersifat trusses
- Batas displacement adalah 0,001 m sebelum buckling pada trusses paling atas
- Ketinggian trusses dianggap sama per lantai yaitu 0,6 m.
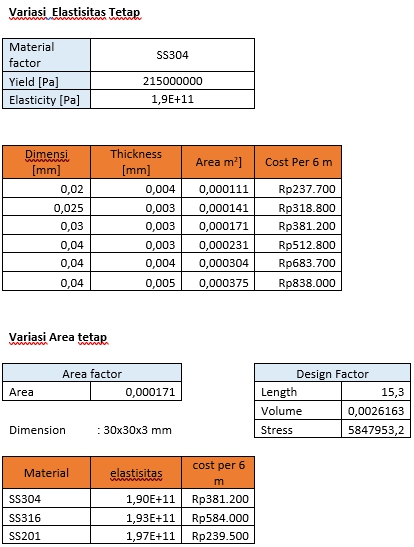
Data Material
Model Numerik
- Untuk perhitungan displacement, reaction force, stress, dan safety factor:
model Trusses_3D_Tugas_Besar_Safety
//define initial variable
parameter Integer Points=size(P,1); //Number of Points
parameter Integer Trusses=size(C,1); //Number of Trusses
parameter Real Yield=215e6; //Yield Strength (Pa)
parameter Real Area=0.000224; //Area L Profile (Dimension=0.03, Thickness=0,004) (m2)
parameter Real Elas=193e9; //Elasticity SS 304 (Pa)
//define connection
parameter Integer C[:,2]=[1,5;
2,6;
3,7;
4,8;
5,6; //1st floor
6,7; //1st floor
7,8; //1st floor
5,8; //1st floor
5,9;
6,10;
7,11;
8,12;
9,10; //2nd floor
10,11;//2nd floor
11,12;//2nd floor
9,12; //2nd floor
9,13;
10,14;
11,15;
12,16;
13,14;//3rd floor
14,15;//3rd floor
15,16;//3rd floor
13,16];//3rd floor
//define coordinates (please put orderly)
parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1
-0.3,-0.375,0,1,1,1; //2
-0.3,0.375,0,1,1,1; //3
0.3,0.375,0,1,1,1; //4
0.3,-0.375,0.6,0,0,0; //5
-0.3,-0.375,0.6,0,0,0; //6
-0.3,0.375,0.6,0,0,0; //7
0.3,0.375,0.6,0,0,0; //8
0.3,-0.375,1.2,0,0,0; //9
-0.3,-0.375,1.2,0,0,0; //10
-0.3,0.375,1.2,0,0,0; //11
0.3,0.375,1.2,0,0,0; //12
0.3,-0.375,1.8,0,0,0; //13
-0.3,-0.375,1.8,0,0,0; //14
-0.3,0.375,1.8,0,0,0; //15
0.3,0.375,1.8,0,0,0]; //16
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-500,
0,0,-1000,
0,0,-1000,
0,0,-500};
//solution
Real displacement[N], reaction[N];
Real check[3];
Real stress1[Trusses];
Real safety[Trusses];
Real dis[3];
Real Str[3];
protected
parameter Integer N=3*Points;
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
Real err=10e-10, ers=10e-4;
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary
for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for;
//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction
reaction:=(G_star*displacement)-F;
//Eliminating float error
for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor
for i in 1:Trusses loop
if stress1[i]>0 then
safety[i]:=Yield/stress1[i];
else
safety[i]:=0;
end if;
end for;
end Trusses_3D_Tugas_Besar_Safety;
- Untuk membuat kurva curve fitting:
function Curve_Fitting input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coe[order+1]; protected Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1]; algorithm for i in 1:size(X,1) loop for j in 1:(order+1) loop Z[i,j]:=X[i]^(order+1-j); end for; end for; ZTr:=transpose(Z); A:=ZTr*Z; B:=ZTr*Y; Coe:=Modelica.Math.Matrices.solve(A,B); end Curve_Fitting;
- Untuk golden section:
model Opt_Gold
parameter Real xd[:];
parameter Real yd[size(xd,1)];
parameter Real xlo=87e-6;
parameter Real xhi=504e-6;
parameter Integer N=10; // maximum iteration
parameter Real es=0.0001; // maximum error
Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3];
Real xopt, fx;
protected
Real d, xl, xu, xint, R=(5^(1/2)-1)/2;
algorithm
xl := xlo;
xu := xhi;
y := Curve_Fitting(xd,yd);
for i in 1:N loop
d:= R*(xu-xl);
x1[i]:=xl+d;
x2[i]:=xu-d;
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
xint:=xu-xl;
if f1[i]>f2[i] then
xl:=x2[i];
xopt:=x1[i];
fx:=f1[i];
else
xu:=x1[i];
xopt:=x2[i];
fx:=f2[i];
end if;
ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
break;
end if;
end for;
end Opt_Gold;
Hasil Perhitungan
Koefisien yang didapat dari data harga variasi area dan variasi material adalah sebagai berikut (coef untuk variasi area dan coef 2-4 untuk variasi material)
Kemudian, coefisien tersebut digunakan untuk mendapatkan variasi yang tidak tersedia dari sumber
Jawaban UAS