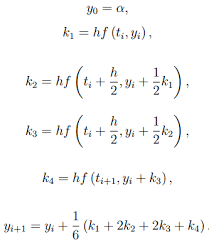Difference between revisions of "Abraham Theodorus"

From ccitonlinewiki
Jump to: navigation, search
(→‎Artificial Neural Network)
 
(30 intermediate revisions by the same user not shown)
Line 11: Line 11:
  
  
−
== '''Kelas 1''' ==
+
== '''Deret Taylor''' ==
  
 
Tanggal : 3 September 2019
 
Tanggal : 3 September 2019
Line 25: Line 25:
 
Kami pun ditugaskan untuk mencoba mencari hasil dari sebuah fungsi menggunakan deret Taylor dalam Microsoft Excel. Kami harus mencari nilai sinus dari π/7. Dengan menggunakan rumus tersebut dapat didapatkan sebuah pola, yaitu -x^2/2n(2n+1). Pola ini dapat dimasukkan kedalam sistem equation dalam Excel dan nilai sinus dari π/7 pun dapat ditemukan.
 
Kami pun ditugaskan untuk mencoba mencari hasil dari sebuah fungsi menggunakan deret Taylor dalam Microsoft Excel. Kami harus mencari nilai sinus dari π/7. Dengan menggunakan rumus tersebut dapat didapatkan sebuah pola, yaitu -x^2/2n(2n+1). Pola ini dapat dimasukkan kedalam sistem equation dalam Excel dan nilai sinus dari π/7 pun dapat ditemukan.
  
−
== '''Kelas 2''' ==
+
== '''Pseudocoding''' ==
  
 
Tanggal : 10 September 2019
 
Tanggal : 10 September 2019
Line 89: Line 89:
 
Adapun bahasa - bahasa pemrograman yang kami bahas diantara lain adalah C++, Phyton, dan Java.
 
Adapun bahasa - bahasa pemrograman yang kami bahas diantara lain adalah C++, Phyton, dan Java.
  
−
== '''Kelas 3''' ==
+
== '''Turunan Numerik''' ==
  
 
Tanggal : 17 September 2019
 
Tanggal : 17 September 2019
Line 101: Line 101:
 
Persoalan Turunan Numerik adalah menentukan nilai hampiran nilai turunan fungsi f. Meskipun metode numerik untuk menghitung turunan fungsi tersedia, tetapi perhitungan turunan sedapat mungkin dihindari. Alasannya, nilai turunan numerik umumnya kurang teliti dibandingkan dengan nilai fungsinya. Dalam kenyataannya, turunan adalah limit dari hasil bagi selisih: yaitu pengurangan dua buah nilai yang besar (fx+h) - fx) ) dan membaginya dengan bilangan yang kecil (h). Pembagian ini dapat menghasilkan turunan dengan galat yang besar.
 
Persoalan Turunan Numerik adalah menentukan nilai hampiran nilai turunan fungsi f. Meskipun metode numerik untuk menghitung turunan fungsi tersedia, tetapi perhitungan turunan sedapat mungkin dihindari. Alasannya, nilai turunan numerik umumnya kurang teliti dibandingkan dengan nilai fungsinya. Dalam kenyataannya, turunan adalah limit dari hasil bagi selisih: yaitu pengurangan dua buah nilai yang besar (fx+h) - fx) ) dan membaginya dengan bilangan yang kecil (h). Pembagian ini dapat menghasilkan turunan dengan galat yang besar.
  
−
== '''Kelas 4''' ==
+
== '''Metode Secant, Bisect, dan Newton-Raphson''' ==
  
 
Tanggal : 24 September 2019
 
Tanggal : 24 September 2019
  
−
Pengajar : Dr. Ir. engkos Achmad Kosasih, M.T.
+
Pengajar : Dr. Ir. Engkos Achmad Kosasih, M.T.
  
  
Line 122: Line 122:
 
Metode Newton-Raphson adalah metode pencarian akar suatu fungsi f(x) dengan pendekatan satu titik, dimana fungsi f(x mempunyai turunan. Metode ini dianggap lebih mudah dari Metode Bagi-Dua (Bisection Method) karena metode ini menggunakan pendekatan satu titik sebagai titik awal. Semakin dekat titik awal yang kita pilih dengan akar sebenarnya, maka semakin cepat konvergen ke akarnya.
 
Metode Newton-Raphson adalah metode pencarian akar suatu fungsi f(x) dengan pendekatan satu titik, dimana fungsi f(x mempunyai turunan. Metode ini dianggap lebih mudah dari Metode Bagi-Dua (Bisection Method) karena metode ini menggunakan pendekatan satu titik sebagai titik awal. Semakin dekat titik awal yang kita pilih dengan akar sebenarnya, maka semakin cepat konvergen ke akarnya.
  
−
== '''Kelas 5''' ==
+
== '''Error''' ==
  
 
Tanggal : 1 Oktober 2019
 
Tanggal : 1 Oktober 2019
Line 144: Line 144:
  
  
−
== '''Tugas 1''' ==
+
== '''Pengenalan Phyton''' ==
 +
 
 +
Tanggal : 29 Oktober 2019
  
 
Pengajar : Dr. Ir. Ahmad Indra Siswantara
 
Pengajar : Dr. Ir. Ahmad Indra Siswantara
  
−
Pada pertemuan kali ini, Pak Dai memberi kami tugas kelompok untuk membuat Governing Equation dari sebuah mobil yang bergerak
+
 
 +
Pada pertemuan kali ini, kami membahas bahasa pemrograman Phyton.
 +
 
 +
 
 +
Pyhton merupakan salah satu bahasa pemrograman dalam metode numerik. Beberapa hal diterangkan pada pertemuan ini, baik bahasa-bahasa tertentu, penulisan hingga praktik secara langsung menggunakan aplikasi yang ada. Python sendiri adalah salah satu metode agar manusia dapat berkomunikasi dengan komputer serta tentunya mempermudah pekerjaan manusia. Terdapat beberapa perintah mudah yang diterapkan pada kelas hari ini. Seperti penjumlahan angka dan kata-kata. Contohnya sebagai berikut:
 +
 
 +
>>>a = 50
 +
 
 +
>>>b = 25
 +
 
 +
>>>a+b
 +
 
 +
75
 +
 
 +
 
 +
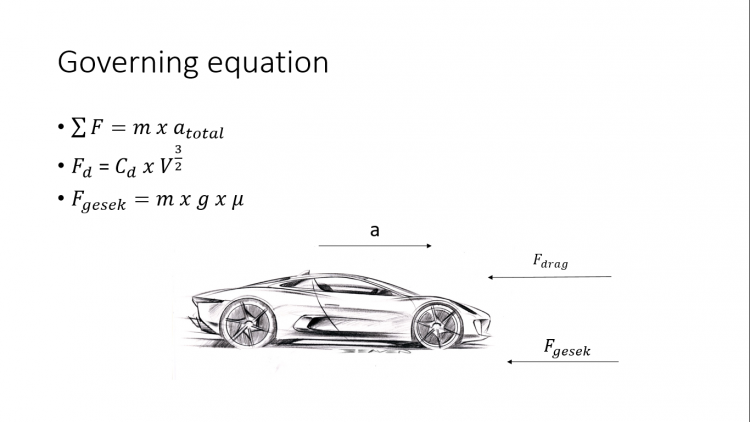
Kelas diakhiri dengan pemberian tugas kelompok yang akan diselesaikan pada pertemuan selanjutnya dalam bentuk video. Tugas yang diberikan adalah membuat Governing Equation yang dapat mengukur top speed dari sebuah kendaraan.
 +
 
 +
 
 +
[[file:Mobilmobil.png|750px]] 
 +
 
 +
[[file:Mobil1mobil.png|750px]]
 +
 
 +
[[file:Mobil2mobil.png|750px]]
 +
 
 +
 
 +
Berikut adalah video tugas kelompok saya:
  
  
−
Kelompok kami:
+
[[file:dimastugas.mp4|600px]]
  
−
1. Abraham Theodorus
+
== '''Metode Runge-Kutta''' ==
  
−
2. Dimas Fahrul Rozi
+
Tanggal : 5 November 2019
  
−
3. Muhammad Ichsan
+
Pengajar : Dr. Ir. Ahmad indra Siswantara
  
  
−
Berikut ini adalah Governing Equation dari mobil yang bergerak:
+
Pada pertemuan kali ini, kami membahas metode Runge-Kutta.
  
−
[[File:Mobilmobil.png]]
+
[[File:rungekutta.png|350px]]
−
[[File:Mobil1mobil.png]]
 
−
[[File:Mobil2mobil.png]]
 
  
−
Pseudocoding dengan memasukkan nilai variabel yang diperlukan:
 
  
−
g= float(9.8) #gravitational_acceleration
+
Metode Runge-Kutta adalah sebuah metode penyelesaian persamaan diferensial dengan pendekatan iterasi numerik. Tidak seperti deret Taylor, metode ini tidak membutuhkan perhitungan dengan turunan. Metode ini bertujuan untuk mencapai derajat ketelitian yang lebih tinggi.
−
cd=eval(input("drag coefficient: "))
 
−
myu= float(input("koefisien gesek dinamis: "))
 
−
v0=eval(input("initial velocity (m/s): "))
 
−
m=eval(input("mass (kg): "))
 
−
a=eval(input("acceleration (m/s^2): "))
 
−
vt=eval(input("top speed (m/s): "))
 
−
semua dibagi m
 
−
fgesek=g*myu
 
−
fdrag=(cd*vt**(3/2))/m
 
−
ft=a
 
−
atot=ft-fdrag-fgesek
 
−
t=(vt-v0)/atot
 
−
print("waktu mobil untuk mencapai top speed: ",t, "detik")
 
  
−
==='''Kelas 1'''===
+
== '''Artificial Neural Network''' ==
  
−
Tanggal : 29 Oktober 2019
+
Tanggal : 3 Desember 2019
  
 
Pengajar : Dr. Ir. Ahmad Indra Siswantara
 
Pengajar : Dr. Ir. Ahmad Indra Siswantara
  
  
−
Pada pertemuan kali ini, kami membahas bahasa pemrograman Phyton dan metode Runge-Kutta.
+
Pada pertemuan kali ini, kami membahas Artificial Neural Network.
 +
 
 +
 
 +
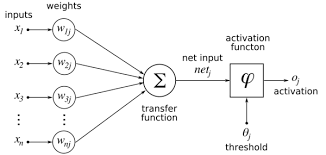
Artificial Neural Network (ANN) atau Jaringan Saraf Tiruan (JST) adalah sebuah alat pemodelan data statistik non-linier. JST dapat digunakan untuk memodelkan hubungan yang kompleks antara input dan output untuk menemukan pola-pola pada data. Menurut suatu teorema yang disebut "teorema penaksiran universal", JST dengan minimal sebuah lapis tersembunyi dengan fungsi aktivasi non-linear dapat memodelkan seluruh fungsi terukur Boreal apapun dari suatu dimensi ke dimensi lainnya.
 +
 
 +
[[File:artifneurnet1.png|350px]]  [[File:artifneurnet2.png|350px]]
 +
 
 +
 
 +
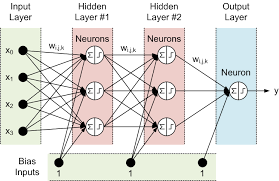
Secara umum, lapisan pada ANN dibagi menjadi 3 bagian:
 +
 
 +
''Input Layer'' terdiri dari neuron yang menerima data masukan dari variabel X. Semua neuron pada lapis ini dapat terhubung ke neuron pada lapisan tersembunyi atau
 +
langsung ke lapisan luaran jika jaringan tidak menggunakan lapisan tersembunyi.
 +
 
 +
''Hidden Layer'' terdiri dari neuron yang menerima data dari lapisan masukan.
 +
 
 +
''Output Layer'' terdiri dari neuron yang menerima data dari lapisan tersembunyi atau langsung dari lapisan masukan yang nilai luarannya melambangkan hasil kalkulasi dari
 +
X menjadi nilai Y.
 +
 
 +
 
 +
Berikut adalah langkah - langkah yang diperlukan untuk membangun ANN:
 +
 
 +
a. Data Preprocessing.
  
 +
b. Menambahkan Input Layer.
  
−
'''Pengenalan Phyton'''
+
c. Randomisasi dengan Init.
  
−
Python adalah bahasa pemrograman interpretatif multiguna[9] dengan filosofi perancangan yang berfokus pada tingkat keterbacaan kode.[10] Python diklaim sebagai bahasa yang menggabungkan kapabilitas, kemampuan, dengan sintaksis kode yang sangat jelas,[11] dan dilengkapi dengan fungsionalitas pustaka standar yang besar serta komprehensif. Python juga didukung oleh komunitas yang besar.
+
d. Menambahkan Hidden Layers.
  
−
Python mendukung multi paradigma pemrograman, utamanya; namun tidak dibatasi; pada pemrograman berorientasi objek, pemrograman imperatif, dan pemrograman fungsional. Salah satu fitur yang tersedia pada python adalah sebagai bahasa pemrograman dinamis yang dilengkapi dengan manajemen memori otomatis. Seperti halnya pada bahasa pemrograman dinamis lainnya, python umumnya digunakan sebagai bahasa skrip meski pada praktiknya penggunaan bahasa ini lebih luas mencakup konteks pemanfaatan yang umumnya tidak dilakukan dengan menggunakan bahasa skrip. Python dapat digunakan untuk berbagai keperluan pengembangan perangkat lunak dan dapat berjalan di berbagai platform sistem operasi.
+
e. Memilih Optimizer, Loss, dan Performance Metrics.
  
 +
f. Meng-''compile'' model.
  
−
'''Metode Runge-Kutta'''
+
g. Menggunakan model.fit untuk melatih model.
  
−
Persamaan Diferensial Biasa (PDB) adalah persamaan yang melibatkan satu atau lebih turunan fungsi satu peubah. Solusi dari PDB adalah fungsi tertentu yang memenuhi persamaan.
+
h. Mengevaluasi model.
−
 
−
Penyelesaian PDB dengan metode deret Taylor tidak praktis karena metode tersebut membutuhkan perhitungan turunan f(x, y). Lagipula, tidak semua fungsi mudah dihitung turunannya, terutama bagi fungsi yang bentuknya rumit. Semakin tinggi orde metode deret Taylor, semakin tinggi turunan fungsi yang harus dihitung. Karena pertimbangan ini, metode deret Taylor yang berorde tinggi pun tidak dapat dapat diterima dalam masalah praktek.
 
  
−
Metode Runge-Kutta adalah alternatif lain dari metode deret Taylor yang tidak membutuhkan perhitungan turunan. Metode ini berusaha mendapatkan derajat ketelitian yang lebih tinggi, dan sekaligus menghindarkan keperluan mencari turunan yang lebih tinggi dengan jalan mengevaluasi fungsi f(x, y) pada titik terpilih dalam setiap selang langkah [CON80]. Metode Runge-Kutta adalah metode PDB yang paling popuper karena banyak dipakai dalam praktek.
+
i. Mengatur parameter optimisasi jika dibutuhkan.

Latest revision as of 19:42, 26 December 2019

Profil

Nama  : Abraham Theodorus M

NPM  : 1706036103

Prodi  : Teknik Mesin


Pra-UTS

Deret Taylor

Tanggal : 3 September 2019

Pengajar: Dr. Ir. Ahmad Indra Siswantara dan Dr. Ir. Engkos Achmad Kosasih, M.T.


Pada kali ini pak Engkos mengajarkan kelas tentang deret Taylor dan pengaplikasiannya, lebih spesifik lagi pengaplikasiannya dalam Microsoft Excel. Deret Taylor dalam matematika adalah representasi fungsi matematika sebagai jumlahan tak hingga dari suku-suku yang nilainya dihitung dari turunan fungsi tersebut di suatu titik. Deret ini dapat dianggap sebagai limit polinomial Taylor. Deret Taylor mendapat nama dari matematikawan Inggris, Brook Taylor. Bila deret tersebut terpusat di titik nol, deret tersebut dinamakan sebagai deret Maclaurin, dari nama matematikawan Skotlandia, Colin Maclaurin.

Download.png

Kami pun ditugaskan untuk mencoba mencari hasil dari sebuah fungsi menggunakan deret Taylor dalam Microsoft Excel. Kami harus mencari nilai sinus dari π/7. Dengan menggunakan rumus tersebut dapat didapatkan sebuah pola, yaitu -x^2/2n(2n+1). Pola ini dapat dimasukkan kedalam sistem equation dalam Excel dan nilai sinus dari π/7 pun dapat ditemukan.

Pseudocoding

Tanggal : 10 September 2019

Pengajar : Dr. Ir. Engkos Achmad Kosasih, M.T.


Pada pertemuan kali ini kami membahas topik Pseudocoding.


Pseudocoding adalah penulisan algoritma yang hampir menyerupai Bahasa Pemrograman, namun Pseudocode ditulis lebih sederhana dengan menggunakan bahasa baku yang mudah dipahami oleh manusia.

Tujuan menggunakan Pseudocode dalam mendeskripsikan suatu algoritma supaya programer dapat memahami suatu kerangka awal (ide) suatu program dengan jelas, meskipun programmer tersebut belum bisa memahami bahasa pemrograman yang akan digunakan.

Kami pun ditugaskan untuk membuat pseudocode untuk fungsi sinus, kosinus, dan eksponensial, yang adalah sebagai berikut:


Fungsi Sinus:

i=1, err=1; suku=x sin=suku while err>1e-7

ratio=-(x^2)/(2*i)/(2*i+1)

suku=suku*ratio

err=abs(suku/sin)

sin=sin+suku

i=i+1


Fungsi Kosinus:

i=1, err=1; suku=1 cos=suku while err>1e-7

ratio=-(x^2)/(2*i)/(2*i-1)

suku=suku*ratio

err=abs(suku/cos)

cos=cos+suku

i=i+1

Fungsi Eksponensial:

i=1, err=1; suku=1 exp=suku while err>1e-7

ratio=(x^2)/i

suku=suku*ratio

err=abs(suku/exp)

exp=exp+suku

i=i+1

Setelah itu, kami pun membahas bahasa pemrograman dan jenis - jenisnya. Bahasa pemrograman, atau sering diistilahkan juga dengan bahasa komputer atau bahasa pemrograman komputer, adalah instruksi standar untuk memerintah komputer. Bahasa pemrograman ini merupakan suatu himpunan dari aturan sintaks dan semantik yang dipakai untuk mendefinisikan program komputer.

Adapun bahasa - bahasa pemrograman yang kami bahas diantara lain adalah C++, Phyton, dan Java.

Turunan Numerik

Tanggal : 17 September 2019

Pengajar : Dr. Ir. Engkos Achmad Kosasih, M.T.


Pada pertemuan kali ini kami membahas Turunan Numerik.


Persoalan Turunan Numerik adalah menentukan nilai hampiran nilai turunan fungsi f. Meskipun metode numerik untuk menghitung turunan fungsi tersedia, tetapi perhitungan turunan sedapat mungkin dihindari. Alasannya, nilai turunan numerik umumnya kurang teliti dibandingkan dengan nilai fungsinya. Dalam kenyataannya, turunan adalah limit dari hasil bagi selisih: yaitu pengurangan dua buah nilai yang besar (fx+h) - fx) ) dan membaginya dengan bilangan yang kecil (h). Pembagian ini dapat menghasilkan turunan dengan galat yang besar.

Metode Secant, Bisect, dan Newton-Raphson

Tanggal : 24 September 2019

Pengajar : Dr. Ir. Engkos Achmad Kosasih, M.T.


Pada pertemuan kali ini, kami membahas tiga topik, yaitu Secant Method, Bisect Method, dan Newton-Raphson Method.


Metode Secant merupakan perbaikan dari metode regula-falsi dan newton raphson dimana kemiringan dua titik dinyatakan sacara diskrit, dengan mengambil bentuk garis lurus yang melalui satu titik.

Tujuan metode Secant adalah untuk menyelesaikan masalah yang terdapat pada metode Newton-Raphson yang terkadang sulit mendapatkan turunan pertama yaitu f‘ (x). Fungsi metode Secant adalah untuk menaksirkan akar dengan menggunakan diferensi daripada turunan untuk memperkirakan kemiringan/slope.


Metode Bagi-Dua (Bisect) adalah algoritma pencarian akar pada sebuah interval. Interval tersebut membagi dua bagian, lalu memilih dari dua bagian ini dipilih bagian mana yang mengandung akar dan bagian yang tidak mengandung akar dibuang. Hal ini dilakukan berulang-ulang hingga diperoleh akar persamaan atau mendekati akar persamaan. Metode ini berlaku ketika ingin memecahkan persamaan f(x)=0 dengan f(x) merupakan fungsi kontinyu.


Metode Newton-Raphson adalah metode pencarian akar suatu fungsi f(x) dengan pendekatan satu titik, dimana fungsi f(x mempunyai turunan. Metode ini dianggap lebih mudah dari Metode Bagi-Dua (Bisection Method) karena metode ini menggunakan pendekatan satu titik sebagai titik awal. Semakin dekat titik awal yang kita pilih dengan akar sebenarnya, maka semakin cepat konvergen ke akarnya.

Error

Tanggal : 1 Oktober 2019

Pengajar : Dr. Ir. Engkos Achmad Kosasih, M.T


Pada pertemuan kali ini, kami membahas berbagai macam sumber kesalahan/Error dalam metode numerik.


Perlu disadari bahwa komputasi numerik adalah komputasi pendekatan (approksimasi) untuk menyelesaikan suatu persoalan, dengan demikian maka hasilnya mengandung “kesalahan” (error).

Beberapa sumber kesalahan adalah:

Round-off errors : kesalahan yang timbul akibat adanya pembulatan angka. Truncation errors : kesalahan yang timbul karena pemotongan suku pada suatu deret / rumus approksimasi, misalnya suatu rumus rumit diganti dengan rumus yang lebih sederhana. Range errors : kesalahan yang terjadi karena nilai hasil komputasi melampaui batas angka yang diperbolehkan oleh komputer, misalnya sangat kecil atau sangat besar.


Pasca UTS

Pengenalan Phyton

Tanggal : 29 Oktober 2019

Pengajar : Dr. Ir. Ahmad Indra Siswantara


Pada pertemuan kali ini, kami membahas bahasa pemrograman Phyton.


Pyhton merupakan salah satu bahasa pemrograman dalam metode numerik. Beberapa hal diterangkan pada pertemuan ini, baik bahasa-bahasa tertentu, penulisan hingga praktik secara langsung menggunakan aplikasi yang ada. Python sendiri adalah salah satu metode agar manusia dapat berkomunikasi dengan komputer serta tentunya mempermudah pekerjaan manusia. Terdapat beberapa perintah mudah yang diterapkan pada kelas hari ini. Seperti penjumlahan angka dan kata-kata. Contohnya sebagai berikut:

>>>a = 50

>>>b = 25

>>>a+b

75


Kelas diakhiri dengan pemberian tugas kelompok yang akan diselesaikan pada pertemuan selanjutnya dalam bentuk video. Tugas yang diberikan adalah membuat Governing Equation yang dapat mengukur top speed dari sebuah kendaraan.


Mobilmobil.png

Mobil1mobil.png

Mobil2mobil.png


Berikut adalah video tugas kelompok saya:


Metode Runge-Kutta

Tanggal : 5 November 2019

Pengajar : Dr. Ir. Ahmad indra Siswantara


Pada pertemuan kali ini, kami membahas metode Runge-Kutta.

Rungekutta.png


Metode Runge-Kutta adalah sebuah metode penyelesaian persamaan diferensial dengan pendekatan iterasi numerik. Tidak seperti deret Taylor, metode ini tidak membutuhkan perhitungan dengan turunan. Metode ini bertujuan untuk mencapai derajat ketelitian yang lebih tinggi.

Artificial Neural Network

Tanggal : 3 Desember 2019

Pengajar : Dr. Ir. Ahmad Indra Siswantara


Pada pertemuan kali ini, kami membahas Artificial Neural Network.


Artificial Neural Network (ANN) atau Jaringan Saraf Tiruan (JST) adalah sebuah alat pemodelan data statistik non-linier. JST dapat digunakan untuk memodelkan hubungan yang kompleks antara input dan output untuk menemukan pola-pola pada data. Menurut suatu teorema yang disebut "teorema penaksiran universal", JST dengan minimal sebuah lapis tersembunyi dengan fungsi aktivasi non-linear dapat memodelkan seluruh fungsi terukur Boreal apapun dari suatu dimensi ke dimensi lainnya.

Artifneurnet1.png Artifneurnet2.png


Secara umum, lapisan pada ANN dibagi menjadi 3 bagian:

Input Layer terdiri dari neuron yang menerima data masukan dari variabel X. Semua neuron pada lapis ini dapat terhubung ke neuron pada lapisan tersembunyi atau langsung ke lapisan luaran jika jaringan tidak menggunakan lapisan tersembunyi.

Hidden Layer terdiri dari neuron yang menerima data dari lapisan masukan.

Output Layer terdiri dari neuron yang menerima data dari lapisan tersembunyi atau langsung dari lapisan masukan yang nilai luarannya melambangkan hasil kalkulasi dari X menjadi nilai Y.


Berikut adalah langkah - langkah yang diperlukan untuk membangun ANN:

a. Data Preprocessing.

b. Menambahkan Input Layer.

c. Randomisasi dengan Init.

d. Menambahkan Hidden Layers.

e. Memilih Optimizer, Loss, dan Performance Metrics.

f. Meng-compile model.

g. Menggunakan model.fit untuk melatih model.

h. Mengevaluasi model.

i. Mengatur parameter optimisasi jika dibutuhkan.

Retrieved from "http://air.eng.ui.ac.id/index.php?title=Abraham_Theodorus&oldid=18687"