Difference between revisions of "Muhammad Luqman Sugiyono"
(→Pertemuan pada 30 Oktober 2019) |
|||
| (2 intermediate revisions by the same user not shown) | |||
| Line 297: | Line 297: | ||
[[File:luqman30oktobermetnum.jpg|400px|center]] | [[File:luqman30oktobermetnum.jpg|400px|center]] | ||
| + | dengan kode sebagai berikut: | ||
| + | t = eval(input("pada saat t berapa: ")) | ||
| + | h = 1 # dtnya | ||
| + | t0 = 0.1 | ||
| + | y0 = 0 # disemprotkan dari darat denga ketinggian 0 | ||
| + | def F(t0, y0): | ||
| + | return ((y0 + 5*t*t)/t) | ||
| + | # Finds value of y for a given x using step size h | ||
| + | def rungeKutta(t0, y0, t, h): | ||
| + | # Count number of iterations using step size or | ||
| + | # step height h | ||
| + | n = (int)((t - t0) / h) | ||
| + | # mendefinisikan y= y0 | ||
| + | y = y0 | ||
| + | for i in range(1, n + 1): | ||
| + | "Apply Runge Kutta Formulas to find next value of y" | ||
| + | k1 = h * F(t0, y) | ||
| + | k2 = h * F(t0 + 0.5 * h, y + 0.5 * k1) | ||
| + | k3 = h * F(t0 + 0.5 * h, y + 0.5 * k2) | ||
| + | k4 = h * F(t0 + h, y + k3) | ||
| + | # Update next value of y | ||
| + | y = y + (1.0 / 6.0) * (k1 + 2 * k2 + 2 * k3 + k4) | ||
| + | # Update next value of t | ||
| + | t0 = t0 + h | ||
| + | return y | ||
| + | print('posisi air padaman pertama telah sampai pada ketinggian:', | ||
| + | rungeKutta(t0, y0, t, h)) | ||
| + | |||
| + | [[File:luqman30oktobermetnum2.jpg|800px|center]] | ||
Komentar dari teman-teman: | Komentar dari teman-teman: | ||
<comments voting="Plus" /> | <comments voting="Plus" /> | ||
Latest revision as of 15:07, 6 November 2019
Muhammad Luqman Sugiyono lahir di Bogor, pada 10 September 1999, merupakan seorang mahasiswa Teknik Mesin Universitas Indonesia angkatan tahun 2018. Luqman dibesarkan di Bogor. Luqman merupakan lulusan dari SMAN 3 Bogor. Saat ini, Luqman tinggal di Kos Pondok Bukit Pisang.
Contents
Pertemuan 1
Mengapa kita sebagai anak mesin perlu belajar kalkulus? Kalkulus merupakan ilmu hitung dasar. Sebagai anak mesin, kita akan banyak dihadapkan dengan masalah. Masalah ini dapat diselesaikan dengan hitungan matematis. Dalam perhitungan tersebut, dibutuhkan logika matematika (seperti permodelan, penyederhanaan, simulasi, dll) yang baik sehingga penyelesaian masalahnya tepat. Karena itulah, kita perlu belajar kalkulus.
Apa itu Python? Python merupakan salah satu bahasa pemograman yang ada di dunia ini. Python dikenal sebagai bahasa yang mudah dipelajari dan dipahami, karena struktur sintaksnya rapi. Bahasa ini sangat penting, seperti sebuah bahasa yang kita gunakan untuk berkomunikasi pada umumnya, dimana bahasa ini dapat dimengerti oleh manusia maupun komputer. Logika manusia perlu di-compile sehingga jadilah bahasa yang dimengerti oleh komputer. Bahasa Python ini kita gunakan ketika kita akan meminta bantuan komputer untuk menyelesaikan masalah kita.
Kita dapat menyelesaikan masalah dengan metode matematika. Terkadang kita mengerti logika penyelesaian masalah, namun kita tidak mampu menghitungnya karena perhitungan yang rumit. Disinilah hadir Python. Komputer tidak akan kesulitan untuk menghitung banyak hal dan bilangan, selama kita meminta tolong kepada komputer dengan bahasa yang dapat dimengerti komputer. Kita dapat memberi tahu komputer dengan menuliskan langkah-langkah pengerjaannya. US bisa memprediksi kapan badai akan datang hanya dengan meminta tolong komputer untuk menyelesaikan model matematika dengan model numeris. Komputer ini tidak mengerti ilmu kalkulus melainkan hanya mengerti tambah kurang kali dan bagi. Kitalah yang menyusun langkah-langkah pengerjaannya.
Flowchart dapat digunakan untuk membantu menyusun langkah-langkah sistematis. Flowchart juga dapat memudahkan pembacaan logika.
asas yang baik sebagai mahasiswa di UI:
hari ini harus lebih baik dari kemarin.
kalau hari ini lebih baik dari kemarin, maka berungtung. kalau hari ini sama dengan kemaren, ia merugi. kalau hari ini lebih buruk dari kemarin, ia adalah orang yg celaka
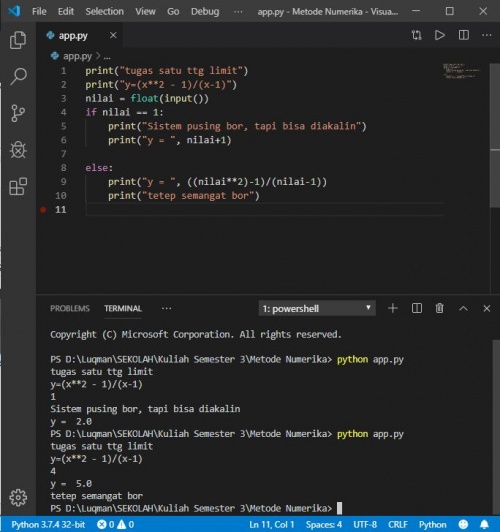
Berikut ini adalah hasil program yang telah saya uji coba:
Pertemuan 2
Saat ini sudah mulai memasuki revolusi industri 4.0, dimana semua orang sudah harus melek akan teknologi. Terlebih lagi, kita sebagai calon insinyur teknik mesin, harus memahami akan numerik. Kenapa demikian? Karena daya tampung otak kita tidak akan cukup menyimpan dan mengingat seluruh informasi yang tersedia saat ini. Kita butuh bantuan komputer. Komputer itu memang dirancang untuk menampung, mengingat, bahkan mengolah data-data informasi. Komputer sampai saat ini sudah berkempang sangat pesat, mulai dari software maupun hardware. Komputer zaman dahulu masih 32bit, namun yang sekarang sudah banyak beredar ialah versi 64bit, dimana besarnya bit ini merepresentasikan kecepatan dalam mengolah data.
Lalu kita diingatkan untuk selalu belajar dan belajar. Pak DAI menyampaikan, bahwa kalau kita semakin banyak mempelajari, maka kita akan semakin menunduk. Hal itu dikarenakan bahwa kita akan semakain sadar kalau ilmu yang kita miliki ini masih sangat sedikit. Intinya adalah tetap rendah hati. Kita yang hanya tahu sedikit ini jangan pernah sombong. Jangan juga melemah sehingga kita menjadi generasi yang idiot. Harus selalu semangat untuk membuka mata pada dunia. Jangan mau disetir oleh keadaan. Nah agar tidak mudah disetir, maka kita harus tahu akan ilmunya. Disinilah kesempatan besar untuk mempelajari metode numerik.
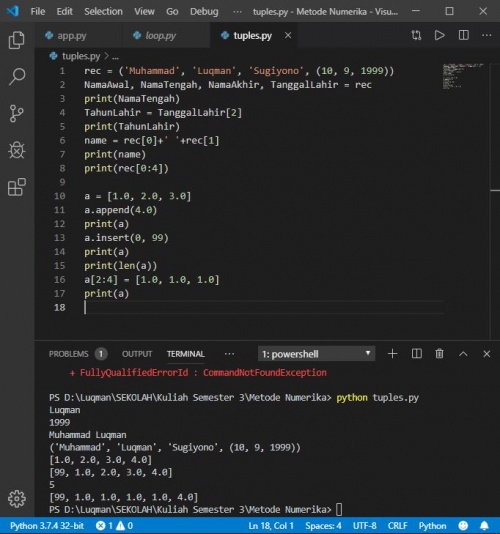
Berikut ini adalah hasil pembelajaran tentang tuples dan list:
Pertemuan 3
Pada pertemuan ketiga, kami ditantang untuk membuat sebuah program python yang mampu menjawab sebuah nilai di barisan fibonacci ke-n. Kira-kira seperti inilah program pyhton yang telah saya diskusikan bersama teman saya:
Pertemuan 4
Pada pertemuan keempat, kami ditantang untuk membuat sebuah program python yang mampu menjawab eliminasi Gauss dari sebuh matriks. Eliminasi Gauss adalah suatu cara mengoperasikan nilai-nilai di dalam matriks sehingga menjadi matriks yang lebih sederhana. Caranya adalah dengan melakukan operasi baris sehingga matriks tersebut menjadi matriks yang eselon-baris. Ini dapat digunakan sebagai salah satu metode penyelesaian persamaan linear dengan menggunakan matriks. Caranya dengan mengubah persamaan linear tersebut ke dalam matriks teraugmentasi dan mengoperasikannya. Setelah menjadi matriks Eselon-baris, lakukan substitusi balik untuk mendapatkan nilai dari variabel-variabel tersebut.
Eliminasi Gauss ini disempurnakan kembali dengan yang namanya Eliminasi Gauss Jordan. Dalam aljabar linear, eliminasi Gauss-Jordan adalah versi dari eliminasi Gauss. Pada metode eliminasi Gauss-Jordan kita membuat nol elemen-elemen di bawah maupun di atas diagonal utama suatu matriks. Hasilnya adalah matriks tereduksi yang berupa matriks diagonal satuan (semua elemen pada diagonal utama bernilai 1, elemen-elemen lainnya nol).
Berikut ini adalah kode program python yang telah saya pelajari:
from fractions import Fraction
def pprint(A):
n = len(A)
for i in range(0, n):
line = ""
for j in range(0, n+1):
line += str(A[i][j]) + "\t"
if j == n-1:
line += "| "
print(line)
print("")
# Performs and returns the gauss elimination
# @A : matrix
def gauss(A):
n = len(A)
for i in range(0, n):
# Search for maximum in this column
maxE1 = abs(A[i][i])
maxRow = i
for k in range(i+1, n):
# compares rows, first row can't start with zero
if abs(A[k][i]) < maxE1 or maxE1 == 0:
maxE1 = abs(A[k][i])
maxRow = k
# Swap maximum row with current row (column by column)
for k in range(i, n+1):
tmp = A[maxRow][k]
A[maxRow][k] = A[i][k]
A[i][k] = tmp
# Make all rows below this one 0 in current column
for k in range(i+1, n):
c = -A[k][i]/A[i][i]
for j in range(i, n+1):
if i == j:
A[k][j] = 0
else:
A[k][j] += c * A[i][j]
# Print echelon matrix
print("Echelon Matrix:\t")
pprint(A)
# Solve equation Ax = b for echelon matrix
x = [0 for i in range(n)]
for i in range(n - 1, -1, -1):
# there is no solution
if A[i][i] == 0:
return [0 for i in range(n)]
# normal solution
else:
x[i] = A[i][n]/A[i][i]
for k in range(i-1, -1, -1):
A[k][n] -= A[k][i]*x[i]
return x
# test code
print('Please input the number of variables:')
n = int(input())
# creates a matrix of zeros A = [[0 for j in range(n+1)] for i in range(n)]
# Read input data
print("Please enter each row separated by a new line:")
for i in range(0, n):
line = map(Fraction, input().split(" "))
for j, el in enumerate(line):
A[i][j] = el
print("Please enter the solution column with values separated by spaces:")
line = input().split(" ")
lastLine = list(map(Fraction, line))
for i in range(0, n):
A[i][n] = lastLine[i]
# Print input
print("\nMatrix:")
pprint(A)
# Calculate solution x = gauss(A)
# Print solution
print("Result:")
# check results
solution = False
for i in range(n):
if x[i] != 0:
solution = True
# a solution exists
if solution:
for i in range(len(x)):
print("x", i+1, " = ", x[i])
# a solution does not exist
else:
print("No Solution")
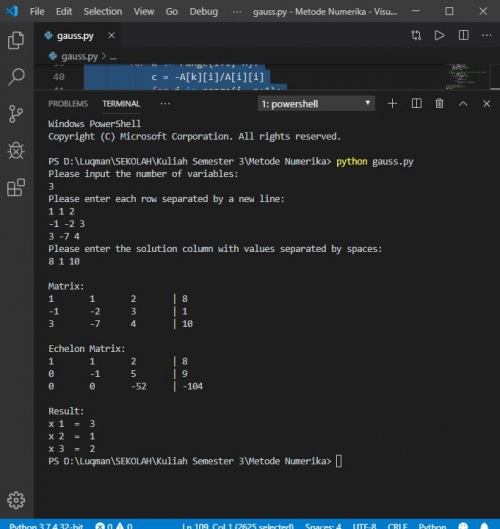
Ketika program tersebut dijalankan, maka akan muncul hasil sebagai berikut:
Pertemuan 5
Pertemuan 6
Quiz 16 Oktober 2019
Kodingan untuk penyelsaian prob. 2.1 nomor 6:
from numpy import linalg
import numpy as np
A = np.array([[0, 0, 2, 1, 2], [0, 1, 0, 2, -1],
[1, 2, 0, -2, 0], [0, 0, 0, -1, 1], [0, 1, -1, 1, -1]]) #input matriks
B = np.array([1, 1, -4, -2, -1]) #input solusi matriks
Z = np.linalg.solve(A, B) #oprasi aljabar
print(Z) #print hasil
maka didapatkan hasil [2. -2. 1. 1. -1].
Sedangkan, untuk kodingan penyelesaian prob. 7.1 nomer 2:
x0 = 0 # ini permisalan saja
y = 1 # ini permisalan saja
x = 0.33 # ini permisalan saja
h = 0.01 # permisalan step size sebesar 0.01
def dydx(x, y):
# Ini merupakan implementasi perhitungan Runge-Kutta.
return ((x**2 - 4*y))
def rungeKutta(x0, y0, x, h):
n = (int)((x - x0)/h)
y = y0
for i in range(1, n + 1):
k1 = h * dydx(x0, y)
k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)
k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)
k4 = h * dydx(x0 + h, y + k3)
# untuk y selanjutnya
y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
# untuk x selanjutnya
x0 = x0 + h
return y
print("Nilai y pada t =", t, "adalah", rungeKutta(x0, y, x, h))
Dengan demikian, akan didapatkan hasil sebesar 0.886929175...
UTS, 23 Oktober 2019
Video Muhasabah diri by Muhammad Luqman Sugiyono
Koding untuk soal A:
from math import*
print("Ini ada aplikasi untuk mencari solusi dari soal UTS metnum nomor A.")
g = 9.8 # pengenalan kalau gaya gravitasi pada saat itu adalah 9.8m/s^2
m1 = eval(input("massa beban 1 = "))
m2 = eval(input("massa beban 2 = "))
m3 = eval(input("massa beban 3 = "))
miu = eval(input("koef. gesek bidang = "))
teta = eval(input("sudut kemiringan bidang = "))
sinteta = sin(teta)
costeta = cos(teta)
T1 = g*sinteta*m1 - m1*g*costeta*miu
T2 = g*sinteta*m2 - m2*g*costeta*miu + T1
T3 = g*sinteta*m3 - m3*g*costeta*miu + T2
print("tegangan pada T1 adalah ", T1)
print("tegangan pada T2 adalah ", T2)
print("tegangan pada T3 adalah ", T3)
Untuk soal A, saya telah mengubah kodingan sehingga isi kodingan berupa proses eliminasi matriks. Persamaan tegangan tali yang sudah ada dibuat menjadi matriks terlebih dahulu ada dapat diproses secara eliminasi gauss jordan. Berikut adalah kodingan untuk soal A dengan metode eliminasi linear:
from math import*
from numpy import*
import numpy as np
print("Ini ada aplikasi untuk mencari solusi dari soal UTS metnum nomor A.")
g = 9.8 # pengenalan kalau gaya gravitasi pada saat itu adalah 9.8m/s^2
m1 = eval(input("massa beban 1 = "))
m2 = eval(input("massa beban 2 = "))
m3 = eval(input("massa beban 3 = "))
# koefisien gesek bidang dianggap sama untuk ketiga beban
miu = eval(input("koef. gesek bidang = "))
teta = eval(input("sudut kemiringan bidang = "))
phi = 3.14
rad = teta * phi / 180
sinteta = sin(rad)
costeta = cos(rad)
TA = np.array([[1/(sinteta - miu*costeta), 0, 0],
[0, 1/(sinteta - miu*costeta), 0],
[0, 0, 1/(sinteta - miu*costeta)]])
TB = np.array([[m1*g],
[m2*g],
[m3*g]])
TT = np.linalg.solve(TA, TB)
TT1 = TT[0]
TT2 = TT[1] + TT1
TT3 = TT[2] + TT2
print(TT)
print("Tegangan T1 adalah ", TT1, "Newton")
print("Tegangan T2 adalah ", TT2, "Newton")
print("Tegangan T3 adalah ", TT3, "Newton")
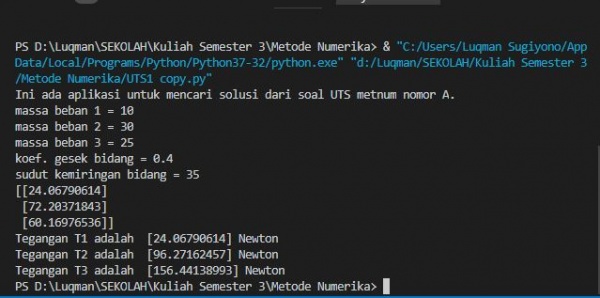
Hasil run padaprogram diatas adalah seperti ini:
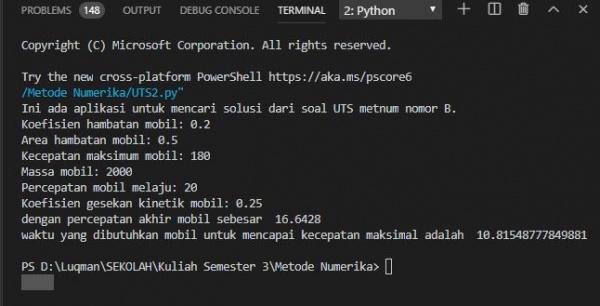
Untuk soal B, saya telah menyelesaikan kodingannya dengan metode numerik, yakni sebagai berikut:
print("Ini ada aplikasi untuk mencari solusi dari soal UTS metnum nomor B.")
# mobil yang digunakan peugeot 504
# karena mobil dari diam, maka v0 = 0
rho = 1.12 # massa jening udara
Cd = eval(input("Koefisien hambatan mobil: "))
A = eval(input("Area hambatan mobil: ")) # 0.533 #asumsi untuk luasan drag
V = eval(input("Kecepatan maksimum mobil: ")) # 186 #asumsi topspeed
m = eval(input("Massa mobil: ")) # 1540 #asusmsi berat mobil
a = eval(input("Percepatan mobil melaju: ")) # 25 #asumsi akselerasi mobil
miu = eval(input("Koefisien gesekan kinetik mobil: ")) # 0.14
g = 9.8 # percepatan gravitasi
fs = g*miu
fdrag = (1/2)*(1/m)*rho*Cd*A*V**2
atot = a - (fs + fdrag)
t = V/atot
print("dengan percepatan akhir mobil sebesar ", atot)
print("waktu yang dibutuhkan mobil untuk mencapai kecepatan maksimal adalah ", t)
Hasil run padaprogram diatas adalah seperti ini:
Pertemuan pada 30 Oktober 2019
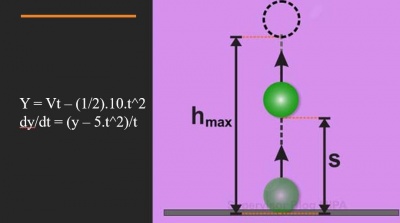
Saya membawakan kasus sederhana, yaitu seorang pemadam kebakaran yang sedang menyemprotkan air padaman ke atas gedung dari bawah. gedung yang kebakaran sangatlah tinggi sehingga sudut yang dibentuk antara selang pancuran air padaman dengan daratan hampir 90 derajat yang membuat nilai cos dari sudut tersebut sangatlah kecil dan dapat kita anggap nol.
dengan kode sebagai berikut:
t = eval(input("pada saat t berapa: "))
h = 1 # dtnya
t0 = 0.1
y0 = 0 # disemprotkan dari darat denga ketinggian 0
def F(t0, y0):
return ((y0 + 5*t*t)/t)
# Finds value of y for a given x using step size h
def rungeKutta(t0, y0, t, h):
# Count number of iterations using step size or
# step height h
n = (int)((t - t0) / h)
# mendefinisikan y= y0
y = y0
for i in range(1, n + 1):
"Apply Runge Kutta Formulas to find next value of y"
k1 = h * F(t0, y)
k2 = h * F(t0 + 0.5 * h, y + 0.5 * k1)
k3 = h * F(t0 + 0.5 * h, y + 0.5 * k2)
k4 = h * F(t0 + h, y + k3)
# Update next value of y
y = y + (1.0 / 6.0) * (k1 + 2 * k2 + 2 * k3 + k4)
# Update next value of t
t0 = t0 + h
return y
print('posisi air padaman pertama telah sampai pada ketinggian:',
rungeKutta(t0, y0, t, h))
Komentar dari teman-teman:



Enable comment auto-refresher