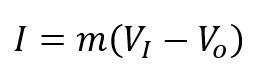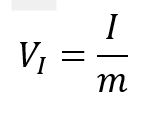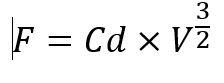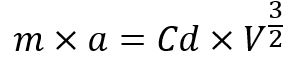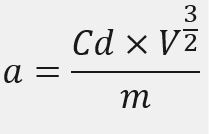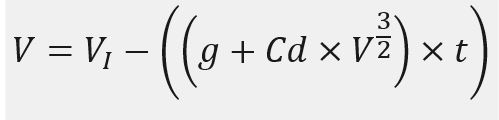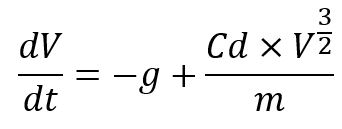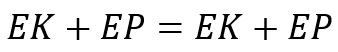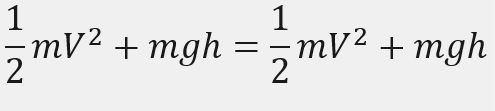Difference between revisions of "Pemodelan Persamaan Gerakan Lemparan Vertikal"
(→Algoritma) |
(→Flowchart) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 75: | Line 75: | ||
7. Mendefinisikan apakah genteng telah menyentuh tanah kembali atau belum dengan batasan kecepatan yang merupakan hasil penurunan dari persamaan energi | 7. Mendefinisikan apakah genteng telah menyentuh tanah kembali atau belum dengan batasan kecepatan yang merupakan hasil penurunan dari persamaan energi | ||
| − | == Flowchart == | + | == Flowchart == |
| − | + | [[File:Flowchart Umas Tugas 3.JPG]] | |
== Coding == | == Coding == | ||
| Line 98: | Line 98: | ||
h = 0.01 | h = 0.01 | ||
| − | step_size = np.arange(0,i,h) | + | step_size = np.arange(0,i,h) #fungsi ini adalah untuk mendefinisikan suatu range denga suatu lompatan tertentu |
#membuat looping | #membuat looping | ||
Latest revision as of 09:47, 6 November 2019
Studi Kasus
Persamaan yang ditulis dengan inisial RAU merupakan suatu persamaan mengenai gerakan melempar vertikal keatas, contoh aplikasi yang ada di dunia nyata adalah lemparan genteng keatas dari tukang bangunan. Persamaan matematika dari kegiatan melempar genteng ke atas rumah ini saya buat dengan metode numerik runge kutta, dengan memperhitungkan gravitasi dan gaya drag yang dihasilkan dari geometri genteng.
Berikut ini video pelemparan genteng yang saya maksidkan . Klik disini => [1]
Dengan asumsi lemparan vertikal ke atas, tidak membentuk sudut terhadap sumbu vertikal, maka berikut ini adalah pemodelan matematis dari kasus ini:
Model Matematika
Impuls yang diberikan Tukang Bangunan
Dalam pemodelan matematika dari kasus ini diperlukan kecepatan awal yang saya cari dengan memperhitungkan impuls yang diberikan oleh tukang bangunan. Persamaan impuls tersebut adalah sebagai berikut:
dengan kecepatan awal nol karena genteng tidak memiliki kecepatan sebelum diberikan impuls oleh tukang bangunan, sehingga rumus untuk mencari kecepatan awal menjadi seperti berikut:
Perlambatan Kecepatan oleh Gravitasi dan Gaya Drag Udara
Perlambatan kecepatan atau percepatan untuk kasus ini diperoleh dari gaya berat yang dimiliki oleh genteng dan gaya drag udara:
Gaya Drag Udara
Persamaan gaya drag dari udara adalah sebagai berikut:
Sehingga dihasilkan komponen percepatan sebagai berikut:
Sehingga, persamaan kecepatan yang dihasilkan setelah memperhitungkan hambatan gravitasi dan drag yang ada sehingga menghasilkan fungsi kecepatan sebagai berikut ini:
yang jika diturunkan menjadi persamaan berikut:
persamaan inilah yang nantinya akan dipakai untuk membuat persamaan Runge-Kutta Orde 4 untuk menyelesaikan permasalahan ini. Namun masih ada beberapa batasan yang harus diberikan. Persamaan runge-kutta ini belum bisa mendeteksi bahwa benda sudah menyentuh tanah lagi sehingga perlu adanya batasan kecepatan yang menunjukkan bahwa hasil tersebut berarti genteng telah menyentuh tanah kembali.
Kondisi genteng telah menyentuh tanah kembali
Ada beberapa cara untuk mengetahui bahwa genteng telah menyentuh tanah kembali. Yaitu dengan memodelkan posisi terhadap waktu atau dengan energi. Untuk kasus ini saya hanya ingin memodelkan kecepatannya sehingga saya menggunakan batasan dari kekalan energi:
Persamaan energi tersebut dapat juga ditunjukkan menjadi seperti ini, dengan asumsi tidak ada energi selain energi kinetik dan potensial yang bekerja.
Pada kondisi ketinggian yang sama maka kecepatan yang dihasilkan akan sama, sehingga itu menjadi batasan yang akan digunakan dalam output pada pengerjaan tugas ini. Ketika kecepatannya sudah sesuai dengan kecepatan awal maka diasumsikan genteng telah menyentuh tanah kembali dan kecepatannya 0
Algoritma
Persamaan ini dapat diselesaikan dengan metode runge kutta, dalam kasus ini saya ingin mencoba mencari kecepatan genteng yang dilemparkan pada suatu waktu tertentu dengan memperhitungkan gaya berat dan gaya drag dari genteng tersebut. Sebenarnya coding yang saya buat ini sifatnya universal untuk benda apapun ketika dilempar secara vertikal, karena ada komponen Cd yang harus dimasukkan oleh pengguna. Cara-cara yang akan saya lakukan adalah sebagai berikut:
1. Menyusun input yang akan digunakan yaitu terdiri dari impuls yang diberikan, nilai gravitasi, koefisien drag, masa genteng , dan waktu dimana kecepatan ingin diketahui.
2. Mendefinisikan percepatan sesuai dengan turunan kecepatan yang ada di model matematika yang ada di atas.
3. Mendefinisikan kecepatan awal sebagai fungsi impuls sesuai dengan model matematika yang sudah dituliskan di atas.
4. Mendefinisikan kecepatan awal v dengan abjad lain yang gunanya untuk menjadi batasan genteng telah menyentuh tanah kembali atau belum
5. Menentukan "step size" atau increment untuk runge kutta berikut ini. Saya menentukan incrementnya sebesar 0.01
6. Membuat iterasi untuk runge kutta dengan batasan waktu sesuai dengan yang diminta di awal untuk menentukan kecepatannya
7. Mendefinisikan apakah genteng telah menyentuh tanah kembali atau belum dengan batasan kecepatan yang merupakan hasil penurunan dari persamaan energi
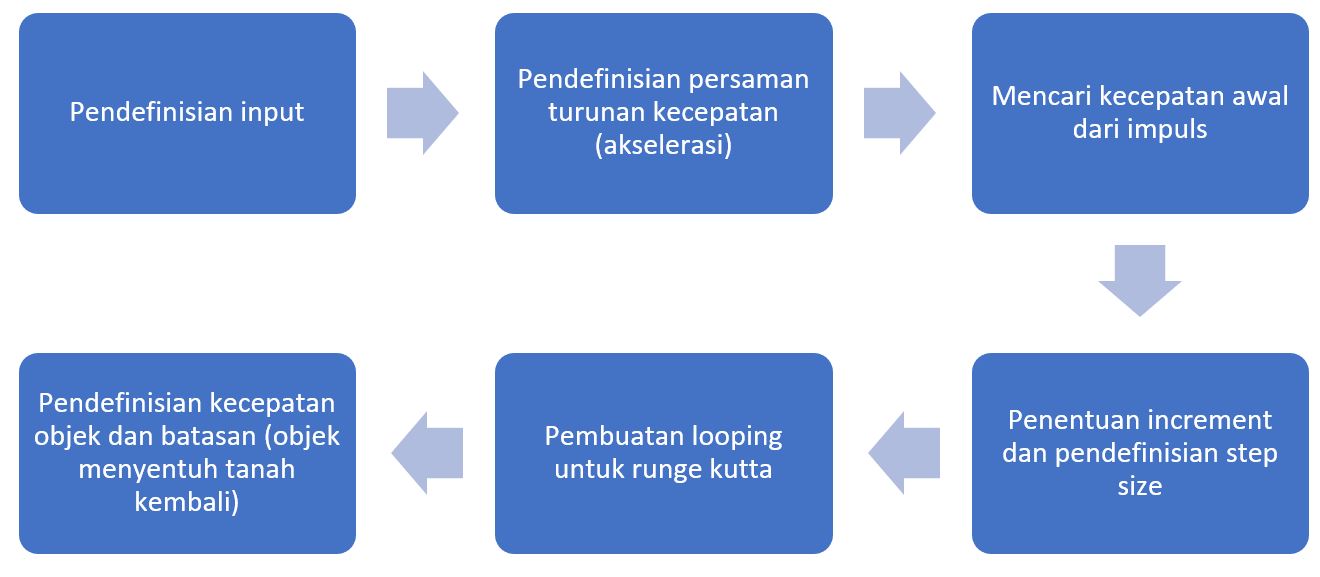
Flowchart
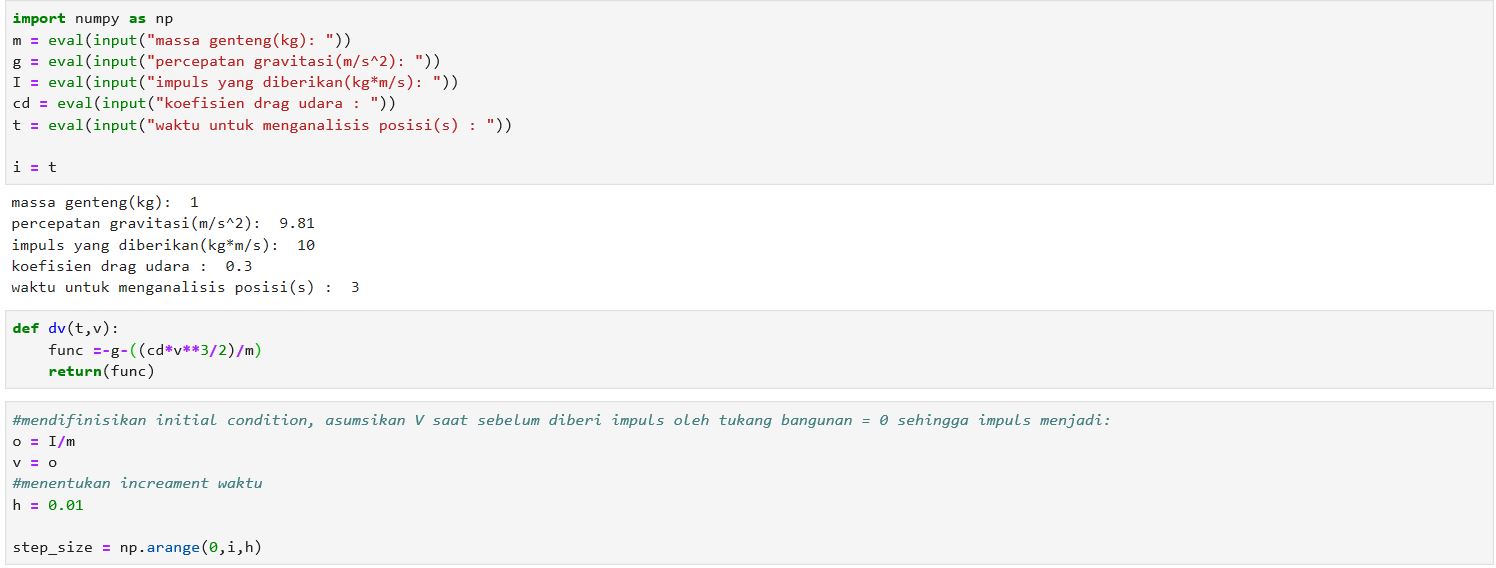
Coding
import numpy as np
m = eval(input("massa genteng(kg): "))
g = eval(input("percepatan gravitasi(m/s^2): "))
I = eval(input("impuls yang diberikan(kg*m/s): "))
cd = eval(input("koefisien drag udara : "))
t = eval(input("waktu untuk menganalisis posisi(s) : "))
i = t
def dv(t,v):
func =-g-((cd*v**3/2)/m)
return(func)
#mendifinisikan initial condition, asumsikan V saat sebelum diberi impuls oleh tukang bangunan = 0 sehingga impuls menjadi: o = I/m v = o #menentukan increament waktu h = 0.01
step_size = np.arange(0,i,h) #fungsi ini adalah untuk mendefinisikan suatu range denga suatu lompatan tertentu
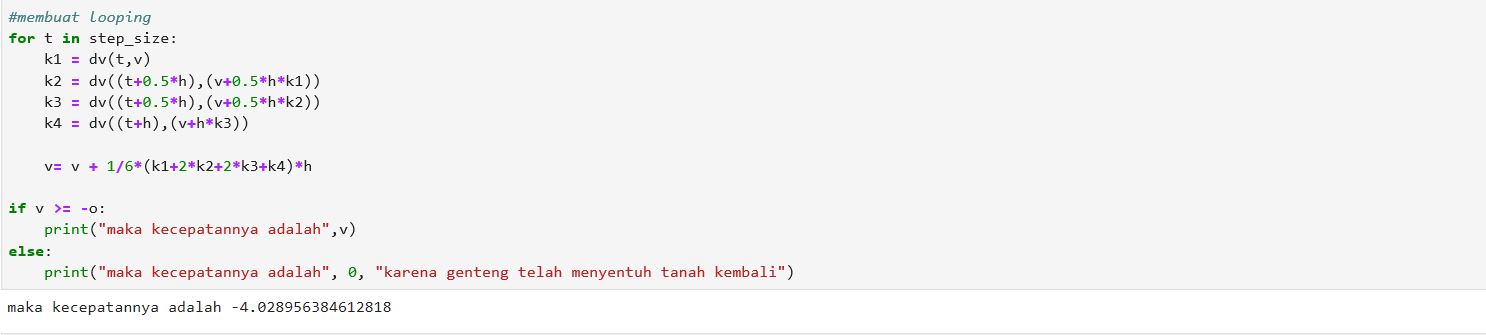
#membuat looping
for t in step_size:
k1 = dv(t,v)
k2 = dv((t+0.5*h),(v+0.5*h*k1))
k3 = dv((t+0.5*h),(v+0.5*h*k2))
k4 = dv((t+h),(v+h*k3))
v= v + 1/6*(k1+2*k2+2*k3+k4)*h
#pendefinisian if dan else berikut ini berdasarkan pada konservasi energi kinetik dan potensial bahwa jumlah energi kinetik dan potensialnya selalu konstan
if v >= -o:
print("maka kecepatannya adalah",v)
else:
print("maka kecepatannya adalah", 0, "karena genteng telah menyentuh tanah kembali")