Difference between revisions of "Almacho Rachmanudiputra"
(→UTS Metode Numerik) |
|||
| (20 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | [[File:IMG-20190901-WA0001.jpg]]Nama : Almacho Rachmanudiputra | + | [[File:IMG-20190901-WA0001.jpg]] |
| + | |||
| + | Nama : Almacho Rachmanudiputra | ||
Jurusan : Teknik Mesin Paralel Universitas Indonesia | Jurusan : Teknik Mesin Paralel Universitas Indonesia | ||
| Line 98: | Line 100: | ||
== Hiburan 2 == | == Hiburan 2 == | ||
| − | Konversi | + | Konversi dari Eliminasi dengan metode Gaussian |
6x1 + 4x2 = 50 | 6x1 + 4x2 = 50 | ||
| Line 141: | Line 143: | ||
X[m] = (B[m] - np.dot(A[m,m+1:n],x[m+1:n])/A[m,m] | X[m] = (B[m] - np.dot(A[m,m+1:n],x[m+1:n])/A[m,m] | ||
| + | |||
| + | == Hiburan 3 == | ||
| + | |||
| + | [[File:hiburan 3.jpg]] | ||
| + | |||
| + | Langkah 1 | ||
| + | |||
| + | Tentukan persamaan pada gambar tersebut : | ||
| + | |||
| + | <div border-style: inset;"> | ||
| + | 6x<sub>1</sub> + 4x<sub>2</sub> = 50 | ||
| + | 2x<sub>1</sub> + x<sub>3</sub> + 4x<sub>4</sub> = 50 | ||
| + | 7x<sub>2</sub> + 3x<sub>3</sub> + 4x<sub>4</sub> = 50 | ||
| + | 4x<sub>1</sub> + 4x<sub>3</sub> = 50 | ||
| + | |||
| + | matriks : | ||
| + | |||
| + | [6. -4. 0. 0.] | ||
| + | [-4. 0. 4. 0.] | ||
| + | [-2. 0. -1. 4.] | ||
| + | [0. 7. -3. -4.] | ||
| + | </div> | ||
| + | |||
| + | Langkah 2 | ||
| + | |||
| + | tulis matriks di python seperti berikut : | ||
| + | |||
| + | <div border-style: inset;"> | ||
| + | import numpy as np | ||
| + | <br> A = np.array([[6, -4, 0, 0], [-4, 0 ,4, 0], [-2, 0, -1, 4], [ 0, 7, -3, -4]], float) | ||
| + | B = np.array([50, 0, 50, 0], float) | ||
| + | <br>n = len(A) | ||
| + | </div> | ||
| + | |||
| + | menggunakan eliminasi gauss | ||
| + | |||
| + | <div border-style: inset;"> | ||
| + | for k in range(0,n-1): | ||
| + | for i in range(k+1,n): | ||
| + | if A[i,k]!=0 : | ||
| + | lam = A[i,k]/A[k,k] | ||
| + | A[i,k:n] = A[i,k:n]-(A[k,k:n]*lam) | ||
| + | B[i] = B[i]-(B[k]*lam) | ||
| + | </div> | ||
| + | |||
| + | lalu dengan back subs | ||
| + | |||
| + | <div border-style: inset;"> | ||
| + | x = np.zeros(n,float) | ||
| + | for m in range(n-1,-1,-1): | ||
| + | x[m]=(B[m]-np.dot(A[m,m+1:n],x[m+1:n]))/A[m,m] | ||
| + | </div> | ||
| + | |||
| + | maka hasilnya adalah : | ||
| + | |||
| + | [[File:Screenshot 3.png]] | ||
== Hiburan 4 dan 5 == | == Hiburan 4 dan 5 == | ||
| Line 270: | Line 328: | ||
== UTS Metode Numerik == | == UTS Metode Numerik == | ||
| + | |||
| + | SOAL A | ||
| + | |||
| + | import math | ||
| + | |||
| + | #1. Pertanyaan Fungsi | ||
| + | |||
| + | print('diberikan fungsi sin theta = m4/(m1+m2+m3)') | ||
| + | |||
| + | print('Nilai m1?') | ||
| + | |||
| + | m1=eval(input()) | ||
| + | |||
| + | print('Nilai m2?') | ||
| + | |||
| + | m2=eval(input()) | ||
| + | |||
| + | print('Nilai m3?') | ||
| + | |||
| + | m3=eval(input()) | ||
| + | |||
| + | print('Nilai m4?') | ||
| + | |||
| + | m4=eval(input()) | ||
| + | |||
| + | #2. Menentukan nilai a | ||
| + | |||
| + | a = 0 | ||
| + | |||
| + | #3. Menentukan fungsi sin theta | ||
| + | |||
| + | x = m4 | ||
| + | |||
| + | y = (m1+m2+m3) | ||
| + | |||
| + | alfa = m4 / (m1+m2+m3) | ||
| + | |||
| + | #4. Mendapatkan hasil sin theta | ||
| + | |||
| + | print('maka, hasil sin theta adalah', alfa) | ||
| + | |||
| + | |||
| + | sudutalfa=math.asin(alfa) | ||
| + | |||
| + | sudutalfa2=math.degrees(sudutalfa) | ||
| + | |||
| + | print('jadi nilai sudut alfa adalah',sudutalfa2) | ||
| + | |||
| + | Hasil : | ||
| + | |||
| + | |||
| + | RESTART: C:\Users\Almacho R\AppData\Local\Programs\Python\Python37-32\UTS A.py | ||
| + | |||
| + | diberikan fungsi sin theta = m4/(m1+m2+m3) | ||
| + | |||
| + | Nilai m1? | ||
| + | 3 | ||
| + | |||
| + | Nilai m2? | ||
| + | 2 | ||
| + | |||
| + | Nilai m3? | ||
| + | 2 | ||
| + | |||
| + | Nilai m4? | ||
| + | 1 | ||
| + | |||
| + | maka, hasil sin theta adalah 0.14285714285714285 | ||
| + | |||
| + | jadi nilai sudut alfa adalah 8.213210701738188 | ||
| + | |||
| + | |||
| + | SOAL B | ||
import numpy as np | import numpy as np | ||
| + | |||
def diff_y (x,y): | def diff_y (x,y): | ||
fungsi = x**2 - 4*y | fungsi = x**2 - 4*y | ||
| Line 280: | Line 412: | ||
a = 1 | a = 1 | ||
j = 1 | j = 1 | ||
| − | step_size = -np. | + | step_size = -np.arrange (0,0.5,h) |
for t in step_size: | for t in step_size: | ||
k1 = diff_y (x,y) - (a + j) | k1 = diff_y (x,y) - (a + j) | ||
| Line 288: | Line 420: | ||
print ('maka x(0.5) adalah', w1) | print ('maka x(0.5) adalah', w1) | ||
| + | |||
| + | Hasil : | ||
| + | |||
| + | RESTART: C:/Users/Almacho R/AppData/Local/Programs/Python/Python37-32/UTS B.py | ||
| + | maka x(0.5) adalah 40.666666666666664 | ||
| + | |||
| + | == Video Penjelasan Soal UTS Metode Numerik == | ||
| + | |||
| + | SOAL A dan SOAL B | ||
| + | |||
| + | https://www.youtube.com/watch?v=tnnizR9b9Pw&t=100s | ||
| + | |||
| + | == Video Manfaat Metode Numerik == | ||
| + | |||
| + | Apa yang telah saya dapatkan selama belajar metode numerik? | ||
| + | |||
| + | https://www.youtube.com/watch?v=0Y1U8NkC7ko | ||
Latest revision as of 23:38, 27 October 2019
Nama : Almacho Rachmanudiputra
Jurusan : Teknik Mesin Paralel Universitas Indonesia
NPM : 1706026701
Contents
Biografi dan Riwayat Pendidikan
Lahir : Jakarta, 23 Oktober 1998
2002-2003 : Sakinah Al Azhar Rawamangun
2003-2005 : TK Islam Al Azhar Rawamangun
2005-2011 : SDI Al Azhar 13 Rawamangun
2011-2014 : SMP Negeri 115 Jakarta
2014-2017 : SMA Negeri 8 Jakarta
2017- : S1 Teknik Mesin Paralel Universitas Indonesia
Hasil Belajar Pemrograman Python/C++
Di minggu pertama saya mencoba untuk mengunduh aplikasi python namun saya belum menemukan crack file tersebut. Lalu saya membaca e-book panduan python, disitu saya membaca peraturan penulisan sintaks pada python yang harus dipenuhi, antara lain penulisan statement, penulisan string, penulisan case, penulisan blok, serta cara menulis komentar di python. Untuk penulisan komentar biasanya menggunakan tanda baca pagar (#), serta menggunakan tanda petik ('). Terakhir saya membaca berbagai macam penulisan blok seperti blok percabangan, blok fungsi, blok perulangan, blok class, blok exception, dan block with.
Statement = instruksi yang akan dieksekusi oleh komputer.
String = teks atau kumpulan karakter.
Blok program = kumpulan dari beberapa statement yang dikumpulkan menjadi satu blok.
Contoh Pengerjaan Phython :
x1 = 0
dx1 = ('0.1')
dx = float (dx1)
x2 = x1+dx
Fx_1 = ((x2**2)-1) / (x1-1)
n = 1 error = 0
print ("n x F(x) error")
print (n," ",x1," ",Fx_1," ",error)
while x2<1 :
Fx_2 = ((x2**2)-1) / (x2-1)
error = ((Fx_2-Fx_1) / Fx_1)
Fx_1 = Fx_2
n = n+1
print (n," ",x1," ",Fx_1," ",error)
x2=x2+dx
Hiburan 1
x1 = 0
dx1 = ('0.1')
dx = float (dx1)
x2 = x1+dx
Fx_1 = ((x2**2)-1) / (x1-1)
n = 1 error = 0
print ("n x F(x) error")
print (n," ",x1," ",Fx_1," ",error)
while x2<1 :
Fx_2 = ((x2**2)-1) / (x2-1)
error = ((Fx_2-Fx_1) / Fx_1)
Fx_1 = Fx_2
n = n+1
print (n," ",x1," ",Fx_1," ",error)
x2=x2+dx
Hiburan 2
Konversi dari Eliminasi dengan metode Gaussian
6x1 + 4x2 = 50
2x1 + x3 + 4x4 = 50
7x2 + 3x3 + 4x4 = 50
4x1 + 4x3 = 50
Masukkan kedalam persamaan matriks
[[6, 4, 0, 0,][2, 0, 1, 4][0, 7, 3, 4][4, 0, 4, 0]]
Lalu masukkan matriks kedalam program Phyton
import numpy as np
A = np. array ([[6, 4, 0, 0], [2, 0, 1, 4], [0, 7, 3, 4], [4, 0, 4, 0]], float)
B = np.array ([50, 50, 0, 0], float)
n = len (A)
Gunakan eliminasi Gauss
for k in range(0,n-1) :
for i in range (k+1,n) :
if A[i,k]! = 0 :
lam = A[i,k]/A[k,k]
A[i,k:n] = A[i,k:n] - (A[k,k:n]*lam)
B[i] = B[i] - B[k]*lam
x = np.zeros(n,float)
for m in range(n-1,-1,-1) :
X[m] = (B[m] - np.dot(A[m,m+1:n],x[m+1:n])/A[m,m]
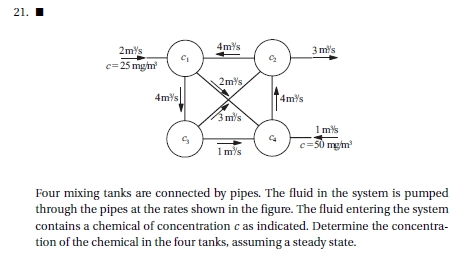
Hiburan 3
Langkah 1
Tentukan persamaan pada gambar tersebut :
6x1 + 4x2 = 50 2x1 + x3 + 4x4 = 50 7x2 + 3x3 + 4x4 = 50 4x1 + 4x3 = 50
matriks :
[6. -4. 0. 0.] [-4. 0. 4. 0.] [-2. 0. -1. 4.] [0. 7. -3. -4.]
Langkah 2
tulis matriks di python seperti berikut :
import numpy as np
A = np.array([[6, -4, 0, 0], [-4, 0 ,4, 0], [-2, 0, -1, 4], [ 0, 7, -3, -4]], float) B = np.array([50, 0, 50, 0], float)
n = len(A)
menggunakan eliminasi gauss
for k in range(0,n-1):
for i in range(k+1,n):
if A[i,k]!=0 :
lam = A[i,k]/A[k,k]
A[i,k:n] = A[i,k:n]-(A[k,k:n]*lam)
B[i] = B[i]-(B[k]*lam)
lalu dengan back subs
x = np.zeros(n,float)
for m in range(n-1,-1,-1):
x[m]=(B[m]-np.dot(A[m,m+1:n],x[m+1:n]))/A[m,m]
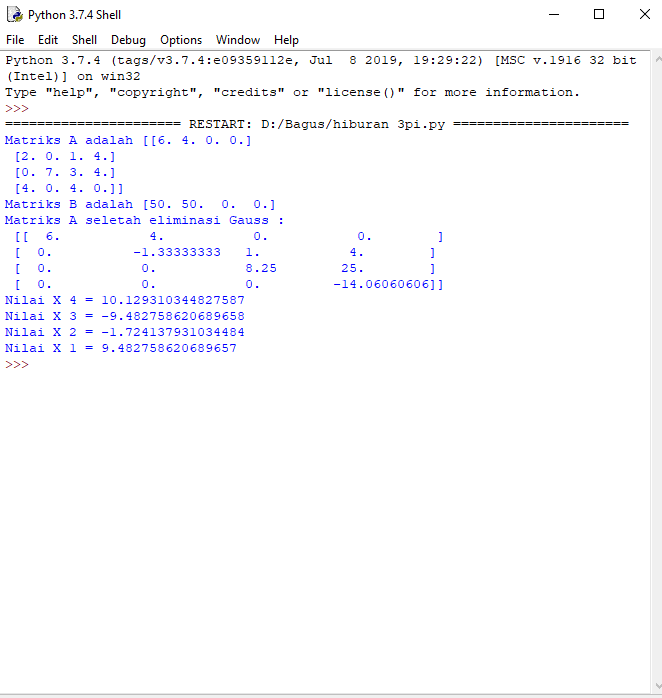
maka hasilnya adalah :
Hiburan 4 dan 5
Pada hiburan minggu ke-4 & ke-5, saya menggunakan matriks dalam menyelesaikan suatu persoalan yang menggunakan persamaan. Dikerjakan dalam Python dengan memasukkan modul pengerjaan.
Secara teori, digunakan hukum kontinuitas massa sehingga didapati rumus Q*p=Q*p dan didapatakan 4 persamaan dengan 4 variabel
6C1 - 4C2 = 50
-2C1 - 1C3 + 4C4 = 50
7C2 - 3C3 - 4C4 = 0
-4C1 + 4C3 = 0
6C1 - 4C2 + 0C3 + 0C4 = 50
-2C1 + 0C2 - 1C3 + 4C4 = 50
0C1 + 7C2 - 3C3 - 4C4 = 0
-4C1 + 0C2 + 4C3 + 0C4 = 0
Kemudian, persamaan - persamaan ini dimasukkan kedalam python untuk di hitung hasil persamaannya.
Kuis
Nomor 1 :
import numpy as np
class GEPP():
def __init__(self, A, b, doPricing=True):
#super(GEPP, self).__init__()
self.A = A # input: A is an n x n numpy matrix
self.b = b # b is an n x 1 numpy array
self.doPricing = doPricing
self.n = None # n is the length of A
self.x = None # x is the solution of Ax=b
self._validate_input() # method that validates input
self._elimination() # method that conducts elimination
self._backsub() # method that conducts back-substitution
def _validate_input(self):
self.n = len(self.A)
if self.b.size != self.n:
raise ValueError("Invalid argument: incompatible sizes between" +
"A & b.", self.b.size, self.n)
def _elimination(self):
# Elimination
for k in range(self.n - 1):
if self.doPricing:
# Pivot
maxindex = abs(self.A[k:, k]).argmax() + k
if self.A[maxindex, k] == 0:
raise ValueError("Matrix is singular.")
# Swap
if maxindex != k:
self.Ak, maxindex = self.Amaxindex, k
self.bk, maxindex = self.bmaxindex, k
else:
if self.A[k, k] == 0:
raise ValueError("Pivot element is zero. Try setting doPricing to True.")
# Eliminate
for row in range(k + 1, self.n):
multiplier = self.A[row, k] / self.A[k, k]
self.A[row, k:] = self.A[row, k:] - multiplier * self.A[k, k:]
self.b[row] = self.b[row] - multiplier * self.b[k]
def _backsub(self):
# Back Substitution
self.x = np.zeros(self.n)
for k in range(self.n - 1, -1, -1):
self.x[k] = (self.b[k] - np.dot(self.A[k, k + 1:], self.x[k + 1:])) / self.A[k, k]
def main():
A = np.array([[1., 2., 0., -2., 0.],
[0., 1., 0., 2., -1.],
[0., 0., 2., 1., 2.],
[0., 0., 0., -1., 1.],
[0., 1., -1., 1., -1.]])
b = np.array([[-4.],
[1.],
[1.],
[-2.],
[-1.]])
GaussElimPiv = GEPP(np.copy(A), np.copy(b), doPricing=False)
print(GaussElimPiv.x)
print(GaussElimPiv.A)
print(GaussElimPiv.b)
GaussElimPiv = GEPP(A, b)
print(GaussElimPiv.x)
if __name__ == "__main__":
main()
Nomor 2 :
import numpy as np
def diff_y (x,y) :
fungsi = x**2 - 4*y return (fungsi)
x = 0 y = 1 h = 0.01 step_size = np.arrange (0,0.03,h)
for t in step_size :
k1 = diff_y (x,y) k2 = diff_y ((x+0,5*h), (y+0.5*k1*h))
y = y + k1*h
print ('maka y(0.03) adalah', y)
UTS Metode Numerik
SOAL A
import math
- 1. Pertanyaan Fungsi
print('diberikan fungsi sin theta = m4/(m1+m2+m3)')
print('Nilai m1?')
m1=eval(input())
print('Nilai m2?')
m2=eval(input())
print('Nilai m3?')
m3=eval(input())
print('Nilai m4?')
m4=eval(input())
- 2. Menentukan nilai a
a = 0
- 3. Menentukan fungsi sin theta
x = m4
y = (m1+m2+m3)
alfa = m4 / (m1+m2+m3)
- 4. Mendapatkan hasil sin theta
print('maka, hasil sin theta adalah', alfa)
sudutalfa=math.asin(alfa)
sudutalfa2=math.degrees(sudutalfa)
print('jadi nilai sudut alfa adalah',sudutalfa2)
Hasil :
RESTART: C:\Users\Almacho R\AppData\Local\Programs\Python\Python37-32\UTS A.py
diberikan fungsi sin theta = m4/(m1+m2+m3)
Nilai m1? 3
Nilai m2? 2
Nilai m3? 2
Nilai m4? 1
maka, hasil sin theta adalah 0.14285714285714285
jadi nilai sudut alfa adalah 8.213210701738188
SOAL B
import numpy as np
def diff_y (x,y):
fungsi = x**2 - 4*y
return (fungsi)
x=0
y=10
h=10
a = 1
j = 1
step_size = -np.arrange (0,0.5,h)
for t in step_size:
k1 = diff_y (x,y) - (a + j) k2 = diff_y ((x+0.5*h),(y+0.05*k1*h)) - (a + j)
w1 = y + 1/3*(k1+2*k2)
print ('maka x(0.5) adalah', w1)
Hasil :
RESTART: C:/Users/Almacho R/AppData/Local/Programs/Python/Python37-32/UTS B.py
maka x(0.5) adalah 40.666666666666664
Video Penjelasan Soal UTS Metode Numerik
SOAL A dan SOAL B
https://www.youtube.com/watch?v=tnnizR9b9Pw&t=100s
Video Manfaat Metode Numerik
Apa yang telah saya dapatkan selama belajar metode numerik?