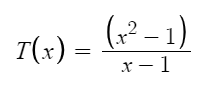Difference between revisions of "Ahmad Fadhil Nugraha"

From ccitonlinewiki
Jump to: navigation, search
 
(7 intermediate revisions by the same user not shown)
Line 1: Line 1:
 
== Biografi ==
 
== Biografi ==
 +
 +
[[File:Pon bio.jpg]]
 
Ahmad Fadhil Nugraha (lahir di Jakarta, 3 November 1998) biasa dipanggil fadhil atau pon. Mengawali pendidikan di Depok (SD-SMA) dan sekarang sedang mengabdi ilmu di Teknik Mesin Universitas Indonesia. Hobi saya adalah berolahraga dan bermain musik.
 
Ahmad Fadhil Nugraha (lahir di Jakarta, 3 November 1998) biasa dipanggil fadhil atau pon. Mengawali pendidikan di Depok (SD-SMA) dan sekarang sedang mengabdi ilmu di Teknik Mesin Universitas Indonesia. Hobi saya adalah berolahraga dan bermain musik.
  
Line 14: Line 16:
  
 
[[File:H1pon3.png]]
 
[[File:H1pon3.png]]
 +
 +
== Hiburan Minggu 2 ==
 +
 +
Mencari nilai x pada persamaan menggunakan python
 +
 +
'''8x**4 + 2x**3 + x**2 - x = 0'''
 +
 +
def f(x):
 +
  return 8*x**3 + 2*x**2 + x - 1
 +
def fprime(x):
 +
  return 24*x**2 + 4*x +1
 +
 +
ep = 0.001
 +
 +
gu = -10
 +
i = 0
 +
 +
print('8*x**3 + 2*x**2 + x - 1')
 +
 +
print('Results by Python 3.7')
 +
 +
while abs(f(gu)) >= ep:
 +
  gu = gu - (f(gu)/fprime(gu))
 +
  i += 1
 +
  print(' ' + str(i) + ' ' + str(round(gu,7)))
 +
 +
print('The root approach is ' + str(round(gu,2)) + '| failed to calculate: ' + str(i) + ' times' )
 +
 +
 +
setelah dilakukan run pada python maka akan keluar hasil :
 +
 +
Results by Python 3.7
 +
1 -6.6916561
 +
2 -4.4843577
 +
3 -3.0097929
 +
4 -2.0212238
 +
5 -1.351617
 +
6 -0.8837556
 +
7 -0.5232533
 +
8 -0.1359299
 +
9 1.1078572
 +
10 0.7226116
 +
11 0.4921017
 +
12 0.3862078
 +
13 0.3624733
 +
14 0.3613595
 +
The root approach is 0.36| failed to calculate: 14 times
 +
 +
 +
== HIBURAN 3 ==
 +
 +
Kali ini tugas diberikan untuk mencari nilai x pada
 +
 +
[[File:hiburan 3.jpg]]
 +
 +
pertama-tama harus mencari persamaannya terlebih dahulu :
 +
 +
<div border-style: inset;">
 +
6x<sub>1</sub> + 4x<sub>2</sub> = 50
 +
2x<sub>1</sub> + x<sub>3</sub> + 4x<sub>4</sub> = 50
 +
7x<sub>2</sub> + 3x<sub>3</sub> + 4x<sub>4</sub> = 50
 +
4x<sub>1</sub> + 4x<sub>3</sub> = 50
 +
 +
Maka akan menghasilkan matriks :
 +
 +
[6. -4. 0. 0.]
 +
  [-4. 0. 4. 0.]
 +
  [-2. 0. -1. 4.]
 +
  [0. 7. -3. -4.]
 +
</div>
 +
 +
Setelah itu di python kita menuliskan :
 +
 +
import numpy as np
 +
 +
A = np.array([[6, -4, 0, 0], [-4, 0 ,4, 0], [-2, 0, -1, 4], [ 0, 7, -3, -4]], float)
 +
B = np.array([50, 0, 50, 0], float)
 +
 +
n = len(A)
 +
for k in range(0,n-1):
 +
    for i in range(k+1,n):
 +
        if A[i,k]!=0 :
 +
            lam = A[i,k]/A[k,k]
 +
            A[i,k:n] = A[i,k:n]-(A[k,k:n]*lam)
 +
            B[i] = B[i]-(B[k]*lam)
 +
               
 +
x = np.zeros(n,float)
 +
for m in range(n-1,-1,-1):
 +
    x[m]=(B[m]-np.dot(A[m,m+1:n],x[m+1:n]))/A[m,m]
 +
 +
setelah di run kita akan mendapatkan bahwa
 +
 +
Nilai x 1 = 9.48275
 +
Nilai x 2 = -1.72413
 +
Nilai x 3 = -9.48275
 +
Nilai x 4 = 10.12931
 +
  
 
== UTS ==
 
== UTS ==
Line 81: Line 180:
  
 
print ('maka nilai v adalah',integral)
 
print ('maka nilai v adalah',integral)
 +
 +
 +
==Perbaikan UTS==
 +
 +
 +
*'''SOAL A'''
 +
 +
[[File:video pon 1.mp4]]
 +
 +
import math
 +
from math import *
 +
import numpy as np
 +
 +
m1 = float(input("massa benda 1: "))
 +
m2 = float(input("massa benda 2: "))
 +
m3 = float(input("massa benda 3: "))
 +
m4 = float(input("massa benda 4: "))
 +
tetta = float(input("sudut bidang miring: "))
 +
g = 9.81
 +
 +
sin_tetta = math.sin(tetta)
 +
print ("nilai sin tetta: ", sin_tetta)
 +
 +
w1 = (m1 + m2 +m3) * g
 +
w2 = m4 * g
 +
 +
a = (w2 - (w1 * sin_tetta)) / (m1 + m2 + m3 + m4)
 +
print ("percepatan sistem: ", a ," m/s2")
 +
 +
T = (m4*g) - (m4*a)
 +
print ("besarnya tegangan tali: ", T ," N")
 +
 +
 +
 +
*'''SOAL B'''
 +
 +
[[File:video pon 2.mp4]]
 +
import math
 +
 +
v0 = 0
 +
t0 = 0
 +
t = float(input("waktu yang ditempuh: "))
 +
x0 = 0
 +
xt = float(input("jarak yang ditempuh: "))
 +
m = float(input("massa mobil: "))
 +
g = 9.81
 +
cd = float(input("koefisien gesek dengan udara: "))
 +
p = 1.2  #nilai untuk massa jenis udara
 +
area = float(input("luas daerah yang terkena gesekan dengan udara: "))
 +
fr = float(input("koefisien gesek dengan jalanan: "))
 +
 +
#total gaya gesek
 +
gg = (fr * m *g) + (cd * p * (xt**2 / t**2) * area / 2)
 +
 +
a = ( xt / t**2 ) - ( gg / m )
 +
 +
v = (((v0**2) + 2) * a * xt )
 +
print ("kecepatan pada jarak ", xt , " adalah ", v)

Latest revision as of 12:34, 28 October 2019

Biografi

Pon bio.jpg Ahmad Fadhil Nugraha (lahir di Jakarta, 3 November 1998) biasa dipanggil fadhil atau pon. Mengawali pendidikan di Depok (SD-SMA) dan sekarang sedang mengabdi ilmu di Teknik Mesin Universitas Indonesia. Hobi saya adalah berolahraga dan bermain musik.

Hiburan Minggu 1

Pada minggu pertama kelas metode numerik, ada suatu permasalahan yang diberikan yaitu:

H1pon1.png

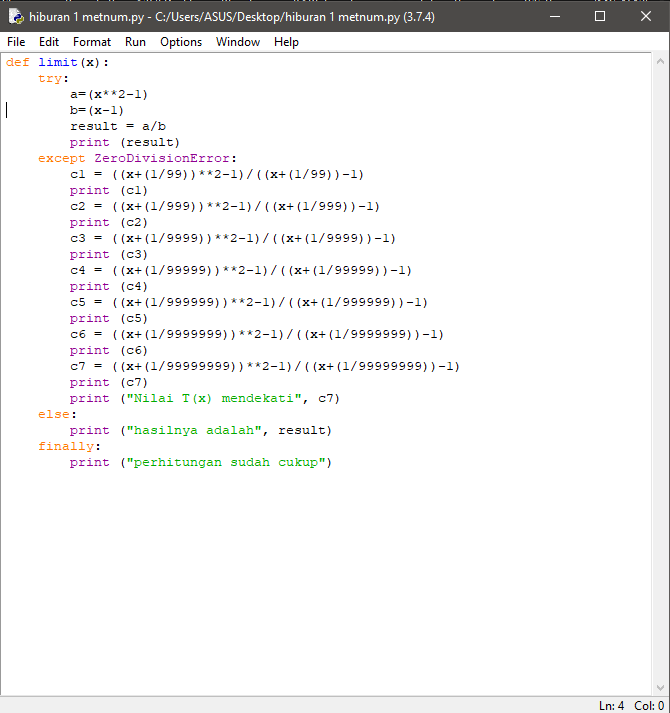
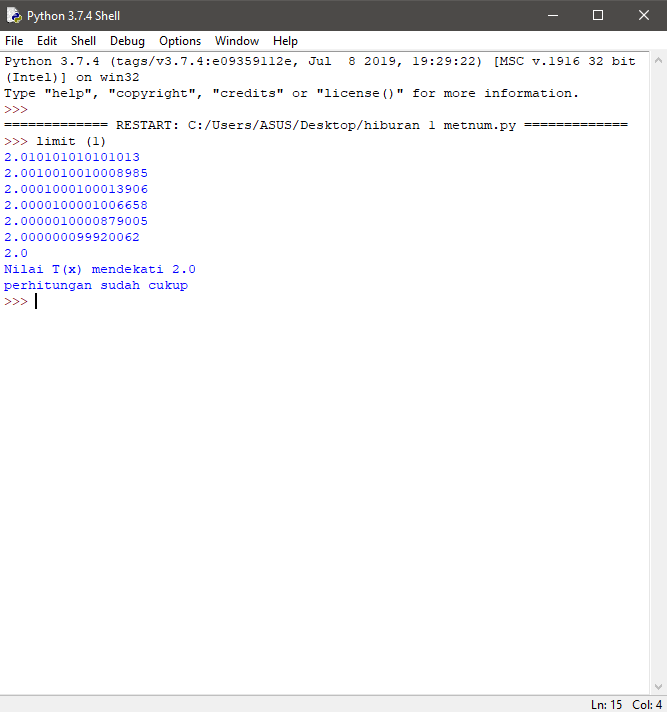
Jika nilai x sama dengan 1 maka nilai persamaan tersebut adalah 0/0 sehingga perlu diterapakan rumus pendekatan limit. pendekatan limit yang digunakan adalah limit mendekati n, dimana n nilainya adalah 1. Jika persamaan tersebut diolah menggunakan python maka tampilannya akan seperti :

H1pon2.png

dari coding tersebut, computer akan memproses dan mendapatkan hasil seperti dibawah ini:

H1pon3.png

Hiburan Minggu 2

Mencari nilai x pada persamaan menggunakan python

8x**4 + 2x**3 + x**2 - x = 0 

def f(x): 
  return 8*x**3 + 2*x**2 + x - 1
def fprime(x):
  return 24*x**2 + 4*x +1

ep = 0.001

gu = -10
i = 0

print('8*x**3 + 2*x**2 + x - 1')

print('Results by Python 3.7')

while abs(f(gu)) >= ep:
  gu = gu - (f(gu)/fprime(gu))
  i += 1
  print(' ' + str(i) + ' ' + str(round(gu,7)))

print('The root approach is ' + str(round(gu,2)) + '| failed to calculate: ' + str(i) + ' times' )


setelah dilakukan run pada python maka akan keluar hasil : 

Results by Python 3.7
1 -6.6916561
2 -4.4843577
3 -3.0097929
4 -2.0212238
5 -1.351617
6 -0.8837556
7 -0.5232533
8 -0.1359299
9 1.1078572
10 0.7226116
11 0.4921017
12 0.3862078
13 0.3624733
14 0.3613595
The root approach is 0.36| failed to calculate: 14 times


HIBURAN 3

Kali ini tugas diberikan untuk mencari nilai x pada

Hiburan 3.jpg

pertama-tama harus mencari persamaannya terlebih dahulu : 

6x1 + 4x2 = 50
2x1 + x3 + 4x4 = 50
7x2 + 3x3 + 4x4 = 50
4x1 + 4x3 = 50

Maka akan menghasilkan matriks : 

[6. -4. 0. 0.]
 [-4. 0. 4. 0.]
 [-2. 0. -1. 4.]
 [0. 7. -3. -4.]

Setelah itu di python kita menuliskan : 

import numpy as np

A = np.array([[6, -4, 0, 0], [-4, 0 ,4, 0], [-2, 0, -1, 4], [ 0, 7, -3, -4]], float)
B = np.array([50, 0, 50, 0], float)

n = len(A)
for k in range(0,n-1):
    for i in range(k+1,n):
        if A[i,k]!=0 :
            lam = A[i,k]/A[k,k] 
            A[i,k:n] = A[i,k:n]-(A[k,k:n]*lam)
            B[i] = B[i]-(B[k]*lam)
               
x = np.zeros(n,float)
for m in range(n-1,-1,-1):
   x[m]=(B[m]-np.dot(A[m,m+1:n],x[m+1:n]))/A[m,m]

setelah di run kita akan mendapatkan bahwa 

Nilai x 1 = 9.48275
Nilai x 2 = -1.72413
Nilai x 3 = -9.48275
Nilai x 4 = 10.12931


UTS

SOAL A

import math

m1=input("m1?")

m2=input("m2?")

m3=input("m3?")

m4=input("m4?")

x=asin((m1+m2+m3)/m4)

print ('jika nilai m1 adalah ',m1,' m2 adalah ',m2,' m3 adalah ',m3,' m4 adalah ',m4,'maka nilai sudutnya sebesar',x)


SOAL B


Fgesek = input("Nilai F gesek?")

Fangin = input("NIlai F angin?")

Mmobil = input("Nilai Massa Mobil?")

t = input("waktu?")

a=0

b= t

n=10

h=(b-a)/float(n)

x=[]

gx=[]

print ('nilai x') for i in arange(n): 

 x.append(a+i*h)
 print ('x',i,' = ',x[i])

print ('nilai g(x)') for i in arange(n): 

 gx.append((Fgesek+Fangin)*t/Mmobil)
 print ('g(x',i,') = ',gx[i])

print ('jumlah nilainya') jml=0 for i in arange(n): 

 jml=jml+gx[i]

print ('jumlah= ',jml)

print ()

print ('bagi dengan n dan dikalikan (b-a)')

integral=jml*h

print ('maka nilai v adalah',integral)


Perbaikan UTS

  • SOAL A

import math
from math import *
import numpy as np

m1 = float(input("massa benda 1: "))
m2 = float(input("massa benda 2: "))
m3 = float(input("massa benda 3: "))
m4 = float(input("massa benda 4: "))
tetta = float(input("sudut bidang miring: "))
g = 9.81

sin_tetta = math.sin(tetta)
print ("nilai sin tetta: ", sin_tetta)

w1 = (m1 + m2 +m3) * g
w2 = m4 * g

a = (w2 - (w1 * sin_tetta)) / (m1 + m2 + m3 + m4)
print ("percepatan sistem: ", a ," m/s2")

T = (m4*g) - (m4*a)
print ("besarnya tegangan tali: ", T ," N")


  • SOAL B

import math

v0 = 0
t0 = 0
t = float(input("waktu yang ditempuh: "))
x0 = 0
xt = float(input("jarak yang ditempuh: "))
m = float(input("massa mobil: "))
g = 9.81
cd = float(input("koefisien gesek dengan udara: "))
p = 1.2  #nilai untuk massa jenis udara
area = float(input("luas daerah yang terkena gesekan dengan udara: "))
fr = float(input("koefisien gesek dengan jalanan: "))

#total gaya gesek
gg = (fr * m *g) + (cd * p * (xt**2 / t**2) * area / 2)

a = ( xt / t**2 ) - ( gg / m )

v = (((v0**2) + 2) * a * xt )
print ("kecepatan pada jarak ", xt , " adalah ", v)
Retrieved from "http://air.eng.ui.ac.id/index.php?title=Ahmad_Fadhil_Nugraha&oldid=14694"