Difference between revisions of "Muhammad Alief Guntur Raharjo"
(→PEMODELAN BALOK PADA PONDASI RUMAH DENGAN 3DD FRAME) |
|||
| (105 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | ==''' | + | =='''IDENTITAS'''== |
| + | |||
| + | Nama : Muhammad Alief Guntur Raharjo/ Guntur | ||
| + | |||
| + | NPM : 1806244484 | ||
| + | |||
| + | Peminatan : Perancangan dan Manufaktur Produk | ||
| + | |||
| + | Program Studi : Magister Teknik Mesin | ||
| + | |||
| + | Instansi : Universitas Indonesia | ||
| + | |||
| + | Motto hidup | ||
| + | |||
| + | إِنْ أَحْسَنتُمْ أَحْسَنتُمْ لِأَنفُسِكُمْ ۖ وَإِنْ أَسَأْتُمْ فَلَهَا ۚ فَإِذَا جَآءَ وَعْدُ ٱلْءَاخِرَةِ لِيَسُۥٓـُٔوا۟ وُجُوهَكُمْ وَلِيَدْخُلُوا۟ ٱلْمَسْجِدَ كَمَا دَخَلُوهُ أَوَّلَ مَرَّةٍ وَلِيُتَبِّرُوا۟ مَا عَلَوْا۟ تَتْبِيرًا | ||
| + | |||
| + | Jika kamu berbuat baik (berarti) kamu berbuat baik bagi dirimu sendiri dan jika kamu berbuat jahat, maka (kejahatan) itu bagi dirimu sendiri, dan apabila datang saat hukuman bagi (kejahatan) yang kedua, (Kami datangkan orang-orang lain) untuk menyuramkan muka-muka kamu dan mereka masuk ke dalam masjid, sebagaimana musuh-musuhmu memasukinya pada kali pertama dan untuk membinasakan sehabis-habisnya apa saja yang mereka kuasai. (Al-Israa': 7) | ||
| Line 11: | Line 27: | ||
Penulis dilahirkan pada 25 September 1995 dan dibesarkan di sebuah desa bernama Banjarasri. Sebuah desa di kabupaten kecil nan asri, Sragen, Jawa Tengah. Namun sejak tahun 1999, penulis bersama kedua orang tua merantau ke Surakarta, Jawa Tengah dan masih menetap di sana. | Penulis dilahirkan pada 25 September 1995 dan dibesarkan di sebuah desa bernama Banjarasri. Sebuah desa di kabupaten kecil nan asri, Sragen, Jawa Tengah. Namun sejak tahun 1999, penulis bersama kedua orang tua merantau ke Surakarta, Jawa Tengah dan masih menetap di sana. | ||
| − | Saat ini, penulis sedang menempuh studi pada peminatan '''Perancangan dan Manufaktur''' di Program Studi Magister Teknik Mesin, Fakultas Teknik, Universitas Indonesia (UI). Penulis tinggal di Kompleks Pondok Pesantren Al-Hikam 2 Jalan Haji Amat No. 4 RT. 01/ III Kukusan, Beji, Depok, Jawa Barat. Aktivitas penulis selain kuliah dan melakukan riset, juga aktif berorganisasi di Keluarga Mahasiswa Nadhatul Ulama (KMNU) UI. Sebelum hijrah ke Depok, penulis merupakan alumnus Universitas Sebelas Maret (UNS) Surakarta angkatan 2013 yang hobi | + | Saat ini, penulis sedang menempuh studi pada peminatan '''Perancangan dan Manufaktur Produk''' di Program Studi Magister Teknik Mesin, Fakultas Teknik, Universitas Indonesia (UI). Penulis tinggal di Kompleks Pondok Pesantren Al-Hikam 2 Jalan Haji Amat No. 4 RT. 01/ III Kukusan, Beji, Depok, Jawa Barat. Aktivitas penulis selain kuliah dan melakukan riset, juga aktif berorganisasi di Keluarga Mahasiswa Nadhatul Ulama (KMNU) UI. Sebelum hijrah ke Depok, penulis merupakan alumnus Universitas Sebelas Maret (UNS) Surakarta angkatan 2013 yang hobi berenang. |
| + | |||
| + | Lebih jauh, jika Saudara/ i memiliki kritik, saran, maupun uneg-uneg yang ingin disampaikan, dapat menghubungi kontak penulis berikut | ||
| − | + | [[File:Contoh7.jpg|200px|thumb|left|Penulis: Muhammad Alief Guntur Raharjo]] | |
Surel : muhammad.alief82@ui.ac.id | Surel : muhammad.alief82@ui.ac.id | ||
Instagram : @muhatur | Instagram : @muhatur | ||
| + | |||
| + | WhatsApp : 081328101724 | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| Line 23: | Line 55: | ||
Wassalamu'alaykum Wr. Wb. | Wassalamu'alaykum Wr. Wb. | ||
| − | |||
| − | |||
=='''TUGAS KOMPUTASI TEKNIK'''== | =='''TUGAS KOMPUTASI TEKNIK'''== | ||
| Line 70: | Line 100: | ||
''3. Bagaimana anda menjelaskan secara rasional dari pertanyaan berapa nilai (x^2-1)/(x-1) jika x=1?'' | ''3. Bagaimana anda menjelaskan secara rasional dari pertanyaan berapa nilai (x^2-1)/(x-1) jika x=1?'' | ||
| − | Dalam kasus tersebut, jika nilai x=1 disubstitusikan dalam fungsi tersebut maka bernilai 0/0. Hasil ini merupakan bentuk tak tentu karena hasilnya yang tidak terhingga. Berikut penjelasannya. Ketika hasil 0/0 dimisalkan sama dengan x (0/0=x maka 0.x=0) artinya kita harus menentukan nol dikalikan bilangan berapa (x) yang menghasilkan sama dengan nol, sehingga bilangan yang memenuhi tersebut (x) adalah berapapun bilangan tersebut. Hal ini yang menjadikannya tidak tentu karena penyelesaian yang tidak terhingga. Solusinya adalah mendekati fungsi tersebut dengan metode pendekatan limit fungsi. | + | Dalam kasus tersebut, jika nilai x=1 disubstitusikan dalam fungsi tersebut maka bernilai 0/0. Hasil ini merupakan bentuk tak tentu karena hasilnya yang tidak terhingga. Berikut penjelasannya. Ketika hasil 0/0 dimisalkan sama dengan x (0/0=x maka 0.x=0) artinya kita harus menentukan nol dikalikan bilangan berapa (x) yang menghasilkan sama dengan nol, sehingga bilangan yang memenuhi tersebut (x) adalah berapapun bilangan tersebut. Hal ini yang menjadikannya tidak tentu karena penyelesaian yang tidak terhingga. Oleh karena itu, saya mencoba menyelesaikan fungsi tersebut dengan pendekatan-pendekatan sebagai berikut. |
| + | |||
| + | Tabel 1 | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | !x!! (x^2 − 1)/(x − 1)! | ||
| + | |- | ||
| + | |0.5|| 1.50000 | ||
| + | |- | ||
| + | |0.9|| 1.90000 | ||
| + | |- | ||
| + | |0.99|| 1.99000 | ||
| + | |- | ||
| + | |0.999|| 1.99900 | ||
| + | |- | ||
| + | |0.9999 || 1.99990 | ||
| + | |- | ||
| + | |0.99999|| 1.99999 | ||
| + | |- | ||
| + | |…|| … | ||
| + | |} | ||
| + | |||
| + | Dari tabel 1, saya mengetahui bahwa saat x mendekati 1 maka f(x)=(x^2-1)/(x-1) mendekati 2. | ||
| + | |||
| + | Kemudian saya mencoba untuk mendekati dari sisi sebelahnya, nilainya juga mendekati 2 seperti dalam tabel 2. | ||
| + | |||
| + | Tabel 2 | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | !x !! (x^2 − 1)/ (x − 1)! | ||
| + | |- | ||
| + | |1.5|| 2.50000 | ||
| + | |- | ||
| + | |1.1 || 2.10000 | ||
| + | |- | ||
| + | |1.01 || 2.01000 | ||
| + | |- | ||
| + | |1.001 || 2.00100 | ||
| + | |- | ||
| + | |1.0001 || 2.00010 | ||
| + | |- | ||
| + | |1.00001 || 2.00001 | ||
| + | |- | ||
| + | |… || … | ||
| + | |} | ||
| + | |||
| + | Sekarang saya mempunyai 2 kondisi yaitu saat x=1 kita tidak mengetahui jawabannya ''(indeterminate)'' namun nilainya mendekati 2. Saat kita menjawab 2 juga tidak sepenuhnya benar, karena menggunakan metode pendekatan limit fungsi f(x) mendekati 1. Solusinya adalah mendekati fungsi tersebut dengan metode pendekatan limit fungsi. | ||
lim┬(x→1)〖 (x^2-1)/(x-1)〗= lim┬(x→1)〖 ((x+1) (x-1))/(x-1)〗 | lim┬(x→1)〖 (x^2-1)/(x-1)〗= lim┬(x→1)〖 ((x+1) (x-1))/(x-1)〗 | ||
| Line 83: | Line 161: | ||
| − | =='''DISKUSI | + | =='''DISKUSI KELAS'''== |
''1. Diskusi 11 Februari 2019'' | ''1. Diskusi 11 Februari 2019'' | ||
| Line 89: | Line 167: | ||
'''Pemodelan (Modelling)''' | '''Pemodelan (Modelling)''' | ||
| − | + | '''Pemodelan''' adalah sebuah proses penyederhanaan dari sebuah sistem yang rumit. Tujuan pemodelan adalah untuk mempelajari behaviour dari target masalah yang dikaji. Misal dalam permasalahan perencanaan jembatan di selat Sunda yang menghubungkan antara pulau Jawa dan Sumatera, maka dilakukan simplifikasi dalam pemodelannya. Hal ini dilakukan simplifikasi khususnya factor dominan yang mempengaruhi konstruksi dan keamanan dari jembatan yang akan dibuat, factor dominan tersebut adalah kecepatan dan arah angin yang berpotensi membebani struktur jembatan tersebut. | |
| + | |||
| + | '''Komputasi teknik''' adalah suatu pelajaran yang memiliki tujuan membekali diri dengan pengetahuan untuk menyelesaikan permasalahan Teknik dengan metode pemodelan/modeling. Misal pada permasalahan perancangan dan pembuatan jembatan, dilakukan dengan memodelkan secara numerik. Komputasi Teknik dimulai dari adanya permasalahan (problem). Dalam memahami masalah yang akan diselesaikan, tahap pertama adalah melakukan analisis awal (pemikiran awal). Pemikiran awal merupakan suatu hipotesis, yaitu sebuah tesis yang belum ''firmly accepted'' yang akan dibuktikan dengan percobaan. | ||
| + | |||
| + | '''Tahap-tahap pemodelan''' | ||
| + | |||
| + | 1. Menentukan permasalahan | ||
| + | |||
| + | 2. Melakukan analisis awal (pemikiran awal). Dalam tahap ini dilakukan asumsi-asumsi yang berupa hipotesis untuk dibuktikan dalam percobaan. | ||
| + | |||
| + | 3. Algoritma | ||
| + | |||
| + | 4. Model Komputasi | ||
| + | |||
| + | 5. Eksekusi model (simulasi) | ||
| + | |||
| + | 6. Hasil perhitungan | ||
| + | |||
| + | 7. Report | ||
| + | |||
| + | '''Komputasi Teknik''' dapat digunakan untuk mengembangkan ilmu atau mendapatkan ilmu, sehingga pada akhirnya memperoleh pemahaman dengan akal bahwa hasil yang diperoleh dari pembelajaran tersebut bermanfaat/berguna bagi diri sendiri, bukan untuk Tuhan (karena Tuhan memiliki sifat infinite). | ||
| + | Ilmu mekanik adalah disiplin ilmu yang mempelajari gerak laku sebuah benda. material disini memiliki arti luas tidak terbatas pada material logam, tapi seluruh material baik tubuh manusia, angina, tumbuhan dan seterusnya. Sebuah gaya adalah tarikan atau dorongan. jadi mekanikal bisa berbentukfisik atau non fisik. Dalam fisik, gaya berlaku pada suatu materi. | ||
| + | |||
| + | '''''Contoh Kasus''''' : Salah satu tantangan dalam desain adalah menghasilkan desain yang kuat, tahan lama, dan ekonomis. Misal dalam kasus pembuatan pondasi bangunan rumah panggung. Parameter dari desain pondasi tersebut adalah tahan lama, kuat, dan ekonomis. Hal ini disebut dengan structure integrity, dimana integrity disini bermakna struktur yang didesain bersifat kuat, tahan lama, dan ekonomis, dengan mengikuti batas ijin dan memasukkan FOS (Factor of Safety) | ||
| + | |||
| + | |||
| + | Sekian. | ||
| + | |||
| + | |||
| + | |||
| + | =='''ANALISIS STRUKTUR PONDASI RUMAH PANGGUNG'''== | ||
| + | |||
| + | ''Dosen Pengampu : Bapak Dr. Ir. Ahmad Indra Siswantara (Pak DAI)'' | ||
| + | |||
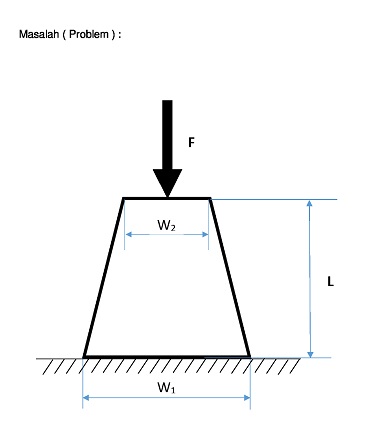
| + | [[File:Problem.jpg]] | ||
| + | [[File:Alur.jpg]] | ||
| + | |||
| + | [[File:Flowchart gtr.jpg]] | ||
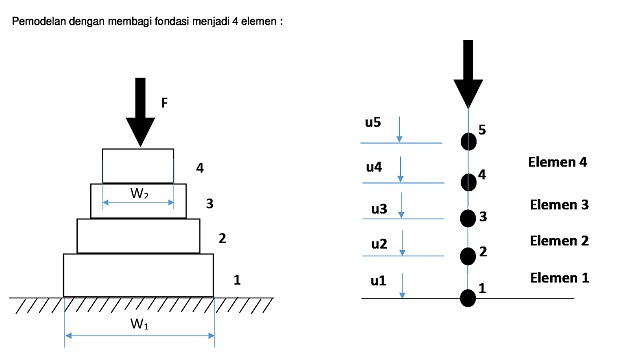
| + | [[File:Pemodelan.jpg]] | ||
| + | |||
| + | Asumsi untuk tiap-tiap notasi adalah : | ||
| + | |||
| + | E = 215*10^3 [N/mm^2] | ||
| + | |||
| + | W1 = 25 [mm] | ||
| + | |||
| + | W2 = 15 [mm] | ||
| + | |||
| + | t = 2 [mm] | ||
| + | |||
| + | L = 20 [mm] | ||
| + | |||
| + | La = L/4 | ||
| + | |||
| + | u1 = 0 [mm] | ||
| + | |||
| + | F = 15 [N] | ||
| + | |||
| + | |||
| + | A1 = (W1+(((W2-W1)/L)*0))*t | ||
| + | |||
| + | A2 = (W1+(((W2-W1)/L)*5))*t | ||
| + | |||
| + | A3 = (W1+(((W2-W1)/L)*10))*t | ||
| + | |||
| + | A4 = (W1+(((W2-W1)/L)*15))*t | ||
| + | |||
| + | A5 = (W1+(((W2-W1)/L)*20))*t | ||
| + | |||
| + | |||
| + | K1 = ((A2+A1)*E)/(2*La) | ||
| + | |||
| + | K2 = ((A3+A2)*E)/(2*La) | ||
| + | |||
| + | K3 = ((A4+A3)*E)/(2*La) | ||
| + | |||
| + | K4 = ((A5+A4)*E)/(2*La) | ||
| + | |||
| + | |||
| + | Teg1 = E*((u2-u1)/La | ||
| + | |||
| + | Teg2 = E*((u3-u2)/La | ||
| + | |||
| + | Teg3 = E*((u4-u3)/La | ||
| + | |||
| + | Teg4= E*((u5-u4)/La | ||
| − | |||
| − | + | ((K1+K2)*u2)+(-K2*u3)=0 | |
| + | |||
| + | (-K2*u2)+((K2+K3)*u3)+(-K3*u4)=0 | ||
| + | |||
| + | (-K3*u3)+((K3+K4)*u4)+(-K4*u5)=0 | ||
| + | |||
| + | (-K4+u4)+(-K4*u5)=F | ||
| + | |||
| + | EES (Engineering Equation Solver) | ||
| + | |||
| + | [[File:EES.png]] | ||
| + | |||
| + | Output EES | ||
| + | |||
| + | [[File:Output.png]] | ||
| + | |||
| + | |||
| + | Sekian. | ||
| + | |||
| + | ''2. Diskusi Kelas 11 Maret 2019'' | ||
| + | |||
| + | Sharing masalah mengenai penggunaan perangkat lunak 3DD Software | ||
| + | |||
| + | |||
| + | |||
| + | =='''RANCANGAN ANGGARAN BIAYA RUMAH'''== | ||
| + | |||
| + | ''Dosen Pengampu : Bapak Dr. Ir. Ahmad Indra Siswantara (Pak DAI)'' | ||
| + | |||
| + | Rumah adalah sebuah bangunan yang dibutuhkan oleh setiap makhluk hidup untuk menunjang kehidupan. Dalam membangun sebuah rumah, hal kecil namun penting yang harus kita lakukan adalah menyusun dan merancang Rancangan Anggaran dan Biaya (RAB). Berikut penulis sajikan contoh simulasi sederhana mengenai RAB rumah tipe 80 [https://drive.google.com/file/d/1hb-rjjlvJxYWn8aqa2TVzhVT5jax7srR/view?usp=sharing] | ||
| + | |||
| + | '''''Detail Engineering Design (DED)''''' | ||
| + | |||
| + | [[File:Contoh1.png]] | ||
| + | |||
| + | Sumber : Desain Griya | ||
| + | |||
| + | Itu merupakan contoh RAB, bagaimana sudah ada gambaran kan ya untuk membangun rumah. Saat ini penulis baru dapat memberikan contoh simulasi pembangunan rumah, mohon do'anya untuk bisa segera membangun rumah tangga. Hehee ^_^ | ||
| + | |||
| + | |||
| + | Sekian. | ||
| + | |||
| + | |||
| + | |||
| + | =='''QUIZ KOMPUTASI TEKNIK'''== | ||
| + | |||
| + | ''Dosen Pengampu : Bapak Dr. Ir. Ahmad Indra Siswantara (Pak DAI)'' | ||
| + | |||
| + | Anda diminta untuk membuat sebuah model komputasi untuk membuat bangunan yang akan digunakan untuk usaha ''service'' (layanan) penyewaan rumah/ kamar. Jalankan simulasi terhadap model tersebut untuk memutuskan kelayakan usaha tersebut (teknis dan ekonomis)! | ||
| + | |||
| + | '''Analisa awal :''' | ||
| + | |||
| + | Saya memiliki sebidang tanah dengan '''luas tanah dan bangunan 300 m2''' (10x30 m). Saya merencanakan membangun suatu unit usaha berupa penyewaan kamar (indekos). Dari luasan itu akan dibuat '''kamar''' sebanyak '''17 buah''' dengan luas setiap kamar 3x5,8 m dengan kamar mandi dalam. | ||
| + | |||
| + | [[File:Contoh2.jpg]] | ||
| + | |||
| + | '''Asumsi :''' | ||
| + | |||
| + | Harga tanah per m2 di daerah Surakarta adalah Rp 1.000.000,00 [1 juta] | ||
| + | |||
| + | Harga membangun rumah indekos di daerah Surakarta adalah Rp 700.000,00 [0,7 juta] | ||
| + | |||
| + | Biaya pembelian berbagai perabotan Rp 500.000,00 [0,5 juta] | ||
| + | |||
| + | Pengurusan perizinan usaha Rp 10.000.000,00 [10 juta] | ||
| + | |||
| + | TDL listrik setiap bulan Rp 250.000,00 [0,25 juta] | ||
| + | |||
| + | TDA air setiap bulan Rp 100.000,00 [0,1 juta] | ||
| + | |||
| + | Pemeliharaan setiap bulan Rp 500.000,00 [0,5 juta] | ||
| + | |||
| + | '''Harga sewa kamar indekos setiap bulan Rp 500.000,00 [0,5 juta]''' | ||
| + | |||
| + | '''Rancangan Anggaran Bangunan :''' | ||
| + | |||
| + | Biaya pembelian tanah = luas tanah (m2) x harga tanah (/m2) = Rp 300.000.000,00 [300 juta] | ||
| + | |||
| + | Biaya pembangunan indekos = luas tanah (m2) x biaya (/m2) = Rp 210.000.000,00 [210 juta] | ||
| + | |||
| + | Beli perabotan = biaya beli x jumlah kamar = Rp 8.500.000,00 [8,5 juta] | ||
| + | |||
| + | '''Total pembangunan = tanah + bangunan + perabotan + izin = Rp 528.500.000,00 [528,5 juta]''' | ||
| + | |||
| + | TDL listrik setahun = TDL bulanan x 12 = Rp 3.000.000,00 [3 juta] | ||
| + | |||
| + | TDA air setahun = operasional bulanan x 12 = Rp 1.200.000,00 [1,2 juta] | ||
| + | |||
| + | Pemeliharaan setahun = pemeliharaan bulanan x 12 = Rp 6.000.000,00 [6 juta] | ||
| + | |||
| + | '''Biaya operasional setahun = (TDL + TDA + pemeliharaan) = Rp 10.200.000,00 [10,2 juta]''' | ||
| + | |||
| + | '''Perhitungan Break Event Point (BEP) :''' | ||
| + | |||
| + | Jika saya mengasumsikan kamar indekos penuh setiap bulan sepanjang tahun maka pemasukan yang dapat diperoleh sebesar | ||
| + | |||
| + | Pemasukan/ tahun = banyak kamar x harga sewa x 12 bulan = Rp 120.000.000,00 [120 juta] | ||
| + | |||
| + | Laba/ tahun = pemasukan/ tahun – biaya operasional/ tahun = Rp 109.800.000,00 [109,8 juta] | ||
| + | |||
| + | '''BEP (tahun)''' = (total pembangunan)/(laba setiap tahun) = 4,813 ≃ '''4 tahun 9 bulan''' | ||
| + | |||
| + | '''Komputasi''' | ||
| + | |||
| + | Simulasi analisis perhitungan komputer (komputasi) menggunakan Engineering Equation Solver (EES) sebagai berikut : | ||
| + | |||
| + | EES Formula | ||
| + | |||
| + | [[File:Contoh3.png]] | ||
| + | [[File:Contoh4.png]] | ||
| + | |||
| + | [[File:Contoh5.png]] | ||
| + | |||
| + | EES Solving | ||
| + | |||
| + | [[File:Contoh6.png]] | ||
| + | |||
| + | |||
| + | Saudara/ i dapat mengetahui selengkapnya dengan mengklik tautan berikut | ||
| + | |||
| + | '''Analisa Kelayakan Bangunan Untuk Usaha Penyewaan Kamar''' [https://drive.google.com/file/d/1yk6HEslxSXzj_LM2GHZDEEO-SsPdaUjQ/view?usp=sharing] | ||
| + | |||
| + | |||
| + | Sekian. | ||
| + | |||
| + | |||
| + | |||
| + | =='''PEMODELAN ATAP RUMAH DENGAN 3DD FRAME'''== | ||
| + | |||
| + | Pada pembahasan kali ini, penulis ingin membagikan mengenai pemodelan atap dengan perangkat lunak 3DD Frame. Atap dirancang mengikuti konstruksi bangunan rumah kos. Adapun konstruksi bangunan rumah kos tersebut telah dirancang sebelumnya. | ||
| + | |||
| + | Untuk melakukan analisa Truss pada atap tersebut, penulis melakukan rekayasa program (coding). Coding ini akan membantu dalam melakukan pengolahan pada 3DD Frame. Coding dibuat dalam bentuk file .csv dimana didalamnya memuat beberapa informasi, seperti | ||
| + | |||
| + | 1. Jumlah Node dan koordinat tiap node pada desain atap | ||
| + | |||
| + | 2. Constraint dari atap tersebut, dimana pada simuasi ini constrint diletakan pada seluruh node pada bagian bawah | ||
| + | |||
| + | 3. Jumlah frame yang terdapat pada desain atap, ditambah dengan beberapa informasi seperti: besar luas penampang dari tiap frame, inersia frame, modulus elastisitas, modulus geser dan massa jenis | ||
| + | |||
| + | 4. Arah dan gaya gravitasi yang bekerja pada model uji | ||
| + | |||
| + | 5. Jumlah kasus pembebanan statis yang dialami oleh model uji | ||
| + | |||
| + | Berikut coding untuk melakukan analisa Truss atap [https://drive.google.com/file/d/1X1Z7AgVFigOZlfw9fp63izAtb6Liq_PT/view?usp=sharing] | ||
| + | |||
| + | Setelah melakukan coding, kemudian dilakukan simulasi menggunakan 3DD Frame. Simulasi dilakukan dengan memasukkan file ekstensi .csv dan memberikan nama file untuk hasil simulasinya dalam 3DD Frame | ||
| + | |||
| + | [[File:Contoh10.png]] | ||
| + | |||
| + | [[File:Contoh11.png]] | ||
| + | |||
| + | '''Hasil simulasi 3DD Frame''' | ||
| + | |||
| + | Hasil simulasi oleh 3DD Framen ini berisi data displacement pada tiap node, gaya yang diterima oleh tiap frame, dan reaksi yang diberikan oleh tiap-tiap node. Hasil plotingan simulasi sebagai berikut | ||
| + | |||
| + | [[File:Contoh12.png]] | ||
| + | |||
| + | |||
| + | Sekian. | ||
| + | |||
| + | |||
| + | |||
| + | =='''PEMODELAN BEAM RUMAH DENGAN 3DD FRAME'''== | ||
| + | |||
| + | Pemodelan beam sangat diperlukan dalam pembangunan konstruksi suatu bangunan. Pada kesempatan ini, penulis ingin membagikan ilmu mengenai analisa dan pemodelan beam pada rumah kos dengan perangkat lunak 3DD Frame. Berikut analisanya | ||
| + | |||
| + | Langkah-langkah dalam analisa beam sebagai berikut | ||
| + | |||
| + | 1. Membuat dan menyimpan coding dalam dokumen Microsoft Excel berektensi '.csv'. Berikut coding beam tersebut [https://drive.google.com/file/d/1tbMnetyyYz5FWFjZ_rtuulRYato1Ijhi/view?usp=sharing] | ||
| + | |||
| + | 2. Double klik program 3DD Frame untuk membuka dan menjalankannya | ||
| + | |||
| + | 3. Masukkan inputan sesuai nama dokumen .csv tersebut | ||
| + | |||
| + | 4. Memberikan nama dokumen output yang Saudara kehendaki | ||
| + | |||
| + | 5. Pemodelan telah selesai dilakukan. | ||
| + | |||
| + | Berikut hasil analisa dan pemodelan beam rumah penulis | ||
| + | |||
| + | Hasil analisa [https://drive.google.com/file/d/1l-vKNtT2snwiz6EycZ4CRNsXI9ue48zf/view?usp=sharing] | ||
| + | |||
| + | Hasil pemodelan | ||
| + | |||
| + | [[File:Contoh9.png]] | ||
| + | |||
| + | |||
| + | Sekian. | ||
| + | |||
| + | |||
| + | |||
| + | =='''PEMODELAN BALOK PONDASI RUMAH DENGAN 3DD FRAME'''== | ||
| + | |||
| + | Pemodelan balok pada suatu pondasi rumah menjadi salah satu hal penting yang juga harus dianalisa untuk mengetahui besarnya beban yang dapat ditumpu dengan pemilihan profil material yang sesuai. Berikut analisa sederhana balok pondasi penulis. | ||
| + | |||
| + | 1. Coding balok [https://drive.google.com/file/d/15Tl_a9vhcY2ANF0TIRdOyVghrnDy5jAF/view?usp=sharing] | ||
| + | |||
| + | 2. Hasil analisa [https://drive.google.com/file/d/1iEc6WiKgycGm84UykYvEXZvGfg3991Zg/view?usp=sharing] | ||
| + | |||
| + | 3. Hasil pemodelan | ||
| + | |||
| + | [[File:Contoh13.png]] | ||
| + | |||
| + | |||
| + | Sekian. | ||
| + | |||
| + | =='''UJIAN TENGAH SEMESTER (UTS)'''== | ||
| + | |||
| + | UTS ini diadakan pada tanggal 25 Maret 2019 dengan sistematika membuat pertanyaan dan jawaban secara mandiri berdasarkan tujuan pembelajaran komputasi teknik, yaitu | ||
| + | |||
| + | 1. Memahami konsep-konsep dalam Komputasi Teknik dan mengaplikasikannya, | ||
| + | |||
| + | 2. Mampu mengenali diri sendiri lebih baik, | ||
| + | |||
| + | 3. Skor kelayakan nilai yang patut didapatkan, | ||
| + | |||
| + | 4. Menuliskan 5 orang teman yang memiliki kapabilitas dalam komputasi teknik beserta alasannya, | ||
| + | |||
| + | |||
| + | Sekian. | ||
| + | |||
| + | |||
| + | |||
| + | =='''MOMEN INERSIA'''== | ||
| + | |||
| + | Tugas-tugas berikut mengenai analisa profil beam, seperti yang dijelaskan berikut | ||
| + | |||
| + | 1. Menghitung Momen Inertia pada sembarang bentuk profil [https://drive.google.com/file/d/1MgFuUxvsQEqMC1vMYrGb4TZmxPyZ5KCX/view?usp=sharing] | ||
| + | |||
| + | 2. Menghitung Momen Inertia pada H beam dengan bentuk profil I [https://drive.google.com/file/d/1OBDFQdKsoT2FOgOoZDZASSvKhvoCWibM/view?usp=sharing] | ||
| + | |||
| + | |||
| + | Sekian. | ||
| + | |||
| + | |||
| + | |||
| + | =='''TUGAS BESAR (PROYEK)'''== | ||
| + | |||
| + | ''Tema'' | ||
| + | |||
| + | Aplikasi Komputasi Teknik Dalam Desain dan Analitis “Zero Energy Building (ZEB)” | ||
| + | |||
| + | ''Topik/ Judul'' | ||
| + | |||
| + | '''APLIKASI KOMPUTASI TEKNIK DALAM PERANCANGAN RUMAH KOS BAROKAH BERKONSEP ''ZERO ENERGY BUILDINGS'' (ZEBs)''' | ||
| + | |||
| + | ''Subtopik" | ||
| + | |||
| + | Analisis Struktur | ||
| + | |||
| + | ''Sinopsis'' | ||
| + | |||
| + | ZEB merupakan bangunan dengan konsumsi energi nol. Bangunan ZEB diinisiasi karena kebutuhan dan kesadaran dalam mengurangi emisi karbon yang timbul akibat penggunaan energi fosil yang massif. Dalam tugas besar (proyek) komputasi teknik ini, kami mencoba untuk merancang sebuah bangunan berupa rumah yang dapat disewakan setiap kamarnya. Proyek ini dikerjakan dan diawasi bersama secara gotong-royong oleh : | ||
| + | |||
| + | 1. Helmi Surya Putra | ||
| + | |||
| + | 2. Muchamad Panji | ||
| + | |||
| + | 3. Muhammad Alief Guntur Raharjo | ||
| + | |||
| + | 4. Yunus Bakhtiar Arafat | ||
| + | |||
| + | Perancangan rumah tinggal ini direncanakan berlokasi di Depok, Jawa Barat. Konsep bangunan yang akan kami bangun berupa rumah tiga lantai yang dilengkapi berbagai sumber energi terbarukan untuk menerapkan konsep ZEB. Adapun luas bangunan 18x25 m2 dan luas kamar 3x5 m2. Pada setiap lantai terdapat 20 kamar tidur yang dapat disewakan dengan kamar mandi dalam. | ||
| + | |||
| + | Analisis yang akan kami kerjakan berupa : | ||
| + | |||
| + | • '''Analisis biaya''' pembangunan dan operasional, meliputi pemilihan material dalam pembangunan, perhitungan BEP ''(Break Event Point)'', dan penentuan harga sewa | ||
| + | |||
| + | • '''Analisis struktur''', meliputi analisis statis dan dinamis (angin dan guncangan gempa) bangunan | ||
| + | |||
| + | • '''Analisis energi ZEB''', meliputi pemenuhan kebutuhan energi dasar seperti listrik, air, dan gas bangunan | ||
| + | |||
| + | |||
| + | Sekian. | ||
| + | |||
| + | |||
| + | |||
| + | =='''PROGRESS TUGAS BESAR (PROYEK)'''== | ||
| + | |||
| + | APLIKASI KOMPUTASI TEKNIK DALAM PERANCANGAN RUMAH KOS BAROKAH BERKONSEP ''ZERO ENERGY BUILDINGs'' (ZEBs) - Muh. Alief Guntur R. | ||
| + | |||
| + | 1. Senin, 29 April 2019 (Progress 30%) [http://air.eng.ui.ac.id/index.php?title=Aplikasi_Komputasi_Teknik_Dalam_Perancangan_Rumah_Kos_Barokah_Berkonsep_Zero_Energy_Building] | ||
| + | |||
| + | |||
| + | Sekian. | ||
Latest revision as of 08:48, 6 May 2019
Contents
- 1 IDENTITAS
- 2 TENTANG PENULIS
- 3 TUGAS KOMPUTASI TEKNIK
- 4 DISKUSI KELAS
- 5 ANALISIS STRUKTUR PONDASI RUMAH PANGGUNG
- 6 RANCANGAN ANGGARAN BIAYA RUMAH
- 7 QUIZ KOMPUTASI TEKNIK
- 8 PEMODELAN ATAP RUMAH DENGAN 3DD FRAME
- 9 PEMODELAN BEAM RUMAH DENGAN 3DD FRAME
- 10 PEMODELAN BALOK PONDASI RUMAH DENGAN 3DD FRAME
- 11 UJIAN TENGAH SEMESTER (UTS)
- 12 MOMEN INERSIA
- 13 TUGAS BESAR (PROYEK)
- 14 PROGRESS TUGAS BESAR (PROYEK)
IDENTITAS
Nama : Muhammad Alief Guntur Raharjo/ Guntur
NPM : 1806244484
Peminatan : Perancangan dan Manufaktur Produk
Program Studi : Magister Teknik Mesin
Instansi : Universitas Indonesia
Motto hidup
إِنْ أَحْسَنتُمْ أَحْسَنتُمْ لِأَنفُسِكُمْ ۖ وَإِنْ أَسَأْتُمْ فَلَهَا ۚ فَإِذَا جَآءَ وَعْدُ ٱلْءَاخِرَةِ لِيَسُۥٓـُٔوا۟ وُجُوهَكُمْ وَلِيَدْخُلُوا۟ ٱلْمَسْجِدَ كَمَا دَخَلُوهُ أَوَّلَ مَرَّةٍ وَلِيُتَبِّرُوا۟ مَا عَلَوْا۟ تَتْبِيرًا
Jika kamu berbuat baik (berarti) kamu berbuat baik bagi dirimu sendiri dan jika kamu berbuat jahat, maka (kejahatan) itu bagi dirimu sendiri, dan apabila datang saat hukuman bagi (kejahatan) yang kedua, (Kami datangkan orang-orang lain) untuk menyuramkan muka-muka kamu dan mereka masuk ke dalam masjid, sebagaimana musuh-musuhmu memasukinya pada kali pertama dan untuk membinasakan sehabis-habisnya apa saja yang mereka kuasai. (Al-Israa': 7)
TENTANG PENULIS
Assalamu'alaykum Wr. Wb.
Mohon izin memperkenalkan diri ya :))
Penulis dilahirkan pada 25 September 1995 dan dibesarkan di sebuah desa bernama Banjarasri. Sebuah desa di kabupaten kecil nan asri, Sragen, Jawa Tengah. Namun sejak tahun 1999, penulis bersama kedua orang tua merantau ke Surakarta, Jawa Tengah dan masih menetap di sana.
Saat ini, penulis sedang menempuh studi pada peminatan Perancangan dan Manufaktur Produk di Program Studi Magister Teknik Mesin, Fakultas Teknik, Universitas Indonesia (UI). Penulis tinggal di Kompleks Pondok Pesantren Al-Hikam 2 Jalan Haji Amat No. 4 RT. 01/ III Kukusan, Beji, Depok, Jawa Barat. Aktivitas penulis selain kuliah dan melakukan riset, juga aktif berorganisasi di Keluarga Mahasiswa Nadhatul Ulama (KMNU) UI. Sebelum hijrah ke Depok, penulis merupakan alumnus Universitas Sebelas Maret (UNS) Surakarta angkatan 2013 yang hobi berenang.
Lebih jauh, jika Saudara/ i memiliki kritik, saran, maupun uneg-uneg yang ingin disampaikan, dapat menghubungi kontak penulis berikut
Surel : muhammad.alief82@ui.ac.id
Instagram : @muhatur
WhatsApp : 081328101724
Terima kasih ^_^
Wassalamu'alaykum Wr. Wb.
TUGAS KOMPUTASI TEKNIK
Dosen Pengampu : Bapak Dr. Ir. Ahmad Indra Siswantara (Pak DAI)
1. Resume Diskusi Kelas 04 Februari
Penciptaan manusia oleh Allah SWT sebagai makhluk hidup dianugerahi oleh akal. Akal ini yang membedakan antara manusia, binatang, dan tumbuhan sebagai makhluk hidup. Kemudian sebagai insan pelajar yang sedang belajar komputasi teknik, diperlukan prasayaray berupa akal untuk menunjang kesuksesan dalam proses belajar tersebut. Dalam pembelajaran komputasi teknik hendaknya kita harus memahami beberapa konsep berikut :
1. Konsep algoritma
2. Konsep flowchart
3. Konsep model matematis
4. Konsep akurat
5. Konsep error
6. Konsep iterasi
Proses pembelajaran terkadang menemui kendala. Kendala ini hendaknya dijadikan refleksi agar menjadi pribadi yang lebih mengetahui dalam mengenali dan memahami diri sendiri serta menghindarkan dari kebodohan dalam mengenali diri tersebut. Adapun beberapa kendalanya antara lain :
1. Kedudukan
2. Harta atau materi
3. Pengikut atau follower
4. Maksiat
Hal tersebut merupakan kendala dalam mengenali diri yang dapat berujung pada kebodohan manusia yang berakal. Sejatinya manusia berakal adalah manusia yang selalu mengingat Allah ketika berdiri, duduk, atau dalam keadan berbaring dan memikirkan tentang penciptaan langit dan bumi (seraya berkata): “Ya Tuhan Kami, tiada Engkau menciptakan ini dengan sia-sia, Maha Suci Engkau, maka peliharalah Kami dari siksa neraka (Q.S. Ali ‘Imran: 91). Asbabun Nuzul Q.S. Ali ‘Imran: 91. Penciptaan Allah yang ada di langit dan bumi tentunya banyak (infinite) dan tidak ada yang tidak bermanfaat, sesuai terkandung dalam Al-Qur’an tersebut. Kita sebagai insan yang berakal diharuskan mampu menggunakan akal secara sehat (rasio) untuk menyusun, mengenali, dan menafsirkan segala penciptaanNya (persepsi) yang akan membawa kita mendekati ke suatu titik yaitu menambah rasa syukur pada Sang Pencipta.
2. Jelaskan konsep “Infinite”!
Konsep infinite dalam dunia komputasi erat kaitannya dengan permasalahan limit fungsi yang berbentuk pecahan ketika fungsi tersebut didekati oleh bilangan tak terhingga. Sebagai contoh sederhana,
lim┬(x→∞)〖 1/x〗=⋯
Suatu pecahan bernilai semakin besar ketika penyebutnya semakin kecil dan pembilangnya semakin besar, begitupun sebaliknya. Pada kasus tersebut, penyebut pecahannya didekati oleh bilangan tak terhingga yang nilainya semakin besar, dengan pembilang yang hanya bernilai 1. Akibatnya, nilai limit pecahan tersebut semakin kecil mendekati 0. Penjelasan konsep infinite yaitu jika suatu pecahan limit fungsi didekati oleh suatu bilangan tak terhingga maka pecahan limit fungsi tersebut bernilai semakin besar atau kecil dimana bergantung pada pembilang dan penyebutnya, lalu hasilnya akan mendekati suatu nilai tertentu.
3. Bagaimana anda menjelaskan secara rasional dari pertanyaan berapa nilai (x^2-1)/(x-1) jika x=1?
Dalam kasus tersebut, jika nilai x=1 disubstitusikan dalam fungsi tersebut maka bernilai 0/0. Hasil ini merupakan bentuk tak tentu karena hasilnya yang tidak terhingga. Berikut penjelasannya. Ketika hasil 0/0 dimisalkan sama dengan x (0/0=x maka 0.x=0) artinya kita harus menentukan nol dikalikan bilangan berapa (x) yang menghasilkan sama dengan nol, sehingga bilangan yang memenuhi tersebut (x) adalah berapapun bilangan tersebut. Hal ini yang menjadikannya tidak tentu karena penyelesaian yang tidak terhingga. Oleh karena itu, saya mencoba menyelesaikan fungsi tersebut dengan pendekatan-pendekatan sebagai berikut.
Tabel 1
| x | (x^2 − 1)/(x − 1)! |
|---|---|
| 0.5 | 1.50000 |
| 0.9 | 1.90000 |
| 0.99 | 1.99000 |
| 0.999 | 1.99900 |
| 0.9999 | 1.99990 |
| 0.99999 | 1.99999 |
| … | … |
Dari tabel 1, saya mengetahui bahwa saat x mendekati 1 maka f(x)=(x^2-1)/(x-1) mendekati 2.
Kemudian saya mencoba untuk mendekati dari sisi sebelahnya, nilainya juga mendekati 2 seperti dalam tabel 2.
Tabel 2
| x | (x^2 − 1)/ (x − 1)! |
|---|---|
| 1.5 | 2.50000 |
| 1.1 | 2.10000 |
| 1.01 | 2.01000 |
| 1.001 | 2.00100 |
| 1.0001 | 2.00010 |
| 1.00001 | 2.00001 |
| … | … |
Sekarang saya mempunyai 2 kondisi yaitu saat x=1 kita tidak mengetahui jawabannya (indeterminate) namun nilainya mendekati 2. Saat kita menjawab 2 juga tidak sepenuhnya benar, karena menggunakan metode pendekatan limit fungsi f(x) mendekati 1. Solusinya adalah mendekati fungsi tersebut dengan metode pendekatan limit fungsi.
lim┬(x→1)〖 (x^2-1)/(x-1)〗= lim┬(x→1)〖 ((x+1) (x-1))/(x-1)〗
lim┬(x→1)〖 (x^2-1)/(x-1)〗= lim┬(x→1)〖 (x+1)〗
lim┬(x→1)〖 (x^2-1)/(x-1)〗=2
Sekian.
DISKUSI KELAS
1. Diskusi 11 Februari 2019
Pemodelan (Modelling)
Pemodelan adalah sebuah proses penyederhanaan dari sebuah sistem yang rumit. Tujuan pemodelan adalah untuk mempelajari behaviour dari target masalah yang dikaji. Misal dalam permasalahan perencanaan jembatan di selat Sunda yang menghubungkan antara pulau Jawa dan Sumatera, maka dilakukan simplifikasi dalam pemodelannya. Hal ini dilakukan simplifikasi khususnya factor dominan yang mempengaruhi konstruksi dan keamanan dari jembatan yang akan dibuat, factor dominan tersebut adalah kecepatan dan arah angin yang berpotensi membebani struktur jembatan tersebut.
Komputasi teknik adalah suatu pelajaran yang memiliki tujuan membekali diri dengan pengetahuan untuk menyelesaikan permasalahan Teknik dengan metode pemodelan/modeling. Misal pada permasalahan perancangan dan pembuatan jembatan, dilakukan dengan memodelkan secara numerik. Komputasi Teknik dimulai dari adanya permasalahan (problem). Dalam memahami masalah yang akan diselesaikan, tahap pertama adalah melakukan analisis awal (pemikiran awal). Pemikiran awal merupakan suatu hipotesis, yaitu sebuah tesis yang belum firmly accepted yang akan dibuktikan dengan percobaan.
Tahap-tahap pemodelan
1. Menentukan permasalahan
2. Melakukan analisis awal (pemikiran awal). Dalam tahap ini dilakukan asumsi-asumsi yang berupa hipotesis untuk dibuktikan dalam percobaan.
3. Algoritma
4. Model Komputasi
5. Eksekusi model (simulasi)
6. Hasil perhitungan
7. Report
Komputasi Teknik dapat digunakan untuk mengembangkan ilmu atau mendapatkan ilmu, sehingga pada akhirnya memperoleh pemahaman dengan akal bahwa hasil yang diperoleh dari pembelajaran tersebut bermanfaat/berguna bagi diri sendiri, bukan untuk Tuhan (karena Tuhan memiliki sifat infinite). Ilmu mekanik adalah disiplin ilmu yang mempelajari gerak laku sebuah benda. material disini memiliki arti luas tidak terbatas pada material logam, tapi seluruh material baik tubuh manusia, angina, tumbuhan dan seterusnya. Sebuah gaya adalah tarikan atau dorongan. jadi mekanikal bisa berbentukfisik atau non fisik. Dalam fisik, gaya berlaku pada suatu materi.
Contoh Kasus : Salah satu tantangan dalam desain adalah menghasilkan desain yang kuat, tahan lama, dan ekonomis. Misal dalam kasus pembuatan pondasi bangunan rumah panggung. Parameter dari desain pondasi tersebut adalah tahan lama, kuat, dan ekonomis. Hal ini disebut dengan structure integrity, dimana integrity disini bermakna struktur yang didesain bersifat kuat, tahan lama, dan ekonomis, dengan mengikuti batas ijin dan memasukkan FOS (Factor of Safety)
Sekian.
ANALISIS STRUKTUR PONDASI RUMAH PANGGUNG
Dosen Pengampu : Bapak Dr. Ir. Ahmad Indra Siswantara (Pak DAI)
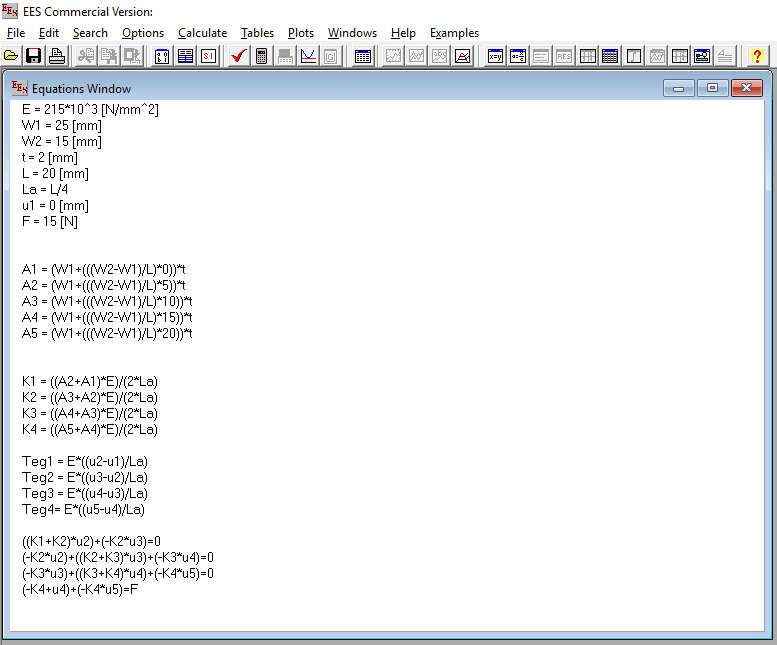
Asumsi untuk tiap-tiap notasi adalah :
E = 215*10^3 [N/mm^2]
W1 = 25 [mm]
W2 = 15 [mm]
t = 2 [mm]
L = 20 [mm]
La = L/4
u1 = 0 [mm]
F = 15 [N]
A1 = (W1+(((W2-W1)/L)*0))*t
A2 = (W1+(((W2-W1)/L)*5))*t
A3 = (W1+(((W2-W1)/L)*10))*t
A4 = (W1+(((W2-W1)/L)*15))*t
A5 = (W1+(((W2-W1)/L)*20))*t
K1 = ((A2+A1)*E)/(2*La)
K2 = ((A3+A2)*E)/(2*La)
K3 = ((A4+A3)*E)/(2*La)
K4 = ((A5+A4)*E)/(2*La)
Teg1 = E*((u2-u1)/La
Teg2 = E*((u3-u2)/La
Teg3 = E*((u4-u3)/La
Teg4= E*((u5-u4)/La
((K1+K2)*u2)+(-K2*u3)=0
(-K2*u2)+((K2+K3)*u3)+(-K3*u4)=0
(-K3*u3)+((K3+K4)*u4)+(-K4*u5)=0
(-K4+u4)+(-K4*u5)=F
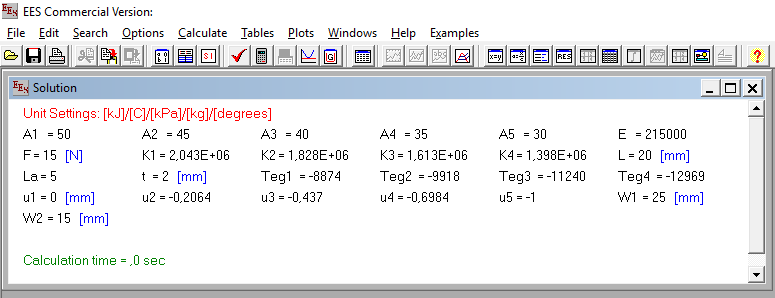
EES (Engineering Equation Solver)
Output EES
Sekian.
2. Diskusi Kelas 11 Maret 2019
Sharing masalah mengenai penggunaan perangkat lunak 3DD Software
RANCANGAN ANGGARAN BIAYA RUMAH
Dosen Pengampu : Bapak Dr. Ir. Ahmad Indra Siswantara (Pak DAI)
Rumah adalah sebuah bangunan yang dibutuhkan oleh setiap makhluk hidup untuk menunjang kehidupan. Dalam membangun sebuah rumah, hal kecil namun penting yang harus kita lakukan adalah menyusun dan merancang Rancangan Anggaran dan Biaya (RAB). Berikut penulis sajikan contoh simulasi sederhana mengenai RAB rumah tipe 80 [1]
Detail Engineering Design (DED)
Sumber : Desain Griya
Itu merupakan contoh RAB, bagaimana sudah ada gambaran kan ya untuk membangun rumah. Saat ini penulis baru dapat memberikan contoh simulasi pembangunan rumah, mohon do'anya untuk bisa segera membangun rumah tangga. Hehee ^_^
Sekian.
QUIZ KOMPUTASI TEKNIK
Dosen Pengampu : Bapak Dr. Ir. Ahmad Indra Siswantara (Pak DAI)
Anda diminta untuk membuat sebuah model komputasi untuk membuat bangunan yang akan digunakan untuk usaha service (layanan) penyewaan rumah/ kamar. Jalankan simulasi terhadap model tersebut untuk memutuskan kelayakan usaha tersebut (teknis dan ekonomis)!
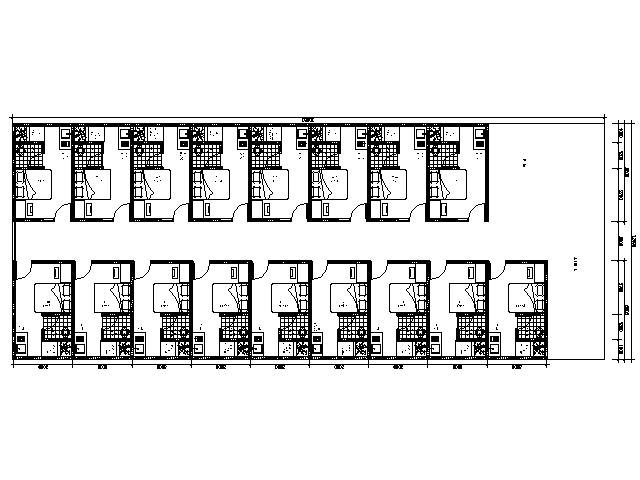
Analisa awal :
Saya memiliki sebidang tanah dengan luas tanah dan bangunan 300 m2 (10x30 m). Saya merencanakan membangun suatu unit usaha berupa penyewaan kamar (indekos). Dari luasan itu akan dibuat kamar sebanyak 17 buah dengan luas setiap kamar 3x5,8 m dengan kamar mandi dalam.
Asumsi :
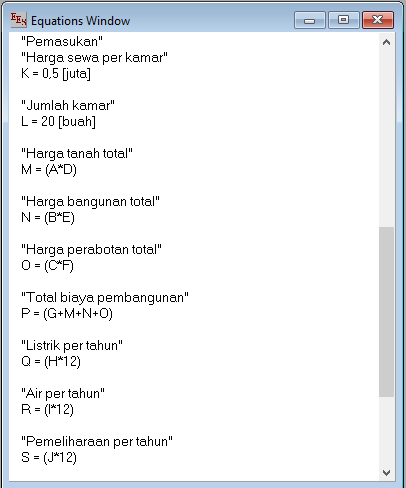
Harga tanah per m2 di daerah Surakarta adalah Rp 1.000.000,00 [1 juta]
Harga membangun rumah indekos di daerah Surakarta adalah Rp 700.000,00 [0,7 juta]
Biaya pembelian berbagai perabotan Rp 500.000,00 [0,5 juta]
Pengurusan perizinan usaha Rp 10.000.000,00 [10 juta]
TDL listrik setiap bulan Rp 250.000,00 [0,25 juta]
TDA air setiap bulan Rp 100.000,00 [0,1 juta]
Pemeliharaan setiap bulan Rp 500.000,00 [0,5 juta]
Harga sewa kamar indekos setiap bulan Rp 500.000,00 [0,5 juta]
Rancangan Anggaran Bangunan :
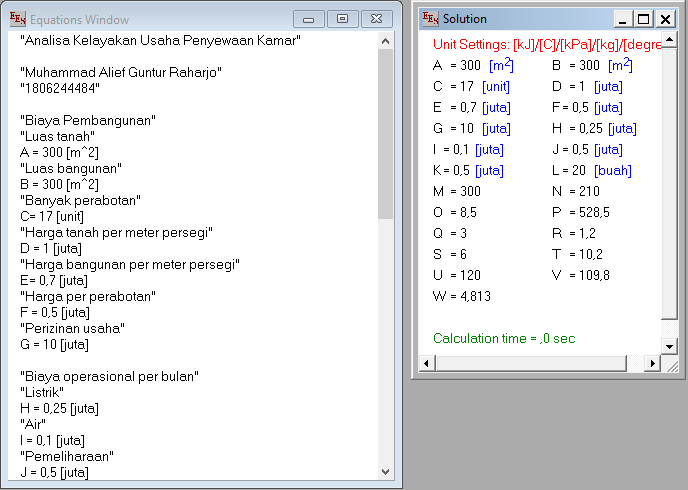
Biaya pembelian tanah = luas tanah (m2) x harga tanah (/m2) = Rp 300.000.000,00 [300 juta]
Biaya pembangunan indekos = luas tanah (m2) x biaya (/m2) = Rp 210.000.000,00 [210 juta]
Beli perabotan = biaya beli x jumlah kamar = Rp 8.500.000,00 [8,5 juta]
Total pembangunan = tanah + bangunan + perabotan + izin = Rp 528.500.000,00 [528,5 juta]
TDL listrik setahun = TDL bulanan x 12 = Rp 3.000.000,00 [3 juta]
TDA air setahun = operasional bulanan x 12 = Rp 1.200.000,00 [1,2 juta]
Pemeliharaan setahun = pemeliharaan bulanan x 12 = Rp 6.000.000,00 [6 juta]
Biaya operasional setahun = (TDL + TDA + pemeliharaan) = Rp 10.200.000,00 [10,2 juta]
Perhitungan Break Event Point (BEP) :
Jika saya mengasumsikan kamar indekos penuh setiap bulan sepanjang tahun maka pemasukan yang dapat diperoleh sebesar
Pemasukan/ tahun = banyak kamar x harga sewa x 12 bulan = Rp 120.000.000,00 [120 juta]
Laba/ tahun = pemasukan/ tahun – biaya operasional/ tahun = Rp 109.800.000,00 [109,8 juta]
BEP (tahun) = (total pembangunan)/(laba setiap tahun) = 4,813 ≃ 4 tahun 9 bulan
Komputasi
Simulasi analisis perhitungan komputer (komputasi) menggunakan Engineering Equation Solver (EES) sebagai berikut :
EES Formula
EES Solving
Saudara/ i dapat mengetahui selengkapnya dengan mengklik tautan berikut
Analisa Kelayakan Bangunan Untuk Usaha Penyewaan Kamar [2]
Sekian.
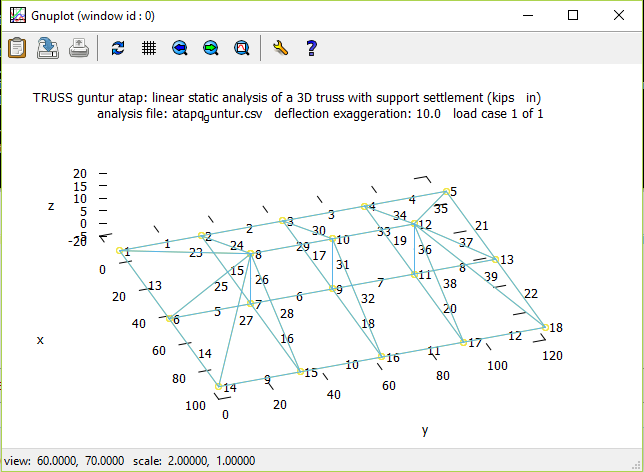
PEMODELAN ATAP RUMAH DENGAN 3DD FRAME
Pada pembahasan kali ini, penulis ingin membagikan mengenai pemodelan atap dengan perangkat lunak 3DD Frame. Atap dirancang mengikuti konstruksi bangunan rumah kos. Adapun konstruksi bangunan rumah kos tersebut telah dirancang sebelumnya.
Untuk melakukan analisa Truss pada atap tersebut, penulis melakukan rekayasa program (coding). Coding ini akan membantu dalam melakukan pengolahan pada 3DD Frame. Coding dibuat dalam bentuk file .csv dimana didalamnya memuat beberapa informasi, seperti
1. Jumlah Node dan koordinat tiap node pada desain atap
2. Constraint dari atap tersebut, dimana pada simuasi ini constrint diletakan pada seluruh node pada bagian bawah
3. Jumlah frame yang terdapat pada desain atap, ditambah dengan beberapa informasi seperti: besar luas penampang dari tiap frame, inersia frame, modulus elastisitas, modulus geser dan massa jenis
4. Arah dan gaya gravitasi yang bekerja pada model uji
5. Jumlah kasus pembebanan statis yang dialami oleh model uji
Berikut coding untuk melakukan analisa Truss atap [3]
Setelah melakukan coding, kemudian dilakukan simulasi menggunakan 3DD Frame. Simulasi dilakukan dengan memasukkan file ekstensi .csv dan memberikan nama file untuk hasil simulasinya dalam 3DD Frame
Hasil simulasi 3DD Frame
Hasil simulasi oleh 3DD Framen ini berisi data displacement pada tiap node, gaya yang diterima oleh tiap frame, dan reaksi yang diberikan oleh tiap-tiap node. Hasil plotingan simulasi sebagai berikut
Sekian.
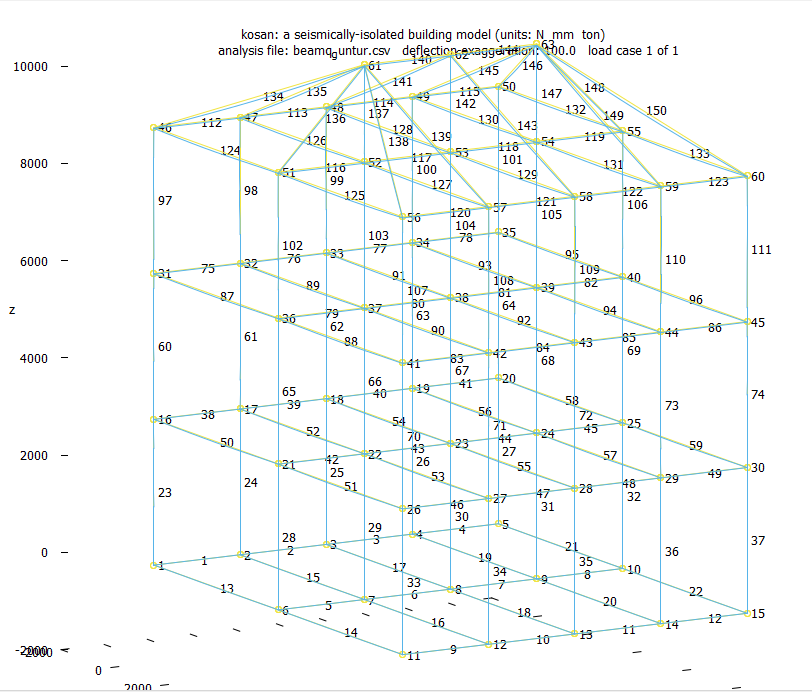
PEMODELAN BEAM RUMAH DENGAN 3DD FRAME
Pemodelan beam sangat diperlukan dalam pembangunan konstruksi suatu bangunan. Pada kesempatan ini, penulis ingin membagikan ilmu mengenai analisa dan pemodelan beam pada rumah kos dengan perangkat lunak 3DD Frame. Berikut analisanya
Langkah-langkah dalam analisa beam sebagai berikut
1. Membuat dan menyimpan coding dalam dokumen Microsoft Excel berektensi '.csv'. Berikut coding beam tersebut [4]
2. Double klik program 3DD Frame untuk membuka dan menjalankannya
3. Masukkan inputan sesuai nama dokumen .csv tersebut
4. Memberikan nama dokumen output yang Saudara kehendaki
5. Pemodelan telah selesai dilakukan.
Berikut hasil analisa dan pemodelan beam rumah penulis
Hasil analisa [5]
Hasil pemodelan
Sekian.
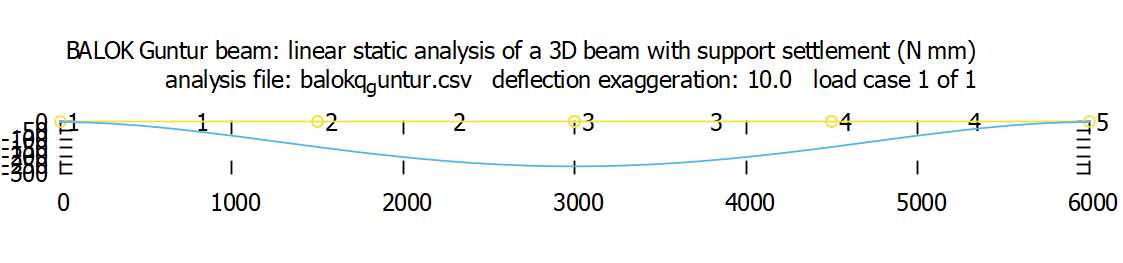
PEMODELAN BALOK PONDASI RUMAH DENGAN 3DD FRAME
Pemodelan balok pada suatu pondasi rumah menjadi salah satu hal penting yang juga harus dianalisa untuk mengetahui besarnya beban yang dapat ditumpu dengan pemilihan profil material yang sesuai. Berikut analisa sederhana balok pondasi penulis.
1. Coding balok [6]
2. Hasil analisa [7]
3. Hasil pemodelan
Sekian.
UJIAN TENGAH SEMESTER (UTS)
UTS ini diadakan pada tanggal 25 Maret 2019 dengan sistematika membuat pertanyaan dan jawaban secara mandiri berdasarkan tujuan pembelajaran komputasi teknik, yaitu
1. Memahami konsep-konsep dalam Komputasi Teknik dan mengaplikasikannya,
2. Mampu mengenali diri sendiri lebih baik,
3. Skor kelayakan nilai yang patut didapatkan,
4. Menuliskan 5 orang teman yang memiliki kapabilitas dalam komputasi teknik beserta alasannya,
Sekian.
MOMEN INERSIA
Tugas-tugas berikut mengenai analisa profil beam, seperti yang dijelaskan berikut
1. Menghitung Momen Inertia pada sembarang bentuk profil [8]
2. Menghitung Momen Inertia pada H beam dengan bentuk profil I [9]
Sekian.
TUGAS BESAR (PROYEK)
Tema
Aplikasi Komputasi Teknik Dalam Desain dan Analitis “Zero Energy Building (ZEB)”
Topik/ Judul
APLIKASI KOMPUTASI TEKNIK DALAM PERANCANGAN RUMAH KOS BAROKAH BERKONSEP ZERO ENERGY BUILDINGS (ZEBs)
Subtopik"
Analisis Struktur
Sinopsis
ZEB merupakan bangunan dengan konsumsi energi nol. Bangunan ZEB diinisiasi karena kebutuhan dan kesadaran dalam mengurangi emisi karbon yang timbul akibat penggunaan energi fosil yang massif. Dalam tugas besar (proyek) komputasi teknik ini, kami mencoba untuk merancang sebuah bangunan berupa rumah yang dapat disewakan setiap kamarnya. Proyek ini dikerjakan dan diawasi bersama secara gotong-royong oleh :
1. Helmi Surya Putra
2. Muchamad Panji
3. Muhammad Alief Guntur Raharjo
4. Yunus Bakhtiar Arafat
Perancangan rumah tinggal ini direncanakan berlokasi di Depok, Jawa Barat. Konsep bangunan yang akan kami bangun berupa rumah tiga lantai yang dilengkapi berbagai sumber energi terbarukan untuk menerapkan konsep ZEB. Adapun luas bangunan 18x25 m2 dan luas kamar 3x5 m2. Pada setiap lantai terdapat 20 kamar tidur yang dapat disewakan dengan kamar mandi dalam.
Analisis yang akan kami kerjakan berupa :
• Analisis biaya pembangunan dan operasional, meliputi pemilihan material dalam pembangunan, perhitungan BEP (Break Event Point), dan penentuan harga sewa
• Analisis struktur, meliputi analisis statis dan dinamis (angin dan guncangan gempa) bangunan
• Analisis energi ZEB, meliputi pemenuhan kebutuhan energi dasar seperti listrik, air, dan gas bangunan
Sekian.
PROGRESS TUGAS BESAR (PROYEK)
APLIKASI KOMPUTASI TEKNIK DALAM PERANCANGAN RUMAH KOS BAROKAH BERKONSEP ZERO ENERGY BUILDINGs (ZEBs) - Muh. Alief Guntur R.
1. Senin, 29 April 2019 (Progress 30%) [10]
Sekian.