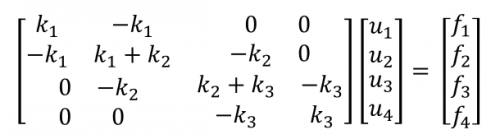Difference between revisions of "Kelompok 12"

From ccitonlinewiki
Jump to: navigation, search
(→‎Tugas metode Runge Kutta pada pegas)
 
(10 intermediate revisions by 2 users not shown)
Line 66: Line 66:
  
 
terdapat pegas dengan konstanta 75 N/m. yang dihubungkan dengan benda bermassa 2,5 kg kemudian benda itu ditarik dengan gaya P(t). jika gaya ditarik kurang dari 2 detik maka gaya yang berlaku adalah 10t N. dan jika gaya ditarik lebih dari sama dengan 2 detik maka yang gaya yang berlaku 20 N. dengan gaya-gaya itu akan menghasilkan regangan. dan regangan terjauh dapat diselesaikan dengan metode runge kutta brdasarkan persamaan y"= (p(t)/m)-(k.y/m).
 
terdapat pegas dengan konstanta 75 N/m. yang dihubungkan dengan benda bermassa 2,5 kg kemudian benda itu ditarik dengan gaya P(t). jika gaya ditarik kurang dari 2 detik maka gaya yang berlaku adalah 10t N. dan jika gaya ditarik lebih dari sama dengan 2 detik maka yang gaya yang berlaku 20 N. dengan gaya-gaya itu akan menghasilkan regangan. dan regangan terjauh dapat diselesaikan dengan metode runge kutta brdasarkan persamaan y"= (p(t)/m)-(k.y/m).
 +
 +
[[File:agakagak.png]]
 +
 +
 +
'''kode untuk menyelesaikan metode runge kutta'''
 +
# Di sini, kita akan menggunakan x0 dan y sebagai titik asal, x sebagai t yang diinginkan, dan h sebagai increment. Kita menggunakan h = 0.01.
 +
x0 = 0
 +
list =[]
 +
 +
 +
y = 0
 +
h = 0.01
 +
x = float(input("Masukkan nilai t: "))
 +
if 0 <= x < 2:
 +
  # dydx menyatakan persamaan awal dalam soal.
 +
  # Didapat hasil 4x - 30y karena dipakai massa m = 2,5 kg dan konstanta pegas k = 75 N/m.
 +
  # P(t) dinyatakan dalam x.
 +
  def dydx(x, y):
 +
    return (4*x - 30*y)
 +
  # Ini merupakan implementasi perhitungan Runge-Kutta.
 +
  def rungeKutta(x0, y0, x, h):
 +
    n = (int)((x - x0)/h) 
 +
    y = y0
 +
    for i in range(1, n + 1):
 +
      k1 = h * dydx(x0, y)
 +
      k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)
 +
      k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)
 +
      k4 = h * dydx(x0 + h, y + k3)
 +
 +
      # untuk y selanjutnya
 +
      y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
 +
 +
      # untuk x selanjutnya
 +
      x0 = x0 + h
 +
      list.append(y)
 +
    return y
 +
  print("Nilai y pada t =", x, "adalah", rungeKutta(x0, y, x, h))
 +
elif x >= 2:
 +
  # Ketika x >= 2, maka variabel x sudah tidak lagi memengaruhi persamaan.
 +
  def dydx(x, y):
 +
    return (8 - 30*y)
 +
  def rungeKutta(x0, y0, x, h):
 +
    n = (int)((x - x0)/h) 
 +
    y = y0
 +
    for i in range(1, n + 1):
 +
      k1 = h * dydx(x0, y)
 +
      k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)
 +
      k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)
 +
      k4 = h * dydx(x0 + h, y + k3)
 +
      y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
 +
      x0 = x0 + h
 +
      list.append(y)
 +
    return y
 +
  print("Nilai y pada t =", x, "adalah", rungeKutta(x0, y, x, h))
 +
else:
 +
  print("Mohon masukkan nilai t positif.")
 +
 +
print(list)
 +
print("nilai maksimal adalah ", max(list))
 +
 +
 +
sehingga apabila memasukkan t=1 akan didapat
 +
 +
[[File:hasilrunge1.PNG]]
 +
 +
 +
dan apabila memasukkan t=2 maka akan didapat
 +
[[File:hasilrunge22.PNG]]
 +
 +
 +
== Tugas Airfoil ==
 +
 +
Untuk tugas ini, kami menggunakan referensi airfoil NACA-0009 9.0% smoothed untuk mendapatkan nilai drag force dan lift force pada kecepatan 30 m/s
 +
 +
 +
[[File:Airfoil Kel.12.png]]
 +
 +
 +
Variabel pada tugas ini adalah angle airfoil dari -15° hingga 90°
 +
 +
dengan bantuan aplikasi CFDSOF dan Paraview
 +
 +
didapatkan nilai-nilai sebagai berikut
 +
 +
 +
[[File:Data Airfoil Kel.12.png]]
 +
 +
 +
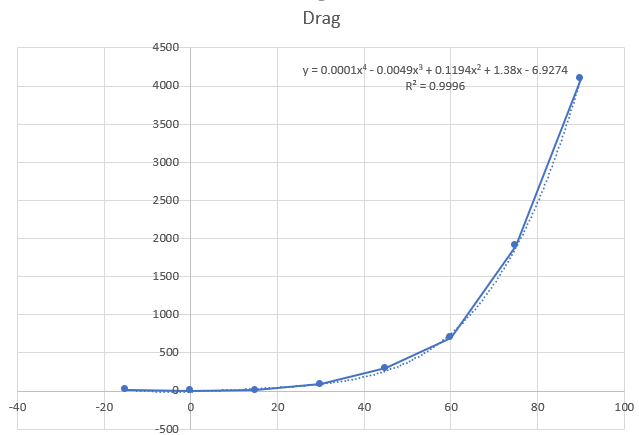
'''Grafik Drag'''
 +
 +
[[File:Grafik Drag versi 2 Kel.12.png]]
 +
 +
 +
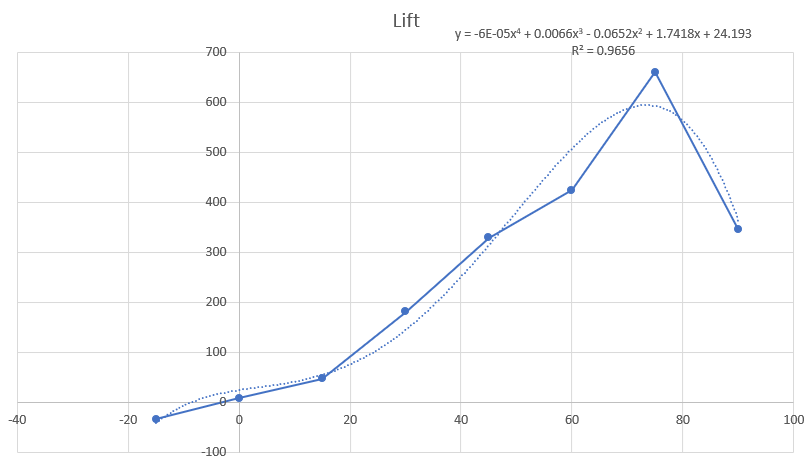
'''Grafik Lift'''
 +
 +
[[File:Grafik Lift versi 2 Kel.12.png]]
 +
 +
 +
'''Hasil Optimasi'''
 +
 +
import numpy as np
 +
from scipy.optimize import minimize
 +
 +
def drag(x):#drag
 +
    x = x[0]
 +
    d = 0.0001*x**4 -0.0049*x**3 + 0.1194*x**2 - 1.38*x - 6.927
 +
    return d
 +
 +
def lift(x): #lift
 +
    x = x[0]
 +
    l =  -0.00006*x**4 + 0.0066*x**3 - 0.0652*x**2 + 1.7418*x + 24.193
 +
    return l
 +
 +
def obj(x): #sudut yang diminimalkan
 +
    return drag(x)
 +
 +
def c1(x): #variable SUDUT yang meminimalkan persamaan garis drag
 +
    return drag(x)
 +
def c2(x): #variable SUDUT yang meminimalkan persamaan garis lift
 +
    return lift(x)
 +
 +
 +
con1=({'type':'ineq','fun':c1})
 +
con2=({'type':'ineq','fun':c2})
 +
cons = (con1,con2)
 +
 +
a = (10,90)
 +
batas = [a]
 +
 +
x1_guess = 20
 +
 +
x0 = np.array([x1_guess])
 +
 +
sol = minimize(obj,x0, method='SLSQP', bounds=batas, constraints=cons, options={'disp':True})
 +
 +
xopt = sol.x
 +
fopt = -sol.fun
 +
 +
dopt = drag(xopt) # drag optimal
 +
lopt = lift(xopt) # lift optimal
 +
 +
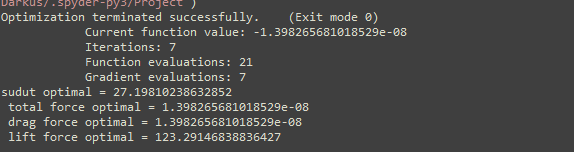
print ('sudut optimal = '+str(xopt[0]), "\n", 'total force optimal = '+str(fopt), "\n", 'drag force optimal = '+str(-dopt), "\n", 'lift force optimal = '+str(lopt))
 +
 +
 +
[[File:Optimasi Elvin 1.png]]
 +
 +
 +
 +
== Aplikasi ANN pada Data CFD ==
 +
 +
'''Koding ANN (Dengan Google Colab)'''
 +
 +
import tensorflow as tf
 +
from tensorflow import keras
 +
from tensorflow.keras import Sequential
 +
from tensorflow.keras.layers import Flatten, Dense
 +
import numpy as np
 +
import pandas as pd
 +
print(tf.__version__)
 +
 +
from google.colab import files
 +
uploaded = files.upload()
 +
 +
import io
 +
database = pd.read_excel(io.BytesIO(uploaded['ANN ELVIN.xlsx']))
 +
 +
x = database['angle of attack']
 +
#y1 = dataset['Fdrag']
 +
#y2 = dataset['Flift']
 +
y = database['drag/lift']
 +
 +
import matplotlib.pyplot as plt
 +
plt.plot(x,y)
 +
 +
norm_x = [(a-np.min(x))/(np.max(x)-np.min(x)) 
 +
                              for a in x]
 +
norm_y = [(a-np.min(y))/(np.max(y)-np.min(y)) 
 +
                              for a in y]
 +
 +
from sklearn.preprocessing import StandardScaler
 +
from sklearn.model_selection import train_test_split
 +
 +
x_train, x_test, y_train, y_test = train_test_split(norm_x, norm_y, test_size = 0.3, random_state =
 +
0)
 +
 +
x_train = np.asarray(x_train)
 +
x_test = np.asarray (x_test)
 +
y_train = np.asarray (y_train)
 +
y_test = np.asarray (y_test)
 +
 +
 +
import matplotlib.pyplot as plt
 +
unnorm_y_awal=  [a*(np.max(y)-np.min(y))+np.min(y) 
 +
                              for a in y_test]
 +
plt.suptitle('Output Real')
 +
plt.plot(unnorm_y_awal)
 +
 +
model = Sequential()
 +
model.add(Dense(3, activation='relu', input_dim = 1)) # input layer
 +
model.add(Dense(4, activation='relu')) # hidden layer
 +
model.add(Dense(1, activation = 'sigmoid'))
 +
 +
model.compile(optimizer='adam', loss = 'binary_crossentropy', metrics=['accuracy'])
 +
 +
history = model.fit(x_train, y_train, batch_size = 64, epochs = 5, verbose = 1, validation_split = 0.16)
 +
 +
Train on 3 samples, validate on 1 samples
 +
Epoch 1/5
 +
3/3 [==============================] - 0s 34ms/sample - loss: 0.7800 - acc: 0.0000e+00 - val_loss: 0.8347 - val_acc: 0.0000e+00
 +
Epoch 2/5
 +
3/3 [==============================] - 0s 2ms/sample - loss: 0.7782 - acc: 0.0000e+00 - val_loss: 0.8323 - val_acc: 0.0000e+00
 +
Epoch 3/5
 +
3/3 [==============================] - 0s 1ms/sample - loss: 0.7765 - acc: 0.0000e+00 - val_loss: 0.8299 - val_acc: 0.0000e+00
 +
Epoch 4/5
 +
3/3 [==============================] - 0s 1ms/sample - loss: 0.7748 - acc: 0.0000e+00 - val_loss: 0.8275 - val_acc: 0.0000e+00
 +
Epoch 5/5
 +
3/3 [==============================] - 0s 2ms/sample - loss: 0.7731 - acc: 0.0000e+00 - val_loss: 0.8252 - val_acc: 0.0000e+00
 +
 +
unnorm_x=  [a*(np.max(x)-np.min(x))+np.min(x) 
 +
                              for a in x_test]
 +
unnorm_y=  [a*(np.max(y)-np.min(y))+np.min(y) 
 +
                              for a in y_test]
 +
 +
plt.suptitle('Output Real vs Output Prediction ANN')
 +
plt.subplot(2, 1, 1)
 +
plt.plot(unnorm_y_awal)
 +
plt.subplot(2, 1, 2)
 +
plt.plot(unnorm_y)
 +
 +
 +
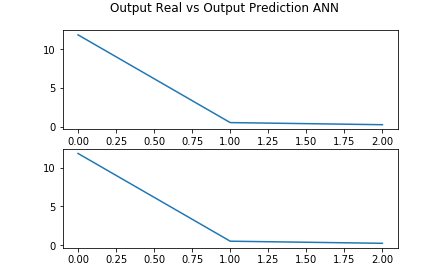
'''Hasil'''
 +
 +
Dapat dilihat bahwa output real dengan output prediction ANN sama persis
 +
 +
[[File:ANN Elvin 1.png]]

Latest revision as of 23:07, 16 December 2019

Perkenalkan, kami kelompok 12 dengan anggota kelompok sebagai berikut:

1. Elvin

2. Khairun Naziri Batubara

3. Adam Ilham Maulana


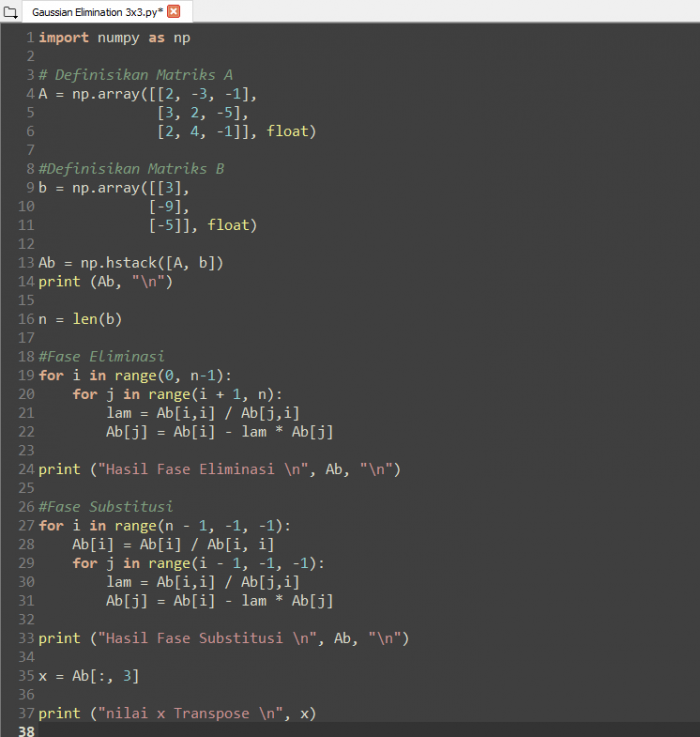
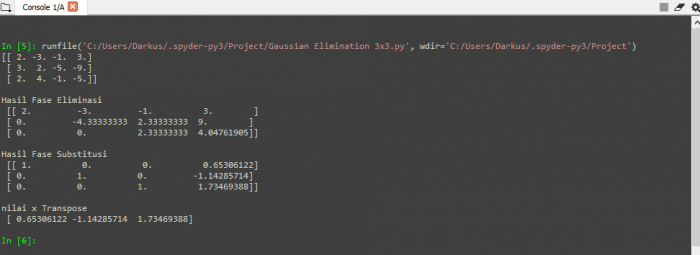
Tugas Metode Eliminasi Gauss

Video diatas merupakan penjelasan program eliminasi Gauss yang dibuat pada python. Rangkaian kode dari video diatas ditampilkan sebagai berikut:

Code Gauss Elimination Kel.12.png

Console Gauss Elimination Kel.12.png


Tugas Finite Element Analysis dengan Eliminasi Gauss

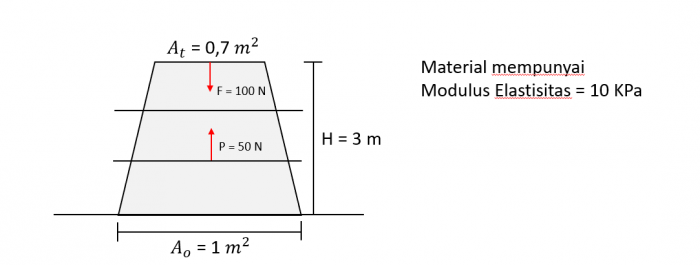
Dengan kode yang telah dibuat untuk menyelesaikan masalah pada sistem persamaan linear, kode tersebut juga dapat diaplikasikan pada simulasi Finite Element Analysis Contoh Soal

Soal Gauss Simulasi.png

Seperti pada gambar diatas, suatu struktur diberikan gaya P keatas pada jarak 1 m dari lantai dan gaya F kebawah pada ujung struktur, hitunglah nodal displacement yang terjadi.

Penyelesaian

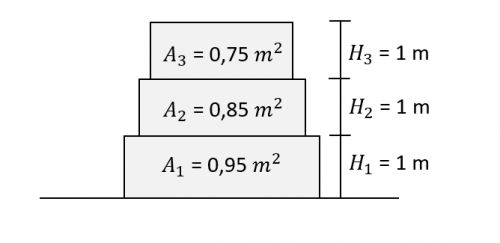
Element.png

  • untuk menyelesaikan masalah ini, kita dapat membagikan struktur tersebut menjadi 3 element dengan tinggi 1 meter dengan luas penampang rata-rata berturut-turut dari lantai 950 m2, 850 m2, dan 750 m2
  • dengan rumus stiffness k = A*E/L kita dapat menghitung k1, k2, k3 berturut-turut 9500 N/m, 8500 N/m, dan 7500 N/m
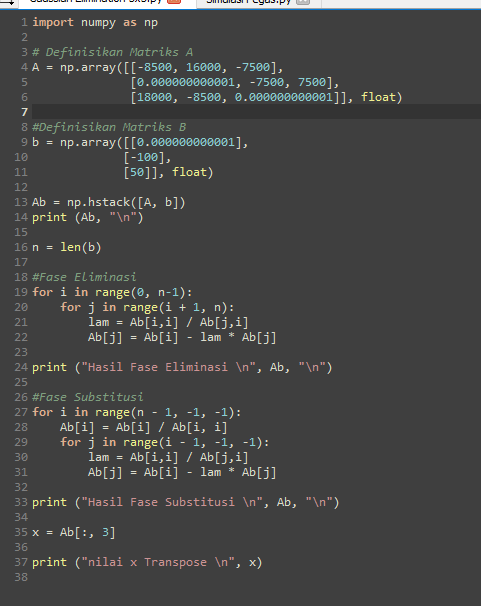
  • kemudian kita masukkan nilai-nilai stiffness k dan gaya F dan P beserta constraint yang ada ke matriks untuk penyelesaian

Matrix Simulasi.png

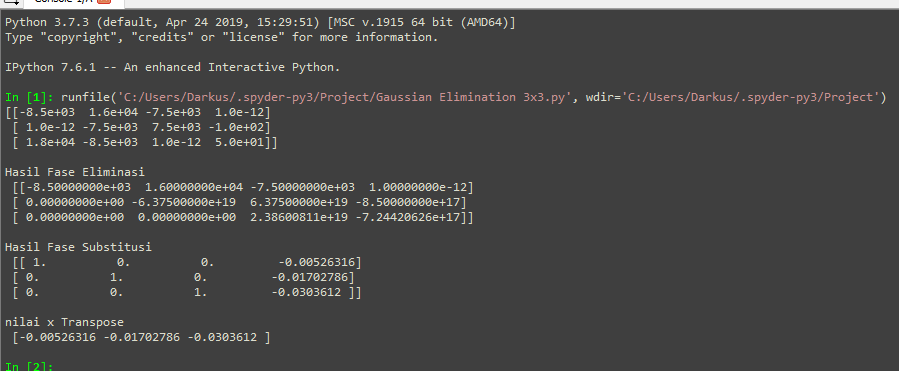
Penyelesaian yang didapatkan akan seperti berikut

Simulasi Gauss Kode.png Simulasi Gauss Konsol.png

dan didapatkan nodal displacement secara berturut-turut 0,00526 , 0,0170 , dan 0,030 kearah bawah

berikut adalah video penjelasan untuk tugas ini


Tugas metode Runge Kutta pada pegas

1. Persoalan dan analisis fisika

terdapat sebuah sistem pegas dan massa yang menempel pada dinding. Pegas tersebut memiliki konstanta sebesar 75 N/m dan Benda bermassa 2,5 kg. Gaya P yang diberikan pada sistem menjauhi dinding dengan besaran 10t apabila terjadi saat t<2s dan 20N apabila terjadi saat t>=2s. Terdapat juga persamaan untuk percepatan sistem yaitu y"= (P(t)/m)-((k/m)y). Disini kita harus mencari perpindahan maksimum sistem, dan diplotkan pada grafik perubahan posisi sistem terhadap waktu dimana sistem awal berada pada keadaan diam (v=0)

Analisis Fisika pada keadaan tersebut berlaku Hukum Newton ke-2 yaitu F=a.m, dimana a=percepatan benda dan m = massa benda. Selain itu berlaku juga hukum tentang gaya pegas, f=k.y, dimana k = konstanta pegas dan y = perubahan panjang pegas. Kedua gaya ini dapat memengaruhi perpindahan benda. Dikarenakan adany gaya tarik P dan gaya reaksi oleh pegas yang berlawanan dengan gaya tarik P atau dapat dirumuskan. Gaya total = gaya yang diberikan pada sistem - gaya reaksi pegas. m.y"=P(t)-ky dan apabila kedua ruas dibagi dengan massa maka persamaan akan menjadi y"=P(t)/m-(k/m)y

2. algoritma penyelesaian

terdapat pegas dengan konstanta 75 N/m. yang dihubungkan dengan benda bermassa 2,5 kg kemudian benda itu ditarik dengan gaya P(t). jika gaya ditarik kurang dari 2 detik maka gaya yang berlaku adalah 10t N. dan jika gaya ditarik lebih dari sama dengan 2 detik maka yang gaya yang berlaku 20 N. dengan gaya-gaya itu akan menghasilkan regangan. dan regangan terjauh dapat diselesaikan dengan metode runge kutta brdasarkan persamaan y"= (p(t)/m)-(k.y/m).

Agakagak.png


kode untuk menyelesaikan metode runge kutta

  1. Di sini, kita akan menggunakan x0 dan y sebagai titik asal, x sebagai t yang diinginkan, dan h sebagai increment. Kita menggunakan h = 0.01.

x0 = 0 list =[]


y = 0 h = 0.01 x = float(input("Masukkan nilai t: ")) if 0 <= x < 2: 

 # dydx menyatakan persamaan awal dalam soal.
 # Didapat hasil 4x - 30y karena dipakai massa m = 2,5 kg dan konstanta pegas k = 75 N/m.
 # P(t) dinyatakan dalam x. 
 def dydx(x, y): 
   return (4*x - 30*y) 
 # Ini merupakan implementasi perhitungan Runge-Kutta.
 def rungeKutta(x0, y0, x, h): 
   n = (int)((x - x0)/h)  
   y = y0 
   for i in range(1, n + 1): 
      k1 = h * dydx(x0, y) 
      k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1) 
      k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2) 
      k4 = h * dydx(x0 + h, y + k3) 

      # untuk y selanjutnya 
      y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4) 

      # untuk x selanjutnya
      x0 = x0 + h 
      list.append(y)
   return y 
 print("Nilai y pada t =", x, "adalah", rungeKutta(x0, y, x, h))

elif x >= 2: 

 # Ketika x >= 2, maka variabel x sudah tidak lagi memengaruhi persamaan.
 def dydx(x, y): 
   return (8 - 30*y) 
 def rungeKutta(x0, y0, x, h): 
   n = (int)((x - x0)/h)  
   y = y0 
   for i in range(1, n + 1): 
      k1 = h * dydx(x0, y) 
      k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1) 
      k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2) 
      k4 = h * dydx(x0 + h, y + k3) 
      y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
      x0 = x0 + h 
      list.append(y)
   return y 
 print("Nilai y pada t =", x, "adalah", rungeKutta(x0, y, x, h))

else: 

 print("Mohon masukkan nilai t positif.")

print(list) print("nilai maksimal adalah ", max(list))


sehingga apabila memasukkan t=1 akan didapat

Hasilrunge1.PNG


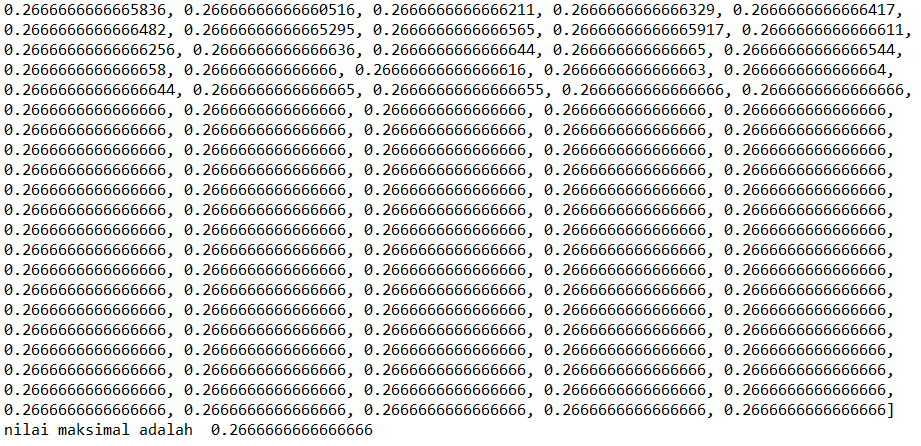
dan apabila memasukkan t=2 maka akan didapat Hasilrunge22.PNG


Tugas Airfoil

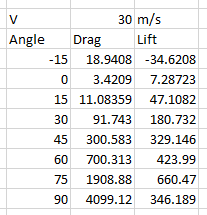
Untuk tugas ini, kami menggunakan referensi airfoil NACA-0009 9.0% smoothed untuk mendapatkan nilai drag force dan lift force pada kecepatan 30 m/s


Airfoil Kel.12.png


Variabel pada tugas ini adalah angle airfoil dari -15° hingga 90°

dengan bantuan aplikasi CFDSOF dan Paraview

didapatkan nilai-nilai sebagai berikut


Data Airfoil Kel.12.png


Grafik Drag

Grafik Drag versi 2 Kel.12.png


Grafik Lift

Grafik Lift versi 2 Kel.12.png


Hasil Optimasi 

import numpy as np
from scipy.optimize import minimize

def drag(x):#drag
    x = x[0]
    d = 0.0001*x**4 -0.0049*x**3 + 0.1194*x**2 - 1.38*x - 6.927
    return d

def lift(x): #lift
    x = x[0]
    l =  -0.00006*x**4 + 0.0066*x**3 - 0.0652*x**2 + 1.7418*x + 24.193
    return l

def obj(x): #sudut yang diminimalkan
    return drag(x)

def c1(x): #variable SUDUT yang meminimalkan persamaan garis drag
    return drag(x)
def c2(x): #variable SUDUT yang meminimalkan persamaan garis lift
    return lift(x)


con1=({'type':'ineq','fun':c1})
con2=({'type':'ineq','fun':c2})
cons = (con1,con2)

a = (10,90)
batas = [a]

x1_guess = 20

x0 = np.array([x1_guess])

sol = minimize(obj,x0, method='SLSQP', bounds=batas, constraints=cons, options={'disp':True})

xopt = sol.x
fopt = -sol.fun

dopt = drag(xopt) # drag optimal
lopt = lift(xopt) # lift optimal

print ('sudut optimal = '+str(xopt[0]), "\n", 'total force optimal = '+str(fopt), "\n", 'drag force optimal = '+str(-dopt), "\n", 'lift force optimal = '+str(lopt))


Optimasi Elvin 1.png


Aplikasi ANN pada Data CFD

Koding ANN (Dengan Google Colab) 

import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Flatten, Dense
import numpy as np
import pandas as pd
print(tf.__version__)

from google.colab import files
uploaded = files.upload()

import io
database = pd.read_excel(io.BytesIO(uploaded['ANN ELVIN.xlsx']))

x = database['angle of attack']
#y1 = dataset['Fdrag']
#y2 = dataset['Flift']
y = database['drag/lift']

import matplotlib.pyplot as plt
plt.plot(x,y)

norm_x = [(a-np.min(x))/(np.max(x)-np.min(x))  
                             for a in x]
norm_y = [(a-np.min(y))/(np.max(y)-np.min(y))  
                             for a in y]

from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split

x_train, x_test, y_train, y_test = train_test_split(norm_x, norm_y, test_size = 0.3, random_state = 
0)

x_train = np.asarray(x_train)
x_test = np.asarray (x_test)
y_train = np.asarray (y_train)
y_test = np.asarray (y_test)


import matplotlib.pyplot as plt
unnorm_y_awal=  [a*(np.max(y)-np.min(y))+np.min(y)  
                              for a in y_test]
plt.suptitle('Output Real')
plt.plot(unnorm_y_awal)

model = Sequential()
model.add(Dense(3, activation='relu', input_dim = 1)) # input layer
model.add(Dense(4, activation='relu')) # hidden layer
model.add(Dense(1, activation = 'sigmoid'))

model.compile(optimizer='adam', loss = 'binary_crossentropy', metrics=['accuracy'])

history = model.fit(x_train, y_train, batch_size = 64, epochs = 5, verbose = 1, validation_split = 0.16)

Train on 3 samples, validate on 1 samples
Epoch 1/5
3/3 [==============================] - 0s 34ms/sample - loss: 0.7800 - acc: 0.0000e+00 - val_loss: 0.8347 - val_acc: 0.0000e+00
Epoch 2/5
3/3 [==============================] - 0s 2ms/sample - loss: 0.7782 - acc: 0.0000e+00 - val_loss: 0.8323 - val_acc: 0.0000e+00
Epoch 3/5
3/3 [==============================] - 0s 1ms/sample - loss: 0.7765 - acc: 0.0000e+00 - val_loss: 0.8299 - val_acc: 0.0000e+00
Epoch 4/5
3/3 [==============================] - 0s 1ms/sample - loss: 0.7748 - acc: 0.0000e+00 - val_loss: 0.8275 - val_acc: 0.0000e+00
Epoch 5/5
3/3 [==============================] - 0s 2ms/sample - loss: 0.7731 - acc: 0.0000e+00 - val_loss: 0.8252 - val_acc: 0.0000e+00

unnorm_x=  [a*(np.max(x)-np.min(x))+np.min(x)  
                             for a in x_test]
unnorm_y=  [a*(np.max(y)-np.min(y))+np.min(y)  
                             for a in y_test]

plt.suptitle('Output Real vs Output Prediction ANN')
plt.subplot(2, 1, 1)
plt.plot(unnorm_y_awal)
plt.subplot(2, 1, 2)
plt.plot(unnorm_y)


Hasil

Dapat dilihat bahwa output real dengan output prediction ANN sama persis

ANN Elvin 1.png

Retrieved from "http://air.eng.ui.ac.id/index.php?title=Kelompok_12&oldid=18009"