Difference between revisions of "Kelompok 1"
| (11 intermediate revisions by one other user not shown) | |||
| Line 97: | Line 97: | ||
*Apabila kedua ruas kita bagi dengan m, maka akan kita dapatkan persamaan seperti yang tertulis pada soal | *Apabila kedua ruas kita bagi dengan m, maka akan kita dapatkan persamaan seperti yang tertulis pada soal | ||
*y" = P(t)/m - (k/m)y | *y" = P(t)/m - (k/m)y | ||
| + | |||
| + | *Kami menggunakan aplikasi pycharm dan kodingan yang kami gunakan adalah: | ||
| + | |||
| + | import numpy as np; from numpy import sin, asarray, zeros, interp | ||
| + | from run_kut4 import integrate | ||
| + | from printSoln import printSoln | ||
| + | import pylab | ||
| + | |||
| + | k = 75 | ||
| + | m = 2.5 | ||
| + | |||
| + | def P(t): | ||
| + | if t < 2: | ||
| + | return 10.*t | ||
| + | else: | ||
| + | return 20. | ||
| + | |||
| + | def F(x,y): | ||
| + | F = zeros( (2,), dtype=float ) | ||
| + | F[0] = y[1] | ||
| + | F[1] = P(x)/m - (k/m) * y[0] | ||
| + | return F | ||
| + | |||
| + | x0 = 0.0 # start of the integration | ||
| + | xStop = 6.0 # end of the integration | ||
| + | y0 = asarray( [ 0., 0. ], dtype=float ) | ||
| + | h = 0.01 | ||
| + | freq = 20 | ||
| + | |||
| + | X,Y = integrate(F,x0,y0,xStop,h) | ||
| + | #printSoln(X,Y,freq) | ||
| + | |||
| + | pylab.plot( X, Y[:,0] ) | ||
| + | pylab.xlabel('time (t)'); | ||
| + | pylab.ylabel('y(t)'); | ||
| + | pylab.axhline(y=0,color='green') | ||
| + | pylab.grid('on') | ||
| + | pylab.title("Kelompok 1") | ||
| + | pylab.show() | ||
| + | |||
| + | [[File:Koding(1).jpg|700px|center|]] | ||
| + | |||
| + | [[File:Koding(2).jpg|700px|center|]] | ||
| + | |||
| + | pertama kami install modul numpy dan install modul matplotlib | ||
| + | setelah itu kami menggunakan modul run_kut4 dan juga modul pprintSoln yang dua-duanya terdapat di github.com | ||
| + | |||
| + | ## module run_kut4 | ||
| + | ''' X,Y = integrate(F,x,y,xStop,h). | ||
| + | 4th-order Runge-Kutta method for solving the | ||
| + | initial value problem {y}' = {F(x,{y})}, where | ||
| + | {y} = {y[0],y[1],...y[n-1]}. | ||
| + | x,y = initial conditions | ||
| + | xStop = terminal value of x | ||
| + | h = increment of x used in integration | ||
| + | F = user-supplied function that returns the | ||
| + | array F(x,y) = {y'[0],y'[1],...,y'[n-1]}. | ||
| + | ''' | ||
| + | from numpy import array | ||
| + | def integrate(F,x,y,xStop,h): | ||
| + | |||
| + | def run_kut4(F,x,y,h): | ||
| + | K0 = h*F(x,y) | ||
| + | K1 = h*F(x + h/2.0, y + K0/2.0) | ||
| + | K2 = h*F(x + h/2.0, y + K1/2.0) | ||
| + | K3 = h*F(x + h, y + K2) | ||
| + | return (K0 + 2.0*K1 + 2.0*K2 + K3)/6.0 | ||
| + | |||
| + | X = [] | ||
| + | Y = [] | ||
| + | X.append(x) | ||
| + | Y.append(y) | ||
| + | while x < xStop: | ||
| + | h = min(h,xStop - x) | ||
| + | y = y + run_kut4(F,x,y,h) | ||
| + | x = x + h | ||
| + | X.append(x) | ||
| + | Y.append(y) | ||
| + | return array(X),array(Y) | ||
| + | |||
| + | [[File:run_kut4.jpg|700px|center|]] | ||
| + | |||
| + | ## module printSoln | ||
| + | ''' printSoln(X,Y,freq). | ||
| + | Prints X and Y returned from the differential | ||
| + | equation solvers using printput frequency 'freq'. | ||
| + | freq = n prints every nth step. | ||
| + | freq = 0 prints initial and final values only. | ||
| + | ''' | ||
| + | def printSoln(X,Y,freq): | ||
| + | |||
| + | def printHead(n): | ||
| + | print "\n x ", | ||
| + | for i in range (n): | ||
| + | print " y[",i,"] ", | ||
| + | print | ||
| + | |||
| + | def printLine(x,y,n): | ||
| + | print "%13.4e"% x, | ||
| + | for i in range (n): | ||
| + | print "%13.4e"% y[i], | ||
| + | print | ||
| + | |||
| + | m = len(Y) | ||
| + | try: n = len(Y[0]) | ||
| + | except TypeError: n = 1 | ||
| + | if freq == 0: freq = m | ||
| + | printHead(n) | ||
| + | for i in range(0,m,freq): | ||
| + | printLine(X[i],Y[i],n) | ||
| + | if i != m - 1: printLine(X[m - 1],Y[m - 1],n) | ||
| + | |||
| + | [[File:printSoln.jpg|700px|center|]] | ||
| + | Setelah semua telah dimasukkan dalam aplikasi pycharm maka kami melakukan run dan kemudian akan langsung muncul grafik. | ||
| + | |||
| + | [[File:Grafik kelompok 1.jpg|700px|center|]] | ||
| + | [[File:Kelompok 1 PR1.mp4]] | ||
| + | |||
| + | '''Tugas optimasi aerodinamika''' | ||
| + | *Membuat geometri aerofoil di software CAD yang digunakan (kelompok kami menggunakan ukuran airfoil standar NACA dengan nomor 63-412). | ||
| + | *Melakukan simulasi aliran udara untuk geometri airfoil di software CFDSOF untuk mendapatkan nilai ''lift'' dan ''drag'' dari airfoil pada berbagai ''angle of attack''. | ||
| + | *Menggunakan program Python yang ditujukan untuk optimasi nilai ''angle of attack'', dimana nilai tersebut akan memiliki gaya ''lift'' besar dan ''drag'' kecil. | ||
| + | *Program Python yang digunakan: | ||
| + | |||
| + | import numpy as np | ||
| + | from scipy.optimize import minimize | ||
| + | |||
| + | |||
| + | def calc_drag(x):#drag | ||
| + | x1 = x[0] | ||
| + | drag = 0.0193*x1**5 - 0.3797*x1**4 + 2.1688*x1**3 - 2.2064*x1**2 - 3.0016*x1 + 4.0659 | ||
| + | return drag | ||
| + | |||
| + | def calc_lift(x): #lift | ||
| + | x1 = x[0] | ||
| + | lift = -0.0179*x1**5 + 0.55*x1**4 - 6.0283*x1**3 + 26.852*x1**2 - 38.461*x1 + 21.939 | ||
| + | return lift | ||
| + | |||
| + | def objective(x): #volume yang diminimalkan | ||
| + | return calc_drag(x) | ||
| + | |||
| + | def constraint1(x): #variable SUDUT yang meminimalkan persamaan garis drag | ||
| + | return calc_drag(x) | ||
| + | |||
| + | def constraint2(x): #variable SUDUT yang meminimalkan persamaan garis lift | ||
| + | return calc_lift(x) | ||
| + | |||
| + | con1=({'type':'ineq','fun':constraint1}) | ||
| + | con2=({'type':'ineq','fun':constraint2}) | ||
| + | cons = (con1,con2) | ||
| + | a = (0,90) | ||
| + | batas = [a] | ||
| + | |||
| + | x1_guess = 50 | ||
| + | |||
| + | x0 = np.array([x1_guess]) | ||
| + | |||
| + | sol = minimize(objective,x0, method='SLSQP',bounds=batas, constraints=cons, options={'disp':True}) | ||
| + | |||
| + | xopt = sol.x | ||
| + | forceopt = -sol.fun | ||
| + | |||
| + | dragopt = calc_drag(xopt) # drag optimal | ||
| + | liftopt = calc_lift(xopt) # lift optimal | ||
| + | |||
| + | print ('sudut optimal = '+str(xopt[0])) | ||
| + | print ('total force optimal = '+str(forceopt)) | ||
| + | print ('drag force optimal = '+str(dragopt)) | ||
| + | print ('lift force optimal = '+str(liftopt)) | ||
| + | |||
| + | |||
| + | # In[10]: | ||
| + | |||
| + | |||
| + | import numpy as np | ||
| + | from scipy.optimize import minimize | ||
| + | |||
| + | |||
| + | def calc_drag(x):#drag | ||
| + | x1 = x[0] | ||
| + | drag = 0.0193*x1**5 - 0.3797*x1**4 + 2.1688*x1**3 - 2.2064*x1**2 - 3.0016*x1 + 4.0659 | ||
| + | return drag | ||
| + | |||
| + | def calc_lift(x): #lift | ||
| + | x1 = x[0] | ||
| + | lift = -0.0179*x1**5 + 0.55*x1**4 - 6.0283*x1**3 + 26.852*x1**2 - 38.461*x1 + 21.939 | ||
| + | return lift | ||
| + | |||
| + | def objective(x): #volume yang diminimalkan | ||
| + | return calc_lift(x) | ||
| + | |||
| + | def constraint1(x): #variable SUDUT yang meminimalkan persamaan garis drag | ||
| + | return calc_drag(x) | ||
| + | |||
| + | def constraint2(x): #variable SUDUT yang meminimalkan persamaan garis lift | ||
| + | return calc_lift(x) | ||
| + | |||
| + | con1=({'type':'ineq','fun':constraint1}) | ||
| + | con2=({'type':'ineq','fun':constraint2}) | ||
| + | cons = (con1,con2) | ||
| + | a = (0,90) | ||
| + | batas = [a] | ||
| + | |||
| + | x1_guess = 50 | ||
| + | |||
| + | x0 = np.array([x1_guess]) | ||
| + | |||
| + | sol = minimize(objective,x0, method='SLSQP',bounds=batas, constraints=cons, options={'disp':True}) | ||
| + | |||
| + | xopt = sol.x | ||
| + | forceopt = -sol.fun | ||
| + | |||
| + | dragopt = calc_drag(xopt) # drag optimal | ||
| + | liftopt = calc_lift(xopt) # lift optimal | ||
| + | |||
| + | print ('sudut optimal = '+str(xopt[0])) | ||
| + | print ('total force optimal = '+str(forceopt)) | ||
| + | print ('drag force optimal = '+str(dragopt)) | ||
| + | print ('lift force optimal = '+str(liftopt)) | ||
Latest revision as of 16:22, 11 December 2019
Kelompok 1 Anggota:
- Andika Ramadhan Gurnida
- M. Pasha Wibisono
- M. Yusuf Abdurrahman
- Rizkyawan Wibawa
Tugas: Menyelesaikan problem set bab 2 dengan program Python
- Agenda untuk tugas ini berdasarkan pemahaman kami atas informasi yang ada adalah pembuatan program Python untuk melakukan eliminasi Gauss, yang kemudian akan digunakan untuk menyelesaikan salah satu soal pada problem set yang terdapat pada Bab 2.
- Kami memilih soal nomor 4 di Problem Set 2.1 dari buku untuk diselesaikan.
- Langkah-langkah yang terdapat dalam program yang kami buat adalah sebagai berikut:
- 1. Mengimpor modul numpy untuk membuat matriks
- 2. Membuat matriks persamaan yang terdapat pada soal untuk diselesaikan
- 3. Menulis algoritma untuk melakukan fase eliminasi
- 4. Menulis algoritma untuk melakukan back substitution
- 5. Mencetak matriks penyelesaian soal
- Program yang telah kami buat secara spesifik untuk menyelesaikan soal tersebut sebagai berikut:
import numpy as np
A = np.array ([[2,-3,-1],[3,2,-5],[2,4,-1]]) b = np.array ([[3],[-9],[-5]])
def gaussElimin(A,b):
n = len(b) for k in range (0,n-1): for i in range(k+1,n): if A[i,k] != 0.0: lam = A[i,k]/A[k,k] A[i,k+1:n] = A[i,k+1:n] - lam*A[k,k+1:n] b[i] = b[i] - lam*b[k]
for k in range(n-1,-1,-1): b[k] = (b[k] - np.dot(A[k,k+1:n],b[k+1:n]))/A[k,k] return b
x = gaussElimin(A,b) print (x)
Tugas: Aplikasi Metode Numerik pada masalah statika struktur
- Agenda untuk tugas ini berdasarkan pemahaman kami atas informasi yang ada adalah menjelaskan aplikasi dari apa yang telah dipelajari pada mata kuliah metode numerik untuk menyelesaikan permasalahan statika struktur satu dimensi.
- Kami memilih menggunakan analisa finite element untuk menyelesaikan contoh soal statika struktur satu dimensi.
- Soal tersebut sebagai berikut:
- Sebuah batang baja dengan panjang 600mm memiliki luas daerah cross-section sebesar 650mm^2 dan 350mm^2 pada kedua ujungnya. Ujung dengan luasan yang lebih besar menempel pada dinding dan diberikan dua gaya aksial sebesar 40kN pada ujung yang kecil dengan arah menjauhi dinding, dan 10kN pada posisi 200mm dari ujung yang kecil dengan arah mendekati dinding. Modelkan batang tersebut dengan tiga finite element dan tentukan nodal displacement yang terjadi.
- Pertama-tama, kami memodelkan batang tersebut dengan tiga finite element terlebih dulu.
- Ketiga elemen tersebut dipisahkan berdasarkan rata-rata luas daerah cross-section pada ujung-ujungnya, dengan panjang masing-masing elemen sebesar 200mm. Elemen yang paling dekat dengan dinding memiliki rata-rata luas daerah cross-section sebesar 600mm^2, elemen di tengah sebesar 500mm^2, dan elemen paling ujung sebesar 400mm^2.
- Titik-titik tempat menyatunya elemen-elemen tersebut diperlakukan sebagai node yang akan dihitung perpindahannya.
- Kita juga menentukan posisi konektivitas antar elemen, yang nantinya akan berguna untuk membuat matriks.
- Node yang dimiliki batang tersebut ada 4 buah (1 pada ujung setiap elemen), maka dapat kita tentukan bahwa elemen paling dekat dengan dinding memiliki konektivitas dengan dinding dan elemen tengah di titik 1 dan 2, elemen tengah terhubung dengan elemen dekat dinding dan elemen ujung di titik 2 dan 3, dan elemen ujung terhubung dengan elemen tengah dan bagian ujung batang di titik 3 dan 4.
- Informasi ini digunakan untuk membuat matriks global stiffness terlebih dahulu, dimana matriks tersebut diisi dengan nilai stiffness dari masing-masing elemen. Nilai tersebut ditentukan oleh rumus k = (E.A) / l, dimana k adalah nilai stiffness, E adalah modulus Young untuk baja (200 GPa = 200 x 10^3 MPa [N/mm^2]), A adalah luas daerah cross-section, dan l adalah panjang setiap elemen.
- Kita juga membuat matriks global load vector, dengan nilai beban sesuai pada beban yang terdapat di setiap node.
- Setelah kita membuat kedua matriks tersebut, maka nodal displacement dapat dicari (dengan catatan node dinding memiliki perpindahan 0 sehingga kita hanya akan mendapatkan tiga nilai perpindahan) dengan program berikut:
# Mengimpor modul untuk membuat matriks import numpy as np
# Membuat matriks stiffness dan matriks gaya pada objek K = np.array ([[5.5,-2.5,0],[-2.5,4.5,-2],[0,-2,2]]) F = np.array ([[0],[-0.05],[0.2]])
# Mendefinisikan eliminasi Gauss def gaussElimin(K,F):
# Algoritma fase eliminasi n = len(F) for k in range (0,n-1): for i in range(k+1,n): if K[i,k] != 0.0: lam = K [i,k]/K[k,k] K[i,k+1:n] = K[i,k+1:n] - lam*K[k,k+1:n] F[i] = F[i] - lam*F[k]
# Algoritma back substitution for k in range(n-1,-1,-1): F[k] = (F[k] - np.dot(K[k,k+1:n],F[k+1:n]))/K[k,k] return F
# Mendefinisikan variabel untuk dicetak pada layar Q = gaussElimin(K,F) print (Q)
- Catatan 1: nilai matriks beban dibagi dengan nilai modulus Young untuk mempermudah pembuatan matriks.
- Catatan 2: hasil matriks Q dalam satuan mm
- Catatan 3: untuk tugas aplikasi metode numerik untuk memodelkan masalah statika struktur, video tidak dapat kami upload ke wiki karena ukurannya yang terlalu besar. Kami mohon pemakluman dari Pak Indra dan Pak Radon mengenai hal ini, dan apabila berkenan, kami bersedia menunjukkan video yang telah kami buat secara langsung.
Tugas: Spring-mass system
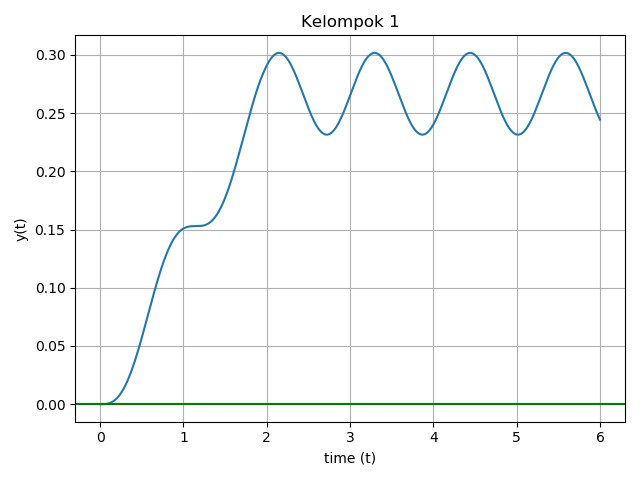
- Soal: Diilustrasikan sebuah sistem pegas-massa yang terpasang pada suatu dinding. Pegas tersebut memiliki konstanta kekakuan 75 N/m dan massa benda adalah 2,5 kg. Gaya P diberikan pada sistem ke arah menjauhi dinding dengan besaran 10t N selama 2 detik pertama dan 20 N setelahnya. Persamaan untuk percepatan sistem diberikan sebagai berikut: y" = (P(t)/m) - ((k/m)y). Sistem awalnya berada dalam keadaan diam. Hitung perpindahan maksimum sistem, dan plotkan pada grafik perubahan posisi sistem terhadap waktu!
- Analisa fenomena fisika: Pada sistem pegas-massa akan berlaku hukum II Newton, dimana arah percepatan sistem sama dengan arah total gaya yang bekerja pada sistem. Kita tahu bahwa benda dengan massa memiliki perumusan gaya F = m.a, dimana m adalah massa benda dan a (atau y") adalah percepatan benda, dan pegas memiliki perumusan gaya F = k.y, dimana k adalah konstanta kekakuan pegas dan y adalah perubahan panjang pegas dari panjang awal. Pada sistem pegas-massa dalam soal, gaya yang diberikan pada sistem arahnya menjauhi dinding. Hal ini akan mengakibatkan massa bergerak menjauhi dinding dengan percepatan tertentu. Pegas yang terpasang pada dinding akan memberikan gaya reaksi akibat meregang, yang arahnya berlawanan dengan gaya yang bekerja pada sistem. Oleh karena itu, perumusan gaya pada sistem dapat dinyatakan dengan:
- Gaya yang bekerja pada benda = Gaya yang diberikan pada sistem - gaya reaksi pegas
- m.y" = P(t) - k.y
- Apabila kedua ruas kita bagi dengan m, maka akan kita dapatkan persamaan seperti yang tertulis pada soal
- y" = P(t)/m - (k/m)y
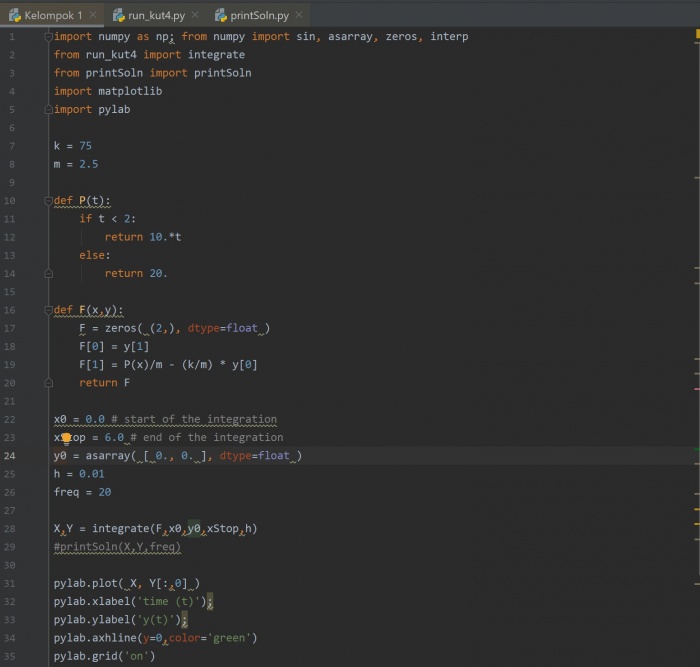
- Kami menggunakan aplikasi pycharm dan kodingan yang kami gunakan adalah:
import numpy as np; from numpy import sin, asarray, zeros, interp from run_kut4 import integrate from printSoln import printSoln import pylab
k = 75 m = 2.5
def P(t):
if t < 2:
return 10.*t
else:
return 20.
def F(x,y):
F = zeros( (2,), dtype=float )
F[0] = y[1]
F[1] = P(x)/m - (k/m) * y[0]
return F
x0 = 0.0 # start of the integration xStop = 6.0 # end of the integration y0 = asarray( [ 0., 0. ], dtype=float ) h = 0.01 freq = 20
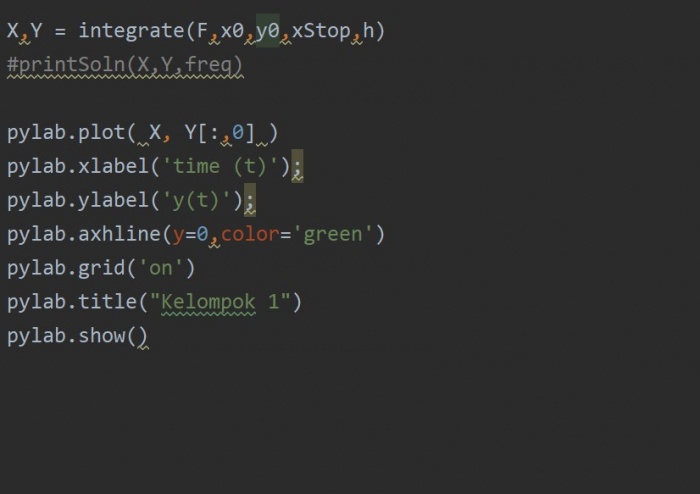
X,Y = integrate(F,x0,y0,xStop,h) #printSoln(X,Y,freq)
pylab.plot( X, Y[:,0] )
pylab.xlabel('time (t)');
pylab.ylabel('y(t)');
pylab.axhline(y=0,color='green')
pylab.grid('on')
pylab.title("Kelompok 1")
pylab.show()
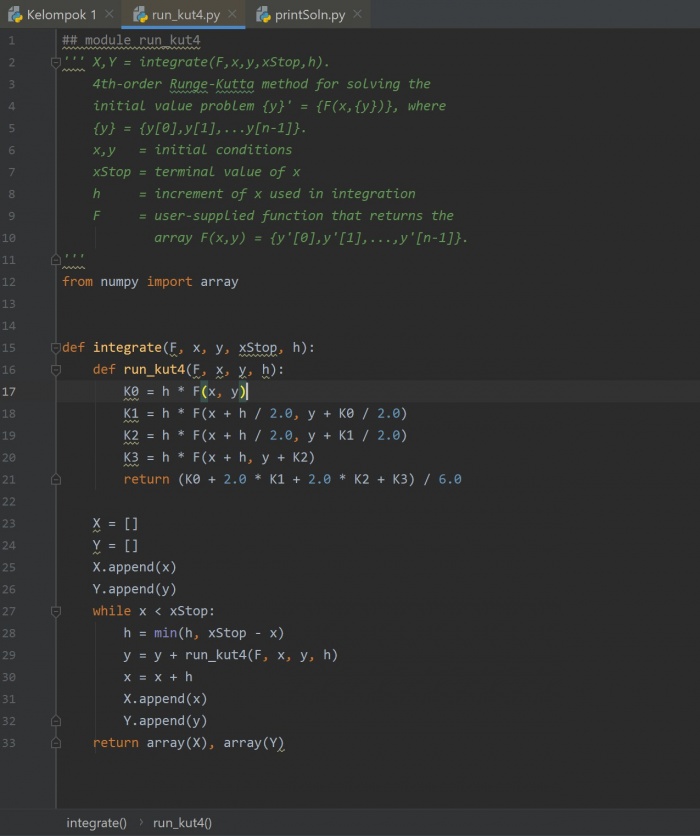
pertama kami install modul numpy dan install modul matplotlib setelah itu kami menggunakan modul run_kut4 dan juga modul pprintSoln yang dua-duanya terdapat di github.com
## module run_kut4
X,Y = integrate(F,x,y,xStop,h).
4th-order Runge-Kutta method for solving the
initial value problem {y}' = {F(x,{y})}, where
{y} = {y[0],y[1],...y[n-1]}.
x,y = initial conditions
xStop = terminal value of x
h = increment of x used in integration
F = user-supplied function that returns the
array F(x,y) = {y'[0],y'[1],...,y'[n-1]}.
from numpy import array
def integrate(F,x,y,xStop,h):
def run_kut4(F,x,y,h):
K0 = h*F(x,y)
K1 = h*F(x + h/2.0, y + K0/2.0)
K2 = h*F(x + h/2.0, y + K1/2.0)
K3 = h*F(x + h, y + K2)
return (K0 + 2.0*K1 + 2.0*K2 + K3)/6.0
X = []
Y = []
X.append(x)
Y.append(y)
while x < xStop:
h = min(h,xStop - x)
y = y + run_kut4(F,x,y,h)
x = x + h
X.append(x)
Y.append(y)
return array(X),array(Y)
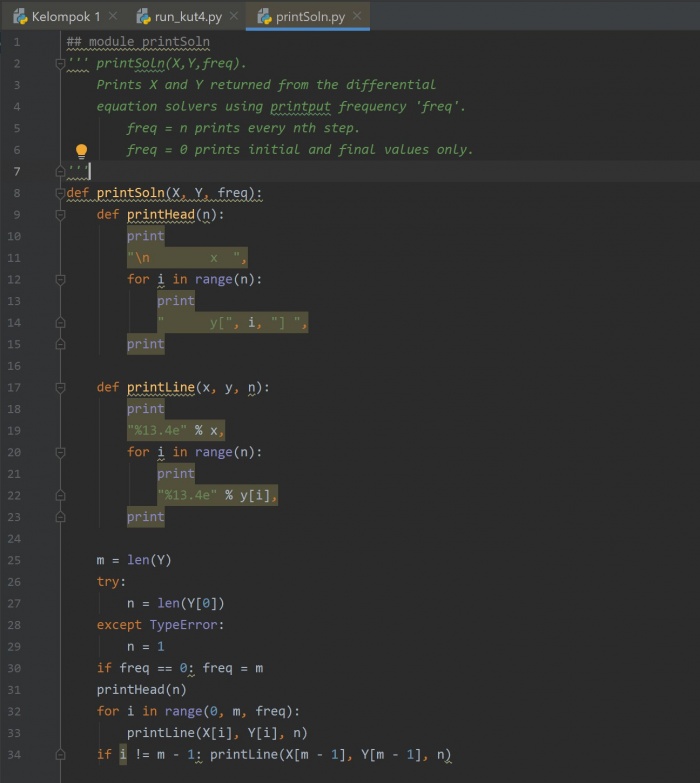
## module printSoln
printSoln(X,Y,freq).
Prints X and Y returned from the differential
equation solvers using printput frequency 'freq'.
freq = n prints every nth step.
freq = 0 prints initial and final values only.
def printSoln(X,Y,freq):
def printHead(n):
print "\n x ",
for i in range (n):
print " y[",i,"] ",
print
def printLine(x,y,n):
print "%13.4e"% x,
for i in range (n):
print "%13.4e"% y[i],
print
m = len(Y)
try: n = len(Y[0])
except TypeError: n = 1
if freq == 0: freq = m
printHead(n)
for i in range(0,m,freq):
printLine(X[i],Y[i],n)
if i != m - 1: printLine(X[m - 1],Y[m - 1],n)
Setelah semua telah dimasukkan dalam aplikasi pycharm maka kami melakukan run dan kemudian akan langsung muncul grafik.
Tugas optimasi aerodinamika
- Membuat geometri aerofoil di software CAD yang digunakan (kelompok kami menggunakan ukuran airfoil standar NACA dengan nomor 63-412).
- Melakukan simulasi aliran udara untuk geometri airfoil di software CFDSOF untuk mendapatkan nilai lift dan drag dari airfoil pada berbagai angle of attack.
- Menggunakan program Python yang ditujukan untuk optimasi nilai angle of attack, dimana nilai tersebut akan memiliki gaya lift besar dan drag kecil.
- Program Python yang digunakan:
import numpy as np from scipy.optimize import minimize
def calc_drag(x):#drag x1 = x[0] drag = 0.0193*x1**5 - 0.3797*x1**4 + 2.1688*x1**3 - 2.2064*x1**2 - 3.0016*x1 + 4.0659 return drag
def calc_lift(x): #lift x1 = x[0] lift = -0.0179*x1**5 + 0.55*x1**4 - 6.0283*x1**3 + 26.852*x1**2 - 38.461*x1 + 21.939 return lift
def objective(x): #volume yang diminimalkan return calc_drag(x)
def constraint1(x): #variable SUDUT yang meminimalkan persamaan garis drag return calc_drag(x) def constraint2(x): #variable SUDUT yang meminimalkan persamaan garis lift return calc_lift(x)
con1=({'type':'ineq','fun':constraint1})
con2=({'type':'ineq','fun':constraint2})
cons = (con1,con2)
a = (0,90)
batas = [a]
x1_guess = 50
x0 = np.array([x1_guess])
sol = minimize(objective,x0, method='SLSQP',bounds=batas, constraints=cons, options={'disp':True})
xopt = sol.x forceopt = -sol.fun
dragopt = calc_drag(xopt) # drag optimal liftopt = calc_lift(xopt) # lift optimal
print ('sudut optimal = '+str(xopt[0]))
print ('total force optimal = '+str(forceopt))
print ('drag force optimal = '+str(dragopt))
print ('lift force optimal = '+str(liftopt))
# In[10]:
import numpy as np from scipy.optimize import minimize
def calc_drag(x):#drag x1 = x[0] drag = 0.0193*x1**5 - 0.3797*x1**4 + 2.1688*x1**3 - 2.2064*x1**2 - 3.0016*x1 + 4.0659 return drag
def calc_lift(x): #lift x1 = x[0] lift = -0.0179*x1**5 + 0.55*x1**4 - 6.0283*x1**3 + 26.852*x1**2 - 38.461*x1 + 21.939 return lift
def objective(x): #volume yang diminimalkan return calc_lift(x)
def constraint1(x): #variable SUDUT yang meminimalkan persamaan garis drag return calc_drag(x) def constraint2(x): #variable SUDUT yang meminimalkan persamaan garis lift return calc_lift(x)
con1=({'type':'ineq','fun':constraint1})
con2=({'type':'ineq','fun':constraint2})
cons = (con1,con2)
a = (0,90)
batas = [a]
x1_guess = 50
x0 = np.array([x1_guess])
sol = minimize(objective,x0, method='SLSQP',bounds=batas, constraints=cons, options={'disp':True})
xopt = sol.x forceopt = -sol.fun
dragopt = calc_drag(xopt) # drag optimal liftopt = calc_lift(xopt) # lift optimal
print ('sudut optimal = '+str(xopt[0]))
print ('total force optimal = '+str(forceopt))
print ('drag force optimal = '+str(dragopt))
print ('lift force optimal = '+str(liftopt))