Difference between revisions of "Pertemuan Ke-6 (02 Oktober 2019)"
(Created page with "Dalam mennyelesaikan sebuah kasus nyata, terkadang kita melakukan permodelan terhadap kasus tersebut. Pemodelan tersebut dilakukan dengan cara persamaan diferensial. Persama...") |
|||
| (2 intermediate revisions by the same user not shown) | |||
| Line 3: | Line 3: | ||
Persamaan diferensial membahas tentang efek kontinu dari suatu objek jika diberikan gaya atau pengaruh luar. | Persamaan diferensial membahas tentang efek kontinu dari suatu objek jika diberikan gaya atau pengaruh luar. | ||
Penyelesaian Persamaan diferensial dengan Metode Numerik | Penyelesaian Persamaan diferensial dengan Metode Numerik | ||
| − | Metode Runge- | + | Metode Runge-Kutta |
Banyak persamaan diferensial tidak bisa diselesaikan dengan menggunakan metode eksak, oleh karena itu digunakan metode numerik. | Banyak persamaan diferensial tidak bisa diselesaikan dengan menggunakan metode eksak, oleh karena itu digunakan metode numerik. | ||
| − | Metode Runge- | + | Metode Runge-Ktuta |
| − | Persamaan runge - | + | Persamaan runge-Ktuta hanya memerlukan persamaan diferensial awal dan intial value. |
| + | |||
| + | Metode runge kutta dikhususkan untuk penyelesaian model matematika dengan aproksimasi nilai dengan galat yang lebih kecil atau teliti | ||
| + | |||
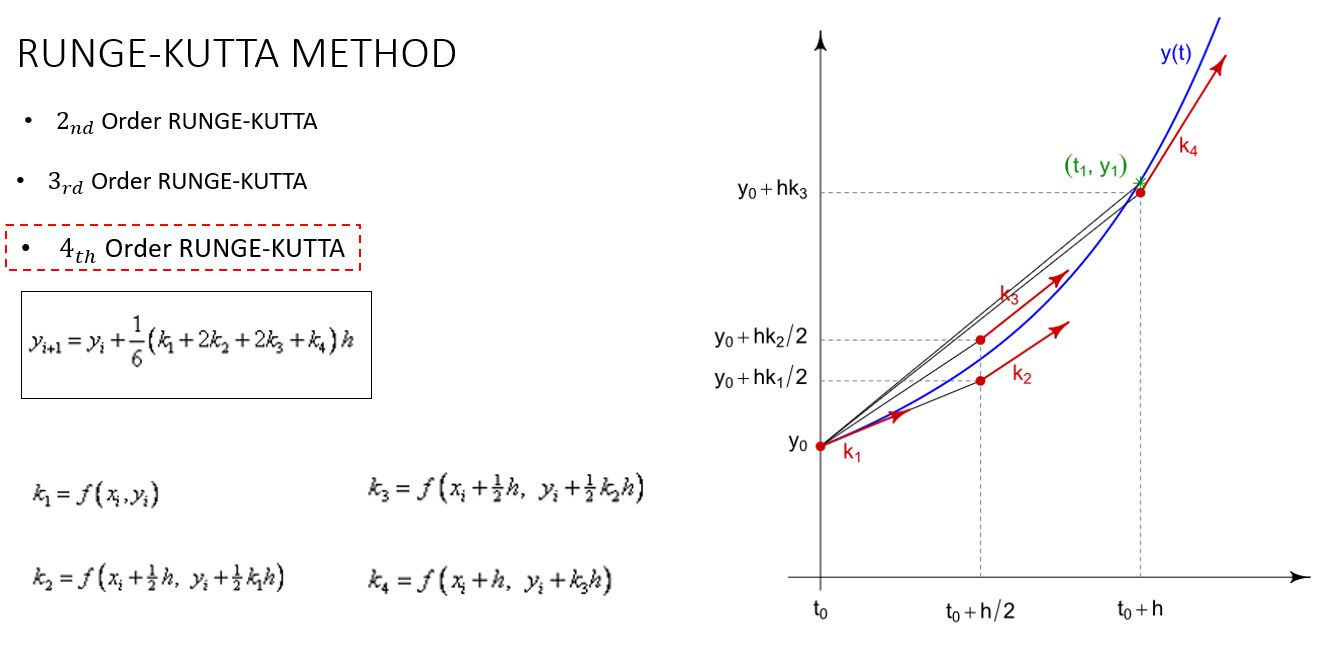
| + | Berikut ini rumus dari runge kutta orde 4 : | ||
| + | [[File:runge-kutta1.JPG]] | ||
Latest revision as of 14:27, 17 October 2019
Dalam mennyelesaikan sebuah kasus nyata, terkadang kita melakukan permodelan terhadap kasus tersebut. Pemodelan tersebut dilakukan dengan cara persamaan diferensial. Persamaan diferensial membahas tentang efek kontinu dari suatu objek jika diberikan gaya atau pengaruh luar. Penyelesaian Persamaan diferensial dengan Metode Numerik Metode Runge-Kutta Banyak persamaan diferensial tidak bisa diselesaikan dengan menggunakan metode eksak, oleh karena itu digunakan metode numerik.
Metode Runge-Ktuta
Persamaan runge-Ktuta hanya memerlukan persamaan diferensial awal dan intial value.
Metode runge kutta dikhususkan untuk penyelesaian model matematika dengan aproksimasi nilai dengan galat yang lebih kecil atau teliti