Difference between revisions of "Andika Ikhsan Kamil"
| (27 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | [[File:emil1.jpg|thumb]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Nama : Andika Ikhsan Kamil | ||
| + | |||
| + | NPM : 1806201176 | ||
| + | TTL : Tangerang, 11 Januari 2001 | ||
| − | |||
| − | |||
| − | + | ==KALKULUS== | |
Apa itu kalkulus? Kalkulus merupakan mata kuliah wajib teknik yang bertujuan untuk mempelajari pelajaran seperti integral, logaritma, trigonometri dan lainnya yang berhubungan dengan matematika teknik secara lanjutan. | Apa itu kalkulus? Kalkulus merupakan mata kuliah wajib teknik yang bertujuan untuk mempelajari pelajaran seperti integral, logaritma, trigonometri dan lainnya yang berhubungan dengan matematika teknik secara lanjutan. | ||
| Line 65: | Line 15: | ||
Tujuan kita dari belajar kalkulus sendiri adalah agar dapat mengerti bagaimana perhitungan matematik yang ada pada fakultas teknik pada saat kuliah nantinya. | Tujuan kita dari belajar kalkulus sendiri adalah agar dapat mengerti bagaimana perhitungan matematik yang ada pada fakultas teknik pada saat kuliah nantinya. | ||
| − | + | ==PHYTON== | |
Proses Belajar Phyton | Proses Belajar Phyton | ||
| Line 84: | Line 34: | ||
Dan Masih Banyak Lainnya | Dan Masih Banyak Lainnya | ||
| − | + | ==TUGAS 1== | |
def tugas(x): | def tugas(x): | ||
| Line 112: | Line 62: | ||
print(hasilnya/jumlah) | print(hasilnya/jumlah) | ||
| − | + | ==TUGAS 2== | |
rec = ('Andika', 'Ikhsan', 'Kamil',(11,1,2001)) | rec = ('Andika', 'Ikhsan', 'Kamil',(11,1,2001)) | ||
| Line 130: | Line 80: | ||
print(rec[0:3]) | print(rec[0:3]) | ||
| − | + | ==TUGAS 3== | |
| − | Fibonacci dengan While Loop | + | ===Fibonacci dengan While Loop=== |
# Python Fibonacci series Program using While Loop | # Python Fibonacci series Program using While Loop | ||
| Line 155: | Line 105: | ||
i = i + 1 | i = i + 1 | ||
| − | Fibonacci dengan Sub Routine (Function) | + | ===Fibonacci dengan Sub Routine (Function)=== |
def recur_fibo(n): | def recur_fibo(n): | ||
| Line 178: | Line 128: | ||
for i in range(nterms): | for i in range(nterms): | ||
print(recur_fibo(i)) | print(recur_fibo(i)) | ||
| + | |||
| + | |||
| + | ==Pertemuan 6== | ||
| + | |||
| + | Metode metode yang dipakai pada metode nnumerik contohnya adalah metode kutta. Dalam analisis numerik , metode Runge-Kutta adalah keluarga metode iteratif implisit dan eksplisit , yang mencakup rutin terkenal yang disebut Metode Euler , yang digunakan dalam diskritisasi temporal untuk solusi perkiraan persamaan diferensial biasa . | ||
| + | |||
| + | Anggota keluarga Runge-Kutta yang paling dikenal secara umum disebut sebagai "RK4", "metode Runge-Kutta" klasik atau hanya sebagai "metode Runge-Kutta". | ||
| + | |||
| + | |||
| + | ==QUIZ== | ||
| + | |||
| + | ===Problem Set 2.1=== | ||
| + | |||
| + | #Gauss Elimination For Matrix Using Numpy | ||
| + | |||
| + | from numpy import linalg | ||
| + | import numpy as np | ||
| + | |||
| + | bar1 = [0,0,2,1,2] | ||
| + | bar2 = [0,1,0,2,-1] | ||
| + | bar3 = [1,2,0,-2,1] | ||
| + | bar4 = [0,0,0,-1,1] | ||
| + | bar5 = [0,1,-1,1,-1] | ||
| + | nmat = np.array ([bar1,bar2,bar3,bar4,bar5]) | ||
| + | print ("n Matrix adalah sebagai berikut:") | ||
| + | print (nmat) | ||
| + | cons = np.array ([1,1,-4,-2,-1]) | ||
| + | print ("Matrix Y adalah sebagai berikut:") | ||
| + | print (cons) | ||
| + | jawab = linalg.solve (nmat,cons) | ||
| + | x1val = int(jawab[0]) | ||
| + | x2val = int(jawab[1]) | ||
| + | x3val = int(jawab[2]) | ||
| + | x4val = int(jawab[3]) | ||
| + | x5val = int(jawab[4]) | ||
| + | print ("hasil X adalah :") | ||
| + | print ("x1= ",x1val) | ||
| + | print ("x2= ",x2val) | ||
| + | print ("x3= ",x3val) | ||
| + | print ("x4= ",x4val) | ||
| + | print ("x5= ",x5val) | ||
| + | |||
| + | ===Problem Set 7.1=== | ||
| + | |||
| + | def dydx(x, y): | ||
| + | return ((x**2 - 4 * y) | ||
| + | |||
| + | # Finds value of y for a given x using step size h | ||
| + | # and initial value y0 at x0. | ||
| + | def rungeKutta(x0, y0, x, h): | ||
| + | # Count number of iterations using step size or | ||
| + | # step height h | ||
| + | n = (int)((x - x0)/h) | ||
| + | # Iterate for number of iterations | ||
| + | y = y0 | ||
| + | for i in range(1, n + 1): | ||
| + | "Apply Runge Kutta Formulas to find next value of y" | ||
| + | k1 = h * dydx(x0, y) | ||
| + | k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1) | ||
| + | k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2) | ||
| + | k4 = h * dydx(x0 + h, y + k3) | ||
| + | |||
| + | # Update next value of y | ||
| + | y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4) | ||
| + | |||
| + | # Update next value of x | ||
| + | x0 = x0 + h | ||
| + | return y | ||
| + | |||
| + | # Driver method | ||
| + | x0 = 0 | ||
| + | y = 1 | ||
| + | x = 0.03 | ||
| + | h = 0.01 | ||
| + | print 'The value of y at x is:', rungeKutta(x0, y, x, h) | ||
| + | |||
| + | |||
| + | Output: | ||
| + | |||
| + | The value of y at x is : 1.003639 | ||
| + | |||
| + | |||
| + | ==CODING UTS== | ||
| + | |||
| + | ===Case 1A=== | ||
| + | |||
| + | |||
| + | from math import * | ||
| + | |||
| + | |||
| + | g=9.81 | ||
| + | M1=eval(input("mau berapa massa benda 1 ?")) | ||
| + | M2=eval(input("Mau berapa massa benda 2 ?")) | ||
| + | M3=eval(input("Mau berapa massa benda 3 ?")) | ||
| + | M3=eval(input("Mau berapa massa benda 4 ?")) | ||
| + | Fk1=eval(input("Koefisien gesek benda 1 ?")) | ||
| + | Fk2=eval(input("koefisien gesek benda 2 ?")) | ||
| + | Fk3=eval(input("Koefisien gesek benda 3 ?")) | ||
| + | alfa=eval(input("sudutnya mau berapa ?")) | ||
| + | a=eval(input("percepatan :")) | ||
| + | x= sin(alfa) | ||
| + | y= cos(alfa) | ||
| + | |||
| + | |||
| + | T1=M1*g*(x-Fk1*y)-M1*a | ||
| + | T2=M2*g*(x-Fk2*y)+T1-M2*a | ||
| + | T3=M3*g*(x-Fk3*y)+T2-M3*a | ||
| + | |||
| + | print("maka T1 adalah ?",T1) | ||
| + | print("maka T2 adalah ?",T2) | ||
| + | print("maka T3 adalah ?",T3) | ||
| + | |||
| + | |||
| + | ===CASE 2A=== | ||
| + | |||
| + | |||
| + | #memasukkan nilai variabel yang diperlukan | ||
| + | cd=eval(input("drag coefficient: ")) | ||
| + | v0=eval(input("Kecepatan Awal (m/s): ")) | ||
| + | m=eval(input("Massa (kg): ")) | ||
| + | a=eval(input("Percepatan (m/s^2): ")) | ||
| + | vt=eval(input("Kecepatan Tertinggi (m/s): ")) | ||
| + | #semua dibagi m | ||
| + | fdrag=(cd*vt**(3/2))/m | ||
| + | ft=a | ||
| + | atot=ft-fdrag | ||
| + | t=(vt-v0)/atot | ||
| + | print("waktu mobil untuk mencapai kecepatan tertinggi: ",t, "detik") | ||
| + | |||
| + | ==TUGAS VIDEO UTS== | ||
| + | |||
| + | |||
| + | 1.'''Video Muhasabah(percerminan diri )''' | ||
| + | |||
| + | [[File:EmilVideo1.mp4]] | ||
| + | |||
| + | |||
| + | 2.'''Video penjelasan soal nomor I.A''' | ||
| + | |||
| + | [[File:EmilVideo6.mp4]] | ||
| + | |||
| + | |||
| + | 3.'''Video penjelasan soal II.A''' | ||
| + | |||
| + | |||
| + | [[File:EmilVideo5.mp4]] | ||
| + | |||
| + | ==Tugas CFDSOF== | ||
| + | Aplikasi CFD SOF digunakan untuk menganalisis suatu persamaan yang melibatkan suatu fluida tertentu yang melewati suatu benda padat. Kali ini mahasiswa Metnum-02 diperlukan untuk menentukan suatu persamaan yang didapatkan dari Drag Coefficient dari sebuah mobil yang sedang melaju. | ||
| + | |||
| + | [[File:tugascfdsof.png|800px]] | ||
| + | |||
| + | Dan setelah melaksanakan percobaan tersebut akan didapatkan hitungan sebagai berikut. | ||
| + | |||
| + | [[File:tugascfdsof2.png|800px]] | ||
| + | |||
| + | Hasil Analisis Drag dan Lift terhadap sudut | ||
| + | |||
| + | [[File:Hasil Data Lift Drag.PNG]] | ||
| + | |||
| + | |||
| + | Grafik Sudut vs Drag | ||
| + | |||
| + | [[File:Sudut vs Drag.PNG]] | ||
| + | |||
| + | |||
| + | Grafik Sudut vs Lift | ||
| + | |||
| + | [[File:Sudut vs Lift.PNG]] | ||
| + | |||
| + | |||
| + | Grafik Sudut vs Drag/Lift | ||
| + | |||
| + | [[File:Perbandingan.PNG]] | ||
| + | |||
| + | Optimasi Sudut | ||
| + | |||
| + | [[File:Optimasi Nyoman Kamaru.PNG]] | ||
| + | |||
| + | |||
| + | ==Artificial Neural Network== | ||
| + | |||
| + | Neural network adalah model yang terinspirasi oleh bagaimana neuron dalam otak manusia bekerja. Tiap neuron pada otak manusia saling berhubungan dan informasi mengalir dari setiap neuron tersebut. | ||
| + | |||
| + | Pada part selanjutnya, akan saya bahas bagaimana proses training pada neural network lebih mendalam. Namun pada part ini akan dijelaskan garis besarnya saja. Proses training terdiri dari 2 tahap : | ||
| + | Forward Pass | ||
| + | Backward Pass | ||
Latest revision as of 17:33, 17 December 2019
Nama : Andika Ikhsan Kamil
NPM : 1806201176
TTL : Tangerang, 11 Januari 2001
Contents
KALKULUS
Apa itu kalkulus? Kalkulus merupakan mata kuliah wajib teknik yang bertujuan untuk mempelajari pelajaran seperti integral, logaritma, trigonometri dan lainnya yang berhubungan dengan matematika teknik secara lanjutan.
Tujuan kita dari belajar kalkulus sendiri adalah agar dapat mengerti bagaimana perhitungan matematik yang ada pada fakultas teknik pada saat kuliah nantinya.
PHYTON
Proses Belajar Phyton
Pengertian Python (bahasa pemrograman) merupakan bahasa pemrograman tinggi yang bisa melakukan eksekusi sejumlah instruksi multi guna secara langsung (interpretatif) dengan metode Object Oriented Programming dan juga menggunakan semantik dinamis untuk memberikan tingkat keterbacaan syntax. Sebagai bahasa pemrograman tinggi, python dapat dipelajari dengan mudah karena telah dilengkapi dengan manajemen memori otomatis.
Ada Banyak fitur fitur pada phyton seperti : Print Variabel, String Integer If List Loop Slicing If Else Block Variable Dan Masih Banyak Lainnya
TUGAS 1
def tugas(x):
result = (x**2-1)/(x-1)
try:
result
except ZeroDivisionError:
result = float('inf')
return result
a = 1 b = a + 0.3 c = 0.05 d = a - c hasilnya = 0 jumlah = 0 while a < b+ 0.5:
d =d + 0.01
print(soal(d))
a = a + 0.1
jumlah = jumlah + 1
if soal(d) != float('inf'):
hasilnya = hasilnya + soal(d)
print("limitnya = ")
print(hasilnya/jumlah)
TUGAS 2
rec = ('Andika', 'Ikhsan', 'Kamil',(11,1,2001))
NamaAwal, NamaTengah, NamaAkhir, tanggallahir = rec
print(NamaTengah)
TahunLahir = tanggallahir [2]
print(TahunLahir)
name = rec[0] ++rec[1]
print(name)
print(rec[0:3])
TUGAS 3
Fibonacci dengan While Loop
- Python Fibonacci series Program using While Loop
- Fibonacci series will start at 0 and travel upto below number
Number = int(input("\nPlease Enter the Range Number: "))
- Initializing First and Second Values of a Series
i = 1 First_Value = 0 Second_Value = 1
- Find & Displaying Fibonacci series
while(i < Number):
if(i <= 1):
Next = i
else:
Next = First_Value + Second_Value
First_Value = Second_Value
Second_Value = Next
print(Next)
i = i + 1
Fibonacci dengan Sub Routine (Function)
def recur_fibo(n):
"""Recursive function to
print Fibonacci sequence"""
if n <= 1:
return n
else:
return(recur_fibo(n-1) + recur_fibo(n-2))
- Change this value for a different result
nterms = 10
- uncomment to take input from the user
- nterms = int(input("How many terms? "))
- check if the number of terms is valid
if nterms <= 0:
print("Plese enter a positive integer")
else:
print("Fibonacci sequence:")
for i in range(nterms):
print(recur_fibo(i))
Pertemuan 6
Metode metode yang dipakai pada metode nnumerik contohnya adalah metode kutta. Dalam analisis numerik , metode Runge-Kutta adalah keluarga metode iteratif implisit dan eksplisit , yang mencakup rutin terkenal yang disebut Metode Euler , yang digunakan dalam diskritisasi temporal untuk solusi perkiraan persamaan diferensial biasa .
Anggota keluarga Runge-Kutta yang paling dikenal secara umum disebut sebagai "RK4", "metode Runge-Kutta" klasik atau hanya sebagai "metode Runge-Kutta".
QUIZ
Problem Set 2.1
#Gauss Elimination For Matrix Using Numpy
from numpy import linalg import numpy as np
bar1 = [0,0,2,1,2]
bar2 = [0,1,0,2,-1]
bar3 = [1,2,0,-2,1]
bar4 = [0,0,0,-1,1]
bar5 = [0,1,-1,1,-1]
nmat = np.array ([bar1,bar2,bar3,bar4,bar5])
print ("n Matrix adalah sebagai berikut:")
print (nmat)
cons = np.array ([1,1,-4,-2,-1])
print ("Matrix Y adalah sebagai berikut:")
print (cons)
jawab = linalg.solve (nmat,cons)
x1val = int(jawab[0])
x2val = int(jawab[1])
x3val = int(jawab[2])
x4val = int(jawab[3])
x5val = int(jawab[4])
print ("hasil X adalah :")
print ("x1= ",x1val)
print ("x2= ",x2val)
print ("x3= ",x3val)
print ("x4= ",x4val)
print ("x5= ",x5val)
Problem Set 7.1
def dydx(x, y):
return ((x**2 - 4 * y)
# Finds value of y for a given x using step size h
# and initial value y0 at x0.
def rungeKutta(x0, y0, x, h):
# Count number of iterations using step size or
# step height h
n = (int)((x - x0)/h)
# Iterate for number of iterations
y = y0
for i in range(1, n + 1):
"Apply Runge Kutta Formulas to find next value of y"
k1 = h * dydx(x0, y)
k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)
k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)
k4 = h * dydx(x0 + h, y + k3)
# Update next value of y
y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
# Update next value of x
x0 = x0 + h
return y
# Driver method x0 = 0 y = 1 x = 0.03 h = 0.01 print 'The value of y at x is:', rungeKutta(x0, y, x, h)
Output:
The value of y at x is : 1.003639
CODING UTS
Case 1A
from math import *
g=9.81
M1=eval(input("mau berapa massa benda 1 ?"))
M2=eval(input("Mau berapa massa benda 2 ?"))
M3=eval(input("Mau berapa massa benda 3 ?"))
M3=eval(input("Mau berapa massa benda 4 ?"))
Fk1=eval(input("Koefisien gesek benda 1 ?"))
Fk2=eval(input("koefisien gesek benda 2 ?"))
Fk3=eval(input("Koefisien gesek benda 3 ?"))
alfa=eval(input("sudutnya mau berapa ?"))
a=eval(input("percepatan :"))
x= sin(alfa)
y= cos(alfa)
T1=M1*g*(x-Fk1*y)-M1*a T2=M2*g*(x-Fk2*y)+T1-M2*a T3=M3*g*(x-Fk3*y)+T2-M3*a
print("maka T1 adalah ?",T1)
print("maka T2 adalah ?",T2)
print("maka T3 adalah ?",T3)
CASE 2A
#memasukkan nilai variabel yang diperlukan
cd=eval(input("drag coefficient: "))
v0=eval(input("Kecepatan Awal (m/s): "))
m=eval(input("Massa (kg): "))
a=eval(input("Percepatan (m/s^2): "))
vt=eval(input("Kecepatan Tertinggi (m/s): "))
#semua dibagi m
fdrag=(cd*vt**(3/2))/m
ft=a
atot=ft-fdrag
t=(vt-v0)/atot
print("waktu mobil untuk mencapai kecepatan tertinggi: ",t, "detik")
TUGAS VIDEO UTS
1.Video Muhasabah(percerminan diri )
2.Video penjelasan soal nomor I.A
3.Video penjelasan soal II.A
Tugas CFDSOF
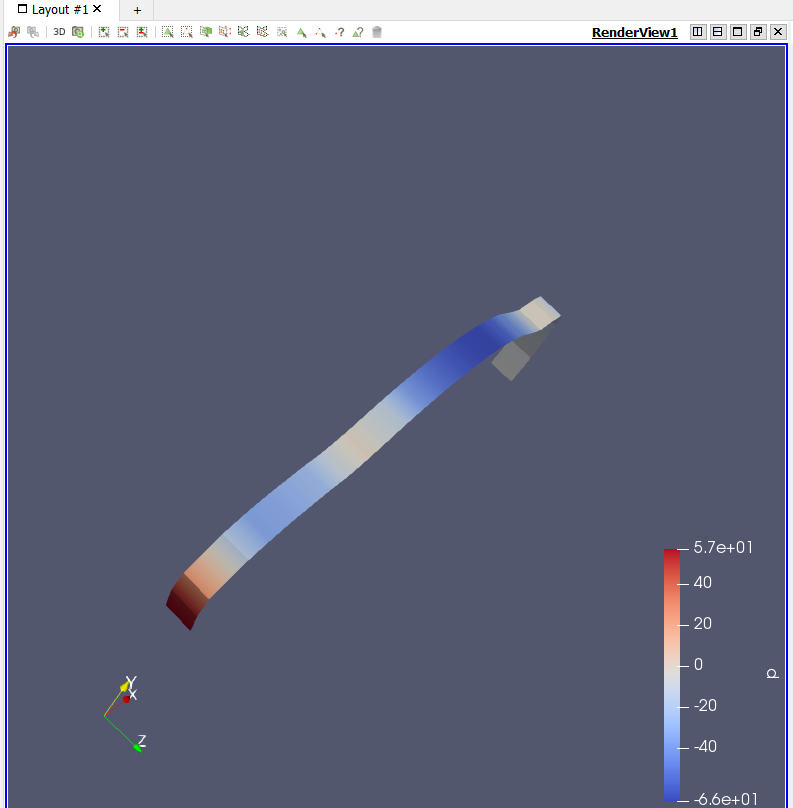
Aplikasi CFD SOF digunakan untuk menganalisis suatu persamaan yang melibatkan suatu fluida tertentu yang melewati suatu benda padat. Kali ini mahasiswa Metnum-02 diperlukan untuk menentukan suatu persamaan yang didapatkan dari Drag Coefficient dari sebuah mobil yang sedang melaju.
Dan setelah melaksanakan percobaan tersebut akan didapatkan hitungan sebagai berikut.
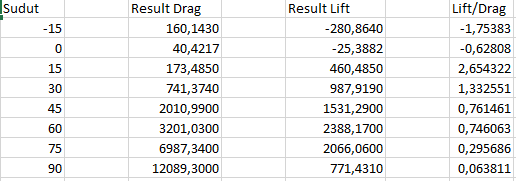
Hasil Analisis Drag dan Lift terhadap sudut
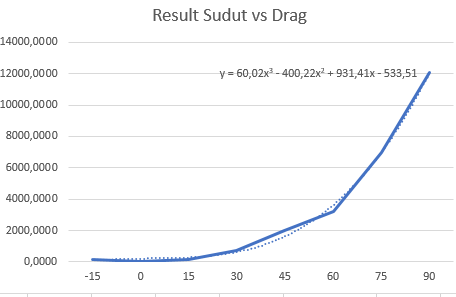
Grafik Sudut vs Drag
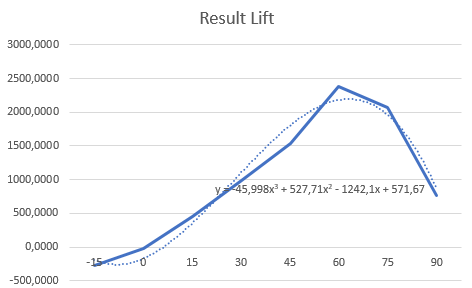
Grafik Sudut vs Lift
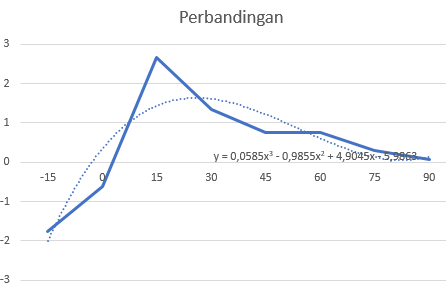
Grafik Sudut vs Drag/Lift
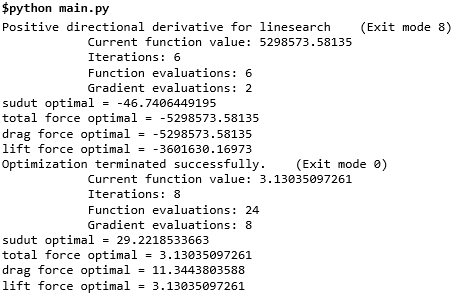
Optimasi Sudut
Artificial Neural Network
Neural network adalah model yang terinspirasi oleh bagaimana neuron dalam otak manusia bekerja. Tiap neuron pada otak manusia saling berhubungan dan informasi mengalir dari setiap neuron tersebut.
Pada part selanjutnya, akan saya bahas bagaimana proses training pada neural network lebih mendalam. Namun pada part ini akan dijelaskan garis besarnya saja. Proses training terdiri dari 2 tahap : Forward Pass Backward Pass