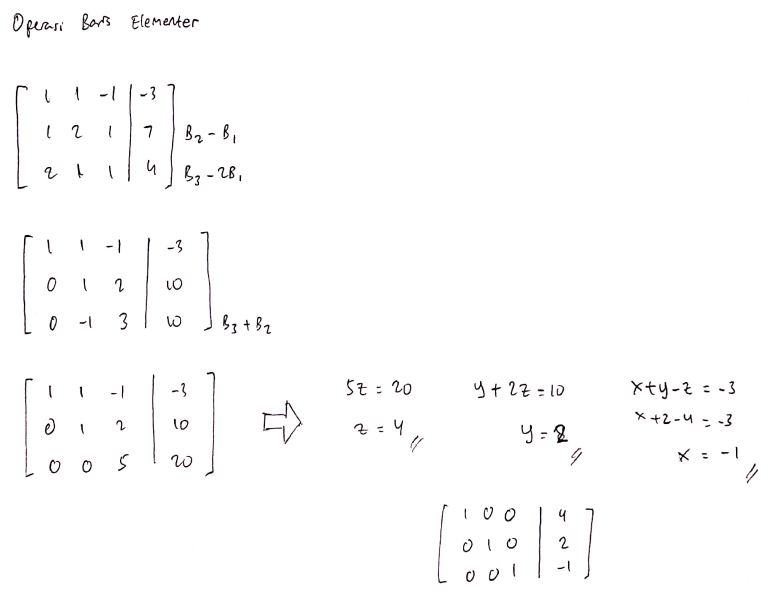Difference between revisions of "Kelompok 14"

From ccitonlinewiki
Jump to: navigation, search
 
(8 intermediate revisions by the same user not shown)
Line 12: Line 12:
 
=== Pengertian ===
 
=== Pengertian ===
  
−
Eliminasi Gauss-Jordan adalah prosedur pemecahan sistem persamaan linear dengan mengubahnya menjadi bentuk matriks '''eselon baris tereduksi''' dengan '''Operasi Baris Elementer'''.
+
Eliminasi Gauss-Jordan adalah prosedur pemecahan sistem persamaan linear dengan mengubahnya menjadi bentuk matriks '''eselon baris tereduksi''' dengan metode '''operasi baris elementer'''.
 +
 
 +
Contoh soal:
 +
 
 +
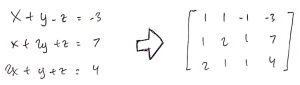
x + y – z = –3
 +
 
 +
x + 2y + z = 7
 +
 
 +
2x + y + z = 4
  
 
Pertama, sistem persamaan linear yang ingin dipecahkan diubah ke matriks:
 
Pertama, sistem persamaan linear yang ingin dipecahkan diubah ke matriks:
  
−
[[File:K14-mengubah_spl_ke_matriks.png]]
+
[[File:K14-mengubah_spl_ke_matriks.png|thumb|center]]
  
 
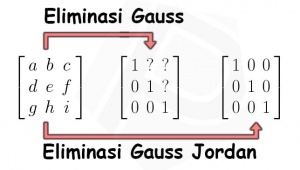
Kemudian, dengan operasi baris elementer, matriks tersebut diubah menjadi matriks eselon baris '''(gauss)''', kemudian diubah lagi menjadi matriks eselon baris tereduksi '''(gauss-jordan)'''.
 
Kemudian, dengan operasi baris elementer, matriks tersebut diubah menjadi matriks eselon baris '''(gauss)''', kemudian diubah lagi menjadi matriks eselon baris tereduksi '''(gauss-jordan)'''.
  
−
[[File:K14-Ilustrasi-eliminasi-gauss-jordan.jpg]]
+
[[File:K14-Ilustrasi-eliminasi-gauss-jordan.jpg|thumb|center]]
 +
 
 +
Berikut penyelesaian secara manual:
 +
 
 +
[[File:K14-obe.png]]
 +
 
  
 
=== Menyelesaikan SPL dengan Eliminasi Gauss-Jordan menggunakan Python ===
 
=== Menyelesaikan SPL dengan Eliminasi Gauss-Jordan menggunakan Python ===
Line 34: Line 47:
  
 
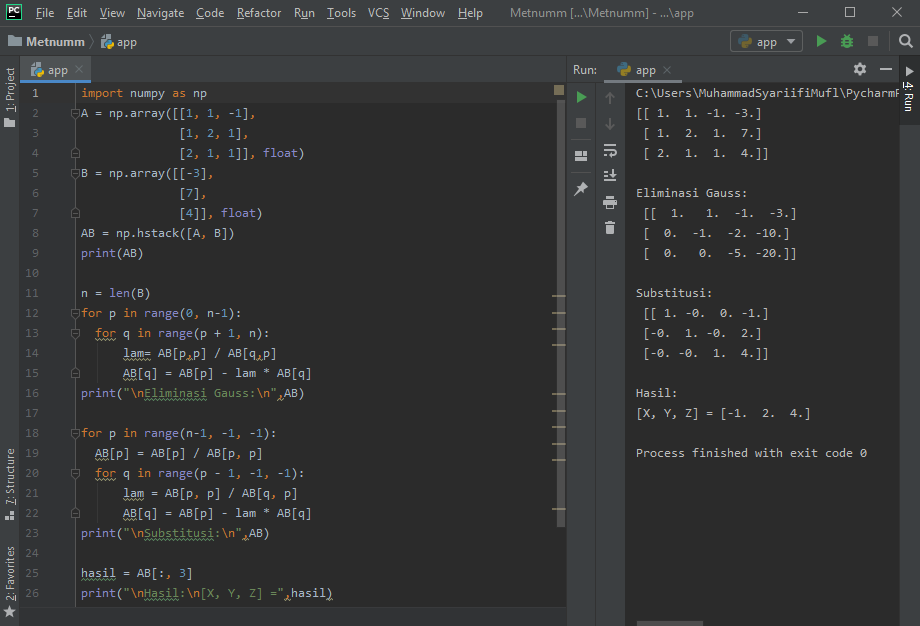
Berikut kode yang kami gunakan di python:
 
Berikut kode yang kami gunakan di python:
−
import numpy as np
 
−
A = np.array([[1, 1, -1],
 
−
              [1, 2, 1],
 
−
              [2, 1, 1]])
 
−
B = np.array([[-3],
 
−
              [7],
 
−
              [4]])
 
−
n = len(A)
 
−
for k in range(0, n-1):
 
−
  for i in range(n-1, k, -1):
 
−
    if A[i][k] != 0.0:
 
−
      lam= A[i][k]/A[k,k]
 
−
      A[i,k:n]=A[i, k:n] - (A[k,k:n]*lam)
 
−
      B[i]= B[i] - (B[k]*lam)
 
−
x=np.zeros(n,float)
 
−
for m in range(n-1, -1, -1):
 
−
  x[m]= (B[m]-np.dot(A[m, m+1:n], x[m+1:n]))/A[m,m]
 
−
  print("X", m+1, "=", x[m])
 
  
 
[[File:K14-gauss-jordan elimination.png]]
 
[[File:K14-gauss-jordan elimination.png]]
  
−
Run dari kode di atas. Ketika dimasukkan nilai dari matriks A (yaitu persamaan linear yang ingin dicari solusinya) dan matriks B (konstanta persamaan di sebelah tanda "="), program menampilkan solusi dari x (X1), y (X2), dan z (X3).
+
=== Video ===
 +
 
 +
[[File:K14-metnum_gauss-jordan.mp4]]
 +
 
 +
 
 +
 
 +
== Menyelesaikan Soal dengan Runge-Kutta ==
 +
 
 +
[[File:K14-Runge_kutta_2.png]]
 +
 
 +
 
 +
=== Kode di python ===
 +
 
 +
# x0 dan y sebagai titik asal, x sebagai t yang diinput, dan h sebagai tingkat peningkatan, di sini digunakan h = 0.001 supaya cukup akurat
 +
x0 = 0
 +
y = 0
 +
h = 0.001
 +
x = float(input("Nilai t: "))  # perintah untuk memasukkan nilai t sebagai x
 +
 +
if 0 <= x < 2:  # untuk 0 <= t < 2
 +
    def dydx(x, y):  # dydx menyatakan persamaan awal dalam soal
 +
        return (4 * x - 30 * y) # diperoleh 4x - 30y karena diketahui di soal m = 2,5 kg dan k = 75 N/m, P(t) dinyatakan dalam x
 +
 +
    def rungeKutta(x0, y0, x, h):  # perhitungan Runge-Kutta
 +
        n = (int)((x - x0) / h)
 +
        y = y0
 +
        for i in range(1, n + 1):
 +
            k1 = h * dydx(x0, y)
 +
            k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)
 +
            k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)
 +
            k4 = h * dydx(x0 + h, y + k3)
 +
            y = y + (1.0 / 6.0) * (k1 + 2 * k2 + 2 * k3 + k4)
 +
            x0 = x0 + h
 +
        return y
 +
 +
    print("Nilai y pada t =", x, "adalah", rungeKutta(x0, y, x, h))
 +
 +
elif x >= 2:  # untuk t > 2
 +
    def dydx(x, y):  # dydx menyatakan persamaan awal dalam soal
 +
        return (8 - 30 * y)  # diperoleh 8 - 30y karena diketahui di soal P(t) = 20 N , m = 2,5 kg , k = 75 N/m
 +
 +
    def rungeKutta(x0, y0, x, h):  # perhitungan Runge-Kutta
 +
        n = (int)((x - x0) / h)
 +
        y = y0
 +
        for i in range(1, n + 1):
 +
            k1 = h * dydx(x0, y)
 +
            k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)
 +
            k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)
 +
            k4 = h * dydx(x0 + h, y + k3)
 +
            y = y + (1.0 / 6.0) * (k1 + 2 * k2 + 2 * k3 + k4)
 +
            x0 = x0 + h
 +
        return y
 +
 +
    print("Nilai y pada t =", x, "adalah", rungeKutta(x0, y, x, h)) # print nilai y pada t yang diinput
 +
 +
else:
 +
    print("Nilai t harus positif.")  # memberitahu nilai t harus positif jika t yang dimasukkan negatif
 +
 
 +
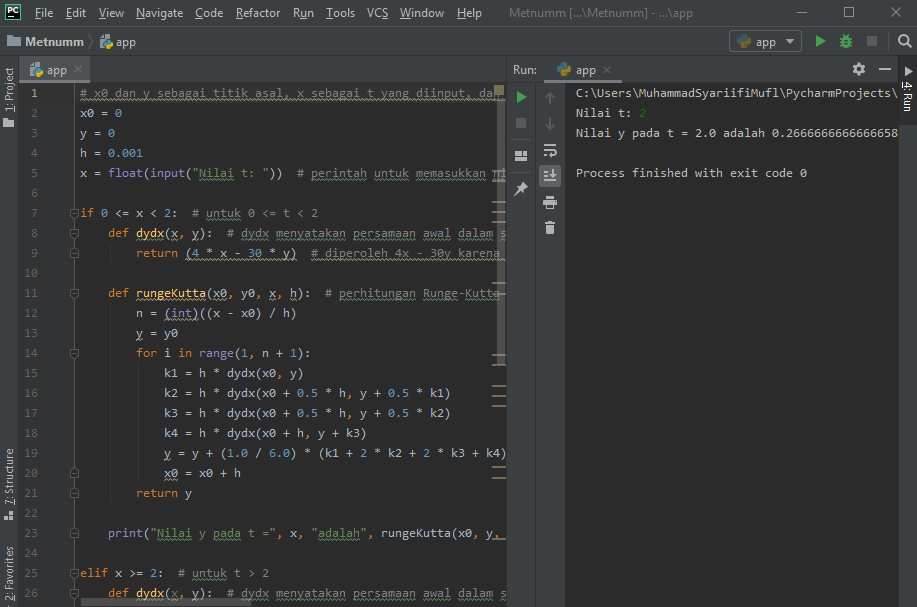
[[File:K14-Runge_kutta.png]]
 +
 
 +
Run dari kode di atas, ketika dimasukkan t = 2, program menampilkan nilai y pada t = 2 yaitu 0.2666666666666658
 +
 
 +
 
 +
 
 +
== Optimasi Angle of Attack pada Airfoil ==
 +
 
 +
=== Airfoil ===
 +
 
 +
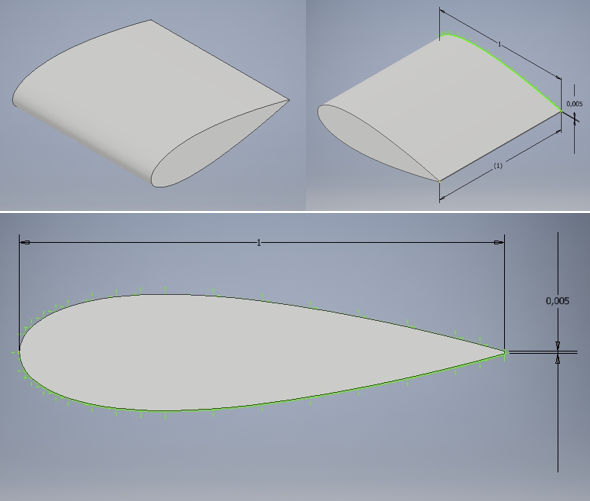
Pada tugas kali ini, kami mendesain sebuah airfoil dengan menggunakan program Autodesk Inventor untuk dites seberapa besar gaya angkat (lift force) dan gaya hambatan udara (drag force) yang dihasilkan ketika menabrak udara dengan kecepatan 100 m/s. Berikut adalah bentuk desain airfoil yang kami buat:
 +
 
 +
[[File:Airfoil_kelompok_14.png]]
 +
 
 +
 
 +
 
 +
=== Data Drag Force & Lift Force ===
 +
 
 +
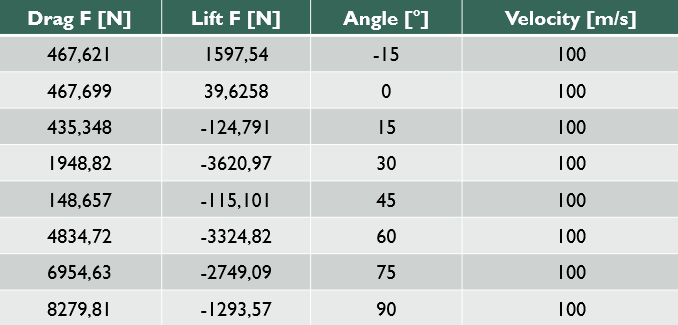
Dengan menggunakan software CFDSOF-NG V1.00, diperoleh data besarnya drag force & lift force terhadap kemiringan sudut airfoil sebagai berikut:
 +
 
 +
[[File:Data_airfoil_kelompok_14.png]]
 +
 
 +
 
 +
 
 +
=== Kurva drag force & lift force terhadap kemiringan sudut airfoil ===
 +
 
 +
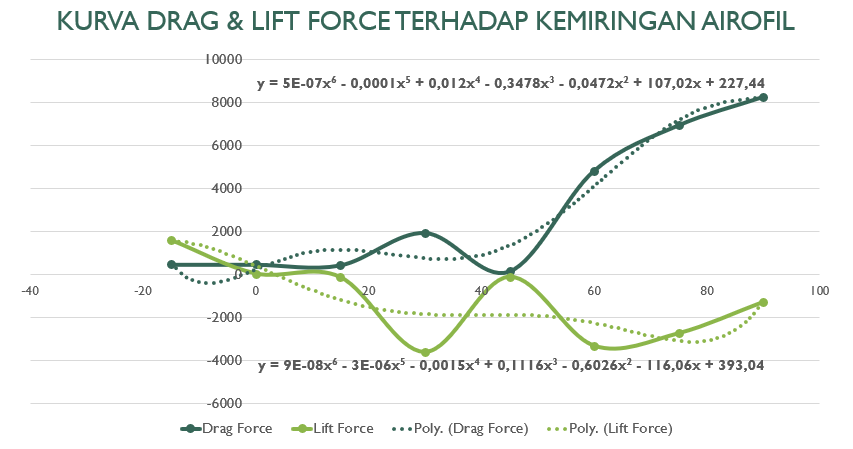
Berikut kurva dari drag force & lift force terhadap kemiringan sudut airfoil:
 +
 
 +
[[File:Kurva_airfoil_kelompok_14.png]]
 +
 
 +
 
 +
 
 +
=== Optimasi ===
 +
 
 +
Dari persamaan kurva tersebut, kami mencari nilai optimasi dari masing-masing force dengan menggunakan kode berikut:
 +
 
 +
import numpy as np
 +
from scipy.optimize import minimize
 +
 +
def cdrag(x):
 +
    x1 = x[0]
 +
    drag = 0.0000005*x1**6-0.0001*x1**5+0.012*x1**4-0.3478*x1**3-0.0472*x1**2+107.02*x1+227.44
 +
    return drag
 +
 +
def clift(x):
 +
    x1 = x[0]
 +
    lift = 0.00000009*x1**6-0.000003*x1**5-0.0015*x1**4+0.1116*x1**3-0.6026*x1**2-116.06*x1+393.04
 +
    return lift
 +
 +
def objective(x):
 +
    return cdrag(x)
 +
 +
def constraint1(x):
 +
    return 90 - cdrag(x)
 +
def constraint2(x):
 +
    return 90 - clift(x)
 +
 +
con1=({'type':'ineq','fun':constraint1})
 +
con2=({'type':'ineq','fun':constraint2})
 +
cons = (con1,con2)
 +
 +
x1_guess = 50
 +
 +
x0 = np.array([x1_guess])  
 +
 +
sol = minimize(objective,x0, method='SLSQP',constraints=cons, options={'disp':True})
 +
 +
xopt = sol.x
 +
forceopt = -sol.fun
 +
 +
dragopt = cdrag(xopt)
 +
liftopt = clift(xopt)
 +
 +
print ("")
 +
print ("Hasil optimasi:")
 +
print ("Sudut optimal = "+str(-xopt[0]))
 +
print ("Total force optimal = "+str(forceopt))
 +
print ("Drag force optimal = "+str(-dragopt))
 +
print ("Lift force optimal = "+str(liftopt))
 +
 
 +
'''Hasil optimasi''':
 +
 +
Sudut optimal = -18.824361039981582 °
 +
Total force optimal = -1197.981206594249 N
 +
Drag force optimal = -1197.981206594249 N
 +
Lift force optimal = -1452.2582614781118 N

Latest revision as of 19:11, 16 December 2019

Anggota Kelompok 14

Muhammad Syariifi Muflih (1806149210)

Fabio Almer Agoes (1806201296)

Oimolala Putrawan (1706036412)

Eliminasi Gauss-Jordan

Pengertian

Eliminasi Gauss-Jordan adalah prosedur pemecahan sistem persamaan linear dengan mengubahnya menjadi bentuk matriks eselon baris tereduksi dengan metode operasi baris elementer.

Contoh soal:

x + y – z = –3

x + 2y + z = 7

2x + y + z = 4

Pertama, sistem persamaan linear yang ingin dipecahkan diubah ke matriks:

K14-mengubah spl ke matriks.png

Kemudian, dengan operasi baris elementer, matriks tersebut diubah menjadi matriks eselon baris (gauss), kemudian diubah lagi menjadi matriks eselon baris tereduksi (gauss-jordan).

K14-Ilustrasi-eliminasi-gauss-jordan.jpg

Berikut penyelesaian secara manual:

K14-obe.png


Menyelesaikan SPL dengan Eliminasi Gauss-Jordan menggunakan Python

Contoh soal sistem persamaan linear 3 variabel:

x + y – z = –3

x + 2y + z = 7

2x + y + z = 4


Berikut kode yang kami gunakan di python:

K14-gauss-jordan elimination.png

Video


Menyelesaikan Soal dengan Runge-Kutta

K14-Runge kutta 2.png


Kode di python

# x0 dan y sebagai titik asal, x sebagai t yang diinput, dan h sebagai tingkat peningkatan, di sini digunakan h = 0.001 supaya cukup akurat
x0 = 0
y = 0
h = 0.001
x = float(input("Nilai t: "))  # perintah untuk memasukkan nilai t sebagai x

if 0 <= x < 2:  # untuk 0 <= t < 2
   def dydx(x, y):  # dydx menyatakan persamaan awal dalam soal
       return (4 * x - 30 * y)  # diperoleh 4x - 30y karena diketahui di soal m = 2,5 kg dan k = 75 N/m, P(t) dinyatakan dalam x

   def rungeKutta(x0, y0, x, h):  # perhitungan Runge-Kutta
       n = (int)((x - x0) / h)
       y = y0
       for i in range(1, n + 1):
           k1 = h * dydx(x0, y)
           k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)
           k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)
           k4 = h * dydx(x0 + h, y + k3)
           y = y + (1.0 / 6.0) * (k1 + 2 * k2 + 2 * k3 + k4)
           x0 = x0 + h
       return y

   print("Nilai y pada t =", x, "adalah", rungeKutta(x0, y, x, h))

elif x >= 2:  # untuk t > 2
   def dydx(x, y):  # dydx menyatakan persamaan awal dalam soal
       return (8 - 30 * y)  # diperoleh 8 - 30y karena diketahui di soal P(t) = 20 N , m = 2,5 kg , k = 75 N/m

   def rungeKutta(x0, y0, x, h):  # perhitungan Runge-Kutta
       n = (int)((x - x0) / h)
       y = y0
       for i in range(1, n + 1):
           k1 = h * dydx(x0, y)
           k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)
           k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)
           k4 = h * dydx(x0 + h, y + k3)
           y = y + (1.0 / 6.0) * (k1 + 2 * k2 + 2 * k3 + k4)
           x0 = x0 + h
       return y

   print("Nilai y pada t =", x, "adalah", rungeKutta(x0, y, x, h))  # print nilai y pada t yang diinput

else:
   print("Nilai t harus positif.")  # memberitahu nilai t harus positif jika t yang dimasukkan negatif

K14-Runge kutta.png

Run dari kode di atas, ketika dimasukkan t = 2, program menampilkan nilai y pada t = 2 yaitu 0.2666666666666658


Optimasi Angle of Attack pada Airfoil

Airfoil

Pada tugas kali ini, kami mendesain sebuah airfoil dengan menggunakan program Autodesk Inventor untuk dites seberapa besar gaya angkat (lift force) dan gaya hambatan udara (drag force) yang dihasilkan ketika menabrak udara dengan kecepatan 100 m/s. Berikut adalah bentuk desain airfoil yang kami buat:

Airfoil kelompok 14.png


Data Drag Force & Lift Force

Dengan menggunakan software CFDSOF-NG V1.00, diperoleh data besarnya drag force & lift force terhadap kemiringan sudut airfoil sebagai berikut:

Data airfoil kelompok 14.png


Kurva drag force & lift force terhadap kemiringan sudut airfoil

Berikut kurva dari drag force & lift force terhadap kemiringan sudut airfoil:

Kurva airfoil kelompok 14.png


Optimasi

Dari persamaan kurva tersebut, kami mencari nilai optimasi dari masing-masing force dengan menggunakan kode berikut: 

import numpy as np
from scipy.optimize import minimize

def cdrag(x):
   x1 = x[0]
   drag = 0.0000005*x1**6-0.0001*x1**5+0.012*x1**4-0.3478*x1**3-0.0472*x1**2+107.02*x1+227.44
   return drag

def clift(x):
   x1 = x[0]
   lift = 0.00000009*x1**6-0.000003*x1**5-0.0015*x1**4+0.1116*x1**3-0.6026*x1**2-116.06*x1+393.04
   return lift

def objective(x):
   return cdrag(x)

def constraint1(x): 
   return 90 - cdrag(x)
def constraint2(x):
   return 90 - clift(x)

con1=({'type':'ineq','fun':constraint1})
con2=({'type':'ineq','fun':constraint2})
cons = (con1,con2)

x1_guess = 50

x0 = np.array([x1_guess]) 

sol = minimize(objective,x0, method='SLSQP',constraints=cons, options={'disp':True})

xopt = sol.x
forceopt = -sol.fun 

dragopt = cdrag(xopt)
liftopt = clift(xopt) 

print ("")
print ("Hasil optimasi:")
print ("Sudut optimal = "+str(-xopt[0]))
print ("Total force optimal = "+str(forceopt))
print ("Drag force optimal = "+str(-dragopt))
print ("Lift force optimal = "+str(liftopt))

Hasil optimasi:

Sudut optimal = -18.824361039981582 °
Total force optimal = -1197.981206594249 N
Drag force optimal = -1197.981206594249 N
Lift force optimal = -1452.2582614781118 N
Retrieved from "http://air.eng.ui.ac.id/index.php?title=Kelompok_14&oldid=17923"