Difference between revisions of "Kelompok 9"
| (23 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | Perkenalkan kami dari kelompok 9 kelas Metode Numerik Kelas Reguler-2 yang beranggotakan : | |
| + | |||
| + | 1. Muhamad Ilham Santoso 1706986422 | ||
| + | |||
| + | 2. Irfan Rahadi K. 1706036255 | ||
| + | |||
| + | 3. Muhammad Fakhri Saputra 1806201030 | ||
| + | |||
| + | |||
| + | == '''Tugas Pertama Kelompok 9''' == | ||
| + | |||
| + | |||
| + | Eliminasi Gauss adalah suatu metode untuk mengoperasikan nilai-nilai di dalam matriks sehingga menjadi matriks yang lebih sederhana lagi. Dengan melakukan operasi baris sehingga matriks tersebut menjadi matriks yang baris. Ini dapat digunakan sebagai salah satu metode penyelesaian persamaan linear dengan menggunakan matriks. Caranya dengan mengubah persamaan linear tersebut ke dalam matriks teraugmentasi dan mengoperasikannya. Setelah menjadi matriks baris, lakukan substitusi balik untuk mendapatkan nilai dari variabel-variabel tersebut. Berikut adalah penjelasan penggunaaan aplikasi metode numerik pada eliminasi Gauss | ||
| + | |||
| + | |||
[[File:Tugas_1_Kelompok_9.mp4]] | [[File:Tugas_1_Kelompok_9.mp4]] | ||
| − | + | ||
| + | Berikut ini merupakan sebuah contoh dari penggunaan kode python ini dan hasil setelah melakukan running pada program yaitu | ||
| + | |||
| + | [[File:Tugas1.jpg]] | ||
| + | |||
| + | |||
| + | |||
| + | == '''Tugas Kedua Kelompok 9''' == | ||
| + | |||
| + | |||
| + | Berikut adalah video penjelasan tugas kedua yaitu penggunaan aplikasi Metode Numerik pada Statika Struktur menggunakan metode Finite Element untuk menyelesaikan persoalan pada sebuah batang panjang 5 m diberi beban 1000N di tengah batang. Lalu kami menghitung support reaction yang terjadi pada dua ujung batang | ||
| + | |||
| + | |||
[[File:Tugas_2_Kelompok_9.mp4]] | [[File:Tugas_2_Kelompok_9.mp4]] | ||
| + | |||
| + | Berikut ini merupakan sebuah contoh dari penggunaan kode python ini dan hasil setelah melakukan running pada program yaitu | ||
| + | |||
| + | [[File:Tugas2.jpg]] | ||
| + | |||
| + | == '''Tugas Ketiga Kelompok 9''' == | ||
| + | |||
| + | [[File:Tugas3Spring.png]] | ||
| + | |||
| + | Terdapat sebuah beban m sebesar 2.5 kg, terhubungan dengan sebuah pegas dalam keaadan horizontal yang memiliki konstanta pegas k sebesar 75 N/m. Beban tersebut diberi gaya eksternal sebesar P (t). Jika beban ditarik selama kurang dari 2 sekon (t<2s) maka besaran gaya memiliki fungsi (10t). Jika gaya yang diberikan 2 sekon atau lebih (t≥ 2), maka besar gaya yaitu 20N. | ||
| + | |||
| + | Flowchart : | ||
| + | |||
| + | [[File:FlowchartKelompok9.png]] | ||
| + | |||
| + | |||
| + | |||
| + | Berikut adalah video penjelasan tugas kedua yaitu penggunaan methode runge kutta untuk menyelesaikan soal di atas | ||
| + | |||
| + | [[File:Videotugas3.mp4]] | ||
| + | |||
| + | |||
| + | Berikut ini merupakan sebuah contoh dari penggunaan kode python ini dan hasil setelah melakukan running pada program yaitu | ||
| + | |||
| + | |||
| + | [[File:HasilRunnig.jpg]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | == Tugas CFD Drag Force == | ||
| + | |||
| + | |||
| + | Setelah kami melakukan percobaan dengan 10 variabel kecepatan berbeda menggunakan aplikasi CFDSOF-NG, didapat data sebagai berikut yang nantinya akan di-plotting dan dilakukan curve fitting : | ||
| + | |||
| + | [[File:Data.png]] | ||
| + | |||
| + | |||
| + | [[File:Data1.png]] | ||
| + | |||
| + | |||
| + | Hasil curve fitting yang kami lakukan di excel seperti pada grafik berikut | ||
| + | |||
| + | |||
| + | [[File:Data22.png]] | ||
| + | |||
| + | |||
| + | Berdasarkan pengolahan tersebut, dapat disimpulkan bahwa hubungan drag force dengan kecepatan pada permasalahan ini sesuai dengan persamaan berikut: | ||
| + | |||
| + | y = 1.0196x2 + 1.7495x + 3.9384 | ||
| + | |||
| + | |||
| + | y = Drag Force | ||
| + | |||
| + | x = Velocity | ||
| + | |||
| + | |||
| + | R² = 0.9996 | ||
| + | |||
| + | Menunjukan keakuratan dari regresi yang telah dilakukan. Semakin besar nilainya (mendekati 1) maka semakin akurat | ||
| + | |||
| + | |||
| + | |||
| + | == Tugas Analisis Flow pada Airfoil == | ||
| + | |||
| + | '''Angle of Attack = -15 derajat''' | ||
| + | |||
| + | [[File:l-15d.png]] | ||
| + | |||
| + | [[File:l-15.png]] | ||
| + | |||
| + | |||
| + | '''Angle of Attack = 0 derajat''' | ||
| + | |||
| + | |||
| + | [[File:0drag.png]] | ||
| + | |||
| + | [[File:0lift.png]] | ||
| + | |||
| + | |||
| + | '''Angle of Attack = 15 derajat''' | ||
| + | |||
| + | |||
| + | [[File:dragggg15.png]] | ||
| + | |||
| + | [[File:lift5515.png]] | ||
| + | |||
| + | |||
| + | '''Angle of Attack = 30 derajat''' | ||
| + | |||
| + | |||
| + | [[File:30drag.png]] | ||
| + | |||
| + | [[File:30lift.png]] | ||
| + | |||
| + | '''Angle of Attack = 45 derajat''' | ||
| + | |||
| + | [[File:45draag.png]] | ||
| + | |||
| + | [[File:45liift.png]] | ||
| + | |||
| + | |||
| + | '''Angle of Attack = 60 derajat''' | ||
| + | |||
| + | |||
| + | [[File:60drag.png]] | ||
| + | |||
| + | [[File:60lift.png]] | ||
| + | |||
| + | '''Angle of Attack = 75 derajat''' | ||
| + | |||
| + | |||
| + | [[File:75draag.png]] | ||
| + | |||
| + | [[File:75lift.png]] | ||
| + | |||
| + | '''Angle of Attack = 90 derajat''' | ||
| + | |||
| + | [[File:90drag.png]] | ||
| + | |||
| + | [[File:90lift.png]] | ||
| + | |||
| + | |||
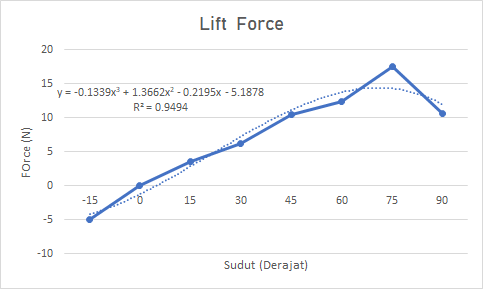
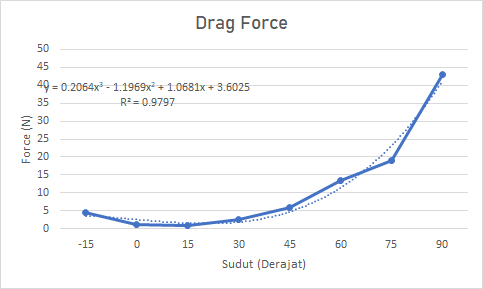
| + | '''Grafik Optimalisasi menggunakan Excel''' | ||
| + | |||
| + | |||
| + | [[File:opt1.png]] | ||
| + | |||
| + | |||
| + | [[File:opt2.png]] | ||
| + | |||
| + | |||
| + | [[File:opt3.png]] | ||
| + | |||
| + | |||
| + | |||
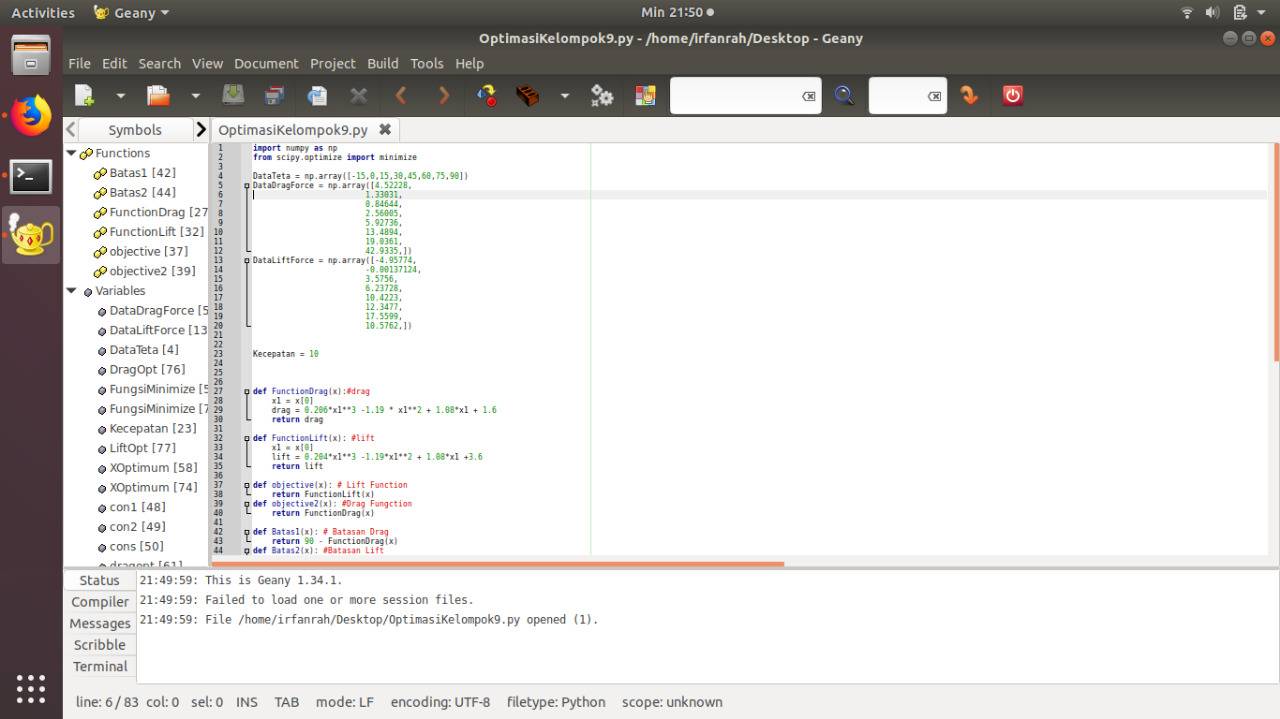
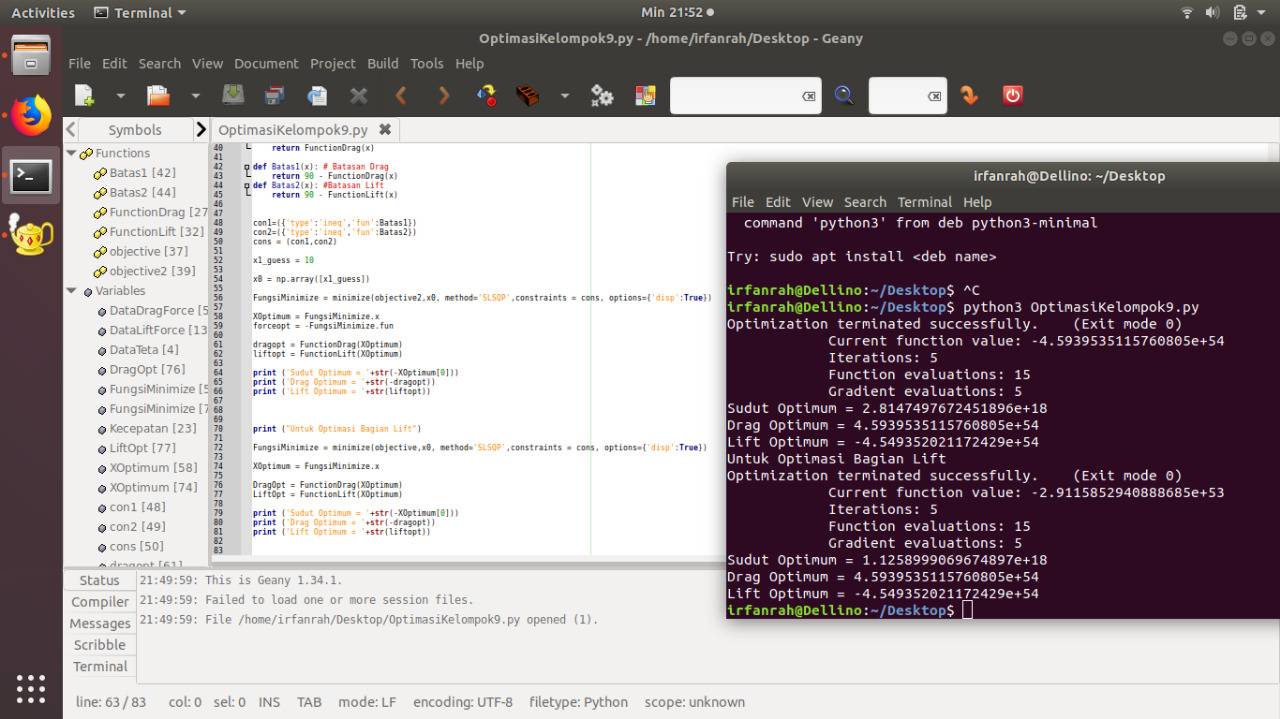
| + | '''Hasil Optimalisasi menggunakan Python''' | ||
| + | |||
| + | [[File:optimalisasipyth1.jpg]] | ||
| + | |||
| + | [[File:optimalisasipyth2.jpg]] | ||
Latest revision as of 22:58, 1 December 2019
Perkenalkan kami dari kelompok 9 kelas Metode Numerik Kelas Reguler-2 yang beranggotakan :
1. Muhamad Ilham Santoso 1706986422
2. Irfan Rahadi K. 1706036255
3. Muhammad Fakhri Saputra 1806201030
Contents
Tugas Pertama Kelompok 9
Eliminasi Gauss adalah suatu metode untuk mengoperasikan nilai-nilai di dalam matriks sehingga menjadi matriks yang lebih sederhana lagi. Dengan melakukan operasi baris sehingga matriks tersebut menjadi matriks yang baris. Ini dapat digunakan sebagai salah satu metode penyelesaian persamaan linear dengan menggunakan matriks. Caranya dengan mengubah persamaan linear tersebut ke dalam matriks teraugmentasi dan mengoperasikannya. Setelah menjadi matriks baris, lakukan substitusi balik untuk mendapatkan nilai dari variabel-variabel tersebut. Berikut adalah penjelasan penggunaaan aplikasi metode numerik pada eliminasi Gauss
Berikut ini merupakan sebuah contoh dari penggunaan kode python ini dan hasil setelah melakukan running pada program yaitu
Tugas Kedua Kelompok 9
Berikut adalah video penjelasan tugas kedua yaitu penggunaan aplikasi Metode Numerik pada Statika Struktur menggunakan metode Finite Element untuk menyelesaikan persoalan pada sebuah batang panjang 5 m diberi beban 1000N di tengah batang. Lalu kami menghitung support reaction yang terjadi pada dua ujung batang
Berikut ini merupakan sebuah contoh dari penggunaan kode python ini dan hasil setelah melakukan running pada program yaitu
Tugas Ketiga Kelompok 9
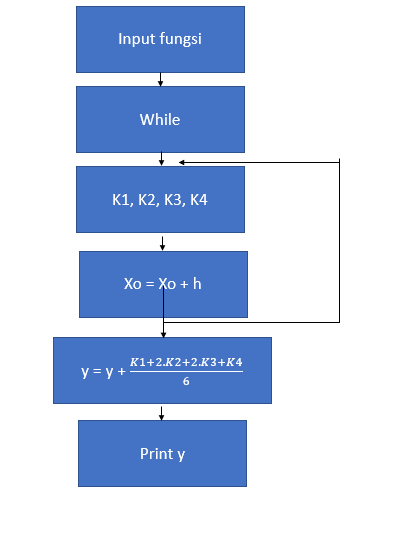
Terdapat sebuah beban m sebesar 2.5 kg, terhubungan dengan sebuah pegas dalam keaadan horizontal yang memiliki konstanta pegas k sebesar 75 N/m. Beban tersebut diberi gaya eksternal sebesar P (t). Jika beban ditarik selama kurang dari 2 sekon (t<2s) maka besaran gaya memiliki fungsi (10t). Jika gaya yang diberikan 2 sekon atau lebih (t≥ 2), maka besar gaya yaitu 20N.
Flowchart :
Berikut adalah video penjelasan tugas kedua yaitu penggunaan methode runge kutta untuk menyelesaikan soal di atas
Berikut ini merupakan sebuah contoh dari penggunaan kode python ini dan hasil setelah melakukan running pada program yaitu
Tugas CFD Drag Force
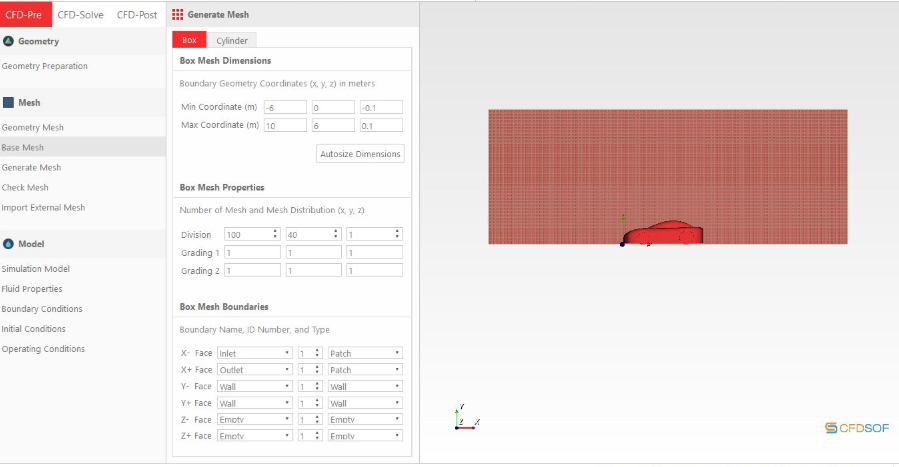
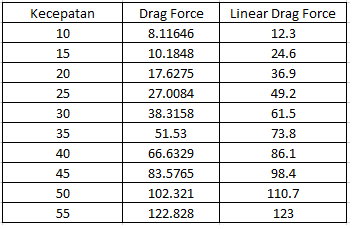
Setelah kami melakukan percobaan dengan 10 variabel kecepatan berbeda menggunakan aplikasi CFDSOF-NG, didapat data sebagai berikut yang nantinya akan di-plotting dan dilakukan curve fitting :
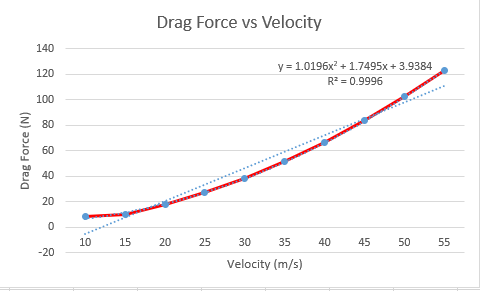
Hasil curve fitting yang kami lakukan di excel seperti pada grafik berikut
Berdasarkan pengolahan tersebut, dapat disimpulkan bahwa hubungan drag force dengan kecepatan pada permasalahan ini sesuai dengan persamaan berikut:
y = 1.0196x2 + 1.7495x + 3.9384
y = Drag Force
x = Velocity
R² = 0.9996
Menunjukan keakuratan dari regresi yang telah dilakukan. Semakin besar nilainya (mendekati 1) maka semakin akurat
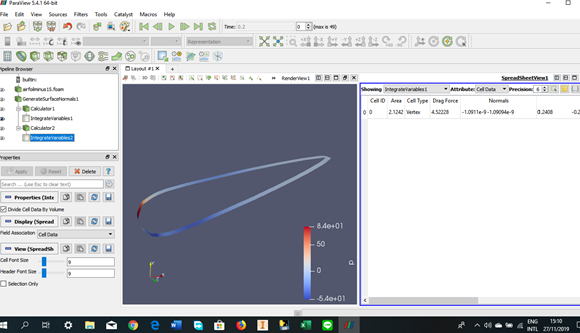
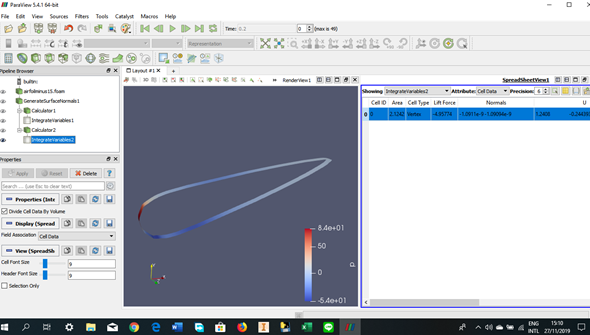
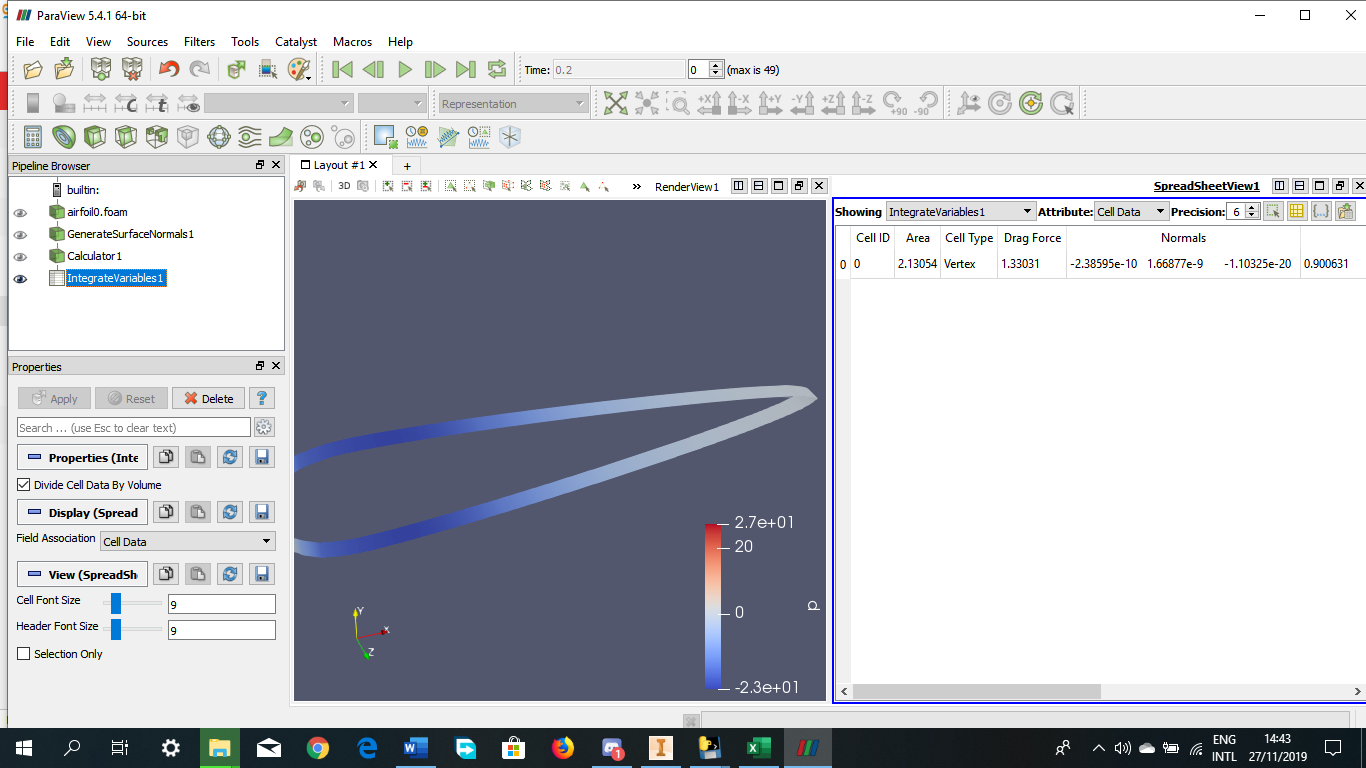
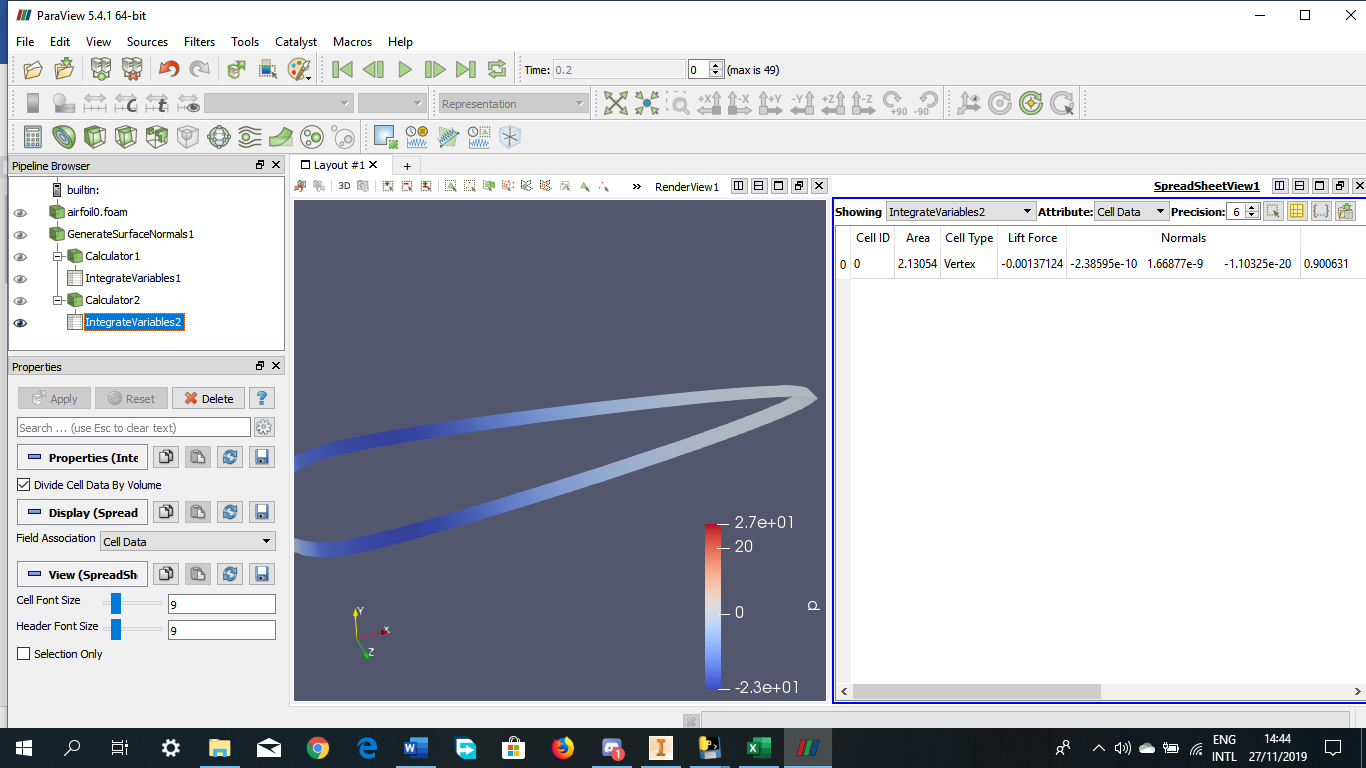
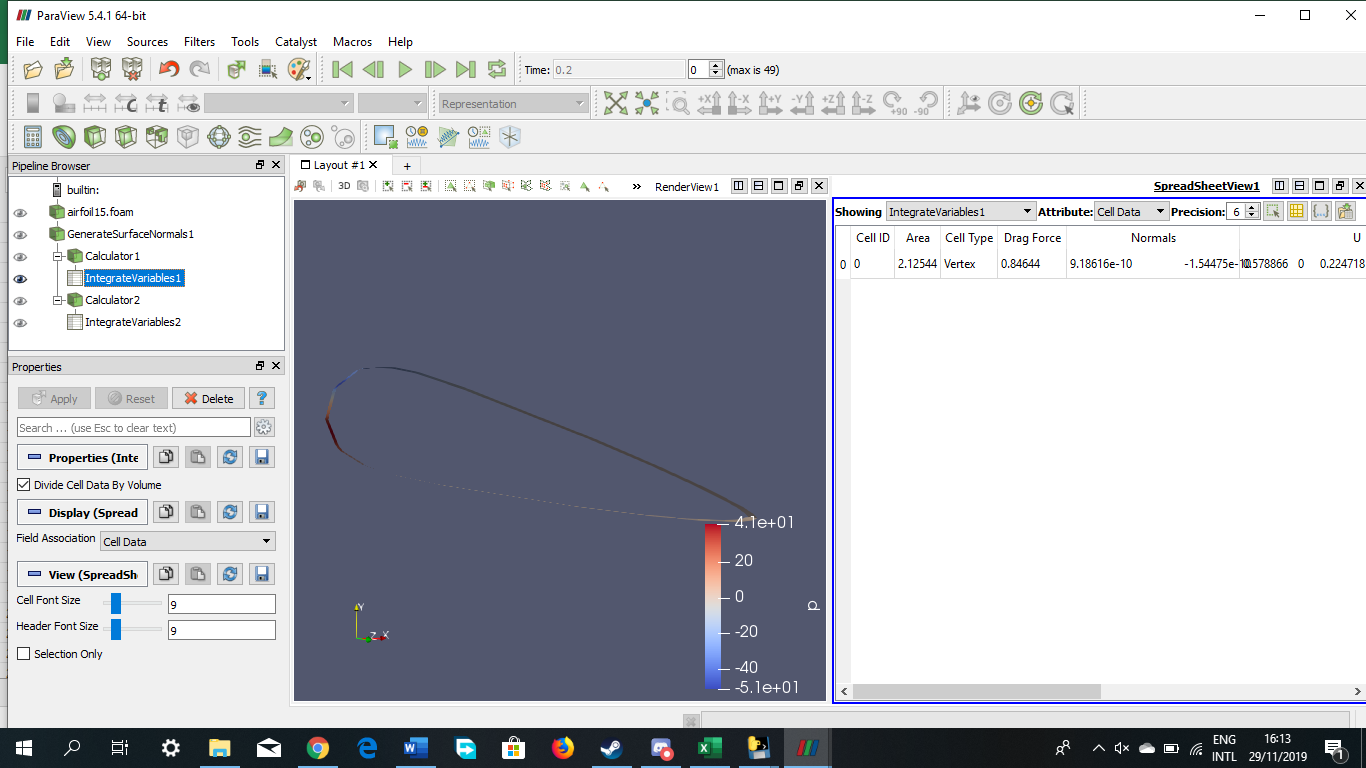
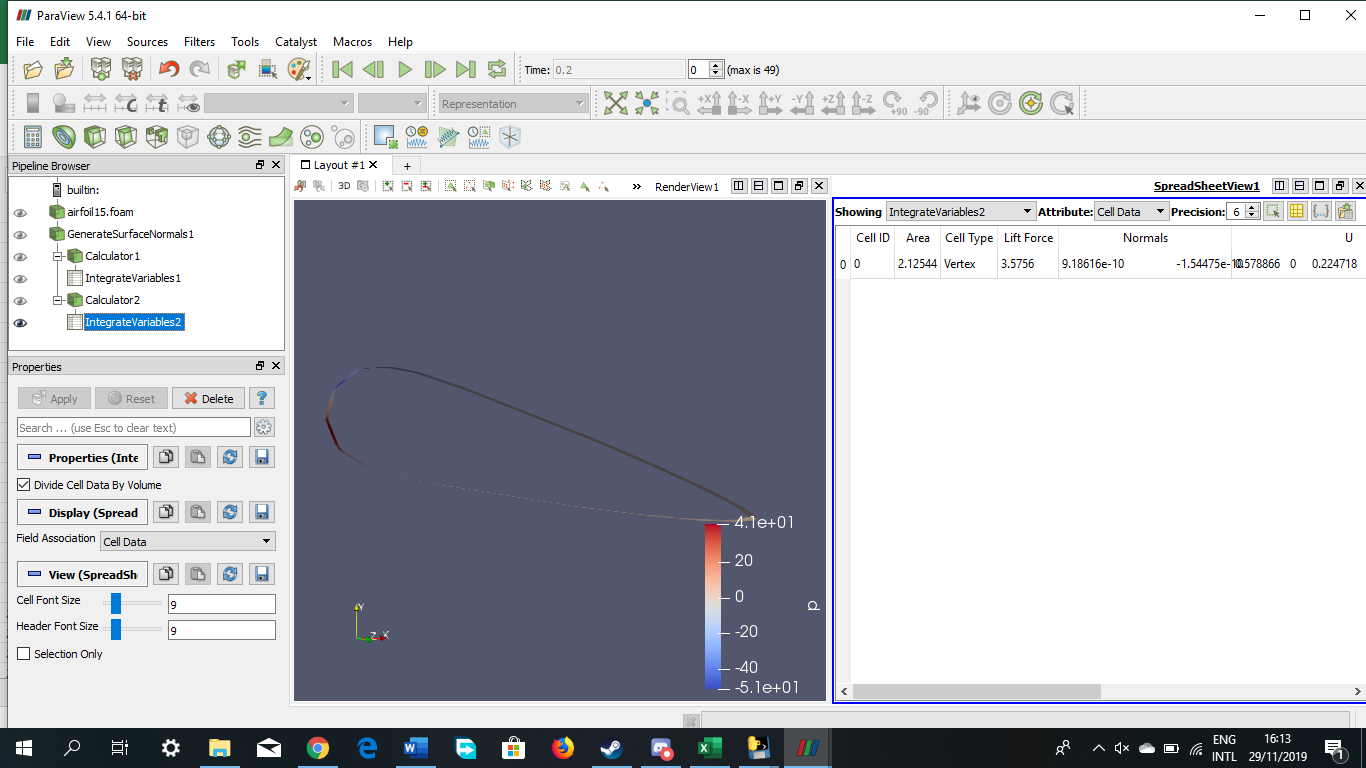
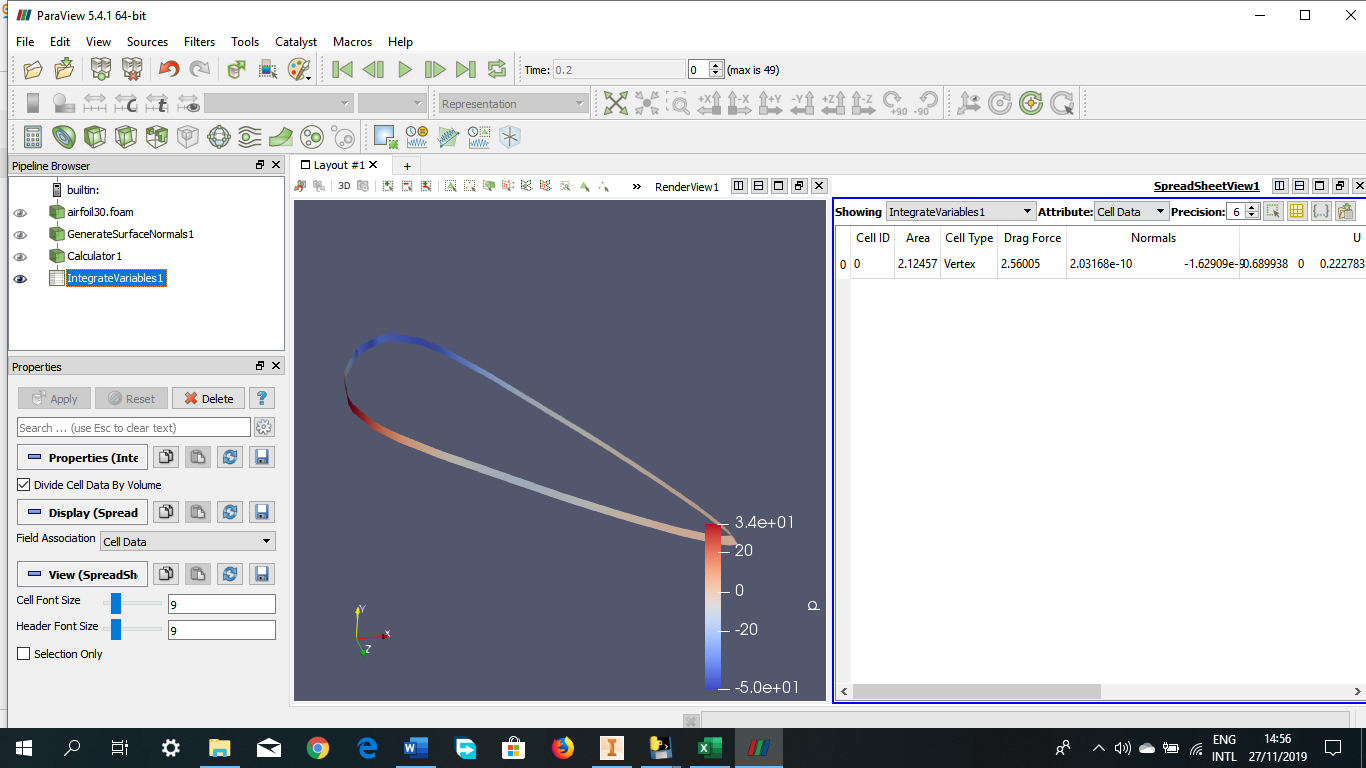
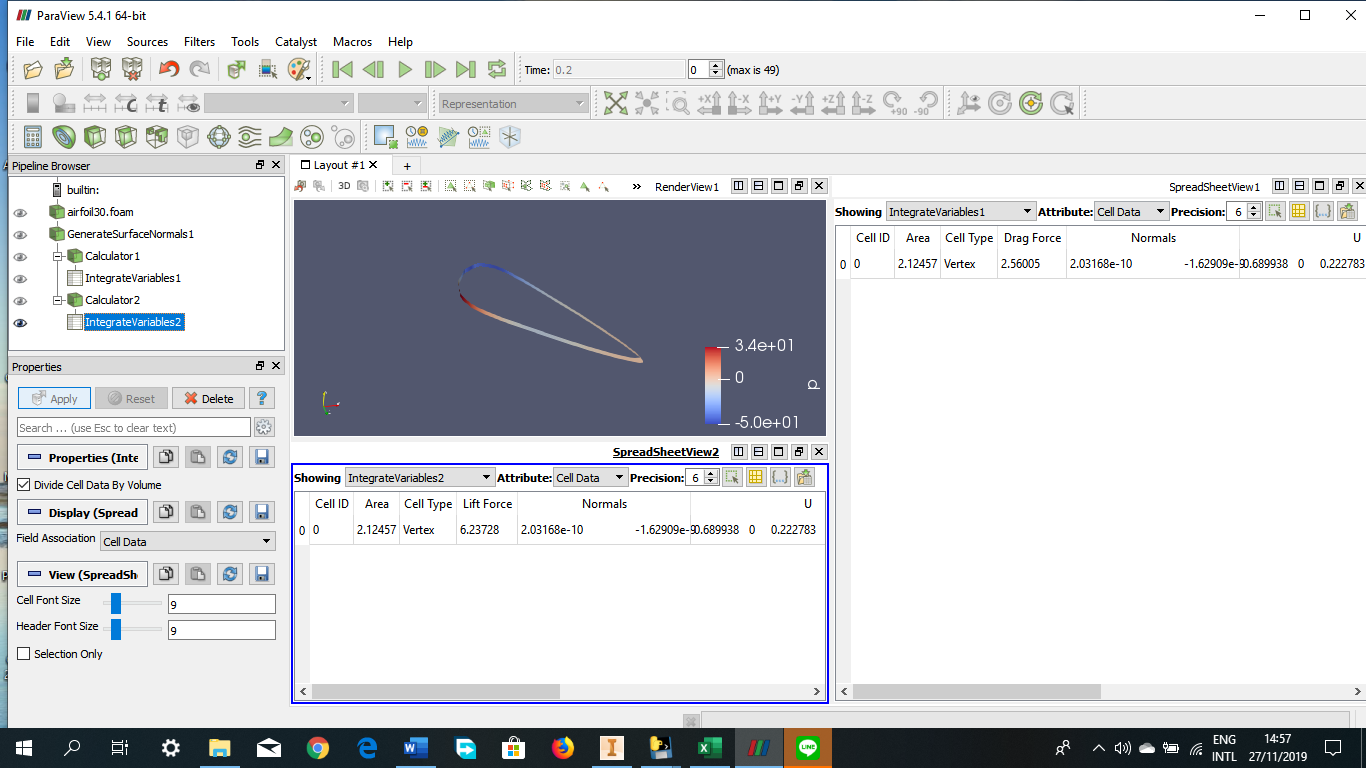
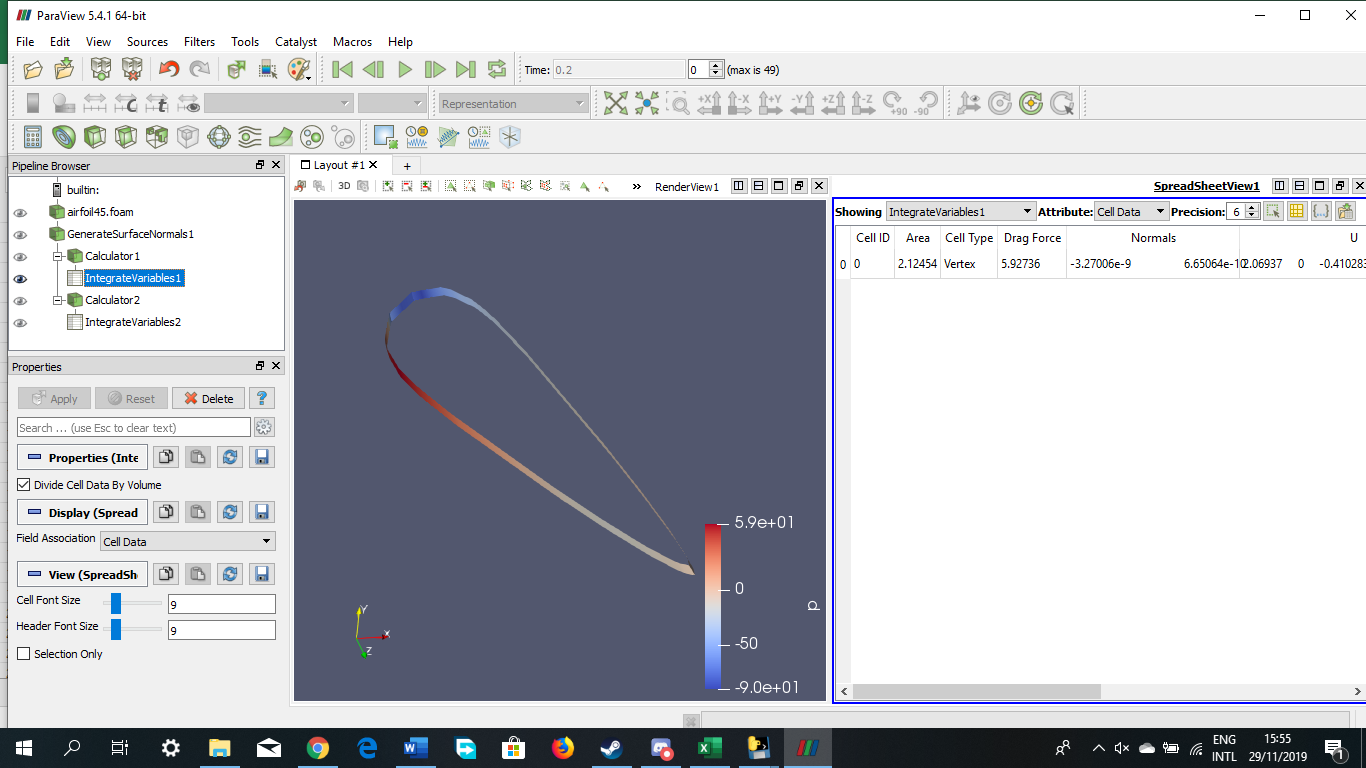
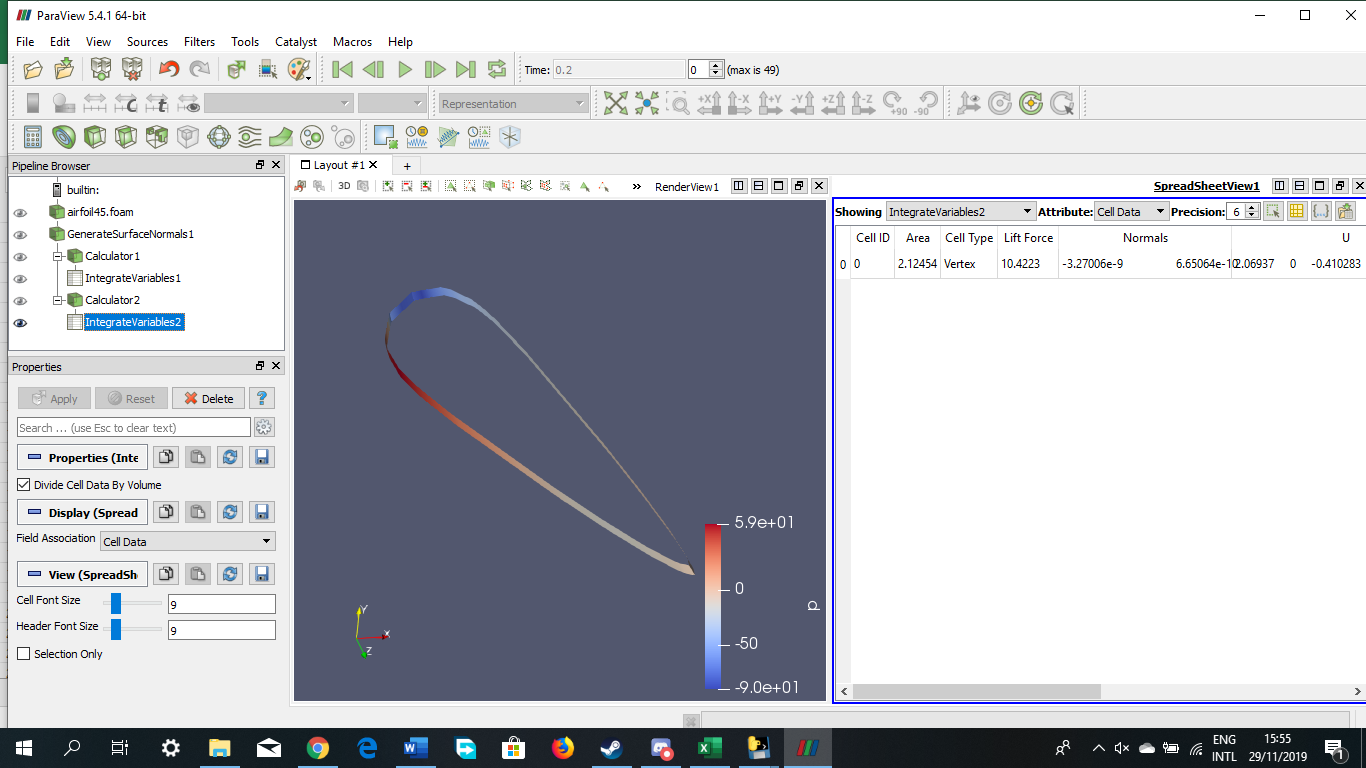
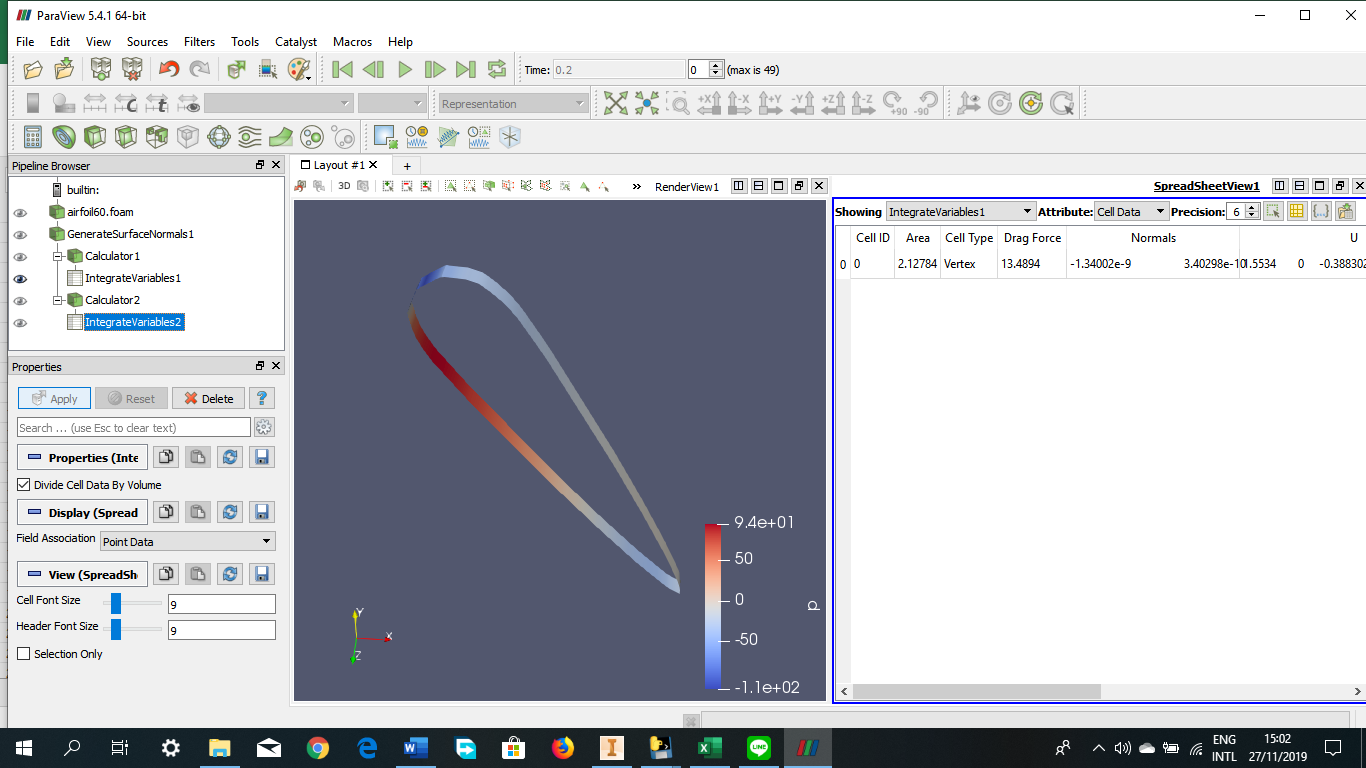
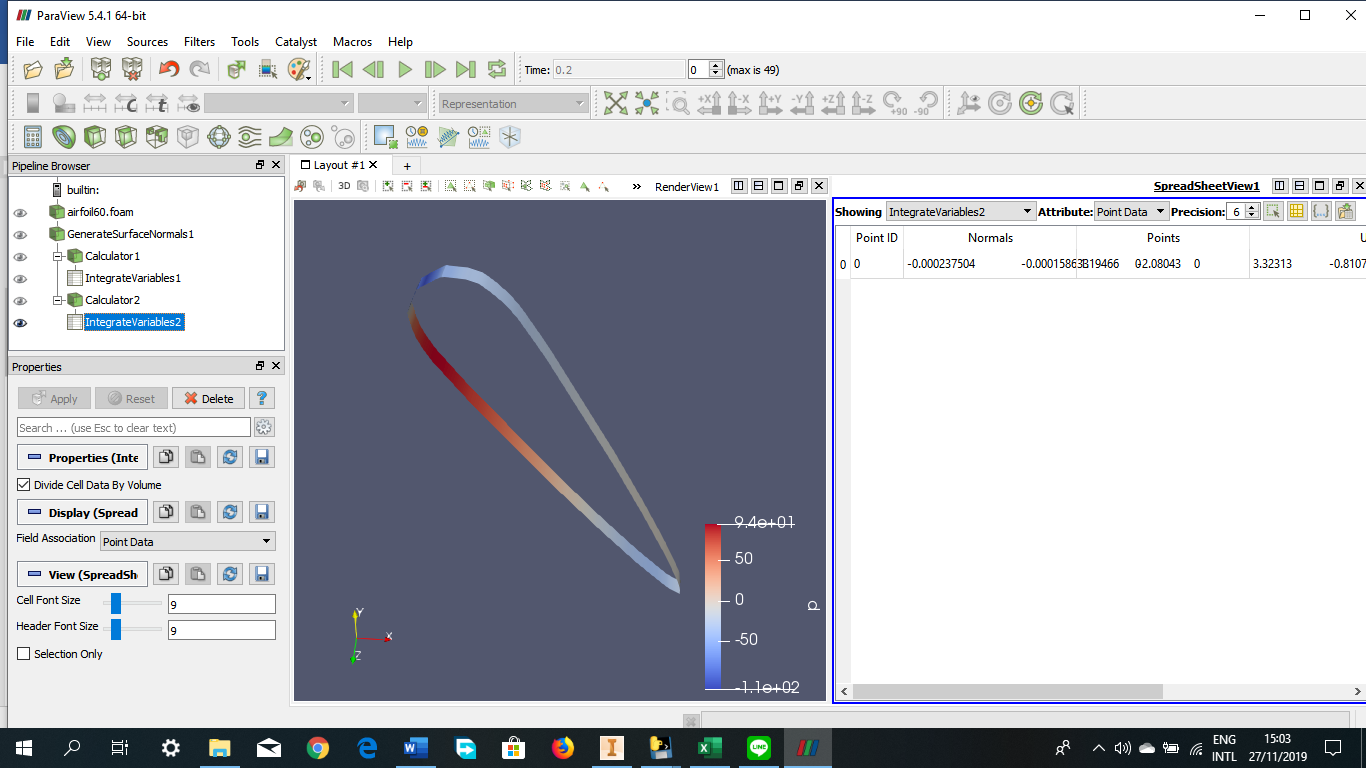
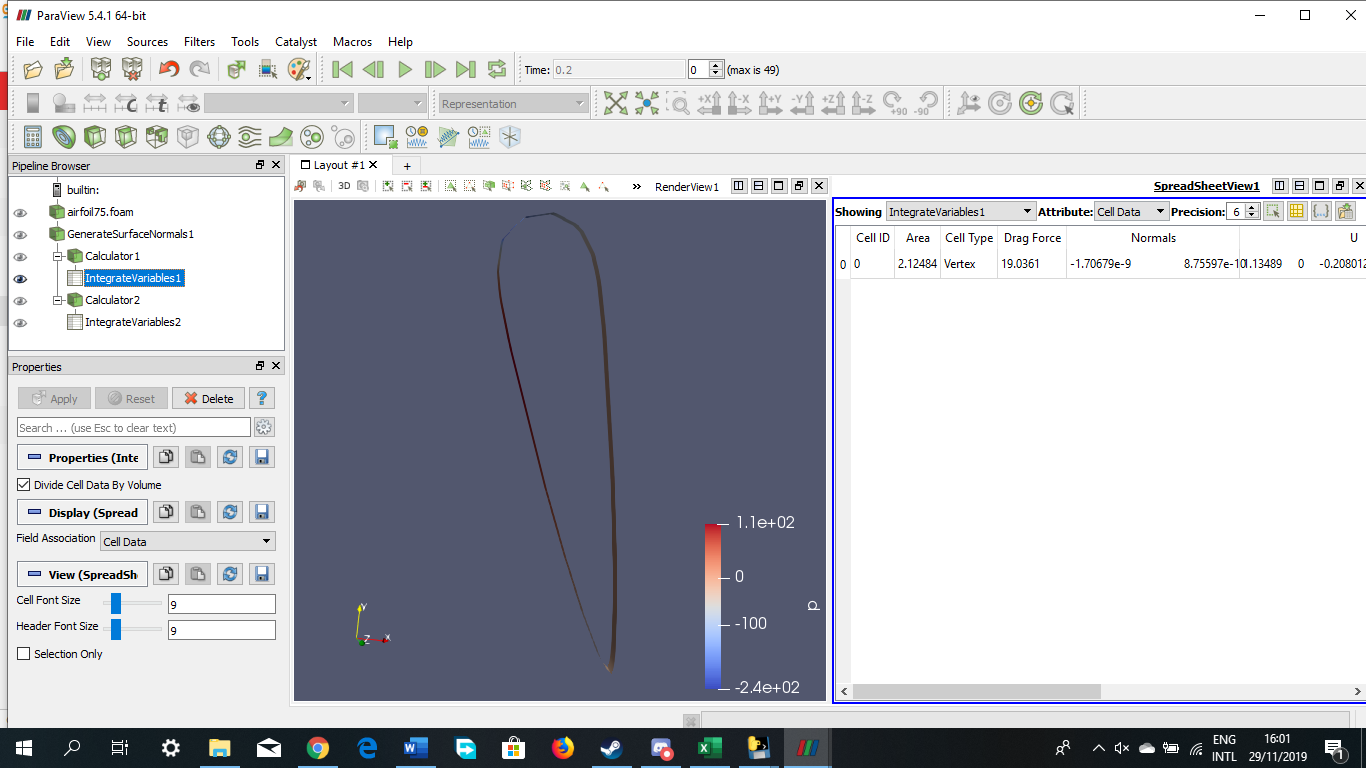
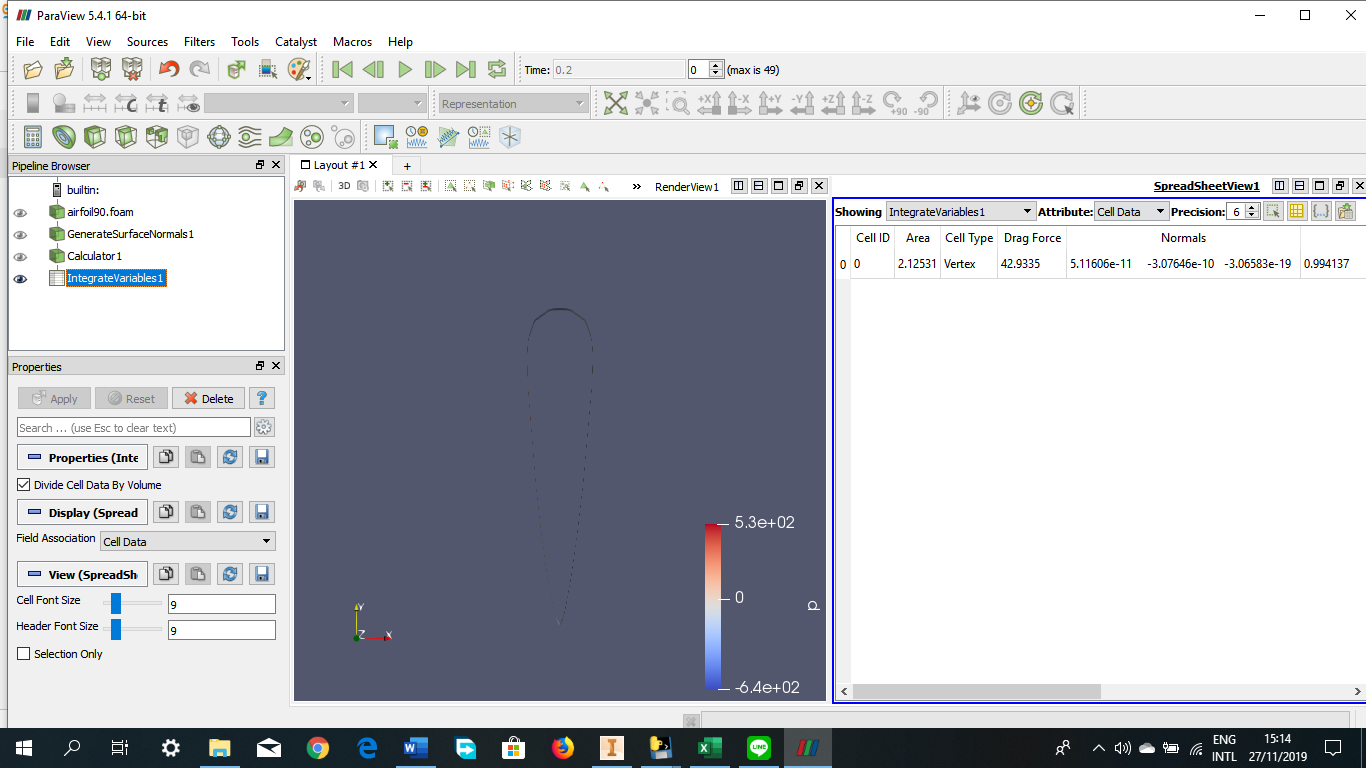
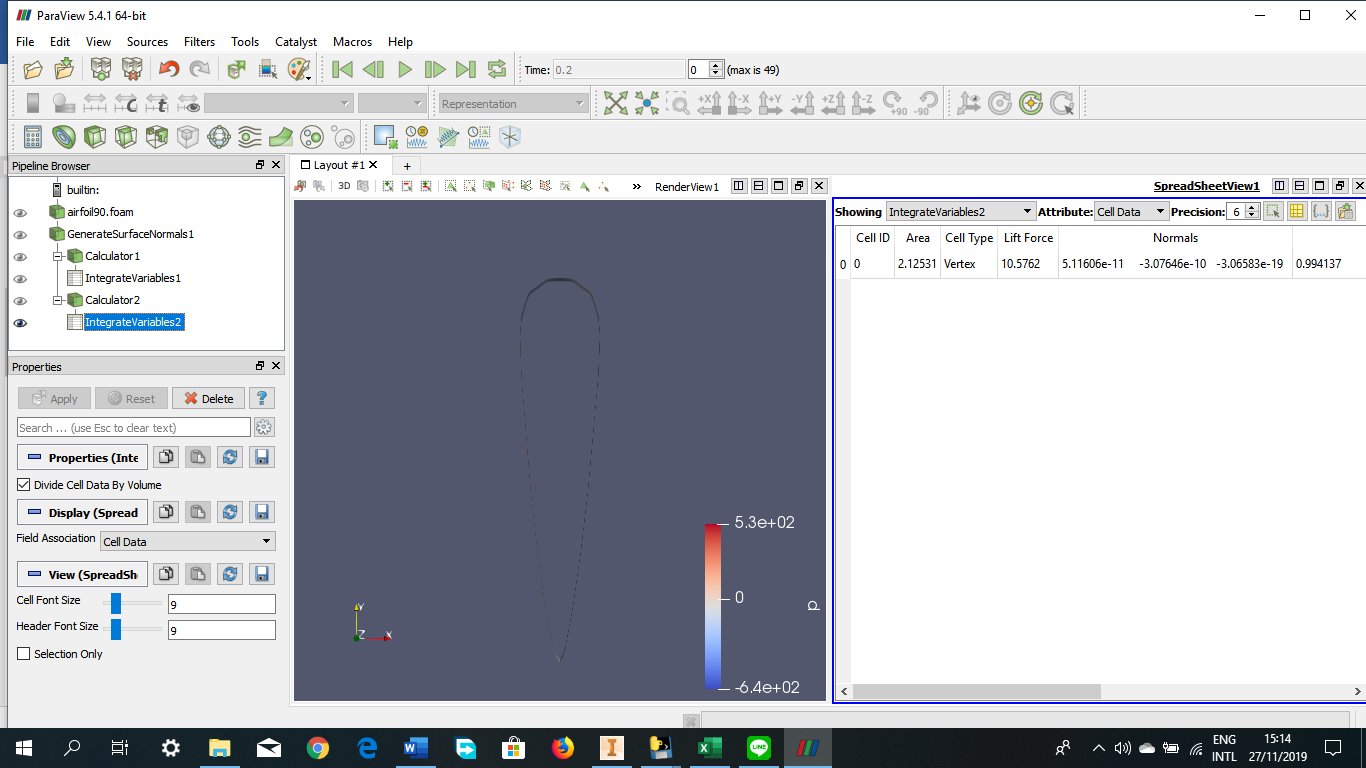
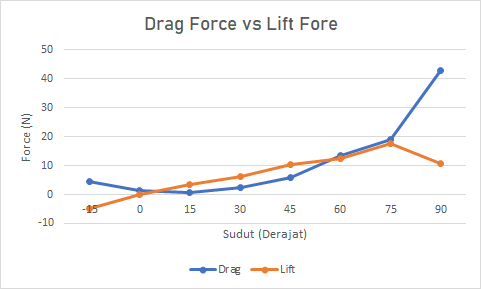
Tugas Analisis Flow pada Airfoil
Angle of Attack = -15 derajat
Angle of Attack = 0 derajat
Angle of Attack = 15 derajat
Angle of Attack = 30 derajat
Angle of Attack = 45 derajat
Angle of Attack = 60 derajat
Angle of Attack = 75 derajat
Angle of Attack = 90 derajat
Grafik Optimalisasi menggunakan Excel
Hasil Optimalisasi menggunakan Python