Difference between revisions of "Elvin"
| (39 intermediate revisions by the same user not shown) | |||
| Line 15: | Line 15: | ||
|} | |} | ||
| + | [[Progress Tugas Merancang - Elvin]] | ||
== Pertemuan 1 (4 September 2019) == | == Pertemuan 1 (4 September 2019) == | ||
| Line 96: | Line 97: | ||
'''1.a. Loop''' | '''1.a. Loop''' | ||
| − | Algoritma | + | '''Algoritma''' |
* Definisikan nilai a = 0 dan b = 1 (a dan b berturut-turut akan menjadi suku ke-0 dan ke-1 serta menjadi dasar untuk penjumlahan fibonacci) | * Definisikan nilai a = 0 dan b = 1 (a dan b berturut-turut akan menjadi suku ke-0 dan ke-1 serta menjadi dasar untuk penjumlahan fibonacci) | ||
* Input suku ke - n Fibonacci yang diinginkan | * Input suku ke - n Fibonacci yang diinginkan | ||
| Line 103: | Line 104: | ||
* jika n lebih dari 1 maka c = a + b, nilai a akan diubah menjadi b, nilai b akan diubah menjadi c. Proses akan di loop hingga mencapai nilai n yang diinginkan | * jika n lebih dari 1 maka c = a + b, nilai a akan diubah menjadi b, nilai b akan diubah menjadi c. Proses akan di loop hingga mencapai nilai n yang diinginkan | ||
| − | Flowchart | + | '''Flowchart''' |
| − | |||
| + | [[File:FlowchartV2 Fibonacci Elvin.png|600px]] | ||
| + | |||
| + | |||
| + | '''Program Python''' | ||
| + | |||
| + | [[File:LoopV2 Fibonacci Elvin.JPG]][[File:Loop Fibonacci Elvin Console.JPG]] | ||
| − | |||
| − | |||
'''1.b. Function''' | '''1.b. Function''' | ||
| − | Algoritma | + | '''Algoritma''' |
| − | * | + | * Definisikan fungsi f(n) = f(n-1) + f(n-2) |
| − | * | + | * Nilai n hanya berlaku untuk n >= 0, jika n < 0 maka print "error" |
| − | * | + | * Jika n = 0 atau n = 1 maka print nilai n tersebut |
| − | * | + | * Jika n > 1 maka input nilai tersebut ke fungsi f(n) |
| − | + | ||
| + | '''Flowchart''' | ||
| + | |||
| + | [[File:Flowchart Fibonacci Function Elvin.png|600px]] | ||
| − | |||
| − | |||
| + | '''Program Python''' | ||
| − | + | [[File:Function Fibonacci Elvin.JPG]][[File:Function Fibonacci Elvin Console.JPG]] | |
| − | [[File: | ||
'''2. Tugas''' | '''2. Tugas''' | ||
| − | Selain kuis yang diberikan, Pak DAI dan Pak Radon mengelompokkan mahasiswa dengan satu sama lain agar proses pembelajaran lebih baik. Setelah itu, tugas untuk | + | Selain kuis yang diberikan, Pak DAI dan Pak Radon mengelompokkan mahasiswa dengan satu sama lain agar proses pembelajaran lebih baik. Setelah itu, tugas untuk mennyelesaikan salah satu soal eliminasi gauss yang terdapat pada buku referensi mata kuliah Metode Numerik. |
| + | |||
| + | Pengerjaan tugas ini dapat dilihat pada Page [[Kelompok 12]] | ||
| + | |||
| + | |||
| + | == Pertemuan 4 (25 September 2019) == | ||
| + | |||
| + | '''1. Pemodelan''' | ||
| + | |||
| + | Pada pertemuan kelas Metode Numerik kali ini, Pak Dai memberikan materi mengenai pemodelan. '''Model''' merupakan suatu representasi, simplifikasi atau asumsi dari sebuah benda ataupun sistem yang dibuat untuk mendekati benda ataupun kondisi nyata. Model diperlukan agar kita dapat melaksanakan analisis ataupun eksperimen secara lebih mudah tanpa menghabiskan sumber daya yang ada. Model yang dibuat hanya mendekati kondisi nyata sehingga eksperimen atau simulasi yang dilakukan tidak selalu menunjukkan hasil yang 100% akurat. Seperti berbagai bidang ilmu lainnya, arsitek dengan maket, sipil dengan jembatan miniatur, dan teknik aerodinamika dengan wind tunnel, semua model dibuat agar dapat diuji terlebih dahulu tanpa menghasilkan dampak yang besar. Model harus ada karena saat kita mendesign, kita harus memastikan apa yang kita design itu berfungsi, bekerja dan reliable. | ||
| + | |||
| + | |||
| + | '''2. Tugas''' | ||
| + | |||
| + | Tugas yang diberikan minggu ini adalah aplikasi eliminasi gauss untuk melaksanakan Finite Element Analysis. | ||
| + | |||
| + | Pengerjaan tugas ini dapat dilihat pada Page [[Kelompok 12]] | ||
| + | |||
| + | |||
| + | == Pertemuan 5 (2 Oktober 2019) == | ||
| + | |||
| + | '''1. Membuat Program Simulasi dengan Eliminasi Gauss''' | ||
| + | |||
| + | Pertemuan hari ini diisi dengan penjelasan materi oleh bang Edo dan Bang Timothy asisten dosen untuk kelas Metode Numerik. Mereka menjelaskan kembali bagaimana membuat program simulasi dengan eliminasi gauss yang merupakan tugas dari minggu sebelumnya. Materi ini dijelaskan dengan pendekatan menggunakan pegas sebagai elemen untuk finite element analysis yang akan dilakukan. Kemudian mereka juga menjelaskan beda mengkode dengan bantuan module numpy, sympy, dan manual di python. Dapat dilihat bahwa panjang dan kerumitan dari kode yang ditulis berbeda-beda berdasarkan tidak atau digunakannya module tersebut. | ||
| + | |||
| + | |||
| + | '''2. Rangkuman Bab 4 buku Numerical Methods Python''' | ||
| + | |||
| + | Masalah dimana kita harus menentukan nilai x agar f(x) = 0 sering ditemukan di analisis ilmu teknik yang kemudian dapat dikenal sebagai akar dari persamaan atau nilai nol dari fungsi f(x). sebuah fungsi terdiri atas 3 komponen, yaitu input (x), output (y), dan aturan f untuk mendapatkan hasil y. untuk mendapatkan suatu akar dari persamaan, terdapat berbagai metode yang mencakupi: | ||
| + | |||
| + | * '''Metode Incremental Search''' | ||
| + | |||
| + | Cara yang paling baik untuk memperkirakan nilai suatu akar adalah dengan menggambarkan fungsi itu sendiri. Jika suatu f(x1) dan f(x2) memiliki nilai yang berlawanan (+-) maka terdapat setidaknya satu nilai akar pada interval x1 hingga x2. Jika intervalnya sangat kecil, maka sangat memungkinkan untuk terdapat 1 akar. Sehingga nilai 0 dari fungsi f(x) dapat ditemukan dengan mengevaluasi fungsi pada interval tersebut. | ||
| + | |||
| + | Masalah yang terdapat pada metode ini adalah: | ||
| + | |||
| + | '''a.''' Sangat mungkin untuk melewatkan 2 nilai akar dengan interval yang lebih kecil dari interval x1-x2 | ||
| + | |||
| + | '''b.''' Akar ganda tidak akan terdeteksi | ||
| + | |||
| + | '''c.''' Beberapa pole dapat dikeliru sebagai akar. | ||
| + | |||
| + | * '''Metode Bisection''' | ||
| + | Metode bisection bekerja dengan mengurangi separuh nilai akar yang terdapat pada interval x1 dan x2 hingga sangat kecil. Metode ini juga merupakan metode yang sangat cepat dan dapat diandalkan. | ||
| + | Metode ini mempunyai proses yang sama dengan incremental scratch dimana jika terdapat sebuah akar pada interval x1 dan x2 maka f(x1) dan f(x2) memiliki tanda yang berlawanan. Untuk mengurangi separuh nilai interval, kita menghitung f(x3) dimana x3 = 1/2*(x1+x2). Kemudian jika nilai f(x2) dan f(x3) mempunyai nilai yang berlawanan maka akar terdapat pada interval x2 dan x3, jika tidak maka akar terdapat pada interval x1 dan x3. Kemudian proses diulang hingga nilai interval menjadi suatu nilai P yang sangat kecil dimana, | ||
| + | |||
| + | |x2 – x1| =< P | ||
| + | |||
| + | * '''Metode Secant and False Position''' | ||
| + | Metode secant dan false position sangat mirip satu sama lain dimana kedua metode ini membutuhkan estimasi mula untuk mencari nilai akar, dengan demikian nilai x3 dari akar dapat diestimasi dari interpolasi antara x1 dan x2. | ||
| + | |||
| + | Metode false position membutuhkan nilai x1 dan x2 untuk mendapatkan interval yang berisi akar. Setelah kita mendapatkan nilai x3 hasil interpolasi, kita dapat menggantikan salah satu nilai x1 atau x2 dengan nilai x3. Kemudian, jika f(x3) mempunyai tanda yang sama dengan nilai f(x1) maka x1 <- x3; sebaliknya kita memilih x2 <- x3. Prosedur diulang hingga suatu konvergen tercapai | ||
| + | |||
| + | Metode Secant berbeda dari false position dimana ia tidak perlu interval x1 dan x2 dan menggantikan nilai estimasi tertua dari akar (x1 <- x2 dan x2 <- x3) | ||
| + | |||
| + | |||
| + | |||
| + | * '''Metode Ridder''' | ||
| + | Metode ini merupakan modifikasi dari metode false position dimana jika akar terdapat pada interval x1 dan x2, maka kita dapat menghitung f(x3) dari x3 hasil interpolasi dimana x3 adalah titik tengah dari interval. | ||
| + | Kemudian kita dapat menggunakan fungsi | ||
| + | |||
| + | g(x) = f(x)e^(x-x)Q | ||
| + | |||
| + | dimana Q adalah konstanta yang ditentukan dari mendapatkan nilai (x1, g1), (x2, g2), dan (x3, g3) seperti pada gambar (b). Nilai akar yang baru kemudian akan didapatkan dari interpolasi linear dari nilai-nilai g(x). | ||
| + | |||
| + | [[File:SS metnum 1.png]] | ||
| + | |||
| + | dari persamaan g(x) kita mendapatkan bahwa h=(x2-x1)/2. Syarat agar ketiga titik di gambar (b) terletak pada sebuah garis lurus adalah | ||
| + | |||
| + | [[File:SS metnum 2.png]] | ||
| + | |||
| + | yang merupakan sebuah persaman kuadrat pada e^hQ dengan solusi | ||
| + | |||
| + | [[File:SS metnum 3.png]] | ||
| + | |||
| + | Dengan me-interpolasi linear titik (x1,g1) dan (x2,g2) maka kita mendapatkan akar baru dengan persamaan berikut | ||
| + | |||
| + | [[File:SS metnum 4.png]] | ||
| + | |||
| + | * '''Metode Newton-Raphson''' | ||
| + | Metode ini menggunakan turunan f’(x) dari fungsi dan fungsi f(x) itu sendiri. Kemudian metode ini hanya bisa digunakan jika f’(x) dapat dihitung. | ||
| + | |||
| + | Metode ini didapatkan dengan menurunkan rumus dari seri taylor f(x) | ||
| + | |||
| + | [[File:SS metnum 5.png]] | ||
| + | |||
| + | jika xi+1 adalah akar dari f(x) = 0 maka persamaan diatas menjadi | ||
| + | |||
| + | [[File:SS metnum 7.png]] | ||
| + | |||
| + | dengan mengasumsi xi mendekati nilai xi+1, kita dapat menghapus bilangan terakhir pada persamaan dan mendapatkan persamaan berikut | ||
| + | |||
| + | [[File:SS metnum 6.png]] | ||
| + | |||
| + | Kita hanya perlu mengulangi kalkulasi persamaan diatas dengan nilai awal x0 hingga mencapai suatu kriteria konvergen | ||
| + | |||
| + | |xi+1 - xi| < E | ||
| + | |||
| + | |||
| + | == Pertemuan 6 (9 Oktober 2019) == | ||
| + | |||
| + | |||
| + | |||
| + | == Pertemuan 7 (16 Oktober 2019) == | ||
| + | |||
| + | Program Python untuk Solusi Aljabar Simultan | ||
| + | |||
| + | import numpy as np | ||
| + | |||
| + | # Definisikan Matriks A | ||
| + | A = np.array([[1, 2, 0, -2, 0], | ||
| + | [0, 1, -1, 1, -1], | ||
| + | [0, 1, 0, 2, -1], | ||
| + | [0, 0, 2, 1, 2], | ||
| + | [0, 0, 0, -1, 1]], float) | ||
| + | |||
| + | #Definisikan Matriks B | ||
| + | b = np.array([[-4], | ||
| + | [-1], | ||
| + | [1], | ||
| + | [1], | ||
| + | [-2]], float) | ||
| + | |||
| + | Ab = np.hstack([A, b]) | ||
| + | print (Ab, "\n") | ||
| + | |||
| + | n = len(b) | ||
| + | |||
| + | #Fase Eliminasi | ||
| + | for i in range(0, n-1): | ||
| + | for j in range(i + 1, n): | ||
| + | if Ab[i,i] != 0.0: | ||
| + | lam = Ab[i,i] / Ab[j,i] | ||
| + | Ab[j] = Ab[i] - lam * Ab[j] | ||
| + | |||
| + | print ("Hasil Fase Eliminasi \n", Ab, "\n") | ||
| + | |||
| + | #Fase Substitusi | ||
| + | for i in range(n - 1, -1, -1): | ||
| + | Ab[i] = Ab[i] / Ab[i, i] | ||
| + | for j in range(i - 1, -1, -1): | ||
| + | lam = Ab[i,i] / Ab[j,i] | ||
| + | Ab[j] = Ab[i] - lam * Ab[j] | ||
| + | |||
| + | print ("Hasil Fase Substitusi \n", Ab, "\n") | ||
| + | |||
| + | x = Ab[:, 3] | ||
| + | |||
| + | print ("nilai x Transpose \n", x) | ||
| + | |||
| + | |||
| + | Program Python untuk Solusi Aljabar Simultan | ||
| + | |||
| + | def rungeKutta(t0, y0, t, h): | ||
| + | def dydx(x, y): # mendefinisikan persamaan yang ingin dicari jawabannya | ||
| + | if x < 2: | ||
| + | return ((x**2) - (4*y)) | ||
| + | |||
| + | # hitung jumlah iterasi data | ||
| + | n = (int)((t - t0)/h) | ||
| + | y = y0 | ||
| + | for i in range(1, n + 1): | ||
| + | k1 = h * dydt(t0, y0) | ||
| + | k2 = h * dydt(t0 + 0.5 * h, y0 + 0.5 * k1) | ||
| + | k3 = h * dydt(t0 + 0.5 * h, y0 + 0.5 * k2) | ||
| + | k4 = h * dydt(t0 + h, y0 + k3) | ||
| + | |||
| + | # memperbarui nilai y | ||
| + | y = y0 + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4) | ||
| + | |||
| + | # memperbarui nilai x berdasarkan step height | ||
| + | x = x + h | ||
| + | return y | ||
| + | |||
| + | #masukkan nilai x, y, x0, dan h | ||
| + | x0 = 0 | ||
| + | y = 1 | ||
| + | t = 0.03 | ||
| + | h = 0.01 | ||
| + | print ('nilai y:', rungeKutta(x0, y, x, h)) | ||
| + | |||
| + | |||
| + | |||
| + | == Pertemuan 8 (UTS) == | ||
| + | |||
| + | '''Koding untuk Eliminasi Gauss Tegangan Tali''' | ||
| + | |||
| + | import numpy as np | ||
| + | import math | ||
| + | |||
| + | |||
| + | # input nilai-nilai yang perlu didefinisikan | ||
| + | |||
| + | m1 = eval(input("nilai m1 :")) | ||
| + | m2 = eval(input("nilai m2 :")) | ||
| + | m3 = eval(input("nilai m3 :")) | ||
| + | g = 9.81 | ||
| + | alpha = eval(input("nilai derajat kemiringan :")) | ||
| + | myu = eval(input("nilai koefisien gesek :")) | ||
| + | |||
| + | sudut = alpha*22/(7*180) | ||
| + | |||
| + | theta = sin ((sudut)) | ||
| + | |||
| + | u1 = m1*g*(theta-myu) | ||
| + | u2 = m2*g*(theta-myu) | ||
| + | u3 = m3*g*(theta-myu) | ||
| + | |||
| + | # Definisikan Matriks A | ||
| + | A = np.array([[1, 0, 0], | ||
| + | [-1, 1, 0], | ||
| + | [0, -1, 1]], float) | ||
| + | |||
| + | #Definisikan Matriks B | ||
| + | b = np.array([[u1], | ||
| + | [u2], | ||
| + | [u3]], float) | ||
| + | |||
| + | |||
| + | def EG(A, b, Pivot = True): | ||
| + | n = len(A) | ||
| + | #Fase Eliminasi | ||
| + | for k in range(n-1): | ||
| + | if Pivot: #Fase Pivot | ||
| + | j = abs(A[k:,k]).argmax() + k | ||
| + | if A[j, k] == 0: | ||
| + | raise ValueError("Matriks bersifat singular") | ||
| + | if j != k: | ||
| + | A[ [k , j]] = A[ [j , k]] | ||
| + | b[ [k , j]] = b[ [j , k]] | ||
| + | #Eliminasi | ||
| + | for i in range(k+1, n): | ||
| + | lam = A[i,k]/A[k,k] | ||
| + | A[i, k:] = A[i, k:] - lam*A[k, k:] | ||
| + | b[i] = b[i] - lam*b[k] | ||
| + | |||
| + | #Fase Substitusi | ||
| + | x = np.zeros(n) | ||
| + | for k in range(n-1, -1, -1): | ||
| + | x[k] = (b[k] - np.dot(A[k,k+1:], x[k+1:]))/A[k,k] | ||
| + | |||
| + | return x | ||
| + | |||
| + | print ("nilai t1, t2, dan t3 adalah :", EG (A,b)) | ||
| + | |||
| + | Asumsi nilai yang ingin dimasukkan | ||
| + | |||
| + | m1 = 10 kg | ||
| + | |||
| + | m2 = 20 kg | ||
| + | |||
| + | m3 = 30 kg | ||
| + | |||
| + | derajat kemiringan = 30° | ||
| + | |||
| + | koefisien gesek = 0,1 | ||
| + | |||
| + | |||
| + | kita akan mendapatkan hasil t1, t2, dan t3 | ||
| + | |||
| + | t1 = 39.25790347 | ||
| + | t2 = 117.7737104 | ||
| + | t3 = 235.54742079 | ||
| + | |||
| + | [[File:UTS Elvin Console.png]] | ||
| + | |||
| + | Video Penjelasan Soal Tegangan Tali dengan Eliminasi Gauss | ||
| + | |||
| + | [[File:Eliminasi Gauss Tegangan Tali.mp4]] | ||
| + | |||
| + | |||
| + | |||
| + | '''Koding Untuk Runge Kutta Top Speed Mobil''' | ||
| + | |||
| + | m = eval(input("massa mobil : ")) | ||
| + | g = 9.81 | ||
| + | a = eval(input("percepatan mobil : ")) | ||
| + | cd = eval(input("koefisien drag udara : ")) | ||
| + | myu = eval(input("koefisien gesek jalan : ")) | ||
| + | v0 = 0 | ||
| + | t0 = 0 | ||
| + | dt = 1 #tinggi step atau waktu | ||
| + | error = 100 | ||
| + | p = a - g*myu | ||
| + | q = cd/m | ||
| + | |||
| + | lst = [] | ||
| + | |||
| + | def dvdt(t0, v0): | ||
| + | return p-(q*(v0)**(1.5)) | ||
| + | |||
| + | while error > 0.005: | ||
| + | k1 = dvdt(t0, v0) | ||
| + | k2 = dvdt(t0 + 0.5 * dt, v0 + 0.5 * dt * k1) | ||
| + | k3 = dvdt(t0 + 0.5 * dt, v0 + 0.5 * dt * k2) | ||
| + | k4 = dvdt(t0 + dt, v0 + dt * k3) | ||
| + | v1 = v0 + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4) | ||
| + | t0 = t0 + dt | ||
| + | error = ((v1 - v0) / v1)*100 #persentase error | ||
| + | v0 = v1 | ||
| + | lst.append(v1) | ||
| + | |||
| + | waktu = len(lst) | ||
| + | |||
| + | print ("waktu untuk mencapai velocity maksimal adalah: ", waktu+1) | ||
| + | print ("velocity maksimal adalah: ", v1) | ||
| + | |||
| + | |||
| + | Asumsi nilai yang ingin dimasukkan | ||
| + | |||
| + | massa mobil = 1000 kg | ||
| + | |||
| + | percepatan awal mobil = 10 m/2 | ||
| + | |||
| + | koefisien drag udara = 0.6 | ||
| + | |||
| + | koefisien gesek jalan = 0.5 | ||
| + | |||
| + | kecepatan awal = 0 m/s | ||
| + | |||
| + | dengan | ||
| + | |||
| + | dt (tinggi step) = 1 | ||
| + | |||
| + | t0 = 0 | ||
| + | |||
| + | v0 = 0 m/s (diam) | ||
| + | |||
| + | kita akan mendapatkan nilai terminal velocity | ||
| + | |||
| + | vt = 415.11 m/s | ||
| + | |||
| + | dengan waktu untuk mencapai terminal velocity adalah 342 s | ||
| + | |||
| + | [[File:Console Runge Kutta Elvin UTS.png]] | ||
| + | |||
| + | berikut adalah grafik waktu terhadap kecepatan dimana kita bisa melihat waktu yang dicapai terminal velocity dengan kondisi yang diasumsikan | ||
| + | |||
| + | [[File:UTS runge kutta Elvin grafik ver 2.png|500px]] | ||
| + | |||
| + | Video Penjelasan Soal Top Speed Mobil | ||
| + | |||
| + | [[File:Runge Kutta Top Speed I.mp4]] | ||
| + | |||
| + | [[File:Runge Kutta Top Speed II.mp4]] | ||
| + | |||
| + | |||
| + | '''Video Muhasabah''' | ||
| + | |||
| + | [[File:Muhasabah Elvin I.mp4]] | ||
| + | |||
| + | [[File:Muhasabah Elvin II.mp4]] | ||
| + | |||
| + | |||
| + | |||
| + | == Pertemuan 9 (30 Oktober 2019) == | ||
| + | |||
| + | '''Perbaikan Koding Terminal Velocity Mobil''' | ||
| + | |||
| + | m = eval(input("massa mobil : ")) | ||
| + | g = 9.81 | ||
| + | cd = eval(input("koefisien drag udara : ")) | ||
| + | myu = eval(input("koefisien gesek jalan : ")) | ||
| + | hp = eval(input("Besar Horsepower mobil : ")) | ||
| + | rpm = eval(input("Besar RPM mobil : ")) | ||
| + | v0 = 0 | ||
| + | t0 = 0 | ||
| + | dt = 1 #tinggi step atau waktu | ||
| + | error = 100 | ||
| + | |||
| + | Fmobil = (hp * 9550) / (rpm * ((2 * 3.14)/60)) | ||
| + | |||
| + | p = (Fmobil/m) - g*myu | ||
| + | q = cd/m | ||
| + | |||
| + | lst = [] | ||
| + | |||
| + | def dvdt(t0, v0): | ||
| + | return p-(q*(v0)**(1.5)) | ||
| + | |||
| + | while error > 0.005: | ||
| + | k1 = dvdt(t0, v0) | ||
| + | k2 = dvdt(t0 + 0.5 * dt, v0 + 0.5 * dt * k1) | ||
| + | k3 = dvdt(t0 + 0.5 * dt, v0 + 0.5 * dt * k2) | ||
| + | k4 = dvdt(t0 + dt, v0 + dt * k3) | ||
| + | v1 = v0 + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4) | ||
| + | t0 = t0 + dt | ||
| + | error = ((v1 - v0) / v1)*100 #persentase error | ||
| + | v0 = v1 | ||
| + | lst.append(v1) | ||
| + | |||
| + | waktu = len(lst) | ||
| + | |||
| + | print ("waktu untuk mencapai velocity maksimal adalah: ", waktu+1) | ||
| + | print ("velocity maksimal adalah: ", v1) | ||
| + | |||
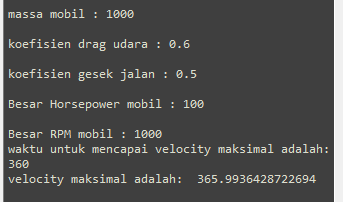
| + | diatas merupakan perbaikan dari koding terminal velocity pada minggu UTS dimana pada kode ini, saya memperhitungkan horsepower dan rpm dari mobil | ||
| + | |||
| + | dengan input nilai dan hasil berikut | ||
| + | |||
| + | massa mobil : 1000 kg | ||
| + | |||
| + | koefisien drag : 0.6 | ||
| + | |||
| + | koefisien gesekan jalan : 0.5 | ||
| + | |||
| + | Horsepower mobil : 100 hp | ||
| + | |||
| + | RPM mobil : 1000 rpm | ||
| + | |||
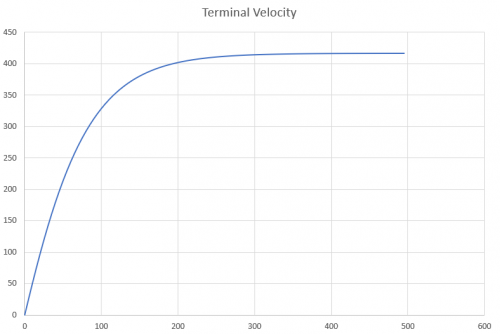
| + | akan menghasilkan top speed sebesar 365.99 m/s pada waktu 360 s | ||
| + | |||
| + | [[File:New runge kutta Elvin Console.png]] | ||
| + | |||
| + | |||
| + | '''Tugas Persamaan Diferensial''' | ||
| + | |||
| + | rho = eval(input("Rho material : ")) | ||
| + | k = eval(input("k material : ")) | ||
| + | cp = eval(input("Cp material : ")) | ||
| + | qin = eval(input("kalor yang dihasilkan dalam dinding : ")) | ||
| + | T0 = eval(input("Suhu awal dalam dinding : ")) | ||
| + | t = eval(input("lama waktu : ")) | ||
| + | t0 = 0 | ||
| + | |||
| + | dt = 1 #tinggi step atau waktu | ||
| + | |||
| + | p = qin/(rho*cp) | ||
| + | q = k/(rho*cp) | ||
| + | |||
| + | def dTdt(t0, T0): | ||
| + | return p+(q*(T0)) | ||
| + | |||
| + | def RK4(t0, T0, t, dt): | ||
| + | n = (t-t0)//dt #jumlah iterasi yang dibutuhkan | ||
| + | |||
| + | for i in range (1, n+1): | ||
| + | k1 = dTdt(t0, T0) | ||
| + | k2 = dTdt(t0 + 0.5 * dt, T0 + 0.5 * dt * k1) | ||
| + | k3 = dTdt(t0 + 0.5 * dt, T0 + 0.5 * dt * k2) | ||
| + | k4 = dTdt(t0 + dt, T0 + dt * k3) | ||
| + | T1 = T0 + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4) | ||
| + | T0 = T1 #memperbarui nilai T untuk iterasi berikutnya | ||
| + | |||
| + | t0 = t0 + dt | ||
| + | |||
| + | return T0 | ||
| + | |||
| + | |||
| + | print ("suhu akhir dalam dinding pada t =", t, "adalah ", RK4(t0, T0, t, dt)) | ||
| + | |||
| + | |||
| + | |||
| + | Diatas merupakan koding yang dibuat untuk menyelesaikan persamaan diferensial saya sendiri yaitu konduksi secara transien dengan persamaan berikut: | ||
| + | |||
| + | [[File:Persamaan Elvin Konduksi.png|300px]] | ||
| + | |||
| + | dimana kasusnya adalah mencari nilai temperatur pada jarak x dalam sebuah dinding setelah 10 sekon | ||
| + | |||
| + | nilai-nilai yang saya input adalah | ||
| + | |||
| + | Qin = 1000 W/m3 | ||
| + | |||
| + | K = 100 W/m K | ||
| + | |||
| + | Cp = 4 kJ/kg K | ||
| + | |||
| + | rho = 1600 kg/m3 | ||
| + | |||
| + | T0 = 50°C | ||
| + | |||
| + | t = 10 s | ||
| + | |||
| + | dan menghasilkan nilai T pada jarak x setelah 10 sekon adalah 60.147°C | ||
| + | |||
| + | [[File:Console Runge Kutta 2 Elvin.png]] | ||
| + | |||
| + | berikut merupakan video penjelasan untuk pemodelan, persamaan, dan koding tugas ini | ||
| + | |||
| + | [[File:Persamaan Runge Kutta Elvin 1.mp4]] | ||
| + | |||
| + | [[File:Persamaan Runge Kutta Elvin 2.mp4]] | ||
| + | |||
| + | |||
| + | |||
| + | == Pertemuan 10 (6 November 2019) == | ||
| + | |||
| + | Pada pertemuan minggu ini, kami melanjutkan kelas seperti biasa dan membahas salah satu soal yang dipertanyakan Ujian Tengah Semester kemarin mengenai terminal velocity sebuah mobil. | ||
| + | |||
| + | '''1. Wawasan Pak Dai''' | ||
| + | |||
| + | Sebelum membahas soal tersebut kami juga diberikan beberapa wawasan dari Pak Dai mengenai pentingnya logika dan cara berpikir. Berbagai masalah matematis yang ada tidak boleh hanya diselesaikan dengn diketahui, ditanya, mencari rumus yang digunakan, dan menjawab itu adalah kerja seorang operator yang jalan secara terbuku. Akan tetapi, penyelesaian suatu masalah harus melalui proses yang lebih mendalam yaitu dengan memahami masalah tersebut terlebih dahulu. Dengan bisa memahami masalah tersebut, kita bisa berfungsi sesuai seorang mahasiswa teknik mesin dengan menyusun masalah mennjadi suatu persamaan yang kemudian bisa diselesaikan. | ||
| + | |||
| + | '''2. Soal UTS Terminal Velocity (Modifikasi)''' | ||
| + | |||
| + | Soal Ujian Tengah Semester yang dikeluarkan sebelumnya mengenai terminal velocity suatu mobil dibahas oleh Pak Dai. Soal yang sudah diselesaikan kami sebelumnya ini diselesaikan dengan menginput data percepatan. Padahal percepatan sendiri tidak diketahui secara nyata jika dilihat pada spesifikasi mobil yang biasa dijual. Dengan demikian, kami diarahkan untuk mencoba mengerjakan ulang soal tersebut dengan menginput data Horsepower dan RPM Mobil. | ||
| + | |||
| + | Hasil Bisa dilihat di Pertemuan 9 | ||
| + | |||
| + | == Pertemuan 11 (13 November 2019) == | ||
| + | |||
| + | '''1. Regresi Linear''' | ||
| + | |||
| + | Pada pertemuan ini, kami diberi materi oleh Pak Radon mengenai proses untuk mengelola data suatu grafik yaitu dengan regresi linier, curve fitting, dan least square. hal ini dapat dilaksanakan dengan menggunakan data yang sudah dikumpulkan sebelumnya untuk diproses. Bagaimana cara untuk memilih proses yang dibutuhkan tergantung oleh fenomena fisika serta output yang diinginkan. | ||
| + | |||
| + | Salah satu aplikasi dari regresi linier, curve fitting, dan least square ini merupakan Optimasi. Optimasi sendiri merupakan proses yang bertujuan untuk mencari nilai minimum atau maksimum dari suatu fungsi. fungsi ini dapat berasal dari data yang dikumpulkan atau model matematis yang dibuat. Dengan melakukan optimasi, kita bisa mendapatkan nilai efektif atau efisien dari suatu sistem. Contohnya, volume mobil agar bensin dapat diiritkan, desain suatu panel surya agar output daya maksimal, dan seterusnya. Asisten Dosen Bang Timothy juga kemudian menjelaskan beberapa metode optimasi yang dapat digunakan seperti basin hopping, metode powell, dan lainnya. Kemudian, kelas dilanjutkan dengan pembahsan contoh soal dibuku referensi hingga waktu selesai. | ||
| + | |||
| + | == Pertemuan 12 (20 November 2019) == | ||
| + | |||
| + | '''1. Materi CFD''' | ||
| + | |||
| + | Pada pertemuan minggu ini, kami diajarkan mengenai penggunaan software didunia engineering. Computer Aided Engineering sendiri terdiri atas beberapa bidang umum seperti, Computer Aided Design (CAD), Computer Aided Manufacturing (CAM), Computational Fluid Dynamics (CFD), Finite Element Analysis (FEA), dan lain-lainnya. Kali ini, kami diajarkan CFD dengan sebuah program yang dikembangkan oleh CCIT FTUI yaitu CFDSOF. CFDSOF adalah software yang digunakan untuk menganalisis gerak atau pengaruh suatu fluida dalam suatu Boundary Volume. secara langsung materi minggu ini juga berhubungan dengan salah satu jenis masalah matematis yaitu Boundary Value Problem. | ||
| + | |||
| + | Masing-masing mahasiswa kelas Metode Numerik mempelajari CFDSOF ini dengan sebuah model contoh mobil yang sudah disediakan oleh asisten dosen bang timo dan bang edo. mereka mengajarkan kita langkah per langkah dari bagaimana mengimport model, membuat meshing volume serta konfigurasi jumlah mesh dan boundary, kemudian pemilihan model simulasi, input data boundary, running simulasi, hingga analisis hasil yang ada dengan aplikasi paraview. | ||
| + | |||
| + | '''2. Tugas CFD Mobil''' | ||
| + | |||
| + | Setelah mempelajari CFDSOF tersebut, setiap kelompok diarahkan untuk mencoba mengumpulkan data mobil menggunakan CFDSOF untuk bisa membuat sebuah grafik yang kemudian diproses dengan regresi linier atau curve fitting. | ||
| + | |||
| + | [[File:CFDSOF 1 Elvin.png|500px]] | ||
| + | |||
| + | Model Mobil | ||
| + | |||
| + | [[File:CFDSOF 2 Elvin.png|500px]] | ||
| + | |||
| + | Meshing | ||
| + | |||
| + | [[File:CFDSOF 3 Elvin.png|500px]] | ||
| + | |||
| + | Solver Study Case | ||
| + | |||
| + | [[File:CFDSOF 4 Elvin.png|500px]] | ||
| + | |||
| + | Analisis dengan paraview | ||
| + | |||
| + | [[File:CFDSOF 5 Elvin.png|500px]] | ||
| + | |||
| + | Hasil proses data dengan excel | ||
| + | |||
| + | '''3. Tugas Airfoil''' | ||
| + | |||
| + | Sebelumnya tugas CFD Mobil dilaksanakan dengan membuat airfoil pada mobil tersebut dengan angle of attack -15 hingga 90 derajat. Akan tetapi, tugas diubah untuk hanya menganalisis Airfoil tersebut pada angle -15 hingga 90 derajat dan kemudian dioptimasi | ||
| + | |||
| + | == Pertemuan 13 (27 November 2019) == | ||
| + | |||
| + | '''1. Kuis''' | ||
| + | |||
| + | Pada pertemuan minggu ini, kami diberi kuis dadakan oleh Pak Dai untuk mengetes pemahaman diri kami terhadap metode numerik dari awal semester hingga pertemuan ini. Kuis ini sendiri membahas beberapa hal dasar seperti soal yang pertama kali diberikan pada pertemuan 1 serta penyelesaiannya dengan metode numerik dan analitik. Selain itu, juga menanya mengenai apa yang kita ketahui mengenai optimasi sistem dan juga kontribusi masing-masing untuk tugas airfoil. | ||
| + | |||
| + | '''2. Presentasi Kelas''' | ||
| + | |||
| + | Setelah Kuis, kelompok mahasiswa diarahkan untuk melaksanakan presentasi mengenai tugas yang diberikan sebelumnya yaitu analisis CFD pada airfoil pesawat dan optimasinya dengan python. Kelompok saya sendiri maju pada hari ini untuk mempresentasikan progress. | ||
| + | |||
| + | Hasil dapat dilihat disini [[Kelompok 12]] | ||
| + | |||
| + | == Pertemuan 14 (4 Desember 2019) == | ||
| + | |||
| + | '''1. Presentasi Kelas (Lanjutan)''' | ||
| + | |||
| + | Pertemuan minggu ini dilanjutkan dengan presentasi kelompok yang belum melaksanakan pada minggu sebelumnya dari awal pembelajaran kelas hingga selesai. Dan dari pengamatan saya sendiri banyak sekali tahapan dan progress yang sudah dicapai teman-teman sekelas saya. | ||
| + | |||
| + | '''2. Materi Artificial Neural Network''' | ||
| + | |||
| + | Setelah beberapa kelompok sudah mempresentasikan hasil optimasi airfoil masing-masing, kelas dilanjutkan dengan pembelajaran mengenai Artificial Neural Network secara dasar hingga selesai. Materi juga diberikan oleh Asisten Dosen bang timo untuk dibaca-baca kembali | ||
| + | |||
| + | '''3. Tugas''' | ||
| + | |||
| + | Tugas Minggu ini adalah untuk membuat sebuah ANN untuk diaplikasikan ke data CFD Airfoil yang sebelumnya sudah didapatkan | ||
| + | |||
| + | == Pertemuan 15 (11 Desember 2019) == | ||
| + | |||
| + | '''1. Wawasan Pak Dai''' | ||
| + | |||
| + | Pada pertemuan terakhir sebelum Ujian Akhir Semester, Pak Dai memberikan beberapa wawasan ke mahasiswa yang hadir di kelas. Seperti yang kita ketahui tujuan pembelajaran metode numerik ini adalah | ||
| + | * Memahami konsep dan prinsip dasar yang ada di metode numerik | ||
| + | * Mengaplikasi konsep tersebut ke permasalahan engineering | ||
| + | * Menjadi Lebih mengenal diri | ||
| + | Kami diingatkan kembali akan tujuan pembelajaran ini dan juga mengambil intisari pembelajaran dari awal semester hingga selesai. Apa yang kita pelajari di kelas ini belum tentu akan digunakan pada kemudian hari, akan tetapi pengalaman yang dialami selama menjalani proses itu lah yang penting untuk perkembangan diri. | ||
| + | |||
| + | |||
| + | '''2. Materi Kelas''' | ||
| + | |||
| + | Materi kelas minggu ini kembali mencakupi pembelajaran ANN dan juga langsung dipraktekkan oleh Asisten Dosen Bang Timo dan Bang Edo. kami diajarkan bagaimana me-running ANN tersebut untuk memproses data CFD yang kami miliki sebelumnya. | ||
| + | |||
| + | Hasil dapat dilihat disini [[Kelompok 12]] | ||
| + | |||
| + | |||
| + | <comments voting="Plus" /> | ||
Latest revision as of 17:31, 17 November 2020
"Everything will be 大丈夫"
| Profile | ||
|---|---|---|

|
Nama | Elvin |
| NPM | 1706036381 | |
| Jurusan | Teknik Mesin | |
Progress Tugas Merancang - Elvin
Contents
- 1 Pertemuan 1 (4 September 2019)
- 2 Pertemuan 2 (11 September 2019)
- 3 Pertemuan 3 (18 september 2019)
- 4 Pertemuan 4 (25 September 2019)
- 5 Pertemuan 5 (2 Oktober 2019)
- 6 Pertemuan 6 (9 Oktober 2019)
- 7 Pertemuan 7 (16 Oktober 2019)
- 8 Pertemuan 8 (UTS)
- 9 Pertemuan 9 (30 Oktober 2019)
- 10 Pertemuan 10 (6 November 2019)
- 11 Pertemuan 11 (13 November 2019)
- 12 Pertemuan 12 (20 November 2019)
- 13 Pertemuan 13 (27 November 2019)
- 14 Pertemuan 14 (4 Desember 2019)
- 15 Pertemuan 15 (11 Desember 2019)
Pertemuan 1 (4 September 2019)
1. Pengenalan Kelas Metode Numerik
Perkenalkan nama saya Elvin, saya adalah seorang mahasiswa teknik mesin di Universitas Indonesia yang sedang mengambil mata kuliah Metode Numerik yang diajarkan Bapak Dr. Ir. Ahmad Indra Siswantara dan Bapak Dr. Eng. Radon Dhelika. Pada kelas ini, mahasiswa diberi pertanyaan "Mengapa harus mempelajari kalkulus?" oleh Bapak DAI (Dr. Ahmad Indra). Kalkulus merupakan ilmu dasar yang banyak digunakan pada banyak bidang ilmu lainnya, serta juga digunakan untuk membuat model matematika untuk pendekatan suatu kasus nyata serta menganalisa dan proses agar dapat mencapai penyelesaian. Dari kelas Metode Numerik ini sendiri, kami sebagai mahasiswa teknik mesin diharapkan dapat menyelesaikan masalah model matematika secara manual ataupun melalui pembelajaran bahasa pemrograman seperti bahasa C++, Python, Javascript, dan lainnya. Pada kelas Metode Numerik ini, pembelajaran kami akan berfokus pada bahasa pemrograman python yang sudah banyak digunakan secara internasional dan juga dipelajari oleh perguruan tinggi luar negeri seperti Massachusets Institute of Technology dan lainnya.
2. Bahasa Pemrograman Python
Python adalah sebuah bahasa pemrograman tingkat tinggi yang biasa digunakan oleh programmer untuk menulis rangkaian kode logik yang kemudian dapat digunakan sebagai sebuah program yang bekerja sesuai dengan keinginan atau tujuan programmer itu sendiri.
3. Tugas
Tugas yang diberikan pada 4 September 2019 adalah membuat algoritma dan program di Python untuk menyelesaikan persamaan berikut.
T(x) = (x^2 - 1) / (x - 1) (1)
secara manual, persamaan (1) dapat diselesaikan dengan mudah dengan penggunaan limit ataupun l'hopital. Akan tetapi, dikarenakan tugas ini diwajibkan untuk menggunakan Phyton, saya sendiri perlu mempelajari phyton secara keseluruhan terlebih dahulu. Dari hal sederhana seperti print ("Hello World") hingga bagaimana mengoperasikan sebuah kalkulator dengan variabel, string, operator aritmatika, conditionals (if, else, dan elif).
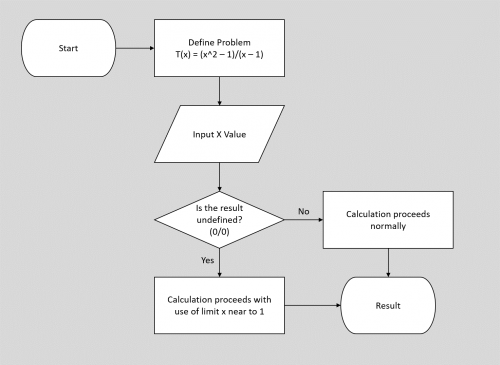
Untuk menyelesaikan persamaan (1), saya merancang algoritma yang diperlukan terlebih dahulu seperti pada gambar berikut.
Proses dimulai dari mendefinisikan masalah terlebih dahulu yaitu persamaan (1). Setelah itu nilai x dimasukkan ke persamaan (1) untuk mendapatkan hasil. Berdasarkan hasil yang didapatkan akan terdapat 2 pilihan. Jika hasil terdefinisi (tidak 0/0), maka perhitungan dilanjutkan seperti biasa. Akan tetapi, jika hasil tidak terdefinisi (0/0), maka perhitungan dilanjutkan dengan menggunakan limit x mendekati 1. Setelah itu, proses akan berakhir dengan mendapatkan nilai akhir dari persamaan.
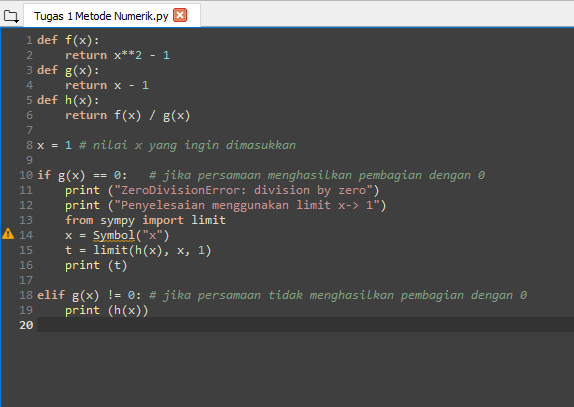
Berdasarkan algoritma yang dirancang, saya menggunakan language interpreter Spyder untuk membuat rangkaian kode sebagai berikut.
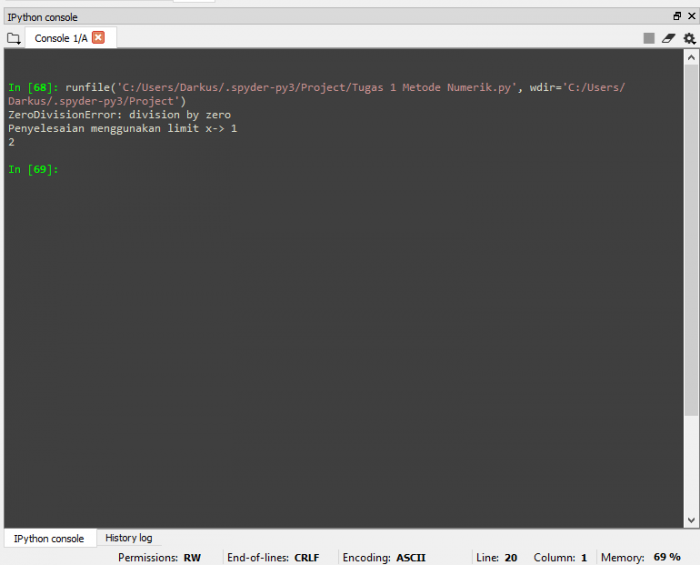
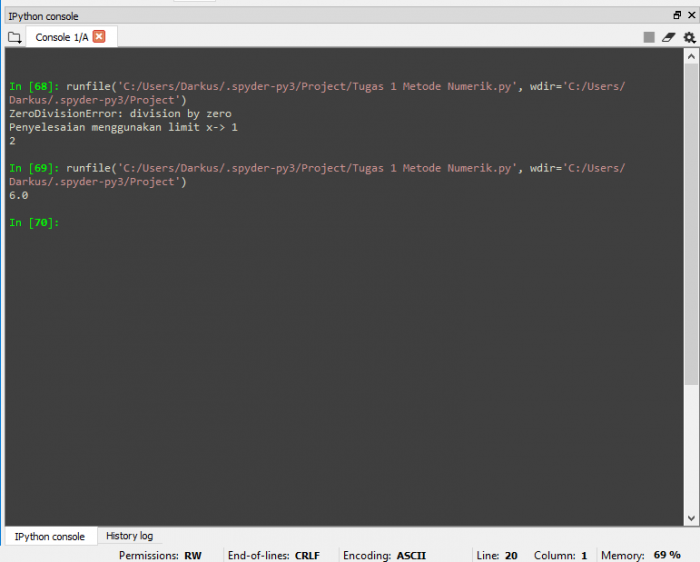
Pada kode ini saya mendefinisikan persamaan (1) sebagai fungsi h(x)=f(x)/g(x) dimana fungsi f(x)=x^2-1 dan fungsi g(x)=x-1. Kemudian, mendefinisikan nilai x yang ingin dimasukkan ke persamaan. Berdasarkan nilai x tersebut, jika terjadi pembagian dengan 0 (tidak terdefinisikan), maka penyelesaian menggunakan limit yang diimport dari library sympy. berdasarkan gambar diatas yang menggunakan nilai x = 1, didapatkan hasil berikut yang terprint pada console spyder.
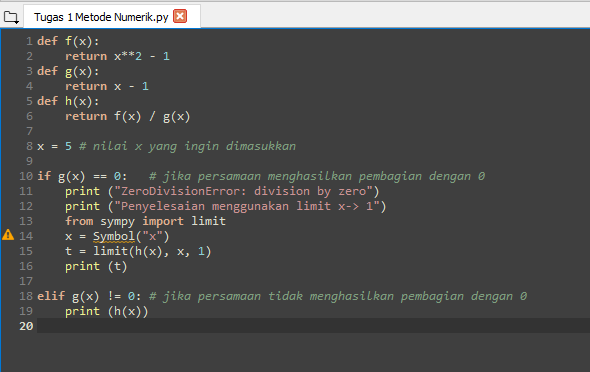
Sebaliknya, jika tidak terjadi pembagian dengan 0 (terdefinisikan), maka perhitungan dilanjutkan dengan biasa seperti pada gambar kode dan hasil pada console yang dibawah yang menggunakan nilai x = 5 dan mendapatkan hasil 6.
Pertemuan 2 (11 September 2019)
1. Wawasan oleh Pak DAI
Pertemuan kelas Metode Numerik pada minggu ke-2 melanjutkan pembelajaran dalam bahasa pemrograman python. Sebelum memasuki materi tersebut, Pak DAI memberikan beberapa wawasan yang penting dan menarik yang berkaitan mengenai pembelajaran metode numerik python dan pemrograman secara umum dari sudut luar pandang mahasiswa. Seperti yang kita tahu, Metode Numerik dapat digunakan untuk menyelesaikan masalah model matematika apapun dengan pendekatan yang menyerupai kondisi nyata. Hal ini dapat dibantu melalui penggunaan pemrograman contohnya python. Selain itu, manfaat dari pemrograman tidak hanya terbatas pada aplikasi metode numerik tetapi juga banyak digunakan untuk menghasilkan berbagai aplikasi/perangkat lunak yang banyak digunakan oleh manusia. Aplikasi ataupun perangkat lunak ini berisi berbagai algoritma dan rangkaian kode yang diisi oleh programmer yang membuatnya. Contoh secara umum adalah permainan catur digital yang banyak dimainkan memiliki puluhan ribu langkah yang diprogram untuk mengalahkan pemain. Di kasus ini, semakin banyak pemrograman ataupun langkah yang dibuat oleh programmer untuk programnya, maka semakin banyak hal atau langkah yang dapat dilakukan program tersebut hingga dapat disebut sebagai Artificial Intelligence (AI). Pak DAI sendiri mengatakan bahwa AI merupakan serangkaian logika yang dibuat oleh manusia yang mempunyai peran sebagai Natural Intelligence. Terlebih dari itu, Pak DAI juga mengatakan bahwa kita perlu memahami batasan yang dimiliki masing-masing sehingga kita dapat memanfaatkan perkembangan teknologi secara pesat seperti dari revolusi industri 1.0 hingga 4.0 sekarang. Dan kemudian, kita dapat memanfaatkan teknologi tersebut agar dapat ter-empower sehingga pada revolusi industri 5.0 berikutnya.
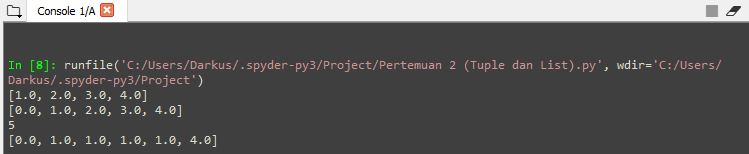
2. Python: List and Tuples
Materi Python yang diberi oleh Pak Radon pada pertemuan ini berfokus pada pengenalan python dari dasar. Selain itu, kami dianjurkan dari Pak Radon dan Pak DAI untuk aktif dan intensif untuk mempelajari phyton diluar jam mata kuliah. Dengan mencari sumber yang sesuai dengan cara pembelajaran masing-masing dari buku, video, ataupun website pembelajaran. Salah satu website yang dianjurkan adalah introtopython.org dimana web ini memiliki materi python yang sangat lengkap mengenai pemakaian dasar hingga kompleks. Materi hari ini difokuskan agar mahasiswa minimal sudah mengalami pemrograman python dengan memrogram print ("Hello World"). Setelah itu, materi dilanjutkan ke pembelajaran Tuples dan List.
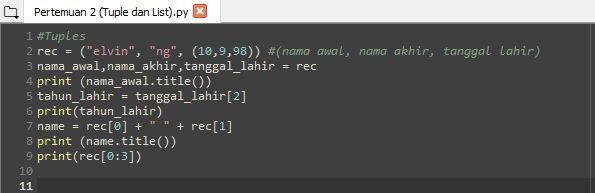
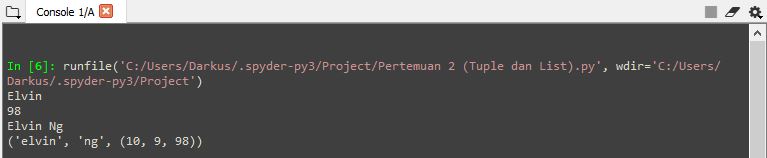
Tuples Tuples adalah struktur data yang digunakan untuk mengelompokkan data yang terpisahkan oleh sebuah tanda koma (','). data ini kemudian dapat di ditetapkan sebagai suatu kode contohnya pada line 2 dan 3 gambar interpreter dibawah. Dengan demikian kita dapat me-print data spesifik yang dibutuhkan seperti kode yang terdapat dibawah beserta hasil yang diconsole.
Lists
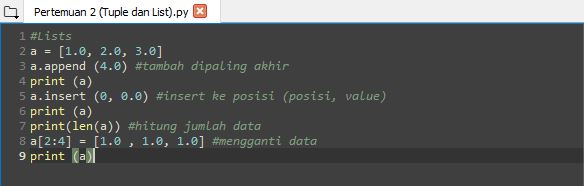
Lists adalah struktur data yang digunakan untuk mengelompokkan data yang dapat diubah posisi ataupun nilainya. setiap data (item) yang terdapat pada lists ini juga memiliki pasangan angka yang terhitung dari 0 hingga seterusnya. Contoh-contoh pemakaian list terdapat pada gambar interpreter dan console berikut.
Tuples dan Lists ini mungkin terlihat menyerupai satu sama lain. Akan tetapi, perbedaan utama antara dua struktur data ini adalah data yang terdapat pada list dapat diubah (mutable) sedangkan data yang terdapat pada tuples tidak dapat diubah. selain itu, tuples menggunakan tanda kurung ( ) sedangkan lists menggunakan tanda kurung kotak [ ]
Pertemuan 3 (18 september 2019)
1. Kuis
Pada pertemuan kelas Metode Numerik 18 September 2019, Pak DAI dan Pak Radon memberikan kuis untuk menguji pemahaman mahasiswa dalam bahasa pemrograman Python.
Soal yang diberikan adalah sebagai berikut
1, 1, 2, 3, 5, 8, 13, 21, ...., n-1, n Dari deret Fibonacci diatas, buatlah algoritma, flowchart, serta Program Python untuk menghasilkan angka dari suku yang diinginkan
Soal ini dapat diselesaikan dengan menggunakan loop ataupun function pada python
1.a. Loop
Algoritma
- Definisikan nilai a = 0 dan b = 1 (a dan b berturut-turut akan menjadi suku ke-0 dan ke-1 serta menjadi dasar untuk penjumlahan fibonacci)
- Input suku ke - n Fibonacci yang diinginkan
- jika n=0 maka hasil adalah a
- jika n=1 maka hasil adalah b
- jika n lebih dari 1 maka c = a + b, nilai a akan diubah menjadi b, nilai b akan diubah menjadi c. Proses akan di loop hingga mencapai nilai n yang diinginkan
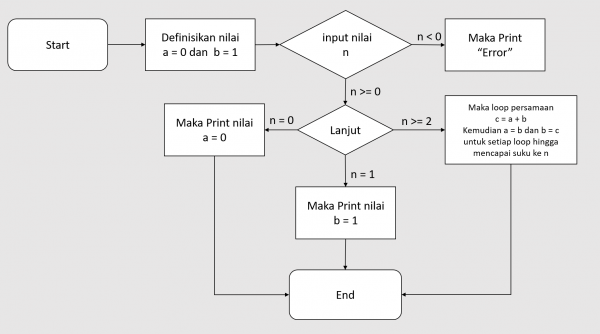
Flowchart
Program Python
1.b. Function
Algoritma
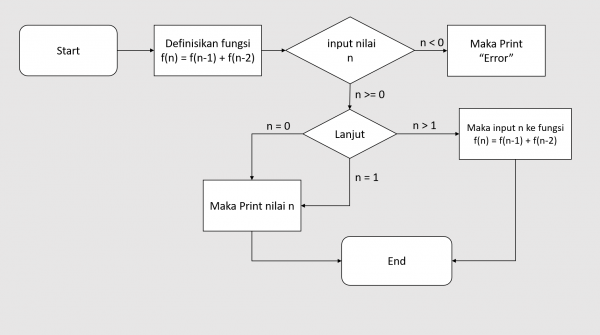
- Definisikan fungsi f(n) = f(n-1) + f(n-2)
- Nilai n hanya berlaku untuk n >= 0, jika n < 0 maka print "error"
- Jika n = 0 atau n = 1 maka print nilai n tersebut
- Jika n > 1 maka input nilai tersebut ke fungsi f(n)
Flowchart
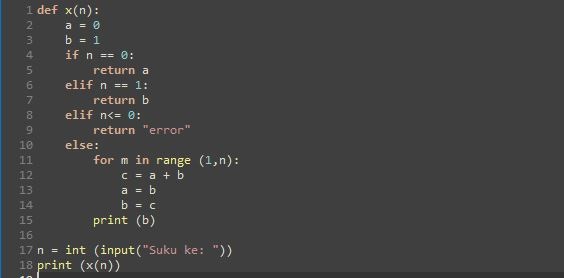
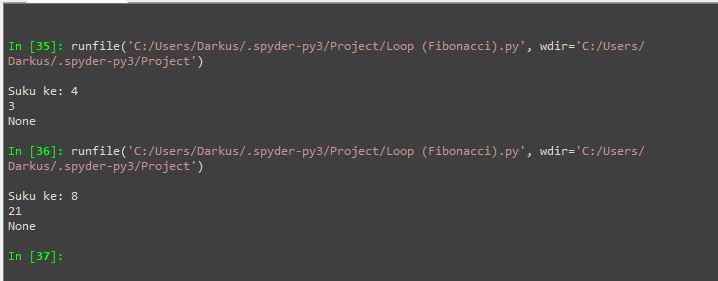
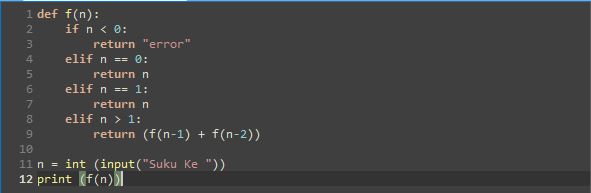
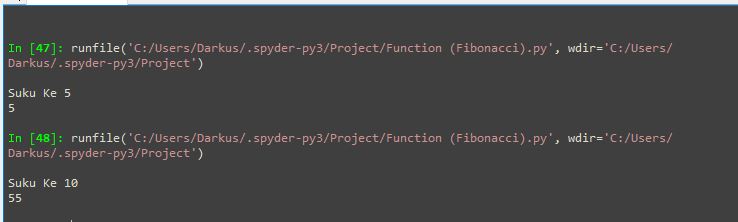
Program Python
2. Tugas
Selain kuis yang diberikan, Pak DAI dan Pak Radon mengelompokkan mahasiswa dengan satu sama lain agar proses pembelajaran lebih baik. Setelah itu, tugas untuk mennyelesaikan salah satu soal eliminasi gauss yang terdapat pada buku referensi mata kuliah Metode Numerik.
Pengerjaan tugas ini dapat dilihat pada Page Kelompok 12
Pertemuan 4 (25 September 2019)
1. Pemodelan
Pada pertemuan kelas Metode Numerik kali ini, Pak Dai memberikan materi mengenai pemodelan. Model merupakan suatu representasi, simplifikasi atau asumsi dari sebuah benda ataupun sistem yang dibuat untuk mendekati benda ataupun kondisi nyata. Model diperlukan agar kita dapat melaksanakan analisis ataupun eksperimen secara lebih mudah tanpa menghabiskan sumber daya yang ada. Model yang dibuat hanya mendekati kondisi nyata sehingga eksperimen atau simulasi yang dilakukan tidak selalu menunjukkan hasil yang 100% akurat. Seperti berbagai bidang ilmu lainnya, arsitek dengan maket, sipil dengan jembatan miniatur, dan teknik aerodinamika dengan wind tunnel, semua model dibuat agar dapat diuji terlebih dahulu tanpa menghasilkan dampak yang besar. Model harus ada karena saat kita mendesign, kita harus memastikan apa yang kita design itu berfungsi, bekerja dan reliable.
2. Tugas
Tugas yang diberikan minggu ini adalah aplikasi eliminasi gauss untuk melaksanakan Finite Element Analysis.
Pengerjaan tugas ini dapat dilihat pada Page Kelompok 12
Pertemuan 5 (2 Oktober 2019)
1. Membuat Program Simulasi dengan Eliminasi Gauss
Pertemuan hari ini diisi dengan penjelasan materi oleh bang Edo dan Bang Timothy asisten dosen untuk kelas Metode Numerik. Mereka menjelaskan kembali bagaimana membuat program simulasi dengan eliminasi gauss yang merupakan tugas dari minggu sebelumnya. Materi ini dijelaskan dengan pendekatan menggunakan pegas sebagai elemen untuk finite element analysis yang akan dilakukan. Kemudian mereka juga menjelaskan beda mengkode dengan bantuan module numpy, sympy, dan manual di python. Dapat dilihat bahwa panjang dan kerumitan dari kode yang ditulis berbeda-beda berdasarkan tidak atau digunakannya module tersebut.
2. Rangkuman Bab 4 buku Numerical Methods Python
Masalah dimana kita harus menentukan nilai x agar f(x) = 0 sering ditemukan di analisis ilmu teknik yang kemudian dapat dikenal sebagai akar dari persamaan atau nilai nol dari fungsi f(x). sebuah fungsi terdiri atas 3 komponen, yaitu input (x), output (y), dan aturan f untuk mendapatkan hasil y. untuk mendapatkan suatu akar dari persamaan, terdapat berbagai metode yang mencakupi:
- Metode Incremental Search
Cara yang paling baik untuk memperkirakan nilai suatu akar adalah dengan menggambarkan fungsi itu sendiri. Jika suatu f(x1) dan f(x2) memiliki nilai yang berlawanan (+-) maka terdapat setidaknya satu nilai akar pada interval x1 hingga x2. Jika intervalnya sangat kecil, maka sangat memungkinkan untuk terdapat 1 akar. Sehingga nilai 0 dari fungsi f(x) dapat ditemukan dengan mengevaluasi fungsi pada interval tersebut.
Masalah yang terdapat pada metode ini adalah:
a. Sangat mungkin untuk melewatkan 2 nilai akar dengan interval yang lebih kecil dari interval x1-x2
b. Akar ganda tidak akan terdeteksi
c. Beberapa pole dapat dikeliru sebagai akar.
- Metode Bisection
Metode bisection bekerja dengan mengurangi separuh nilai akar yang terdapat pada interval x1 dan x2 hingga sangat kecil. Metode ini juga merupakan metode yang sangat cepat dan dapat diandalkan. Metode ini mempunyai proses yang sama dengan incremental scratch dimana jika terdapat sebuah akar pada interval x1 dan x2 maka f(x1) dan f(x2) memiliki tanda yang berlawanan. Untuk mengurangi separuh nilai interval, kita menghitung f(x3) dimana x3 = 1/2*(x1+x2). Kemudian jika nilai f(x2) dan f(x3) mempunyai nilai yang berlawanan maka akar terdapat pada interval x2 dan x3, jika tidak maka akar terdapat pada interval x1 dan x3. Kemudian proses diulang hingga nilai interval menjadi suatu nilai P yang sangat kecil dimana,
|x2 – x1| =< P
- Metode Secant and False Position
Metode secant dan false position sangat mirip satu sama lain dimana kedua metode ini membutuhkan estimasi mula untuk mencari nilai akar, dengan demikian nilai x3 dari akar dapat diestimasi dari interpolasi antara x1 dan x2.
Metode false position membutuhkan nilai x1 dan x2 untuk mendapatkan interval yang berisi akar. Setelah kita mendapatkan nilai x3 hasil interpolasi, kita dapat menggantikan salah satu nilai x1 atau x2 dengan nilai x3. Kemudian, jika f(x3) mempunyai tanda yang sama dengan nilai f(x1) maka x1 <- x3; sebaliknya kita memilih x2 <- x3. Prosedur diulang hingga suatu konvergen tercapai
Metode Secant berbeda dari false position dimana ia tidak perlu interval x1 dan x2 dan menggantikan nilai estimasi tertua dari akar (x1 <- x2 dan x2 <- x3)
- Metode Ridder
Metode ini merupakan modifikasi dari metode false position dimana jika akar terdapat pada interval x1 dan x2, maka kita dapat menghitung f(x3) dari x3 hasil interpolasi dimana x3 adalah titik tengah dari interval. Kemudian kita dapat menggunakan fungsi
g(x) = f(x)e^(x-x)Q
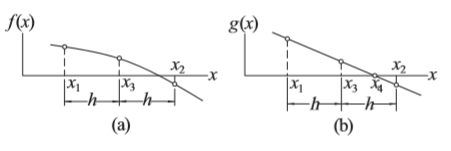
dimana Q adalah konstanta yang ditentukan dari mendapatkan nilai (x1, g1), (x2, g2), dan (x3, g3) seperti pada gambar (b). Nilai akar yang baru kemudian akan didapatkan dari interpolasi linear dari nilai-nilai g(x).
dari persamaan g(x) kita mendapatkan bahwa h=(x2-x1)/2. Syarat agar ketiga titik di gambar (b) terletak pada sebuah garis lurus adalah
yang merupakan sebuah persaman kuadrat pada e^hQ dengan solusi
Dengan me-interpolasi linear titik (x1,g1) dan (x2,g2) maka kita mendapatkan akar baru dengan persamaan berikut
- Metode Newton-Raphson
Metode ini menggunakan turunan f’(x) dari fungsi dan fungsi f(x) itu sendiri. Kemudian metode ini hanya bisa digunakan jika f’(x) dapat dihitung.
Metode ini didapatkan dengan menurunkan rumus dari seri taylor f(x)
jika xi+1 adalah akar dari f(x) = 0 maka persamaan diatas menjadi
dengan mengasumsi xi mendekati nilai xi+1, kita dapat menghapus bilangan terakhir pada persamaan dan mendapatkan persamaan berikut
Kita hanya perlu mengulangi kalkulasi persamaan diatas dengan nilai awal x0 hingga mencapai suatu kriteria konvergen
|xi+1 - xi| < E
Pertemuan 6 (9 Oktober 2019)
Pertemuan 7 (16 Oktober 2019)
Program Python untuk Solusi Aljabar Simultan
import numpy as np
# Definisikan Matriks A
A = np.array([[1, 2, 0, -2, 0],
[0, 1, -1, 1, -1],
[0, 1, 0, 2, -1],
[0, 0, 2, 1, 2],
[0, 0, 0, -1, 1]], float)
#Definisikan Matriks B
b = np.array([[-4],
[-1],
[1],
[1],
[-2]], float)
Ab = np.hstack([A, b])
print (Ab, "\n")
n = len(b)
#Fase Eliminasi
for i in range(0, n-1):
for j in range(i + 1, n):
if Ab[i,i] != 0.0:
lam = Ab[i,i] / Ab[j,i]
Ab[j] = Ab[i] - lam * Ab[j]
print ("Hasil Fase Eliminasi \n", Ab, "\n")
#Fase Substitusi
for i in range(n - 1, -1, -1):
Ab[i] = Ab[i] / Ab[i, i]
for j in range(i - 1, -1, -1):
lam = Ab[i,i] / Ab[j,i]
Ab[j] = Ab[i] - lam * Ab[j]
print ("Hasil Fase Substitusi \n", Ab, "\n")
x = Ab[:, 3]
print ("nilai x Transpose \n", x)
Program Python untuk Solusi Aljabar Simultan
def rungeKutta(t0, y0, t, h):
def dydx(x, y): # mendefinisikan persamaan yang ingin dicari jawabannya
if x < 2:
return ((x**2) - (4*y))
# hitung jumlah iterasi data
n = (int)((t - t0)/h)
y = y0
for i in range(1, n + 1):
k1 = h * dydt(t0, y0)
k2 = h * dydt(t0 + 0.5 * h, y0 + 0.5 * k1)
k3 = h * dydt(t0 + 0.5 * h, y0 + 0.5 * k2)
k4 = h * dydt(t0 + h, y0 + k3)
# memperbarui nilai y
y = y0 + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
# memperbarui nilai x berdasarkan step height
x = x + h
return y
#masukkan nilai x, y, x0, dan h
x0 = 0
y = 1
t = 0.03
h = 0.01
print ('nilai y:', rungeKutta(x0, y, x, h))
Pertemuan 8 (UTS)
Koding untuk Eliminasi Gauss Tegangan Tali
import numpy as np
import math
# input nilai-nilai yang perlu didefinisikan
m1 = eval(input("nilai m1 :"))
m2 = eval(input("nilai m2 :"))
m3 = eval(input("nilai m3 :"))
g = 9.81
alpha = eval(input("nilai derajat kemiringan :"))
myu = eval(input("nilai koefisien gesek :"))
sudut = alpha*22/(7*180)
theta = sin ((sudut))
u1 = m1*g*(theta-myu)
u2 = m2*g*(theta-myu)
u3 = m3*g*(theta-myu)
# Definisikan Matriks A
A = np.array([[1, 0, 0],
[-1, 1, 0],
[0, -1, 1]], float)
#Definisikan Matriks B
b = np.array([[u1],
[u2],
[u3]], float)
def EG(A, b, Pivot = True):
n = len(A)
#Fase Eliminasi
for k in range(n-1):
if Pivot: #Fase Pivot
j = abs(A[k:,k]).argmax() + k
if A[j, k] == 0:
raise ValueError("Matriks bersifat singular")
if j != k:
A[ [k , j]] = A[ [j , k]]
b[ [k , j]] = b[ [j , k]]
#Eliminasi
for i in range(k+1, n):
lam = A[i,k]/A[k,k]
A[i, k:] = A[i, k:] - lam*A[k, k:]
b[i] = b[i] - lam*b[k]
#Fase Substitusi
x = np.zeros(n)
for k in range(n-1, -1, -1):
x[k] = (b[k] - np.dot(A[k,k+1:], x[k+1:]))/A[k,k]
return x
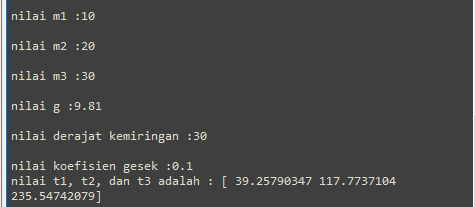
print ("nilai t1, t2, dan t3 adalah :", EG (A,b))
Asumsi nilai yang ingin dimasukkan
m1 = 10 kg
m2 = 20 kg
m3 = 30 kg
derajat kemiringan = 30°
koefisien gesek = 0,1
kita akan mendapatkan hasil t1, t2, dan t3
t1 = 39.25790347 t2 = 117.7737104 t3 = 235.54742079
Video Penjelasan Soal Tegangan Tali dengan Eliminasi Gauss
Koding Untuk Runge Kutta Top Speed Mobil
m = eval(input("massa mobil : "))
g = 9.81
a = eval(input("percepatan mobil : "))
cd = eval(input("koefisien drag udara : "))
myu = eval(input("koefisien gesek jalan : "))
v0 = 0
t0 = 0
dt = 1 #tinggi step atau waktu
error = 100
p = a - g*myu
q = cd/m
lst = []
def dvdt(t0, v0):
return p-(q*(v0)**(1.5))
while error > 0.005:
k1 = dvdt(t0, v0)
k2 = dvdt(t0 + 0.5 * dt, v0 + 0.5 * dt * k1)
k3 = dvdt(t0 + 0.5 * dt, v0 + 0.5 * dt * k2)
k4 = dvdt(t0 + dt, v0 + dt * k3)
v1 = v0 + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
t0 = t0 + dt
error = ((v1 - v0) / v1)*100 #persentase error
v0 = v1
lst.append(v1)
waktu = len(lst)
print ("waktu untuk mencapai velocity maksimal adalah: ", waktu+1)
print ("velocity maksimal adalah: ", v1)
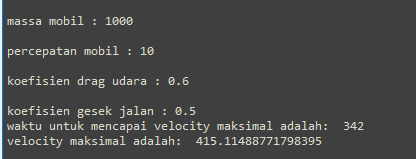
Asumsi nilai yang ingin dimasukkan
massa mobil = 1000 kg
percepatan awal mobil = 10 m/2
koefisien drag udara = 0.6
koefisien gesek jalan = 0.5
kecepatan awal = 0 m/s
dengan
dt (tinggi step) = 1
t0 = 0
v0 = 0 m/s (diam)
kita akan mendapatkan nilai terminal velocity
vt = 415.11 m/s
dengan waktu untuk mencapai terminal velocity adalah 342 s
berikut adalah grafik waktu terhadap kecepatan dimana kita bisa melihat waktu yang dicapai terminal velocity dengan kondisi yang diasumsikan
Video Penjelasan Soal Top Speed Mobil
Video Muhasabah
Pertemuan 9 (30 Oktober 2019)
Perbaikan Koding Terminal Velocity Mobil
m = eval(input("massa mobil : "))
g = 9.81
cd = eval(input("koefisien drag udara : "))
myu = eval(input("koefisien gesek jalan : "))
hp = eval(input("Besar Horsepower mobil : "))
rpm = eval(input("Besar RPM mobil : "))
v0 = 0
t0 = 0
dt = 1 #tinggi step atau waktu
error = 100
Fmobil = (hp * 9550) / (rpm * ((2 * 3.14)/60))
p = (Fmobil/m) - g*myu
q = cd/m
lst = []
def dvdt(t0, v0):
return p-(q*(v0)**(1.5))
while error > 0.005:
k1 = dvdt(t0, v0)
k2 = dvdt(t0 + 0.5 * dt, v0 + 0.5 * dt * k1)
k3 = dvdt(t0 + 0.5 * dt, v0 + 0.5 * dt * k2)
k4 = dvdt(t0 + dt, v0 + dt * k3)
v1 = v0 + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
t0 = t0 + dt
error = ((v1 - v0) / v1)*100 #persentase error
v0 = v1
lst.append(v1)
waktu = len(lst)
print ("waktu untuk mencapai velocity maksimal adalah: ", waktu+1)
print ("velocity maksimal adalah: ", v1)
diatas merupakan perbaikan dari koding terminal velocity pada minggu UTS dimana pada kode ini, saya memperhitungkan horsepower dan rpm dari mobil
dengan input nilai dan hasil berikut
massa mobil : 1000 kg
koefisien drag : 0.6
koefisien gesekan jalan : 0.5
Horsepower mobil : 100 hp
RPM mobil : 1000 rpm
akan menghasilkan top speed sebesar 365.99 m/s pada waktu 360 s
Tugas Persamaan Diferensial
rho = eval(input("Rho material : "))
k = eval(input("k material : "))
cp = eval(input("Cp material : "))
qin = eval(input("kalor yang dihasilkan dalam dinding : "))
T0 = eval(input("Suhu awal dalam dinding : "))
t = eval(input("lama waktu : "))
t0 = 0
dt = 1 #tinggi step atau waktu
p = qin/(rho*cp)
q = k/(rho*cp)
def dTdt(t0, T0):
return p+(q*(T0))
def RK4(t0, T0, t, dt):
n = (t-t0)//dt #jumlah iterasi yang dibutuhkan
for i in range (1, n+1):
k1 = dTdt(t0, T0)
k2 = dTdt(t0 + 0.5 * dt, T0 + 0.5 * dt * k1)
k3 = dTdt(t0 + 0.5 * dt, T0 + 0.5 * dt * k2)
k4 = dTdt(t0 + dt, T0 + dt * k3)
T1 = T0 + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
T0 = T1 #memperbarui nilai T untuk iterasi berikutnya
t0 = t0 + dt
return T0
print ("suhu akhir dalam dinding pada t =", t, "adalah ", RK4(t0, T0, t, dt))
Diatas merupakan koding yang dibuat untuk menyelesaikan persamaan diferensial saya sendiri yaitu konduksi secara transien dengan persamaan berikut:
dimana kasusnya adalah mencari nilai temperatur pada jarak x dalam sebuah dinding setelah 10 sekon
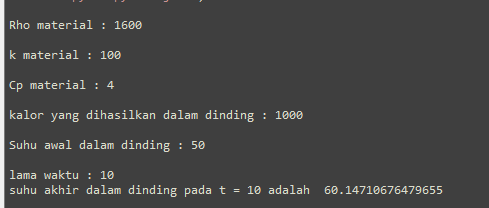
nilai-nilai yang saya input adalah
Qin = 1000 W/m3
K = 100 W/m K
Cp = 4 kJ/kg K
rho = 1600 kg/m3
T0 = 50°C
t = 10 s
dan menghasilkan nilai T pada jarak x setelah 10 sekon adalah 60.147°C
berikut merupakan video penjelasan untuk pemodelan, persamaan, dan koding tugas ini
Pertemuan 10 (6 November 2019)
Pada pertemuan minggu ini, kami melanjutkan kelas seperti biasa dan membahas salah satu soal yang dipertanyakan Ujian Tengah Semester kemarin mengenai terminal velocity sebuah mobil.
1. Wawasan Pak Dai
Sebelum membahas soal tersebut kami juga diberikan beberapa wawasan dari Pak Dai mengenai pentingnya logika dan cara berpikir. Berbagai masalah matematis yang ada tidak boleh hanya diselesaikan dengn diketahui, ditanya, mencari rumus yang digunakan, dan menjawab itu adalah kerja seorang operator yang jalan secara terbuku. Akan tetapi, penyelesaian suatu masalah harus melalui proses yang lebih mendalam yaitu dengan memahami masalah tersebut terlebih dahulu. Dengan bisa memahami masalah tersebut, kita bisa berfungsi sesuai seorang mahasiswa teknik mesin dengan menyusun masalah mennjadi suatu persamaan yang kemudian bisa diselesaikan.
2. Soal UTS Terminal Velocity (Modifikasi)
Soal Ujian Tengah Semester yang dikeluarkan sebelumnya mengenai terminal velocity suatu mobil dibahas oleh Pak Dai. Soal yang sudah diselesaikan kami sebelumnya ini diselesaikan dengan menginput data percepatan. Padahal percepatan sendiri tidak diketahui secara nyata jika dilihat pada spesifikasi mobil yang biasa dijual. Dengan demikian, kami diarahkan untuk mencoba mengerjakan ulang soal tersebut dengan menginput data Horsepower dan RPM Mobil.
Hasil Bisa dilihat di Pertemuan 9
Pertemuan 11 (13 November 2019)
1. Regresi Linear
Pada pertemuan ini, kami diberi materi oleh Pak Radon mengenai proses untuk mengelola data suatu grafik yaitu dengan regresi linier, curve fitting, dan least square. hal ini dapat dilaksanakan dengan menggunakan data yang sudah dikumpulkan sebelumnya untuk diproses. Bagaimana cara untuk memilih proses yang dibutuhkan tergantung oleh fenomena fisika serta output yang diinginkan.
Salah satu aplikasi dari regresi linier, curve fitting, dan least square ini merupakan Optimasi. Optimasi sendiri merupakan proses yang bertujuan untuk mencari nilai minimum atau maksimum dari suatu fungsi. fungsi ini dapat berasal dari data yang dikumpulkan atau model matematis yang dibuat. Dengan melakukan optimasi, kita bisa mendapatkan nilai efektif atau efisien dari suatu sistem. Contohnya, volume mobil agar bensin dapat diiritkan, desain suatu panel surya agar output daya maksimal, dan seterusnya. Asisten Dosen Bang Timothy juga kemudian menjelaskan beberapa metode optimasi yang dapat digunakan seperti basin hopping, metode powell, dan lainnya. Kemudian, kelas dilanjutkan dengan pembahsan contoh soal dibuku referensi hingga waktu selesai.
Pertemuan 12 (20 November 2019)
1. Materi CFD
Pada pertemuan minggu ini, kami diajarkan mengenai penggunaan software didunia engineering. Computer Aided Engineering sendiri terdiri atas beberapa bidang umum seperti, Computer Aided Design (CAD), Computer Aided Manufacturing (CAM), Computational Fluid Dynamics (CFD), Finite Element Analysis (FEA), dan lain-lainnya. Kali ini, kami diajarkan CFD dengan sebuah program yang dikembangkan oleh CCIT FTUI yaitu CFDSOF. CFDSOF adalah software yang digunakan untuk menganalisis gerak atau pengaruh suatu fluida dalam suatu Boundary Volume. secara langsung materi minggu ini juga berhubungan dengan salah satu jenis masalah matematis yaitu Boundary Value Problem.
Masing-masing mahasiswa kelas Metode Numerik mempelajari CFDSOF ini dengan sebuah model contoh mobil yang sudah disediakan oleh asisten dosen bang timo dan bang edo. mereka mengajarkan kita langkah per langkah dari bagaimana mengimport model, membuat meshing volume serta konfigurasi jumlah mesh dan boundary, kemudian pemilihan model simulasi, input data boundary, running simulasi, hingga analisis hasil yang ada dengan aplikasi paraview.
2. Tugas CFD Mobil
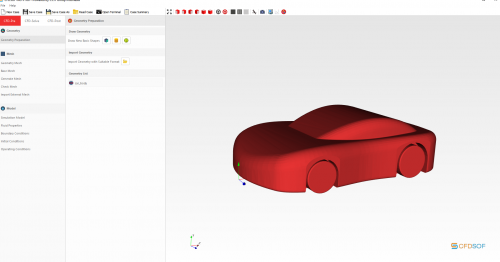
Setelah mempelajari CFDSOF tersebut, setiap kelompok diarahkan untuk mencoba mengumpulkan data mobil menggunakan CFDSOF untuk bisa membuat sebuah grafik yang kemudian diproses dengan regresi linier atau curve fitting.
Model Mobil
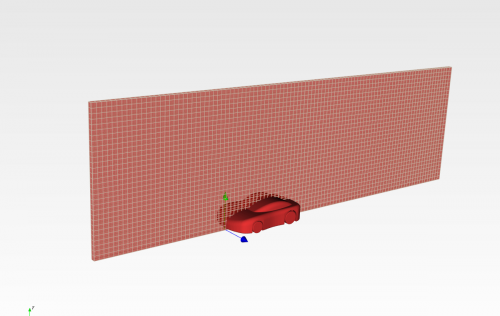
Meshing
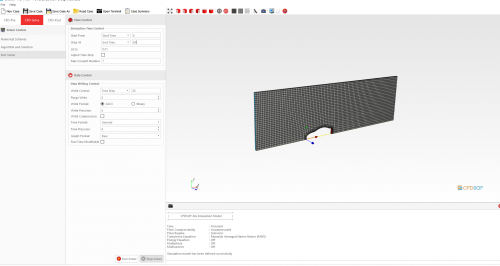
Solver Study Case
Analisis dengan paraview
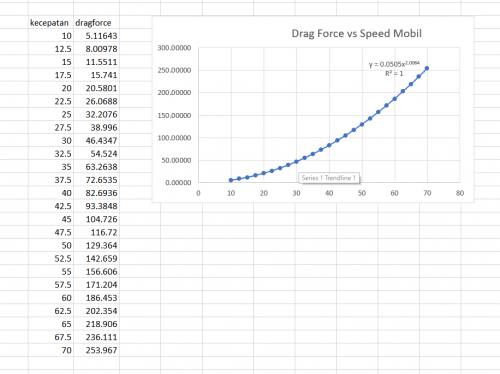
Hasil proses data dengan excel
3. Tugas Airfoil
Sebelumnya tugas CFD Mobil dilaksanakan dengan membuat airfoil pada mobil tersebut dengan angle of attack -15 hingga 90 derajat. Akan tetapi, tugas diubah untuk hanya menganalisis Airfoil tersebut pada angle -15 hingga 90 derajat dan kemudian dioptimasi
Pertemuan 13 (27 November 2019)
1. Kuis
Pada pertemuan minggu ini, kami diberi kuis dadakan oleh Pak Dai untuk mengetes pemahaman diri kami terhadap metode numerik dari awal semester hingga pertemuan ini. Kuis ini sendiri membahas beberapa hal dasar seperti soal yang pertama kali diberikan pada pertemuan 1 serta penyelesaiannya dengan metode numerik dan analitik. Selain itu, juga menanya mengenai apa yang kita ketahui mengenai optimasi sistem dan juga kontribusi masing-masing untuk tugas airfoil.
2. Presentasi Kelas
Setelah Kuis, kelompok mahasiswa diarahkan untuk melaksanakan presentasi mengenai tugas yang diberikan sebelumnya yaitu analisis CFD pada airfoil pesawat dan optimasinya dengan python. Kelompok saya sendiri maju pada hari ini untuk mempresentasikan progress.
Hasil dapat dilihat disini Kelompok 12
Pertemuan 14 (4 Desember 2019)
1. Presentasi Kelas (Lanjutan)
Pertemuan minggu ini dilanjutkan dengan presentasi kelompok yang belum melaksanakan pada minggu sebelumnya dari awal pembelajaran kelas hingga selesai. Dan dari pengamatan saya sendiri banyak sekali tahapan dan progress yang sudah dicapai teman-teman sekelas saya.
2. Materi Artificial Neural Network
Setelah beberapa kelompok sudah mempresentasikan hasil optimasi airfoil masing-masing, kelas dilanjutkan dengan pembelajaran mengenai Artificial Neural Network secara dasar hingga selesai. Materi juga diberikan oleh Asisten Dosen bang timo untuk dibaca-baca kembali
3. Tugas
Tugas Minggu ini adalah untuk membuat sebuah ANN untuk diaplikasikan ke data CFD Airfoil yang sebelumnya sudah didapatkan
Pertemuan 15 (11 Desember 2019)
1. Wawasan Pak Dai
Pada pertemuan terakhir sebelum Ujian Akhir Semester, Pak Dai memberikan beberapa wawasan ke mahasiswa yang hadir di kelas. Seperti yang kita ketahui tujuan pembelajaran metode numerik ini adalah
- Memahami konsep dan prinsip dasar yang ada di metode numerik
- Mengaplikasi konsep tersebut ke permasalahan engineering
- Menjadi Lebih mengenal diri
Kami diingatkan kembali akan tujuan pembelajaran ini dan juga mengambil intisari pembelajaran dari awal semester hingga selesai. Apa yang kita pelajari di kelas ini belum tentu akan digunakan pada kemudian hari, akan tetapi pengalaman yang dialami selama menjalani proses itu lah yang penting untuk perkembangan diri.
2. Materi Kelas
Materi kelas minggu ini kembali mencakupi pembelajaran ANN dan juga langsung dipraktekkan oleh Asisten Dosen Bang Timo dan Bang Edo. kami diajarkan bagaimana me-running ANN tersebut untuk memproses data CFD yang kami miliki sebelumnya.
Hasil dapat dilihat disini Kelompok 12
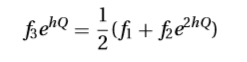
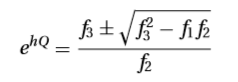
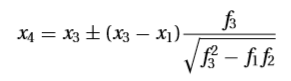
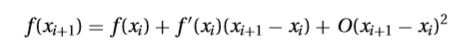
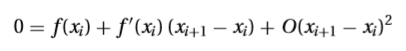
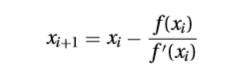
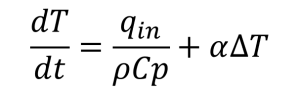

Enable comment auto-refresher
RyansonJ
Permalink |
Elvin
Stefanus.nandiwardhana
Permalink |