Difference between revisions of "Kevin Kameswara"
| (16 intermediate revisions by 2 users not shown) | |||
| Line 15: | Line 15: | ||
== Kegiatan pada Selasa, 10 September 2019 == | == Kegiatan pada Selasa, 10 September 2019 == | ||
| − | * Mempelajari dasar-dasar algoritma untuk kalkulator sinus, cosinus, dan e^x dengan menggunakan pseudocode | + | * Mempelajari dasar-dasar algoritma untuk kalkulator sinus, cosinus, dan e^x dengan menggunakan pseudocode. |
| + | * Pseudo code adalah algoritma dasar untuk dijadikan dasar(atau diterjemahkan) ke dalam berbagai macam bahasa pemrograman, seperti C++, python, atau pascal. | ||
| + | * Semakin dasar suatu kode, semakin panjang kodenya, namun semakin dekat bahasa tersebut dengan bahasa mesin (1 dan 0), semakin tinggi bahasa, semakin mudah dan pendek namun semakin jauh dari bahasa mesin. | ||
| + | * Bahasa tingkat 1 adalah bahasa mesin, bahasa tingkat 3 contohnya adalah C++, dan bahasa tingkat 4 contohnya adalah python. | ||
| + | * Value/Nilai dari suatu bahasa untuk dipelajari adalah tingkat kompatibilitasnya, semakin sering digunakan suatu bahasa dalam operasi-operasi, semakin berharga suatu bahasa untuk dipelajari. C++ dipakai di kelas ini salah satunya adalah karena kompatibel dengan ANSYS. | ||
| + | * Contoh dari pseudocode untuk sinus adalah : | ||
| + | suku = x <br> | ||
| + | sin = suku <br> | ||
| + | i = 1 <br> | ||
| + | er = 1 <br> | ||
| + | while er > 1/10000000: | ||
| + | rat = -x**2/(2*i)/(2*i+1) <br> | ||
| + | suku = suku*rat <br> | ||
| + | er = suku/sin <br> | ||
| + | if er > 0: <br> | ||
| + | er = er <br> | ||
| + | else: <br> | ||
| + | er = er*(-1) <br> | ||
| + | sin = sin + suku <br> | ||
| + | i = i + 1 <br> | ||
| + | |||
| + | * Dikelas juga di minta untuk menerjemahkan pseudocode tersebut kedalam kode. | ||
| + | * Kode sinus dalam bahasa python: | ||
| + | def sine(x): <br> | ||
| + | suku = x <br> | ||
| + | sin = suku <br> | ||
| + | i = 1 <br> | ||
| + | er = 1 <br> | ||
| + | while er > 1/10000000: <br> | ||
| + | rat = -x**2/(2*i)/(2*i+1) <br> | ||
| + | suku = suku*rat <br> | ||
| + | er = suku/sin <br> | ||
| + | if er > 0: <br> | ||
| + | er = er <br> | ||
| + | else: <br> | ||
| + | er = er*(-1) <br> | ||
| + | sin = sin + suku <br> | ||
| + | i = i + 1 <br> | ||
| + | print(sin) <br> | ||
| + | return sin <br> | ||
| + | [[File:Kode sin.png]] | ||
| + | |||
| + | ==Kegiatan pada Selasa, 17 September 2019== | ||
| + | *Belajar mengenai turunan numerik | ||
| + | *Turunan numerik bisa di nyatakan sebagai: | ||
| + | turunan = (f(x + x*e-6) - f(x))/(x*e-6) <br> | ||
| + | """contoh""" <br> | ||
| + | turunansine30 = (sine(30+30*(10**(-10)) - sine(30))/(30*10**(-10)) <br> | ||
| + | ==Kegiatan pada Selasa, 1 Oktober 2019== | ||
| + | *Truncation error adalah error karena pemotongan deret taylor | ||
| + | *pendekatan dy/dx mendekati deltay/deltax menghasilkan truncation error. | ||
| + | *Artinya dy/dx = Deltay/Deltax + Truncation error | ||
| + | *misalkan kkita ingain menghitung nilai y diantara x 1 = 0 dan x 2 = 1000 | ||
| + | *misalnya delta x = 1000, maka ada 1 mesh | ||
| + | *misakan Delta x nya samadengan 500, maka ada 2 mesh | ||
| + | *misalkan delta x nya sama dengan 10, maka ada 100 mesh | ||
| + | *oke, misalkan meshnya sangat banyak, delta x makin kecil, maka truncation error semakin kecil, karena pemotongan deret taylor semakin sedikit | ||
| + | *Tapi karena banyak mesh yang harus dihitung, maka jumlah pembulatan akan semakin banyak, maka error pembulatan akan semakin besar. Maka Rounding Error semakin besar | ||
| + | *Bila ditarik garis rounding error dan truncation error, maka titik potong antara 2 garis tersebut merupakan jumlah mesh optimal, dengan total error tersedikit. | ||
| + | *Konfirmasi metode numerik dapat dilakukan apabila terjadi kecenderungan yang sama antara hasil numerik dan hasil eksperimen. | ||
| + | |||
| + | |||
| + | == Kegiatan kelas Selasa, 29 Oktober 2019 == | ||
| + | *Mempelajari dasar-dasar Bahasa pemrograman python seperti operasi matematika dasar, string, modul math dan lain sebagainya | ||
| + | *Membahas sekilas tentang Runge Kutta methods | ||
| + | *Memberikan tugas untuk mencari waktu yang dibutuhkan oleh sebuah mobil dengan spesifikasi tertentu untuk mencapai kecepatan maksimumnya, diberikan spesifikasi motornya. | ||
| + | *Hasil diskusi kami adalah: <br> | ||
| + | 1. Gaya eksternal yang bekerja adalah gaya berat, gaya kontak 2 roda belakang, gaya kontak 2 roda depan, gaya gesek 2 roda belakang sebagai penggerak, gaya gesek 2 roda depan sebagai penghambat dan gaya Drag aerodinamik. <br> | ||
| + | 2. Analisa 2 Dimensi <br> | ||
| + | 3. Hitungan 2 roda dijadikan 1, misalnya gaya 2 roda belakang diwakilkan menjadi fb <br> | ||
| + | 4. Titik nol adalah titik kontak antara roda belakang mobil dan jalan <br> | ||
| + | 5. kemiringan jalan dianggap nol <br> | ||
| + | 6. Gaya berat W bekerja pada pusat massa yang terletak X secara horizontaldan Y secara vertical dari titik 0. <br> | ||
| + | 7. Gaya gesek roda depan bekerja pada titik kontak antara roda depan dengan tanah dan dipengaruhi oleh koefisien gesek static ban-tanah dan koefisien gesek bearing. Kedua koefisien tersebut dianggap konstan. <br> | ||
| + | 8. Gaya drag bekerja pada pusat massa, dipengaruhi oleh konstanta drag Cd, yang diasumsikan konstan <br>. | ||
| + | 9. Segala integral yang dilakukan dilakukan dengan cara penjumlahan Riemann. <br> | ||
| + | |||
| + | [[File:Pr Metnum 1_1.jpg]] | ||
| + | [[File:Pr Metnum 1 2 Kevin.jpg]] | ||
| + | ok <br> | ||
| + | kedua gambar terseb akan dijelaskan dengan kode berikut:<br> | ||
| + | kode:<br> | ||
| + | def fbx(gef,gr,T,R): | ||
| + | Fb = gef*gr*T/R | ||
| + | return Fb | ||
| + | #Gef = total gear ratio efficiancy | ||
| + | #gr = gear ratio | ||
| + | #T = engine torque | ||
| + | #R = rearwheel radius | ||
| + | #fbx = friction force of 2 rearwheels | ||
| + | |||
| + | def alpha(gef,gr,T,R,x,L,ub,us,W): | ||
| + | fbx = fbx(gef,gr,T,R) | ||
| + | alfa = fbx - (x/L)*us*ub*W | ||
| + | return alfa | ||
| + | |||
| + | # x = jarak horizontal antara roda belakang dan pusat massa | ||
| + | # L = jarak antara roda depan dan roda belakang | ||
| + | # ub = koefisien gesek bearing roda depan (dianggap konstan) | ||
| + | # us = koefisien gesek statis ban dan jalan (dianggap konstan) | ||
| + | # W = berat mobil (Newton) | ||
| + | |||
| + | def beta(ub,us,y,L,ro,A,Cd): | ||
| + | bet = (ub*us*y/L + 1)*0.5*ro*A*Cd | ||
| + | return bet | ||
| + | |||
| + | # y = jarak vertikal antara roda belakang dan pusat massa | ||
| + | # ro * massa jenis udara | ||
| + | # A = area efektif dari mobil tersebut | ||
| + | # Cd = konstanta drag (dianggap konstan) | ||
| + | |||
| + | def vmax(gef,gr,T,R,x,L,ub,us,W,y,ro,A,Cd): | ||
| + | vamx = (beta(ub,us,y,L,ro,A,Cd)/alpha(gef,gr,T,R,x,L,ub,us,W))**0.5 | ||
| + | return vamx | ||
| + | |||
| + | #Vmax adalah kecepatan maksimal | ||
| + | #berdasarkan gambar di foto, waktu yang dibutuhkan untuk mencapai kecepatan maksimum adalah bentuk integral | ||
| + | #Fungsi integral tersebut akan dideakati dengan metode jumlah Riemann | ||
| + | |||
| + | def tmax(gef,gr,T,R,x,L,ub,us,W,y,ro,A,Cd): | ||
| + | m = W/9.8 | ||
| + | V = 0 | ||
| + | Vmaks = vmax(gef,gr,T,R,x,L,ub,us,W,y,ro,A,Cd) | ||
| + | alf = alpha(gef,gr,T,R,x,L,ub,us,W) | ||
| + | beet = beta(ub,us,y,L,ro,A,Cd) | ||
| + | T = 0 | ||
| + | h = (Vmax - V)/10000 | ||
| + | while V != Vmax: | ||
| + | T = T + m/(alf-beet*(V**2)) | ||
| + | V = V + h | ||
| + | return T | ||
| + | |||
| + | == Tugas Video 1 == | ||
| + | *Kode dibuat dengan asumsi bahwa pusat massa mobil terletak di tengah-tengah antara kiri dan kanan mobil | ||
| + | *Asumsi berikutnya adalah konstanta drag independen terhadap kecepatan mobil | ||
| + | *Kemudian koefisien gesek total pada roda depan mobil independen terhadap kecepatan mobil | ||
| + | *Mobil berjalan lurus, tidak sedang menanjak atau menurun | ||
| + | *Karena grafik yang dihasilkan berupa asimtot, maka waktu yang ditempuh di set menjadi ketika v = 98% dari v maksimal, di video dijelaskan bahwa waktu nya sangat besar sekali, itu disebabkan karena fungsinya membentuk asimtot di v = vmax. | ||
| + | * Notes : kode di video belum diubah menjadi 98% sehingga waktu yang di hasilkan sangat besar. | ||
| + | * Penjelasan berikutnya dapat dilihat di foto yang terlampir | ||
| + | [[File:Turunan 1 1.png|200px|thumb|center|Halaman 1 dan 2]] | ||
| + | [[File:Turunan 1 2.png|200px|thumb|center|Halaman 3 dan 4]] | ||
| + | [[File:Turunan 1 3.png|200px|thumb|center|Halaman 5 dan 6]] | ||
| + | [[File:Python_1_1.png|200px|thumb|right|python Halaman 1]] | ||
| + | [[File:Python_1_2.png|200px|thumb|right|python Halaman 2]] | ||
| + | [[File:Python_1_3.png|200px|thumb|right|python Halaman 3]] | ||
| + | [[File:Vspeed.mp4]] | ||
| + | |||
| + | |||
| + | ==5 November 2019, analysis kecepatan maksimum dengan Cd(V) == | ||
| + | * Menganalisa Cd untuk beberapa jenis kecepatan (biasanya linear) di CFD | ||
| + | * Kemudian plot di Microsoft Excel untuk di lakukan regresi linear | ||
| + | *Dari regresi linear tersebut didapatkan persamaan. Persamaan tersebut kemudian dimasukkan ke persamaan turunan F terhadap V. | ||
| + | * Selanjutnya persamaan dF/dV tersebut di Runge-Kutta, plot grafik dan bisa didapatkan hasilnya | ||
| + | |||
| + | |||
| + | ==19 November 2019, Optimasi sudut pesawat == | ||
| + | *GUnakan CFD untuk iterasi Drag dari sudut 1 hingga 15 (karena stall terjadi pada sudut kurang dari 15, sehingga iterasi lebih dari 15 menjadi sia sia) | ||
| + | *Masukkan data data CFD kedalam excel untuk di regresi. | ||
| + | * Optimasi. Dalam hal ini kelompok kami menggunakan golden rule section. Mengapa golden rule section? karena metode ini lebih superior dibandingkan metode turunan=0 maupun metode newton karena metode ini tidak akan terkecoh dengan titik ekstrim lokal, namun fokus pada titik ekstrim universal pada rentang yang ditentukan. | ||
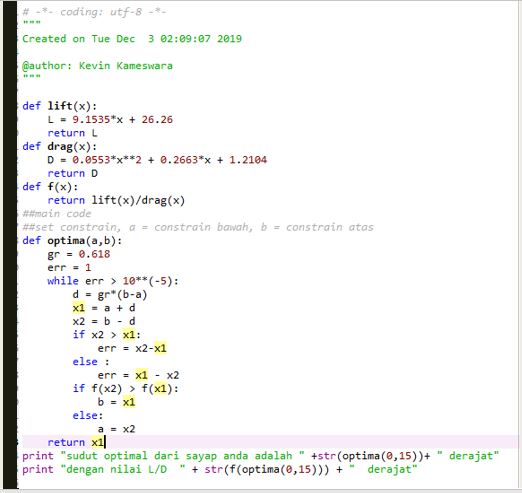
| + | [[File:Kode.JPG]] | ||
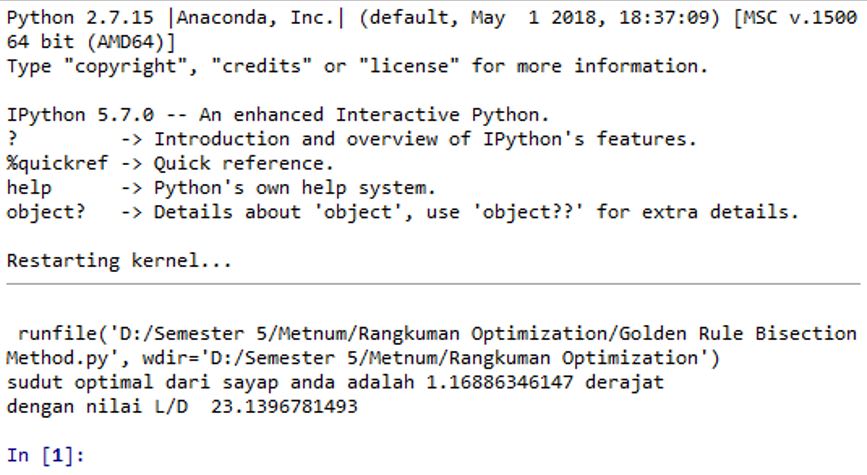
| + | [[File:Hasilkod.JPG]] | ||
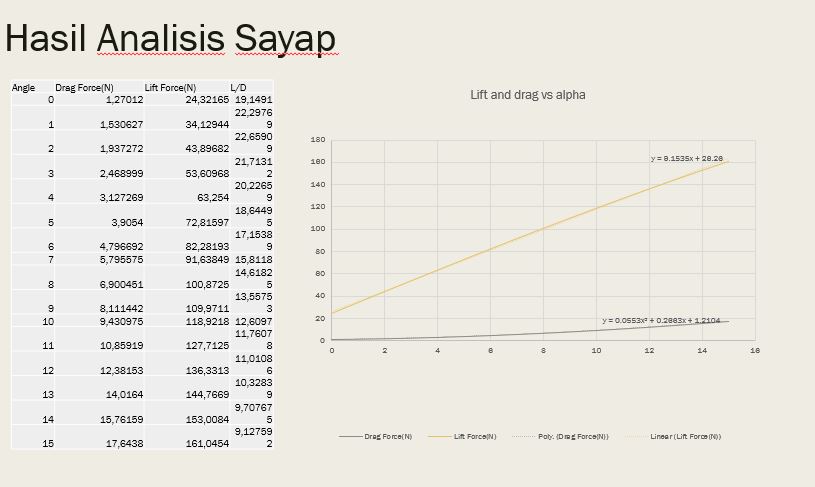
| + | [[File:Grafikod.JPG]] | ||
Latest revision as of 05:31, 17 December 2019
Contents
- 1 Profil
- 2 Kegiatan pada Selasa, 3 September 2019
- 3 Kegiatan pada Selasa, 10 September 2019
- 4 Kegiatan pada Selasa, 17 September 2019
- 5 Kegiatan pada Selasa, 1 Oktober 2019
- 6 Kegiatan kelas Selasa, 29 Oktober 2019
- 7 Tugas Video 1
- 8 5 November 2019, analysis kecepatan maksimum dengan Cd(V)
- 9 19 November 2019, Optimasi sudut pesawat
Profil
- Nama : Kevin Kameswara
- NPM : 1706036596
Kegiatan pada Selasa, 3 September 2019
- Membahas ulang tentang taylor series
- Memperjelas bagaimana aplikasi taylor series untuk penghitungan numerik:
- menjelaskan ulang secara detail bagaimana taylor series bekerja seperti apa itu dan bagaimana kerja dari suku, radius, error, dan significant number.
- menjelaska bahwa apabila kita ingin mendapatkan ketelitian sebanyak N significant number maka kita harus menjalankan taylor series hingga sampai ke suku dengan error ber order -(N+1). Sebenarnya -N saja sudah cukup, hanya sebaiknya -(N+1)
- mahasiswa diminta untuk mencari nilai dari sin pi/7 dengan menggunakan kalkulator yang dibuat sendiri menggunakan taylor series yang dikomputasi menggunakan microsoft excel. Caranya adalah dengan pertama mengerjakan terlebih dahulu taylor series dengan pulpen hingga suku ke enam, kemudian didapatkan bahwa setengah dari mereka adalah nol, karena sinusoidal. Kemudian fungsi dirapihkan dan didapatkan 3 suku. 3 suku tersebut dilihat pola nya, suku kedua adalah r2*suku pertama, dan suku ketiga adalah r3*suku kedua. r2 dan r3 berhubungan satu sama lain, kemudian dari hubugnan tersebut dapat dicari nilai r yang merupakan fungsi dari suku. Kemudian fungsi-fungsi tersebut dimasukkan ke dalam excel untuk dikomputasi. Dibuat kolom i, x(yang merupakan pi/7 untuk semua i), suku, fungsi dan error. i merupakan suku ke berapa,fungsi di dapat dengan menambahkan fungsi n-1 dengan suku n. Fungsi juga merupakan penjumlahan seluruh suku hingga suku tersebut. Suku n merupakan suku n-1*r(dari suku tersebut). r merupakan fungsi dari i.
- setelah selesai, sebagai pekerjaan rumah, mahasiswa diminta melakukan hal serupa kepada fungsi cosinus x dan fungsi e^x.
- mahasiswa juga diminta mengerjakan diary sebagai pekerjaan rumah.
Kegiatan pada Selasa, 10 September 2019
- Mempelajari dasar-dasar algoritma untuk kalkulator sinus, cosinus, dan e^x dengan menggunakan pseudocode.
- Pseudo code adalah algoritma dasar untuk dijadikan dasar(atau diterjemahkan) ke dalam berbagai macam bahasa pemrograman, seperti C++, python, atau pascal.
- Semakin dasar suatu kode, semakin panjang kodenya, namun semakin dekat bahasa tersebut dengan bahasa mesin (1 dan 0), semakin tinggi bahasa, semakin mudah dan pendek namun semakin jauh dari bahasa mesin.
- Bahasa tingkat 1 adalah bahasa mesin, bahasa tingkat 3 contohnya adalah C++, dan bahasa tingkat 4 contohnya adalah python.
- Value/Nilai dari suatu bahasa untuk dipelajari adalah tingkat kompatibilitasnya, semakin sering digunakan suatu bahasa dalam operasi-operasi, semakin berharga suatu bahasa untuk dipelajari. C++ dipakai di kelas ini salah satunya adalah karena kompatibel dengan ANSYS.
- Contoh dari pseudocode untuk sinus adalah :
suku = x
sin = suku
i = 1
er = 1
while er > 1/10000000: rat = -x**2/(2*i)/(2*i+1)
suku = suku*rat
er = suku/sin
if er > 0:
er = er
else:
er = er*(-1)
sin = sin + suku
i = i + 1
- Dikelas juga di minta untuk menerjemahkan pseudocode tersebut kedalam kode.
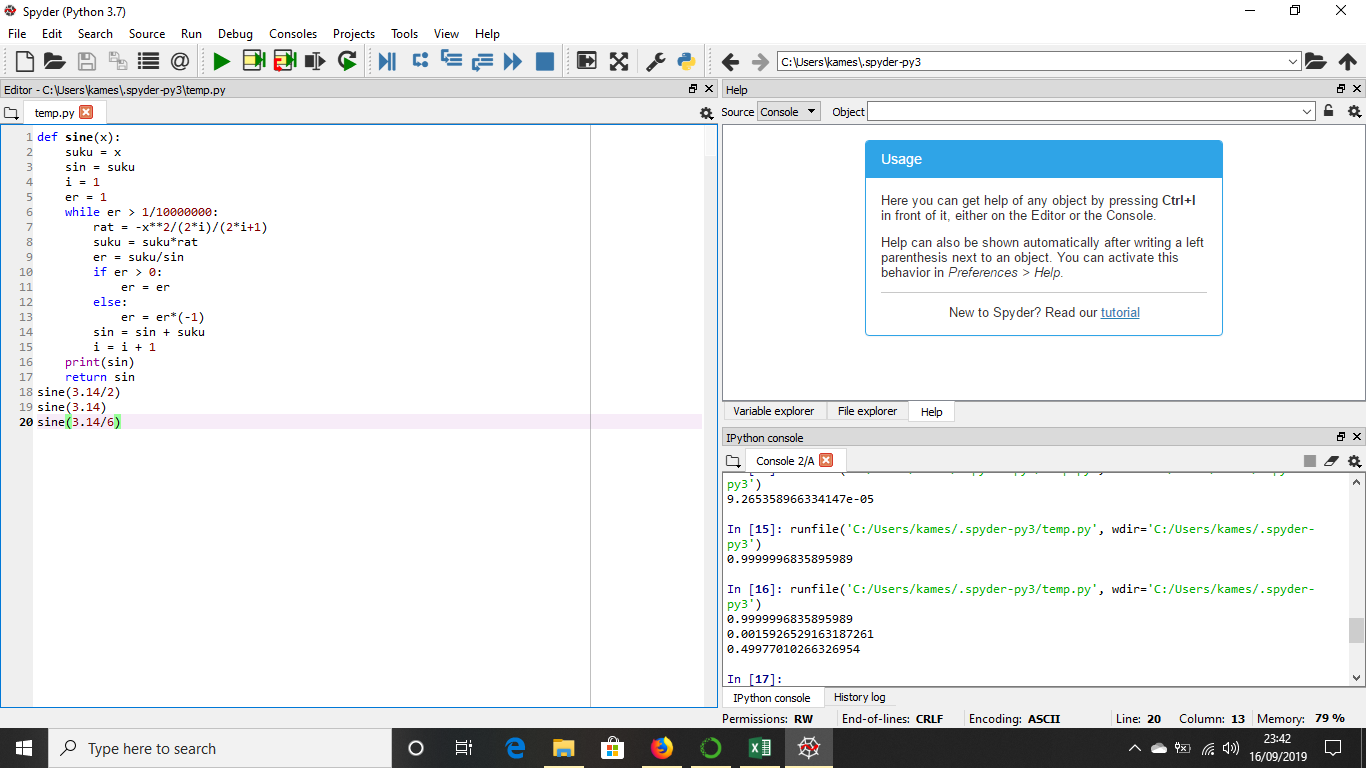
- Kode sinus dalam bahasa python:
def sine(x):
suku = x
sin = suku
i = 1
er = 1
while er > 1/10000000:
rat = -x**2/(2*i)/(2*i+1)
suku = suku*rat
er = suku/sin
if er > 0:
er = er
else:
er = er*(-1)
sin = sin + suku
i = i + 1
print(sin)
return sin
Kegiatan pada Selasa, 17 September 2019
- Belajar mengenai turunan numerik
- Turunan numerik bisa di nyatakan sebagai:
turunan = (f(x + x*e-6) - f(x))/(x*e-6)
"""contoh"""
turunansine30 = (sine(30+30*(10**(-10)) - sine(30))/(30*10**(-10))
Kegiatan pada Selasa, 1 Oktober 2019
- Truncation error adalah error karena pemotongan deret taylor
- pendekatan dy/dx mendekati deltay/deltax menghasilkan truncation error.
- Artinya dy/dx = Deltay/Deltax + Truncation error
- misalkan kkita ingain menghitung nilai y diantara x 1 = 0 dan x 2 = 1000
- misalnya delta x = 1000, maka ada 1 mesh
- misakan Delta x nya samadengan 500, maka ada 2 mesh
- misalkan delta x nya sama dengan 10, maka ada 100 mesh
- oke, misalkan meshnya sangat banyak, delta x makin kecil, maka truncation error semakin kecil, karena pemotongan deret taylor semakin sedikit
- Tapi karena banyak mesh yang harus dihitung, maka jumlah pembulatan akan semakin banyak, maka error pembulatan akan semakin besar. Maka Rounding Error semakin besar
- Bila ditarik garis rounding error dan truncation error, maka titik potong antara 2 garis tersebut merupakan jumlah mesh optimal, dengan total error tersedikit.
- Konfirmasi metode numerik dapat dilakukan apabila terjadi kecenderungan yang sama antara hasil numerik dan hasil eksperimen.
Kegiatan kelas Selasa, 29 Oktober 2019
- Mempelajari dasar-dasar Bahasa pemrograman python seperti operasi matematika dasar, string, modul math dan lain sebagainya
- Membahas sekilas tentang Runge Kutta methods
- Memberikan tugas untuk mencari waktu yang dibutuhkan oleh sebuah mobil dengan spesifikasi tertentu untuk mencapai kecepatan maksimumnya, diberikan spesifikasi motornya.
- Hasil diskusi kami adalah:
1. Gaya eksternal yang bekerja adalah gaya berat, gaya kontak 2 roda belakang, gaya kontak 2 roda depan, gaya gesek 2 roda belakang sebagai penggerak, gaya gesek 2 roda depan sebagai penghambat dan gaya Drag aerodinamik.
2. Analisa 2 Dimensi
3. Hitungan 2 roda dijadikan 1, misalnya gaya 2 roda belakang diwakilkan menjadi fb
4. Titik nol adalah titik kontak antara roda belakang mobil dan jalan
5. kemiringan jalan dianggap nol
6. Gaya berat W bekerja pada pusat massa yang terletak X secara horizontaldan Y secara vertical dari titik 0.
7. Gaya gesek roda depan bekerja pada titik kontak antara roda depan dengan tanah dan dipengaruhi oleh koefisien gesek static ban-tanah dan koefisien gesek bearing. Kedua koefisien tersebut dianggap konstan.
8. Gaya drag bekerja pada pusat massa, dipengaruhi oleh konstanta drag Cd, yang diasumsikan konstan
.
9. Segala integral yang dilakukan dilakukan dengan cara penjumlahan Riemann.

 ok
ok
kedua gambar terseb akan dijelaskan dengan kode berikut:
kode:
def fbx(gef,gr,T,R):
Fb = gef*gr*T/R return Fb
- Gef = total gear ratio efficiancy
- gr = gear ratio
- T = engine torque
- R = rearwheel radius
- fbx = friction force of 2 rearwheels
def alpha(gef,gr,T,R,x,L,ub,us,W):
fbx = fbx(gef,gr,T,R) alfa = fbx - (x/L)*us*ub*W return alfa
- x = jarak horizontal antara roda belakang dan pusat massa
- L = jarak antara roda depan dan roda belakang
- ub = koefisien gesek bearing roda depan (dianggap konstan)
- us = koefisien gesek statis ban dan jalan (dianggap konstan)
- W = berat mobil (Newton)
def beta(ub,us,y,L,ro,A,Cd):
bet = (ub*us*y/L + 1)*0.5*ro*A*Cd return bet
- y = jarak vertikal antara roda belakang dan pusat massa
- ro * massa jenis udara
- A = area efektif dari mobil tersebut
- Cd = konstanta drag (dianggap konstan)
def vmax(gef,gr,T,R,x,L,ub,us,W,y,ro,A,Cd):
vamx = (beta(ub,us,y,L,ro,A,Cd)/alpha(gef,gr,T,R,x,L,ub,us,W))**0.5 return vamx
- Vmax adalah kecepatan maksimal
- berdasarkan gambar di foto, waktu yang dibutuhkan untuk mencapai kecepatan maksimum adalah bentuk integral
- Fungsi integral tersebut akan dideakati dengan metode jumlah Riemann
def tmax(gef,gr,T,R,x,L,ub,us,W,y,ro,A,Cd):
m = W/9.8
V = 0
Vmaks = vmax(gef,gr,T,R,x,L,ub,us,W,y,ro,A,Cd)
alf = alpha(gef,gr,T,R,x,L,ub,us,W)
beet = beta(ub,us,y,L,ro,A,Cd)
T = 0
h = (Vmax - V)/10000
while V != Vmax:
T = T + m/(alf-beet*(V**2))
V = V + h
return T
Tugas Video 1
- Kode dibuat dengan asumsi bahwa pusat massa mobil terletak di tengah-tengah antara kiri dan kanan mobil
- Asumsi berikutnya adalah konstanta drag independen terhadap kecepatan mobil
- Kemudian koefisien gesek total pada roda depan mobil independen terhadap kecepatan mobil
- Mobil berjalan lurus, tidak sedang menanjak atau menurun
- Karena grafik yang dihasilkan berupa asimtot, maka waktu yang ditempuh di set menjadi ketika v = 98% dari v maksimal, di video dijelaskan bahwa waktu nya sangat besar sekali, itu disebabkan karena fungsinya membentuk asimtot di v = vmax.
- Notes : kode di video belum diubah menjadi 98% sehingga waktu yang di hasilkan sangat besar.
- Penjelasan berikutnya dapat dilihat di foto yang terlampir
5 November 2019, analysis kecepatan maksimum dengan Cd(V)
- Menganalisa Cd untuk beberapa jenis kecepatan (biasanya linear) di CFD
- Kemudian plot di Microsoft Excel untuk di lakukan regresi linear
- Dari regresi linear tersebut didapatkan persamaan. Persamaan tersebut kemudian dimasukkan ke persamaan turunan F terhadap V.
- Selanjutnya persamaan dF/dV tersebut di Runge-Kutta, plot grafik dan bisa didapatkan hasilnya
19 November 2019, Optimasi sudut pesawat
- GUnakan CFD untuk iterasi Drag dari sudut 1 hingga 15 (karena stall terjadi pada sudut kurang dari 15, sehingga iterasi lebih dari 15 menjadi sia sia)
- Masukkan data data CFD kedalam excel untuk di regresi.
- Optimasi. Dalam hal ini kelompok kami menggunakan golden rule section. Mengapa golden rule section? karena metode ini lebih superior dibandingkan metode turunan=0 maupun metode newton karena metode ini tidak akan terkecoh dengan titik ekstrim lokal, namun fokus pada titik ekstrim universal pada rentang yang ditentukan.