Difference between revisions of "Jonathan Surya"
(→Minggu kesebelas 4 Desember 2019) |
|||
| (52 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
Nama :Jonathan Surya | Nama :Jonathan Surya | ||
| Line 12: | Line 8: | ||
== '''Minggu Pertama (4 September)''' == | == '''Minggu Pertama (4 September)''' == | ||
| − | + | Pada minggu pertama Pak Dai dan Pak Radon menjelaskan akan pentingnya pemrograman dan teknik mesin merupakan salah satu yang memperlajarinya. | |
'''Kenapa anak mesin harus belajar kalkulus?''' | '''Kenapa anak mesin harus belajar kalkulus?''' | ||
| Line 36: | Line 32: | ||
== Minggu kedua (11 september) == | == Minggu kedua (11 september) == | ||
| − | + | Pada Minggu kedua Pak Dai menjelaskan bahwa seberapa penting machine learning yang berkembang saat ini salah satu contohnya google search engine. | |
| + | |||
| + | menurut Pak Dai Industry 5.0 adalah dasar-dasar pancasila karena teknologi merupakan ciptaan manusia dan sebisa mungkin empowering to human juga agar setiap teknologi yang kita buat dapat membantu sesama. | ||
| + | |||
| + | |||
| + | Artificial Intelligence atau disebut rekayasa buatan yang dibuat oleh manusia. Namun pemilik kepintaran sesungguhnya adalah manusia. hal tersebut dubuat dengan tujuan untuk membantu sesama karena keterbatasan manusia juga. | ||
| + | |||
| + | Pembelajaran minggu kedua mempelajari cara penggunaan Software Python dimana kita membuat coding Hello Python world dan mempelajari dasar dasar coding seperti tuples dan list. untuk mempelajari lebih banyak lagi dapat melalui python anywhere. | ||
| + | |||
| + | [[File:List and tuples 1.JPG]] | ||
Minggu depan tgl 18 sept Quiz bab 1 pemrograman jam 4 sore | Minggu depan tgl 18 sept Quiz bab 1 pemrograman jam 4 sore | ||
| + | |||
| + | == Minggu ketiga (18 september) == | ||
| + | |||
| + | Pada pertemuan ketiga diadakan quiz dasar-dasar pemrograman. Soal quiz membuat algoritma dengan bahasa sendiri,flowchart dan pythonnya untuk suku ke-n dari sebuah bilangan fibronacci yang dimulai dari 1,1,2,3,5,8,.... | ||
| + | |||
| + | untuk soal tersebut dapat diselesaikan dengan 2 cara yaitu function dan loop dengan While Condition | ||
| + | |||
| + | Metode Function | ||
| + | |||
| + | [[File:Function Fibonacci Josur.JPG]] | ||
| + | |||
| + | |||
| + | |||
| + | Metode Loop dengan While Condition | ||
| + | |||
| + | [[File:While loop Fibonacci Josur.JPG]] | ||
| + | |||
| + | == Minggu keempat (25 september) == | ||
| + | |||
| + | |||
| + | Pada pertemuan keempat mempelajari Computer modelling yang terdiri dari computation dan modelling. Modelling sendiri adalah sebuah representasi/simplifikasi/asumsi dari suatu yang bersifat rumit menjadi lebih mudah untuk dipahami. namun tidak sepenuhnya 100 persen sama dari aslinya karena suatu pendekatan saja. | ||
| + | |||
| + | |||
| + | Contoh mechanical modelling yang dapat digunakan dalam Computer modelling adalah | ||
| + | tekanan atau stress= F/A, | ||
| + | elastisitas adalah laju perubahan bentuknya. | ||
| + | oleh karena itu kasus engineering dapat diselesaikan dengan metode numerik | ||
| + | |||
| + | |||
| + | |||
| + | Pr untuk minggu depan menyusun kesetimbangan 4 titik sehingga mendapatkan fungsi aljabar linearnya displacementnya yang terjadi. diskritisasi membuat menjadi titik tak hingga | ||
| + | |||
| + | == Minggu kelima (2 Oktober) == | ||
| + | |||
| + | Pada pertemuan kelima. Asistensi dari asisten mengenai dasar cara kerja eliminasi gauss jordan dalam pengaplikasiannya dalam sistem pegas dimana codingnya dapat dibuat menggunakan import from numpy yang bersifat lebih simple dan menghemat proses penghitungan juga dalam python. Efisiensi pemograman adalah dimana program yang memiliki fungsi yang sama dapat dihasilkan dengan penulisan coding yang lebih sedikit. | ||
| + | |||
| + | pada dasarnya NUMPY, SYMPY dll merupakan suatu external library yang dapat didownload dimana didalamnya sudah terbuat codingan yang dinginkan untuk dipakai sehingga tidak perlu membuat codingan dari awal lagi. | ||
| + | |||
| + | hanya menuliskan Import from sympy fibronacci. lalu data fibronacci pun bisa langsung diproses | ||
| + | |||
| + | |||
| + | Pr untuk minggu depan membaca bab 4 dan membuat rangkuman | ||
| + | |||
| + | == Minggu keenam (9 Oktober) == | ||
| + | |||
| + | merefrensikan kasus fisik yang dapat direferensikan ke komputer. | ||
| + | peran engineer bagimana punya skill untuk memodelkannya. Metode direct kesetimbangan gaya (hukum dasar). sebuah persamaan matematika | ||
| + | orang yang punya wawasannya futuristik. | ||
| + | there is a god | ||
| + | masalah atau benda yang kita hitung ketika terkena beban untuk mendapatkan area criticalnya untuk dilakukan upgrade. | ||
| + | semua rumus dimesin dianggap continu atau berdislokasi atau berpindah tempat. displacement adanya perpindahan tempat | ||
| + | diferensial | ||
| + | |||
| + | == Minggu ketujuh (16 Oktober) == | ||
| + | |||
| + | Codingan Quiz 2 | ||
| + | exercise 7.1 no 2 hal 253 | ||
| + | |||
| + | J0 = input("masukan nilai x0 possitif = ") | ||
| + | K0 = input ("masukan nilai y0 positif = ") | ||
| + | N0 = input("masukan nilai count number biasayanya 1 = ") | ||
| + | def F(x, y): | ||
| + | return (x**2 - 4*y) | ||
| + | def rungeKutta(x0, y0, h): | ||
| + | n = int(N0) | ||
| + | #mendefinisikan y= y0 | ||
| + | y = y0 | ||
| + | for i in range(1, n + 1): | ||
| + | "Apply Runge Kutta Formulas to find next value of y" | ||
| + | k1 = h * F(x0, y) | ||
| + | k2 = h * F(x0 + 0.5 * h, y + 0.5 * k1) | ||
| + | k3 = h * F(x0 + 0.5 * h, y + 0.5 * k2) | ||
| + | k4 = h * F(x0 + h, y + k3) | ||
| + | |||
| + | # Update next value of y | ||
| + | y = y + (1.0 / 6.0) * (k1 + 2 * k2 + 2 * k3 + k4) | ||
| + | |||
| + | # Update next value of x | ||
| + | x0 = x0 + h | ||
| + | return y | ||
| + | |||
| + | # misalkan : | ||
| + | x0 = int(J0) | ||
| + | y = int(K0) | ||
| + | h = 0.2 | ||
| + | print('The value of y at x is:', rungeKutta(x0, y, h)) | ||
| + | |||
| + | exercise bab 2.1 no 6 hal 55 | ||
| + | import numpy | ||
| + | a = [[0, 0, 2, 1, 2], | ||
| + | [0, 1, 0, 2, -1], | ||
| + | [1, 2, 0, -2, 0], | ||
| + | [0, 0, 0, -1, 1], | ||
| + | [0, 1, -1, 1, -1]] | ||
| + | |||
| + | b = [[1], | ||
| + | [1], | ||
| + | [-4], | ||
| + | [-2], | ||
| + | [-1]] | ||
| + | |||
| + | c = [1, 1, 1, 1, 1,] | ||
| + | n = len(b) | ||
| + | |||
| + | # Elimination | ||
| + | for k in range(0, n - 1): | ||
| + | for i in range(n - 1, k, -1): | ||
| + | if a[i][k] != 0.0: | ||
| + | op = a[i][k] / a[i - 1][k] | ||
| + | b[i][0] = b[i][0] - op * b[i - 1][0] | ||
| + | for f in range(0, n): | ||
| + | a[i][f] = a[i][f] - op * a[i - 1][f] | ||
| + | |||
| + | # Subtitution | ||
| + | if a[n - 1][n - 1] != 0: | ||
| + | c[n - 1] = b[n - 1][0] / a[n - 1][n - 1] | ||
| + | else: | ||
| + | c[n - 1] = 0 | ||
| + | for i in range(n - 2, -1, -1): | ||
| + | sigma = 0 | ||
| + | for k in range(0, n, 1): | ||
| + | y = a[i][k] * c[k] | ||
| + | sigma = sigma + y | ||
| + | sigma = sigma - a[i][i] | ||
| + | if a[i][i] != 0: | ||
| + | c[i] = (b[i][0] - sigma) / a[i][i] | ||
| + | else: | ||
| + | a[i][i] = 0 | ||
| + | |||
| + | for v in range(0, n, 1): | ||
| + | print(a[v]) | ||
| + | print(c[0:n]) | ||
| + | |||
| + | namun masih error pada EGJ | ||
| + | |||
| + | == UTS == | ||
| + | '''Hari: Rabu, 23 Oktober 2019''' | ||
| + | |||
| + | '''Oleh : Dr. Ahmad Indra & Dr. Eng. Radon Dhelika''' | ||
| + | |||
| + | Berikut video muhasabah metnum Jonathan Surya | ||
| + | |||
| + | [[File:UTS Muhasabah Jonathan Surya.mp4]] | ||
| + | |||
| + | '''untuk soal 3a''' | ||
| + | |||
| + | from math import | ||
| + | g = 10 | ||
| + | m1 = input("masukan berat massa 1 = ") | ||
| + | m2 = input ("masukan berat massa 2 = ") | ||
| + | m3 = input("masukan berat massa 3 = ") | ||
| + | u1 = input("masukan koef gesek massa 1 = ") | ||
| + | u2 = input("masukan koef gesek massa 2 = ") | ||
| + | u3 = input("masukan koef gesek massa 3 = ") | ||
| + | alfa = input("masukan sudut alfa = ") | ||
| + | a = input("percepatan = ") | ||
| + | x = sin (alfa) | ||
| + | y = cos (alfa) | ||
| + | t1 = m1*g*(x-u1*y) - m1*a | ||
| + | t2 = m2*g*(x-u2*y) + t1 -m2*a | ||
| + | t3 = m3*g*(x-u3*y) + t2 -m3*a | ||
| + | print(t1) | ||
| + | print(t2) | ||
| + | print(t3) | ||
| + | |||
| + | berikut video penjelasan pengerjan soal 3a | ||
| + | |||
| + | [[File:Uts no 3a part 1 Jonathan Surya.mp4]] | ||
| + | |||
| + | [[File:Uts no 3a part 2 Jonathan Surya.mp4]] | ||
| + | |||
| + | '''untuk soal 3b cara 1''' | ||
| + | |||
| + | p udara = 1.1 #massa jenis udara | ||
| + | cd= eval(input("drag coefficient: ")) | ||
| + | area= eval(input("area (m^2): ")) | ||
| + | v0= eval(input("velocity udara: ")) | ||
| + | #masukan nilai yang diketahui pada mobil | ||
| + | mm = eval(input("massa benda/mobil (kg): ")) | ||
| + | g= 9.81 | ||
| + | a = eval(input("percepatan mobil (m/s^2): ")) | ||
| + | v2 = eval(input("kecepatan mobil max (m/s): ")) | ||
| + | v1 = 0 #mobil pada saat diam | ||
| + | #masukan nilai yang diketahui pada F gesek | ||
| + | u = eval(input(" koefisien gesekan: ")) | ||
| + | t = eval(input("waktu dari diam ke gerak(s): ")) | ||
| + | # a drag | ||
| + | ages = g*u | ||
| + | adrag = (cd*area*p udara*v0**2)/2*mm | ||
| + | amobil = a | ||
| + | atot = amobil-(ages+adrag) | ||
| + | t = (v1-v2)/atot | ||
| + | print ("waktu yang diperlukan mobil untuk mencapai kecepatan max (s): ", t) | ||
| + | |||
| + | '''untuk soal 3b cara 2''' | ||
| + | m = eval(input("masukan massa mobil: ")) | ||
| + | g = 10 | ||
| + | p = 1.2 | ||
| + | am = eval(input("percepatan mobil: ")) | ||
| + | Cd = eval(input("koefisien drag: ")) | ||
| + | mu = eval(input("koefisien gesekan: ")) | ||
| + | A = eval(input("area [m^2]: ")) | ||
| + | v0 = eval(input("velocity mobil awal [m/s]: ")) | ||
| + | vf = eval(input("kecepatan mobil max [m/s]: ")) | ||
| + | |||
| + | # total perceptan adalah gabungan dari am, af , ad | ||
| + | Ff = m * g * mu # rumusnya Ff = m * g * mu | ||
| + | Fd = (Cd * A * p * v0 ** 2) / 2 # rumusnya Fd = (Cd * A * p * v0 ** 2) / 2 | ||
| + | a2 = (am) - (Fd / m) - (Ff / m) | ||
| + | def dtdtv(t, y): | ||
| + | return ((m) / (am*g - m * g * mu - 0.5 * Cd * A * p * v0 ** 2)) | ||
| + | t = 0 | ||
| + | h = 0.01 | ||
| + | def rungekutta(v0, t0, vf, h): | ||
| + | n = (int)((vf - v0) / h) | ||
| + | t = t0 | ||
| + | for i in range(1, n + 1): | ||
| + | #rumus Runge kutta | ||
| + | k1 = h * dtdtv(v0, t) | ||
| + | k2 = h * dtdtv(v0 + 0.5 * h, t + 0.5 * k1) | ||
| + | k3 = h * dtdtv(v0 + 0.5 * h, t + 0.5 * k2) | ||
| + | k4 = h * dtdtv(v0 + h, t + k3) | ||
| + | #mendapatkan nilai t yang diperlukan hingga mencapai kecepatan tersebut | ||
| + | t = t + (1.0 / 6.0) * (k1 + 2 * k2 + 2 * k3 + k4) | ||
| + | # nilai Vo | ||
| + | v0 = v0 + h | ||
| + | return t | ||
| + | tfinal = rungekutta(v0, t, vf, h) | ||
| + | print(tfinal) | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | berikut video penjelasan pengerjan soal 3b | ||
| + | |||
| + | [[File:UTS 3b Jonathan Surya.mp4]] | ||
| + | |||
| + | <comments voting="Plus" /> | ||
| + | |||
| + | |||
| + | |||
| + | == Minggu kedelapan 30 Oktober 2019 == | ||
| + | |||
| + | persamaan differensial bola yang di lempar | ||
| + | [[File:Persamaan bola dilempar keatas josur.PNG]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | t = eval(input("pada saat t berapa: ")) | ||
| + | h = 1 #dtnya | ||
| + | # misalkan : | ||
| + | t0 = 0.1 | ||
| + | y0 = eval(input("ketinggian gedung: ")) | ||
| + | def F(t0, y0): | ||
| + | return ((y0 + 5*t*t)/t) | ||
| + | |||
| + | |||
| + | # Finds value of y for a given x using step size h | ||
| + | def rungeKutta(t0, y0, t, h): | ||
| + | # Count number of iterations using step size or | ||
| + | # step height h | ||
| + | n = (int)((t - t0) / h) | ||
| + | #mendefinisikan y= y0 | ||
| + | y = y0 | ||
| + | for i in range(1, n + 1): | ||
| + | "Apply Runge Kutta Formulas to find next value of y" | ||
| + | k1 = h * F(t0, y) | ||
| + | k2 = h * F(t0 + 0.5 * h, y + 0.5 * k1) | ||
| + | k3 = h * F(t0 + 0.5 * h, y + 0.5 * k2) | ||
| + | k4 = h * F(t0 + h, y + k3) | ||
| + | |||
| + | # Update next value of y | ||
| + | y = y + (1.0 / 6.0) * (k1 + 2 * k2 + 2 * k3 + k4) | ||
| + | |||
| + | # Update next value of t | ||
| + | t0 = t0 + h | ||
| + | return y | ||
| + | print('The value of posisi bola at t is:', rungeKutta(t0, y0, t, h)) | ||
| + | |||
| + | |||
| + | [[File:Bola dilempar keatas josur (2).PNG]] | ||
| + | |||
| + | == Minggu kesepuluh 2019 == | ||
| + | pada minggu ini kami mempelajari mengenai CFD solv. contoh yang diambil adalah drag pada mobil yang bergerak. dengan bimbingan bang edo dan bang timo mengenai cara menggunakan softeare | ||
| + | |||
| + | [[File:CFDSOF1.png|700px|thumb|center]] | ||
| + | [[File:CFDSOF2.jpg|700px|thumb|center]] | ||
| + | [[File:CFDSOF3.jpg|700px|thumb|center]] | ||
| + | [[File:CFDSOF4.jpg|700px|thumb|center]] | ||
| + | |||
| + | import,meshing,memasukan initial condition, lalu di import ke paraview dilakukan perhitungan menggunakan fdrag kalkulator dan flift kalkulator | ||
| + | |||
| + | Cfdsof. Input = geometric. Output =IMS. Masuk ke paraview 5.5.4. input= IMS. Output= hasil lift&drag | ||
| + | |||
| + | lalu kita diberi tugas untuk mencari fdrag dari flift dari air foil | ||
| + | |||
| + | == Minggu kesebelas 4 Desember 2019 == | ||
| + | pada minggu ini kami belajar mengenai optimasi untuk mencari nilai optimum dengan meminimal dan maksimal dari suatu fungsi . optimasi aka dibatasi dengan berbagai batas. iterasi salah satu caranya untuk meminimalisir menentukan variabel awalnya | ||
| + | |||
| + | lalu kita diberi tugas untuk mencari nilai optimum dari data fdrag dan flift | ||
| + | |||
| + | Grafik AirFoil Drag Force dan Lift Force | ||
| + | |||
| + | [[File:Grafik Air Foil kelompok 6.PNG|700px|thumb|center]] | ||
| + | |||
| + | Grafik gabungan drag dan lift dari airfoil. Dimana drag force semakin bertambah besar seiring naiknya sudut serang. sedangkan nilai Lift diperoleh optimumnya pada sudut serang 60 | ||
| + | |||
| + | [[File:Grafik Air Foil kelompok 61.png|700px|thumb|center]] | ||
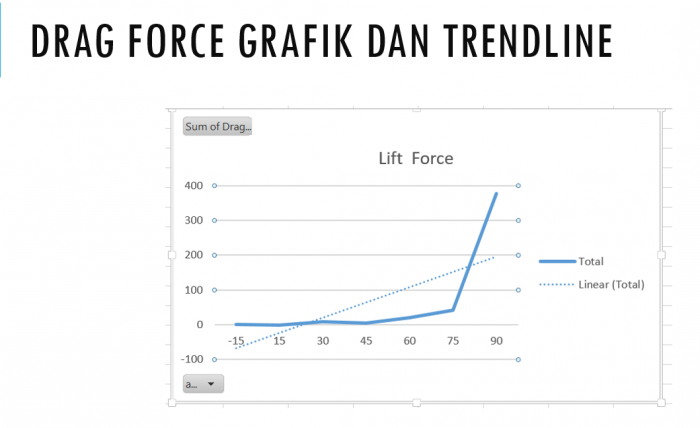
| + | Grafik Drag Force dengan trendline nilai linear y= 43,867x-110,54 | ||
| + | |||
| + | Grafik Drag Force dengan trendline nilai polinomial y= 21,185x^2-125,62x + 143,69 | ||
| + | |||
| + | [[File:Grafik Air Foil kelompok 62.png|700px|thumb|center]] | ||
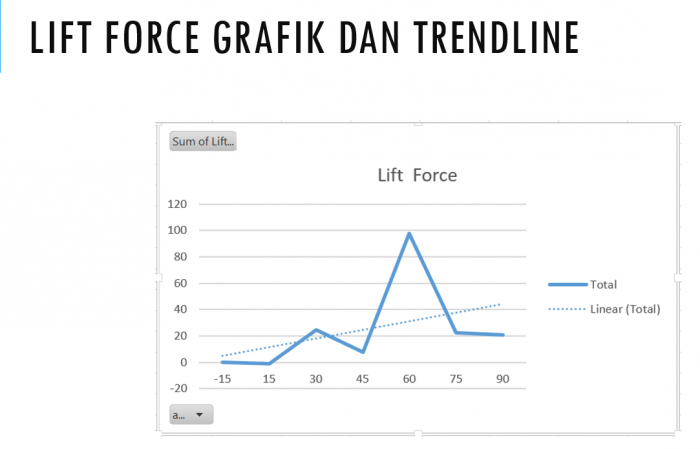
| + | Grafik Lift Force dengan trendline nilai linear y= 6,5549x-1,5127 | ||
| + | |||
| + | Grafik Lift Force dengan trendline nilai polinomial y= -3,5089x^2 + 34,626x - 43,619 | ||
| + | |||
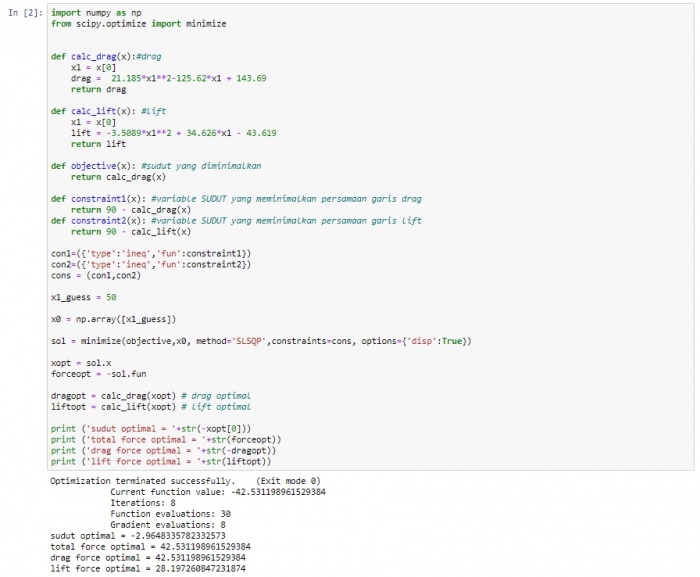
| + | Optimasi | ||
| + | |||
| + | [[File:optimasi7.jpg|700px|thumb|center]] | ||
| + | |||
| + | == Minggu keduabelas 11 Desember 2019 == | ||
| + | pada minggu ini kami mempelajari tentang ANN yaitu artificial neural network yang membahas tentang sistem pembelajaran terawasi yang dibangun dari sejumlah besar elemen sederhana, yang disebut neuron atau perceptron. Setiap neuron dapat membuat keputusan sederhana, dan memberi makan keputusan itu ke neuron lain, yang diorganisasikan dalam lapisan yang saling berhubungan. | ||
Latest revision as of 16:00, 17 December 2019
Nama :Jonathan Surya
NPM :1706036210
Dept :Departemen Teknik Mesin
Contents
- 1 Minggu Pertama (4 September)
- 2 Minggu kedua (11 september)
- 3 Minggu ketiga (18 september)
- 4 Minggu keempat (25 september)
- 5 Minggu kelima (2 Oktober)
- 6 Minggu keenam (9 Oktober)
- 7 Minggu ketujuh (16 Oktober)
- 8 UTS
- 9 Minggu kedelapan 30 Oktober 2019
- 10 Minggu kesepuluh 2019
- 11 Minggu kesebelas 4 Desember 2019
- 12 Minggu keduabelas 11 Desember 2019
Minggu Pertama (4 September)
Pada minggu pertama Pak Dai dan Pak Radon menjelaskan akan pentingnya pemrograman dan teknik mesin merupakan salah satu yang memperlajarinya.
Kenapa anak mesin harus belajar kalkulus?
karena kalkulus merupakan dasar ilmu matematika yang diperlukan mahasiswa teknik. selain itu, kalkulus juga melatih kemampuan perhitungan kita akan angka dan ketelitian juga.Pada dasarnya merupakan cabang dari ilmu matematika yang akan diaplikasikan dalam Engineering
program yang akan digunakan untuk matakuliah metode Numerik ini adalah PYTHON 3.
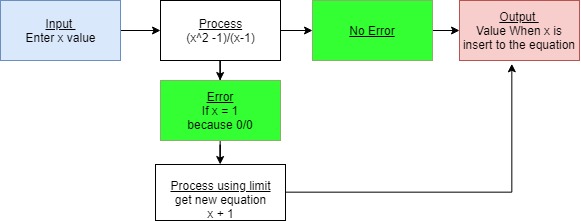
Tugas untuk minggu depan membaca buku python 3, pr membuat algoritma (bisa flowchart) dan menulis coding programnya untuk persamaan (x^2 -1)/(x-1) ,untuk x = 1
Algoritma
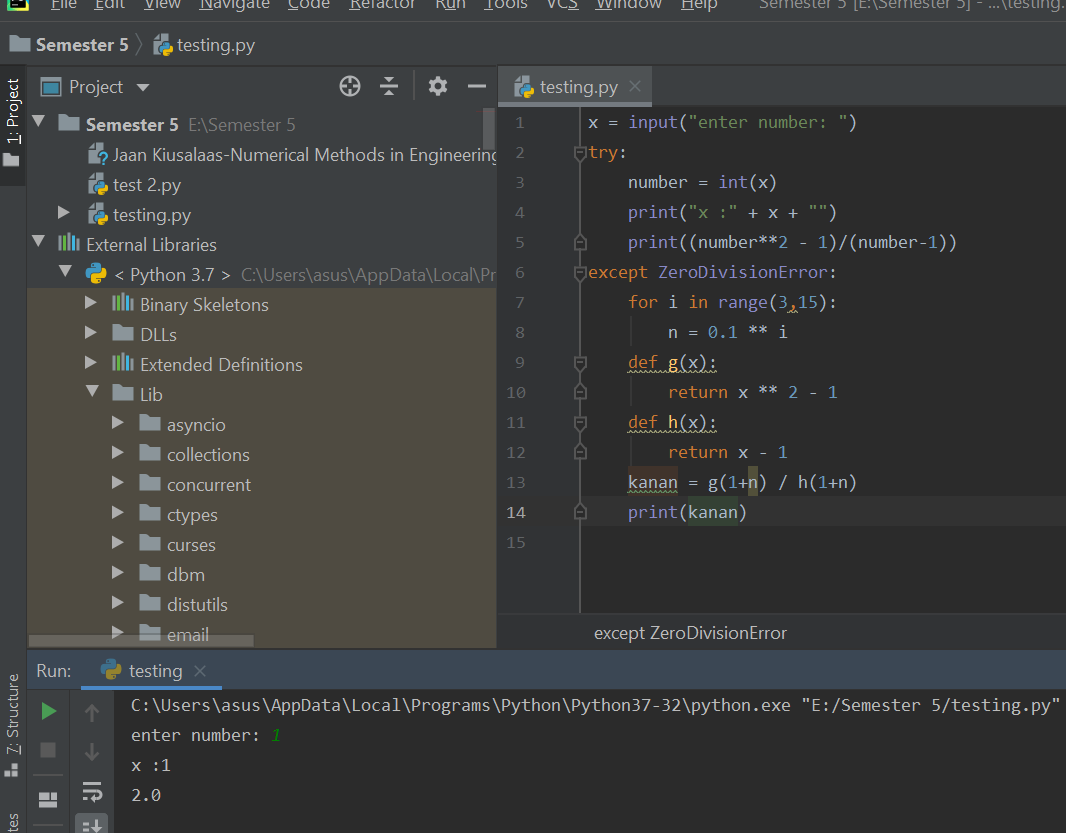
untuk Tugas pertama setelah membuat algoritmanya saya berusaha membuat pythonnya dengan bantuan internet mempelajari simbol-simbol dasar dan bebrapa fungsi seperti pangkat dengan simbol (**). setelah itu saya mencoba membuat code python tersebut dalam pycharm yaitu salah satu program yang menggunakan bahasa python.
Minggu kedua (11 september)
Pada Minggu kedua Pak Dai menjelaskan bahwa seberapa penting machine learning yang berkembang saat ini salah satu contohnya google search engine.
menurut Pak Dai Industry 5.0 adalah dasar-dasar pancasila karena teknologi merupakan ciptaan manusia dan sebisa mungkin empowering to human juga agar setiap teknologi yang kita buat dapat membantu sesama.
Artificial Intelligence atau disebut rekayasa buatan yang dibuat oleh manusia. Namun pemilik kepintaran sesungguhnya adalah manusia. hal tersebut dubuat dengan tujuan untuk membantu sesama karena keterbatasan manusia juga.
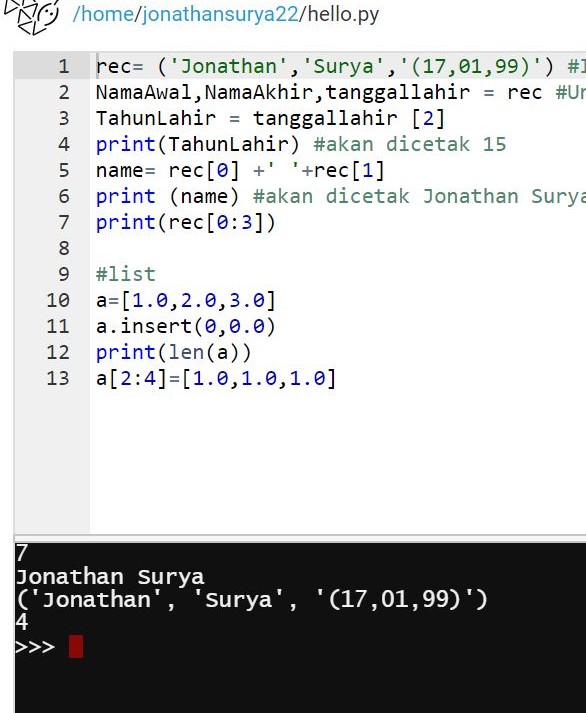
Pembelajaran minggu kedua mempelajari cara penggunaan Software Python dimana kita membuat coding Hello Python world dan mempelajari dasar dasar coding seperti tuples dan list. untuk mempelajari lebih banyak lagi dapat melalui python anywhere.
Minggu depan tgl 18 sept Quiz bab 1 pemrograman jam 4 sore
Minggu ketiga (18 september)
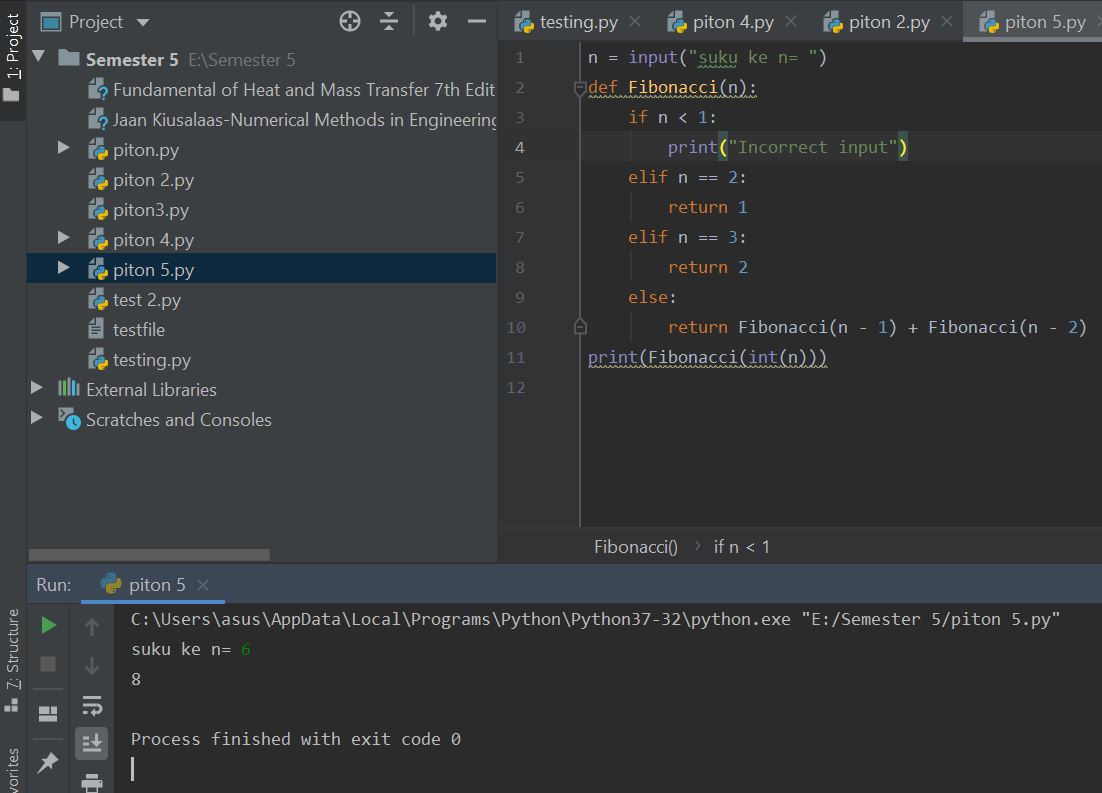
Pada pertemuan ketiga diadakan quiz dasar-dasar pemrograman. Soal quiz membuat algoritma dengan bahasa sendiri,flowchart dan pythonnya untuk suku ke-n dari sebuah bilangan fibronacci yang dimulai dari 1,1,2,3,5,8,....
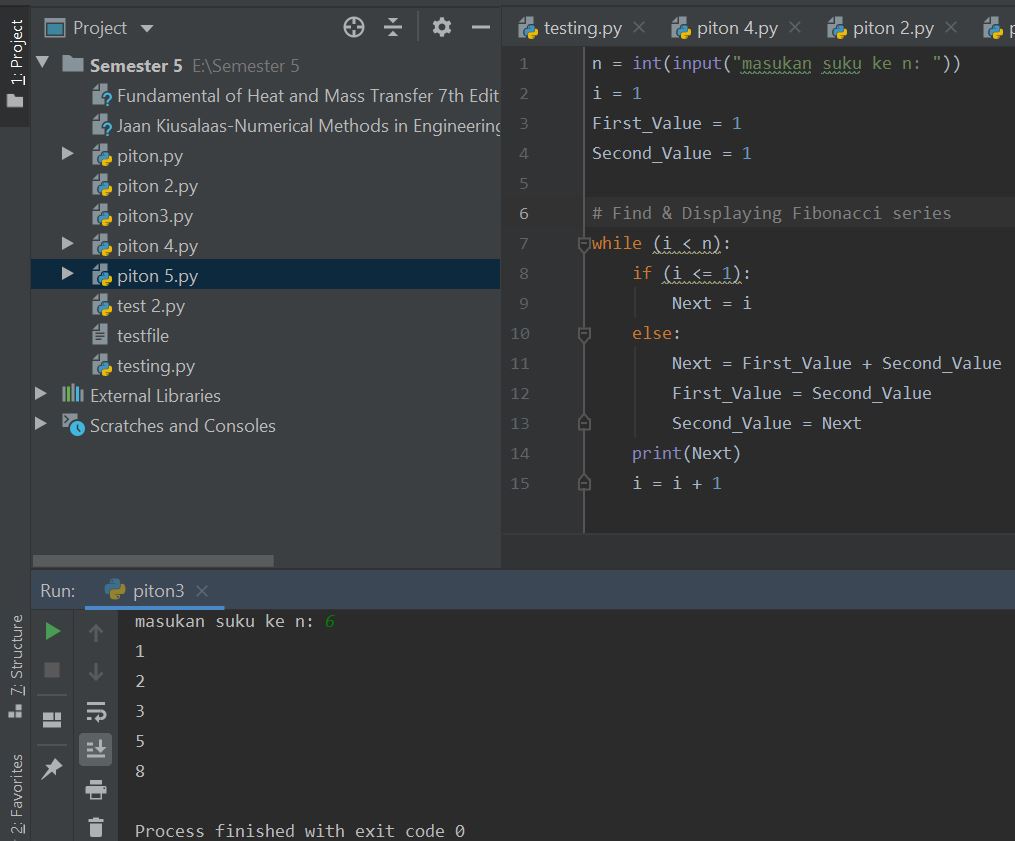
untuk soal tersebut dapat diselesaikan dengan 2 cara yaitu function dan loop dengan While Condition
Metode Function
Metode Loop dengan While Condition
Minggu keempat (25 september)
Pada pertemuan keempat mempelajari Computer modelling yang terdiri dari computation dan modelling. Modelling sendiri adalah sebuah representasi/simplifikasi/asumsi dari suatu yang bersifat rumit menjadi lebih mudah untuk dipahami. namun tidak sepenuhnya 100 persen sama dari aslinya karena suatu pendekatan saja.
Contoh mechanical modelling yang dapat digunakan dalam Computer modelling adalah
tekanan atau stress= F/A,
elastisitas adalah laju perubahan bentuknya.
oleh karena itu kasus engineering dapat diselesaikan dengan metode numerik
Pr untuk minggu depan menyusun kesetimbangan 4 titik sehingga mendapatkan fungsi aljabar linearnya displacementnya yang terjadi. diskritisasi membuat menjadi titik tak hingga
Minggu kelima (2 Oktober)
Pada pertemuan kelima. Asistensi dari asisten mengenai dasar cara kerja eliminasi gauss jordan dalam pengaplikasiannya dalam sistem pegas dimana codingnya dapat dibuat menggunakan import from numpy yang bersifat lebih simple dan menghemat proses penghitungan juga dalam python. Efisiensi pemograman adalah dimana program yang memiliki fungsi yang sama dapat dihasilkan dengan penulisan coding yang lebih sedikit.
pada dasarnya NUMPY, SYMPY dll merupakan suatu external library yang dapat didownload dimana didalamnya sudah terbuat codingan yang dinginkan untuk dipakai sehingga tidak perlu membuat codingan dari awal lagi.
hanya menuliskan Import from sympy fibronacci. lalu data fibronacci pun bisa langsung diproses
Pr untuk minggu depan membaca bab 4 dan membuat rangkuman
Minggu keenam (9 Oktober)
merefrensikan kasus fisik yang dapat direferensikan ke komputer. peran engineer bagimana punya skill untuk memodelkannya. Metode direct kesetimbangan gaya (hukum dasar). sebuah persamaan matematika orang yang punya wawasannya futuristik. there is a god masalah atau benda yang kita hitung ketika terkena beban untuk mendapatkan area criticalnya untuk dilakukan upgrade. semua rumus dimesin dianggap continu atau berdislokasi atau berpindah tempat. displacement adanya perpindahan tempat diferensial
Minggu ketujuh (16 Oktober)
Codingan Quiz 2 exercise 7.1 no 2 hal 253
J0 = input("masukan nilai x0 possitif = ")
K0 = input ("masukan nilai y0 positif = ")
N0 = input("masukan nilai count number biasayanya 1 = ")
def F(x, y):
return (x**2 - 4*y)
def rungeKutta(x0, y0, h):
n = int(N0)
#mendefinisikan y= y0
y = y0
for i in range(1, n + 1):
"Apply Runge Kutta Formulas to find next value of y"
k1 = h * F(x0, y)
k2 = h * F(x0 + 0.5 * h, y + 0.5 * k1)
k3 = h * F(x0 + 0.5 * h, y + 0.5 * k2)
k4 = h * F(x0 + h, y + k3)
# Update next value of y
y = y + (1.0 / 6.0) * (k1 + 2 * k2 + 2 * k3 + k4)
# Update next value of x
x0 = x0 + h
return y
# misalkan :
x0 = int(J0)
y = int(K0)
h = 0.2
print('The value of y at x is:', rungeKutta(x0, y, h))
exercise bab 2.1 no 6 hal 55
import numpy
a = [[0, 0, 2, 1, 2],
[0, 1, 0, 2, -1],
[1, 2, 0, -2, 0],
[0, 0, 0, -1, 1],
[0, 1, -1, 1, -1]]
b = [[1],
[1],
[-4],
[-2],
[-1]]
c = [1, 1, 1, 1, 1,]
n = len(b)
# Elimination
for k in range(0, n - 1):
for i in range(n - 1, k, -1):
if a[i][k] != 0.0:
op = a[i][k] / a[i - 1][k]
b[i][0] = b[i][0] - op * b[i - 1][0]
for f in range(0, n):
a[i][f] = a[i][f] - op * a[i - 1][f]
# Subtitution
if a[n - 1][n - 1] != 0:
c[n - 1] = b[n - 1][0] / a[n - 1][n - 1]
else:
c[n - 1] = 0
for i in range(n - 2, -1, -1):
sigma = 0
for k in range(0, n, 1):
y = a[i][k] * c[k]
sigma = sigma + y
sigma = sigma - a[i][i]
if a[i][i] != 0:
c[i] = (b[i][0] - sigma) / a[i][i]
else:
a[i][i] = 0
for v in range(0, n, 1):
print(a[v])
print(c[0:n])
namun masih error pada EGJ
UTS
Hari: Rabu, 23 Oktober 2019
Oleh : Dr. Ahmad Indra & Dr. Eng. Radon Dhelika
Berikut video muhasabah metnum Jonathan Surya
untuk soal 3a
from math import
g = 10
m1 = input("masukan berat massa 1 = ")
m2 = input ("masukan berat massa 2 = ")
m3 = input("masukan berat massa 3 = ")
u1 = input("masukan koef gesek massa 1 = ")
u2 = input("masukan koef gesek massa 2 = ")
u3 = input("masukan koef gesek massa 3 = ")
alfa = input("masukan sudut alfa = ")
a = input("percepatan = ")
x = sin (alfa)
y = cos (alfa)
t1 = m1*g*(x-u1*y) - m1*a
t2 = m2*g*(x-u2*y) + t1 -m2*a
t3 = m3*g*(x-u3*y) + t2 -m3*a
print(t1)
print(t2)
print(t3)
berikut video penjelasan pengerjan soal 3a
untuk soal 3b cara 1
p udara = 1.1 #massa jenis udara
cd= eval(input("drag coefficient: "))
area= eval(input("area (m^2): "))
v0= eval(input("velocity udara: "))
#masukan nilai yang diketahui pada mobil
mm = eval(input("massa benda/mobil (kg): "))
g= 9.81
a = eval(input("percepatan mobil (m/s^2): "))
v2 = eval(input("kecepatan mobil max (m/s): "))
v1 = 0 #mobil pada saat diam
#masukan nilai yang diketahui pada F gesek
u = eval(input(" koefisien gesekan: "))
t = eval(input("waktu dari diam ke gerak(s): "))
# a drag
ages = g*u
adrag = (cd*area*p udara*v0**2)/2*mm
amobil = a
atot = amobil-(ages+adrag)
t = (v1-v2)/atot
print ("waktu yang diperlukan mobil untuk mencapai kecepatan max (s): ", t)
untuk soal 3b cara 2
m = eval(input("masukan massa mobil: "))
g = 10
p = 1.2
am = eval(input("percepatan mobil: "))
Cd = eval(input("koefisien drag: "))
mu = eval(input("koefisien gesekan: "))
A = eval(input("area [m^2]: "))
v0 = eval(input("velocity mobil awal [m/s]: "))
vf = eval(input("kecepatan mobil max [m/s]: "))
# total perceptan adalah gabungan dari am, af , ad
Ff = m * g * mu # rumusnya Ff = m * g * mu
Fd = (Cd * A * p * v0 ** 2) / 2 # rumusnya Fd = (Cd * A * p * v0 ** 2) / 2
a2 = (am) - (Fd / m) - (Ff / m)
def dtdtv(t, y):
return ((m) / (am*g - m * g * mu - 0.5 * Cd * A * p * v0 ** 2))
t = 0
h = 0.01
def rungekutta(v0, t0, vf, h):
n = (int)((vf - v0) / h)
t = t0
for i in range(1, n + 1):
#rumus Runge kutta
k1 = h * dtdtv(v0, t)
k2 = h * dtdtv(v0 + 0.5 * h, t + 0.5 * k1)
k3 = h * dtdtv(v0 + 0.5 * h, t + 0.5 * k2)
k4 = h * dtdtv(v0 + h, t + k3)
#mendapatkan nilai t yang diperlukan hingga mencapai kecepatan tersebut
t = t + (1.0 / 6.0) * (k1 + 2 * k2 + 2 * k3 + k4)
# nilai Vo
v0 = v0 + h
return t
tfinal = rungekutta(v0, t, vf, h)
print(tfinal)
berikut video penjelasan pengerjan soal 3b
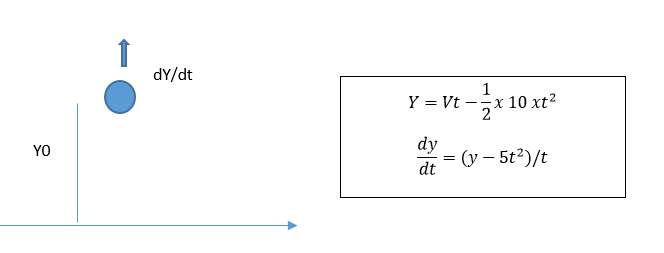
Minggu kedelapan 30 Oktober 2019
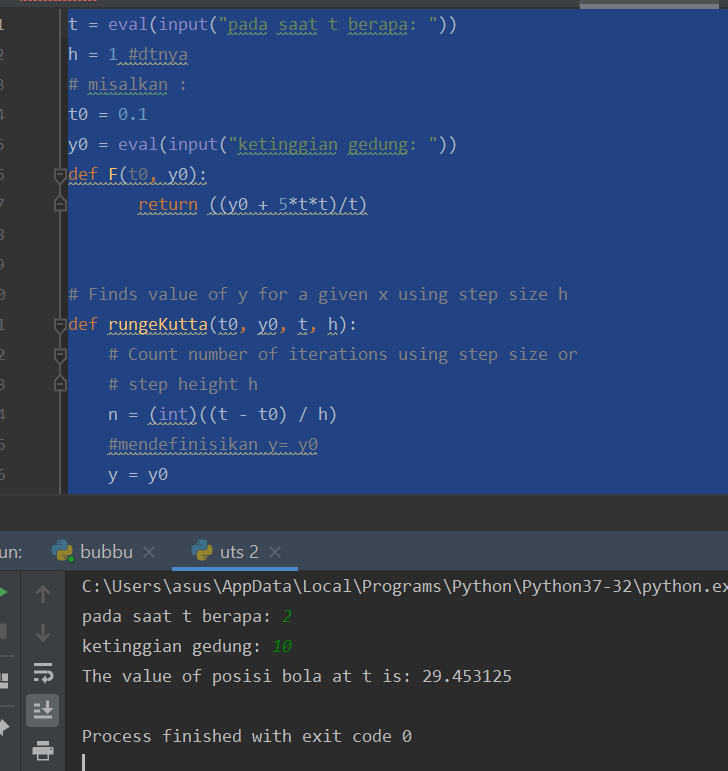
persamaan differensial bola yang di lempar
t = eval(input("pada saat t berapa: "))
h = 1 #dtnya
# misalkan :
t0 = 0.1
y0 = eval(input("ketinggian gedung: "))
def F(t0, y0):
return ((y0 + 5*t*t)/t)
# Finds value of y for a given x using step size h
def rungeKutta(t0, y0, t, h):
# Count number of iterations using step size or
# step height h
n = (int)((t - t0) / h)
#mendefinisikan y= y0
y = y0
for i in range(1, n + 1):
"Apply Runge Kutta Formulas to find next value of y"
k1 = h * F(t0, y)
k2 = h * F(t0 + 0.5 * h, y + 0.5 * k1)
k3 = h * F(t0 + 0.5 * h, y + 0.5 * k2)
k4 = h * F(t0 + h, y + k3)
# Update next value of y
y = y + (1.0 / 6.0) * (k1 + 2 * k2 + 2 * k3 + k4)
# Update next value of t
t0 = t0 + h
return y
print('The value of posisi bola at t is:', rungeKutta(t0, y0, t, h))
Minggu kesepuluh 2019
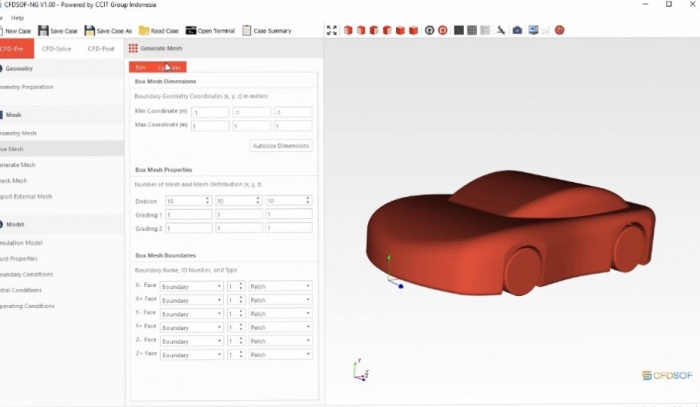
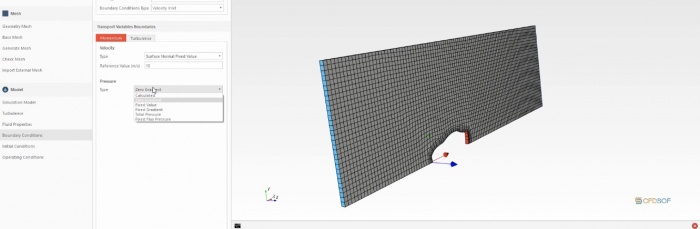
pada minggu ini kami mempelajari mengenai CFD solv. contoh yang diambil adalah drag pada mobil yang bergerak. dengan bimbingan bang edo dan bang timo mengenai cara menggunakan softeare
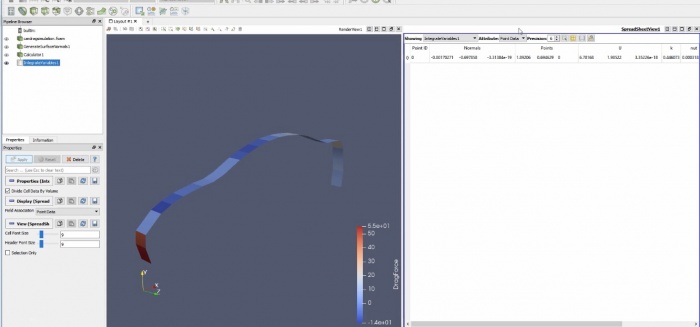
import,meshing,memasukan initial condition, lalu di import ke paraview dilakukan perhitungan menggunakan fdrag kalkulator dan flift kalkulator
Cfdsof. Input = geometric. Output =IMS. Masuk ke paraview 5.5.4. input= IMS. Output= hasil lift&drag
lalu kita diberi tugas untuk mencari fdrag dari flift dari air foil
Minggu kesebelas 4 Desember 2019
pada minggu ini kami belajar mengenai optimasi untuk mencari nilai optimum dengan meminimal dan maksimal dari suatu fungsi . optimasi aka dibatasi dengan berbagai batas. iterasi salah satu caranya untuk meminimalisir menentukan variabel awalnya
lalu kita diberi tugas untuk mencari nilai optimum dari data fdrag dan flift
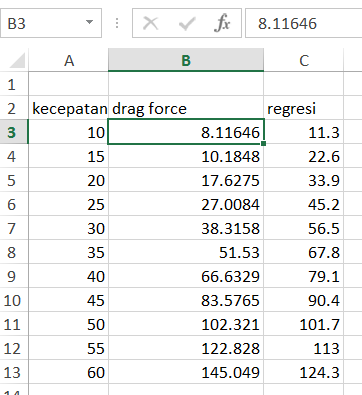
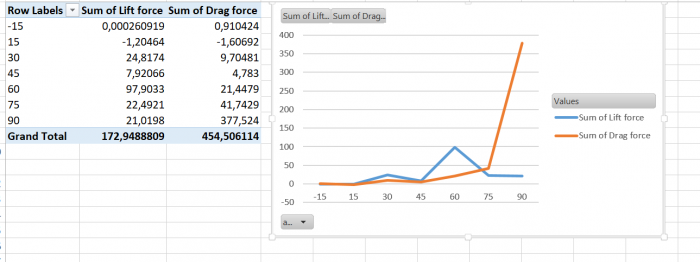
Grafik AirFoil Drag Force dan Lift Force
Grafik gabungan drag dan lift dari airfoil. Dimana drag force semakin bertambah besar seiring naiknya sudut serang. sedangkan nilai Lift diperoleh optimumnya pada sudut serang 60
Grafik Drag Force dengan trendline nilai linear y= 43,867x-110,54
Grafik Drag Force dengan trendline nilai polinomial y= 21,185x^2-125,62x + 143,69
Grafik Lift Force dengan trendline nilai linear y= 6,5549x-1,5127
Grafik Lift Force dengan trendline nilai polinomial y= -3,5089x^2 + 34,626x - 43,619
Optimasi
Minggu keduabelas 11 Desember 2019
pada minggu ini kami mempelajari tentang ANN yaitu artificial neural network yang membahas tentang sistem pembelajaran terawasi yang dibangun dari sejumlah besar elemen sederhana, yang disebut neuron atau perceptron. Setiap neuron dapat membuat keputusan sederhana, dan memberi makan keputusan itu ke neuron lain, yang diorganisasikan dalam lapisan yang saling berhubungan.
Enable comment auto-refresher