Difference between revisions of "Marcellino Lorenzo"
Marcellino (talk | contribs) |
Marcellino (talk | contribs) (→Video UTS) |
||
| (36 intermediate revisions by the same user not shown) | |||
| Line 25: | Line 25: | ||
== Progress Belajar Python == | == Progress Belajar Python == | ||
| − | Minggu, 8 September 2019, saya bermain ke kost teman saya. Dia bernama Jovi Handono, mahasiswa fakultas ilmu komputer yang kebetulan 1 kost dengan saya. Dia adalah teman saya sejak SD. Saya datang ke kamar dia untuk belajar Python. Malam ini saya diajarkan banyak hal dasar oleh Jovi mulai dari dasar-dasar bahasa pemrograman. Saya memulai dengan mendownload Python di https://python.org . Setelah itu Jovi mulai mengajarkan berbagai hal tentang dasar-dasar bahasa python dengan referensi buku ''Numerical Method for Engineering with Python 3''. | + | Minggu, 8 September 2019, saya bermain ke kost teman saya. Dia bernama Jovi Handono, mahasiswa fakultas ilmu komputer yang kebetulan 1 kost dengan saya. Dia adalah teman saya sejak SD. Saya datang ke kamar dia untuk belajar Python. Malam ini saya diajarkan banyak hal dasar oleh Jovi mulai dari dasar-dasar bahasa pemrograman. Saya memulai dengan mendownload Python di https://python.org . Setelah itu Jovi mulai mengajarkan berbagai hal tentang dasar-dasar bahasa python dengan referensi buku '''''Numerical Method for Engineering with Python 3'''''. |
Malam ini saya belajar = | Malam ini saya belajar = | ||
Print | Print | ||
| Line 45: | Line 45: | ||
rec = ("Marcellino","Lorenzo",(18,4,00)) | rec = ("Marcellino","Lorenzo",(18,4,00)) | ||
| − | |||
NamaAwal,NamaAkhir,tanggallahir = rec | NamaAwal,NamaAkhir,tanggallahir = rec | ||
| − | |||
print(NamaAwal) | print(NamaAwal) | ||
| − | |||
TahunLahir = tanggallahir[0] | TahunLahir = tanggallahir[0] | ||
| − | |||
print(TahunLahir) | print(TahunLahir) | ||
| − | |||
name = rec[0]+" "+rec[1] | name = rec[0]+" "+rec[1] | ||
| − | |||
print(name) | print(name) | ||
| − | |||
print(rec[0:2]) | print(rec[0:2]) | ||
| Line 65: | Line 58: | ||
Marcellino | Marcellino | ||
| − | |||
18 | 18 | ||
| − | |||
Marcellino Lorenzo | Marcellino Lorenzo | ||
| − | |||
('Marcellino', 'Lorenzo') | ('Marcellino', 'Lorenzo') | ||
| − | |||
4 | 4 | ||
| Line 80: | Line 69: | ||
a = [1.0,2.0,3.0] | a = [1.0,2.0,3.0] | ||
| − | |||
a.append(4.0) | a.append(4.0) | ||
| − | |||
print(a) | print(a) | ||
| − | |||
a.insert(0,0.0) | a.insert(0,0.0) | ||
| − | |||
print(len(a)) | print(len(a)) | ||
| − | |||
a[2:4] = [1.0, 1.0, 1.0] | a[2:4] = [1.0, 1.0, 1.0] | ||
| Line 94: | Line 78: | ||
[1.0, 2.0, 3.0, 4.0] | [1.0, 2.0, 3.0, 4.0] | ||
| − | |||
5 | 5 | ||
| Line 103: | Line 86: | ||
Maka saat perintah ini di ''run'' akan menghasilkan baris baru yaitu (1,2,3,4). | Maka saat perintah ini di ''run'' akan menghasilkan baris baru yaitu (1,2,3,4). | ||
| + | |||
| + | |||
| + | == Pertemuan Ketiga == | ||
| + | Rabu, 18 September 2019, kami mengerjakan test tentang baris Fibonacci dengan menggunakan Python. Kami wajib membuat algoritma, "flow chart", dan bahasa Python-nya. | ||
| + | |||
| + | Algoritma nya adalah : Fn = F(n-2) + F(n-1) | ||
| + | |||
| + | Untuk bahasa Python nya (dengan While.loop) | ||
| + | |||
| + | nNum = 15 | ||
| + | num = 1 | ||
| + | num1 = 1 | ||
| + | num2 = 1 | ||
| + | count = 0 | ||
| + | |||
| + | while (count<nNum): | ||
| + | print(num1) | ||
| + | num = num1 +num2 | ||
| + | num1 = num2 | ||
| + | num2 = num | ||
| + | count +=1 | ||
| + | |||
| + | nNum menunjukkan hingga baris ke berapa baris Fibonacci yang ingin ditampilkan. num1 = 1 menunjukkan baris dimulai dari 1 bukan 0. Count +=1 sebagai operasi hitung. | ||
| + | |||
| + | |||
| + | (dengan Subroutine) | ||
| + | |||
| + | # Subroutine | ||
| + | # Recurrence Relation | ||
| + | # Fn = Fn-1 + Fn-2 | ||
| + | def recur_fibo(n): | ||
| + | if n <= 1: | ||
| + | return n | ||
| + | else: | ||
| + | return(recur_fibo(n-1)+recur_fibo(n-2)) | ||
| + | |||
| + | nNum = 15 | ||
| + | for i in range(nNum): | ||
| + | print(recur_fibo(i)) | ||
| + | |||
| + | == Pertemuan Keempat == | ||
| + | (Sebelum Hilang dari page Pemodelan Komputer) | ||
| + | |||
| + | Dari diskusi hari ini, kita dapat mempelajari pentingnya mempelajari suatu model. model dapat berarti representasi, simplifikasi, dan asumsi. Dengan mempelajari suatu pemodelan kita dapat memahami cara pikir dan alur berpikir suatu proses. Sebagai contoh dari suatu fondasi yang terlihat 3D dan memiliki banyak unsur, agar mempermudahnya kita dapat membuat suatu pemodelan dan menjadikan nya 2D. Kita dapat melihat gaya2 yang bekerja di dalam fondasi secara lebih jelas saat kita membelahnya menjadi 2D. Ini lah contoh kecil dari pemodelan. | ||
| + | |||
| + | |||
| + | |||
| + | == 9/10/19 == | ||
| + | hari ini mempelajari apa yang bisa dilakukan komputer dalam membantu kita menghitung | ||
| + | |||
| + | mempelajari sistem persamaan | ||
| + | |||
| + | mau sampai 1 juta juga masih bisa dihitung komputer | ||
| + | |||
| + | aspek metnum dalam mesin : | ||
| + | |||
| + | 1. (tidak dilanjutkan) | ||
| + | |||
| + | |||
| + | kita harus menjadi orang cerdas bukan hanya pintar. apakah surga dan neraka ada sedangkan belum terbukti ? | ||
| + | |||
| + | kita harus memperhatikan hal-hal kecil seperti udara. | ||
| + | |||
| + | |||
| + | Komputasi Teknik, Differential Equation | ||
| + | |||
| + | Metode Runge Kutta | ||
| + | |||
| + | |||
| + | Metode numerik pasti ada error tapi dapat digunakan untuk pendekatan semua masalah | ||
| + | |||
| + | 1. Pers diferensial | ||
| + | |||
| + | 2. Initial Condition | ||
| + | |||
| + | |||
| + | == Quiz, 16 Oktober 2019 == | ||
| + | Jawaban soal 2.1 dan 7.1 (dari buku Numerical Method for Engineering with Python 3) | ||
| + | |||
| + | Soal 2.1 | ||
| + | #Mendelegasikan perintah dari library | ||
| + | from numpy import linalg | ||
| + | import numpy as np | ||
| + | |||
| + | #Memasukan nilai Matriks per baris | ||
| + | bar1 = [0,0,2,1,2] | ||
| + | bar2 = [0,1,0,2,-1] | ||
| + | bar3 = [1,2,0,-2,1] | ||
| + | bar4 = [0,0,0,-1,1] | ||
| + | bar5 = [0,1,-1,1,-1] | ||
| + | |||
| + | #Mengaplikasikan penghitungan matriks masing-masing baris | ||
| + | nmat = np.array ([bar1,bar2,bar3,bar4,bar5]) | ||
| + | print ("n Matrix adalah sebagai berikut:") | ||
| + | print (nmat) | ||
| + | cons = np.array ([1,1,-4,-2,-1]) | ||
| + | print ("Matrix Y adalah sebagai berikut:") | ||
| + | print (cons) | ||
| + | jawab = linalg.solve (nmat,cons) | ||
| + | |||
| + | #Mencari nilai X | ||
| + | x1val = int(jawab[0]) | ||
| + | x2val = int(jawab[1]) | ||
| + | x3val = int(jawab[2]) | ||
| + | x4val = int(jawab[3]) | ||
| + | x5val = int(jawab[4]) | ||
| + | |||
| + | #Menampilkan hasil nilai X | ||
| + | print ("hasil X adalah :") | ||
| + | print ("x1= ",x1val) | ||
| + | print ("x2= ",x2val) | ||
| + | print ("x3= ",x3val) | ||
| + | print ("x4= ",x4val) | ||
| + | print ("x5= ",x5val) | ||
| + | |||
| + | Maka jika di ''run'' akan menghasilkan hasil : | ||
| + | x1 = 3 | ||
| + | x2 = -2 | ||
| + | x3 = 1 | ||
| + | x4 = 1 | ||
| + | x5 = -1 | ||
| + | |||
| + | |||
| + | |||
| + | Soal 7.1 | ||
| + | def dydx(x, y): | ||
| + | return ((x**2 - 4*y)) | ||
| + | |||
| + | # Mencari nilai Y dari nilai X dengan h | ||
| + | # dan nilai saat X0 dan Y0. | ||
| + | def rungeKutta(x0, y0, x, h): | ||
| + | # Menghitung dengan step size | ||
| + | # step height h | ||
| + | n = (int)((x - x0)/h) | ||
| + | y = y0 | ||
| + | for i in range(1, n + 1): | ||
| + | "Jalankan Runge Kutta Formulas untuk mendapat nilai Y berikutnya" | ||
| + | k1 = h * dydx(x0, y) | ||
| + | k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1) | ||
| + | k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2) | ||
| + | k4 = h * dydx(x0 + h, y + k3) | ||
| + | |||
| + | # Update nilai Y berikutnya | ||
| + | y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4) | ||
| + | |||
| + | # Update nilai X berikutnya | ||
| + | x0 = x0 + h | ||
| + | return y | ||
| + | |||
| + | #Misalkan : | ||
| + | x0 = 0 | ||
| + | y = 1 | ||
| + | x = 0.03 | ||
| + | h = 0.01 | ||
| + | print ('Nilai dari Y saat di X adalah :', rungeKutta(x0, y, x, h)) | ||
| + | |||
| + | Maka jika di ''run'' akan menghasilkan hasil : | ||
| + | Nilai dari Y saat di X adalah : 0.8869291754400297 | ||
| + | |||
| + | == Ujian Tengah Semester == | ||
| + | |||
| + | Untuk soal I.A | ||
| + | |||
| + | from math import * | ||
| + | |||
| + | #Menentukan nilai atau besaran masing-masing benda | ||
| + | g = 9.8 | ||
| + | m1 = eval(input("massa1 : ")) | ||
| + | m2 = eval(input("massa2 : ")) | ||
| + | m3 = eval(input("massa3 : ")) | ||
| + | k1 = eval(input("koefisien gesek1 : ")) | ||
| + | k2 = eval(input("koefisien gesek2 : ")) | ||
| + | k3 = eval(input("koefisien gesek3 : ")) | ||
| + | a = eval(input("percepatan sistem : ")) | ||
| + | teta = eval(input("sudut kemiringan : ")) | ||
| + | s = sin(teta) | ||
| + | c = cos(teta) | ||
| + | |||
| + | t1 = m1*g*(s-k1*c) - m1*a | ||
| + | t2 = m2*g*(s-k2*c) + t1 - m2*a | ||
| + | t3 = m3*g*(s-k3*c) + t2 - m3*a | ||
| + | m4 = -(t3 - m1*a)/g | ||
| + | |||
| + | print ("massa benda 4 adalah :",m4) | ||
| + | |||
| + | Jawaban = | ||
| + | massa1 (kg): 2 | ||
| + | massa2 (kg): 3 | ||
| + | massa3 (kg): 4 | ||
| + | koefisien gesek1 : 0.3 | ||
| + | koefisien gesek2 : 0.2 | ||
| + | koefisien gesek3 : 0.3 | ||
| + | percepatan sistem : 0 | ||
| + | sudut kemiringan (derajat) : 30 | ||
| + | massa benda 4 adalah (kg) : 9.262488096565958 | ||
| + | Dengan memasukkan angka seperti diatas, maka jika ingin membuat sistem statis atau tidak mengalami perpindahan, massa benda 4 harus sebesar 9,26 Kg | ||
| + | |||
| + | |||
| + | |||
| + | Untuk soal I.B | ||
| + | |||
| + | from math import * | ||
| + | |||
| + | #Menentukan besaran | ||
| + | g = 9.8 | ||
| + | rho = 1.2 #massa jenis udara | ||
| + | |||
| + | cd = eval(input("drag coef: ")) | ||
| + | area = eval(input("area: ")) | ||
| + | v0 = eval(input("kecepatan awal: ")) | ||
| + | m = eval(input("massa mobil (kg): ")) | ||
| + | u = eval(input("koef gesek: ")) | ||
| + | a = eval(input("percepatan mobil: ")) | ||
| + | t = eval(input("waktu (s): ")) | ||
| + | |||
| + | fs = g*u | ||
| + | fdrag = (cd*area*rho*v0**2)/2*m | ||
| + | f1 = a | ||
| + | atotal = f1 - (fdrag + fs) | ||
| + | v1 = v0+atotal*t | ||
| + | |||
| + | print ("kecepatan mobil dari diam: ",v1) | ||
| + | |||
| + | Jawaban = | ||
| + | drag coef: 0.8 | ||
| + | lebar area: 12 | ||
| + | kecepatan awal (m/s): 0 | ||
| + | massa mobil (kg): 1000 | ||
| + | koef gesek: 0.3 | ||
| + | percepatan mobil: 6 | ||
| + | waktu (s): 15 | ||
| + | kecepatan mobil dari diam: 45.9 | ||
| + | |||
| + | Dengan memasukkan angka seperti diatas, maka akan didapatkan hasil kecepatan mobil dari keadaan diam hingga 15 detik kemudian adalah 45,9 m/s atau 165,24 km/jam | ||
| + | |||
| + | |||
| + | == Video UTS == | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Video I.A | ||
| + | |||
| + | [[File:UTS 1.mp4]] | ||
| + | |||
| + | Ini adalah video penjelasan dari penyelesaian soal UTS no 1.1 | ||
| + | |||
| + | |||
| + | Video I.B | ||
| + | |||
| + | [[File:UTS 2.mp4]] | ||
| + | |||
| + | |||
| + | Ini adalah video penjelasan dari penyelesaian soal UTS no 1.2 | ||
| + | |||
| + | |||
| + | Video Muhasabah Diri | ||
| + | |||
| + | [[File:Muhasabah.mp4]] | ||
| + | |||
| + | = Tugas, 30 Oktober 2019 = | ||
| + | |||
| + | Pada pertemuan kali ini, kita diminta untuk membuat penyelesaian permasalahan fisika dengan menggunakan metode Range Kutta. | ||
| + | |||
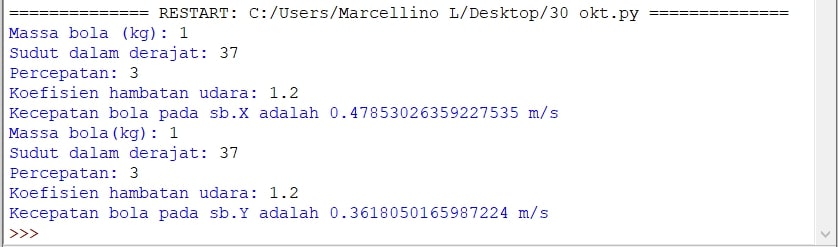
| + | Kita ibaratkan sekelompok mahasiswa mesin sedang bermain basket di laptek belakang. Kita dapat mencari berapa percepatan bola pada sumbu X dan Y dengan menggunakan metode Range Kutta. | ||
| + | |||
| + | '''Sumbu X :''' | ||
| + | |||
| + | from math import * | ||
| + | |||
| + | g = 9.81 | ||
| + | m = eval(input("Massa bola (kg): ")) | ||
| + | sudut = eval(input("Sudut dalam derajat: ")) | ||
| + | a = eval(input("Percepatan: ")) | ||
| + | cd = eval(input("Koefisien hambatan udara: ")) | ||
| + | alpa = sudut*0.0175 | ||
| + | ay = a*(sin(alpa)) | ||
| + | ax = a*(cos(alpa)) | ||
| + | v0 = 0 | ||
| + | x0 = 0 | ||
| + | t0 = 0 | ||
| + | dt = 0.2 | ||
| + | error = 200 | ||
| + | lst = [] | ||
| + | |||
| + | def dxdt(t0, v0): | ||
| + | return ((ax-(cd*v0**3/2)/m)) | ||
| + | |||
| + | while error > 0.01: | ||
| + | k1 = dt*dxdt(t0, v0) | ||
| + | k2 = dt*dxdt(t0+0.5*dt, v0+0.5*dt*k1) | ||
| + | k3 = dt*dxdt(t0+0.5*dt, v0+0.5*dt*k2) | ||
| + | k4 = dt*dxdt(t0+dt, v0+k3*dt) | ||
| + | v1 = v0 + (1/6)*(k1+2*k2+2*k3+k4) | ||
| + | x0 = x0 + dt | ||
| + | v0 = v1 | ||
| + | error = ((v1-v0)/v1) | ||
| + | lst.append(1) | ||
| + | print('Kecepatan bola pada sb.X adalah', v1, 'm/s') | ||
| + | |||
| + | |||
| + | '''Sumbu Y :''' | ||
| + | |||
| + | from math import * | ||
| + | g = 9.81 | ||
| + | m = eval(input("Massa bola(kg): ")) | ||
| + | sudut = eval(input("Sudut dalam derajat: ")) | ||
| + | a = eval(input("Percepatan: ")) | ||
| + | cd = eval(input("Koefisien hambatan udara: ")) | ||
| + | alpa = sudut*0.0175 | ||
| + | ay = a*(sin(alpa)) | ||
| + | ax = a*(cos(alpa)) | ||
| + | v0 = 0 | ||
| + | x0 = 0 | ||
| + | t0 = 0 | ||
| + | dt = 0.2 | ||
| + | error = 200 | ||
| + | lst = [] | ||
| + | |||
| + | def dydt(t0, v0): | ||
| + | |||
| + | return ((ay-(g*(cd*v0**3/2)/m))) | ||
| + | while error > 0.005: | ||
| + | |||
| + | k1 = dt*dydt(t0, v0) | ||
| + | k2 = dt*dydt(t0+0.5*dt, v0+0.5*dt*k1) | ||
| + | k3 = dt*dydt(t0+0.5*dt, v0+0.5*dt*k2) | ||
| + | k4 = dt*dydt(t0+dt, v0+k3*dt) | ||
| + | v2 = v0 + (1/6)*(k1+2*k2+2*k3+k4) | ||
| + | x0 = x0 + dt | ||
| + | v0 = v2 | ||
| + | error = ((v2-v0)/v2) | ||
| + | lst.append(1) | ||
| + | print('Kecepatan bola pada sb.Y adalah', v2, 'm/s') | ||
| + | |||
| + | |||
| + | Setelah itu kita mendapat hasil seperti berikut : | ||
| + | |||
| + | [[File:Gans.jpg]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | = CFD Drag Force (Tugas Kelompok) = | ||
| + | |||
| + | |||
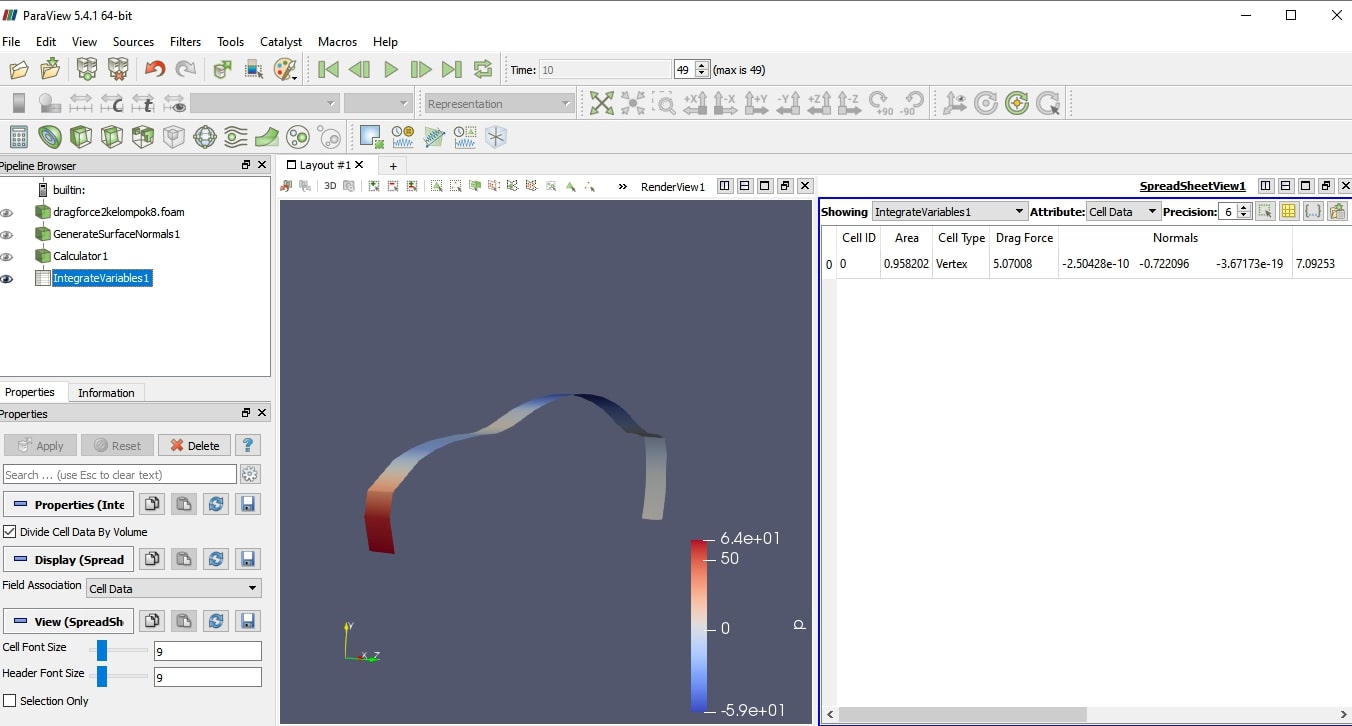
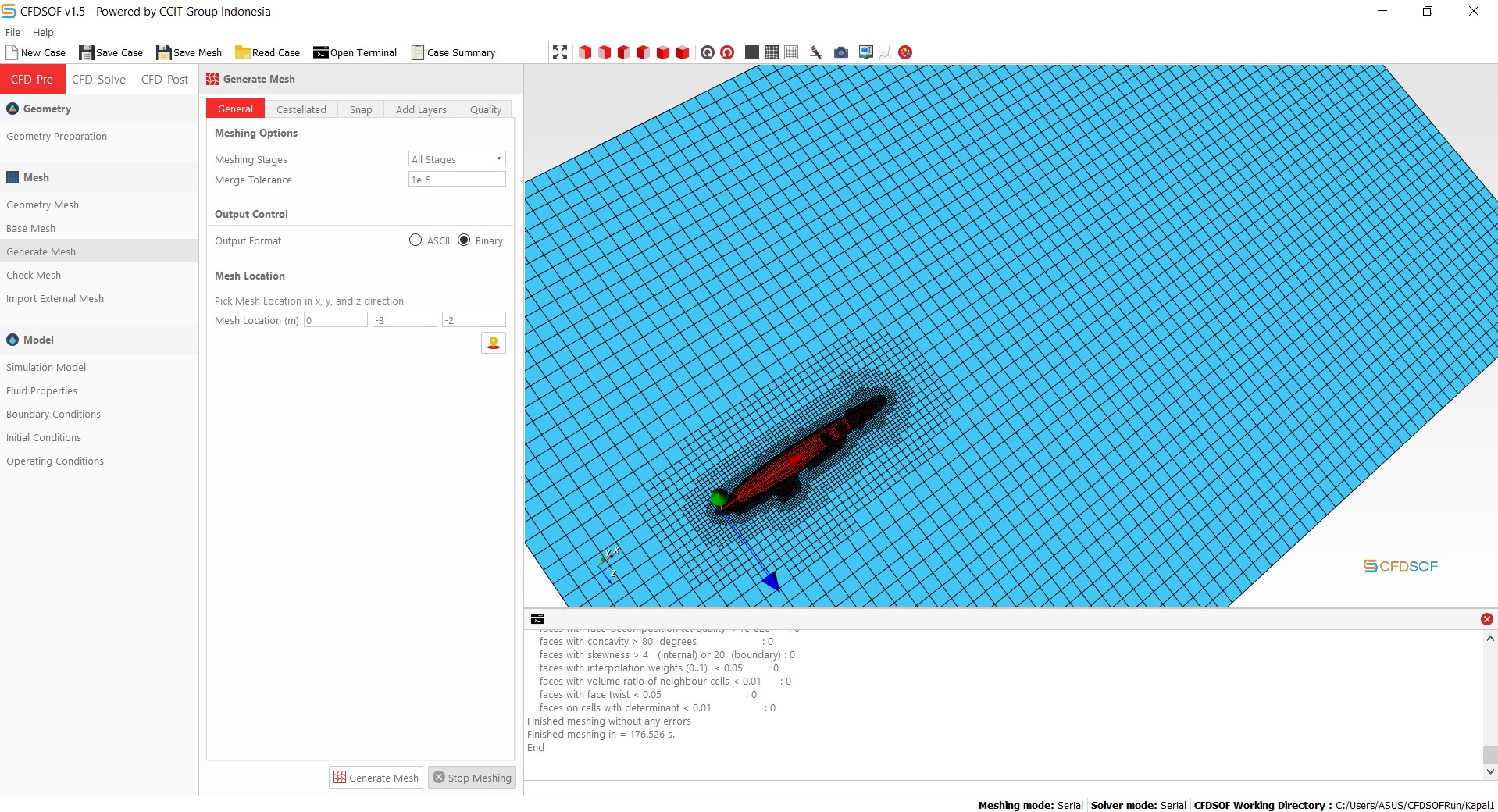
| + | 1) Pertama kita mengambil CAD mobil dari yang sudah disediakan. Lalu kami memmasukan CAD kedalam aplikasi CFD untuk melihat Drag Force dengan variasi kecepatan. Untuk membantu kami, kami menggunakan CFDSOF untuk menghitung hal ini. Awalnya kita menentukan besaran mesh yang kita butuhkan, yang kita ambil pada saat mesh berada di tengah mobil untuk melihat besaran Drag Forcenya. Jadi diasumsikan aliran yang melewati mobil bagian paling teratas. Setelah menentukan mesh, kami berlanjut melakukan perhitungan pada aplikasi Paraview yang menjadi third party dari CFDSOF. Pada applikasi ini, kami dapat menghitung Drag Force menggunakan calculator yaitu dengan mengalikan p*Surface x. Setelah kami melakukan percobaan dengan variasi sebanyak 10 kecepatan didapat 10 macam data sebagai berikut : | ||
| + | |||
| + | [[File:tisya.jpg]] | ||
| + | |||
| + | |||
| + | 2) Setelah mendapatkan 10 hasil Drag Force, kami menginput hasilnya kedalam Excel untuk membuat grafik & hasil persamaan yang didapat dari variasi Drag Force terhadap Kecepatan. Berikut hasil fitting curve : | ||
| + | |||
| + | [[File:cfd1.jpg]] | ||
| + | |||
| + | = Tugas Optimasi Sudut Serang Pada Airfoil = | ||
| + | |||
| + | |||
| + | 1) Melakukan pembuatan airfoil pada aplikasi Inventor dengan variasi 8 sudut caranya dengan merotasi airfoil dengan variasi sudut (-15, 0, 15, 30, 45, 60, 75, 90). Foto dibawah ini merupaka Hasil airfoil buatan kelompok 8 berikut dengan dimensinya. | ||
| + | [[File:Airfoil kelompok8.jpg]] | ||
| + | |||
| + | 2) Mencari besaran Drag Force & Lift Force pada setiap variasi sudut dengan menggunakan aplikasi CFDSOF menggunakan kecepatan internal sebesar 10 m/s. Melakukan perhitungan dengan calculator pada third party yaitu Paraview. Untuk mencari Drag Force mengalikan p*surface x sedangkan untuk mencari Lift Force mengalikan p*surface y. Berikut ditampilkan salah satu hasil paraview pada sudut 75 derajat. | ||
| + | |||
| + | Lift Force pada sudut 75 derajat | ||
| + | [[File:Lift Force 75.Kelompok8.png]] | ||
| + | |||
| + | Drag Force pada sudut 75 derajat | ||
| + | [[File:Drag Force 75.Kelompok8.png]] | ||
| + | |||
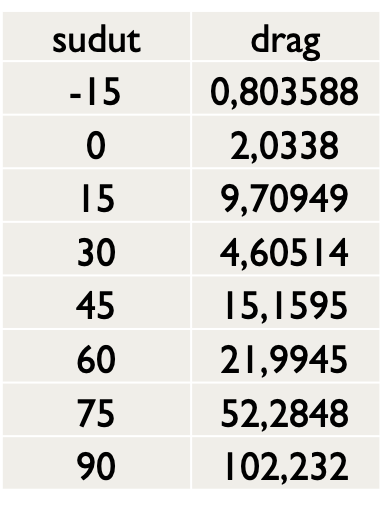
| + | 3) Dari hasil setiap nilai Drag Force dan Lift Force pada setiap sudut, nilai tersebut kami input dan melakukan regresi pada Excel. Hasilnya berupa grafik dan berupa persamaan y(x) yang nantinya digunakan untuk mencari optimasi. Besar hasil Drag Force dan Lift Force berdasarkan sudutnya dapat dilihat dibawah ini : | ||
| + | [[File:Tabel Lift Force.Kelompok8.png]] | ||
| + | |||
| + | [[File:Tabel Drag Force.Kelompok8.png]] | ||
| + | |||
| + | Grafik pada masing-masing force adalah sebagai berikut : | ||
| + | [[File:Grafik Lift Force.Kelompok8.png]] | ||
| + | [[File:Grafik Drag Force.Kelompok8.png]] | ||
| + | |||
| + | 4) Selain membuat grafik pada setiap Force, kami juga menggabungkan dua persamaan antara Lift Force dan Drag Force menjadi satu. Gunanya untuk melihat dititik manakah antara Drag Force dan Lift Force akan bertemu. Hasil dari grafik yang kami buat adalah sebagai berikut : | ||
| + | [[File:Grafik gabungan drag&lift.Kelompok8.png]] | ||
| + | |||
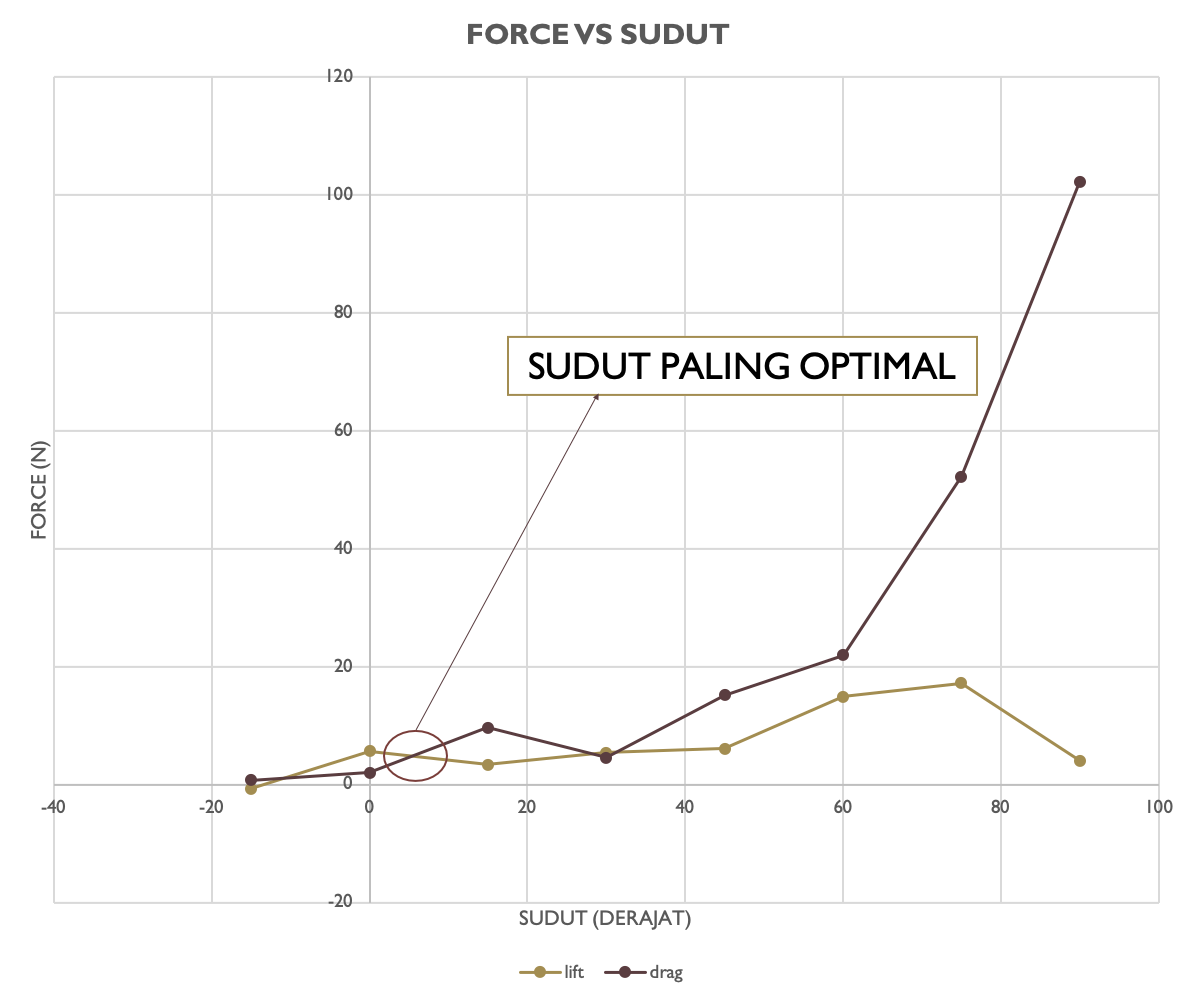
| + | Namun dapat dilihat hasil grafik memperlihatkan bahwa terdapat dua titik yang beririsan. Untuk itu kita perlu mencari menggunakan optimasi untuk melihat dimana persisnya sudut serang paling optimal | ||
| + | |||
| + | 5) Untuk melakukan optimasi, kami membutuhkan persamaan y(x) pada Drag Force dan Lift Force yang sudah dicari tadi menggunakan Excel. Lalu menggunakan Bataan sudut 0-90 derajat. Karena setelah kami coba, hasil jika dimasukkan -15 derajat hasilnya akan sama saja. Lalu setelah itu, kami menggunakan Metode Numerik dengan Bahasa Python dengan aplikasi Jupiter Notebook. Hasil pemograman dibuat dua kali. Yang pertama menggunakan objective persamaan drag lalu yang kedua menggunakan objective persamaan lift. Hasil dari kedua pemograman berupa berikut : | ||
| + | |||
| + | 1. Objective drag Force | ||
| + | Hasil dari program ada di sebelah kanan | ||
| + | [[File:Program Obj Drag.Kelompok8.png]] | ||
| + | |||
| + | 2. Objective Lift Force | ||
| + | Hasil dari program ada di sebelah kanan | ||
| + | [[File:Program Obj Lift.Kelompok8.png]] | ||
| + | |||
| + | 6) Melihat dari kedua hasil optimasi, kami mengambil kesimpulan bahwa titik optimasi didapatkan pada saat sudut sekitar 10 derajat karena force yang diberikan lebih sedikit dibanding pada saat sudut sekitar 30 derajat. Jadi dapat dikatakan bahwa sudut paling optimal pada saat sudut serang sebesar 10.632244814991312 derajat. | ||
| + | |||
| + | [[File:Sudut Paling Optimal.Kelompok8.png]] | ||
| + | |||
| + | |||
| + | = Artificial Neural Networks (ANN) = | ||
| + | |||
| + | |||
| + | [[File:annlast.jpg]] | ||
Latest revision as of 11:19, 1 July 2024
Hello!
Nama : Marcellino Lorenzo
NPM : 1806201011
Mahasiswa Teknik Mesin 2018
Contents
- 1 Pertemuan Pertama
- 2 Progress Belajar Python
- 3 Pertemuan Kedua
- 4 Pertemuan Ketiga
- 5 Pertemuan Keempat
- 6 9/10/19
- 7 Quiz, 16 Oktober 2019
- 8 Ujian Tengah Semester
- 9 Video UTS
- 10 Tugas, 30 Oktober 2019
- 11 CFD Drag Force (Tugas Kelompok)
- 12 Tugas Optimasi Sudut Serang Pada Airfoil
- 13 Artificial Neural Networks (ANN)
Pertemuan Pertama
Rabu, 4 September 2019
Pada pertemuan pertama kelas Metode Numerik pada hari Rabu, 4 September 2019, kami bertemu dengan Dr. Ahmad Indra atau Pak DAI dan Pak Radon. Kami diajarkan brain storming tentang mengapa kami perlu belajar kalkulus di jurusan teknik mesin. Menurut saya, kalkulus penting dipelajari oleh semua calon sarjana teknik karena kalkulus adalah ilmu dasar keteknikan. Di mesin sendiri, kalkulus berguna untuk menghitung segala macam benda terutama saat kami mendesain suatu benda seperti pipa, jalur udara, dll.
To do list 1 minggu kedepan :
- Belajar bahasa pemrograman (Python)
- Coba susun berdasarkan flow chart
- Buat suatu program untuk memecahkan suatu masalah atau menjawab pertanyaan di papan tulis
- Minggu depan jika mau mempresentasikan hasil program akan mendapat bonus atau tambahan nilai
- Semangat !!!
Progress Belajar Python
Minggu, 8 September 2019, saya bermain ke kost teman saya. Dia bernama Jovi Handono, mahasiswa fakultas ilmu komputer yang kebetulan 1 kost dengan saya. Dia adalah teman saya sejak SD. Saya datang ke kamar dia untuk belajar Python. Malam ini saya diajarkan banyak hal dasar oleh Jovi mulai dari dasar-dasar bahasa pemrograman. Saya memulai dengan mendownload Python di https://python.org . Setelah itu Jovi mulai mengajarkan berbagai hal tentang dasar-dasar bahasa python dengan referensi buku Numerical Method for Engineering with Python 3. Malam ini saya belajar =
Print Variabel, String Integer If List Loop Slicing dll
Keesokan hari nya saya mencoba belajar online melalui YouTube dan website sembari berusaha membuat codingan untuk menyelesaikan tugas yang diberi minggu lalu, membuat codingan untuk menyelesaikan T(x) = X^2 - 1 / X - 1
Pertemuan Kedua
Hari ini kami belajar tentang Python. Setelah itu kami diberi syntax seperti ini
Tuples
rec = ("Marcellino","Lorenzo",(18,4,00))
NamaAwal,NamaAkhir,tanggallahir = rec
print(NamaAwal)
TahunLahir = tanggallahir[0]
print(TahunLahir)
name = rec[0]+" "+rec[1]
print(name)
print(rec[0:2])
Saat di run, maka ini akan menghasilkan kalimat
Marcellino
18
Marcellino Lorenzo
('Marcellino', 'Lorenzo')
4
dari hasil ini saya dapat memahami rec adalah merekam data menjadi semacam database dan mirip dengan fungsi list, lalu angka rec[0] dll karena angka dalam Python dimulai dari 0 sehingga, saat mengetikan rec[0] maka yang keluar adalah list pertama yaitu "Marcellino". Beitu juga dengan sistem print untuk mencetak tulisan. Jadi saat semua sudah saya tulis maka akan tercetak nama dan juga tanggal lahir yaitu 18.
List
a = [1.0,2.0,3.0] a.append(4.0) print(a) a.insert(0,0.0) print(len(a)) a[2:4] = [1.0, 1.0, 1.0]
Jika ini di run, maka akan menghasilkan
[1.0, 2.0, 3.0, 4.0] 5
Ini adalah contoh simple penggunaan Python, syntax diatas adalah contoh penggunaan list. Seperti dilihat, awalnya hanya ada 3 angka di dalam list yaitu 1,2,3.
Dibaris berikutnya, ditambahkan perintah untuk menambahkan angka 4 dan juga menambahkan angka 0 di baris pertama (0).
Maka saat perintah ini di run akan menghasilkan baris baru yaitu (1,2,3,4).
Pertemuan Ketiga
Rabu, 18 September 2019, kami mengerjakan test tentang baris Fibonacci dengan menggunakan Python. Kami wajib membuat algoritma, "flow chart", dan bahasa Python-nya.
Algoritma nya adalah : Fn = F(n-2) + F(n-1)
Untuk bahasa Python nya (dengan While.loop)
nNum = 15 num = 1 num1 = 1 num2 = 1 count = 0
while (count<nNum):
print(num1)
num = num1 +num2
num1 = num2
num2 = num
count +=1
nNum menunjukkan hingga baris ke berapa baris Fibonacci yang ingin ditampilkan. num1 = 1 menunjukkan baris dimulai dari 1 bukan 0. Count +=1 sebagai operasi hitung.
(dengan Subroutine)
# Subroutine
# Recurrence Relation
# Fn = Fn-1 + Fn-2
def recur_fibo(n):
if n <= 1:
return n
else:
return(recur_fibo(n-1)+recur_fibo(n-2))
nNum = 15
for i in range(nNum):
print(recur_fibo(i))
Pertemuan Keempat
(Sebelum Hilang dari page Pemodelan Komputer)
Dari diskusi hari ini, kita dapat mempelajari pentingnya mempelajari suatu model. model dapat berarti representasi, simplifikasi, dan asumsi. Dengan mempelajari suatu pemodelan kita dapat memahami cara pikir dan alur berpikir suatu proses. Sebagai contoh dari suatu fondasi yang terlihat 3D dan memiliki banyak unsur, agar mempermudahnya kita dapat membuat suatu pemodelan dan menjadikan nya 2D. Kita dapat melihat gaya2 yang bekerja di dalam fondasi secara lebih jelas saat kita membelahnya menjadi 2D. Ini lah contoh kecil dari pemodelan.
9/10/19
hari ini mempelajari apa yang bisa dilakukan komputer dalam membantu kita menghitung
mempelajari sistem persamaan
mau sampai 1 juta juga masih bisa dihitung komputer
aspek metnum dalam mesin :
1. (tidak dilanjutkan)
kita harus menjadi orang cerdas bukan hanya pintar. apakah surga dan neraka ada sedangkan belum terbukti ?
kita harus memperhatikan hal-hal kecil seperti udara.
Komputasi Teknik, Differential Equation
Metode Runge Kutta
Metode numerik pasti ada error tapi dapat digunakan untuk pendekatan semua masalah
1. Pers diferensial
2. Initial Condition
Quiz, 16 Oktober 2019
Jawaban soal 2.1 dan 7.1 (dari buku Numerical Method for Engineering with Python 3)
Soal 2.1
#Mendelegasikan perintah dari library
from numpy import linalg
import numpy as np
#Memasukan nilai Matriks per baris
bar1 = [0,0,2,1,2]
bar2 = [0,1,0,2,-1]
bar3 = [1,2,0,-2,1]
bar4 = [0,0,0,-1,1]
bar5 = [0,1,-1,1,-1]
#Mengaplikasikan penghitungan matriks masing-masing baris
nmat = np.array ([bar1,bar2,bar3,bar4,bar5])
print ("n Matrix adalah sebagai berikut:")
print (nmat)
cons = np.array ([1,1,-4,-2,-1])
print ("Matrix Y adalah sebagai berikut:")
print (cons)
jawab = linalg.solve (nmat,cons)
#Mencari nilai X
x1val = int(jawab[0])
x2val = int(jawab[1])
x3val = int(jawab[2])
x4val = int(jawab[3])
x5val = int(jawab[4])
#Menampilkan hasil nilai X
print ("hasil X adalah :")
print ("x1= ",x1val)
print ("x2= ",x2val)
print ("x3= ",x3val)
print ("x4= ",x4val)
print ("x5= ",x5val)
Maka jika di run akan menghasilkan hasil :
x1 = 3 x2 = -2 x3 = 1 x4 = 1 x5 = -1
Soal 7.1
def dydx(x, y):
return ((x**2 - 4*y))
# Mencari nilai Y dari nilai X dengan h
# dan nilai saat X0 dan Y0.
def rungeKutta(x0, y0, x, h):
# Menghitung dengan step size
# step height h
n = (int)((x - x0)/h)
y = y0
for i in range(1, n + 1):
"Jalankan Runge Kutta Formulas untuk mendapat nilai Y berikutnya"
k1 = h * dydx(x0, y)
k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)
k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)
k4 = h * dydx(x0 + h, y + k3)
# Update nilai Y berikutnya
y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
# Update nilai X berikutnya
x0 = x0 + h
return y
#Misalkan :
x0 = 0
y = 1
x = 0.03
h = 0.01
print ('Nilai dari Y saat di X adalah :', rungeKutta(x0, y, x, h))
Maka jika di run akan menghasilkan hasil :
Nilai dari Y saat di X adalah : 0.8869291754400297
Ujian Tengah Semester
Untuk soal I.A
from math import *
#Menentukan nilai atau besaran masing-masing benda
g = 9.8
m1 = eval(input("massa1 : "))
m2 = eval(input("massa2 : "))
m3 = eval(input("massa3 : "))
k1 = eval(input("koefisien gesek1 : "))
k2 = eval(input("koefisien gesek2 : "))
k3 = eval(input("koefisien gesek3 : "))
a = eval(input("percepatan sistem : "))
teta = eval(input("sudut kemiringan : "))
s = sin(teta)
c = cos(teta)
t1 = m1*g*(s-k1*c) - m1*a
t2 = m2*g*(s-k2*c) + t1 - m2*a
t3 = m3*g*(s-k3*c) + t2 - m3*a
m4 = -(t3 - m1*a)/g
print ("massa benda 4 adalah :",m4)
Jawaban =
massa1 (kg): 2 massa2 (kg): 3 massa3 (kg): 4 koefisien gesek1 : 0.3 koefisien gesek2 : 0.2 koefisien gesek3 : 0.3 percepatan sistem : 0 sudut kemiringan (derajat) : 30 massa benda 4 adalah (kg) : 9.262488096565958
Dengan memasukkan angka seperti diatas, maka jika ingin membuat sistem statis atau tidak mengalami perpindahan, massa benda 4 harus sebesar 9,26 Kg
Untuk soal I.B
from math import *
#Menentukan besaran
g = 9.8
rho = 1.2 #massa jenis udara
cd = eval(input("drag coef: "))
area = eval(input("area: "))
v0 = eval(input("kecepatan awal: "))
m = eval(input("massa mobil (kg): "))
u = eval(input("koef gesek: "))
a = eval(input("percepatan mobil: "))
t = eval(input("waktu (s): "))
fs = g*u
fdrag = (cd*area*rho*v0**2)/2*m
f1 = a
atotal = f1 - (fdrag + fs)
v1 = v0+atotal*t
print ("kecepatan mobil dari diam: ",v1)
Jawaban =
drag coef: 0.8 lebar area: 12 kecepatan awal (m/s): 0 massa mobil (kg): 1000 koef gesek: 0.3 percepatan mobil: 6 waktu (s): 15 kecepatan mobil dari diam: 45.9
Dengan memasukkan angka seperti diatas, maka akan didapatkan hasil kecepatan mobil dari keadaan diam hingga 15 detik kemudian adalah 45,9 m/s atau 165,24 km/jam
Video UTS
Video I.A
Ini adalah video penjelasan dari penyelesaian soal UTS no 1.1
Video I.B
Ini adalah video penjelasan dari penyelesaian soal UTS no 1.2
Video Muhasabah Diri
Tugas, 30 Oktober 2019
Pada pertemuan kali ini, kita diminta untuk membuat penyelesaian permasalahan fisika dengan menggunakan metode Range Kutta.
Kita ibaratkan sekelompok mahasiswa mesin sedang bermain basket di laptek belakang. Kita dapat mencari berapa percepatan bola pada sumbu X dan Y dengan menggunakan metode Range Kutta.
Sumbu X :
from math import *
g = 9.81
m = eval(input("Massa bola (kg): "))
sudut = eval(input("Sudut dalam derajat: "))
a = eval(input("Percepatan: "))
cd = eval(input("Koefisien hambatan udara: "))
alpa = sudut*0.0175
ay = a*(sin(alpa))
ax = a*(cos(alpa))
v0 = 0
x0 = 0
t0 = 0
dt = 0.2
error = 200
lst = []
def dxdt(t0, v0):
return ((ax-(cd*v0**3/2)/m))
while error > 0.01:
k1 = dt*dxdt(t0, v0)
k2 = dt*dxdt(t0+0.5*dt, v0+0.5*dt*k1)
k3 = dt*dxdt(t0+0.5*dt, v0+0.5*dt*k2)
k4 = dt*dxdt(t0+dt, v0+k3*dt)
v1 = v0 + (1/6)*(k1+2*k2+2*k3+k4)
x0 = x0 + dt
v0 = v1
error = ((v1-v0)/v1)
lst.append(1)
print('Kecepatan bola pada sb.X adalah', v1, 'm/s')
Sumbu Y :
from math import *
g = 9.81
m = eval(input("Massa bola(kg): "))
sudut = eval(input("Sudut dalam derajat: "))
a = eval(input("Percepatan: "))
cd = eval(input("Koefisien hambatan udara: "))
alpa = sudut*0.0175
ay = a*(sin(alpa))
ax = a*(cos(alpa))
v0 = 0
x0 = 0
t0 = 0
dt = 0.2
error = 200
lst = []
def dydt(t0, v0):
return ((ay-(g*(cd*v0**3/2)/m)))
while error > 0.005:
k1 = dt*dydt(t0, v0)
k2 = dt*dydt(t0+0.5*dt, v0+0.5*dt*k1)
k3 = dt*dydt(t0+0.5*dt, v0+0.5*dt*k2)
k4 = dt*dydt(t0+dt, v0+k3*dt)
v2 = v0 + (1/6)*(k1+2*k2+2*k3+k4)
x0 = x0 + dt
v0 = v2
error = ((v2-v0)/v2)
lst.append(1)
print('Kecepatan bola pada sb.Y adalah', v2, 'm/s')
Setelah itu kita mendapat hasil seperti berikut :
CFD Drag Force (Tugas Kelompok)
1) Pertama kita mengambil CAD mobil dari yang sudah disediakan. Lalu kami memmasukan CAD kedalam aplikasi CFD untuk melihat Drag Force dengan variasi kecepatan. Untuk membantu kami, kami menggunakan CFDSOF untuk menghitung hal ini. Awalnya kita menentukan besaran mesh yang kita butuhkan, yang kita ambil pada saat mesh berada di tengah mobil untuk melihat besaran Drag Forcenya. Jadi diasumsikan aliran yang melewati mobil bagian paling teratas. Setelah menentukan mesh, kami berlanjut melakukan perhitungan pada aplikasi Paraview yang menjadi third party dari CFDSOF. Pada applikasi ini, kami dapat menghitung Drag Force menggunakan calculator yaitu dengan mengalikan p*Surface x. Setelah kami melakukan percobaan dengan variasi sebanyak 10 kecepatan didapat 10 macam data sebagai berikut :
2) Setelah mendapatkan 10 hasil Drag Force, kami menginput hasilnya kedalam Excel untuk membuat grafik & hasil persamaan yang didapat dari variasi Drag Force terhadap Kecepatan. Berikut hasil fitting curve :
Tugas Optimasi Sudut Serang Pada Airfoil
1) Melakukan pembuatan airfoil pada aplikasi Inventor dengan variasi 8 sudut caranya dengan merotasi airfoil dengan variasi sudut (-15, 0, 15, 30, 45, 60, 75, 90). Foto dibawah ini merupaka Hasil airfoil buatan kelompok 8 berikut dengan dimensinya.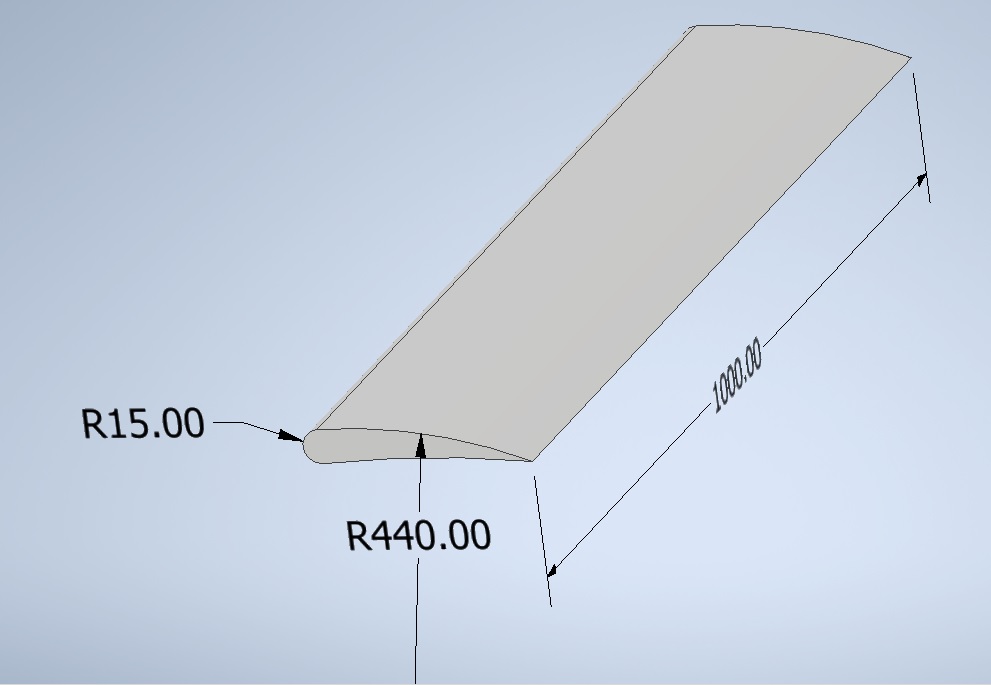
2) Mencari besaran Drag Force & Lift Force pada setiap variasi sudut dengan menggunakan aplikasi CFDSOF menggunakan kecepatan internal sebesar 10 m/s. Melakukan perhitungan dengan calculator pada third party yaitu Paraview. Untuk mencari Drag Force mengalikan p*surface x sedangkan untuk mencari Lift Force mengalikan p*surface y. Berikut ditampilkan salah satu hasil paraview pada sudut 75 derajat.
Lift Force pada sudut 75 derajat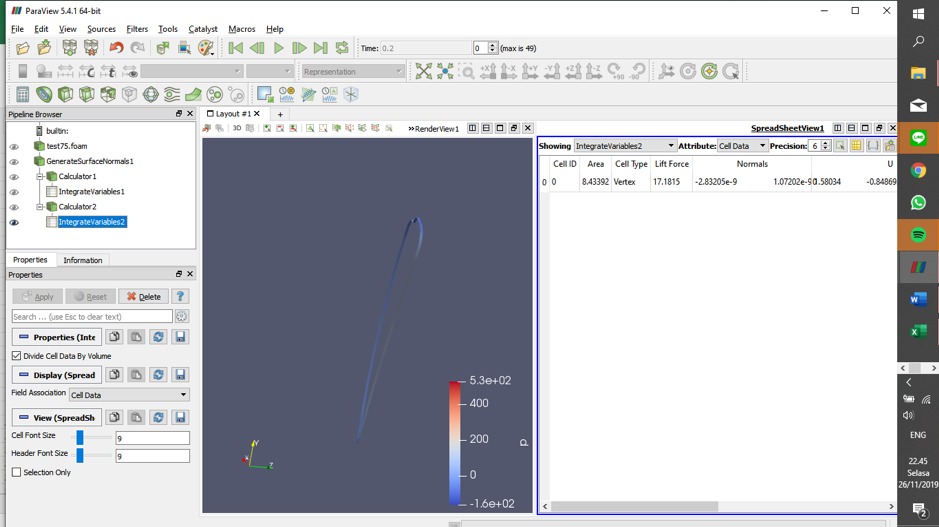
Drag Force pada sudut 75 derajat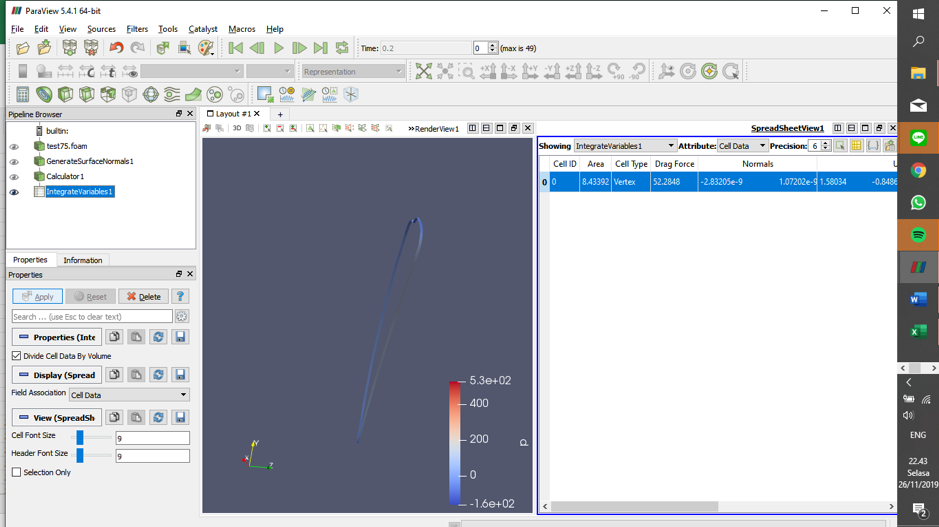
3) Dari hasil setiap nilai Drag Force dan Lift Force pada setiap sudut, nilai tersebut kami input dan melakukan regresi pada Excel. Hasilnya berupa grafik dan berupa persamaan y(x) yang nantinya digunakan untuk mencari optimasi. Besar hasil Drag Force dan Lift Force berdasarkan sudutnya dapat dilihat dibawah ini :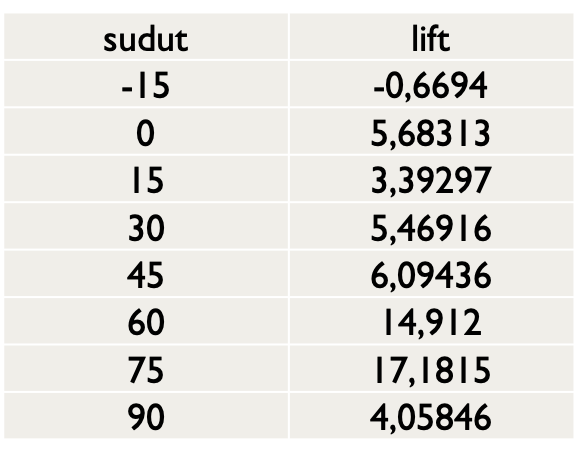
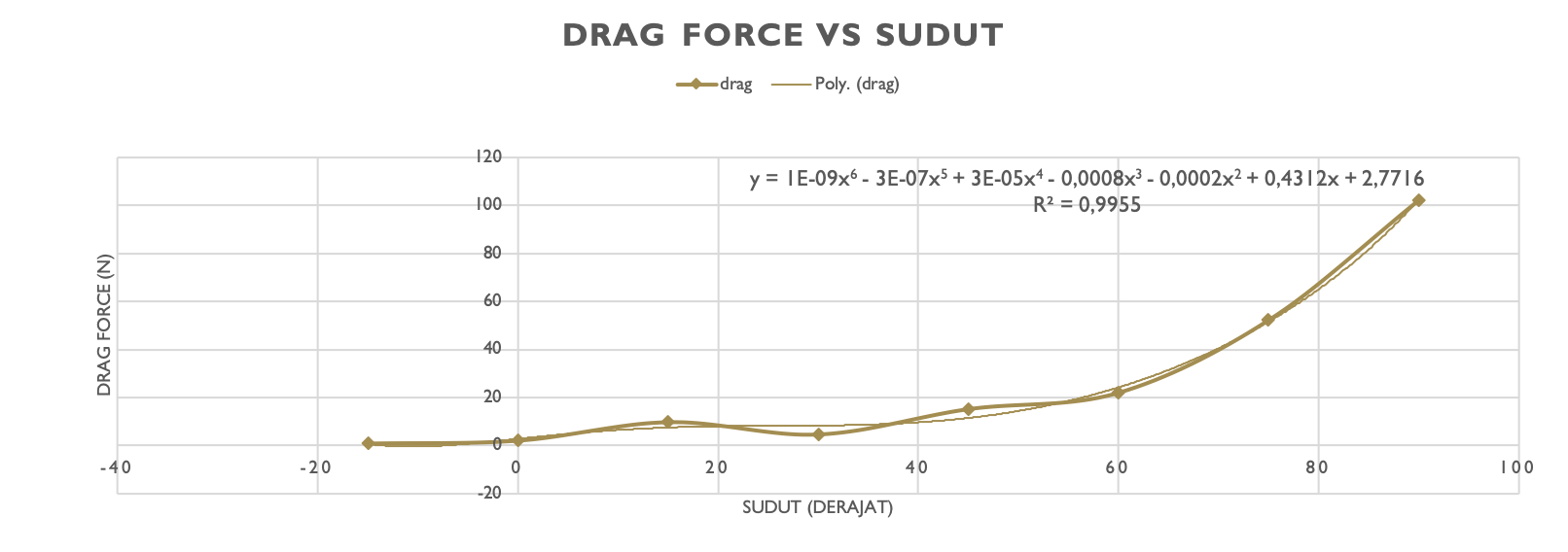
Grafik pada masing-masing force adalah sebagai berikut :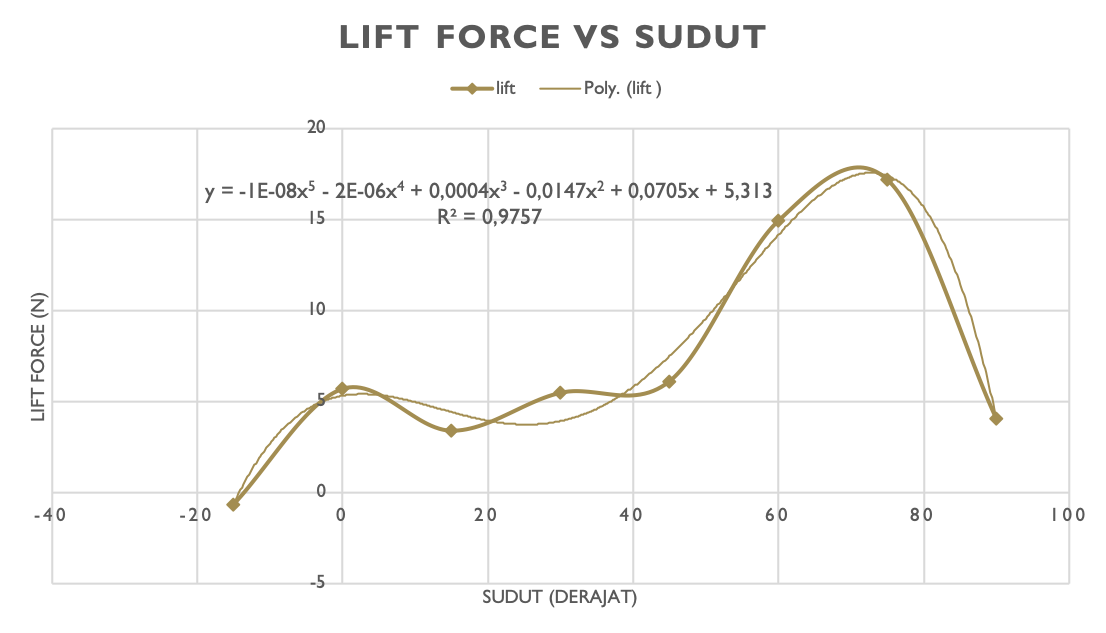
4) Selain membuat grafik pada setiap Force, kami juga menggabungkan dua persamaan antara Lift Force dan Drag Force menjadi satu. Gunanya untuk melihat dititik manakah antara Drag Force dan Lift Force akan bertemu. Hasil dari grafik yang kami buat adalah sebagai berikut :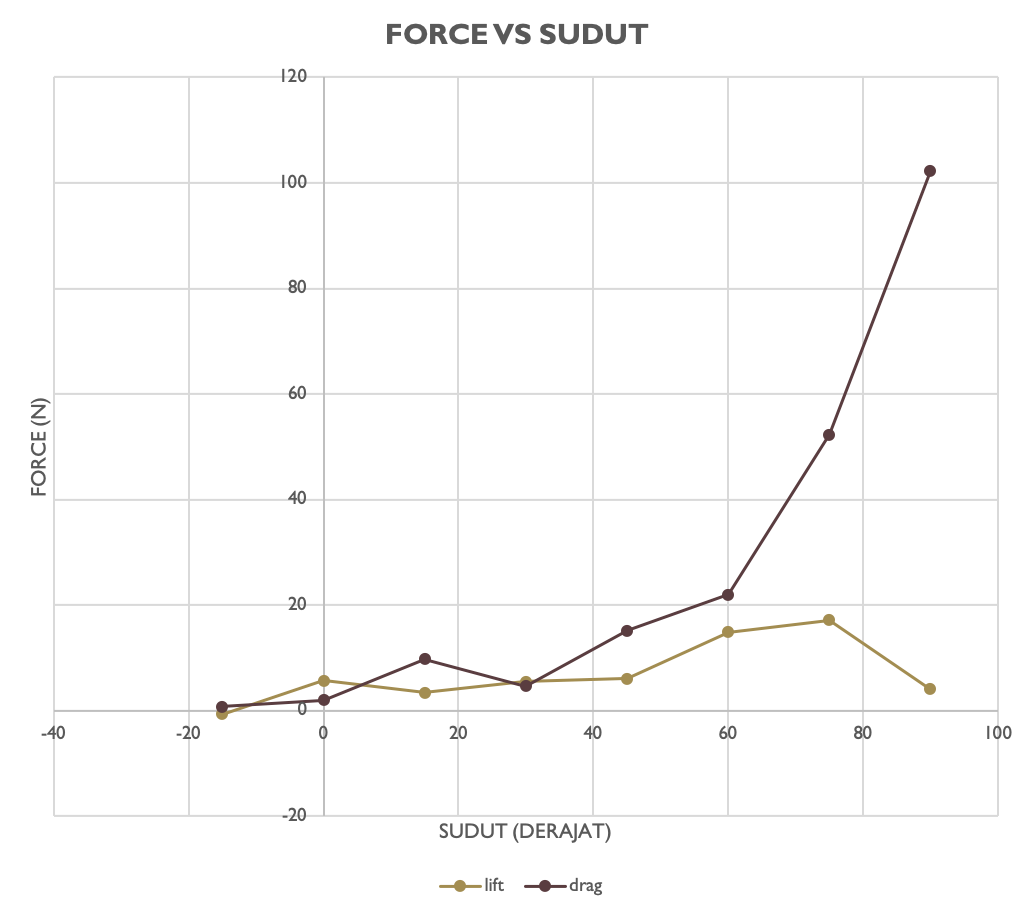
Namun dapat dilihat hasil grafik memperlihatkan bahwa terdapat dua titik yang beririsan. Untuk itu kita perlu mencari menggunakan optimasi untuk melihat dimana persisnya sudut serang paling optimal
5) Untuk melakukan optimasi, kami membutuhkan persamaan y(x) pada Drag Force dan Lift Force yang sudah dicari tadi menggunakan Excel. Lalu menggunakan Bataan sudut 0-90 derajat. Karena setelah kami coba, hasil jika dimasukkan -15 derajat hasilnya akan sama saja. Lalu setelah itu, kami menggunakan Metode Numerik dengan Bahasa Python dengan aplikasi Jupiter Notebook. Hasil pemograman dibuat dua kali. Yang pertama menggunakan objective persamaan drag lalu yang kedua menggunakan objective persamaan lift. Hasil dari kedua pemograman berupa berikut :
1. Objective drag Force Hasil dari program ada di sebelah kanan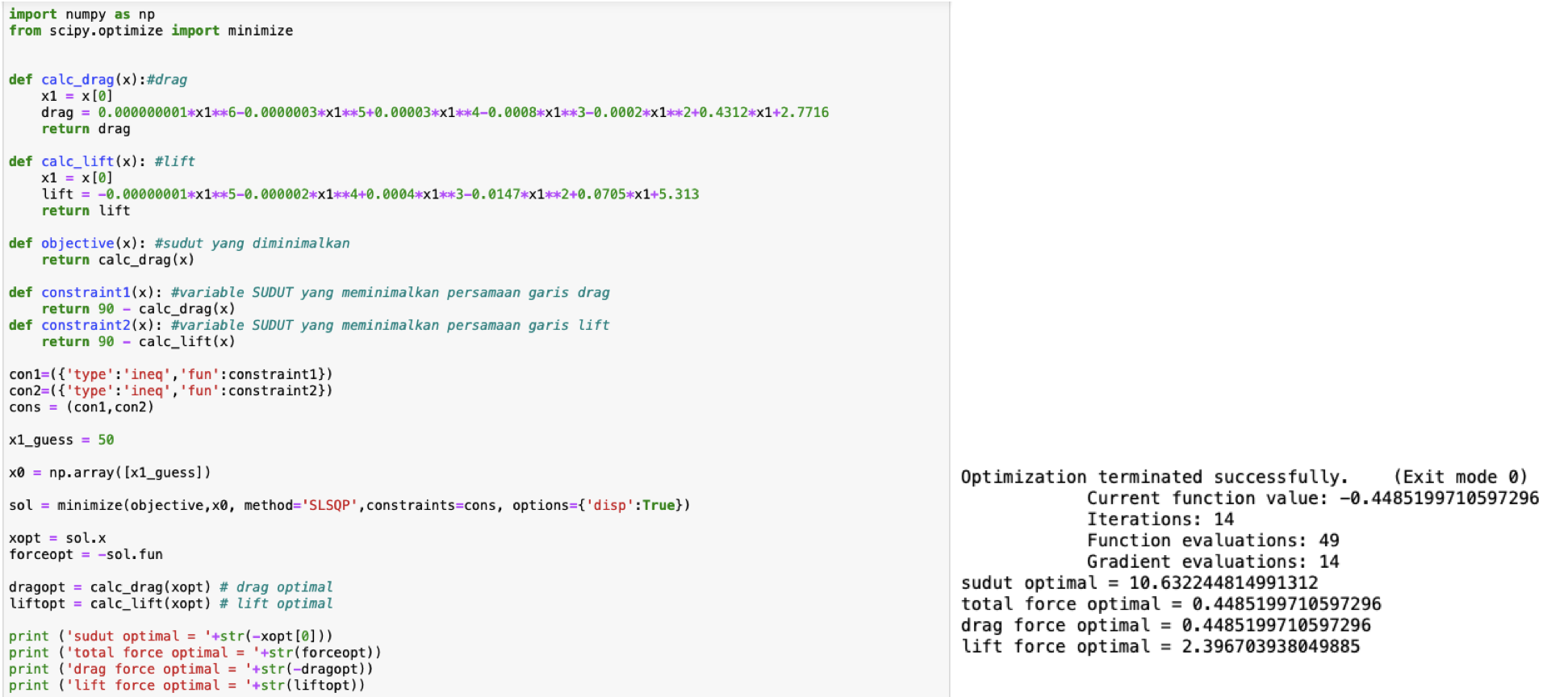
2. Objective Lift Force Hasil dari program ada di sebelah kanan
6) Melihat dari kedua hasil optimasi, kami mengambil kesimpulan bahwa titik optimasi didapatkan pada saat sudut sekitar 10 derajat karena force yang diberikan lebih sedikit dibanding pada saat sudut sekitar 30 derajat. Jadi dapat dikatakan bahwa sudut paling optimal pada saat sudut serang sebesar 10.632244814991312 derajat.