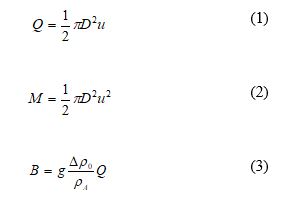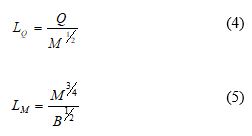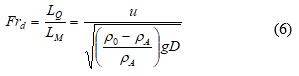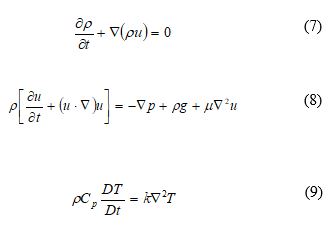Difference between revisions of "Thermal Dispersion Study"
| Line 65: | Line 65: | ||
In this research, the mesh grading is limited only on one axis that is toward the jet flow direction. The grading is concentrated on one point. The point location is varied from 0 m to 10 m from the outfall location (z = 0 m, 5 m, and 6.2 m). | In this research, the mesh grading is limited only on one axis that is toward the jet flow direction. The grading is concentrated on one point. The point location is varied from 0 m to 10 m from the outfall location (z = 0 m, 5 m, and 6.2 m). | ||
| + | |||
| + | == Results and Discussions == | ||
| + | ==== Grid Verification ==== | ||
| + | The model was discretized using a structured-Cartesian grid in which the number of mesh is being controlled at 300,000, 500,000, and 900,000. The velocity contour on the center of the jet is chosen to verify the grid independence. | ||
| + | |||
| + | [[File:Figure_3.png|center|frame|Figure 3]] | ||
| + | |||
| + | [[File:Figure_4.png|center|frame|Figure 4]] | ||
| + | |||
| + | Figure 3 shows the line that is used to map the jet centreline. The results in Figure 4 show that the mesh is considered as independence with 500,000 number of mesh. The results similar to the ZFE region for all of the mesh. It has a difference after the ZFE region and starts aligning again. | ||
| + | |||
| + | [[File:Figure_5a.png|center|frame|Figure 5a]] | ||
| + | [[File:Figure_5b.png|center|frame|Figure 5b]] | ||
| + | |||
| + | The chosen mesh is shown in Figure 5. Furthermore, Figure 5.a shows the mesh towards flow direction. The grading is set to be uniform at first. In the other hands, Figure 5.b shows the mesh configuration facing the inlet surface. The mesh is denser toward the inlet. | ||
Revision as of 11:57, 9 September 2019
Contents
Abstract
Cooling water outfalls of a power plant is one of the engineering applications of discharge that mostly found in coastal areas. It contains buoyant turbulent jets phenomenon that depends on geometry configuration, discharge momentum, and its temperature. Further, thermal dispersion is one of the most critical phenomena that have to be analyzed thoroughly because it directly affects the marine ecosystem and power plant products. With its wide range application in research and engineering problems, computational fluid dynamics (CFD) simulation is done to provide a more detailed analysis of thermal dispersion. Moreover, CFD simulations of discharge are considered to be particularly challenging to perform. The momentum flux, buoyancy flux, and outfall geometry that strongly influence the buoyant jet interaction required the fine mesh to compute. Not only accuracy but also time cost is affected by the mesh. It follows that by optimizing the mesh configuration, an accurate and most economically simulation can be obtained. A three-dimensional model of turbulent jets discharge into stationary ambient seawater is presented in this paper to study certain mesh grading variation that has not been employed before. The simulation is limited only to the near-field area. It is found that mesh with its grading is centered near the outfall could increase the accuracy of the simulation without increasing the number of mesh elements.
Introduction
Cooling Water Outfalls
Thermal or chemical pollutants often discharges to the ocean through outfalls of power plant stations. This activity leads to several changes of condition in the ambient, one of them is the rising of seawater temperature. Consequently, this phenomenon could potentially endanger the seawater ecosystem as well as disturbing the production activity of power plant stations due to the increasing temperature of intake seawater. To overcome those problems, a careful assessment must be done to provide a thorough analysis. The thermal dispersion of discharge occurs in a wide range area. The region close to the outfalls, called by near-field region, that can be characterized as turbulent buoyant jets (Veld, 2013) which the momentum and buoyancy effect are governed the mixing process (Robinson, Wood, Piggott, & Gorman, 2015). Moreover, the discharge in this region form a jet-like flow due to its momentum dominance, however, it becomes plume-like flow when as initial momentum is dissipated and buoyancy dominated.
Theory of Jets and Plumes
The theory about jets-like and plume-like behavior are summarized briefly by Fischer (Fischer, 1979) and Lee and Chu (Lee & Chu, 2003) research. According to Fischer, a pure jet is typically considered as a flow from an orifice with a pure momentum source. He formulated three basic dimensional numbers such as the volume flux, momentum flux, and buoyancy flux to define the influence of momentum and buoyancy force.
From equation (1) to (3), Q, M, and B are volume flux, momentum flux, and buoyancy flux respectively. Further, u is the discharge velocity, D is the outfall diameter, g is the acceleration due to gravity, is the ambient (seawater) density, and
is the initial density differences between the fluid that exit from the outfall and the ambient fluid. These three terms are combined to define two non-dimensional path-lengths.
Where and
area volume length scale and momentum length scale respectively. These length scales will provide useful insight into the dominant processes along the jet trajectory. From equation (4), it becomes clear that
is only depending on the jet geometry. For distances
, the initial outfall geometry has the largest effect on the jet flow, on the other hand, where
, the volume flux becomes less important and the jet is mostly influenced by the initial momentum (Veld, 2013). This distance also makes the flow fully developed. Further, the momentum length scale consists of both momentum- and buoyancy flux. The momentum length scale measures the distance where buoyancy effects become more important than the jet momentum. Research conducted by Veld (2013) proves that momentum length scale is a very important parameter to characterize buoyant jets.
Another important non-dimensional parameter is densimetric Froude number () which gives the hint whether the flow is more jet-like (
) or plume-like (
). The initial densimetric Froude number is given by:
To enrich the understanding of the flow behavior, some researchers had conducted laboratory experiments. One of the studies divides the development of a pure jet into two stages (Albertson, Dal, Jensen, & Rouse, 1950), the zone of the establishment (ZFE) and the zone of established flow (ZEF). Within the ZFE, the jet forms a core that the size of the core is decreasing further from the outfalls. While the core is decreasing, the mixing layer starts to grow. The jet is called fully developed when the mixing layer grows up to the center of the jet. From the experiment, the length of the ZFE is approximately equal to 6.2D. Further than that, the flow enter the ZEF region and assumed to be fully developed. Its axial velocity and concentration profiles are similar to Gaussian distribution (Albertson, Dal, Jensen, & Rouse, 1950).
CFD Research and Exploitation Proposal
Dealing with the near-field region, many studies have been done by CFD to predict how the jet behaves. Robinson et. al. (Robinson, Wood, Piggott, & Gorman, 2015) studied the jet behavior at the near-field region by CFD and compared it with CorJet integral model (Jirka, 2004). They obtained good agreement with the comparison model. The same result is also obtained by Veld (Veld, 2013). The verification process showed good agreement compared with several experimental studies. Further, a question arises on how robust the CFD solution is when it is used in the real object or industrial/engineering needs. The needs of accuracy have to be compromised with the time-cost simulation. The mesh configurations are parameters that directly affect the accuracy and time-cost of the simulation. On previous research conducted by some researchers, some of them stated how they created their mesh, the others are not. It is not a novelty idea on increasing the accuracy without increasing the number of mesh. However, it has not been done in the research of near-field thermal dispersion. The hypothesis starts with changing the mesh grading to gain more accurate results. On Veld (2013), the grading is set finer toward the outfall. However, it could not reach a good accuracy when the number of mesh is decreased. There have to be some ways to exploit the grading configuration to increase accuracy. The present work will study how to increase the results accuracy by varying the mesh grading on a fixed number of elements. The analysis will be done by CFD and use SST k-omega as the turbulence model. Later, the results will be compared with experimental studies. If the hypothesis is proven, then the CFD simulation can be done in less time but still provide good accuracy.
Materials and Methods
Governing Equations
As the high momentum and temperature fluid exit the outflow, the flow field is influenced by the heat and at the same time, the transport of heat is governed by the flow field. Some assumptions are used in these simulations for further elaboration of the governing equations.
- The fluid is assumed to be a continuum
- Incompressible fluid for pressure
- Isotropic
- Constant dynamic viscosity
The flow field is governed by three physical conservation laws such as conservation of mass, momentum, and energy.
Due to the high velocities gradients at the point where the jet enters the ambient fluid, turbulence is introduced into the ambient fluid. Consequently, the jet velocities will fluctuate over time. The SST k-ω turbulence model is employed to construct the mean and fluctuating velocities. According to the assumptions, the density will only change because of the change of temperature. The Boussinesq assumption was used to re-construct the continuity and momentum equation. The density ρ in the gravitational terms is expressed by the linear function of the temperature Τ:
Where β is the thermal expansion coefficient. To define the relation between momentum diffusivity and thermal diffusivity, Prandtl number Pr is introduced.
CFD Modeling
To solve the flow field, the CFD method is used. CFD will discretize the fluid domain into meshes and all the governing equations are calculated within those meshes. The method starts by creating the fluid domain model. The domain volume is 50m x 50m x 30m that is filled with seawater as shown in Figure 1. The outfall is modeled as a circle with a diameter of 1 m on one side with the depth of 15 m from above surface.
The ambient seawater temperature is 293.15 K with thermal expansion 300x10-6 K-1. The jet flow from outfall with a velocity of 3 m/s and temperature of 313.15 K. The computational domain contains six boundary patches, namely inlet, outlet, wall, sea-surface, bottom, and sides. The top part of the domain was sea-surface that is defined as a slip wall. It assumed that there is no heat flux into the seawater from sun radiation. The inlet is where the outfall is. On the same surface at inlet, the wall is defined and applied as a no-slip wall. The bottom surface is located at the bottom of the fluid domain. It is defined as a no-slip wall. Moreover, the outlet is on the opposite surface from the inlet and wall. It is defined as one direction flow boundary. The last is sides, located on the right and left the surface. It is defined as an open boundary where fluid can flow in and out through these surfaces. Next, the grid independency test is being conducted. After finding the independent mesh, that mesh will be used in this mesh grading studies.
Mesh Grading and Study Procedures
Mesh grading is defined as the ratio of the width of the end cell along one edge of a block to the width of the start cell
along that edge.
In this research, the mesh grading is limited only on one axis that is toward the jet flow direction. The grading is concentrated on one point. The point location is varied from 0 m to 10 m from the outfall location (z = 0 m, 5 m, and 6.2 m).
Results and Discussions
Grid Verification
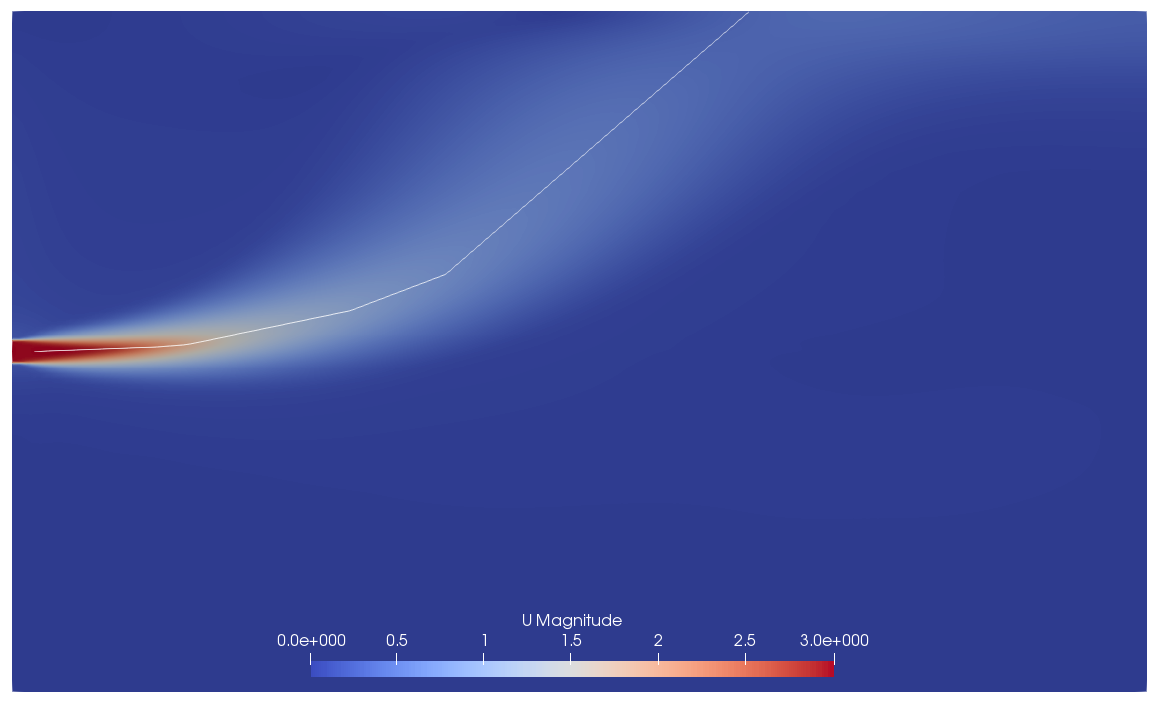
The model was discretized using a structured-Cartesian grid in which the number of mesh is being controlled at 300,000, 500,000, and 900,000. The velocity contour on the center of the jet is chosen to verify the grid independence.
Figure 3 shows the line that is used to map the jet centreline. The results in Figure 4 show that the mesh is considered as independence with 500,000 number of mesh. The results similar to the ZFE region for all of the mesh. It has a difference after the ZFE region and starts aligning again.
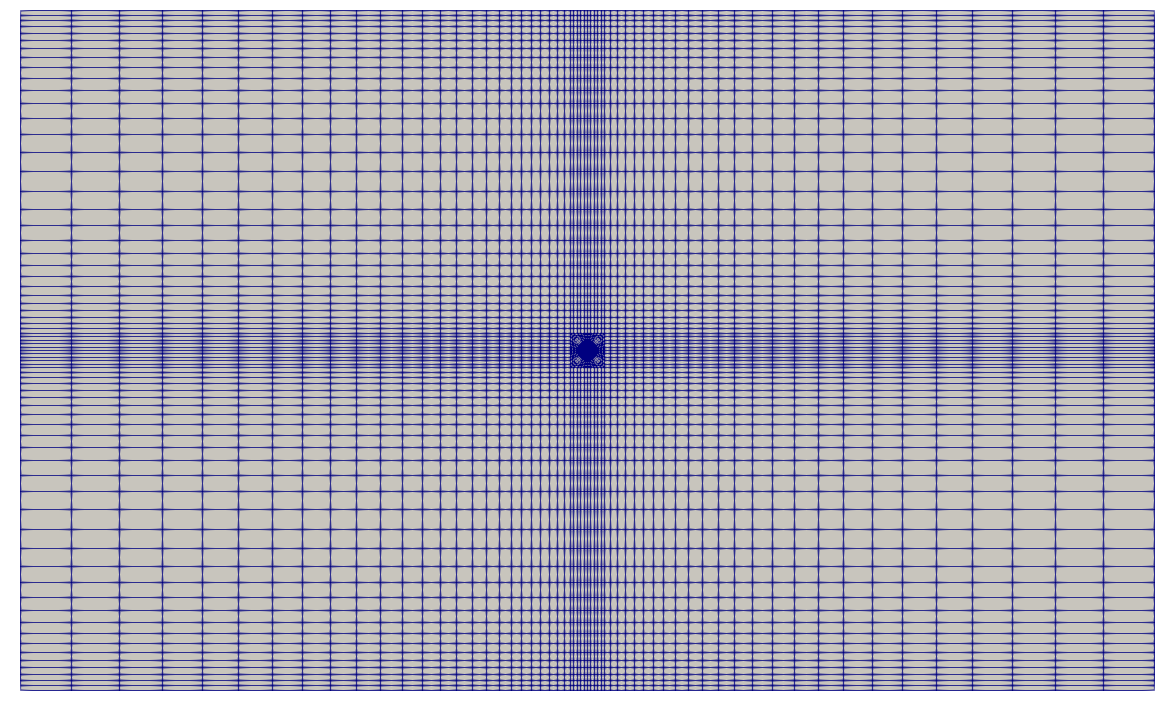
The chosen mesh is shown in Figure 5. Furthermore, Figure 5.a shows the mesh towards flow direction. The grading is set to be uniform at first. In the other hands, Figure 5.b shows the mesh configuration facing the inlet surface. The mesh is denser toward the inlet.