Difference between revisions of "Hazimi Hamar"
Hazimihamar (talk | contribs) |
Hazimihamar (talk | contribs) |
||
| Line 124: | Line 124: | ||
Dalam FEM (Finite Element Method), prinsip Hukum Hooke digunakan untuk menghitung tegangan (stress) dan regangan (strain) dalam elemen-elemen kecil suatu model. Hukum ini diterapkan dalam domain elastis untuk menentukan deformasi atau perpindahan elemen ketika beban diberikan, terutama dalam analisis struktur dan material elastis. Setiap elemen dalam FEM mematuhi hubungan linier antara tegangan dan regangan dalam batas elastisitas, sehingga perpindahan akibat gaya dapat dianalisis secara rinci pada level komponen. Terdapat pada gambar diatas Hukum Hooke menyatakan bahwa gaya (F) yang diterapkan pada sebuah pegas akan menghasilkan perpanjangan (x) yang sebanding, dengan persamaan 𝐹= 𝑘𝑥, di mana 𝑘 adalah kekakuan atau konstanta pegas perpanjangan pegas sebanding dengan gaya yang diterapkan padanya, selama material berada dalam batas elastis. Ini berarti semakin besar gaya, semakin besar perpanjangan yang terjadi. Kedua, ketika gaya dilepaskan, pegas atau material akan kembali ke bentuk atau posisi awalnya jika material tersebut tetap dalam wilayah elastis. Ketiga, Hukum Hooke hanya berlaku selama material berada dalam rentang elastis, di mana deformasi yang terjadi masih bisa pulih sepenuhnya tanpa perubahan permanen pada struktur material. | Dalam FEM (Finite Element Method), prinsip Hukum Hooke digunakan untuk menghitung tegangan (stress) dan regangan (strain) dalam elemen-elemen kecil suatu model. Hukum ini diterapkan dalam domain elastis untuk menentukan deformasi atau perpindahan elemen ketika beban diberikan, terutama dalam analisis struktur dan material elastis. Setiap elemen dalam FEM mematuhi hubungan linier antara tegangan dan regangan dalam batas elastisitas, sehingga perpindahan akibat gaya dapat dianalisis secara rinci pada level komponen. Terdapat pada gambar diatas Hukum Hooke menyatakan bahwa gaya (F) yang diterapkan pada sebuah pegas akan menghasilkan perpanjangan (x) yang sebanding, dengan persamaan 𝐹= 𝑘𝑥, di mana 𝑘 adalah kekakuan atau konstanta pegas perpanjangan pegas sebanding dengan gaya yang diterapkan padanya, selama material berada dalam batas elastis. Ini berarti semakin besar gaya, semakin besar perpanjangan yang terjadi. Kedua, ketika gaya dilepaskan, pegas atau material akan kembali ke bentuk atau posisi awalnya jika material tersebut tetap dalam wilayah elastis. Ketiga, Hukum Hooke hanya berlaku selama material berada dalam rentang elastis, di mana deformasi yang terjadi masih bisa pulih sepenuhnya tanpa perubahan permanen pada struktur material. | ||
| − | ''' | + | '''Stiffness (k)''' pada gambar ini menggambarkan kekakuan pegas, yang berperan serupa dalam elemen-elemen struktural pada model FEM. |
| + | |||
'''Displacement (x)''' menggambarkan perubahan bentuk, yang dalam analisis FEM mengukur deformasi pada titik-titik elemen akibat gaya eksternal. | '''Displacement (x)''' menggambarkan perubahan bentuk, yang dalam analisis FEM mengukur deformasi pada titik-titik elemen akibat gaya eksternal. | ||
| Line 134: | Line 135: | ||
'''Axial Strain''' Regangan aksial (ε) pada arah x, y, dan z dihitung dari tegangan pada ketiga sumbu ini serta efek dari Rasio Poisson, yang menghubungkan tegangan di satu arah dengan perubahan bentuk di arah yang lain. | '''Axial Strain''' Regangan aksial (ε) pada arah x, y, dan z dihitung dari tegangan pada ketiga sumbu ini serta efek dari Rasio Poisson, yang menghubungkan tegangan di satu arah dengan perubahan bentuk di arah yang lain. | ||
| + | |||
'''Shear Strain''' Regangan geser (γ) pada bidang xy, zx, dan yz berhubungan langsung dengan tegangan geser pada bidang yang sama dan Modulus Geser G. Shear strain menunjukkan distorsi atau perubahan bentuk pada bidang tertentu akibat tegangan geser. | '''Shear Strain''' Regangan geser (γ) pada bidang xy, zx, dan yz berhubungan langsung dengan tegangan geser pada bidang yang sama dan Modulus Geser G. Shear strain menunjukkan distorsi atau perubahan bentuk pada bidang tertentu akibat tegangan geser. | ||
'''Axial Stress''' Tegangan aksial (σ) pada arah x, y, dan z diperoleh dengan mengalikan Modulus Young (E), Rasio Poisson (ν), dan regangan aksial pada ketiga arah. Rumus ini menggabungkan pengaruh regangan dari semua arah, yang menunjukkan sifat isotropik dari material tersebut. | '''Axial Stress''' Tegangan aksial (σ) pada arah x, y, dan z diperoleh dengan mengalikan Modulus Young (E), Rasio Poisson (ν), dan regangan aksial pada ketiga arah. Rumus ini menggabungkan pengaruh regangan dari semua arah, yang menunjukkan sifat isotropik dari material tersebut. | ||
| + | |||
'''Shear Stress''' Tegangan geser (τ) pada bidang xy, yz, dan zx berkaitan langsung dengan shear strain pada bidang yang sama dan Modulus Geser (G). Shear stress ini menunjukkan tegangan yang menyebabkan distorsi di bidang tertentu. | '''Shear Stress''' Tegangan geser (τ) pada bidang xy, yz, dan zx berkaitan langsung dengan shear strain pada bidang yang sama dan Modulus Geser (G). Shear stress ini menunjukkan tegangan yang menyebabkan distorsi di bidang tertentu. | ||
'''Diagram Kubus''' di tengah gambar mengilustrasikan tegangan pada berbagai arah pada suatu elemen kubus material. Arah '''tegangan aksial''' (σ_x, σ_y, σ_z) ditunjukkan di sepanjang sumbu utama x, y, dan z, sementara '''tegangan geser''' (τ_xy, τ_yz, τ_zx) ditunjukkan pada bidang antar-sumbu. Diagram ini membantu memvisualisasikan bagaimana tegangan bekerja pada elemen dalam ruang tiga dimensi. Transformasi Stress and Strain persamaan pada gambar menunjukkan bahwa tegangan dan regangan saling berhubungan melalui transformasi berdasarkan Hukum Hooke dalam 3D. Transformasi ini memperhitungkan pengaruh dari semua komponen tegangan pada regangan aksial dan pengaruh regangan pada tegangan aksial, mencerminkan sifat mekanik material isotropik. | '''Diagram Kubus''' di tengah gambar mengilustrasikan tegangan pada berbagai arah pada suatu elemen kubus material. Arah '''tegangan aksial''' (σ_x, σ_y, σ_z) ditunjukkan di sepanjang sumbu utama x, y, dan z, sementara '''tegangan geser''' (τ_xy, τ_yz, τ_zx) ditunjukkan pada bidang antar-sumbu. Diagram ini membantu memvisualisasikan bagaimana tegangan bekerja pada elemen dalam ruang tiga dimensi. Transformasi Stress and Strain persamaan pada gambar menunjukkan bahwa tegangan dan regangan saling berhubungan melalui transformasi berdasarkan Hukum Hooke dalam 3D. Transformasi ini memperhitungkan pengaruh dari semua komponen tegangan pada regangan aksial dan pengaruh regangan pada tegangan aksial, mencerminkan sifat mekanik material isotropik. | ||
Revision as of 07:45, 29 October 2024
Hello, Welcome my first Home Page, in the form of assignment for meeting 1 in the Finite Element & Multhiphysics (27/08/2024)
Dalam kerangka DAI5 Framework yang merupakan konsep dari bapak Dr. Ahmad Indra berperan sebagai inisiator dalam kerangka ini, dengan pandangan filosofis yang mendasar, "I am My Consciousness." Yang dapat digunakan sebagai bentuk pemecahan masalah dan dapat menghasilkan bukti dan solusi.
1. Intention “Niat” sangat penting dalam kerangka DAI5 karena menetapkan tujuan atau hasil yang diinginkan dari proses berpikir. Hal ini selaras dengan filosofi kesadaran, di mana niat merupakan aspek kunci dari keterlibatan mental kita dengan dunia. Memahami niat membantu menjaga fokus dan kejelasan, serta mencegah gangguan, sehingga individu dapat tetap sesuai dengan nilai dan tujuan inti kita. Pemikiran yang disengaja ini menjadi dasar bagi banyak teori kognitif dan emosional, di mana kesadaran akan alasan berpikir dapat membentuk tindakan.
2. Initial Thinking “Pemikiran Awal” Tahap ini merupakan fase eksplorasi di mana individu bebas menggali dan merenungkan masalah. Ini adalah waktu untuk berasosiasi secara bebas tanpa penilaian atau batasan langsung. Pemikiran awal membantu mengenali berbagai aspek suatu masalah, mendorong peserta untuk mengandalkan intuisi dan pengalaman mereka. Tahap ini bertujuan mengumpulkan beragam perspektif sebelum beralih pada solusi yang lebih terfokus.
3. Idealization adalah tentang membayangkan skenario dan solusi terbaik yang mungkin, melampaui keterbatasan saat ini. Tahap ini mendorong berpikir kreatif dan mengajak individu untuk berpikir tanpa batas, membayangkan solusi ideal. Ini sejalan dengan konsep kesadaran yang menantang individu untuk melihat melampaui keadaan dan keterbatasan saat ini. Idealization tidak berarti mengabaikan realitas, melainkan memupuk harapan dan aspirasi untuk memotivasi tindakan lebih lanjut.
4. Instruction Set idealisme yang dikembangkan selama tahap sebelumnya ke dalam langkah-langkah yang dapat ditindaklanjuti. Hal ini penting karena solusi ideal perlu didasarkan pada kenyataan melalui implementasi praktis. Menciptakan seperangkat instruksi yang jelas dan mudah dikelola membantu individu menerjemahkan pemikiran dan aspirasi mereka ke dalam tindakan nyata, memfasilitasi kemajuan menuju tujuan mereka. Efektivitas fase ini bergantung pada kejelasan dan kelayakan langkah-langkah yang dikembangkan, yang menegaskan kembali pentingnya kesengajaan dan refleksi selama proses berlangsung.
Contents
Simple Pipe design Modelling
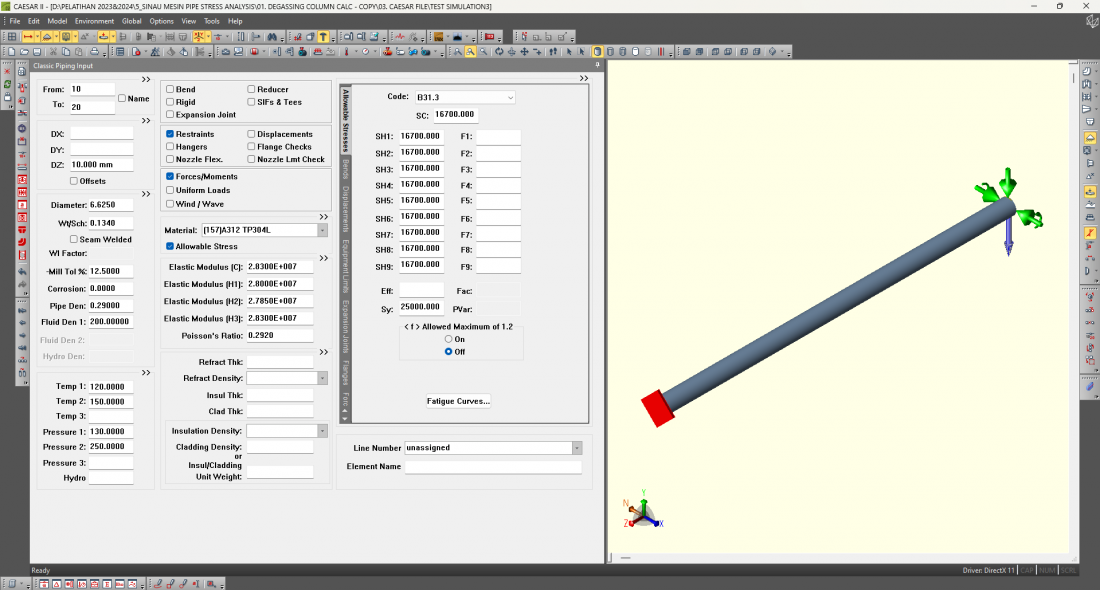
At the 4th meeting the Finite Element & Multhiphysics (4/9/2024) We do simple pipe design using Caesar II with classic piping input >> we make pipe models according to standard code B31.3 and set the layout of the pipe model including pipe length, pipe diameter, pipe wall thickness or sch, pipe fluid density, temperature and pressure are also set.
Material = A312 304L (stainless steel)
Pipe length = 4m
Diameter = 6in
Wallthicknes = 10s
Force/Moment = 8000N
Temp Operation = 120F Temp Design = 150F
Pressure Operation = 130lb./sq.in.
Pressure design = 270lb./sq.in.
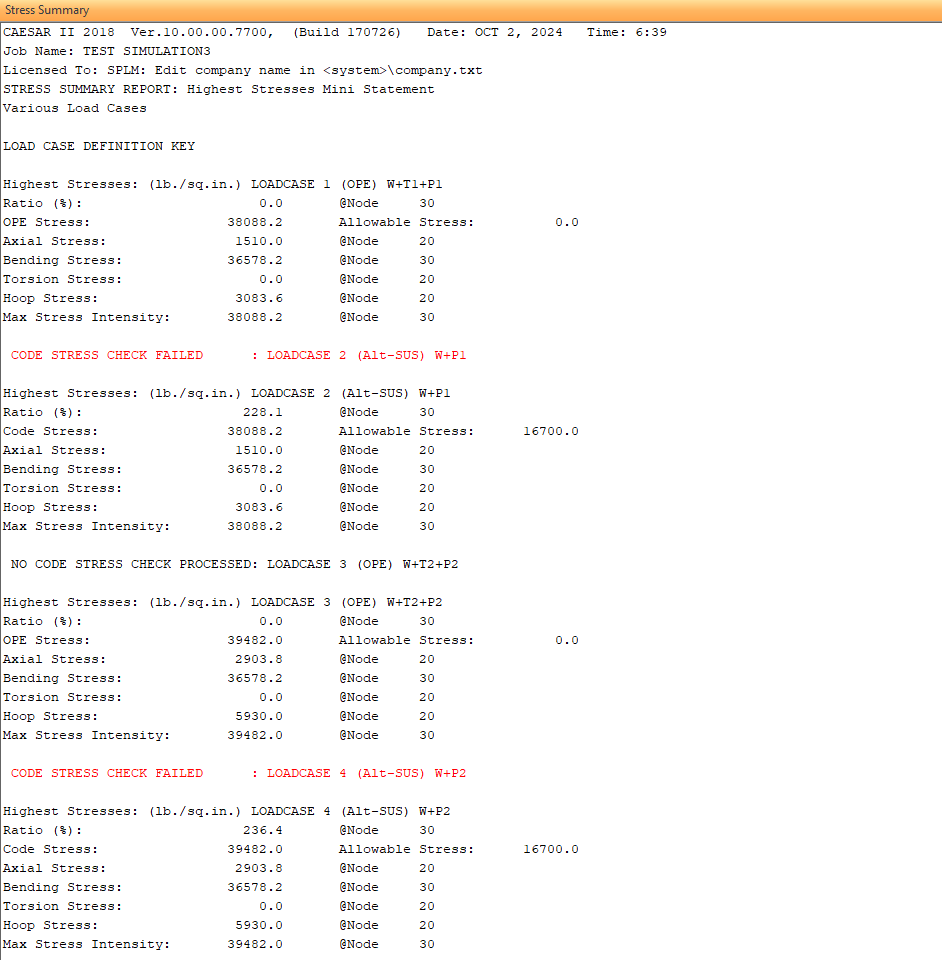
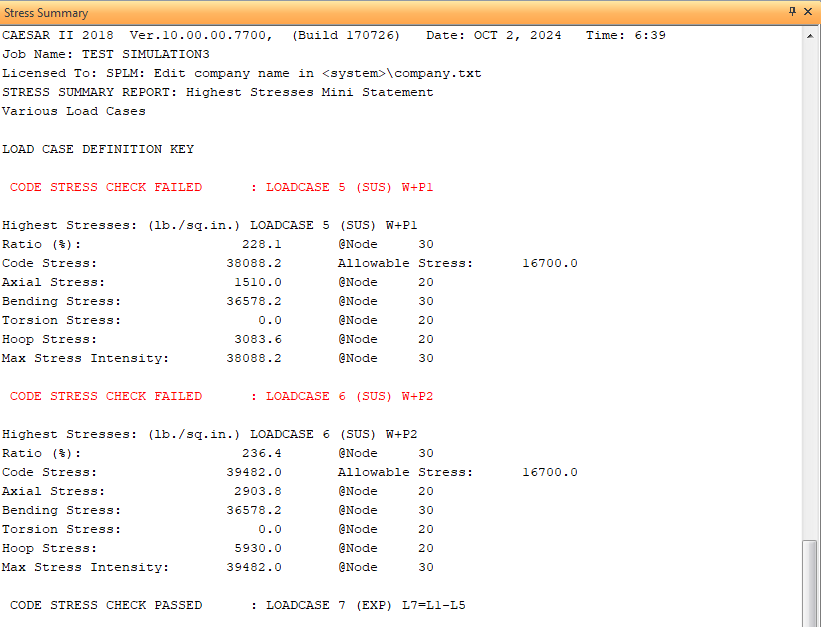
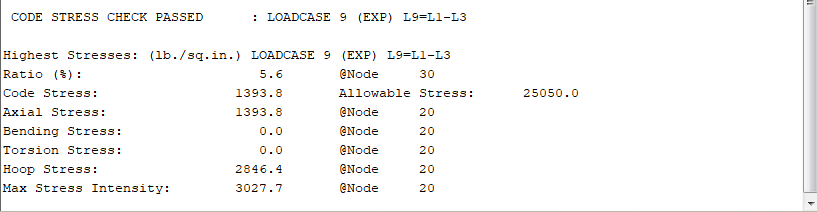
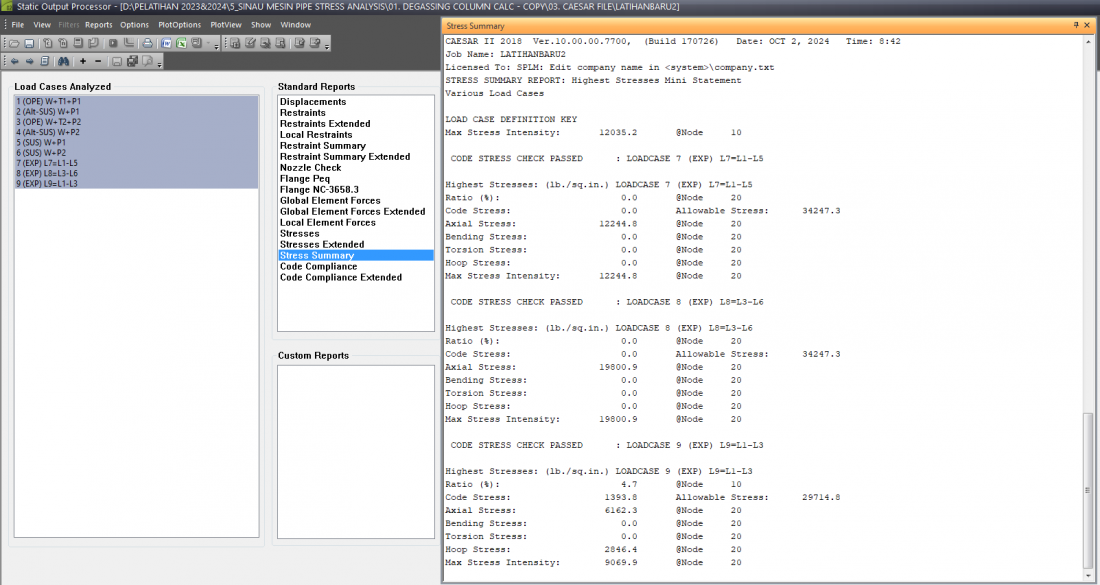
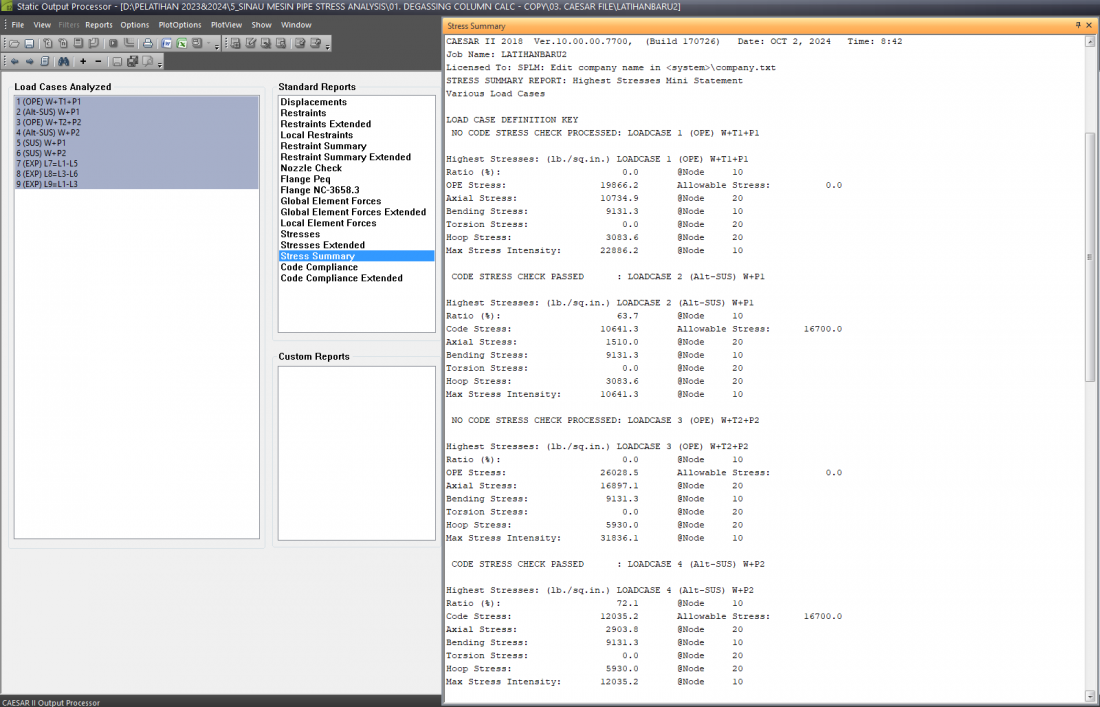
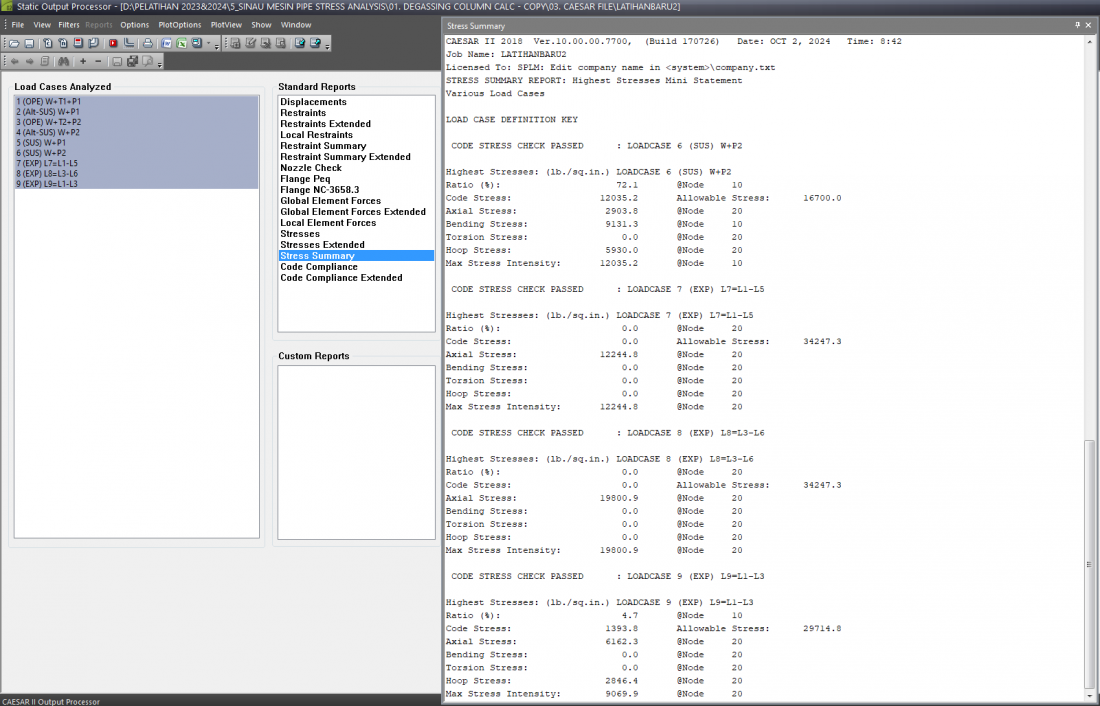
<<<Stress Summary All Conditions:>>>
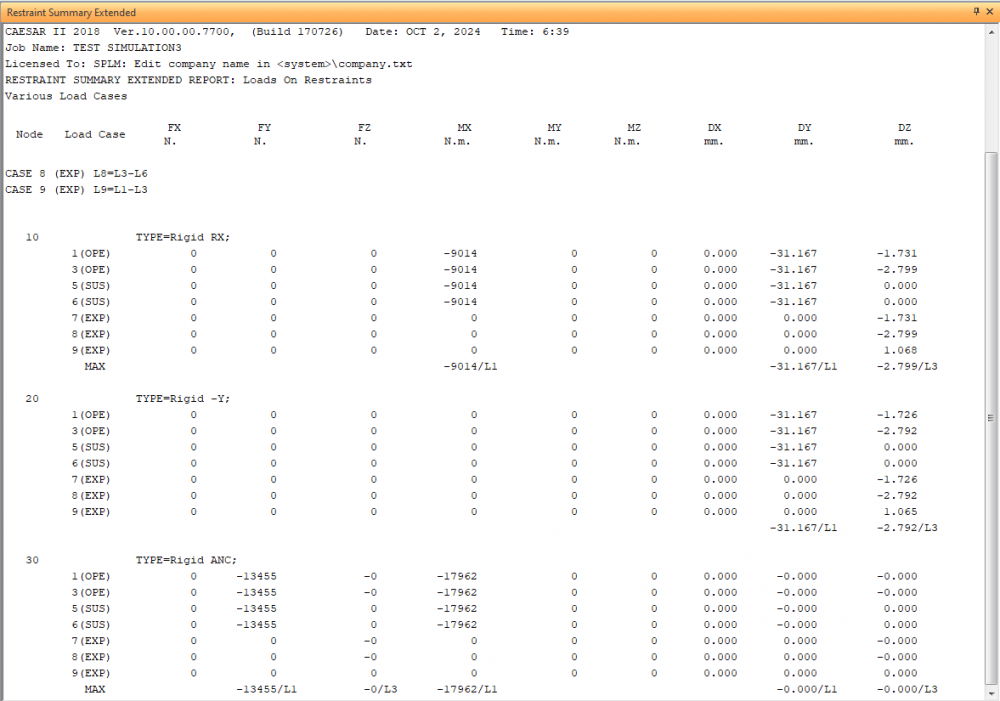
<<<Restraint Summary All Conditions:>>>
Restraint Summary hanya mengeluarkan hasil Force dan Moment pada input pemodelan Temperature dan Pressure dari Design and Operation yang menunjukkan perubahan arah sumbu gaya dan momen.
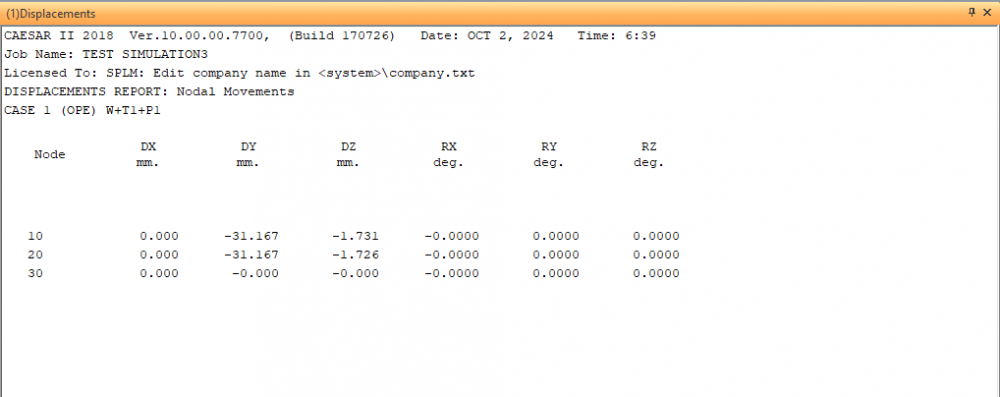
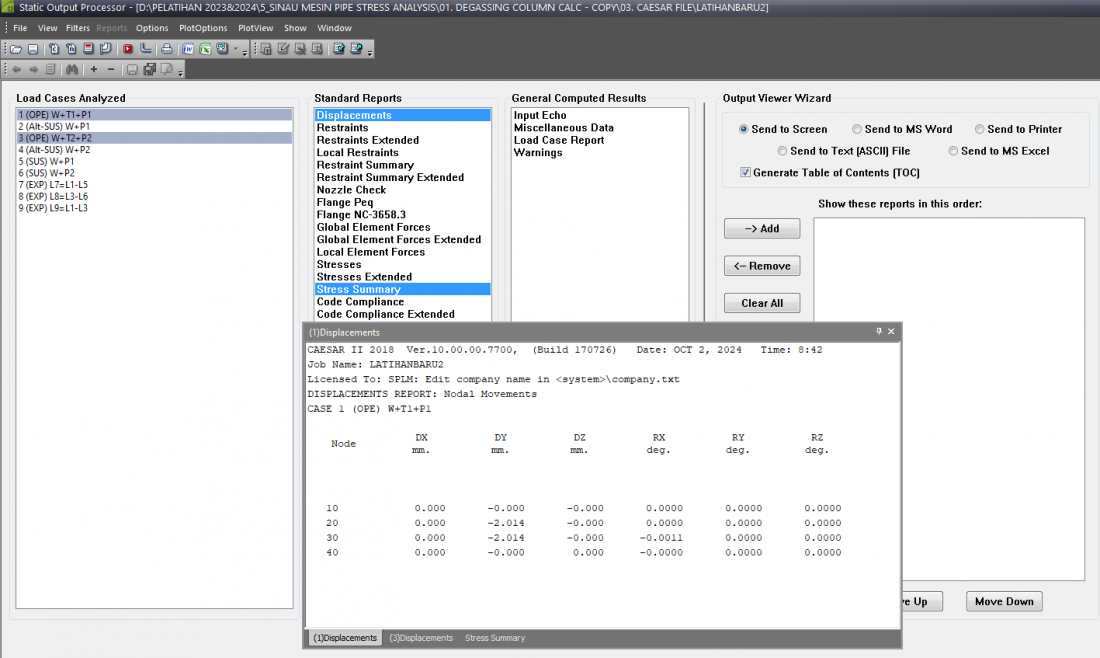
<<<Displacement Conditions:>>>
Displacement pada kondisi Temperatur dan Tekanan dari Desain dan Operasi mengeluarkan hasil defleksi dari semua node pemodelan.
At the 5th meeting the Finite Element & Multhiphysics (10/9/2024)
1. Bagaimana distribusi normal force pada elemen truss ketika mendapatkan beban aksial yang tidak merata?
2. Bagaimana pengaruh variasi kekakuan pada elemen beam terhadap distribusi defleksi akibat beban merata?
1D Element Bar Analysis with Abaqus
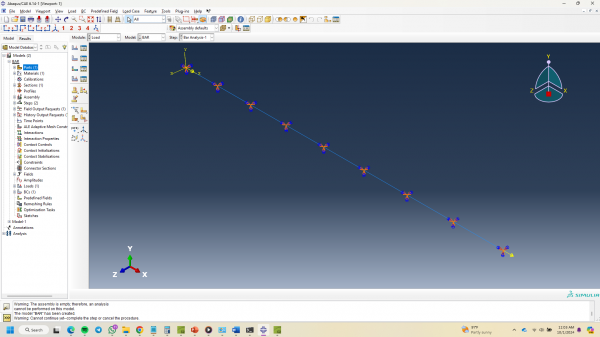
Pada pertemuan berikutnya menggunakan software calculix (Abaqus) untuk kasus sederhana berupa 1D Element Bar. Dengan beberapa parameter sebagai berikut:
Panjang Batang = 4000 mm
E = 200e3 Mpa
F = 10e3 N
Load = 1000 N
Modulus Young = 200kPa
Satu ujung batang fixed, sementara ujung batang lainnya ditarik dengan gaya external sebesar 1000N. Berikut pada gambar dibawah ini:
Pipe 2D Element Hollow Analysis with Caesar 2018
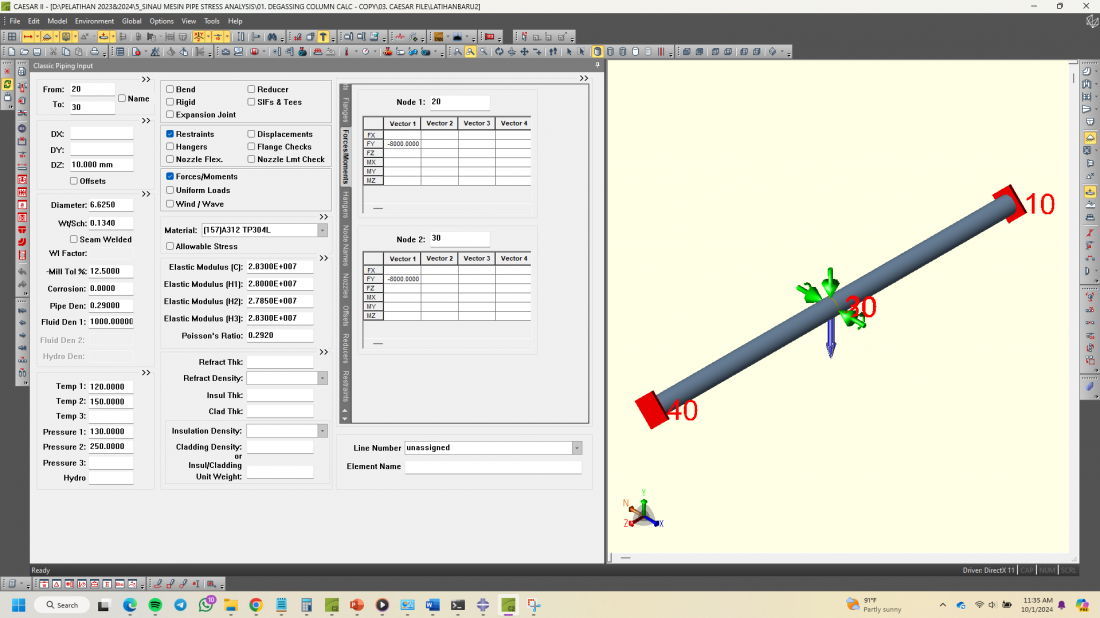
Pada pertemuan berikutnya mencoba untuk melakukan calculix menggunakan Caesar 2018, untuk kasus sederhana. Dengan parameter sebagai berikut:
F = 8000N
Panjang Pipa = 1995 + 1995 = 4000mm
Node titik tengah sebagai tumpuan vertikal load (Force/Moment) = 10mm
dengan koefisient gesek 0.3Mu (karna Steel to Steel)
uniformload ke 2 batang pipa ke arah z 1.5lb.in dari acuan Code B31.3. Displacement dan modelling terdapat pada gambar dibawah ini:
<<<Modelling 2D Element:>>>
<<<Displacement Conditions:>>>
<<<Stress Summary:>>>
Learning Notes
Pada analisis (Finite Element Method/FEM) atau metode elemen hingga terdapat elemen elemen 1D, elemen 2D, dan elemen 3D yang dapat digunakan untuk menyesuaikan bentuk dari kompleksitas objek sebuah bidang yang akan dianalisis. Berikut perbedaan dan penjelasan dari masing-masing elemen berdasarkan analisis multiphysiscs:
1. Elemen 1D Elemen 1D berbentuk garis atau batang dan digunakan untuk merepresentasikan objek fisik yang memiliki satu dimensi dominan, seperti kabel, balok panjang, atau kolom. Elemen ini ideal untuk komponen yang panjang dan ramping, di mana dimensi lainnya (misalnya, lebar atau tinggi) jauh lebih kecil daripada panjangnya. Aplikasi yang biasanya digunakan untuk struktur linier seperti batang, balok, kabel, atau rangka. Elemen 1D memungkinkan analisis tegangan, deformasi, dan gaya dalam elemen tersebut. Contoh dalam Multiphysics pertama Structural Analysis yang dapat menganalisis beban dan tegangan pada balok atau batang. Kedua Thermal Analysis menganalisis distribusi suhu pada pipa panjang atau kabel listrik, di mana panas merambat sepanjang sumbu utama.
2. Elemen 2D Elemen 2D digunakan untuk objek dengan dimensi dominan dalam dua arah (misalnya panjang dan lebar), sementara ketebalannya jauh lebih kecil atau diabaikan. Elemen ini biasanya digunakan untuk memodelkan permukaan atau pelat tipis. Aplikasi yang digunakan dalam analisis pada struktur seperti pelat, membran, atau dinding tipis di mana beban atau pengaruh fisik bekerja pada permukaan besar. Contoh dalam Multiphysics pertama Fluid-Structure Interaction dapat Memodelkan interaksi antara dinding tipis (seperti membran) dan aliran fluida di sekitarnya. Kedua Electromagnetic Analysis menganalisis arus listrik pada permukaan logam tipis, seperti dalam sirkuit. Ketiga Thermal Analysis mendistribusi suhu pada permukaan pelat logam atau dinding.
3. Elemen 3D Elemen 3D berbentuk volumetrik, seperti tetrahedron atau hexahedron, yang mampu menangani objek tiga dimensi penuh dengan geometri kompleks. Elemen ini berguna untuk representasi detail yang mencakup seluruh volume objek dan objek yang memiliki kompleksitas geometris penuh dalam tiga dimensi. Elemen ini cocok untuk objek solid yang tidak dapat direduksi menjadi dua dimensi karena ketebalannya yang signifikan. Aplikasi yang digunakan dalam analisis struktur solid atau kompleks seperti blok, mesin, komponen mekanik besar, atau sistem yang membutuhkan pemodelan volume penuh. Contoh dalam Multiphysics pertama Thermal-Mechanical Analysis menganalisis distribusi suhu dan tegangan dalam objek solid, seperti mesin atau komponen elektronik besar. Kedua Acoustic-Vibration Analysis memodelkan respons getaran dan transmisi suara dalam objek solid seperti blok atau casing. Ketiga Fluid Flow in Porous Media menganalisis aliran fluida melalui objek solid berpori, seperti beton atau tanah.
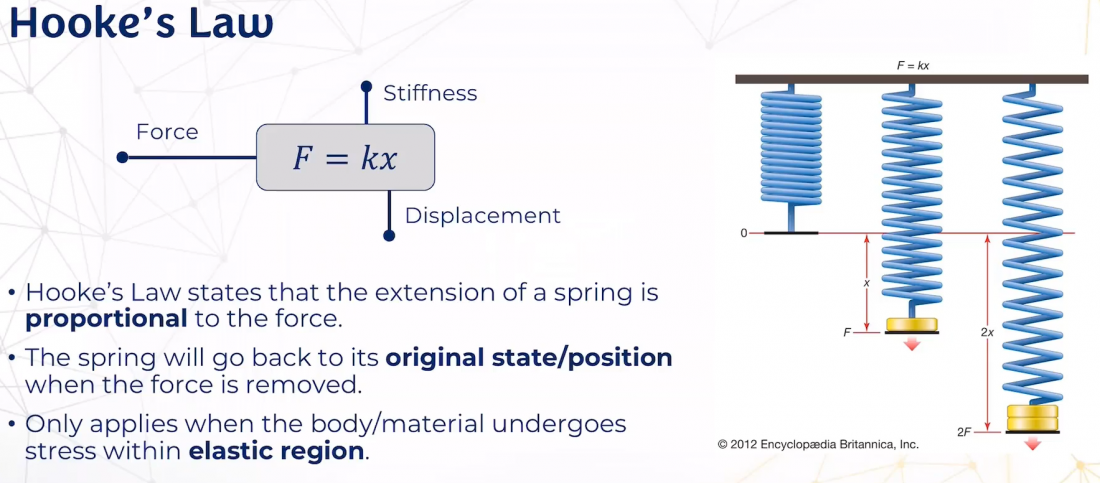
Dalam FEM (Finite Element Method), prinsip Hukum Hooke digunakan untuk menghitung tegangan (stress) dan regangan (strain) dalam elemen-elemen kecil suatu model. Hukum ini diterapkan dalam domain elastis untuk menentukan deformasi atau perpindahan elemen ketika beban diberikan, terutama dalam analisis struktur dan material elastis. Setiap elemen dalam FEM mematuhi hubungan linier antara tegangan dan regangan dalam batas elastisitas, sehingga perpindahan akibat gaya dapat dianalisis secara rinci pada level komponen. Terdapat pada gambar diatas Hukum Hooke menyatakan bahwa gaya (F) yang diterapkan pada sebuah pegas akan menghasilkan perpanjangan (x) yang sebanding, dengan persamaan 𝐹= 𝑘𝑥, di mana 𝑘 adalah kekakuan atau konstanta pegas perpanjangan pegas sebanding dengan gaya yang diterapkan padanya, selama material berada dalam batas elastis. Ini berarti semakin besar gaya, semakin besar perpanjangan yang terjadi. Kedua, ketika gaya dilepaskan, pegas atau material akan kembali ke bentuk atau posisi awalnya jika material tersebut tetap dalam wilayah elastis. Ketiga, Hukum Hooke hanya berlaku selama material berada dalam rentang elastis, di mana deformasi yang terjadi masih bisa pulih sepenuhnya tanpa perubahan permanen pada struktur material.
Stiffness (k) pada gambar ini menggambarkan kekakuan pegas, yang berperan serupa dalam elemen-elemen struktural pada model FEM.
Displacement (x) menggambarkan perubahan bentuk, yang dalam analisis FEM mengukur deformasi pada titik-titik elemen akibat gaya eksternal.
Pada FEM, prinsip dasar Hukum Hooke digunakan untuk mengembangkan matriks kekakuan yang diperlukan untuk menyelesaikan persamaan di berbagai elemen dan menggabungkannya dalam keseluruhan sistem struktur. Proporsionalitas antara Gaya dan Perpanjangan Hukum Hooke menyatakan bahwa perpanjangan pegas sebanding dengan gaya yang diterapkan, selama dalam batas elastisitas. Artinya, semakin besar gaya, semakin besar perpanjangan. Kembali ke Posisi Awal ketika gaya dilepaskan, pegas atau material akan kembali ke bentuk atau posisi aslinya, asalkan material tersebut tetap dalam wilayah elastis. Berlaku dalam Wilayah Elastis hukum ini hanya berlaku selama material atau pegas masih dalam rentang elastis, yaitu ketika deformasi masih dapat pulih sepenuhnya tanpa perubahan permanen pada struktur material.
Berikutnya pada Hukum Hooke dalam 3D untuk material elastis isotropik, yang menjelaskan hubungan antara tegangan (stress) dan regangan (strain) dalam kondisi aksial dan geser, mendefinisikan hubungan linier antara tegangan dan regangan pada material elastis isotropik (material yang sifatnya sama dalam semua arah). Dalam konteks 3D, hukum ini memerlukan konstanta elastisitas material, yaitu Modulus Young (E) dan Rasio Poisson (ν), serta Modulus Geser (G), yang digunakan dalam persamaan tegangan dan regangan. Berikut penjelasan dari bagian-bagian tersebut:
Axial Strain Regangan aksial (ε) pada arah x, y, dan z dihitung dari tegangan pada ketiga sumbu ini serta efek dari Rasio Poisson, yang menghubungkan tegangan di satu arah dengan perubahan bentuk di arah yang lain.
Shear Strain Regangan geser (γ) pada bidang xy, zx, dan yz berhubungan langsung dengan tegangan geser pada bidang yang sama dan Modulus Geser G. Shear strain menunjukkan distorsi atau perubahan bentuk pada bidang tertentu akibat tegangan geser.
Axial Stress Tegangan aksial (σ) pada arah x, y, dan z diperoleh dengan mengalikan Modulus Young (E), Rasio Poisson (ν), dan regangan aksial pada ketiga arah. Rumus ini menggabungkan pengaruh regangan dari semua arah, yang menunjukkan sifat isotropik dari material tersebut.
Shear Stress Tegangan geser (τ) pada bidang xy, yz, dan zx berkaitan langsung dengan shear strain pada bidang yang sama dan Modulus Geser (G). Shear stress ini menunjukkan tegangan yang menyebabkan distorsi di bidang tertentu.
Diagram Kubus di tengah gambar mengilustrasikan tegangan pada berbagai arah pada suatu elemen kubus material. Arah tegangan aksial (σ_x, σ_y, σ_z) ditunjukkan di sepanjang sumbu utama x, y, dan z, sementara tegangan geser (τ_xy, τ_yz, τ_zx) ditunjukkan pada bidang antar-sumbu. Diagram ini membantu memvisualisasikan bagaimana tegangan bekerja pada elemen dalam ruang tiga dimensi. Transformasi Stress and Strain persamaan pada gambar menunjukkan bahwa tegangan dan regangan saling berhubungan melalui transformasi berdasarkan Hukum Hooke dalam 3D. Transformasi ini memperhitungkan pengaruh dari semua komponen tegangan pada regangan aksial dan pengaruh regangan pada tegangan aksial, mencerminkan sifat mekanik material isotropik.