Difference between revisions of "Naufal Aziz Putra"
Naufal.aziz (talk | contribs) |
Naufal.aziz (talk | contribs) |
||
| (24 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | [[File:WhatsApp Image 2020-02-07 at 16.49.28.jpeg| | + | [[File:WhatsApp Image 2020-02-07 at 16.49.28.jpeg|400px|thumb|left|Naufal Aziz Putra]] |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Pertemuan Pertama== | ==Pertemuan Pertama== | ||
| Line 24: | Line 12: | ||
Metode Manual | Metode Manual | ||
| − | [[File:WhatsApp Image 2020-02-13 at 23.21.06.jpeg| | + | [[File:WhatsApp Image 2020-02-13 at 23.21.06.jpeg|300px|thumb|center|Metode Manual]] |
Ketika saya mengerjakan langsung memasukkan angka yang didapat hasilnya adalah 0/0, setelah itu saya memasukkannya dengan menggunakan cara limit dan didapatkan hasil yaitu f(x) = 2. | Ketika saya mengerjakan langsung memasukkan angka yang didapat hasilnya adalah 0/0, setelah itu saya memasukkannya dengan menggunakan cara limit dan didapatkan hasil yaitu f(x) = 2. | ||
| Line 31: | Line 19: | ||
Metode Pyhton | Metode Pyhton | ||
| − | [[File:WhatsApp Image 2020-02-14 at 00.57.15.jpeg| | + | [[File:WhatsApp Image 2020-02-14 at 00.57.15.jpeg|300px|thumb|center|Metode Pyhton]] |
Pada saat menggunakan metode pyhton untuk menyelesaikan proses diatas, kita dapat melakukan dengan memasukkan nilai x dengan memasukkan f(x) kedalam metode pyhton. Kemudian dari aplikasi pyhton tersebut akan otomatis mengeluarkan hasil langsung sesuai dengan yang menggunakan metode manual dengan cara limit. Dari program tersebut didapat hasilnya adalah 2. | Pada saat menggunakan metode pyhton untuk menyelesaikan proses diatas, kita dapat melakukan dengan memasukkan nilai x dengan memasukkan f(x) kedalam metode pyhton. Kemudian dari aplikasi pyhton tersebut akan otomatis mengeluarkan hasil langsung sesuai dengan yang menggunakan metode manual dengan cara limit. Dari program tersebut didapat hasilnya adalah 2. | ||
| Line 51: | Line 39: | ||
Setelah saya membaca beberapa materi dibuku, saya tertarik dengan materi di Bab 9 yaitu tentang Matriks dibuku terdapat bahwa ternyata matriks bisa mencapai hingga 20x20 yang dimana jika saya mengerjakan matriks sampai 5x5 saja secara manual itu sudah sangat sulit untuk dikerjakan. Tetapi di buku bisa mencapai matriks segitu. Saya sangat ingin tau bagaimana jika matriks sebesar itu bisa dikerjakan menggunakan bantuan aplikasi, dan saya sangat ingin tau apakah bisa lebih mudah mengerjakan menggunakan bantuan pengaplikasian?. Seperti dibuku latihan soal nomor 17 mencari hasil dari matriks 20x20 dengan menentukan 5 eigen. | Setelah saya membaca beberapa materi dibuku, saya tertarik dengan materi di Bab 9 yaitu tentang Matriks dibuku terdapat bahwa ternyata matriks bisa mencapai hingga 20x20 yang dimana jika saya mengerjakan matriks sampai 5x5 saja secara manual itu sudah sangat sulit untuk dikerjakan. Tetapi di buku bisa mencapai matriks segitu. Saya sangat ingin tau bagaimana jika matriks sebesar itu bisa dikerjakan menggunakan bantuan aplikasi, dan saya sangat ingin tau apakah bisa lebih mudah mengerjakan menggunakan bantuan pengaplikasian?. Seperti dibuku latihan soal nomor 17 mencari hasil dari matriks 20x20 dengan menentukan 5 eigen. | ||
| − | [[File:WhatsApp Image 2020-02-14 at 17.19.56.jpeg| | + | [[File:WhatsApp Image 2020-02-14 at 17.19.56.jpeg|300px|thumb|center|Bab 9 Soal Nomor 17 Buku Numerical Methods in Engineering with Python 3 oleh Jaan Kiusalaas |
]] | ]] | ||
Bab 7 : Data = Informasi - Pengetahuan - Ilmu yang Bermanfaat - Hikmah - Hidayah | Bab 7 : Data = Informasi - Pengetahuan - Ilmu yang Bermanfaat - Hikmah - Hidayah | ||
| + | |||
| + | ==Tugas 2 Metnum Tanggal 14 Februari 2020== | ||
| + | |||
| + | Soal Gerak Jatuh Bebas | ||
| + | |||
| + | Metode Manual | ||
| + | |||
| + | [[File:WhatsApp Image 2020-02-18 at 15.28.02.jpeg|300px|thumb|center|Soal dan Jawaban Materi Bab 7 Tentang Gerak Jatuh Bebas]] | ||
| + | |||
| + | Metode Software | ||
| + | |||
| + | [[File:Pohon2.png|700px|thumb|center|Memasukkan Data]] | ||
| + | |||
| + | Setelah memasukkan data ke software lalu run | ||
| + | |||
| + | [[File:Pohon1.png|700px|thumb|center|Hasil]] | ||
| + | |||
| + | Setelah itu didapatkan hasil dari soal gerak jatuh bebas | ||
| + | |||
| + | |||
| + | Soal Soal Nomor 17 Buku Numerical Methods in Engineering with Python 3 oleh Jaan Kiusalaas Bab 9 | ||
| + | |||
| + | Penyelesaian Menggunakan Software | ||
| + | |||
| + | Dari penyelesaian menggunakan software didapatkan penyelesaian yang sangat panjang, disini saya menyingkat beberapa cara untuk mempersedikit pengunggahan foto | ||
| + | |||
| + | [[File:1 Naufal.jpg|800px|thumb|center|Cara Pertama]] | ||
| + | |||
| + | [[File:2 Naufal.jpg|800px|thumb|center|Cara Kedua]] | ||
| + | |||
| + | [[File:3 Naufal.jpg|800px|thumb|center|Cara Ketiga]] | ||
| + | |||
| + | [[File:4 Naufal.jpg|800px|thumb|center|Cara Keempat]] | ||
| + | |||
| + | [[File:5 Naufal.jpg|800px|thumb|center|Cara Kelima]] | ||
| + | |||
| + | [[File:6 Naufal.jpg|800px|thumb|center|Cara Keenam]] | ||
| + | |||
| + | Didapatkan hasil dari matriks 20x20 | ||
| + | |||
| + | ==Analisis Tugas 2== | ||
| + | |||
| + | Menurut saya dari soal tentang Bab 7 yaitu Gerak Jatuh Bebas sama seperti apa yang sudah kita pelajari di mata pelajaran Fisika, dan untuk mencari soal tentang Bab 9 yaitu Matriks. Saya mendapat kesulitan untuk mencari 20x20 karna kita mengolah data yang sanagta banyak sehingga itu sangat menyulitkan. Dan akhirnya saya mencoba menggunakan software yang dimana ternyata menggunakan itu juga masih terasa sulit untuk saya. | ||
| + | |||
| + | ==Progres Belajar== | ||
| + | |||
| + | Pelajaran yang saya sudah dapat dari dua pertemuan terakhir | ||
| + | |||
| + | [[File:Metnum Yuk 1.png|800px|thumb|center|Slide 1]] | ||
| + | [[File:Metnum Yuk 2.png|800px|thumb|center|Slide 2]] | ||
| + | [[File:Metnum Yuk 3.png|800px|thumb|center|Slide 3]] | ||
| + | [[File:Metnum Yuk 4.png|800px|thumb|center|Slide 4]] | ||
| + | [[File:Metnum Yuk 5.png|800px|thumb|center|Slide 5]] | ||
| + | |||
| + | ==Pertemuan Ketiga== | ||
| + | |||
| + | Kita harus selalu berserah diri dan bersyukur kepada Tuhan YME, karena apapun yang kita lakukan harus didasari oleh rasa syukur kepada-Nya. Kita sebagai manusia harus selalu bersyukur atas apa yang Allah SWT telah berikan, baik nikmat kesehatan, nikmat kehidupan dan lainnya. | ||
| + | |||
| + | Dipertemuan kemaren diajarkan bahwa hukum fisika maupun matematika dapat dikerjakan dengan aplikasi python. | ||
| + | |||
| + | |||
| + | Ada tiga prinsip dasar ilmu teknik : | ||
| + | |||
| + | 1. Prinsip konservasi massa. v x A = Q= konstan , tetapi rumus ini terbatas. aliran inkompresibel adalah aliran yang massa jenisnya tidak berubah. | ||
| + | |||
| + | 2. Prinsip konservasi momentum. Sering disebut kesetimbangan gaya. F = m.a -> F = M.(dv/dt) | ||
| + | |||
| + | 3. Prinsip konservasi energi. dE/dt = W + Q atau laju perubahan energi. Dalam suatu sistem ada resultan gaya maka sistem itu memiliki percepatan | ||
| + | |||
| + | ==Tugas 3 Metnum Tanggal 21 Februari 2020== | ||
| + | |||
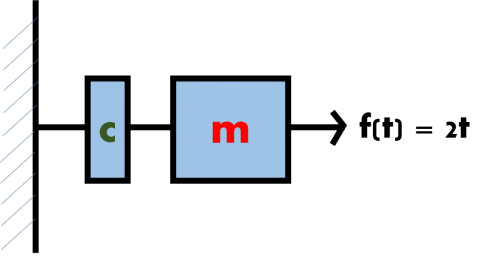
| + | Menurunkan rumus dibawah : | ||
| + | |||
| + | [[File:WhatsApp Image 2020-02-21 at 17.48.42.jpeg|400px|thumb|center|Tugas Pegas]] | ||
| + | |||
| + | |||
| + | -Tugas Soal Baru- | ||
| + | |||
| + | [[File:gaby10.png|500px|thumb|center|-]] | ||
| + | |||
| + | |||
| + | F = m*a (sigma Gaya) | ||
| + | 5t - cv = m*a | ||
| + | a = (5t-cv)/m | ||
| + | dv/dt = (5t-cv)/m | ||
| + | |||
| + | def TurunV(t, v): #Fungsi Turunan V terhadap t | ||
| + | return ((5*t - c*v)/m) | ||
| + | |||
| + | m=eval(input("massa dalam kilogram : ")) | ||
| + | c=eval(input("damper koefisien (Ns/m) : ")) | ||
| + | |||
| + | t0 = 0 #t initial | ||
| + | v0 = 0 #v initial | ||
| + | t = 7 #kecepatan sistem ditanya pada t setelah 7s | ||
| + | h = 0.06 #delta yang digunakan | ||
| + | nilai = (int)((t - t0)/h) #menghitung jumlah increment | ||
| + | for i in range(1, nilai + 1): | ||
| + | |||
| + | k1 = h * TurunV(t0, v0) #runge kutta | ||
| + | k2 = h * TurunV(t0 + 0.5 * h, v0 + 0.5 * k1) | ||
| + | k3 = h * TurunV(t0 + 0.5 * h, v0 + 0.5 * k2) | ||
| + | k4 = h * TurunV(t0 + h, v0 + k3) | ||
| + | |||
| + | v0 = v0 + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4) #sigma nilai k1,k2,k3,k4 ke y' yang baru dan membaginya | ||
| + | t0 = t0 + h | ||
| + | print("Velocity dalam Sistem : ",v0, "m/s") | ||
| + | |||
| + | |||
| + | [[File:gaby11.jpg|600px|thumb|center|-]] | ||
| + | |||
| + | |||
| + | ==Review Pembelajaran== | ||
| + | |||
| + | [[File:cuk1.png|600px|thumb|center|Slide 1]] | ||
| + | [[File:cuk2.png|600px|thumb|center|Slide 2]] | ||
| + | [[File:cuk3.png|600px|thumb|center|Slide 3]] | ||
| + | [[File:cuk4.png|600px|thumb|center|Slide 4]] | ||
| + | [[File:cuk5.png|600px|thumb|center|Slide 5]] | ||
| + | |||
| + | |||
| + | ==Pertemuan Keempat== | ||
| + | |||
| + | Langkah-Langkah pengerjaan CFDSOF v1.5 | ||
| + | |||
| + | 1. Buka CFDSOF v1.5 klik folder pada Geometry preparation => ussAlbacore | ||
| + | 2. Kemudian klik kanan pada Geometry list => Scale => ubah jadi 0.001 semua | ||
| + | 3. Kemudian klik Geometry Mesh ubah min & max pada surface refinement min, max => 3, 4 | ||
| + | 4. Kemudian klik Base Mesh ubah Min coordinate menjadi -2, -5, -5. dan ubah Max Coordinate menjadi 13, 0, 5. | ||
| + | Ubah juga pada Box Mesh Properties pada Divisionnya menjadi 75, 25, 50 | ||
| + | Ubah Box Mesh Boundaries seperti pada gambar dibawah ini | ||
| + | 5. Kemudian klik Generate Mesh lalu ubah Output Format menjadi Binary | ||
| + | lalu ubah Mesh Location menjadi 0, -3, -2 lalu klik pin berwarna kuning di bawah dan klik Generate Mesh | ||
| + | 6. Pastikan Check Mesh Quality sampai muncul Mesh OK. End | ||
| + | 7. Kemudian klik Simulation Model dan ubah menu Turbulance menjadi RANS | ||
| + | 8. Kemudian Klik Turbulance ubah Turbulence Model menjadi Standar k-w dan centang Use Default Coefficient | ||
| + | 9. Kemudian Klik Material ubah Material Name => Water, Density => 1000, Dynamic Viscosity => 0.00089 | ||
| + | 10. Kemudian Klik Boundary Properties | ||
| + | Face Name => Inlet 1, Face Type => Patch, Boundary Conditions Type => Velocity Inlet, lalu ubah Reference Value bebas angkanya | ||
| + | Face Name => Outlet1, Face Type => Patch, Boundary Conditions Type => Outflow | ||
| + | Face Name => Boundary1, Face Type => Patch, Boundary Conditions Type => Far-Field | ||
| + | Face Name => Symmetry1, Face Type => symmetry, Boundary Conditions Type => Symmetry | ||
| + | Face Name => ussAlbacore, Face Type => Wall, Boundary Conditions Type => Stationary Wall | ||
| + | 11. Klik CFD-SOlVE kemudian klik Run solver ubah Write Control => Run Time, 1000 | ||
| + | 12. Lalu klik Run Solver dan tunggu hingga selesai perhitungan dan akan keluarnya grafik | ||
| + | 13. Lalu Klik CFD-POST lalu klik gambar yang 3 warna maka dia akan muncul halaman | ||
| + | 14. Centang ussAlbacore lalu klik Apply maka akan muncul kapal selam | ||
| + | 15. Lalu Klik Calculator lalu samakan kemudian apply | ||
| + | 16. Klik Filters => Alphabetical => Generates Surface Normals | ||
| + | 17. Centang Compute Cell Normalskemudian Apply | ||
| + | 18. Klik calculator dan apply | ||
| + | 19. Lalu klik Filters => Alphabetical => Integrate Variable | ||
| + | 20. Kemudian centang Devide Cell Data By Volume kemudian Apply | ||
| + | 21. Lalu akan muncul tabel | ||
| + | |||
| + | |||
| + | ==Review Asistensi 3 Maret 2020== | ||
| + | |||
| + | [[File:La1.png|600px|thumb|center|Slide 1]] | ||
| + | [[File:La2.png|600px|thumb|center|Slide 2]] | ||
| + | [[File:La3.png|600px|thumb|center|Slide 3]] | ||
| + | [[File:La4.png|600px|thumb|center|Slide 4]] | ||
| + | |||
| + | ==Laporan Asistensi== | ||
| + | |||
| + | [[File:1 - Nopal.png|600px|thumb|center|]] | ||
| + | [[File:2 - Nopal.png|600px|thumb|center|]] | ||
| + | [[File:3 - Nopal.png|600px|thumb|center|]] | ||
| + | |||
| + | |||
| + | ==Tugas Intial Value Problem== | ||
| + | |||
| + | [[File:nopal 10 (2).jpg|600px|thumb|center|]] | ||
| + | [[File:nopal 10 (3).jpg|600px|thumb|center|]] | ||
| + | |||
| + | ==Tugas Boundary Value Problem== | ||
| + | |||
| + | [[File:Nopal 1.png|600px|thumb|center|]] | ||
| + | [[File:Nopal 2.jpg|600px|thumb|center|]] | ||
| + | [[File:Nopal 3.jpg|600px|thumb|center|]] | ||
| + | [[File:Nopal 4.jpg|600px|thumb|center|]] | ||
| + | [[File:Nopal 6.jpg|600px|thumb|center|]] | ||
| + | [[File:Nopal 5.jpg|600px|thumb|center|]] | ||
| + | [[File:Nopal 11.jpg|600px|thumb|center|]] | ||
| + | [[File:Nopal 12.jpg|600px|thumb|center|]] | ||
| + | |||
| + | ==Pertemuan Keenam== | ||
| + | |||
| + | Bang Edo menjelaskan mengenai optimasi pada aplikasi python. | ||
| + | |||
| + | Cara meng-optimasi: | ||
| + | |||
| + | 1. Menentukan persamaan yang dipakai untuk melakukan optimasi | ||
| + | |||
| + | 2. Menentukan alokasi yang efekif dalam memilih sumber yang tersedia | ||
| + | |||
| + | 3. Mendesain dengan karakteristik se-optimal mungkin | ||
| + | |||
| + | 4. Optimasi membutuhkan batasan untuk bekerja dengan baik, maka dari itu diperlukan algoritma optimasi | ||
| + | |||
| + | 5. Melakukan pengecekan pada variable yang dipakai agar sistem bekerja dengan sesuai yang diinginkan/optimal | ||
| + | |||
| + | Bang Edo memberikan sebuah kasus dimana menghitung kayu sepanjang 20 meter untuk dipakai pada pagar rumah. | ||
| + | |||
| + | Kayu sepanjang 20 meter dibutuhkan untuk membuat pagar rumah. Terdapat permintaan dimana di dalamp pagar harus ada minimal panjang kayu yaitu 8 meter yang dibutuhkan untuk bermain bola. Bagaimana agar kayu tersebut dapat memagari rumah dengan luas yang paling besar/optimal. | ||
| + | |||
| + | Fungsi objektif pada kasus ini adalah : Luas halaman (A= P x L) | ||
| + | |||
| + | Dalam mengerjakan proses optimasi pada python dibutuhkan yang namanya constraint/batas/limit. Fungsi constraint adalah untuk membatasi nilai sehingga tidak keluar dari nilai yang diinginkan. | ||
| + | |||
| + | constraint pada soal ini adalah : 20 meter kayu, | ||
| + | |||
| + | jadi 2P + 2L = 20 (2 karena panjang dan lebarnya ada 2). | ||
| + | |||
| + | Panjang minimal 8 meter sehingga terdapat cons lagi yaitu constraint = 2 | ||
| + | |||
| + | |||
| + | ==Tugas Pertemuan Ketujuh Video Optimasi== | ||
| + | |||
| + | Soal : | ||
| + | |||
| + | Sebuah Gelanggang Olahraga Remaja ingin menyimpan bola basket dalam sebuah box besar. Box yang diinginkan berbentuk kubus. Berapa ukuran panjang, lebar, dan tinggi yang diperlukan untuk mencapai volume maksimum yang dapat di gunakan untuk menyimpan bola basket. Syarat Luas Permukaan tidak melebihi 300 cm^2. Gunakan optimasi numerik pada python. | ||
| + | |||
| + | Volume : Panjang x lebar x tinggi | ||
| + | Luas Permukaan : 2 [ (panjang x lebar) + (panjang x tinggi) + (lebar x tinggi) ] | ||
| + | |||
| + | [[File:Tugas_Naufal_Aziz_Putra_Metode_Numerik_Python.mp4|600px|thumb|center|]] | ||
Latest revision as of 01:12, 7 September 2023
Contents
- 1 Pertemuan Pertama
- 2 Tugas 1 Metnum Tanggal 7 Februari 2020
- 3 Analisa Tugas 1
- 4 Pertemuan Kedua
- 5 Tugas 2 Metnum Tanggal 14 Februari 2020
- 6 Analisis Tugas 2
- 7 Progres Belajar
- 8 Pertemuan Ketiga
- 9 Tugas 3 Metnum Tanggal 21 Februari 2020
- 10 Review Pembelajaran
- 11 Pertemuan Keempat
- 12 Review Asistensi 3 Maret 2020
- 13 Laporan Asistensi
- 14 Tugas Intial Value Problem
- 15 Tugas Boundary Value Problem
- 16 Pertemuan Keenam
- 17 Tugas Pertemuan Ketujuh Video Optimasi
Pertemuan Pertama
Pada mata kuliah Metode Numerik ini, saya kurang mengetahui tentang pemrograman. Hingga saat ini program yang saya hanya bisa hanya word dan powerpoint. Selain itu menggunakan internet sebisanya. Tetapi di selama perkuliahan ini di Teknik Perkapalan saya mulai membiasakan diri dengan program excel. Setelah itu saya juga masih belajar dengan penggunaan program AutoCad.
Tugas 1 Metnum Tanggal 7 Februari 2020
Menentukan F(x) = ( x^2 - 1 / x-1 ) menggunakan metode manual dan menggunakan software setelah itu diberikan komentar
Metode Manual
Ketika saya mengerjakan langsung memasukkan angka yang didapat hasilnya adalah 0/0, setelah itu saya memasukkannya dengan menggunakan cara limit dan didapatkan hasil yaitu f(x) = 2.
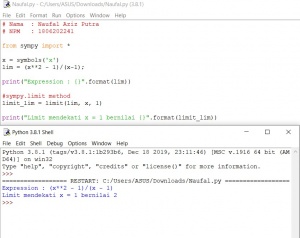
Metode Pyhton
Pada saat menggunakan metode pyhton untuk menyelesaikan proses diatas, kita dapat melakukan dengan memasukkan nilai x dengan memasukkan f(x) kedalam metode pyhton. Kemudian dari aplikasi pyhton tersebut akan otomatis mengeluarkan hasil langsung sesuai dengan yang menggunakan metode manual dengan cara limit. Dari program tersebut didapat hasilnya adalah 2.
Analisa Tugas 1
Menurut saya dengan menggunakan bantuan metode software bisa memudahkan kita dalam perhitungan. Namun menurut saya sampai saat ini menggunakan metode manual lebih mudah mungkin karna mungkin saya yang masih belum terlalu bisa menggunakan aplikasi. Banyak sekali metode penyelesain yang bisa dilakukan seperti menggunakan bantuan alat / software. Tetapi karna kurangnya kemampuan saya dalam melakukan aplikasi tersebut yang semakin kesini perkembangan zaman semakin canggih dalam bidang teknologi sebenarnya kita sangat dapat memanfaatkannya. Untuk sekarang sangat penting mengetahui pemrograman karna dapat memudahkan kita dalam melakukan pekerjaan.
Pertemuan Kedua
Ternyata setelah membuka e-book saya bisa baru tau bahwa sebenarnya perhitungan matematika yang biasa kita lakukan menggunakan manual, bisa dikerjakan melalui bantuan aplikasi.
Di metode numerik kita bisa belajar menyelasaikan fisika dengan metode perhitungan matematik.
Mengurangi rasa malas. Bersyukur kepada Allah SWT, karna sudah diberikan seperti sekarang. Berusahalah setidaknya mencoba apapun terlebih dahulu.
Setelah saya membaca beberapa materi dibuku, saya tertarik dengan materi di Bab 9 yaitu tentang Matriks dibuku terdapat bahwa ternyata matriks bisa mencapai hingga 20x20 yang dimana jika saya mengerjakan matriks sampai 5x5 saja secara manual itu sudah sangat sulit untuk dikerjakan. Tetapi di buku bisa mencapai matriks segitu. Saya sangat ingin tau bagaimana jika matriks sebesar itu bisa dikerjakan menggunakan bantuan aplikasi, dan saya sangat ingin tau apakah bisa lebih mudah mengerjakan menggunakan bantuan pengaplikasian?. Seperti dibuku latihan soal nomor 17 mencari hasil dari matriks 20x20 dengan menentukan 5 eigen.
Bab 7 : Data = Informasi - Pengetahuan - Ilmu yang Bermanfaat - Hikmah - Hidayah
Tugas 2 Metnum Tanggal 14 Februari 2020
Soal Gerak Jatuh Bebas
Metode Manual
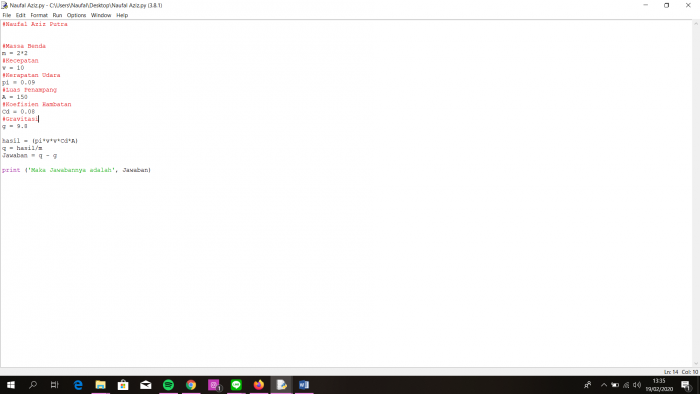
Metode Software
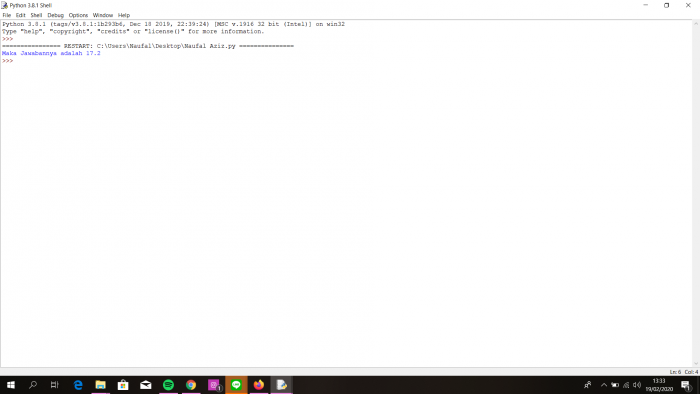
Setelah memasukkan data ke software lalu run
Setelah itu didapatkan hasil dari soal gerak jatuh bebas
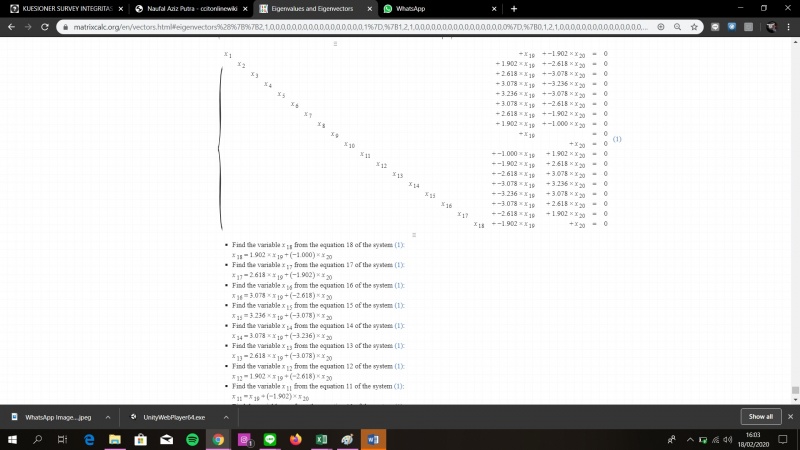
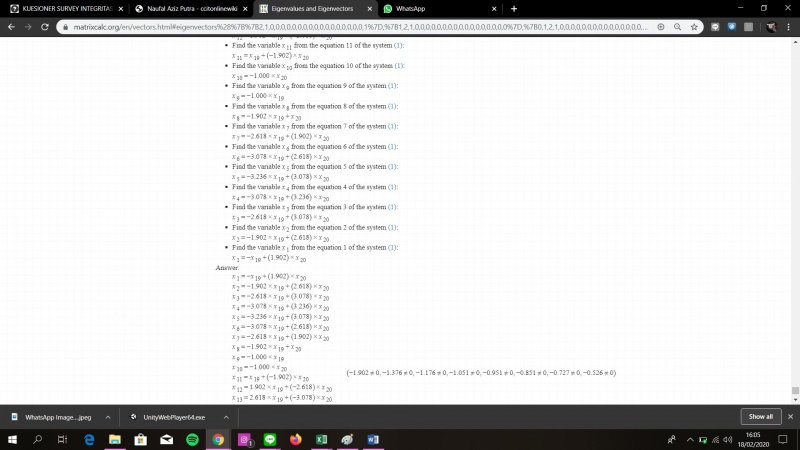
Soal Soal Nomor 17 Buku Numerical Methods in Engineering with Python 3 oleh Jaan Kiusalaas Bab 9
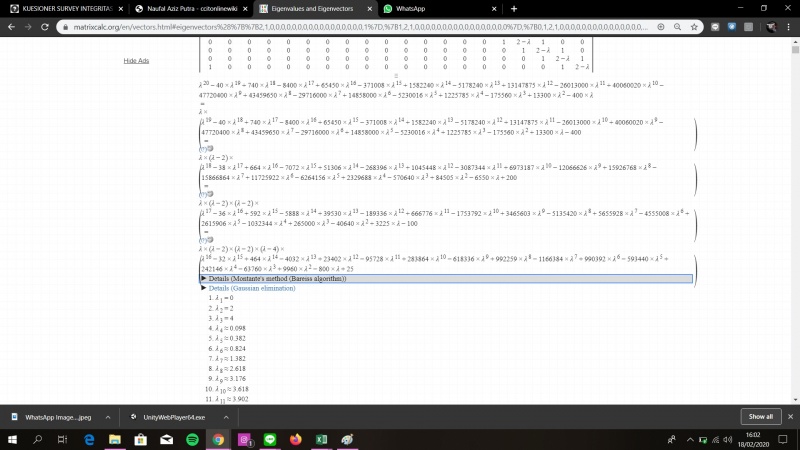
Penyelesaian Menggunakan Software
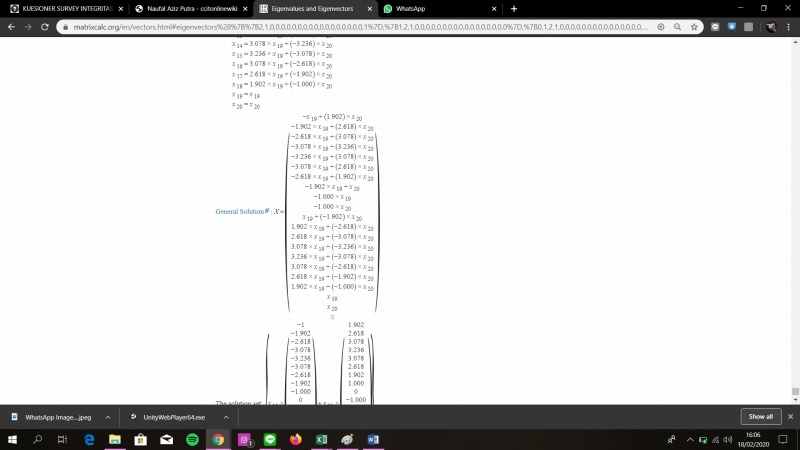
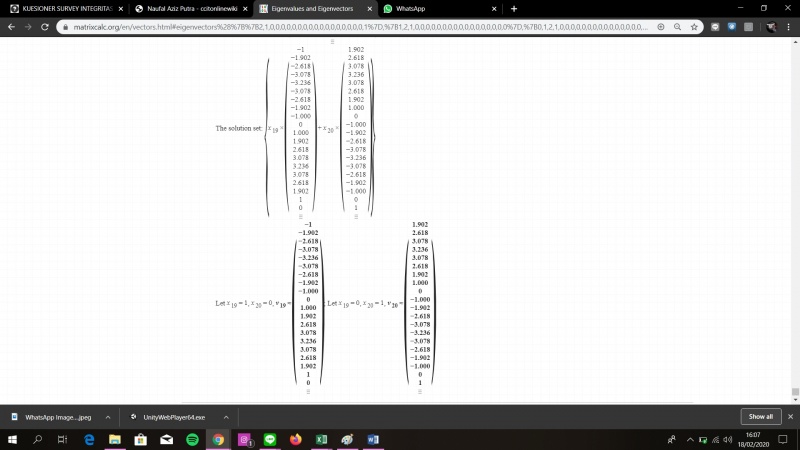
Dari penyelesaian menggunakan software didapatkan penyelesaian yang sangat panjang, disini saya menyingkat beberapa cara untuk mempersedikit pengunggahan foto
Didapatkan hasil dari matriks 20x20
Analisis Tugas 2
Menurut saya dari soal tentang Bab 7 yaitu Gerak Jatuh Bebas sama seperti apa yang sudah kita pelajari di mata pelajaran Fisika, dan untuk mencari soal tentang Bab 9 yaitu Matriks. Saya mendapat kesulitan untuk mencari 20x20 karna kita mengolah data yang sanagta banyak sehingga itu sangat menyulitkan. Dan akhirnya saya mencoba menggunakan software yang dimana ternyata menggunakan itu juga masih terasa sulit untuk saya.
Progres Belajar
Pelajaran yang saya sudah dapat dari dua pertemuan terakhir
Pertemuan Ketiga
Kita harus selalu berserah diri dan bersyukur kepada Tuhan YME, karena apapun yang kita lakukan harus didasari oleh rasa syukur kepada-Nya. Kita sebagai manusia harus selalu bersyukur atas apa yang Allah SWT telah berikan, baik nikmat kesehatan, nikmat kehidupan dan lainnya.
Dipertemuan kemaren diajarkan bahwa hukum fisika maupun matematika dapat dikerjakan dengan aplikasi python.
Ada tiga prinsip dasar ilmu teknik :
1. Prinsip konservasi massa. v x A = Q= konstan , tetapi rumus ini terbatas. aliran inkompresibel adalah aliran yang massa jenisnya tidak berubah.
2. Prinsip konservasi momentum. Sering disebut kesetimbangan gaya. F = m.a -> F = M.(dv/dt)
3. Prinsip konservasi energi. dE/dt = W + Q atau laju perubahan energi. Dalam suatu sistem ada resultan gaya maka sistem itu memiliki percepatan
Tugas 3 Metnum Tanggal 21 Februari 2020
Menurunkan rumus dibawah :
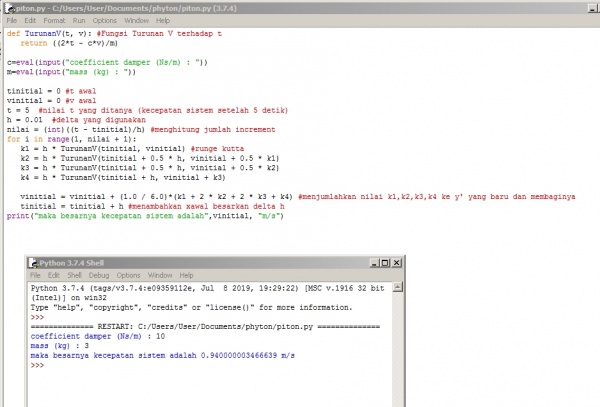
-Tugas Soal Baru-
F = m*a (sigma Gaya) 5t - cv = m*a a = (5t-cv)/m dv/dt = (5t-cv)/m
def TurunV(t, v): #Fungsi Turunan V terhadap t return ((5*t - c*v)/m)
m=eval(input("massa dalam kilogram : "))
c=eval(input("damper koefisien (Ns/m) : "))
t0 = 0 #t initial v0 = 0 #v initial t = 7 #kecepatan sistem ditanya pada t setelah 7s h = 0.06 #delta yang digunakan nilai = (int)((t - t0)/h) #menghitung jumlah increment for i in range(1, nilai + 1): k1 = h * TurunV(t0, v0) #runge kutta k2 = h * TurunV(t0 + 0.5 * h, v0 + 0.5 * k1) k3 = h * TurunV(t0 + 0.5 * h, v0 + 0.5 * k2) k4 = h * TurunV(t0 + h, v0 + k3)
v0 = v0 + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4) #sigma nilai k1,k2,k3,k4 ke y' yang baru dan membaginya
t0 = t0 + h
print("Velocity dalam Sistem : ",v0, "m/s")
Review Pembelajaran
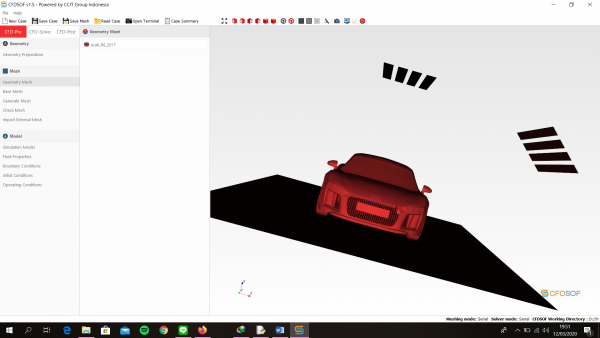
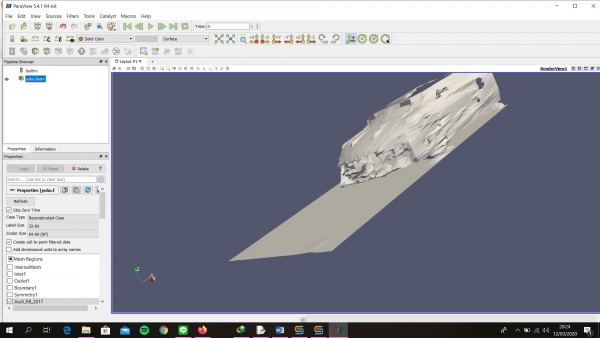
Pertemuan Keempat
Langkah-Langkah pengerjaan CFDSOF v1.5
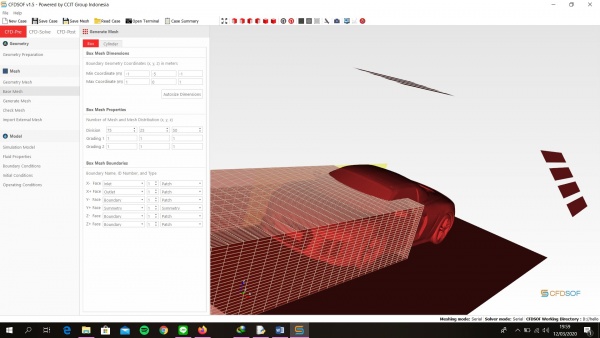
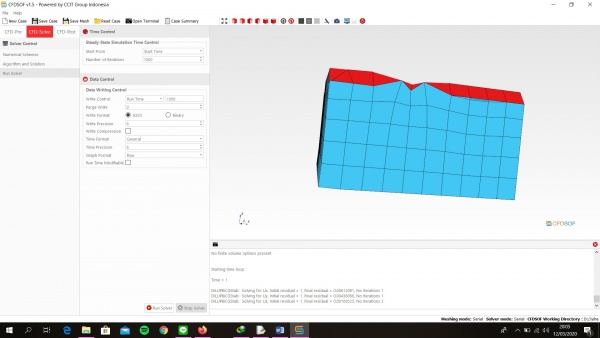
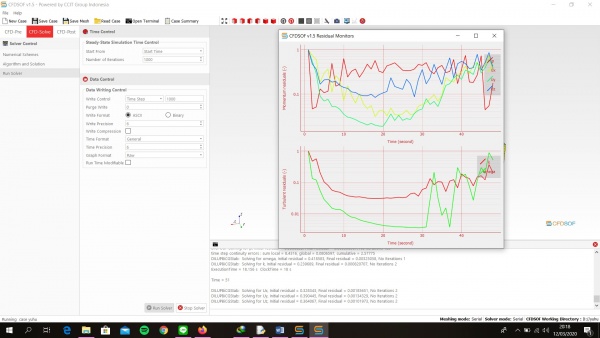
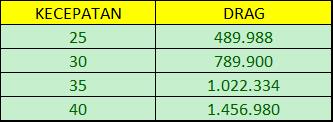
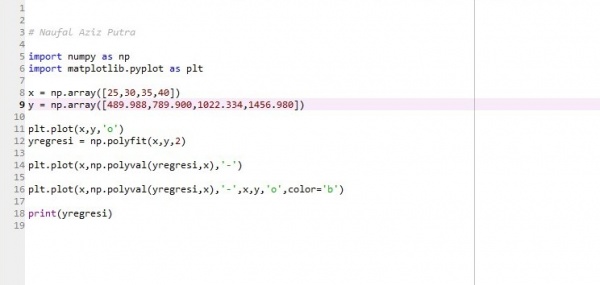
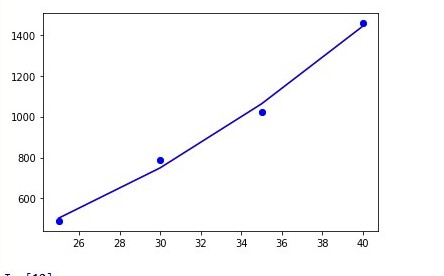
1. Buka CFDSOF v1.5 klik folder pada Geometry preparation => ussAlbacore 2. Kemudian klik kanan pada Geometry list => Scale => ubah jadi 0.001 semua 3. Kemudian klik Geometry Mesh ubah min & max pada surface refinement min, max => 3, 4 4. Kemudian klik Base Mesh ubah Min coordinate menjadi -2, -5, -5. dan ubah Max Coordinate menjadi 13, 0, 5. Ubah juga pada Box Mesh Properties pada Divisionnya menjadi 75, 25, 50 Ubah Box Mesh Boundaries seperti pada gambar dibawah ini 5. Kemudian klik Generate Mesh lalu ubah Output Format menjadi Binary lalu ubah Mesh Location menjadi 0, -3, -2 lalu klik pin berwarna kuning di bawah dan klik Generate Mesh 6. Pastikan Check Mesh Quality sampai muncul Mesh OK. End 7. Kemudian klik Simulation Model dan ubah menu Turbulance menjadi RANS 8. Kemudian Klik Turbulance ubah Turbulence Model menjadi Standar k-w dan centang Use Default Coefficient 9. Kemudian Klik Material ubah Material Name => Water, Density => 1000, Dynamic Viscosity => 0.00089 10. Kemudian Klik Boundary Properties Face Name => Inlet 1, Face Type => Patch, Boundary Conditions Type => Velocity Inlet, lalu ubah Reference Value bebas angkanya Face Name => Outlet1, Face Type => Patch, Boundary Conditions Type => Outflow Face Name => Boundary1, Face Type => Patch, Boundary Conditions Type => Far-Field Face Name => Symmetry1, Face Type => symmetry, Boundary Conditions Type => Symmetry Face Name => ussAlbacore, Face Type => Wall, Boundary Conditions Type => Stationary Wall 11. Klik CFD-SOlVE kemudian klik Run solver ubah Write Control => Run Time, 1000 12. Lalu klik Run Solver dan tunggu hingga selesai perhitungan dan akan keluarnya grafik 13. Lalu Klik CFD-POST lalu klik gambar yang 3 warna maka dia akan muncul halaman 14. Centang ussAlbacore lalu klik Apply maka akan muncul kapal selam 15. Lalu Klik Calculator lalu samakan kemudian apply 16. Klik Filters => Alphabetical => Generates Surface Normals 17. Centang Compute Cell Normalskemudian Apply 18. Klik calculator dan apply 19. Lalu klik Filters => Alphabetical => Integrate Variable 20. Kemudian centang Devide Cell Data By Volume kemudian Apply 21. Lalu akan muncul tabel
Review Asistensi 3 Maret 2020
Laporan Asistensi
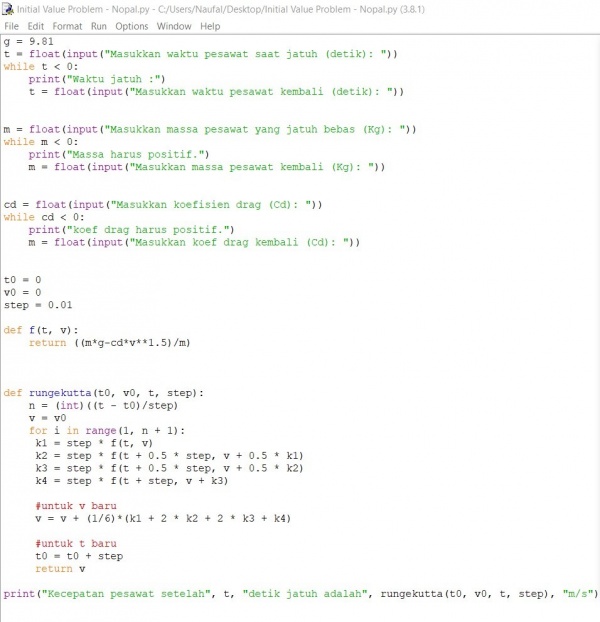
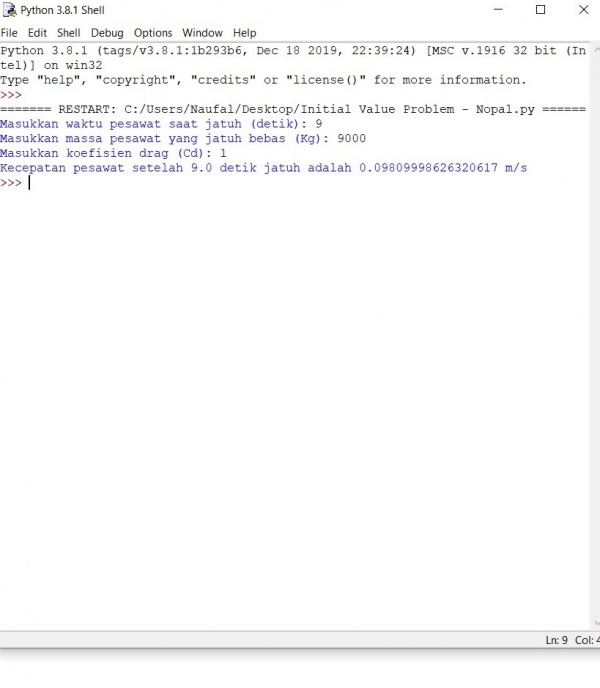
Tugas Intial Value Problem
Tugas Boundary Value Problem
Pertemuan Keenam
Bang Edo menjelaskan mengenai optimasi pada aplikasi python.
Cara meng-optimasi:
1. Menentukan persamaan yang dipakai untuk melakukan optimasi
2. Menentukan alokasi yang efekif dalam memilih sumber yang tersedia
3. Mendesain dengan karakteristik se-optimal mungkin
4. Optimasi membutuhkan batasan untuk bekerja dengan baik, maka dari itu diperlukan algoritma optimasi
5. Melakukan pengecekan pada variable yang dipakai agar sistem bekerja dengan sesuai yang diinginkan/optimal
Bang Edo memberikan sebuah kasus dimana menghitung kayu sepanjang 20 meter untuk dipakai pada pagar rumah.
Kayu sepanjang 20 meter dibutuhkan untuk membuat pagar rumah. Terdapat permintaan dimana di dalamp pagar harus ada minimal panjang kayu yaitu 8 meter yang dibutuhkan untuk bermain bola. Bagaimana agar kayu tersebut dapat memagari rumah dengan luas yang paling besar/optimal.
Fungsi objektif pada kasus ini adalah : Luas halaman (A= P x L)
Dalam mengerjakan proses optimasi pada python dibutuhkan yang namanya constraint/batas/limit. Fungsi constraint adalah untuk membatasi nilai sehingga tidak keluar dari nilai yang diinginkan.
constraint pada soal ini adalah : 20 meter kayu,
jadi 2P + 2L = 20 (2 karena panjang dan lebarnya ada 2).
Panjang minimal 8 meter sehingga terdapat cons lagi yaitu constraint = 2
Tugas Pertemuan Ketujuh Video Optimasi
Soal :
Sebuah Gelanggang Olahraga Remaja ingin menyimpan bola basket dalam sebuah box besar. Box yang diinginkan berbentuk kubus. Berapa ukuran panjang, lebar, dan tinggi yang diperlukan untuk mencapai volume maksimum yang dapat di gunakan untuk menyimpan bola basket. Syarat Luas Permukaan tidak melebihi 300 cm^2. Gunakan optimasi numerik pada python.
Volume : Panjang x lebar x tinggi Luas Permukaan : 2 [ (panjang x lebar) + (panjang x tinggi) + (lebar x tinggi) ]