Difference between revisions of "Arma Lauda Wiratmaja"
Arma.lauda (talk | contribs) (→Optimization of pressurized hydrogen storage) |
Arma.lauda (talk | contribs) |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 5: | Line 5: | ||
== Optimization of pressurized hydrogen storage == | == Optimization of pressurized hydrogen storage == | ||
| + | |||
| + | https://youtube.com/watch?v=URkSN0-hbfw&feature=share | ||
Tujuan : Optimasi pressurized hydrogen storage | Tujuan : Optimasi pressurized hydrogen storage | ||
| Line 11: | Line 13: | ||
batasan parameter : budget yang digunakan dalam optimasi tidak lebih dari 500000 rupiah | batasan parameter : budget yang digunakan dalam optimasi tidak lebih dari 500000 rupiah | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Tidak dapat dipungkiri hidrogen merupakan salah satu unsur yang memiliki potensi yang luar biasa. pemanfaatan hidrogen secara efektif dan efisien diprediksi dapat menjadi salah satu energi alternatif yang tersedia. | ||
| + | Penyimpanan hidrogen menjadi salah satu kunci penting yang masih menjadi bahan penelitian hingga saat ini, pressurized hydrogen storage merupakan sebuah metode untuk menyimpan hidrogen sehingga dapat didistribusikan dengan baik. metode ini memanfaatkan tekanan tinggi dari pompa untuk kemudian memompa hidrogen kedalam tabung. pada umumnya optimasi dapat dilakukan dengan memilih bahan yang kuat dan harga yang lebih murah dibandingkan harga lainnya. | ||
| + | dalam hal ini untuk meningkatkan efisiensi dalam upaya optimasi dengan batasan biaya sebesar 500000 rupiah, maka dapat dilakukan optimasi dengan memilih aluminimum sebagai bahan tabung penyimpanan. optimasi ini cenderung lebih efisien dan efektif dalam meningkatkan masa simpan dari hidrogen selain itu material ini cukup kuat dalam menahan tekanan tinggi. Aluminium juga cenderung lebih stabil dibandingkan logam lain apabila terkena panas dan dingin secara cepat. | ||
| + | |||
| + | Dimisalkan harga tabung pressurized hidrogen menggunakan baja pada umumnya adalah 2-3 juta rupiah, dengan volume dan ketebalan yang sama harga tersebut dapat ditekan menjadi hanya 475000 rupiah dengan mengganti bahan utama. apabila dibandingkan aluminium memiliki efisiensi yang lebih tinggi dalam menyimpan gas, akan tetapi baja memiliki kekuatan daya tahan yang lebih besar terhadap tekanan. jika dihitung pada volume 1 liter dan tekanan 8 bar, aluminium masih memiliki kemampuan yang cukup dalam menahan tekanan tersebut | ||
| + | |||
| + | |||
| + | |||
| + | == Final Report == | ||
| + | |||
| + | Specification : Pressure 8 bar ; Volume 1 Liter ; Cost 500.000 Rupiah | ||
| + | |||
| + | Setelah mendapatkan spesifikasi kita perlu menentukan diameter dari tabung hidrogen, dilakukan asumsi apabila tinggi tabung adalah 60 cm dan volume adalah 1 liter maka diameter tabung yang paling optimal adalah | ||
| + | |||
| + | from scipy.optimize import minimize | ||
| + | import math | ||
| + | |||
| + | def objective(r): | ||
| + | return -math.pi * r**2 * 60 # Negative sign to maximize the volume | ||
| + | |||
| + | def constraint(r): | ||
| + | return math.pi * r**2 * 60 - 1000 # Constraint: volume = 1000 cm³ | ||
| + | |||
| + | # Set the initial guess for the radius | ||
| + | x0 = 1.0 | ||
| + | |||
| + | # Define the optimization problem | ||
| + | problem = { | ||
| + | 'type': 'ineq', | ||
| + | 'fun': constraint | ||
| + | } | ||
| + | |||
| + | # Solve the optimization problem | ||
| + | result = minimize(objective, x0, method='SLSQP', constraints=problem) | ||
| + | |||
| + | # Extract the optimal radius from the result | ||
| + | optimal_radius = result.x[0] | ||
| + | |||
| + | # Calculate the corresponding optimal height | ||
| + | optimal_height = 60 | ||
| + | |||
| + | # Print the results | ||
| + | print(f"Optimal radius: {optimal_radius:.2f} cm") | ||
| + | print(f"Optimal height: {optimal_height} cm") | ||
| + | print(f"Optimal volume: {math.pi * optimal_radius**2 * optimal_height} cm³") | ||
| + | |||
| + | |||
| + | Optimal radius: 4.42 cm | ||
| + | Optimal height: 60 cm | ||
| + | Optimal volume: 1000.01 cm³ | ||
| + | |||
| + | |||
| + | Kemudian didalam membuat Tabung tersebut dipilih material berupa stainless steel 316 karena memiliki kualitas yang lebih baik dibandingkan dengan kompetitior sejenis, selain itu perbedaan harga relatif tinggi sedikit akan tetapi biaya pemeliharaan jauh lebih murah dan efisien. sehingga dalam membuat tabung ini dapat bertahan dalam jangka waktu yang lebih lama dengan mengeluarkan modal yang lebih tapi masih dalam batasan budget. | ||
| + | |||
| + | |||
| + | kemudian dilakukan estimasi ketebalan dinding dengan menghitung | ||
| + | |||
| + | V = π * (R² - r²) * h | ||
| + | r = R - t | ||
| + | |||
| + | dimana t merupakan ketebalan dinding. | ||
| + | |||
| + | R = 4.42 cm (optimal radius) | ||
| + | h = 60 cm (optimal height) | ||
| + | V = 1000.01 cm³ (optimal volume) | ||
| + | |||
| + | lalu dilakukan substitusi | ||
| + | |||
| + | 1000.01 = π * (4.42² - (4.42 - t)²) * 60 | ||
| + | |||
| + | sehingga dibuat coding | ||
| + | |||
| + | from scipy.optimize import fsolve | ||
| + | import math | ||
| + | |||
| + | def equation(t): | ||
| + | R = 4.42 | ||
| + | h = 60 | ||
| + | V = 1000.01 | ||
| + | |||
| + | r = R - t | ||
| + | volume = math.pi * (R**2 - r**2) * h | ||
| + | |||
| + | return volume - V | ||
| + | |||
| + | # Solve the equation to estimate the wall thickness | ||
| + | estimated_wall_thickness = fsolve(equation, 0.01)[0] | ||
| + | |||
| + | print(f"Estimated wall thickness: {estimated_wall_thickness:.2f} cm") | ||
| + | |||
| + | |||
| + | dengan hasil ketebalan 0.02 cm | ||
| + | |||
| + | Lalu dilakukan perhitungan luasan yang digunakan | ||
| + | |||
| + | import math | ||
| + | |||
| + | radius = 4.42 | ||
| + | height = 60 | ||
| + | |||
| + | curved_surface_area = 2 * math.pi * radius * height | ||
| + | base_area = math.pi * radius**2 | ||
| + | |||
| + | total_surface_area = curved_surface_area + 2 * base_area | ||
| + | |||
| + | print(f"Surface Area: {total_surface_area:.2f} cm²") | ||
| + | |||
| + | |||
| + | dan didapatkan hasil 1519.19 cm². | ||
| + | |||
| + | lalu dihitung berat massa tabung | ||
| + | |||
| + | density = 8 # grams/cm³ | ||
| + | volume = 1000.01 # cm³ | ||
| + | |||
| + | mass = volume * density | ||
| + | |||
| + | print(f"Mass of the tube: {mass:.2f} grams") | ||
| + | |||
| + | |||
| + | 8.00 kilograms | ||
| + | |||
| + | |||
| + | |||
| + | lalu dilakukan perhitungan atau estimasi harga pembuatan tabung | ||
| + | |||
| + | [[File:316_Stain.png]] | ||
| + | 8kg * 1.5 $ dengan estimasi kurs 15.000 rupiah / $ | ||
| + | maka hasil yang didapatkan adalah 180.000 rupiah | ||
Latest revision as of 11:44, 16 June 2023
Introduction
Optimization of pressurized hydrogen storage
https://youtube.com/watch?v=URkSN0-hbfw&feature=share
Tujuan : Optimasi pressurized hydrogen storage
Spesifikasi: Volume 1 liter dengan tekanan 8 bar
batasan parameter : budget yang digunakan dalam optimasi tidak lebih dari 500000 rupiah
Tidak dapat dipungkiri hidrogen merupakan salah satu unsur yang memiliki potensi yang luar biasa. pemanfaatan hidrogen secara efektif dan efisien diprediksi dapat menjadi salah satu energi alternatif yang tersedia.
Penyimpanan hidrogen menjadi salah satu kunci penting yang masih menjadi bahan penelitian hingga saat ini, pressurized hydrogen storage merupakan sebuah metode untuk menyimpan hidrogen sehingga dapat didistribusikan dengan baik. metode ini memanfaatkan tekanan tinggi dari pompa untuk kemudian memompa hidrogen kedalam tabung. pada umumnya optimasi dapat dilakukan dengan memilih bahan yang kuat dan harga yang lebih murah dibandingkan harga lainnya.
dalam hal ini untuk meningkatkan efisiensi dalam upaya optimasi dengan batasan biaya sebesar 500000 rupiah, maka dapat dilakukan optimasi dengan memilih aluminimum sebagai bahan tabung penyimpanan. optimasi ini cenderung lebih efisien dan efektif dalam meningkatkan masa simpan dari hidrogen selain itu material ini cukup kuat dalam menahan tekanan tinggi. Aluminium juga cenderung lebih stabil dibandingkan logam lain apabila terkena panas dan dingin secara cepat.
Dimisalkan harga tabung pressurized hidrogen menggunakan baja pada umumnya adalah 2-3 juta rupiah, dengan volume dan ketebalan yang sama harga tersebut dapat ditekan menjadi hanya 475000 rupiah dengan mengganti bahan utama. apabila dibandingkan aluminium memiliki efisiensi yang lebih tinggi dalam menyimpan gas, akan tetapi baja memiliki kekuatan daya tahan yang lebih besar terhadap tekanan. jika dihitung pada volume 1 liter dan tekanan 8 bar, aluminium masih memiliki kemampuan yang cukup dalam menahan tekanan tersebut
Final Report
Specification : Pressure 8 bar ; Volume 1 Liter ; Cost 500.000 Rupiah
Setelah mendapatkan spesifikasi kita perlu menentukan diameter dari tabung hidrogen, dilakukan asumsi apabila tinggi tabung adalah 60 cm dan volume adalah 1 liter maka diameter tabung yang paling optimal adalah
from scipy.optimize import minimize import math
def objective(r):
return -math.pi * r**2 * 60 # Negative sign to maximize the volume
def constraint(r):
return math.pi * r**2 * 60 - 1000 # Constraint: volume = 1000 cm³
- Set the initial guess for the radius
x0 = 1.0
- Define the optimization problem
problem = {
'type': 'ineq', 'fun': constraint
}
- Solve the optimization problem
result = minimize(objective, x0, method='SLSQP', constraints=problem)
- Extract the optimal radius from the result
optimal_radius = result.x[0]
- Calculate the corresponding optimal height
optimal_height = 60
- Print the results
print(f"Optimal radius: {optimal_radius:.2f} cm") print(f"Optimal height: {optimal_height} cm") print(f"Optimal volume: {math.pi * optimal_radius**2 * optimal_height} cm³")
Optimal radius: 4.42 cm
Optimal height: 60 cm
Optimal volume: 1000.01 cm³
Kemudian didalam membuat Tabung tersebut dipilih material berupa stainless steel 316 karena memiliki kualitas yang lebih baik dibandingkan dengan kompetitior sejenis, selain itu perbedaan harga relatif tinggi sedikit akan tetapi biaya pemeliharaan jauh lebih murah dan efisien. sehingga dalam membuat tabung ini dapat bertahan dalam jangka waktu yang lebih lama dengan mengeluarkan modal yang lebih tapi masih dalam batasan budget.
kemudian dilakukan estimasi ketebalan dinding dengan menghitung
V = π * (R² - r²) * h r = R - t
dimana t merupakan ketebalan dinding.
R = 4.42 cm (optimal radius) h = 60 cm (optimal height) V = 1000.01 cm³ (optimal volume)
lalu dilakukan substitusi
1000.01 = π * (4.42² - (4.42 - t)²) * 60
sehingga dibuat coding
from scipy.optimize import fsolve import math
def equation(t):
R = 4.42 h = 60 V = 1000.01
r = R - t volume = math.pi * (R**2 - r**2) * h
return volume - V
- Solve the equation to estimate the wall thickness
estimated_wall_thickness = fsolve(equation, 0.01)[0]
print(f"Estimated wall thickness: {estimated_wall_thickness:.2f} cm")
dengan hasil ketebalan 0.02 cm
Lalu dilakukan perhitungan luasan yang digunakan
import math
radius = 4.42 height = 60
curved_surface_area = 2 * math.pi * radius * height base_area = math.pi * radius**2
total_surface_area = curved_surface_area + 2 * base_area
print(f"Surface Area: {total_surface_area:.2f} cm²")
dan didapatkan hasil 1519.19 cm².
lalu dihitung berat massa tabung
density = 8 # grams/cm³ volume = 1000.01 # cm³
mass = volume * density
print(f"Mass of the tube: {mass:.2f} grams")
8.00 kilograms
lalu dilakukan perhitungan atau estimasi harga pembuatan tabung
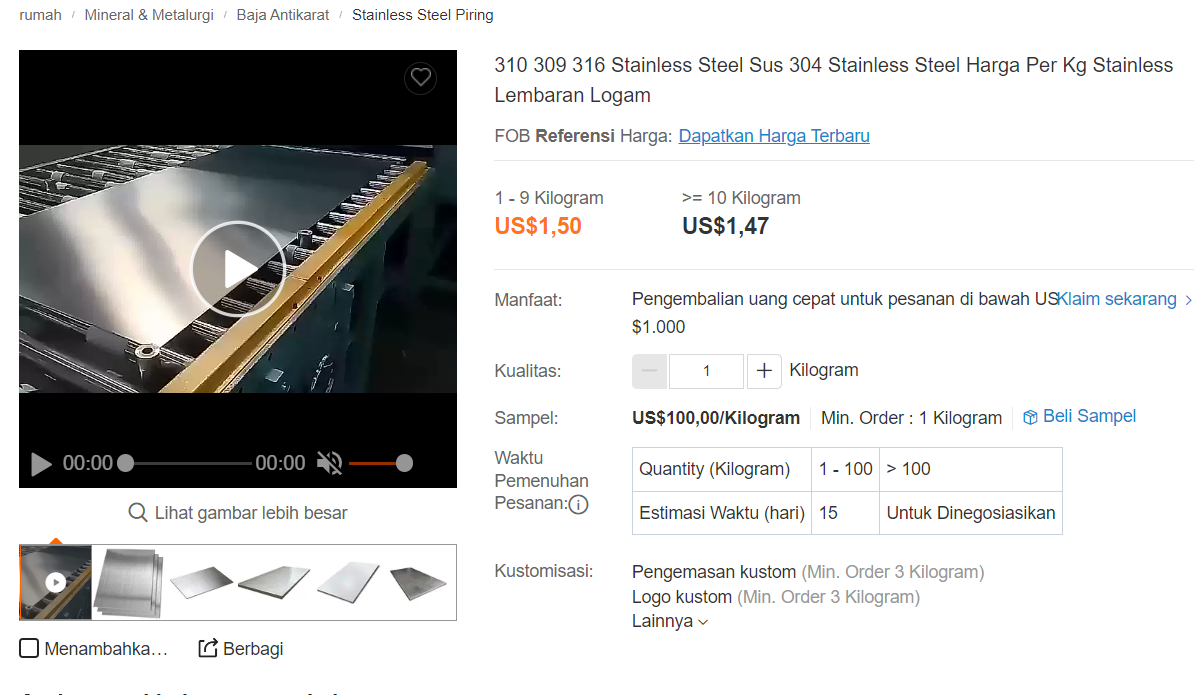 8kg * 1.5 $ dengan estimasi kurs 15.000 rupiah / $
maka hasil yang didapatkan adalah 180.000 rupiah
8kg * 1.5 $ dengan estimasi kurs 15.000 rupiah / $
maka hasil yang didapatkan adalah 180.000 rupiah