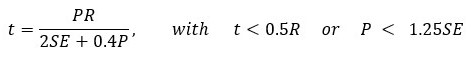Difference between revisions of "Farhan Primatondi Harahap"
Primaxfarhan (talk | contribs) |
Primaxfarhan (talk | contribs) (→Final Report: My Conscious in Design & Optimization of Pressurized Hydrogen Storage (15/06/2023)) |
||
| (8 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | [[File:tondi3. | + | [[File:tondi3.jpg|200px]] |
| + | |||
My name is Farhan Primatondi Harahap, some of my friends call me Farhan/Tondi. But i prefer to be called '''Tondi'''. In my daily life, I simply enjoy the beauty and pleasures that God gave to me ;) | My name is Farhan Primatondi Harahap, some of my friends call me Farhan/Tondi. But i prefer to be called '''Tondi'''. In my daily life, I simply enjoy the beauty and pleasures that God gave to me ;) | ||
| Line 53: | Line 54: | ||
To create a pressured hydrogen storage, there are certainly several materials involved in its construction. Therefore, we must choose wisely in selecting materials that are suitable for building pressured hydrogen storage according to our budget costs. | To create a pressured hydrogen storage, there are certainly several materials involved in its construction. Therefore, we must choose wisely in selecting materials that are suitable for building pressured hydrogen storage according to our budget costs. | ||
| + | According to the ASME Section VIII Pressure Vessel standardization, material Chosen for the design is ASTM A516M sheet metal (Sy = 38 Ksi) | ||
| + | Taking in the safety factor of 2/3, the allowable stress would be 2/3 x Sy = 25.3Ksi | ||
| + | |||
| + | [[File:Stress t1.jpg]] | ||
| + | |||
| + | '''E''' = 0.60 | ||
| + | ''' | ||
| + | P''' = 8 Bar = 0.8 MPa | ||
| + | |||
| + | '''R''' = 54.2 mm | ||
| + | |||
| + | '''S''' = 253000 Psi = 174.4370 MPa | ||
| + | |||
| + | '''Corrosion Allowance''' = 1.5 mm | ||
| + | |||
| + | Calculated t according to the formula is '''t''' = 2.06 mm | ||
| + | |||
| + | Thus the minimal allowable thickness is 2.06 mm | ||
| + | |||
| + | Cost Constrain | ||
determining the proper design for the allocated cost, the analysis of the optimal surface area with respect to the volume is carried out by numerical methods. Using a simple python program: | determining the proper design for the allocated cost, the analysis of the optimal surface area with respect to the volume is carried out by numerical methods. Using a simple python program: | ||
| − | |||
import numpy as np | import numpy as np | ||
from scipy.optimize import minimize | from scipy.optimize import minimize | ||
def objective(x): | def objective(x): | ||
| − | + | radius, height = x | |
| − | + | surface_area = 2 * np.pi * radius * height + 4 * np.pi * radius**2 | |
| − | + | return surface_area | |
def volume_constraint(x): | def volume_constraint(x): | ||
| − | + | radius, height = x | |
| − | + | volume = np.pi * radius**2 * height + (4/3) * np.pi * radius**3 | |
| − | + | return volume - 1000 | |
| − | + | ||
x0 = [2.0, 5.0] | x0 = [2.0, 5.0] | ||
bounds = [(0, None), (0, None)] | bounds = [(0, None), (0, None)] | ||
| Line 77: | Line 97: | ||
optimized_surface_area = problem.fun | optimized_surface_area = problem.fun | ||
| − | + | volume = np.pi * optimized_radius**2 * optimized_height + (4/3) * np.pi * optimized_radius**3 | |
| − | print( | + | |
| − | print( | + | cost_per_cm2 = 780.00 # Cost per cm² in IDR |
| − | print( | + | total_cost = cost_per_cm2 * optimized_surface_area |
| − | + | ||
| − | + | print("Optimized Radius:", optimized_radius) | |
| + | print("Optimized Height:", optimized_height) | ||
| + | print("Optimized Surface Area:", optimized_surface_area) | ||
| + | print("Volume:", volume) | ||
| + | print("Total Cost:", total_cost, "IDR") | ||
| + | |||
| − | + | After running the program, the results are: | |
| − | Optimized | + | Optimized Radius: 5.5270567354775375 |
| + | Optimized Height: 3.0504605712934385 | ||
| + | Optimized Surface Area: 489.81690073075134 | ||
| + | Volume: 1000.0000000000207 | ||
| + | Total Cost: 389211.74600787216 IDR | ||
| − | |||
| − | |||
| − | |||
In this program, we can determine a list of storage options with their characteristics such as capacity, pressure, and cost. By selecting the appropriate material, we then iterate through these options and evaluate whether they meet the target pressure and capacity requirements while considering cost constraints. The appropriate selection that meets all criteria is considered the best choice among all materials. | In this program, we can determine a list of storage options with their characteristics such as capacity, pressure, and cost. By selecting the appropriate material, we then iterate through these options and evaluate whether they meet the target pressure and capacity requirements while considering cost constraints. The appropriate selection that meets all criteria is considered the best choice among all materials. | ||
| − | + | Thus, we know that the '''optimized radius is 5.53 cm''' and '''optimized height is 3.05 cm''' for the minimum '''Surface Area of 489.81 cm^2''' | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | ''' | ||
| − | ''' | ||
| − | |||
| − | |||
| − | ''' | ||
| − | |||
| − | ''' | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | from the result, we also know that it would '''cost''' us '''389211.75 IDR''' to make. The cost is still way below the allocated maximum cost, so this '''design fits all the requirements'''. | |
| − | |||
| − | As the maximum cost is set to 500.000,00 IDR, we have to cross check the price for ASTM A516M sheet metal for a surface area of | + | As the maximum cost is set to 500.000,00 IDR, we have to cross check the price for ASTM A516M sheet metal for a surface area of 489.81 cm^2 Referenced from ali baba, it would cost $680 / Ton. means this material is very cheap and efficient to use |
'''The use of carbon steel regulated by the ASTM A516/A516M specification is generally cost-effective and efficient''' for various applications, including hydrogen storage. Carbon steel is a commonly used material that offers several advantages: | '''The use of carbon steel regulated by the ASTM A516/A516M specification is generally cost-effective and efficient''' for various applications, including hydrogen storage. Carbon steel is a commonly used material that offers several advantages: | ||
| Line 130: | Line 140: | ||
''' | ''' | ||
Therefore, when selecting materials for hydrogen storage, it is crucial to consider various important factors to ensure safety, reliability, and optimal performance according to project requirements. Consultation with experienced engineers or material experts is recommended to choose the appropriate material for your specific needs. | Therefore, when selecting materials for hydrogen storage, it is crucial to consider various important factors to ensure safety, reliability, and optimal performance according to project requirements. Consultation with experienced engineers or material experts is recommended to choose the appropriate material for your specific needs. | ||
| + | |||
| + | == Final Report: Design & Optimization of Pressurized Hydrogen Storage (15/06/2023)== | ||
| + | <youtube width="200" height="100">v=fBmiQwY-568</youtube> | ||
== Resume Pertemuan 2 == | == Resume Pertemuan 2 == | ||
Revision as of 03:19, 16 June 2023
My name is Farhan Primatondi Harahap, some of my friends call me Farhan/Tondi. But i prefer to be called Tondi. In my daily life, I simply enjoy the beauty and pleasures that God gave to me ;)
Contents
Resume Pertemuan 1 - (26/05/2023)
Numerical Methods Mahasiswa diharapkan daat berinteraksi dengan dosen lebih lanjut dalam perkuliahan Mata Kuliah Metode Numerik. Mahasiswa dapat mempelajari metode numerik di Google, sehingga mahasiswa dapat belajar mandiri dan merupakan progress dalam pembelajaran tidak hanya belajar dalam kelas, karena jika hanya di kelas tidak cukup untuk menjawa ujian, karena ujiannya menggunakan metode dia yang membuat soal dia yang menjawab, ini merupakan teknologi yang maju, konten Metode Numerik.
Case study, mengkonversi energi, memecah air, bisa dituliskan menggunakan karya tulis ilmiah ini juga merupakan PKM (Program Kreatifitas Mahasiswa). ChatGPT juga merupakan hasil dari metode numerik. Dapat mendesain 1 liter tabung hidrogen untuk dicampurkan bahan bakar motor. consciousness juga merupakan bahasan yang dibahas pada pertemuan pertama seperti pertanyaan soal (x+1)(x-1)/(x-1) = 2 yang menimbulkan beberapa jawaban oleh karena itu kita harus menggunakan otak kita secara sadar untuk menemukan solusi dari soal tersebut. Oleh karena itu bisa disimpulkan adanya keterkaitan ilmu matematika terhadap conciusness atau kesadaran kita terhadap realitas.
Case Study : Design & Optimization Pressurized Hydrogen Storage (01/06/23)
A pressurized hydrogen storage is a specially designed container for storing hydrogen under high pressure. The storage is designed to withstand higher pressure than the surrounding atmospheric pressure. The main purpose of a pressurized hydrogen storage is to safely and efficiently store and transport hydrogen. Pressurized hydrogen storage are commonly used in applications such as hydrogen storage and transportation for industrial, transportation, and energy storage purposes. The storage are equipped with filling and discharge valves to safely control the flow of hydrogen in and out of the storage. Safety is a crucial factor in the design and use of pressurized hydrogen storage. These storage must meet safety standards and undergo extensive testing to ensure structural reliability and resistance to high pressure.
Hydrogen Storage Spesification : It can accommodate 1 liter of hydrogen, And the pressure inside the storage is 8 bars. And the maximum cost for manufacturing the hydrogen storage is Rp500.000.
How to make a perfect Hydrogen Storage?
To design of pressurized hydrogen storage involves several steps, including Design and Engineering, Material selection, Fabrication, Safety. These are the steps to obtain a Pressurized Hydrogen Storage :
Design and Engineering: Developing the design specifications and engineering calculations for the hydrogen cylinder, considering factors such as capacity, pressure requirements, material selection, and safety considerations. Factors such as shape, volume, and thickness of the tank walls. Cylindrical shape are often used for pressurized gas storage. lets assume to design 1 liter capacity of pressurized hydrogen storage we need to have 300mm height with radius around of 50mm of cylindrical storage.
Material Selection: The choice of material for the storage vessel is critical to ensure safety, weight, and cost considerations. Sourcing and procuring the appropriate materials for the hydrogen cylinder, such as high-strength alloys, carbon fiber composites, or other suitable materials. Material selection is also in accordance with the existing budget.
Manufacturing Techniques: Utilizing manufacturing techniques like filament winding, bladder molding, or other suitable methods to create the desired shape and structure of the hydrogen cylinder. Performing machining operations, such as drilling or threading, and applying finishing treatments, such as cleaning, polishing, or coating, to achieve the desired final specifications.
Safety systems: Integrate safety features such as pressure relief valves, burst discs, or automatic shut-off systems to prevent overpressure or other emergency events. Adding a cover or outer shield to protect the tank from physical damage and external environment that might affect the performance of the tank. Hydrogen storage systems can be complex, and it is important to consult with engineers in the field to ensure the design and optimization process is carried out safely and effectively.
Installation & Operational : Install the storage tank in the intended location, ensuring proper connections and integration with other systems if applicable. Develop guidelines for the safe operation, maintenance, and inspection of the storage tank to ensure its continued performance and integrity.
Finally, for the manufacture of pressurized hydrogen storage, of course you have to think about the initial cost, which is no more than Rp500.000 . Therefore, we must minimize costs on several factors, such as material selection or manufacturing, but sometimes this will cause expensive maintenance costs and security. reduce. so we have to think consciously in this case.
Final Project : Design & Optimization Pressurized Hydrogen Storage (08/06/23)
Based on the description above regarding material selection, form, and system, I believe that the most viable choice for hydrogen storage would be a tank container system with a strong material to store pressurized hydrogen gas storage.
With the following specification requirements:
1. 1 Liter of Hydrogen
2. 8 Bar of pressure
3. Max cost of 500.000,00 IDR
Here's a simplified example of how you could approach the optimization process
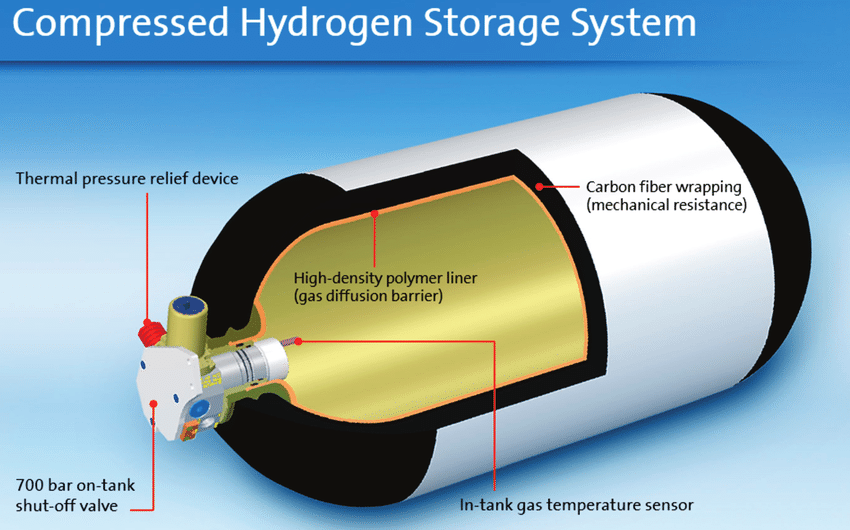 In the picture above is an example of the final planning of a Pressurized Hydrogen Storage cost within Rp 500,000.
In the picture above is an example of the final planning of a Pressurized Hydrogen Storage cost within Rp 500,000.
To create a pressured hydrogen storage, there are certainly several materials involved in its construction. Therefore, we must choose wisely in selecting materials that are suitable for building pressured hydrogen storage according to our budget costs.
According to the ASME Section VIII Pressure Vessel standardization, material Chosen for the design is ASTM A516M sheet metal (Sy = 38 Ksi) Taking in the safety factor of 2/3, the allowable stress would be 2/3 x Sy = 25.3Ksi
E = 0.60 P = 8 Bar = 0.8 MPa
R = 54.2 mm
S = 253000 Psi = 174.4370 MPa
Corrosion Allowance = 1.5 mm
Calculated t according to the formula is t = 2.06 mm
Thus the minimal allowable thickness is 2.06 mm
Cost Constrain determining the proper design for the allocated cost, the analysis of the optimal surface area with respect to the volume is carried out by numerical methods. Using a simple python program:
import numpy as np
from scipy.optimize import minimize
def objective(x):
radius, height = x
surface_area = 2 * np.pi * radius * height + 4 * np.pi * radius**2
return surface_area
def volume_constraint(x):
radius, height = x
volume = np.pi * radius**2 * height + (4/3) * np.pi * radius**3
return volume - 1000
x0 = [2.0, 5.0]
bounds = [(0, None), (0, None)]
constraint = {'type': 'eq', 'fun': volume_constraint}
problem = minimize(objective, x0, bounds=bounds, constraints=constraint)
optimized_radius = problem.x[0]
optimized_height = problem.x[1]
optimized_surface_area = problem.fun
volume = np.pi * optimized_radius**2 * optimized_height + (4/3) * np.pi * optimized_radius**3
cost_per_cm2 = 780.00 # Cost per cm² in IDR
total_cost = cost_per_cm2 * optimized_surface_area
print("Optimized Radius:", optimized_radius)
print("Optimized Height:", optimized_height)
print("Optimized Surface Area:", optimized_surface_area)
print("Volume:", volume)
print("Total Cost:", total_cost, "IDR")
After running the program, the results are:
Optimized Radius: 5.5270567354775375 Optimized Height: 3.0504605712934385 Optimized Surface Area: 489.81690073075134 Volume: 1000.0000000000207 Total Cost: 389211.74600787216 IDR
In this program, we can determine a list of storage options with their characteristics such as capacity, pressure, and cost. By selecting the appropriate material, we then iterate through these options and evaluate whether they meet the target pressure and capacity requirements while considering cost constraints. The appropriate selection that meets all criteria is considered the best choice among all materials.
Thus, we know that the optimized radius is 5.53 cm and optimized height is 3.05 cm for the minimum Surface Area of 489.81 cm^2
from the result, we also know that it would cost us 389211.75 IDR to make. The cost is still way below the allocated maximum cost, so this design fits all the requirements.
As the maximum cost is set to 500.000,00 IDR, we have to cross check the price for ASTM A516M sheet metal for a surface area of 489.81 cm^2 Referenced from ali baba, it would cost $680 / Ton. means this material is very cheap and efficient to use
The use of carbon steel regulated by the ASTM A516/A516M specification is generally cost-effective and efficient for various applications, including hydrogen storage. Carbon steel is a commonly used material that offers several advantages:
Cost-Effective: Carbon steel is generally more affordable compared to alloy steel or other specialized materials. This affordability helps optimize project budgets.
Wide Availability: Carbon steel is widely available in the market and can be produced in large quantities, making it easy to obtain the required material for hydrogen storage projects.
Adequate Mechanical Strength: Carbon steel possesses sufficient mechanical strength to withstand moderate hydrogen pressures. While it may not have the same strength as alloy steel, carbon steel can still meet the required strength requirements for many applications.
However, it is important to note that material selection for hydrogen storage should consider not only cost and efficiency but also factors such as operational pressure, corrosive environments, safety requirements, and compliance with applicable standards or regulations.
In some cases, where higher strength requirements, improved corrosion resistance, or other specific properties are needed, alternative materials such as alloy steel, carbon fiber, or composite materials may be more suitable, despite being more expensive. Therefore, when selecting materials for hydrogen storage, it is crucial to consider various important factors to ensure safety, reliability, and optimal performance according to project requirements. Consultation with experienced engineers or material experts is recommended to choose the appropriate material for your specific needs.