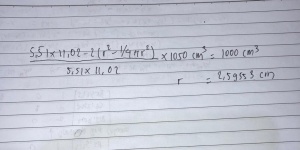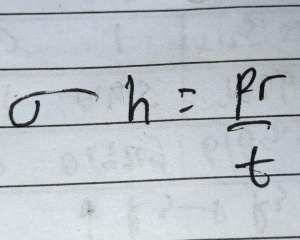Difference between revisions of "Chakra Merdeka Putra Ciya Suhada"
Chakrampcs (talk | contribs) (→Batasan Kekuatan Material (Material Strength Constraint)) |
Chakrampcs (talk | contribs) (→Introduction) |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
== Introduction == | == Introduction == | ||
| + | |||
| + | |||
| + | [[File:Tatagans.jpeg|300x300px]] | ||
Nama saya Chakra Merdeka dengan NPM 2106639711, Saat ini saya sedang berkuliah di Teknik Perkapalan, Departemen Teknik Mesin, Fakultas Teknik, Universitas Indonesia. Hobi saya bermain sepakbola, futsal, dan voli. Saya merupakan orang yang sangat mencintai keluarga. | Nama saya Chakra Merdeka dengan NPM 2106639711, Saat ini saya sedang berkuliah di Teknik Perkapalan, Departemen Teknik Mesin, Fakultas Teknik, Universitas Indonesia. Hobi saya bermain sepakbola, futsal, dan voli. Saya merupakan orang yang sangat mencintai keluarga. | ||
| − | |||
| − | |||
== Resume Pertemuan 1 == | == Resume Pertemuan 1 == | ||
| Line 129: | Line 130: | ||
Setelah ditemukannya parameter-parameter geometris, tahap terakhir dari optimisasi ini adalah membandingkannya dengan batasan biaya yang tidak boleh melebihi Rp500.000,00. Berdasarkan material yang telah dipilih sebelumnya, yaitu AISI 316, kita harus memilih ketebalan dinding tangki yang berada dalam range budget. Berikut adalah list harga beserta perhitungannya. | Setelah ditemukannya parameter-parameter geometris, tahap terakhir dari optimisasi ini adalah membandingkannya dengan batasan biaya yang tidak boleh melebihi Rp500.000,00. Berdasarkan material yang telah dipilih sebelumnya, yaitu AISI 316, kita harus memilih ketebalan dinding tangki yang berada dalam range budget. Berikut adalah list harga beserta perhitungannya. | ||
| − | Harga pelat stainless steel AISI 316 dari PT Citra Anggun Lestari | + | Harga pelat stainless steel AISI 316 dari PT Citra Anggun Lestari <br> |
| − | [[File:PT CITRA.jpg]] | + | [[File:PT CITRA.jpg|400x400px]] |
Berdasarkan perhitungan ini, dengan mengoptimalkan budget constraint, berat minimum yang wajar, tetapi tetap menjaga kekuatan yang wajar, '''dipilih ketebalan sebesar 6 mm''' untuk dinding tangki hidrogen ini. | Berdasarkan perhitungan ini, dengan mengoptimalkan budget constraint, berat minimum yang wajar, tetapi tetap menjaga kekuatan yang wajar, '''dipilih ketebalan sebesar 6 mm''' untuk dinding tangki hidrogen ini. | ||
Latest revision as of 00:57, 16 June 2023
Contents
- 1 Introduction
- 2 Resume Pertemuan 1
- 3 Design & Optimization of Pressurized Hydrogen Storage
- 4 Final Design & Optimization of Pressurized Hydrogen Storage
- 5 Batasan Geometris (Geometrical Constraint)
- 6 Batasan Kekuatan Material (Material Strength Constraint)
- 7 Batasan Biaya (Budget Constraint)
- 8 Final Remarks
- 9 Presentation of My Consciousness
Introduction
Nama saya Chakra Merdeka dengan NPM 2106639711, Saat ini saya sedang berkuliah di Teknik Perkapalan, Departemen Teknik Mesin, Fakultas Teknik, Universitas Indonesia. Hobi saya bermain sepakbola, futsal, dan voli. Saya merupakan orang yang sangat mencintai keluarga.
Resume Pertemuan 1
Mempelajari ilmu apa pun memerlukan kemampuan berpikir yang sadar. Kesadaran diri merupakan kunci dalam membedakan hal-hal yang pantas. Namun, penting untuk diingat bahwa hanya Tuhan yang memiliki kebenaran mutlak serta membahas mengenai apa itu arti dari consciousness dimana pada dasarnya hal tersebut merupakan fundamental yang dimiliki oleh setiap manusia. Jika kita berkaca dari segi kaidah kebahasaan, consciousness atau kesadaran memiliki arti mengerti akan suatu hal yang sedang dialami atau dirasakan oleh suatu objek. Dalam hal metode numerik consciousness dibutuhkan untuk meningkatkan kesadaran akan ketelitian serta pendetailan.
Design & Optimization of Pressurized Hydrogen Storage
Untuk mendesain dan mengoptimalkan penyimpanan hidrogen bertekanan 8 bar dengan kapasitas 1-liter dan budget maksimal Rp500.000, beberapa faktor perlu dipertimbangkan. Berikut adalah beberapa konsep desain dan optimasi yang dapat Anda pertimbangkan:
Bahan Penyimpanan: Pilih bahan yang cocok untuk menyimpan hidrogen secara aman pada tekanan 8 bar. Bahan yang umum digunakan adalah serat karbon yang diperkuat dengan resin epoksi. Material ini ringan, kuat, dan mampu menahan tekanan tinggi.
Tabung Penyimpanan: Cari tabung penyimpanan hidrogen yang sesuai dengan kapasitas dan tekanan yang diinginkan. Pastikan tabung memenuhi standar keamanan dan sertifikasi yang relevan.
Sistem Penguncian: Pastikan tabung memiliki sistem penguncian yang kuat dan aman untuk mencegah kebocoran hidrogen. Sistem penguncian yang baik akan membantu menjaga keamanan penyimpanan.
Sistem Pemantauan: Pertimbangkan pemasangan sensor atau sistem pemantauan untuk memantau tekanan dan suhu di dalam tabung. Hal ini penting untuk memastikan kondisi penyimpanan yang aman.
Sistem Pengeluaran: Perhatikan desain sistem pengeluaran hidrogen yang memungkinkan penggunaan yang mudah dan aman. Misalnya, gunakan katup pengeluaran yang dapat dikontrol dengan mudah dan cepat.
Keamanan: Pastikan bahwa tabung penyimpanan dilengkapi dengan sistem keamanan yang memadai, seperti katup pelepas tekanan berlebih dan katup pengaman termal untuk mencegah peningkatan suhu berlebih.
Biaya: Dalam mempertimbangkan biaya, bandingkan harga tabung dan komponen penyimpanan hidrogen dari berbagai pemasok. Carilah produk yang memenuhi standar keselamatan yang relevan namun tetap terjangkau sesuai dengan anggaran Anda.
Final Design & Optimization of Pressurized Hydrogen Storage
Sebagai mahasiswa Teknik yang mana kita akan menjadi calon insinyur berkualitas, kita harus melakukan pendekatan secara menyeluruh pada segala faktor yang berpengaruh dalam mendesain suatu komponen, terutama efisiensi dan optimisasi yang urgensinya sangat penting. Melalui kelas Metode Numerik dengan tugas mendesain dan mengoptimalkan pressurized hydrogen storage ini, kita dapat belajar untuk berpola pikir layaknya seorang insinyur. Secara tidak langsung, hal ini juga melatih consciousness kita.
Terdapat 3 batasan (constraints) yang menjadi acuan dalam optimisasi desain tangki hidrogen ini, yaitu geometris (geometrical constraint), kekuatan material (strength constraint), dan biaya (budget constraint). Berdasarkan diskusi yang telah dilakukan di kelas bersama teman-teman pada pekan lalu, material yang akan digunakan pada pembuatan tangki hidrogen ini adalah AISI 316 austenitic stainless steel. Austenitic stainless steel juga menjadi salah satu pilihan utama untuk pabrikan-pabrikan pembuat industrial hydrogen storage. Hal ini menandakan juga bahwa austenitic stainless steel sudah teruji secara ketersediaan, durabilitas, kekuatan, machinability, kompatibilitas dengan gas hidrogen (tidak bereaksi dengan hidrogen), dan sebagainya.
Batasan Geometris (Geometrical Constraint)
Geometri Dasar (Base) Ukuran menjadi batasan yang paling utama dalam mendesain tangki hidrogen ini. Optimisasi yang dilakukan adalah membuat surface area seminimal mungkin agar biaya material juga semakin minimum, tetapi tetap dengan volume 1 liter. Namun, karena nanti terdapat reduksi volume akibat end caps, batasan volume pada coding kali ini dibesarkan sedikit menjadi 1,050-liter atau 1050 cm^3. Pada optimisasi geometris ini, dilakukan coding menggunakan Python dengan library NumPy dan SciPy.
Berikut adalah code beserta hasilnya:
import numpy as np from scipy.optimize import minimize
def objective(x):
# x[0] represents the radius, x[1] represents the height radius = x[0] height = x[1]
# Calculate the surface area of the cylindrical structure surface_area = 2 * np.pi * radius * (radius + height)
return surface_area
def constraint(x):
# x[0] represents the radius, x[1] represents the height radius = x[0] height = x[1]
# Calculate the internal volume of the cylindrical structure volume = np.pi * radius**2 * height
# Return the difference between the volume and the desired value (1050 cubic centimeters) return volume - 1050
- Initial guess for the radius and height
x0 = [1.0, 10.0]
- Define the bounds for the variables (radius and height)
bounds = [(0, None), (0, None)]
- Define the constraint dictionary
constraint_dict = {'type': 'eq', 'fun': constraint}
- Use the minimize function to optimize the objective function subject to the constraint
result = minimize(objective, x0, method='SLSQP', bounds=bounds, constraints=constraint_dict)
- Print the optimized results
print("Optimization Results:") print("Radius: {:.2f} cm".format(result.x[0])) print("Height: {:.2f} cm".format(result.x[1])) print("Surface Area: {:.2f} cm^2".format(result.fun))
Hasil run dari code Berdasarkan hasil coding, dapat diketahui bahwa dengan luas area permukaan seminimal mungkin, ukuran tangki tabung yang optimal adalah dengan rasio tinggi:radius = 2:1, dalam hal ini tinggi tabung (h) adalah 11,02 cm dan radiusnya (r) adalah 5,51 cm. Dengan ukuran ini, luas area permukaan yang diperoleh adalah 571,88 cm^2.
Geometri End Cap
Contoh sederhana filleting untuk end caps
Tangki hidrogen dengan bentuk tabung murni saja akan meningkatkan risiko bahaya karena terdapat sudut yang terbentuk antara selimut dan alasnya pada kedua ujungnya, yang mana pada sudut tersebut terdapat konsentrasi stress (tegangan) yang terpusat sehingga dapat meningkatkan risiko kegagalan pada area sudut tersebut. Maka dari itu, dibentuklah end caps dengan metode filleting pada kedua ujung tangki agar stress yang disebabkan oleh tekanan dari gas hidrogen tersebut dapat lebih terdistribusi ke seluruh bagian tangki. 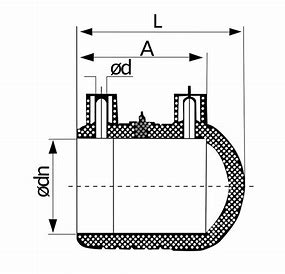
Namun, pembentukan end caps ini tentunya mengurangi volume dari tangki hidrogen. Oleh sebab itu, geometri dasar tangki dibuat dengan volume yang lebih banyak seperti di atas, yaitu 1050 cm^3 agar pengurangan volume akibat end caps ini tidak sampai kurang dari batasan 1 liter yang telah ditetapkan. Luas area proporsional dengan volume sehingga dapat dilakukan perhitungan perbandingan. Melalui perhitungan ini, dapat dicari radius dari fillet.
Hasil perhitungan di atas menunjukkan bahwa radius fillet yang diperoleh untuk end caps pada ujung tangki adalah 2,59553 cm
Batasan Kekuatan Material (Material Strength Constraint)
Pada sistem penyimpanan bertekanan, kekuatan material dan ketebalan pelat dari tangki harus bisa menahan tekanan gas yang menekan ke segala arah pada dinding tangki. Secara spesifikasi, tangki hidrogen 1 liter ini juga memiliki batasan tekanan 8 bar. Ketebalan pelat tangki ini dapat dihitung dengan persamaan hoop stress berikut ini.
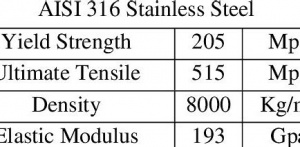
Mechanical Properties of AISI 316
Range ukuran dari ketebalan pelat tidak boleh kurang dari 1/5 radius tangki. Menurut ASME BPV Code Section VIII D.1, ketebalan pelat tangki minimal sebesar 1/16 in atau 1,59 mm tanpa mempertimbangkan korosi, material, ataupun dimensi. Pada perhitungan ini, akan dilakukan iterasi dari radius minimum sebesar 2,7 mm sampai 11,05 mm dengan penambahan sebanyak 1 mm pada setiap iterasinya.
Perhitungan Iterasi Ketebalan Dinding Tangki Iterasi ini dapat dilakukan menggunakan coding Python sebagai berikut:
r = 5.51e-2 #vessel radius p = 800000 #8 bar pressure constraint t = 2.7e-3 #minimum thickness
while t < 11.05e-3:
hoop = (p * r)/(t)
print('Untuk ketebalan', t, 'hoop stress =', hoop, "Pa")
t += 1e-3
if hoop > 205e9: #Yield Strength of AISI 316
break
Berdasarkan hasil perhitungan, range ketebalan 2,7 mm sampai 11,05 mm masih di bawah yield strength sehingga seluruh ketebalan pada range tersebut dapat diaplikasikan. Berikut adalah hasil perhitungan dari code yang menunjukkan bahwa hoop stress-nya jauh di bawah yield strength 205 MPa.
Batasan Biaya (Budget Constraint)
Setelah ditemukannya parameter-parameter geometris, tahap terakhir dari optimisasi ini adalah membandingkannya dengan batasan biaya yang tidak boleh melebihi Rp500.000,00. Berdasarkan material yang telah dipilih sebelumnya, yaitu AISI 316, kita harus memilih ketebalan dinding tangki yang berada dalam range budget. Berikut adalah list harga beserta perhitungannya.
Harga pelat stainless steel AISI 316 dari PT Citra Anggun Lestari
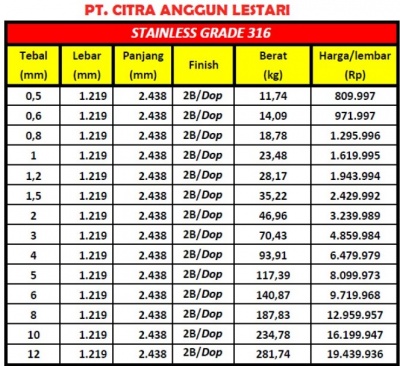
Berdasarkan perhitungan ini, dengan mengoptimalkan budget constraint, berat minimum yang wajar, tetapi tetap menjaga kekuatan yang wajar, dipilih ketebalan sebesar 6 mm untuk dinding tangki hidrogen ini.
Final Remarks
Berdasarkan aplikasi metode numerik pada optimisasi desain sistem penyimpanan hidrogen ini, diperoleh ukuran geometris tangki, yaitu radius sebesar 5,51 cm, tinggi sebesar 11,02 cm, luas permukaan sebesar 571,88 cm, dan radius fillet end cap sebesar 2,59553 cm. Selain itu, melalui batasan kekuatan material dan batasan biaya, diperoleh ukuran ketebalan dinding tangki hidrogen sebesar 6 mm. Namun dibutuhkan beberapa perubahan seperti tinggi kaki diperbesar dan diameter tangki diperkecil hal tersebut dilakukan karena ternyata perhitungan budget constraint masih jauh dibawah RP.500.000,00. Tidak lupa juga dilakukan pemasangan valve di satu sisi tangki untuk melakukan pengisian atau pengosongan tangki hidrogen tersebut menjadi lebih mudah.
Kesimpulannya, optimisasi dengan metode numerik ini masih dibilang cukup sederhana karena masih banyak faktor lain yang harus dipertimbangkan. Namun, optimisasi sederhana ini sudah bisa melatih kita menjadi lebih consciuos.