Difference between revisions of "Irza Lutfi"
Irza Lutfi (talk | contribs) (→Metnum-01) |
Irza Lutfi (talk | contribs) |
||
| (21 intermediate revisions by the same user not shown) | |||
| Line 30: | Line 30: | ||
== Progress 2 Tugas == | == Progress 2 Tugas == | ||
| − | |||
| − | # Harga dan kapasitas | + | from scipy.optimize import minimize |
| − | harga_per_unit = 100000 # Harga per unit penyimpanan hidrogen | + | # Harga dan kapasitas |
| − | + | harga_per_unit = 100000 # Harga per unit penyimpanan hidrogen = 1 | |
| − | + | # Kapasitas penyimpanan hidrogen per unit | |
| − | # Anggaran maksimal | + | # Anggaran maksimal |
| − | budget_maksimal = 500000 | + | budget_maksimal = 500000 |
| − | + | # Fungsi tujuan | |
| − | # Fungsi tujuan | + | def fungsi_tujuan(x): |
| − | def fungsi_tujuan(x): | ||
return -x | return -x | ||
| − | + | # Kendala | |
| − | # Kendala | + | def kendala(anggaran): |
| − | def kendala(anggaran): | ||
return budget_maksimal - (harga_per_unit * anggaran) | return budget_maksimal - (harga_per_unit * anggaran) | ||
| − | + | kendala_anggaran = {'type': 'ineq', 'fun': kendala} | |
| − | kendala_anggaran = {'type': 'ineq', 'fun': kendala} | + | # Nilai awal |
| − | + | x0 = 0 | |
| − | # Nilai awal | + | # Batasan |
| − | x0 = 0 | + | batas = [(0, None)] |
| − | + | # Menyelesaikan masalah optimisasi | |
| − | # Batasan | + | solusi = minimize(fungsi_tujuan, x0, method='SLSQP', bounds=batas, constraints=[kendala_anggaran]) |
| − | batas = [(0, None)] | + | # Menampilkan hasil |
| − | + | print("Status:", solusi.success and "Optimal" or "Tidak ditemukan solusi") | |
| − | # Menyelesaikan masalah optimisasi | ||
| − | solusi = minimize(fungsi_tujuan, x0, method='SLSQP', bounds=batas, constraints=[kendala_anggaran]) | ||
| − | |||
| − | # Menampilkan hasil | ||
| − | print("Status:", solusi.success and "Optimal" or | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
print("Jumlah unit penyimpanan hidrogen yang akan dibeli:", solusi.x[0]) | print("Jumlah unit penyimpanan hidrogen yang akan dibeli:", solusi.x[0]) | ||
print("Total kapasitas penyimpanan:", solusi.x[0] * kapasitas_per_unit, "liter") | print("Total kapasitas penyimpanan:", solusi.x[0] * kapasitas_per_unit, "liter") | ||
print("Total biaya:", solusi.x[0] * harga_per_unit, "Rupiah") | print("Total biaya:", solusi.x[0] * harga_per_unit, "Rupiah") | ||
| − | + | The code above uses the objective function to maximize the number of hydrogen storage units to buy. The budget constraint is set using the constraint function, which ensures that the total cost does not exceed the given maximum budget. The output will display the number of units that must be purchased, the total storage capacity, and the total cost required. | |
| − | |||
| − | + | [[File:Screenshot_2023-06-05_080737.png|400x400px]] | |
| − | |||
| − | |||
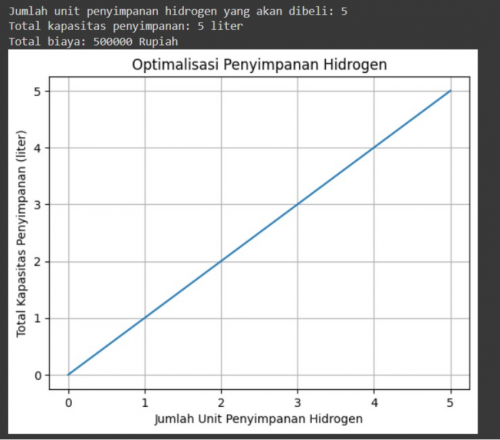
| − | + | Code that shows us a graph of hydrogen storage optimization taking into account the given capacity and budget constraints. | |
| − | + | from scipy.optimize import minimize | |
| + | # Harga dan kapasitas | ||
| + | harga_per_unit = 100000 # Harga per unit penyimpanan hidrogen | ||
| + | kapasitas_per_unit = 1 # Kapasitas penyimpanan hidrogen per unit | ||
| + | # Anggaran maksimal | ||
| + | budget_maksimal = 500000 | ||
| + | # Fungsi tujuan | ||
| + | def fungsi_tujuan(x): | ||
| + | return -x * kapasitas_per_unit | ||
| + | # Kendala | ||
| + | def kendala(anggaran): | ||
| + | return budget_maksimal - (harga_per_unit * anggaran) | ||
| + | kendala_anggaran = {'type': 'ineq', 'fun': kendala} | ||
| + | # Nilai awal | ||
| + | x0 = 0 | ||
| + | # Batasan | ||
| + | batas = [(0, None)] | ||
| + | # Menyelesaikan masalah optimisasi | ||
| + | solusi = minimize(fungsi_tujuan, x0, method='SLSQP', bounds=batas, constraints=[kendala_anggaran]) | ||
| + | # Menampilkan hasil | ||
| + | print("Status:", solusi.success and "Optimal" or "Tidak ditemukan solusi") | ||
| + | print("Jumlah unit penyimpanan hidrogen yang akan dibeli:", solusi.x[0]) | ||
| + | print("Total kapasitas penyimpanan:", solusi.x[0] * kapasitas_per_unit, "liter") | ||
| + | print("Total biaya:", solusi.x[0] * harga_per_unit, "Rupiah") | ||
| − | + | [[File:Screenshot_2023-06-05_080206.png|500x500px]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Hasil Optimasi: | |
| − | + | Radius = 5.50 cm | |
| − | + | Tinggi = 11 cm | |
| − | + | Luas Permukaan = 570 cm | |
| − | |||
| − | |||
| − | + | Pemilihan Material | |
| − | |||
| − | |||
| − | + | Baja paduan nikel dengan kandungan karbon rendah, seperti seri AISI 300 (misalnya, AISI 304, AISI 316), juga dapat menjadi pilihan yang baik untuk tangki hidrogen kecil. Baja paduan nikel memiliki ketahanan yang baik terhadap korosi hidrogen dan tahan terhadap retakan. Meskipun biaya baja paduan nikel mungkin sedikit lebih tinggi daripada baja paduan aluminium, namun tetap dapat dianggap sebagai opsi yang relatif terjangkau. | |
| − | + | [[File:600px-Aisi_Grade_304.png|500x500px]] | |
| − | |||
| − | + | Kekuatan luluh (yield strength) baja AISI 304 adalah sekitar 205 MPa (megapascal) atau sekitar 30,000 psi (pound per square inch). Kekuatan luluh adalah titik ketika baja mulai mengalami deformasi permanen atau perubahan bentuk yang permanen setelah diberikan beban. Kekuatan luluh ini merupakan salah satu parameter penting dalam menentukan kinerja dan kemampuan struktural dari baja 304. | |
| − | |||
| − | + | '''Analisis Biaya''' | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Untuk membuat tangki hidrogen ini diperlukan estimasi biaya pembuatan tangki dengan material Baja AISI 304. Berdasarkan referensi dari Tokopedia, harga baja 30x30cm [1]yang digunakan adalah sebesar Rp165.000. Estimasi biaya machining yang mencakup pengelasan,fit up,machining/taper, dan coating adalah sebesar Rp170.000. Diperlukan pemasangan katup/valve pada salah satu ujung tangki agar dapat dilakukan pengisian/pengosongan gas hidrogen dalam tangki dengan mudah. Biaya katup valve referensi dari tokopedia sebear Rp10.000. | |
| − | |||
| − | + | Maka total biaya Rp165.000 + Rp170.000 + 10.000= Rp345.000 | |
| − | |||
| − | + | '''Kesimpulan''' | |
| − | |||
| − | |||
| − | |||
| − | + | Pada desain tangki hidrogen ini diperoleh ukuran geometris tangki, yaitu radius sebesar 5,42 cm, tinggi sebesar 10,84 cm, luas permukaan sebesar 553.58 cm^2 dengan tebal tangki 8mm. Tangki tersebut menggunakan material Baja AISI304 dengan estimasi biaya produksi dan bahan sekitar RP 345.000 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''Final report video''' | |
| + | [[https://www.youtube.com/watch?v=iqYI1dDki34]] | ||
Latest revision as of 07:11, 12 June 2023
Introduction
Hallo Perkenalkan Saya Irza Lutfi Mahasiswa Teknik Mesin Universitas Indonesia Angkatan 2021 dengan NPM 2106638242!!
Metnum-01
Progress 1 Tugas
Untuk mengoptimalkan tangki hidrogen dengan kapasitas 1 liter dan tekanan 8 bar dengan biaya produksi maksimal Rp. 500.000, ada beberapa faktor yang perlu dipertimbangkan. Berikut adalah langkah-langkah yang dapat diambil untuk mencapai optimasi tersebut:
Material Tangki: Pertimbangkan material tangki yang efisien dan murah untuk digunakan dalam konstruksi tangki hidrogen. Pilihlah material yang memiliki kekuatan yang cukup untuk menahan tekanan 8 bar dan ringan agar tidak menambah berat tangki secara signifikan. Material yang mungkin dapat dipertimbangkan adalah aluminium atau serat karbon.
Desain Tangki: Rancanglah tangki dengan desain yang optimal untuk memaksimalkan kapasitas penyimpanan hidrogen dalam volume 1 liter. Bentuk silinder dengan diameter dan tinggi yang sesuai mungkin merupakan desain yang efisien untuk tujuan ini.
Efisiensi Pengisian: Perhatikan efisiensi pengisian tangki hidrogen. Pastikan sistem pengisian tangki meminimalkan kebocoran dan memastikan pengisian yang cepat dan efisien.
Pemilihan Komponen: Pilihlah komponen seperti katup pengisian, katup pengeluaran, dan sensor tekanan yang efisien dan ekonomis. Pastikan bahwa komponen tersebut memiliki kualitas yang baik agar dapat bekerja secara efektif dan aman.
Proses Produksi: Rancang proses produksi yang efisien untuk meminimalkan biaya produksi. Gunakan metode dan teknologi yang tepat untuk mempercepat produksi dan mengurangi biaya tenaga kerja.
Analisis Biaya: Lakukan analisis biaya mendalam untuk memastikan bahwa biaya produksi tetap di bawah batas maksimal Rp. 500.000. Tinjau biaya bahan baku, biaya tenaga kerja, biaya mesin, dan komponen lainnya yang terlibat dalam produksi tangki hidrogen. Identifikasi area-area di mana penghematan biaya dapat dicapai tanpa mengorbankan kualitas dan keamanan produk.
Optimalisasi Iteratif: Lakukan iterasi dan perbaikan berkelanjutan dalam desain dan proses produksi untuk mencapai hasil yang optimal. Tinjau kembali setiap langkah di atas dan identifikasi cara-cara untuk meningkatkan efisiensi dan mengurangi biaya.
Dengan mengikuti langkah-langkah di atas, diharapkan Anda dapat mengoptimalkan tangki hidrogen dengan kapasitas 1 liter, tekanan 8 bar, dan biaya produksi maksimal Rp. 500.000. Namun, perlu diingat bahwa optimasi ini hanya memberikan panduan umum, dan dapat diperlukan penyesuaian yang lebih rinci tergantung pada kebutuhan dan sumber daya yang tersedia.
Progress 2 Tugas
from scipy.optimize import minimize
# Harga dan kapasitas
harga_per_unit = 100000 # Harga per unit penyimpanan hidrogen = 1
# Kapasitas penyimpanan hidrogen per unit
# Anggaran maksimal
budget_maksimal = 500000
# Fungsi tujuan
def fungsi_tujuan(x):
return -x
# Kendala
def kendala(anggaran):
return budget_maksimal - (harga_per_unit * anggaran)
kendala_anggaran = {'type': 'ineq', 'fun': kendala}
# Nilai awal
x0 = 0
# Batasan
batas = [(0, None)]
# Menyelesaikan masalah optimisasi
solusi = minimize(fungsi_tujuan, x0, method='SLSQP', bounds=batas, constraints=[kendala_anggaran])
# Menampilkan hasil
print("Status:", solusi.success and "Optimal" or "Tidak ditemukan solusi")
print("Jumlah unit penyimpanan hidrogen yang akan dibeli:", solusi.x[0])
print("Total kapasitas penyimpanan:", solusi.x[0] * kapasitas_per_unit, "liter")
print("Total biaya:", solusi.x[0] * harga_per_unit, "Rupiah")
The code above uses the objective function to maximize the number of hydrogen storage units to buy. The budget constraint is set using the constraint function, which ensures that the total cost does not exceed the given maximum budget. The output will display the number of units that must be purchased, the total storage capacity, and the total cost required.
Code that shows us a graph of hydrogen storage optimization taking into account the given capacity and budget constraints.
from scipy.optimize import minimize
# Harga dan kapasitas
harga_per_unit = 100000 # Harga per unit penyimpanan hidrogen
kapasitas_per_unit = 1 # Kapasitas penyimpanan hidrogen per unit
# Anggaran maksimal
budget_maksimal = 500000
# Fungsi tujuan
def fungsi_tujuan(x):
return -x * kapasitas_per_unit
# Kendala
def kendala(anggaran):
return budget_maksimal - (harga_per_unit * anggaran)
kendala_anggaran = {'type': 'ineq', 'fun': kendala}
# Nilai awal
x0 = 0
# Batasan
batas = [(0, None)]
# Menyelesaikan masalah optimisasi
solusi = minimize(fungsi_tujuan, x0, method='SLSQP', bounds=batas, constraints=[kendala_anggaran])
# Menampilkan hasil
print("Status:", solusi.success and "Optimal" or "Tidak ditemukan solusi")
print("Jumlah unit penyimpanan hidrogen yang akan dibeli:", solusi.x[0])
print("Total kapasitas penyimpanan:", solusi.x[0] * kapasitas_per_unit, "liter")
print("Total biaya:", solusi.x[0] * harga_per_unit, "Rupiah")
Hasil Optimasi:
Radius = 5.50 cm
Tinggi = 11 cm
Luas Permukaan = 570 cm
Pemilihan Material
Baja paduan nikel dengan kandungan karbon rendah, seperti seri AISI 300 (misalnya, AISI 304, AISI 316), juga dapat menjadi pilihan yang baik untuk tangki hidrogen kecil. Baja paduan nikel memiliki ketahanan yang baik terhadap korosi hidrogen dan tahan terhadap retakan. Meskipun biaya baja paduan nikel mungkin sedikit lebih tinggi daripada baja paduan aluminium, namun tetap dapat dianggap sebagai opsi yang relatif terjangkau.
Kekuatan luluh (yield strength) baja AISI 304 adalah sekitar 205 MPa (megapascal) atau sekitar 30,000 psi (pound per square inch). Kekuatan luluh adalah titik ketika baja mulai mengalami deformasi permanen atau perubahan bentuk yang permanen setelah diberikan beban. Kekuatan luluh ini merupakan salah satu parameter penting dalam menentukan kinerja dan kemampuan struktural dari baja 304.
Analisis Biaya
Untuk membuat tangki hidrogen ini diperlukan estimasi biaya pembuatan tangki dengan material Baja AISI 304. Berdasarkan referensi dari Tokopedia, harga baja 30x30cm [1]yang digunakan adalah sebesar Rp165.000. Estimasi biaya machining yang mencakup pengelasan,fit up,machining/taper, dan coating adalah sebesar Rp170.000. Diperlukan pemasangan katup/valve pada salah satu ujung tangki agar dapat dilakukan pengisian/pengosongan gas hidrogen dalam tangki dengan mudah. Biaya katup valve referensi dari tokopedia sebear Rp10.000.
Maka total biaya Rp165.000 + Rp170.000 + 10.000= Rp345.000
Kesimpulan
Pada desain tangki hidrogen ini diperoleh ukuran geometris tangki, yaitu radius sebesar 5,42 cm, tinggi sebesar 10,84 cm, luas permukaan sebesar 553.58 cm^2 dengan tebal tangki 8mm. Tangki tersebut menggunakan material Baja AISI304 dengan estimasi biaya produksi dan bahan sekitar RP 345.000
Final report video [[1]]