Difference between revisions of "Muhammad Umar Farhat Al Fatah"
m (→Pressurized Hydrogen Storage Optimization) |
(→My Concious Efforts in Numerical Method Learning and Its Application in Hydrogen Storage Design Optimization) |
||
| (6 intermediate revisions by the same user not shown) | |||
| Line 55: | Line 55: | ||
4. '''Bahan Kimia''': Beberapa senyawa kimia seperti amonia borane (NH3BH3) atau hidrurat logam-organik seperti litium alanat (LiAlH4) dan natrium borohidrida (NaBH4) dapat digunakan sebagai penyimpan hidrogen.<br> | 4. '''Bahan Kimia''': Beberapa senyawa kimia seperti amonia borane (NH3BH3) atau hidrurat logam-organik seperti litium alanat (LiAlH4) dan natrium borohidrida (NaBH4) dapat digunakan sebagai penyimpan hidrogen.<br> | ||
5. '''Material Nanostruktural''': Bahan dengan struktur nanometer seperti nanotube karbon atau graphene memiliki potensi sebagai metode penyimpanan hidrogen. Permukaan yang besar dan sifat-sifat unik dari material nanostruktural ini dapat meningkatkan kapasitas penyerapan hidrogen.<br> | 5. '''Material Nanostruktural''': Bahan dengan struktur nanometer seperti nanotube karbon atau graphene memiliki potensi sebagai metode penyimpanan hidrogen. Permukaan yang besar dan sifat-sifat unik dari material nanostruktural ini dapat meningkatkan kapasitas penyerapan hidrogen.<br> | ||
| + | |||
| + | == Optimasi Penyimpanan == | ||
| + | Ada beberapa tahapan dalam mendesain dan mengoptimasi sistem penyimpanan, dari yang sudah ada menjadi yang sesuai dengan batasan maksimal yang diinginkan.<br> | ||
| + | |||
| + | 1. Tentukan ukuran pelat yang akan digunakan berdasarkan volume yang dibutuhkan, yaitu 1 liter, namun menggunakan luas pelat seminimal mungkin menggunakan perhitungan sebagai berikut:<br> | ||
| + | import math | ||
| + | from scipy.optimize import minimize | ||
| + | |||
| + | def objective(x): | ||
| + | radius, height = x | ||
| + | return 2 * math.pi * radius**2 + 2 * math.pi * radius * height | ||
| + | |||
| + | def constraint(x): | ||
| + | radius, height = x | ||
| + | return math.pi * radius**2 * height - 1000 | ||
| + | |||
| + | initial_guess = [1, 10] # Initial guess for the radius and height | ||
| + | |||
| + | # Define the bounds for the radius and height | ||
| + | bounds = [(0, None), (0, None)] | ||
| + | |||
| + | # Define the volume constraint | ||
| + | volume_constraint = {'type': 'eq', 'fun': constraint} | ||
| + | |||
| + | # Minimize the surface area subject to the volume constraint | ||
| + | result = minimize(objective, initial_guess, method='SLSQP', bounds=bounds, | ||
| + | constraints=volume_constraint) | ||
| + | |||
| + | optimal_radius = result.x[0] | ||
| + | optimal_height = result.x[1] | ||
| + | min_surface_area = result.fun | ||
| + | |||
| + | print(f"\n\nOptimal Radius: {optimal_radius} cm") | ||
| + | print(f"Optimal Height: {optimal_height} cm") | ||
| + | print(f"Minimum Surface Area: {min_surface_area} cm²\n\n") | ||
| + | |||
| + | Dari perhitungan tersebut, didapatkan beberapa nilai ukuran berikut ini,<br> | ||
| + | ● Optimal Radius: 5.419261255088046 cm<br> | ||
| + | ● Optimal Height: 10.838519182022262 cm<br> | ||
| + | ● Minimum Surface Area: 553.5810443894838 cm²<br> | ||
| + | |||
| + | 2. Selanjutnya, dilakukan perhitungan dengan variabel budget yang telah ditetapkan, yaitu Rp. 500.000. Untuk perhitungannya, digunakan perhitungan sebagai berikut menggunakan python: | ||
| + | from scipy.optimize import minimize | ||
| + | |||
| + | # Harga dan kapasitas yang dibutuhkan | ||
| + | harga_per_unit = 500000 # Rupiah | ||
| + | kapasitas_per_unit = 1 # Liter | ||
| + | |||
| + | # Anggaran maksimal | ||
| + | anggaran_maksimal = 500000 | ||
| + | |||
| + | # Fungsi Akhir | ||
| + | def fungsi_akhir(x): | ||
| + | return -x * kapasitas_per_unit | ||
| + | |||
| + | # Kendala yang terjadi | ||
| + | def kendala(anggaran): | ||
| + | return anggaran_maksimal - (harga_per_unit * anggaran) | ||
| + | |||
| + | kendala_anggaran = {'type': 'ineq', 'fun': kendala} | ||
| + | |||
| + | # Nilai awal | ||
| + | x0 = 0 | ||
| + | |||
| + | # Batasan | ||
| + | batas = [(0, None)] | ||
| + | |||
| + | # Menyelesaikan masalah optimisasi | ||
| + | solusi = minimize(fungsi_akhir, x0, method='SLSQP', bounds=batas, constraints=[kendala_anggaran]) | ||
| + | |||
| + | # Menampilkan hasil | ||
| + | print("Status:", solusi.success and "Biaya Optimal" or "Tidak ditemukan solusi") | ||
| + | print("Jumlah unit yang bisa dibeli:", solusi.x[0]) | ||
| + | print("Total kapasitas penyimpanan yang didapat:", solusi.x[0] * kapasitas_per_unit, "liter") | ||
| + | print("Total anggaran:", solusi.x[0] * harga_per_unit, "Rupiah") | ||
| + | |||
| + | Hasil yang didapatkan adalah:<br> | ||
| + | ● Status: Biaya Optimal<br> | ||
| + | ● Jumlah unit yang bisa dibeli: 1<br> | ||
| + | ● Total kapasitas penyimpanan yang didapat: 1.0 liter<br> | ||
| + | ● Total anggaran: 500000.0 Rupiah<br><br> | ||
| + | Menggunakan perhitungan di atas, bisa dilakukan plot terhadap perbandingan kapasitas dan jumlah yang didapatkan dengan code berikut: | ||
| + | # list grafik | ||
| + | unit_list = [] | ||
| + | total_kapasitas_list = [] | ||
| + | |||
| + | # Perhitungan solusi optimal | ||
| + | for jumlah_unit in range(int(budget_maksimal / harga_per_unit) + 1): | ||
| + | total_kapasitas = jumlah_unit * kapasitas_per_unit | ||
| + | total_biaya = jumlah_unit * harga_per_unit | ||
| + | |||
| + | if total_kapasitas > total_kapasitas_optimal and total_biaya <= budget_maksimal: | ||
| + | jumlah_unit_optimal = jumlah_unit | ||
| + | total_kapasitas_optimal = total_kapasitas | ||
| + | total_biaya_optimal = total_biaya | ||
| + | |||
| + | # Menambahkan data ke dalam list untuk grafik | ||
| + | unit_list.append(jumlah_unit) | ||
| + | total_kapasitas_list.append(total_kapasitas) | ||
| + | |||
| + | # Tampilan Hasil | ||
| + | print("Jumlah unit penyimpanan hidrogen yang akan dibeli:", jumlah_unit_optimal) | ||
| + | print("Total kapasitas penyimpanan:", total_kapasitas_optimal, "liter") | ||
| + | print("Total biaya:", total_biaya_optimal, "Rupiah") | ||
| + | |||
| + | # Grafik ditampilkan | ||
| + | plt.plot(unit_list, total_kapasitas_list, color='red') | ||
| + | plt.xlabel('Jumlah Penyimpanan Hidrogen') | ||
| + | plt.ylabel('Total Kapasitas Penyimpanan (liter)') | ||
| + | plt.title('Optimalisasi Penyimpanan Hidrogen') | ||
| + | plt.grid(True) | ||
| + | plt.show() | ||
| + | |||
| + | [[File:Grafik_Umar_1.jpg|300px|thumb|center|Grafik perbandingan kapasitas dan unit]] | ||
| + | |||
| + | Kode yang digunakan di atas, bertujuan untuk melihat optimasi penyimpanan hidrogen dengan mempertimbangkan batasan kapasitas dan anggaran yang diberikan. Tujuan utamanya menemukan jumlah unit penyimpanan hidrogen yang harus dibeli untuk mencapai kapasitas penyimpanan maksimum dengan tetap mempertimbangkan batasan yang digunakan. | ||
| + | |||
| + | Iterasi dilakukan untuk mendapatkan data setiap unit yang dibeli jika dibandingkan dengan kapasitas dan batasan lain yang didapat. Setiap jumlah unit diuji untuk menghitung kapasitas penyimpanan total dan biaya total yang terkait. jika nilai sudah melebihi batasan, iterasi akan berhenti. | ||
| + | |||
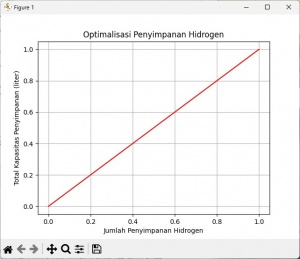
| + | Selain itu, grafik yang terbentuk menunjukkan hubungan antara jumlah unit penyimpanan hidrogen yang akan dibeli dan kapasitas penyimpanan total yang diperoleh dalam merepresentasikan kapasitas total berubah saat unit penyimpanan hidrogen tambahan ditambahkan. | ||
| + | |||
| + | == Hasil desain == | ||
| + | Dengan ukuran yang telah dihitung pada perhitungan sebelumnya, didapatkan gambaran dari tabung yang akan dibuat sebagai berikut: | ||
| + | [[File:Tabung_Umar1.png|300px|thumb|center|Tabung Hidrogen]] | ||
| + | yang memiliki ukuran-ukuran: | ||
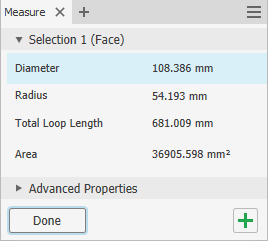
| + | [[File:UkuranTabung_Umar1.png|300px|thumb|center|Hydrogen Storage]] | ||
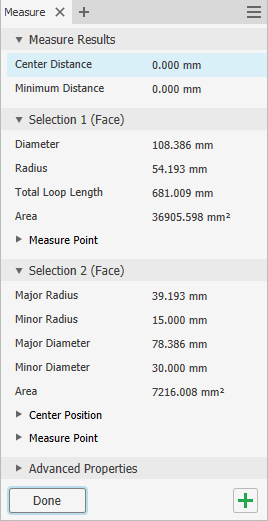
| + | [[File:UkuranTabung_Umar2.png|300px|thumb|center|Hydrogen Storage]] | ||
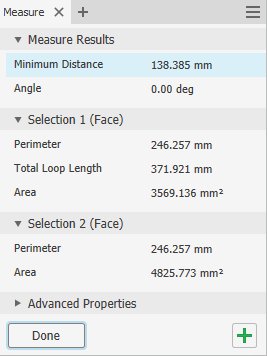
| + | [[File:UkuranTabung_Umar3.png|300px|thumb|center|Hydrogen Storage]] | ||
| + | |||
| + | == Ukuran == | ||
| + | Total ukuran luas plat yang didapat adalah '''(36905.598 + 7216.008 + 4825.773)mm² = 610 cm²''' | ||
| + | |||
| + | == Kesimpulan == | ||
| + | Untuk bisa membuat tabung ini, dibutuhkan<br> | ||
| + | 1. Material<br> | ||
| + | Sesuai dengan harga yang tertera di Tokopedia, harga material plat baja yang digunakan adalah Rp200.000 | ||
| + | |||
| + | 2. Katup tabung<br> | ||
| + | Sesuai dengan harga yang tertera di Tokopedia, harga katup yang digunakan adalah Rp10.000 | ||
| + | |||
| + | 3. Estimasi Biaya pembuatan<br> | ||
| + | Estimasi biaya yang digunakan untuk pembuatan dengan machining adalah Rp150.000 | ||
| + | |||
| + | Oleh karena itu, total biaya yang dibutuhkan dalam pembuatan tabung ini adalah sekitar Rp200.000 + Rp10.000 + Rp150.000= Rp360.000 | ||
| + | |||
| + | = My Concious Efforts in Numerical Method Learning and Its Application in Hydrogen Storage Design Optimization = | ||
| + | [https://www.youtube.com/watch?v=LlrUzyCiMr0 Video Presentasi Umar] | ||
Latest revision as of 00:08, 12 June 2023
Contents
Introduction
Halo semua!
Perkenalkan, nama Saya Muhammad Umar Farhat Al Fatah biasa dipanggil Umar dengan NPM 2106704824.
Saya merupakan Mahasiswa Departemen Teknik Mesin FTUI Angkatan 2021 yang saat ini sedang mengikuti Kelas Metode Numerik 01
Pressurized Hydrogen Storage Optimization
Pertimbangan Desain
Task: Optimasi tangki hidrogen dengan kapasitas 1 liter, pressure 8 bar, dan biaya produksi maksimal Rp. 500.000
Dalam mengoptimasi sistem penyimpanan hidrogen, ada beberapa faktor yang harus dipertimbangkan selama mendesain:
1. Metode penyimpanan
Terdapat beberapa metode penyimpanan yang tersedia untuk hidrogen, antara lain tabung gas terkompresi, logam hidrida, material berbasis karbon, dan penyimpanan kriogenik.
2. Wadah penyimpanan
Berdasarkan metode penyimpanan yang dipilih, cari dan bandingkan berbagai wadah penyimpanan yang tersedia di pasaran dengan mempertimbangkan beberapa faktor, seperti bahan, berat, volume, rating tekanan, fitur keamanan, dan biaya.
3. Persyaratan keamanan
Hidrogen adalah bahan yang sangat mudah terbakar dan faktor keamanan yang baik sehingga perlu dipastikan wadah penyimpanan yang dipilih memenuhi standar dan regulasi keamanan yang berlaku
4. Ukuran wadah
Tentukan ukuran wadah yang optimal berdasarkan volume yang dibutuhkan dan sesuaikan dengan volume yang diinginkan, serta mempertimbangkan beberapa faktor, seperti dimensi wadah, berat, dan biaya.
5. Evaluasi biaya bahan dan konstruksi
Pertimbangkan kembali biaya dari bahan yang diperlukan untuk wadah penyimpanan, seperti logam atau material komposit.
6. Solusi yang hemat biaya
Dari kebutuhan yang telah dievaluasi sebelumnya, temukan alternatif yang lebih hemat biaya yang dapat membantu mengoptimalkan desain. Wadah yang digunakan tidak harus menggunakan yang baru, tetapi menggunakan yang masih bagus kondisinya juga dapat dipertimbangkan
7. Pertimbangkan opsi pengisian ulang
Tentukan apakah terdapat stasiun pengisian ulang lokal atau opsi yang terjangkau untuk mengisi ulang hidrogen karena dapat memengaruhi biaya jangka panjang penggunaan dan pemeliharaan sistem penyimpanan.
8. Estimasi biaya dan optimisasi
Jumlahkan biaya wadah penyimpanan yang dipilih, aksesori keamanan, bahan, dan biaya tambahan yang terlibat. Bandingkan total biaya dengan anggaran yang ditetapkan dan jika estimasi biaya melebihi anggaran, evaluasi kembali pilihan desain dan pertimbangkan opsi alternatif atau penyesuaian untuk memenuhi batasan anggaran.
Dari beberapa faktor tersebut, dalam pembuatannya, keseimbangan dalam efisiensi dan biaya harus benar-benar dipertimbangkan karena kesalahan perhitungan sedikit dapat membahayakan penggunanya
Sifat Hidrogen
Hal yang perlu diketahui dalam mempertimbangkan adalah sifat dari hidrogen itu sendiri. ada beberapa sifat yang penting untuk dipertimbangkan dalam optimasi sistem penyimpanannya, yaitu di antaranya:
1. Gas Ringan: Hidrogen adalah unsur dengan massa atom terkecil di tabel periodik sehingga memiliki kepadatan sangat rendah. Pada suhu dan tekanan standar, hidrogen berada dalam bentuk gas.
2. Reaktivitas: Hidrogen adalah unsur yang sangat reaktif, dapat bereaksi dengan banyak unsur lain, seperti oksigen, halogen, dan logam alkali dan membentuk berbagai senyawa.
3. Pembentuk Air: Hidrogen bereaksi dengan oksigen secara eksotermik untuk membentuk air (H2O).
4. Sifat Asam dan Alkali: Hidrogen dapat bertindak sebagai asam atau alkali dalam reaksi kimia. Ketika hidrogen melepaskan ion H+, ia bertindak sebagai asam dan apabila sebaliknya, ia akan menajdi alkali.
5. Larut dalam Air: Hidrogen adalah gas yang larut dalam air. Ketika hidrogen terlarut dalam air, ia membentuk larutan yang disebut air hidrogen yang memiliki sifat asam atau alkali tergantung pada jumlah ion H+ atau OH- nya.
Material Penyimpanan
Sebagai catatan, hidrogen merupakan bahan yang masih diteliti hingga saat ini sehingga banyak kemungkinan perubahan yang dilakukan oleh manusia dalam menangani hidrogen ini.
Dalam melakukan penyimpanan hidrogen, ada beberapa material yang dapat digunakan:
1. Tangki Logam: Tangki logam seperti tangki baja atau aluminium merupakan metode penyimpanan hidrogen yang umum digunakan. Hidrogen dapat disimpan dalam wadah bertekanan tinggi yang kuat dan tahan terhadap tekanan yang dihasilkan oleh gas hidrogen.
2. Material Absorben: Beberapa material dapat digunakan sebagai penyerap hidrogen, yang dapat mengikat dan menyimpan hidrogen dalam struktur molekulnya. Contohnya termasuk paduan logam seperti paduan magnesium-nikel (Mg-Ni), paduan magnesium-rik (Mg-Ti), atau paduan magnesium-nikel-aluminium (Mg-Ni-Al).
3. Material Adsorben: Material adsorben seperti karbon aktif atau zeolit memiliki kemampuan untuk mengikat hidrogen pada permukaan mereka.
4. Bahan Kimia: Beberapa senyawa kimia seperti amonia borane (NH3BH3) atau hidrurat logam-organik seperti litium alanat (LiAlH4) dan natrium borohidrida (NaBH4) dapat digunakan sebagai penyimpan hidrogen.
5. Material Nanostruktural: Bahan dengan struktur nanometer seperti nanotube karbon atau graphene memiliki potensi sebagai metode penyimpanan hidrogen. Permukaan yang besar dan sifat-sifat unik dari material nanostruktural ini dapat meningkatkan kapasitas penyerapan hidrogen.
Optimasi Penyimpanan
Ada beberapa tahapan dalam mendesain dan mengoptimasi sistem penyimpanan, dari yang sudah ada menjadi yang sesuai dengan batasan maksimal yang diinginkan.
1. Tentukan ukuran pelat yang akan digunakan berdasarkan volume yang dibutuhkan, yaitu 1 liter, namun menggunakan luas pelat seminimal mungkin menggunakan perhitungan sebagai berikut:
import math
from scipy.optimize import minimize
def objective(x):
radius, height = x
return 2 * math.pi * radius**2 + 2 * math.pi * radius * height
def constraint(x):
radius, height = x
return math.pi * radius**2 * height - 1000
initial_guess = [1, 10] # Initial guess for the radius and height
# Define the bounds for the radius and height
bounds = [(0, None), (0, None)]
# Define the volume constraint
volume_constraint = {'type': 'eq', 'fun': constraint}
# Minimize the surface area subject to the volume constraint
result = minimize(objective, initial_guess, method='SLSQP', bounds=bounds,
constraints=volume_constraint)
optimal_radius = result.x[0]
optimal_height = result.x[1]
min_surface_area = result.fun
print(f"\n\nOptimal Radius: {optimal_radius} cm")
print(f"Optimal Height: {optimal_height} cm")
print(f"Minimum Surface Area: {min_surface_area} cm²\n\n")
Dari perhitungan tersebut, didapatkan beberapa nilai ukuran berikut ini,
● Optimal Radius: 5.419261255088046 cm
● Optimal Height: 10.838519182022262 cm
● Minimum Surface Area: 553.5810443894838 cm²
2. Selanjutnya, dilakukan perhitungan dengan variabel budget yang telah ditetapkan, yaitu Rp. 500.000. Untuk perhitungannya, digunakan perhitungan sebagai berikut menggunakan python:
from scipy.optimize import minimize
# Harga dan kapasitas yang dibutuhkan
harga_per_unit = 500000 # Rupiah
kapasitas_per_unit = 1 # Liter
# Anggaran maksimal
anggaran_maksimal = 500000
# Fungsi Akhir
def fungsi_akhir(x):
return -x * kapasitas_per_unit
# Kendala yang terjadi
def kendala(anggaran):
return anggaran_maksimal - (harga_per_unit * anggaran)
kendala_anggaran = {'type': 'ineq', 'fun': kendala}
# Nilai awal
x0 = 0
# Batasan
batas = [(0, None)]
# Menyelesaikan masalah optimisasi
solusi = minimize(fungsi_akhir, x0, method='SLSQP', bounds=batas, constraints=[kendala_anggaran])
# Menampilkan hasil
print("Status:", solusi.success and "Biaya Optimal" or "Tidak ditemukan solusi")
print("Jumlah unit yang bisa dibeli:", solusi.x[0])
print("Total kapasitas penyimpanan yang didapat:", solusi.x[0] * kapasitas_per_unit, "liter")
print("Total anggaran:", solusi.x[0] * harga_per_unit, "Rupiah")
Hasil yang didapatkan adalah:
● Status: Biaya Optimal
● Jumlah unit yang bisa dibeli: 1
● Total kapasitas penyimpanan yang didapat: 1.0 liter
● Total anggaran: 500000.0 Rupiah
Menggunakan perhitungan di atas, bisa dilakukan plot terhadap perbandingan kapasitas dan jumlah yang didapatkan dengan code berikut:
# list grafik
unit_list = []
total_kapasitas_list = []
# Perhitungan solusi optimal
for jumlah_unit in range(int(budget_maksimal / harga_per_unit) + 1):
total_kapasitas = jumlah_unit * kapasitas_per_unit
total_biaya = jumlah_unit * harga_per_unit
if total_kapasitas > total_kapasitas_optimal and total_biaya <= budget_maksimal:
jumlah_unit_optimal = jumlah_unit
total_kapasitas_optimal = total_kapasitas
total_biaya_optimal = total_biaya
# Menambahkan data ke dalam list untuk grafik
unit_list.append(jumlah_unit)
total_kapasitas_list.append(total_kapasitas)
# Tampilan Hasil
print("Jumlah unit penyimpanan hidrogen yang akan dibeli:", jumlah_unit_optimal)
print("Total kapasitas penyimpanan:", total_kapasitas_optimal, "liter")
print("Total biaya:", total_biaya_optimal, "Rupiah")
# Grafik ditampilkan
plt.plot(unit_list, total_kapasitas_list, color='red')
plt.xlabel('Jumlah Penyimpanan Hidrogen')
plt.ylabel('Total Kapasitas Penyimpanan (liter)')
plt.title('Optimalisasi Penyimpanan Hidrogen')
plt.grid(True)
plt.show()
Kode yang digunakan di atas, bertujuan untuk melihat optimasi penyimpanan hidrogen dengan mempertimbangkan batasan kapasitas dan anggaran yang diberikan. Tujuan utamanya menemukan jumlah unit penyimpanan hidrogen yang harus dibeli untuk mencapai kapasitas penyimpanan maksimum dengan tetap mempertimbangkan batasan yang digunakan.
Iterasi dilakukan untuk mendapatkan data setiap unit yang dibeli jika dibandingkan dengan kapasitas dan batasan lain yang didapat. Setiap jumlah unit diuji untuk menghitung kapasitas penyimpanan total dan biaya total yang terkait. jika nilai sudah melebihi batasan, iterasi akan berhenti.
Selain itu, grafik yang terbentuk menunjukkan hubungan antara jumlah unit penyimpanan hidrogen yang akan dibeli dan kapasitas penyimpanan total yang diperoleh dalam merepresentasikan kapasitas total berubah saat unit penyimpanan hidrogen tambahan ditambahkan.
Hasil desain
Dengan ukuran yang telah dihitung pada perhitungan sebelumnya, didapatkan gambaran dari tabung yang akan dibuat sebagai berikut:
yang memiliki ukuran-ukuran:
Ukuran
Total ukuran luas plat yang didapat adalah (36905.598 + 7216.008 + 4825.773)mm² = 610 cm²
Kesimpulan
Untuk bisa membuat tabung ini, dibutuhkan
1. Material
Sesuai dengan harga yang tertera di Tokopedia, harga material plat baja yang digunakan adalah Rp200.000
2. Katup tabung
Sesuai dengan harga yang tertera di Tokopedia, harga katup yang digunakan adalah Rp10.000
3. Estimasi Biaya pembuatan
Estimasi biaya yang digunakan untuk pembuatan dengan machining adalah Rp150.000
Oleh karena itu, total biaya yang dibutuhkan dalam pembuatan tabung ini adalah sekitar Rp200.000 + Rp10.000 + Rp150.000= Rp360.000