Difference between revisions of "Sasikirana Dania Putri"
(→Optimal Hydrogen Tank Dimension Calculations) |
(→Presentation Video) |
||
| (7 intermediate revisions by the same user not shown) | |||
| Line 127: | Line 127: | ||
| − | == Optimal Hydrogen Tank Dimension Calculations == | + | == Optimal Hydrogen Storage Tank Dimension Calculations == |
In order to easily calculate the optimal dimension for a hydrogen tank, one can input certain coding in order to achieve their calculations. For instance, in order to calculate the tank's radius as well as the height; | In order to easily calculate the optimal dimension for a hydrogen tank, one can input certain coding in order to achieve their calculations. For instance, in order to calculate the tank's radius as well as the height; | ||
import math | import math | ||
| − | |||
def calculate_hydrogen_tank_dimensions(volume, max_pressure): | def calculate_hydrogen_tank_dimensions(volume, max_pressure): | ||
# Convert pressure from bar to Pascals | # Convert pressure from bar to Pascals | ||
pressure_pa = max_pressure * 100000 | pressure_pa = max_pressure * 100000 | ||
| − | |||
# Assume a starting radius and height | # Assume a starting radius and height | ||
radius = 0.1 | radius = 0.1 | ||
height = volume / (math.pi * radius**2) | height = volume / (math.pi * radius**2) | ||
| − | |||
# Perform iterative calculations to optimize dimensions | # Perform iterative calculations to optimize dimensions | ||
while True: | while True: | ||
# Calculate stress on the tank wall | # Calculate stress on the tank wall | ||
stress = pressure_pa * radius / (2 * height) | stress = pressure_pa * radius / (2 * height) | ||
| − | |||
# Choose a material with an allowable stress value | # Choose a material with an allowable stress value | ||
# Replace 'allowable_stress' with the appropriate value for your chosen material | # Replace 'allowable_stress' with the appropriate value for your chosen material | ||
allowable_stress = 200000000 # Example value (replace with the actual allowable stress) | allowable_stress = 200000000 # Example value (replace with the actual allowable stress) | ||
| − | |||
# Check if the stress is within the allowable limit | # Check if the stress is within the allowable limit | ||
if stress <= allowable_stress: | if stress <= allowable_stress: | ||
break # Optimal dimensions found, exit the loop | break # Optimal dimensions found, exit the loop | ||
| − | |||
# Adjust the dimensions to decrease the stress | # Adjust the dimensions to decrease the stress | ||
radius += 0.001 | radius += 0.001 | ||
height = volume / (math.pi * radius**2) | height = volume / (math.pi * radius**2) | ||
| − | |||
return radius, height | return radius, height | ||
| − | # | + | # Example when used: |
volume_liters = 1 | volume_liters = 1 | ||
max_pressure_bar = 8 | max_pressure_bar = 8 | ||
| − | |||
radius_cm, height_cm = calculate_hydrogen_tank_dimensions(volume_liters, max_pressure_bar) | radius_cm, height_cm = calculate_hydrogen_tank_dimensions(volume_liters, max_pressure_bar) | ||
radius_m = radius_cm / 100 | radius_m = radius_cm / 100 | ||
height_m = height_cm / 100 | height_m = height_cm / 100 | ||
| − | |||
print(f"Optimal dimensions for a {volume_liters} liter hydrogen tank with a maximum pressure of {max_pressure_bar} bar:") | print(f"Optimal dimensions for a {volume_liters} liter hydrogen tank with a maximum pressure of {max_pressure_bar} bar:") | ||
print(f"Radius: {radius_m} meters") | print(f"Radius: {radius_m} meters") | ||
print(f"Height: {height_m} meters") | print(f"Height: {height_m} meters") | ||
| + | |||
| + | But also keep in mind that we need to calculate the thickness of said tank, which can be calculated by this code; | ||
| + | |||
| + | import math | ||
| + | def calculate_tank_thickness(volume, pressure): | ||
| + | radius = math.sqrt(volume / (math.pi * 1000)) # 1 liter = 1000 cm^3 | ||
| + | allowable_stress = 200 * 10**6 # Assumed allowable stress in Pascal (Pa) | ||
| + | safety_factor = 2 # Assumed safety factor | ||
| + | thickness = (pressure * radius) / (allowable_stress * safety_factor) | ||
| + | return thickness | ||
| + | |||
| + | # Example when in use: | ||
| + | volume = 1000 # 1 liter = 1000 cm^3 | ||
| + | pressure = 800000 # 8 bar = 800,000 Pa | ||
| + | tank_thickness = calculate_tank_thickness(volume, pressure) | ||
| + | print("Required tank thickness:", tank_thickness, "m") | ||
| + | |||
| + | |||
| + | == Presentation Video == | ||
| + | |||
| + | [https://www.youtube.com/watch?v=B4RW7tFHWKI Watch my presentation here!] | ||
Latest revision as of 23:23, 11 June 2023
Contents
Introduction
My name is Sasikirana Dania Putri, with my friends usually calling me Sasi. Currently I'm very interested in learning more about mechanical engineering !! ^O^/
Wish me luck !!
Consciousness Learning
As a student and learner for most of my life; Mr. DAI's teachings is odd - and I'm saying this in a good way of course.
I've met lots of teachers and educators as I myself and have been a students for maybe almost 17 years, give or take; so I assumed that I've seen a fair amount of different types of teachers, all who teaches in their own way. Some asks us to just open a book and memorize, some gives us endless amount of homework to learn from, and some started from the surface, slowly teaching us on what the formula really means. Mr. DAI himself, I think he fits more on the third type, though, in a much more unique way.
Not only does Mr. DAI wants us to understand the materials he was teaching, but he also wants us to actually think about the things outside of the stuffy classroom walls; and that was how we ended up learning about Consciousness.
Being an english speaker for half of my life, the word "consciousness" isn't a stranger; but I've never really thought of it that much otherwise. After hearing his question, I was a bit shocked at first, but it genuinely made me think a lot. The question was, why does 1 divided by 0 equals "infinity"? It's something I've never thought of deeply, since it's been engrained in my brain that 1 divided by 0 is just infinity; I've never question why that is.
As homework; he told us to explain what the solution is to (x^2-1)/(x-1) if the x was 1, told us to give our reasoning on why we think our answer is correct. For me, if we were to insert x = 1 into the equation; it would result in 0/0, undefined. The more I think about it, the more I'm convinced the reason why 0/0 is undefined is because you physically cannot separate and take apart nothing and gave it to, again, nothing or no one. It was why 0/0 would equal as undefined. However, if you look at the equation in a different angle, simplifying it into (x-1)(x+1)/(x-1) form, you'd be able to have the number 2 as an answer.
What does consciousness have to do with this? Well, my answer was everything. Because consciousness means a state where we are aware of our surroundings. Because of consciousness, we were able to read, comprehend, and think about what the equation is before finally able to solve them. Even then, we were able to get two different answers just by how we perceive and what angle we choose to do the equation. All of that was because of consciousness - us being able to comprehend everything and think for ourselves.
Why is this important? As student, especially university students, it is important for us to be able to think for ourselves. Not only is this important when it comes to education, but also for our everyday lives. We should be able to think for ourselves, learn for ourselves, and make choices for ourselves; that is why I think learning about consciousness is important.
Hydrogen Storage
In order to design and optimize a pressurized hydrogen tank (specifically an 8 bar storage with capacity of 1 liters and maximum budget of 500 thousand rupiah) there is a few things I've compiled in my head to do so, which includes;
1. Design the storage container with lightweight and high-strength materials, which are also strong and cost effective such as carbon fiber, aluminum, or other composite materials. This will help to reduce the weight and ensure that the container can withstand the pressure.
2. Consider using a pressure regulator to control the pressure of the hydrogen being stored. This will help to prevent over-pressurization and ensure safe storage. We'd also looks for affordable and yet reliable valves and pressure regulators that are suitable for hydrogen applications
3. Optimize the design of the valve and fitting system to ensure that they are compatible with the high-pressure hydrogen gas. This will help to prevent any leaks or other safety issues.
4. Use a pressure relief device to ensure that the container can release pressure in the event of an emergency. This is used for a safety feature, to make sure there is no burst when an over pressurization happens
5. Efficient Space Utilization: Design the storage system to fit in compact spaces, enabling easy integration into various applications, such as hydrogen-powered vehicles or portable energy systems.
6. Testing and Certification: Ensure that the storage system meets relevant safety standards and undergoes appropriate testing and certification processes to ensure its reliability and performance.
7. Cost-Effective Manufacturing: Explore cost-effective manufacturing methods, such as extrusion or casting, for the pressure vessel. These methods can help keep the production cost within the budget.
Calculating an Optimal Hydrogen Storage Tank
Beforehand, I’ve mentioned a few things we could focus on if we were to optimize a hydrogen tank; for instance I talked about the design of the container as well as the valve, manufacturing, materials, and encouraging users to use a few devices things such as a pressure regulator and relief. Now comes another question? As a mechanical engineer, we should not only be able to only think about how to optimize something, but to count the formulas as well as to design it.
When talking about a hydrogen storage tank, we first must think about the design; how large is it? How big is the length of the said tank? The optimal length and largeness, or volume, of a 1-liter hydrogen storage tank will depend on various factors, including the desired pressure rating, material strength, and safety considerations. In this case, with a maximum pressure of 8 bar, we can explore a general approach to estimating the tank dimensions.
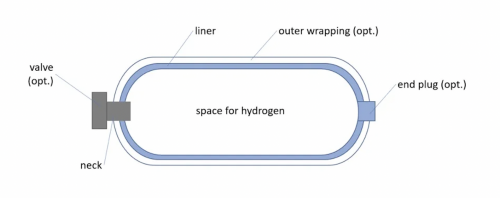
I've attached a picture below as an inspiration of what a hydrogen storage tank is commonly designed as;
To begin, we need to determine the specific requirements for the tank's dimensions, such as the allowable stress in the tank material, safety factors, and design codes and standards. These factors will help ensure the tank's integrity and safety.
Assuming a cylindrical tank shape, we can use the following formula to estimate the required dimensions:
V = π * r^2 * h
where V is the desired volume (1 liter or 0.001 m³), π is a mathematical constant (approximately 3.14159), r is the radius, and h is the height of the tank.
To calculate the dimensions, we can rearrange the formula as follows:
h = V / (π * r^2)
Now, calculate the thickness of a hydrogen storage tank, you will need additional information, such as the material properties, safety factors, and design codes. However, the general outline of the calculation process would be the following;
1. Determine the desired volume: which is a 1-liter hydrogen storage tank.
2. Convert the pressure from bar to Pascals (Pa): 1 bar is approximately equal to 100,000 Pa. Therefore, the maximum pressure of 8 bar is equivalent to 800,000 Pa.
3. Determine the material properties: The specific material you choose for the tank will have a maximum allowable stress value (σ_allowable). This value represents the stress that the material can handle without experiencing permanent deformation or failure.
4. Apply safety factors: Safety factors are used to account for uncertainties and ensure the tank's structural integrity and safety. Typical safety factors range between 2 to 4, depending on the design standards and regulations.
5. Calculate the required thickness: Using the formula for the cylindrical pressure vessel's wall thickness, you can determine the thickness (t) needed to withstand the pressure:
t = (P * r) / (σ_allowable * SF)
where P is the pressure in Pascals, r is the radius of the tank, σ_allowable is the allowable stress of the material, and SF is the safety factor.
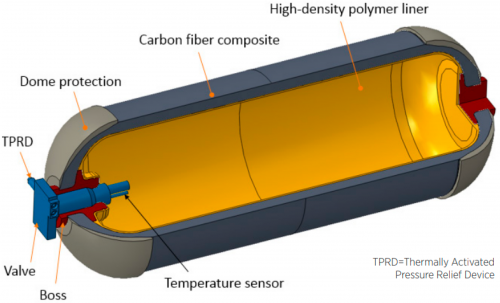
This would be what the final design of a hydrogen storage tank would look;
Let's consider the pressure rating of 8 bar. The pressure in the tank is directly related to the thickness and material properties of the tank walls. However, determining the exact thickness requires additional information about the material strength, safety factors, and design codes.
Typically, pressure vessels like hydrogen storage tanks are made from high-strength materials, such as carbon fiber composite, steel, or aluminum alloy, that can withstand the desired pressure. The thickness of the tank walls will depend on the material's strength and the safety factors applied.
When selecting the best material for a hydrogen storage tank, several factors should be considered, including safety, weight, cost, and compatibility with hydrogen. Here are some key considerations when evaluating materials:
1. Hydrogen Compatibility: The material must be compatible with hydrogen gas to prevent leakage and maintain the integrity of the tank. Hydrogen can cause embrittlement or permeation in certain materials, so it's important to select a material that exhibits good compatibility.
2. Strength and Durability: The material should have sufficient strength to withstand the desired pressure and ensure the tank's structural integrity. It should also possess good durability to withstand cyclic loading and potential impacts.
3. Weight: Lighter materials offer advantages in terms of weight reduction, allowing for improved mobility and efficiency. Materials such as carbon fiber composites are known for their high strength-to-weight ratio and are commonly used in hydrogen storage tanks.
4. Cost: Consider the cost of the material, including manufacturing, fabrication, and any additional surface treatments or coatings required. Cost considerations are vital, especially for large-scale production or commercial applications.
5. Manufacturing Feasibility: Evaluate the feasibility of manufacturing the tank with the chosen material. Consider factors such as availability, ease of fabrication, and compatibility with manufacturing processes.
6. Safety: Assess the material's safety characteristics, including its resistance to fire, impact, and failure modes. Materials with good safety profiles help ensure the overall integrity of the tank and minimize risks.
7. Regulations and Standards: Consider applicable regulations and standards for hydrogen storage systems. Regulatory bodies may have specific material requirements or guidelines to ensure safety and compliance.
To determine the best material, it is crucial to conduct detailed evaluations, including experimental testing, computer simulations, and thorough analysis. Consulting with fellow engineers is something I would highly recommend also, especially to those with a wider and larger experience.
Several materials are commonly used for hydrogen storage tanks, each with its advantages and considerations, for instance;
1. Carbon Fiber Composites: Carbon fiber reinforced composites, such as carbon fiber epoxy, offer excellent strength-to-weight ratios and are widely used in high-pressure hydrogen storage tanks. They provide high tensile strength, good fatigue resistance, and low weight. However, carbon fiber composites can be expensive and require careful handling and manufacturing processes to ensure their integrity.
2. Aluminum Alloys: Aluminum alloys, specifically those with high strength and good corrosion resistance, are commonly employed in hydrogen tanks. They offer a balance between weight, cost, and mechanical properties. Aluminum tanks can be manufactured using various methods, including welding and forging, making them relatively easier to produce compared to some other materials.
3. Steel: High-strength steel alloys, such as steel with advanced heat treatment and alloying, are used in hydrogen storage tanks. Steel tanks are known for their durability, toughness, and relatively lower cost compared to carbon fiber composites. However, steel tanks can be heavier and may require additional anti-corrosion measures.
4. Titanium: Titanium and its alloys possess good hydrogen compatibility and high strength-to-weight ratios. They are particularly suitable for cryogenic hydrogen storage tanks where extremely low temperatures are involved. Titanium tanks are resistant to corrosion and can withstand high-pressure conditions. However, titanium is an expensive material, which limits its widespread use.
5. Polymer-Based Materials: Polymer-based materials, such as high-density polyethylene (HDPE) and polyether ether ketone (PEEK), can be used for low-pressure hydrogen storage tanks. These tanks are lightweight, low-cost, and exhibit good hydrogen compatibility. However, their applications are limited to lower pressure ranges.
Optimal Hydrogen Storage Tank Dimension Calculations
In order to easily calculate the optimal dimension for a hydrogen tank, one can input certain coding in order to achieve their calculations. For instance, in order to calculate the tank's radius as well as the height;
import math
def calculate_hydrogen_tank_dimensions(volume, max_pressure):
# Convert pressure from bar to Pascals
pressure_pa = max_pressure * 100000
# Assume a starting radius and height
radius = 0.1
height = volume / (math.pi * radius**2)
# Perform iterative calculations to optimize dimensions
while True:
# Calculate stress on the tank wall
stress = pressure_pa * radius / (2 * height)
# Choose a material with an allowable stress value
# Replace 'allowable_stress' with the appropriate value for your chosen material
allowable_stress = 200000000 # Example value (replace with the actual allowable stress)
# Check if the stress is within the allowable limit
if stress <= allowable_stress:
break # Optimal dimensions found, exit the loop
# Adjust the dimensions to decrease the stress
radius += 0.001
height = volume / (math.pi * radius**2)
return radius, height
# Example when used:
volume_liters = 1
max_pressure_bar = 8
radius_cm, height_cm = calculate_hydrogen_tank_dimensions(volume_liters, max_pressure_bar)
radius_m = radius_cm / 100
height_m = height_cm / 100
print(f"Optimal dimensions for a {volume_liters} liter hydrogen tank with a maximum pressure of {max_pressure_bar} bar:")
print(f"Radius: {radius_m} meters")
print(f"Height: {height_m} meters")
But also keep in mind that we need to calculate the thickness of said tank, which can be calculated by this code;
import math
def calculate_tank_thickness(volume, pressure):
radius = math.sqrt(volume / (math.pi * 1000)) # 1 liter = 1000 cm^3
allowable_stress = 200 * 10**6 # Assumed allowable stress in Pascal (Pa)
safety_factor = 2 # Assumed safety factor
thickness = (pressure * radius) / (allowable_stress * safety_factor)
return thickness
# Example when in use:
volume = 1000 # 1 liter = 1000 cm^3
pressure = 800000 # 8 bar = 800,000 Pa
tank_thickness = calculate_tank_thickness(volume, pressure)
print("Required tank thickness:", tank_thickness, "m")
Presentation Video
Watch my presentation here!