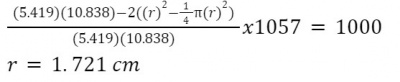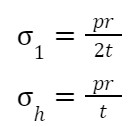Difference between revisions of "Audry Jonathan P. T. Sitompul"
(→Material Strength Constraints) |
|||
| Line 121: | Line 121: | ||
Using a cylindrical shape for the storage tank can pose a safety risk due to stress concentration areas or potential failure points at the corners of the ends. To mitigate this i will curved shapes at the ends to reduce stress concentration. Since our objective is to minimize surface area while maintaining the same volume, the most efficient choice would be a torispherical end cap shape. This shape can be viewed as a cylindrical shape with partial filleting. However, the addition of filleting reduces the overall volume of the structure. Therefore, we need to adjust the geometrical parameters to compensate for this reduction caused by the filleting and ensure the desired volume is maintained. | Using a cylindrical shape for the storage tank can pose a safety risk due to stress concentration areas or potential failure points at the corners of the ends. To mitigate this i will curved shapes at the ends to reduce stress concentration. Since our objective is to minimize surface area while maintaining the same volume, the most efficient choice would be a torispherical end cap shape. This shape can be viewed as a cylindrical shape with partial filleting. However, the addition of filleting reduces the overall volume of the structure. Therefore, we need to adjust the geometrical parameters to compensate for this reduction caused by the filleting and ensure the desired volume is maintained. | ||
[[File:Fillet Tank Audry.png|400px|thumb|right|Fillet Tank(source: researchgate)]][[File:End Cap Equation Audry.jpg|400px|left|]] | [[File:Fillet Tank Audry.png|400px|thumb|right|Fillet Tank(source: researchgate)]][[File:End Cap Equation Audry.jpg|400px|left|]] | ||
| + | |||
| + | |||
====Material Strength Constraints==== | ====Material Strength Constraints==== | ||
Revision as of 02:53, 6 June 2023
INTRODUCTION
Pagi Mesin!
Assalamu'alaikum Wr. Wb.
Halo semua! Perkenalkan, saya Audry Jonathan P. T. Sitompul, akrab dipanggil Jo, dengan NPM 2106709283. Saya adalah mahasiswa Program Studi S1 Teknik Mesin angkatan 2021. Berikut adalah resume-resume saya selama pembelajaran di kelas Metode Numerik 01.
"Trust the process" Kalimat tersebut merupakan motto hidup saya agar selalu memaknai consciousness dalam setiap hal yang saya lakukan.
TUGAS HYDROGEN STORAGE OPTIMIZATION
Method To Optimaze Hydrogen Storage Design
In this study case i will use a commonly used numerical method called "particle swarm optimization" (PSO):
1. Define the Problem: Clearly state the objective function that represents the performance criteria of the hydrogen storage system. It could be maximizing the storage capacity, minimizing the weight or volume, or optimizing any other relevant parameter.
2. Define Variables and Constraints: Identify the variables that can be adjusted to optimize the system, such as tank dimensions, materials, operating conditions, etc. Also, define any constraints that need to be satisfied, such as pressure limits, safety requirements, or cost considerations.
3. Initialize the Swarm: Create a population of potential solutions (particles) that represent different configurations of the hydrogen storage system. Randomly initialize their positions and velocities within the search space.
4. Evaluate Fitness: Evaluate the fitness of each particle by applying the objective function to its corresponding configuration. This step involves performing calculations and simulations to determine the system's performance for each particle.
5. Update Particle's Best Position: For each particle, compare its fitness with the best fitness achieved by that particle so far. If the current fitness is better, update the particle's best position accordingly.
6. Update Global Best Position: Identify the particle with the best fitness among all the particles and record its position as the global best position found so far.
7. Update Velocities and Positions: Update the velocities and positions of each particle based on its own best position and the global best position. This step involves using mathematical equations that incorporate inertia, cognitive, and social parameters to guide the particles' movement.
8. Repeat: Repeat steps 4 to 7 until a termination criterion is met. This criterion could be a maximum number of iterations, reaching a desired fitness threshold, or other convergence criteria.
9. Extract Optimal Solution: Once the algorithm terminates, the particle with the best fitness (global best) represents the optimized design and configuration of the hydrogen storage system. Extract the corresponding parameters and evaluate their values.
10. Validate and Refine: Validate the optimal solution obtained by implementing it in practical applications or conducting further simulations. Refine the solution if necessary based on additional constraints or considerations.
Particle swarm optimization is just one of many numerical methods available for optimization problems. Depending on the specific characteristics of the hydrogen storage system and the optimization goals, other methods like genetic algorithms, simulated annealing, or gradient-based optimization techniques may also be applicable.
Final Project To Optimaze Hydrogen Storage Design
Design of Pressurized Hydrogen Storage
Pressurized hydrogen storage refers to the storage of hydrogen gas at high pressures in a container or vessel. Hydrogen gas, which is highly compressible, can be stored at pressures ranging from a few hundred to several thousand pounds per square inch (psi). By compressing hydrogen, it is possible to store larger quantities of the gas within a smaller volume, making it more practical for transportation and industrial applications.
Requirements Given
The specific requirements are 1 liter (1000 cm^3) of Hydrogen with 8 bar (800 kPa) Pressure with a maximum cost of Rp 500.000
Constraints Used
Geometrical Constraint : The geometrical constraint guarantees that the storage system design adheres to specific volume requirements. By imposing limitations on the volume or dimensions of the storage tank, one can optimize factors like radius and height to ensure that the tank can accommodate the desired 1-liter volume (equivalent to 1000 cm^3). This constraint ensures that the storage tank is appropriately sized and fits within the given space.
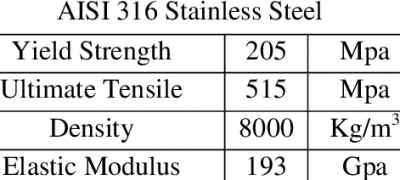
Material Strength Constraint : The material strength constraint focuses on selecting a material capable of withstanding the high-pressure conditions within the hydrogen storage system. Hydrogen is stored at elevated pressures (8 bar or 800 kPa), and choosing a material with suitable strength characteristics is crucial for ensuring safety and integrity. By applying this constraint, it ensures that the chosen material, such as AISI 316 austenitic stainless steel, possesses the necessary mechanical properties to withstand pressure and prevent any material failures or leaks.
Budget Constraint : The budget constraint sets a limit on the cost of the pressurized hydrogen storage system. By considering this constraint, it ensures that the optimization model takes into account the cost-effectiveness of the design. The budget constraint aids in selecting cost-efficient materials and optimizing geometrical parameters to meet the required specifications while remaining within the allocated budget of Rp 500,000. This constraint guarantees that the final design is financially feasible and aligns with the available resources.
Geometrical Constraint
In our scenario, the goal is to minimize the surface area while ensuring that the volume remains constant at 1 liter or 1000 cubic centimeters. By using an optimization function in Python, we can calculate the optimal values for the radius and height of a cylinder that satisfy both criteria.
import scipy.optimize as optimize
import math
# Constants
volume = 1000 # Desired volume in cubic centimeters
# Objective function
def objective(x):
radius, height = x
surface_area = 2 * np.pi * radius * (radius + height)
return surface_area
# Constraint function
def constraint(x):
radius, height = x
volume = np.pi * radius**2 * height
return volume - 1000
# Optimization
initial_guess = [1.0, 10] # Initial guess for radius and height
bounds = [(0, None), (0, None)] # Bounds for radius and height (non-negative values)
constraints = [{'type': 'ineq', 'fun': constraint}] # Volume constraint
result = minimize(objective, initial_guess, bounds=bounds, constraints=constraints)
# Extract optimal radius and height
optimal_radius = result.x[0]
optimal_height = result.x[1]
minimum_surface_area = result.fun
# Display the computed optimal radius, height, and surface area
print("Optimal Radius:", optimal_radius)
print("Optimal Height:", optimal_height)
print("Minimum Surface Area:", minimum_surface_area)In this code, we use the minimize_scalar function from the SciPy library to perform the optimization separately for the radius and height. The objective function calculates the surface area of the cylinder, while the constraint function enforces the desired volume of 1000 cubic centimeters. We define bounds to ensure non-negative values for radius and height.
First, we optimize for the minimum radius by keeping the height fixed at the initial guess value. Then, we optimize for the minimum height by keeping the radius fixed at the initial guess value. Finally, we compute the minimum surface area using the obtained optimal radius and height.
The results for the minimum radius, minimum height, and minimum surface area are
Optimal Radius: 5.419259622871326
Optimal Height: 10.838525719677232
Minimum Surface Area: 553.5810446887042End Cap Fillet
Using a cylindrical shape for the storage tank can pose a safety risk due to stress concentration areas or potential failure points at the corners of the ends. To mitigate this i will curved shapes at the ends to reduce stress concentration. Since our objective is to minimize surface area while maintaining the same volume, the most efficient choice would be a torispherical end cap shape. This shape can be viewed as a cylindrical shape with partial filleting. However, the addition of filleting reduces the overall volume of the structure. Therefore, we need to adjust the geometrical parameters to compensate for this reduction caused by the filleting and ensure the desired volume is maintained.
Material Strength Constraints
In our specific scenario, the hydrogen tank with a volume of 1 liter has a maximum pressure limit of 8 bar.
Within a cylindrical component with thin walls, there are two primary types of stress: circumferential (hoop) stress and longitudinal stress. To calculate the hoop stress and longitudinal stress, the following formulas can be used.
For this case we use High-Strength Steel: Steel alloys AISI 316 austenitic stainless steel because AISI 316 are commonly used due to their high strength, good ductility, and resistance to hydrogen embrittlement. Steel tanks can withstand high pressures and are relatively cost-effective.