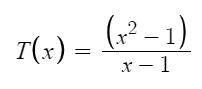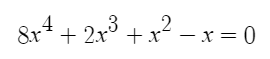Difference between revisions of "Samuel Albert Sitompul"
(→PYTHON CODE) |
(→Data Diri) |
||
| (9 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | == Data Diri == | ||
| + | |||
| + | |||
| + | |||
| + | Nama : Samuel Albert Sitompul | ||
| + | |||
| + | NPM : 1606907556 | ||
| + | |||
| + | Jurusan : Teknik Mesin S1 Paralel | ||
| + | |||
| + | Angkatan: 2016 | ||
| + | |||
| + | ---- | ||
| + | |||
| + | == Riwayat Diri == | ||
| + | |||
| + | Pengalaman Diri: | ||
| + | |||
| + | |||
| + | - Founder dan CFO Agrisia.id (2017-Sekarang) | ||
| + | |||
| + | - Stock Market Trader/Investor (2017-Sekarang) | ||
| + | |||
| + | - BP Litbang IMM FTUI (2017) | ||
| + | |||
| + | ---- | ||
| + | |||
== PROFILE == | == PROFILE == | ||
Nama saya adalah Samuel Albert Sitompul lahir di Medan, 1 Maret 1997. Saya mengawali pendidikan sekolah di Medan (TK-SMA) hingga sekarang saya sedang menempuh perkuliahan saya di Universitas Indonesia pada jurusan Teknik Mesin sejak tahun 2016. Hobi saya adalah berolahraga dan membaca. | Nama saya adalah Samuel Albert Sitompul lahir di Medan, 1 Maret 1997. Saya mengawali pendidikan sekolah di Medan (TK-SMA) hingga sekarang saya sedang menempuh perkuliahan saya di Universitas Indonesia pada jurusan Teknik Mesin sejak tahun 2016. Hobi saya adalah berolahraga dan membaca. | ||
| + | ---- | ||
| + | |||
| + | == Minggu 1 == | ||
| + | |||
| + | Bahasa pemograman adalah bahasa yang dipakai dalam perangkat pintar elektronik guna sebagai acuan dasar komunikasi perangkat dalam menjalankan operasionalnya dalam bentuk ''coding''. Bahasa pemograman yang pernah saya baca adalah Python, namun yang saya baca hanya pengenalan dasar dari Python tersebut. | ||
| + | |||
| + | Python adalah bahasa pemrograman interpretatif multiguna yang memakai filosofi perancangan dengan fokus kepada tingkat keterbacaan kode. Sebagai bahasa pemrograman, Python menggabungkan kemampuan, kapabilitas dan sintaksis kode serta fungsi pustaka yang berkualitas tinggi. | ||
| + | |||
| + | Fitur dalam bahasa pemograman Python secara general : | ||
| + | |||
| + | 1. Berorientasi kepada objek. | ||
| + | |||
| + | 2. Relatif mudah dikembangkan dengan menciptakan modul-modul baru. Asalnya Modul tersebut merupakan kombinasi dari modul lama yang di integrasi. | ||
| + | |||
| + | 3. Memiliki tata bahasa yang relatif mudah dipelajari oleh manusia. | ||
| + | |||
| + | 4. Didukung sistem pengelolaan memori secara otomatis sehingga membutuhkan kinerja saat ''coding''. | ||
| + | |||
| + | 5. Python juga memiliki banyak fasilitas pendukung sehingga ketika menjalankannya, tergolong mudah dan cepat. | ||
| + | |||
| + | ---- | ||
| + | |||
| + | == Minggu 2 == | ||
| + | |||
| + | Pada minggu ke-2 kelas Metode Numerik, membahas apa itu angka eksak dan angka numerik?, lintas apakah bagaimana eksistensinya?, angka eksak mulai dari 0,1,2,3,4,5...dst itu tentu ada, namun itu hanya sebuah perjanjian / kesepakatan pembatasan nilai untuk berkomunikasi verbal agar memudahkan kita manusia untuk bertukar informasi dalam kehidupan nyata. Pada dasarnya komputer hanya mengenal 2 angka, yaitu "0" dan "1", dimana 0 yang berarti tidak bernilai dan 1 yang artinya bernilai, seperti layaknya iya dan tidak. Komputer bekerja berdasarkan perintah, dan perintah itu berisi kombinasi rangkaian angka 0 dan 1 yang menjadi modul dasar komputer untuk bekerja. Loncatan-loncatan elektron listrik yang biasa disebut ''pulse'' merupakan cara komputer bekerja mengirim sinyal untuk melakukan perintah operasional. | ||
| + | |||
| + | Angka eksak merupakan hasil pendekatan perhitungan dari angka numerik, karena pada dasarnya secara keseluruhan nilai yang sebenarnya didapat secara akurat hanya bisa di hitung dengan angka numerik. | ||
| + | |||
| + | Berikut merupakan soal yang diberikan. | ||
| + | |||
| + | [[File:29244.png]] | ||
| + | |||
| + | |||
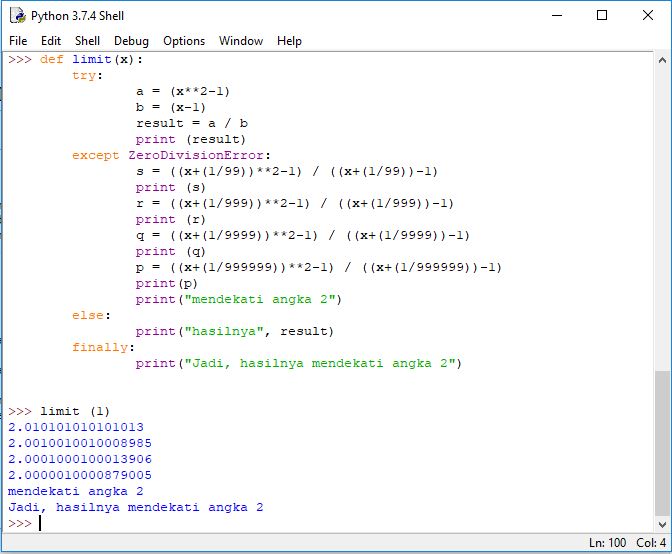
| + | Dalam mengerjakan soal diatas dengan x=1 tidak bisa mendapatkan hasil yang benar dikarenakan 0/0. Oleh sebab itu, saya gunakan limit pendekatan x=1. Saya menambahkan fungsi hingga perbedaan 1/999999 yang mendekati angka nol, sehingga hasil pendekatan dari perhitungan tidak menjauhi hasil sebenarnya dalam eksak. | ||
| + | |||
| + | |||
| + | [[File:Metode Numerik1.jpg]] | ||
| + | |||
| + | Jadi hasilnya secara numerik mendekati angka 2, dan dapat dianggap secara eksak hasilnya adalah 2. Namun, dosen kami Bapak Dr. Ir. Ahmad Indra Siswantara menitip pesan agar tidak lupa diri terhadap yang punya kehidupan kita, walau kita sudah sejauh ini mengerti akan teknologi. Ditengah maraknya perkembangan teknologi yang pesat, kadang kita melunturkan sisi lain dari kehidupan kita, yaitu agama. Dimana hubungan kita pribadi dengan Tuhan YME merupakan dasar acuan kehidupan kita sehari-hari. | ||
| + | |||
| + | ---- | ||
| + | |||
| + | == Minggu 3 == | ||
| + | |||
| + | [[File:80092.png]] | ||
| + | |||
| + | Diberikan persamaan seperti diatas, carilah nilai dari x pada persamaan tersebut! | ||
| + | |||
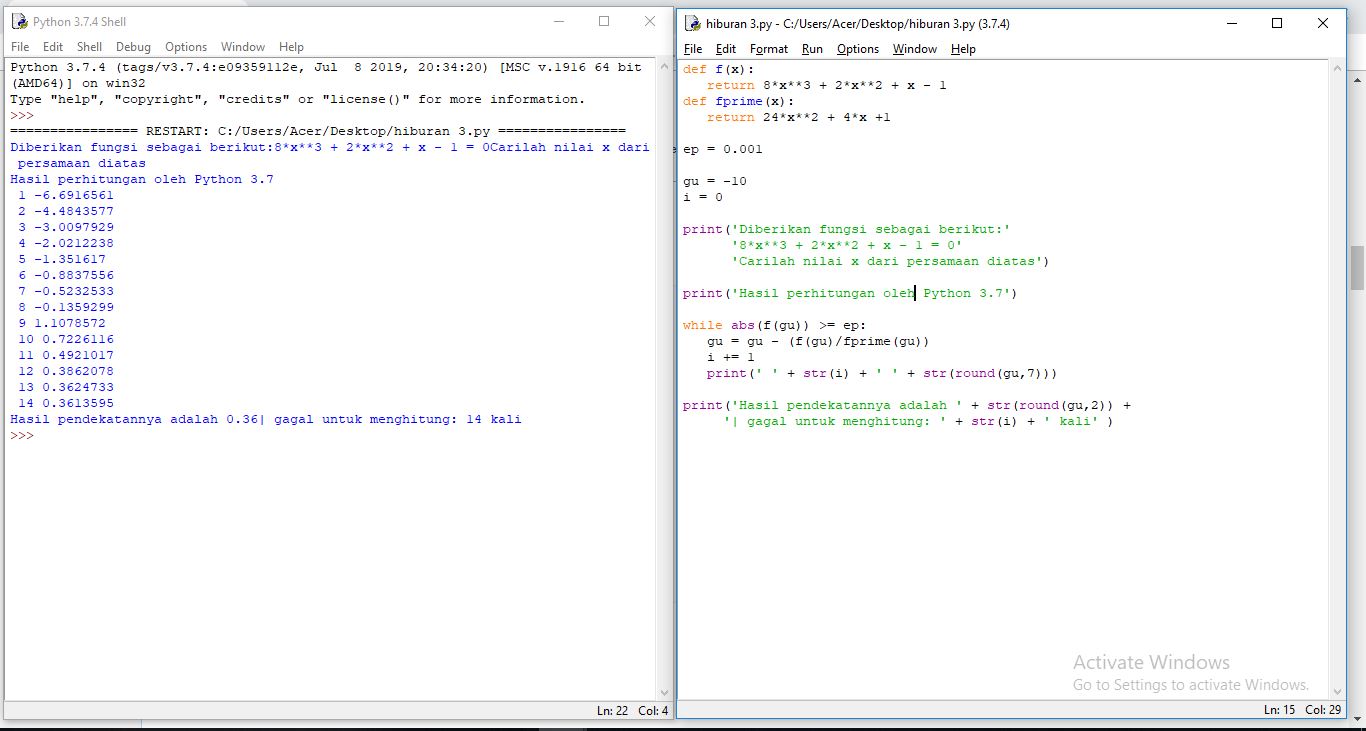
| + | [[File:Hiburan 3.JPG]] | ||
| + | |||
| + | Python Script : | ||
| + | |||
| + | def f(x): | ||
| + | return 8*x**3 + 2*x**2 + x - 1 | ||
| + | def fprime(x): | ||
| + | return 24*x**2 + 4*x +1 | ||
| + | |||
| + | ep = 0.001 | ||
| + | |||
| + | gu = -10 | ||
| + | i = 0 | ||
| + | |||
| + | print('Diberikan fungsi sebagai berikut:' | ||
| + | '8*x**3 + 2*x**2 + x - 1 = 0' | ||
| + | 'Carilah nilai x dari persamaan diatas') | ||
| + | |||
| + | print('Hasil perhitungan oleh Python 3.7') | ||
| + | |||
| + | while abs(f(gu)) >= ep: | ||
| + | gu = gu - (f(gu)/fprime(gu)) | ||
| + | i += 1 | ||
| + | print(' ' + str(i) + ' ' + str(round(gu,7))) | ||
| + | |||
| + | print('Hasil pendekatannya adalah ' + str(round(gu,2)) + | ||
| + | '| gagal untuk menghitung: ' + str(i) + ' kali' ) | ||
---- | ---- | ||
| + | == Minggu 4 == | ||
| − | == QUIZ (14/10/2019) == | + | Pada pertemuan ini kami diajarkan bagaimama cara menggunakan matrix dalam menyelesaikan suatu masalah yang berbentuk persamaan. Dalam hal ini menggunakan program python |
| + | |||
| + | Pada hukum kontinuitas massa terdapat rumus Q*p=Q*p dan didapatakan 4 persamaan dengan 4 variabel | ||
| + | |||
| + | |||
| + | 6C1 - 4C2 = 50 | ||
| + | |||
| + | -2C1 - 1C3 + 4C4 = 50 | ||
| + | |||
| + | 7C2 - 3C3 - 4C4 = 0 | ||
| + | |||
| + | -4C1 + 4C3 = 0 | ||
| + | |||
| + | |||
| + | 6C1 - 4C2 + 0C3 + 0C4 = 50 | ||
| + | |||
| + | -2C1 + 0C2 - 1C3 + 4C4 = 50 | ||
| + | |||
| + | 0C1 + 7C2 - 3C3 - 4C4 = 0 | ||
| + | |||
| + | -4C1 + 0C2 + 4C3 + 0C4 = 0 | ||
| + | |||
| + | Kemudian, persamaan - persamaan ini dimasukkan kedalam python untuk di hitung hasil persamaannya. | ||
| + | |||
| + | ---- | ||
| + | |||
| + | == Minggu 5 == | ||
| + | |||
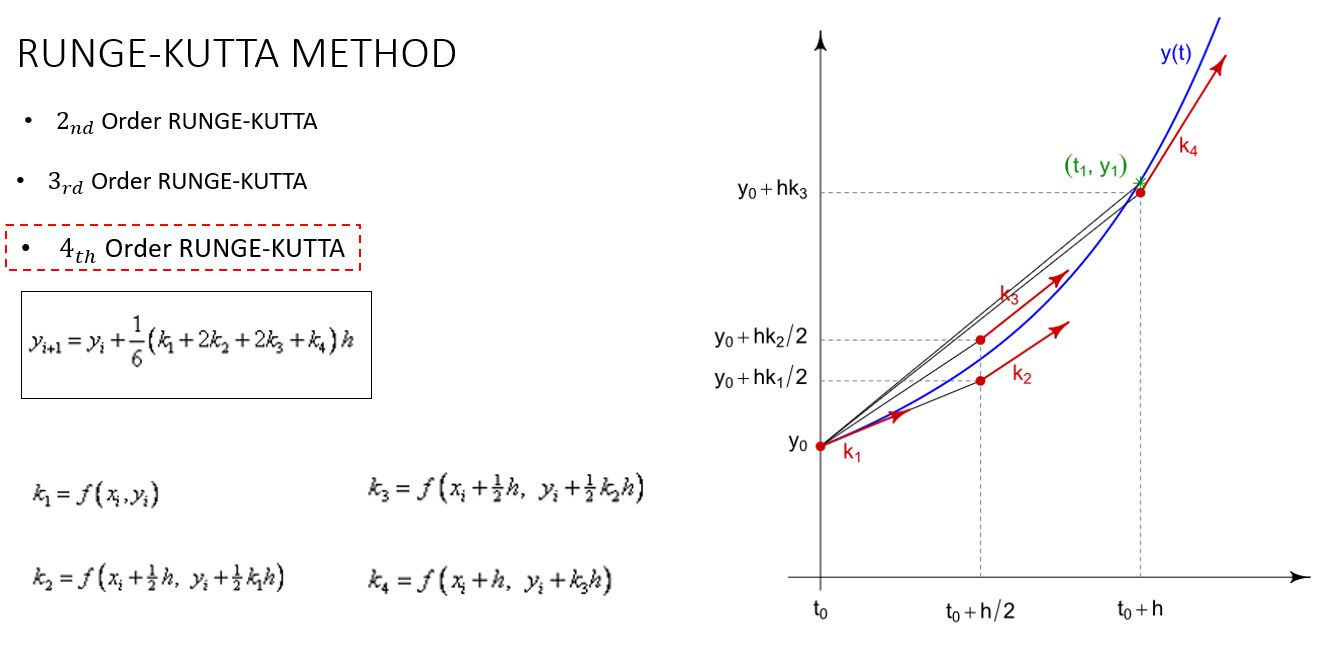
| + | Pada minggu kelima, kami diajarkan cara penggunaan turunan menggunakan Python dengan Metode Runge Kutta orde 4, kali ini diajarkan dengan menggunakan excel terlebih dahulu untuk mempermudah pemahaman terkait pendekatan metode ini terhadap turunan yang berlaku, berikut merupakan penjelasan singkat dari metode ini: | ||
| + | |||
| + | 1. Metode Runge-Kutta adalah alternatif lain dari metode deret Taylor yang tidak membutuhkan perhitungan turunan. | ||
| + | |||
| + | 2. Metode ini menawarkan penyelesaian persamaan diferensial dengan pertumbuhan ''truncation error'' yang jauh lebih kecil. | ||
| + | |||
| + | 3. ''Truncation error'' adalah kesalahan / penyimpangan nilai yang timbul akibat pemotongan suku pada suatu deret atau rumus dalam approksimasi. | ||
| + | |||
| + | [[File:Runge-kutta1.JPG]] | ||
| + | |||
| + | |||
| + | DIberikan contoh soal seperti dibawah ini: | ||
| + | |||
| + | |||
| + | [[File:RungeKuts2.png]] | ||
| + | |||
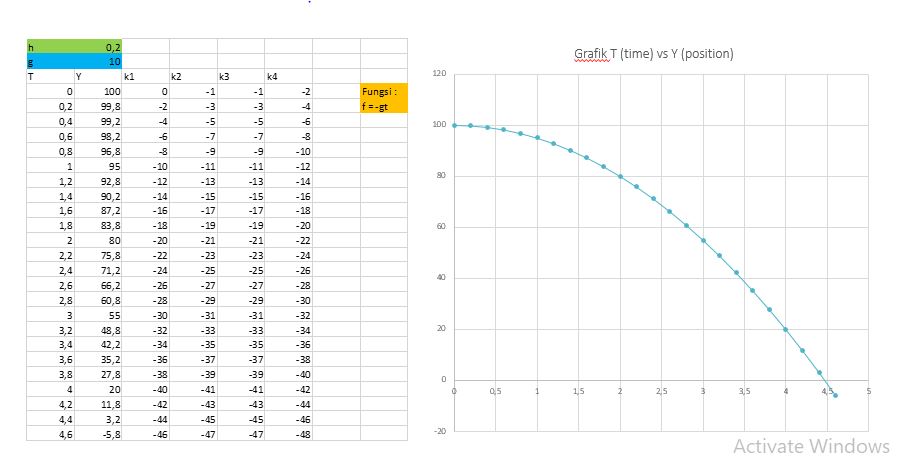
| + | Jawaban dalam excel yang telah dibuat: | ||
| + | |||
| + | |||
| + | [[File:RungeKuts3.JPG]] | ||
| + | |||
| + | ---- | ||
| + | |||
| + | == Minggu 6 - QUIZ (14/10/2019) == | ||
=== Problem set 2.1 Number 6 page 55 === | === Problem set 2.1 Number 6 page 55 === | ||
| Line 38: | Line 192: | ||
==== PYTHON CODE ==== | ==== PYTHON CODE ==== | ||
| − | + | Import numpy as np | |
A=np.array([[1, 2, 0, -2, 0], [0, 1, 0, 2, -1],[0, 1, -1, 1, -1], [0, 0, 0, -1, 1], [0, 0, 2, 1, 2]],float) | A=np.array([[1, 2, 0, -2, 0], [0, 1, 0, 2, -1],[0, 1, -1, 1, -1], [0, 0, 0, -1, 1], [0, 0, 2, 1, 2]],float) | ||
| Line 46: | Line 200: | ||
n=len(A) | n=len(A) | ||
| − | + | Gauss Elimination code | |
for k in range (0,n-1): | for k in range (0,n-1): | ||
| Line 56: | Line 210: | ||
print ('matrix A:', '\n', A) | print ('matrix A:', '\n', A) | ||
| − | + | Back substitution | |
x=np.zeros(n,float) | x=np.zeros(n,float) | ||
| Line 62: | Line 216: | ||
x[m]=(B[m]-np.dot(A[m, m+1:n], x[m+1:n]))/A[m,m] | x[m]=(B[m]-np.dot(A[m, m+1:n], x[m+1:n]))/A[m,m] | ||
print ('nilai X', m+1, '=', x[m]) | print ('nilai X', m+1, '=', x[m]) | ||
| + | |||
| + | [[File:Code1.jpg]] | ||
| + | |||
| + | |||
| + | === Problem set 7.1 Number 1 page 263 === | ||
| + | |||
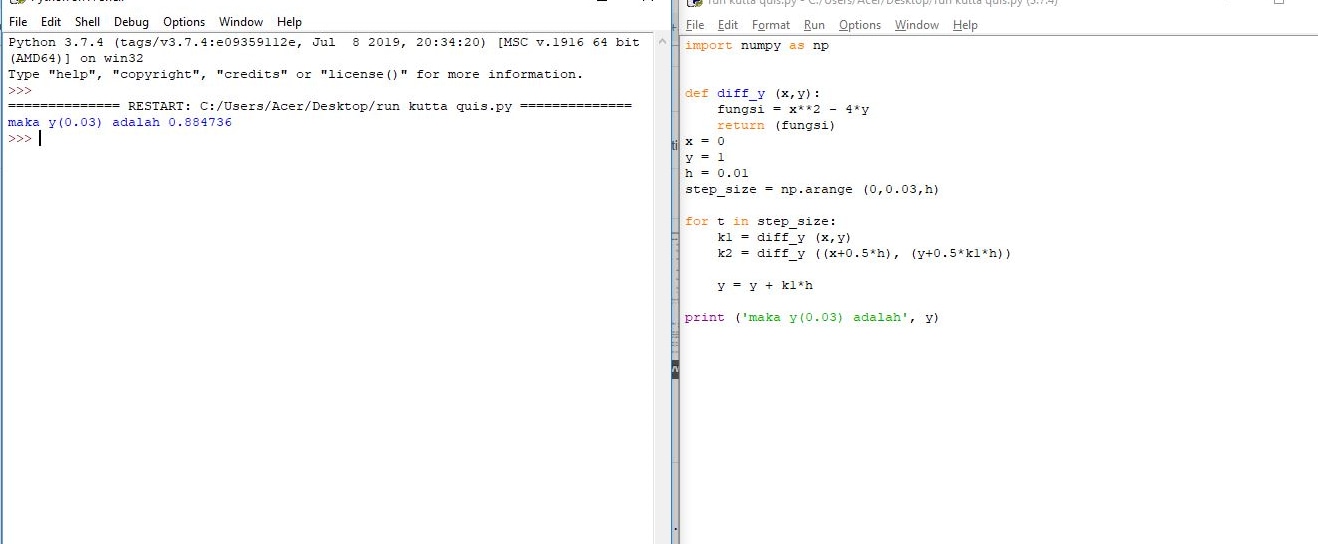
| + | Python Script : | ||
| + | import numpy as np | ||
| + | |||
| + | |||
| + | def diff_y (x,y): | ||
| + | fungsi = x**2 - 4*y | ||
| + | return (fungsi) | ||
| + | x = 0 | ||
| + | y = 1 | ||
| + | h = 0.01 | ||
| + | step_size = np.arange (0,0.03,h) | ||
| + | |||
| + | for t in step_size: | ||
| + | k1 = diff_y (x,y) | ||
| + | k2 = diff_y ((x+0.5*h), (y+0.5*k1*h)) | ||
| + | |||
| + | y = y + k1*h | ||
| + | |||
| + | print ('maka y(0.03) adalah', y) | ||
| + | |||
| + | [[File:Code2.jpg]] | ||
Latest revision as of 02:27, 10 April 2022
Contents
Data Diri
Nama : Samuel Albert Sitompul
NPM : 1606907556
Jurusan : Teknik Mesin S1 Paralel
Angkatan: 2016
Riwayat Diri
Pengalaman Diri:
- Founder dan CFO Agrisia.id (2017-Sekarang)
- Stock Market Trader/Investor (2017-Sekarang)
- BP Litbang IMM FTUI (2017)
PROFILE
Nama saya adalah Samuel Albert Sitompul lahir di Medan, 1 Maret 1997. Saya mengawali pendidikan sekolah di Medan (TK-SMA) hingga sekarang saya sedang menempuh perkuliahan saya di Universitas Indonesia pada jurusan Teknik Mesin sejak tahun 2016. Hobi saya adalah berolahraga dan membaca.
Minggu 1
Bahasa pemograman adalah bahasa yang dipakai dalam perangkat pintar elektronik guna sebagai acuan dasar komunikasi perangkat dalam menjalankan operasionalnya dalam bentuk coding. Bahasa pemograman yang pernah saya baca adalah Python, namun yang saya baca hanya pengenalan dasar dari Python tersebut.
Python adalah bahasa pemrograman interpretatif multiguna yang memakai filosofi perancangan dengan fokus kepada tingkat keterbacaan kode. Sebagai bahasa pemrograman, Python menggabungkan kemampuan, kapabilitas dan sintaksis kode serta fungsi pustaka yang berkualitas tinggi.
Fitur dalam bahasa pemograman Python secara general :
1. Berorientasi kepada objek.
2. Relatif mudah dikembangkan dengan menciptakan modul-modul baru. Asalnya Modul tersebut merupakan kombinasi dari modul lama yang di integrasi.
3. Memiliki tata bahasa yang relatif mudah dipelajari oleh manusia.
4. Didukung sistem pengelolaan memori secara otomatis sehingga membutuhkan kinerja saat coding.
5. Python juga memiliki banyak fasilitas pendukung sehingga ketika menjalankannya, tergolong mudah dan cepat.
Minggu 2
Pada minggu ke-2 kelas Metode Numerik, membahas apa itu angka eksak dan angka numerik?, lintas apakah bagaimana eksistensinya?, angka eksak mulai dari 0,1,2,3,4,5...dst itu tentu ada, namun itu hanya sebuah perjanjian / kesepakatan pembatasan nilai untuk berkomunikasi verbal agar memudahkan kita manusia untuk bertukar informasi dalam kehidupan nyata. Pada dasarnya komputer hanya mengenal 2 angka, yaitu "0" dan "1", dimana 0 yang berarti tidak bernilai dan 1 yang artinya bernilai, seperti layaknya iya dan tidak. Komputer bekerja berdasarkan perintah, dan perintah itu berisi kombinasi rangkaian angka 0 dan 1 yang menjadi modul dasar komputer untuk bekerja. Loncatan-loncatan elektron listrik yang biasa disebut pulse merupakan cara komputer bekerja mengirim sinyal untuk melakukan perintah operasional.
Angka eksak merupakan hasil pendekatan perhitungan dari angka numerik, karena pada dasarnya secara keseluruhan nilai yang sebenarnya didapat secara akurat hanya bisa di hitung dengan angka numerik.
Berikut merupakan soal yang diberikan.
Dalam mengerjakan soal diatas dengan x=1 tidak bisa mendapatkan hasil yang benar dikarenakan 0/0. Oleh sebab itu, saya gunakan limit pendekatan x=1. Saya menambahkan fungsi hingga perbedaan 1/999999 yang mendekati angka nol, sehingga hasil pendekatan dari perhitungan tidak menjauhi hasil sebenarnya dalam eksak.
Jadi hasilnya secara numerik mendekati angka 2, dan dapat dianggap secara eksak hasilnya adalah 2. Namun, dosen kami Bapak Dr. Ir. Ahmad Indra Siswantara menitip pesan agar tidak lupa diri terhadap yang punya kehidupan kita, walau kita sudah sejauh ini mengerti akan teknologi. Ditengah maraknya perkembangan teknologi yang pesat, kadang kita melunturkan sisi lain dari kehidupan kita, yaitu agama. Dimana hubungan kita pribadi dengan Tuhan YME merupakan dasar acuan kehidupan kita sehari-hari.
Minggu 3
Diberikan persamaan seperti diatas, carilah nilai dari x pada persamaan tersebut!
Python Script :
def f(x):
return 8*x**3 + 2*x**2 + x - 1
def fprime(x):
return 24*x**2 + 4*x +1
ep = 0.001
gu = -10
i = 0
print('Diberikan fungsi sebagai berikut:'
'8*x**3 + 2*x**2 + x - 1 = 0'
'Carilah nilai x dari persamaan diatas')
print('Hasil perhitungan oleh Python 3.7')
while abs(f(gu)) >= ep:
gu = gu - (f(gu)/fprime(gu))
i += 1
print(' ' + str(i) + ' ' + str(round(gu,7)))
print('Hasil pendekatannya adalah ' + str(round(gu,2)) +
'| gagal untuk menghitung: ' + str(i) + ' kali' )
Minggu 4
Pada pertemuan ini kami diajarkan bagaimama cara menggunakan matrix dalam menyelesaikan suatu masalah yang berbentuk persamaan. Dalam hal ini menggunakan program python
Pada hukum kontinuitas massa terdapat rumus Q*p=Q*p dan didapatakan 4 persamaan dengan 4 variabel
6C1 - 4C2 = 50
-2C1 - 1C3 + 4C4 = 50
7C2 - 3C3 - 4C4 = 0
-4C1 + 4C3 = 0
6C1 - 4C2 + 0C3 + 0C4 = 50
-2C1 + 0C2 - 1C3 + 4C4 = 50
0C1 + 7C2 - 3C3 - 4C4 = 0
-4C1 + 0C2 + 4C3 + 0C4 = 0
Kemudian, persamaan - persamaan ini dimasukkan kedalam python untuk di hitung hasil persamaannya.
Minggu 5
Pada minggu kelima, kami diajarkan cara penggunaan turunan menggunakan Python dengan Metode Runge Kutta orde 4, kali ini diajarkan dengan menggunakan excel terlebih dahulu untuk mempermudah pemahaman terkait pendekatan metode ini terhadap turunan yang berlaku, berikut merupakan penjelasan singkat dari metode ini:
1. Metode Runge-Kutta adalah alternatif lain dari metode deret Taylor yang tidak membutuhkan perhitungan turunan.
2. Metode ini menawarkan penyelesaian persamaan diferensial dengan pertumbuhan truncation error yang jauh lebih kecil.
3. Truncation error adalah kesalahan / penyimpangan nilai yang timbul akibat pemotongan suku pada suatu deret atau rumus dalam approksimasi.
DIberikan contoh soal seperti dibawah ini:
Jawaban dalam excel yang telah dibuat:
Minggu 6 - QUIZ (14/10/2019)
Problem set 2.1 Number 6 page 55
Matrix given,
A = [[0, 0, 2, 1, 2], [0, 1, 0, 2, -1], [1, 2, 0, -2, 0], [0, 0, 0, -1, 1], [0, 1, -1, 1, -1]]
B = [1, 1, -4, -2, -1]
Before entering Gauss Elimination, matrix should be configured so we could eliminate it,
Matrix configuration,
A = [[1, 2, 0, -2, 0], [0, 1, 0, 2, -1],[0, 1, -1, 1, -1], [0, 0, 0, -1, 1], [0, 0, 2, 1, 2]]
B = [-4, 1, -1, -2, 1]
So the result is,
X1 = 2
X2 = -2
X3 = 1
X4 = 1
X5 = -1
PYTHON CODE
Import numpy as np
A=np.array([[1, 2, 0, -2, 0], [0, 1, 0, 2, -1],[0, 1, -1, 1, -1], [0, 0, 0, -1, 1], [0, 0, 2, 1, 2]],float)
B=np.array([-4, 1, -1, -2, 1],float)
n=len(A)
Gauss Elimination code
for k in range (0,n-1): for i in range (k+1, n): if A[i,k]!=0 : lam= A[i,k]/A[k,k] A[i,k:n]= A[i, k:n]-(A[k,k:n]*lam) B[i]=B[i]-(B[k]*lam) print ('matrix A:', '\n', A)
Back substitution
x=np.zeros(n,float) for m in range (n-1, -1, -1): x[m]=(B[m]-np.dot(A[m, m+1:n], x[m+1:n]))/A[m,m] print ('nilai X', m+1, '=', x[m])
Problem set 7.1 Number 1 page 263
Python Script :
import numpy as np
def diff_y (x,y):
fungsi = x**2 - 4*y
return (fungsi)
x = 0
y = 1
h = 0.01
step_size = np.arange (0,0.03,h)
for t in step_size:
k1 = diff_y (x,y)
k2 = diff_y ((x+0.5*h), (y+0.5*k1*h))
y = y + k1*h
print ('maka y(0.03) adalah', y)