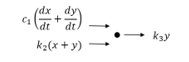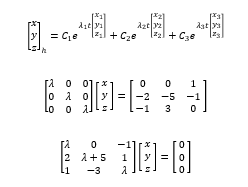Difference between revisions of "Kania Amelia Safitri"
(→Quiz Komputasi Teknik) |
(→Pengetahuan Penulis tentang Komputasi Teknik) |
||
| (35 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
Nama : Kania Amelia Safitri | Nama : Kania Amelia Safitri | ||
| − | |||
| − | |||
Prodi : Konversi Energi | Prodi : Konversi Energi | ||
| − | |||
Perkenalan penulis dengan komputasi teknik berawal dari kegiatan perkuliahan penulis saat menempuh gelar sarjana, penulis diajarkan bagaimana menggunakan beberapa software yang dapat membantu dalam menganalisis dan mengolah data, seperti ''matlab'', ''minitab'' dan ''excel''. | Perkenalan penulis dengan komputasi teknik berawal dari kegiatan perkuliahan penulis saat menempuh gelar sarjana, penulis diajarkan bagaimana menggunakan beberapa software yang dapat membantu dalam menganalisis dan mengolah data, seperti ''matlab'', ''minitab'' dan ''excel''. | ||
| Line 13: | Line 10: | ||
= Pengetahuan Penulis tentang Komputasi Teknik= | = Pengetahuan Penulis tentang Komputasi Teknik= | ||
| − | + | Semasa kuliah komputasi teknik digunakan untuk menyelesaikan permasalahan optimasi dalam bidang keteknikan dengan menggunakan matlab, serta untuk mempermudah analisa numerik dari suatu sebaran data di dalam excel, selain itu aplikasi minitab juga digunakan untuk menganalisis nilai statistik dari sebaran data yang dimiliki. | |
| − | + | Matlab digunakan penulis untuk menunjukan nilai optimum dari suatu pemodelan matematika, dimana pemodelan matematika tersebut dirumuskan dari permasalahan yang ada di lapangan. Sebagai contoh, terdapat dua gudang penyimpanan kayu yang dapat dituliskan sebagai gudang A dan B dimana jarak gudang tersebut dengan tempat pemotongan masing-masing sejauh 10 km dan 8 km biaya pengantaran batang kayu perkilometer adalah $2, serta ongkos pemotongan kayu perbatang sebesar $12. Gudang A dapat menampung sekitar 200 batang kayu dan gudang B dapat menampung sekitar 125 batang kayu. Jika perhari hanya dapat dilakukan pemotongan sebanyak 300-310 batang kayu maka berapa biaya minimum yang harus dikeluarkan untuk mendapatkan hasil potongan kayu maksimum perbulannya? | |
Persoalan seperti di atas dapat diselesaikan dengan pemodelan matematika, lalu dilanjutkan dengan penggunan aplikasi mathlab, meskipun dapat dilakukan perhitungan manual namun penggunaan mathlab dapat membantu menyelesaikan persoalan tersebut dengan cepat. | Persoalan seperti di atas dapat diselesaikan dengan pemodelan matematika, lalu dilanjutkan dengan penggunan aplikasi mathlab, meskipun dapat dilakukan perhitungan manual namun penggunaan mathlab dapat membantu menyelesaikan persoalan tersebut dengan cepat. | ||
| Line 25: | Line 22: | ||
Gambaran di atas merupakan pengetahuan yang penulis dapatkan mengenai komputasi teknik, namun dengan berjalannya waktu penulis perlu melakukan ''review'' kembali mengenai pelajaran yang telah didapatkan, agar penulis dengan mudah mengaplikasikan kembali ilmu yang telah didapatkan. Penulis menilai kemampuan penulis berada pada taraf cukup dalam bidang komputasi teknik, besar harapan dengan adanya pembelajaran lebih lanjut mengenai komputasi teknik, penulis dapat mengembangkan kemampuan penulis menjadi lebih baik dari sebelumnya. | Gambaran di atas merupakan pengetahuan yang penulis dapatkan mengenai komputasi teknik, namun dengan berjalannya waktu penulis perlu melakukan ''review'' kembali mengenai pelajaran yang telah didapatkan, agar penulis dengan mudah mengaplikasikan kembali ilmu yang telah didapatkan. Penulis menilai kemampuan penulis berada pada taraf cukup dalam bidang komputasi teknik, besar harapan dengan adanya pembelajaran lebih lanjut mengenai komputasi teknik, penulis dapat mengembangkan kemampuan penulis menjadi lebih baik dari sebelumnya. | ||
| − | + | ==Draft Paper Komputasi Teknik== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ==Draft | ||
| Line 430: | Line 216: | ||
HASIL DAN ANALISA | HASIL DAN ANALISA | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Quiz Komputasi Teknik== | == Quiz Komputasi Teknik== | ||
| − | ''' | + | '''Initial Thingking''' |
| − | Initial Thingking''' | ||
Sebuah pendulum bergerak dengan kondisi awal; u (kecepatan) sebesar 4 m/s, v (percepatan) sebesar 0 m/s, dan ω (frekuensi sudut) yang konstan sebesar 5 rad/s, untuk mengetahui gerak osilasi dari pendulum maka metode numerik digunakan untuk mempercepat dan mempermudah proses perhitungan, berikut persamaan yang digunakaan dalam metode numerik, | Sebuah pendulum bergerak dengan kondisi awal; u (kecepatan) sebesar 4 m/s, v (percepatan) sebesar 0 m/s, dan ω (frekuensi sudut) yang konstan sebesar 5 rad/s, untuk mengetahui gerak osilasi dari pendulum maka metode numerik digunakan untuk mempercepat dan mempermudah proses perhitungan, berikut persamaan yang digunakaan dalam metode numerik, | ||
| Line 462: | Line 233: | ||
'''Pemodelan''' | '''Pemodelan''' | ||
| − | + | [[File:Gr1.PNG|200px]] | |
| + | |||
Pendulum bergerak dari posisi B menuju ke A lalu berosilasi secara terus menerus (dengan mengasumsikan tidak adanya gaya gesekan yang terjadi di antara pendulum dengan udara). Secara analitikal nilai kecepatan dan percepatan pendulum dapat diketahui melalui persamaan; | Pendulum bergerak dari posisi B menuju ke A lalu berosilasi secara terus menerus (dengan mengasumsikan tidak adanya gaya gesekan yang terjadi di antara pendulum dengan udara). Secara analitikal nilai kecepatan dan percepatan pendulum dapat diketahui melalui persamaan; | ||
| Line 487: | Line 259: | ||
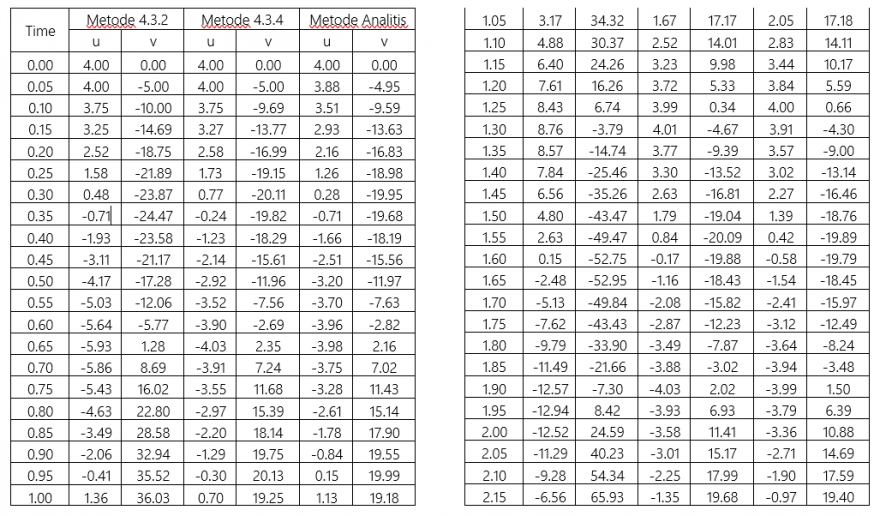
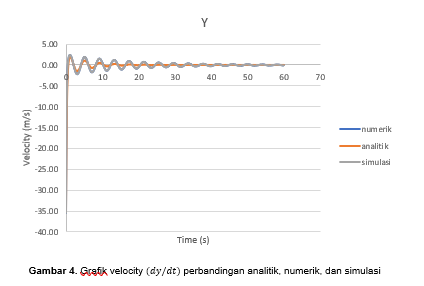
Proses verifikasi dilakukan dengan membandingkan data-data hasil numerik dengan data-data hasil analitikal berdasarkan hasil perhitungan menggunakan excel maka didapatkan grafik osilasi dari gerakkan yang dihasilkan oleh pendulum yang ditunjukkan oleh grafik 1 dan 2, dimana grafik 1 menunjukan kecepatan getaran pendulum sedangkan grafik 2 menunjukan percepatan getaran pendulum. | Proses verifikasi dilakukan dengan membandingkan data-data hasil numerik dengan data-data hasil analitikal berdasarkan hasil perhitungan menggunakan excel maka didapatkan grafik osilasi dari gerakkan yang dihasilkan oleh pendulum yang ditunjukkan oleh grafik 1 dan 2, dimana grafik 1 menunjukan kecepatan getaran pendulum sedangkan grafik 2 menunjukan percepatan getaran pendulum. | ||
| − | + | [[File:Gr2.PNG|800 px]] | |
Grafik 1 dan 2 menunjukan perbedaan hasil antara data perhitungan metode numerik dengan analisis, data hasil perhitungan dengan menggunakan metode analisis ditunjukan oleh garis berwarna merah baik kecepatan maupun percepatan menunjukan trend osilasi yang stabil dari pergerakan pada 0 s hingga 5s, sedangkan untuk metode numerik menghasilkan trend yang tidak selaras dengan data hasil perhitungan analitik, sehingga dapat disimpulkan bahwa persamaan yang digunakan tidak terferifikasi, untuk itu diperlukan suatu persaamaan lain. | Grafik 1 dan 2 menunjukan perbedaan hasil antara data perhitungan metode numerik dengan analisis, data hasil perhitungan dengan menggunakan metode analisis ditunjukan oleh garis berwarna merah baik kecepatan maupun percepatan menunjukan trend osilasi yang stabil dari pergerakan pada 0 s hingga 5s, sedangkan untuk metode numerik menghasilkan trend yang tidak selaras dengan data hasil perhitungan analitik, sehingga dapat disimpulkan bahwa persamaan yang digunakan tidak terferifikasi, untuk itu diperlukan suatu persaamaan lain. | ||
| Line 499: | Line 271: | ||
dan untuk persamaan kecepatan getaran tetap digunakan persamaan | dan untuk persamaan kecepatan getaran tetap digunakan persamaan | ||
| − | u^(n+1)= u^n+ | + | u^(n+1)= u^n+ (∆t v)^n |
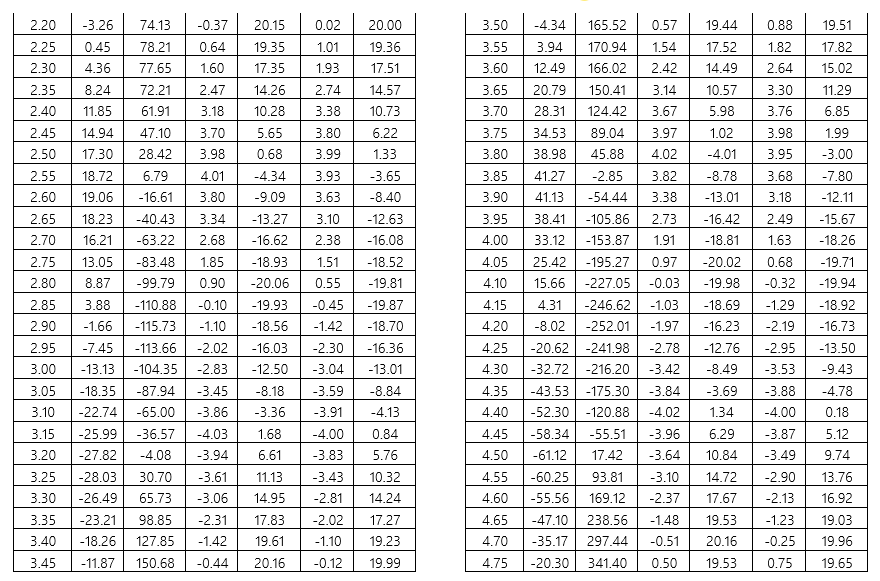
Sehingga, didapatkan grafik antara metode numerik dan analitikal untuk kecepatan dan percepatan sebagai berikut, | Sehingga, didapatkan grafik antara metode numerik dan analitikal untuk kecepatan dan percepatan sebagai berikut, | ||
| − | + | [[File:Gr3.PNG|800 px]] | |
Terlihat pada grafik 3 dan 4 bahwasannya data-data hasil perhitungan dengan metode numerik memiliki kemiripan yang sangat tinggi dengan hasil analitik, dimana hasil keduanya saliang berdempetan sehingga dapat disimpulkan bahwasanya metode numerik yang dilakukan untuk menyelesaikan persoalaan ini terverifikasi. | Terlihat pada grafik 3 dan 4 bahwasannya data-data hasil perhitungan dengan metode numerik memiliki kemiripan yang sangat tinggi dengan hasil analitik, dimana hasil keduanya saliang berdempetan sehingga dapat disimpulkan bahwasanya metode numerik yang dilakukan untuk menyelesaikan persoalaan ini terverifikasi. | ||
| Line 509: | Line 281: | ||
'''Lampiran''' | '''Lampiran''' | ||
| + | |||
| + | [[File:Gr4.PNG|880 px]] | ||
| + | [[File:Gr5.PNG]] | ||
| + | [[File:Gr6.PNG]] | ||
| + | |||
| + | =Artikel Oscillating 1-D Dynamic System= | ||
| + | |||
| + | Tugas Kelompok: | ||
| + | |||
| + | Kania Amelia Safitri (1906324113) | ||
| + | |||
| + | Evi Elisa Ambarita (1906324044) | ||
| + | |||
| + | Dieter Rahmadiawan (1906324031) | ||
| + | |||
| + | Chandra R.M. Simanjuntak (1906324012) | ||
| + | |||
| + | |||
| + | '''1. Pendahuluan''' | ||
| + | |||
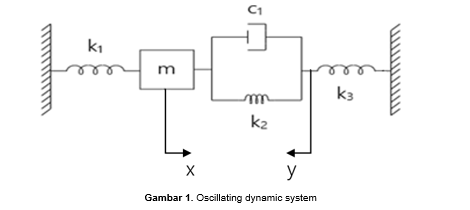
| + | Artikel ini akan membahas penyelesaian permasalahan oscillating 1-D dynamic system pada system damping sesuai gambar di bawah. Pada system di bawah terdapat sebuah massa yang dihubungkan dengan 3 spring, dan 1 dashpot. System tersebut fix pada 2 boundary sisi kiri dan kanan. | ||
| + | |||
| + | [[File:1-1D.PNG]] | ||
| + | |||
| + | Penyelesaian dari permasalahan tersebut akan dilakukan dengan 3 metode, yang kemudian akan dibandingkan hasil dari perhitungan pada tiap metode tersebut. Metode yang digunakan yaitu: analitikal, numerik, dan simulasi. Pada metode analitikal dilakukan tinjauan gaya aksi – reaksi pada free body diagram (FBD) yang muncul dari eksitasi yang diberikan. Kemudian untuk penyelesaian metode numerik akan dilakukan iterasi dengan bantuan software Microsoft Excel menggunakan Forward Euler. Sedangkan untuk proses simulasi akan dilakukan dengan bantuan software MATLAB. | ||
| + | |||
| + | |||
| + | '''2. Metode Penyelesaian''' | ||
| + | |||
| + | |||
| + | '''2.1 Metode Analitikal''' | ||
| + | |||
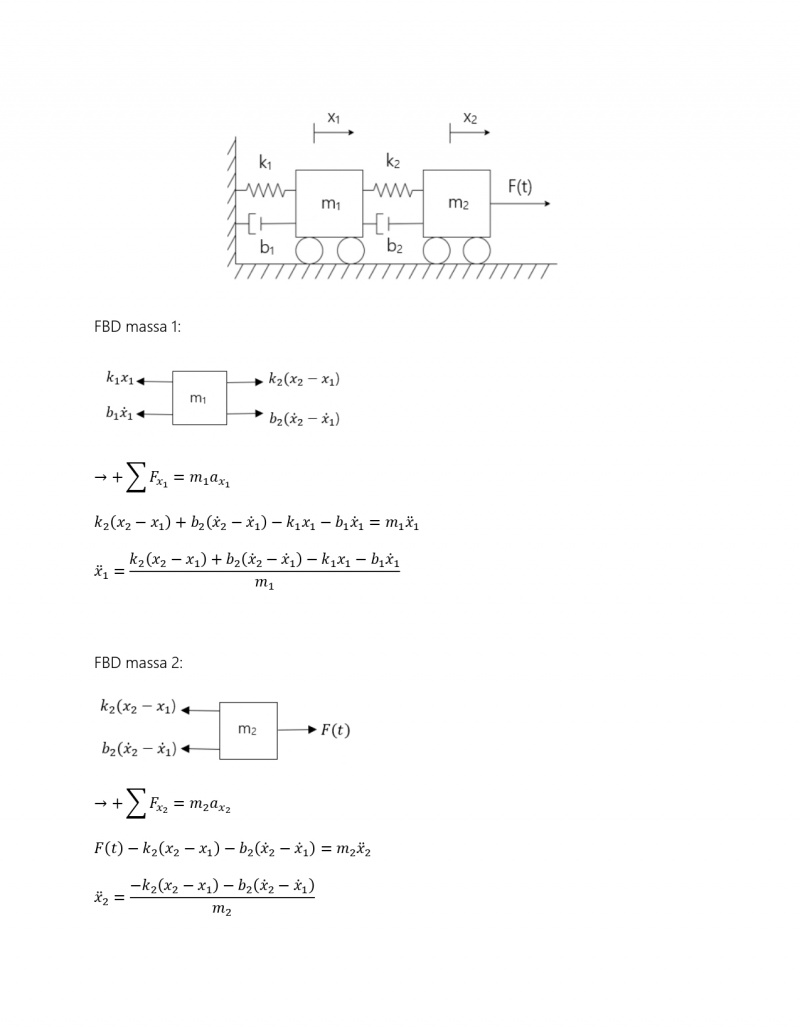
| + | Free Body Diagram (FBD) | ||
| + | |||
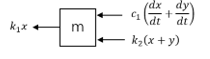
| + | '''Tinjauan Massa''' | ||
| + | |||
| + | [[File:2-1D.PNG]] | ||
| + | |||
| + | Analisa FBD: | ||
| + | |||
| + | 0-k_1 x-c_1 (dx/dt+dy/dt)-k_2 (x+y)=m (d^2 x)/(dt^2) | ||
| + | |||
| + | '''Tinjauan Titik''' (diantara c1, k2, dan k3) | ||
| + | |||
| + | [[File:3-1D.PNG]] | ||
| + | |||
| + | Analisa FBD: | ||
| + | |||
| + | 0-c_1(dx/dt+dy/dt)-k_2 (x+y)-k_3 y=0 (d^2 y)/(dt^2) | ||
| + | |||
| + | '''Diketahui''': | ||
| + | m=1kg | ||
| + | c_1=1 N/m | ||
| + | |||
| + | k_1=1 N/m^2 | ||
| + | |||
| + | k_2=2 N/m^2 | ||
| + | |||
| + | k_3=3 N/m^2 | ||
| + | |||
| + | dx/dt=x ̇ | ||
| + | |||
| + | dy/dt=y ̇ | ||
| + | |||
| + | (d^2 x)/(dt^2 )=x ̈ | ||
| + | |||
| + | (d^2 y)/(dt^2 )=y ̈ | ||
| + | |||
| + | Maka persamaan 1 dan 2 dapat dituliskaan kembali menjadi: | ||
| + | |||
| + | Persamaan 1, | ||
| + | |||
| + | 0-x-(x ̇+y ̇ )-2 (x+y)=x ̈ | ||
| + | |||
| + | -2y-y ̇=3x+x ̇+x ̈ | ||
| + | |||
| + | Persamaan 2, | ||
| + | |||
| + | 0-(x ̇+y ̇ )-2(x+y)-3y=0 | ||
| + | |||
| + | -y ̇-5y=2x+x ̇ | ||
| + | |||
| + | '''Penyelesaian''' | ||
| + | |||
| + | Asumsi | ||
| + | |||
| + | x ̇ =z subtitusi ke persamaan 3 dan 4 maka; | ||
| + | |||
| + | z ̇ =-(3x+2y+y+z) | ||
| + | |||
| + | y ̇ =-(2x+5y+z) | ||
| + | |||
| + | Karena pada persamaan 5 masih terdapat y ̇ maka subtitusi persamaan 6 ke persamaan 5, sehingga didapatkan nilai z ̇ sebagai berikut; | ||
| + | |||
| + | z ̇ =-x+3y | ||
| + | |||
| + | Penyelesaian menggunakan matrix; | ||
| + | |||
| + | [[File:4-1D.PNG]] | ||
| + | |||
| + | Di mana nilai g_x (t), g_y (t), g_z (t)=0 (homogen) | ||
| + | |||
| + | sehingga | ||
| + | |||
| + | [[File:5-1D.PNG]] | ||
| + | |||
| + | {λ^2 (λ+5)+0+((-1)(2)(-3))}-{(-1)(λ+5)+λ(-3)(1)+0}=0 | ||
| + | λ^3+5λ^2+4λ+11=0 | ||
| + | |||
| + | Maka didapatkan nilai λ sebesar | ||
| + | |||
| + | λ_1=-4.65 | ||
| + | |||
| + | λ_2=-0.175±1.52i | ||
| + | |||
| + | Sehingga didapatkan persamaan | ||
| + | |||
| + | x_h=C_1 e^(-4.65t)+e^(-0.175t)(C_2sin[(1.52t)+C_3cos(1.52t)] | ||
| + | |||
| + | Jika diasumsikan nilai C_1,C_2,dan C_3 adalah 1, 2 dan 3 maka; | ||
| + | |||
| + | x_h=e^(-4.65t)+e^(-0.175t)[2sin(1.52t)+3cos(1.52t)] | ||
| + | |||
| + | Nilai x untuk t = 0 s, t = 1 s, dan t = 10 s adalah, | ||
| + | |||
| + | x_0= e^(-4.65(0))+e^(-0.175(0))(2sin(1.52(0))+3cos(1.52(0)) | ||
| + | |||
| + | x_0=4 m | ||
| + | |||
| + | x_1= e^(-4.65(1))+ e^(-0.175(1))(2sin(1.52(1))+3cos(1.52(1)) | ||
| + | |||
| + | x_1=1.81 m | ||
| + | |||
| + | x_10= e^(-4.65(10))+ e^(-0.175(10))(2sin(1.52(10))+3cos(1.52(10)) | ||
| + | |||
| + | x_10=-0,29m | ||
| + | |||
| + | Mencari nilai y_h dengan mensubtitusi nilai x_h ke dalam persamaan | ||
| + | |||
| + | z ̇ =-x+3y, | ||
| + | di mana nilai z ̇ = x ̈. | ||
| + | |||
| + | Mencari nilai x ̇ ; | ||
| + | |||
| + | x_h= e^(-4.65t)+e^(-0.175t)[2sin(1.52t)+3cos(1.52t)] | ||
| + | |||
| + | x ̇ =dx/dt=d/dt [e^(-4.65t)+e^(-0.175t){2sin(1.52t)+3cos(1.52t)}] | ||
| + | |||
| + | d/dt [e^(-4.65t)]= -4.65e^(-4.65t) | ||
| + | |||
| + | d/dt [e^(-0.175t) | ||
| + | {2sin(1.52t)+3cos(1.52t)}]=-4.91e^(-0.175t)sin(1.52t)+2.515e^(-0.175t)cos(1.52t) | ||
| + | |||
| + | x ̇ =-4.65e^(-4.65t)-4.91e^(-0.175t)sin(1.52t)+2.515e^(-0.175t)cos(1.52t) | ||
| + | |||
| + | Nilai x ̇ untuk t = 0 s, t = 1 s, dan t = 10 s adalah | ||
| + | |||
| + | x ̇_0=-4.65e^0-4.91e^0 sin(0)+2.515e^0cos(0) | ||
| + | |||
| + | x ̇_0 =-2.135 m/s | ||
| + | |||
| + | x ̇_1=-4.65e^(-4.65(1))-4.91e^(-0.175(1))sin(1.52(1))+2.515e^(-0.175(1))cos(1.52(1)) | ||
| + | |||
| + | x ̇_1 =-4.05 m/s | ||
| + | |||
| + | x ̇_10=-4.65e^(-4.65(10))-4.91e^(-0.175(10))sin(1.52(10))+2.515e^(-0.175(10))cos(1.52(10)) | ||
| + | |||
| + | x ̇_10 =-0.8 m/s | ||
| + | |||
| + | Mencari nilai x ̈ ; | ||
| + | |||
| + | x ̈ =dx ̇ /dt=d/dt[-4.65e^(-4.65t)-4.91e^(-0.175t)sin(1.52t)+2.515e^(-0.175t)cos(1.52t)] | ||
| + | |||
| + | d/dt[4.65e^(-4.65t)]=-21.62e^(-4.65t) | ||
| + | |||
| + | d/dt[4.91e^(-0.175t)sin(1.52t)]=4.91(-0.175e^(-0.175t)sin(1.52t)+1.52e^(-0.175t)cos(1.52t) | ||
| + | |||
| + | d/dt [2.515e^(-0.175t)cos(1.52t)]=2.515(-0.175e^(-0.175t)cos(1.52t)-1.52e^(-0.175t)sin(1.52t)) | ||
| + | |||
| + | x ̈ =21.62e^(-4.65t)-4.91(-0.175e^(-0.175t)sin(1.52t)+1.52e^(-0.175t) cos(1.52t)+2.515(-0.175e^(-0.175t)cos(1.52t)-1.52e^(-0.175t)sin(1.52t)) | ||
| + | |||
| + | Persamaan x ̈ di atas dapat disederhanakan menjadi; | ||
| + | |||
| + | x ̈ _h=21.62e^(-4.65t)-2.96e^(-0.175t)sin(1.52t)-7.9e^(-0.175t)cos(1.52t) | ||
| + | |||
| + | Nilai x ̈ untuk t = 0 s, t = 1 s, dan t = 10 s adalah | ||
| + | |||
| + | x ̈ _0=21.62e^0-2.96e^0 sin(0)-7.9e^0 cos(0) | ||
| + | |||
| + | x ̈ _0=13.72 m/s^2 | ||
| + | |||
| + | x ̈ _1=21.62e^(-4.65t)-2.96e^(-0.175t) sin(1.52t)-7.9e^(-0.175t)cos(1.52t) | ||
| + | |||
| + | x ̈ _1=-2.61 m/s^2 | ||
| + | |||
| + | x ̈ _10=21.62e^(-4.65(10))-2.96e^(-0.175(10))sin(1.52(10)-7.9e^(-0.175(10))cos(1.52(10)) | ||
| + | |||
| + | x ̈ _10=0.95 m/s^2 | ||
| + | |||
| + | Mencari nilai y; | ||
| + | |||
| + | x ̈ =-x+3y | ||
| + | |||
| + | y =(x ̈ +x)/3 | ||
| + | |||
| + | y_h =1/3 [21.62e^(-4.65t)-2.96e^(-0.175t)sin(1.52t)-7.9e^(-0.175t)cos(1.52t)+ e^(-4.65t)+ e^(-0.175t)(2sin(1.52t)+3 cos(1.52t))] | ||
| + | |||
| + | Persamaan y_h dapat disederhanakan menjadi; | ||
| + | |||
| + | y_h=1/3[22.62e^(-4.65t)-e^(-0.175t)(0.96sin(1.52t)+4.9cos(1.52t))] | ||
| + | |||
| + | Nilai y untuk t = 0 s, t = 1 s, dan t = 10 s adalah | ||
| + | |||
| + | y_0= 1/3 [22.62e^(-4.65(0))-e^(-0.175(0))(0.96 sin(0)+4.9 cos(0))] | ||
| + | |||
| + | y_0= 5.9 m | ||
| + | |||
| + | y_1= 1/3 [22.62e^(-4.65(1))- e^(-0.175(1)) (0.96 sin(1.52)+4.9 cos(1.52))] | ||
| + | |||
| + | y_1= -0.27 m | ||
| + | |||
| + | y_10= 1/3 [22.62e^(-4.65(10))- e^(-0.175(10)) (0.96 sin(15.2)+4.9 cos(15.2))] | ||
| + | |||
| + | y_10= -0.22 m | ||
| + | |||
| + | Mencari nilai y ̇ ; | ||
| + | |||
| + | y ̇ =dy/dt=d/dt {1/3 [22.62e^(-4.65t)- e^(-0.175t)(0.96sin(1.52t)+4.9cos(1.52t))]} | ||
| + | |||
| + | d/dt [22.62e^(-4.65t)]=-105.18e^(-4.65t) | ||
| + | |||
| + | d/dt [e^(-0.175t)(0.96 sin(1.52t)+4.9 cos(1.52t))]=-7.61e^(-0.175t)sin(1.52t)+0.6e^(-0.175t)cos(1.52t) | ||
| + | |||
| + | y ̇=1/3 [-105.18e^(-4.65t)+7.61e^(-0.175t)sin(1.52t)-0.6e^(-0.175t)cos(1.52t)] | ||
| + | |||
| + | Nilai y ̇ ketika t = 0 s, t = 1 s, dan t = 10 s adalah | ||
| + | |||
| + | y ̇_0=1/3 [-105.18e^0+7.61e^0sin(0)-0.6e^0cos(0)] | ||
| + | |||
| + | y ̇ _0= -35.26 m/s | ||
| + | |||
| + | y ̇ _1= 1/3 [-105.18e^(-4.65(1))+7.61e^(-0.175(1))sin(1.52(1))-0.6e^(-0.175(1)) cos(1.52(1))] | ||
| + | |||
| + | y ̇ _1=1.78 m/s | ||
| + | |||
| + | y ̇_10= 1/3 [-105.18e^(-4.65(10))+7.61e^(-0.175(10))sin(1.52(10))-0.6e^(-0.175(10))cos(1.52(10))] | ||
| + | |||
| + | y ̇ _10=0.24 m/s | ||
| + | |||
| + | |||
| + | '''2.2 Metode Numerik''' | ||
| + | |||
| + | Metode ini dilakukan dengan menggunakan software Microsoft Excel. Parameter input yang harus diketahui yaitu x pada t = 0 s, y pada t = 0 s, dan selisih penambahan waktu (∆t). Parameter input x dan y ini dapat juga disebut dengan initial condition. Lalu kemudian dilakukan iterasi sesuai dengan ∆t sampai waktu yang ditentukan. Nilai parameter input tersebut didapat dengan cara analitis seperti sudah disebut di atas, yaitu x_((t=0))=4 m; y_((t=0))=5.9 m; dan selisih waktu ∆t=0.1 second. | ||
| + | |||
| + | Seperti sudah disebutkan sebelumnya bahwa penyelesaiannya menggunakan Forward Euler, yaitu sebagai berikut: | ||
| + | |||
| + | x^(n+1)=x^n+x ̇^n.∆t | ||
| + | |||
| + | Dimana x ̇ pada t = 0 s menggunakan persamaan | ||
| + | |||
| + | y^(n+1)=y^n+y ̇^n.∆t | ||
| + | |||
| + | Dimana y ̇ menggunakan persamaan | ||
| + | |||
| + | x^(n+1)=x ̇^n+x ̈.∆t | ||
| + | |||
| + | Dimana x ̈=z ̇ menggunakan persamaan | ||
| + | |||
| + | |||
| + | '''2.3 Simulasi''' | ||
| + | |||
| + | Simulasi dilakukan dengan bantuan software MATLAB. Adapun agar simulasi dapat berjalan, maka perlu diberikan input coding pada software MATLAB yang isinya sebagai berikut. | ||
| + | |||
| + | % Calculates the position, velocity, and acceleration as a function of time | ||
| + | |||
| + | % of a system of carts connected by springs and dashpots. Euler's Method is | ||
| + | |||
| + | % used to solve the equations of motion numerically. | ||
| + | |||
| + | clear all; close all; clc; | ||
| + | |||
| + | tic | ||
| + | |||
| + | % Problem parameters | ||
| + | |||
| + | k1=1; % cart 1 spring constant (N/m) | ||
| + | |||
| + | k2=2; % cart 1 spring constant (N/m) | ||
| + | |||
| + | b1=1; % cart 1 viscous damping coefficient (kg/s) | ||
| + | |||
| + | m1=1; % cart 1 mass (kg) | ||
| + | |||
| + | k3=3; % cart 1 spring constant (N/m) | ||
| + | |||
| + | x10=4; % cart 1 initial position (m) | ||
| + | |||
| + | x20=5.9; % y movement initial position (m) | ||
| + | |||
| + | v10=-2.135; % cart 1 initial velocity (m/s) | ||
| + | |||
| + | v20=-35.36; % cart 2 initial velocity (m/s) | ||
| + | |||
| + | % Set time step stuff | ||
| + | |||
| + | simTime=60; % simulation time (s) | ||
| + | |||
| + | tStep=0.1; % simulation time step | ||
| + | |||
| + | iterations=simTime/tStep; | ||
| + | |||
| + | t=0:iterations; | ||
| + | |||
| + | % Pre-allocate variables for speed and add initial conditions | ||
| + | |||
| + | x1=zeros(iterations,1); | ||
| + | |||
| + | x1(1,:)=x10; | ||
| + | |||
| + | x2=zeros(iterations,1); | ||
| + | |||
| + | x2(1,:)=x20; | ||
| + | |||
| + | v1=zeros(iterations,1); | ||
| + | |||
| + | v1(1,:)=v10; | ||
| + | |||
| + | v2=zeros(iterations,1); | ||
| + | |||
| + | v2(1,:)=v20; | ||
| + | |||
| + | a1=zeros(iterations,1); | ||
| + | |||
| + | a1(1,:)=((0-(k1*x10)-b1*(v10+v20)-k2*(x20+x10))/m1); | ||
| + | |||
| + | % Solve the ODE's with Euler's Method | ||
| + | |||
| + | for n=2:(iterations+1) | ||
| + | x1(n,:)=x1(n-1,:)+v1(n-1,:)*tStep; % cart 1 position | ||
| + | x2(n,:)=x2(n-1,:)+v2(n-1,:)*tStep; % cart 2 position | ||
| + | v1(n,:)=v1(n-1,:)+a1(n-1,:)*tStep; % cart 1 velocity | ||
| + | v2(n,:)=-(2*x1(n,:)+5*x2(n,:)+v1(n,:)) | ||
| + | |||
| + | % Find cart accelerations | ||
| + | a1(n,:)=((0-k1*x1(n,:))-b1*(v1(n,:)+v2(n,:))-k2*(x2(n,:)+x1(n,:))/m1); | ||
| + | end | ||
| + | |||
| + | % Plot results | ||
| + | |||
| + | subplot(3,1,1) | ||
| + | |||
| + | hold on; | ||
| + | |||
| + | plot(t',x1,'r') | ||
| + | |||
| + | plot(t',x2,'m') | ||
| + | |||
| + | ylabel('Position (m)') | ||
| + | |||
| + | title('Position, Velocity, & Acceleration as a Function of Time') | ||
| + | |||
| + | legend('Pergerakan ke arah X','Pergerakan ke arah Y') | ||
| + | |||
| + | subplot(3,1,2) | ||
| + | |||
| + | hold on; | ||
| + | |||
| + | plot(t',v1,'b') | ||
| + | |||
| + | plot(t',v2,'c') | ||
| + | |||
| + | ylabel('Velocity (m/s)') | ||
| + | |||
| + | legend('Pergerakan ke arah X','Pergerakan ke arah Y') | ||
| + | |||
| + | subplot(3,1,3) | ||
| + | |||
| + | hold on; | ||
| + | |||
| + | plot(t',a1,'g') | ||
| + | |||
| + | ylabel('Acceleration (m/s^2)') | ||
| + | |||
| + | xlabel('time (1 = 0.01 detik)') | ||
| + | |||
| + | legend('Pergerakan ke arah X','Pergerakan ke arah Y') | ||
| + | |||
| + | toc | ||
| + | |||
| + | |||
| + | '''Grafik Hasil Perhitungan''' | ||
| + | |||
| + | [[File:6-1D.PNG]] | ||
| + | |||
| + | [[File:7-1D.PNG]] | ||
| + | |||
| + | [[File:8-1D.PNG]] | ||
| + | |||
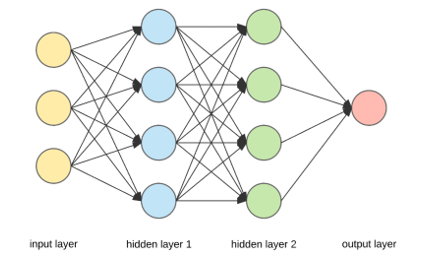
| + | Selanjutnya, untuk memverifikasi hasil numerik menggunakan metode euler yang dijelaskan diatas, digunakan metode Artificial Neural Networks (ANN) pada perangkat lunak matlab. Berikut sedikit pengenalan tentang ANN yang dapat kita temui dari beberapa sumber di internet. ANN adalah beberapa lapisan jaringan saraf (neural network) yang terhubung secara keseluruhan yang dapat dilihat dari gambar dibawah ini. Setiap node pada setiap lapisan terhubung ke setiap node dari lapisan selanjutnya. Jaringan dibuat lebih dalam dengan menambah jumlah lapisan tersembunyi (hidden layer). | ||
| + | |||
| + | [[File:9-1D.PNG]] | ||
| + | |||
| + | Jika salah satu hidden layer atau node output diperbesar, maka akan ditemukan gambar dibawah ini | ||
| + | |||
| + | [[File:10-1D.PNG]] | ||
| + | |||
| + | Node tertentu mengambil jumlah bobot dari inputnya, dan meneruskannya melalui fungsi aktivasi non-linear. Ini merupakan output dari node yang kemudian menjadi input dari node yang lain pada layer selanjutnya. Sinyal mengalir dari kiri ke kanan, dan output akhir dihitung dengan cara melakukan prosedur ini untuk semua node. Melatih jaringan saraf berarti mempelajari bobot yang terkait dengan semua edge. | ||
| + | |||
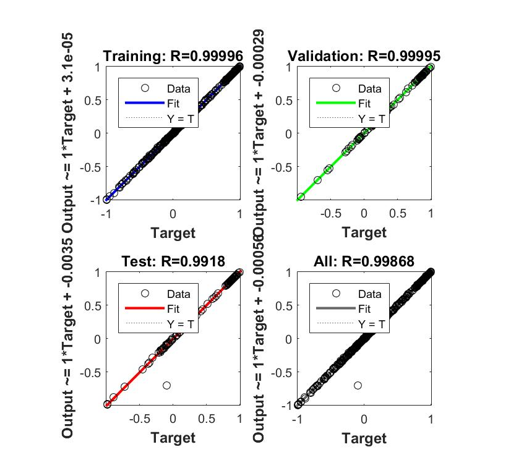
| + | Metode ANN ini digunakan untuk melatih data-data yang didapat dari numerik, dimana nilai posisi pada sumbu x dan y digunakan sebagai nilai input, dan nilai kecepatan pada sumbu x (u) dan sumbu y (v) yang merupakan hasil diferensial dari posisi digunakan sebagai nilai target. Data yang di training sebanyak 400 data. | ||
| + | |||
| + | [[File:11-1D.PNG]] | ||
| + | |||
| + | Dengan demikian, diperoleh hasil yang dapat dilihat pada gambar diatas, dengan nilai R sebesar 0,99996 yang berarti data yang didapat dari metode Euler terverifikasi secara baik dengan persamaan yang dihasilkan dari metode ANN pada matlab. | ||
| + | |||
| + | |||
| + | '''Kesimpulan''' | ||
| + | |||
| + | Dari hasil yang sudah didapat untuk metode analitik, numerik, dan simulasi berikut beberapa hal yang dapat disimpulkan: | ||
| + | |||
| + | a) Hasil perhitungan numerik terhadap simulasi memiliki nilai yang berimpit. Hal ini dikarenakan, pada dasarnya simulasi yang dilakukan dengan MATLAB, menggunakan cara yang sama dengan numerik, hanya saja pada numerik persamaan-persamaannya harus dirubah menjadi 3 persamaan dengan orde 1. Sedangan pada simulasi, persamaan dari FBD langsung menjadi input pada MATLAB. | ||
| + | |||
| + | b) Hasil perhitungan numerik dan simulasi berbeda dengan metode analitik. Seperti sudah disebutkan pada materi perkuliahan sebelum ini, bahwa pada metode Forward Euler terdapat hal yang harus diperhatikan pada perkembangan amplitudonya. | ||
| + | |||
| + | c) Hasil metode forward euler telah terverifikasi dengan metode Artificial Neural Networks (ANN) yang dapat dilihat dari nilai R sebesar 0,99996 (mendekati 1) dari persamaan output metode ANN menggunakan software matlab. | ||
| + | |||
| + | |||
| + | |||
| + | = Tugas Artikel MS dan FES 1 = | ||
| + | |||
| + | Kasus ini menjelaskan sebuah sistem 2 cart spring-mass-damper. Persamaan gerak untuk system 2 degree of freedom yang digunakan adalah Newtonian mechanics dan diselesaikan secara numerik pada matlab. | ||
| + | |||
| + | [[File:FBD-MS-FES.jpg|800 px]] | ||
| + | % Calculates the position, velocity, and acceleration as a function of time | ||
| + | % of a system of carts connected by springs and dashpots. Euler's Method is | ||
| + | % used to solve the equations of motion numerically. | ||
| + | clear all; close all; clc; | ||
| + | tic | ||
| + | |||
| + | % Problem parameters | ||
| + | k1=50; % cart 1 spring constant (N/m) | ||
| + | k2=50; % cart 2 spring constant (N/m) | ||
| + | b1=3; % cart 1 viscous damping coefficient (kg/s) | ||
| + | b2=3; % cart 2 viscous damping coefficient (kg/s) | ||
| + | m1=5; % cart 1 mass (kg) | ||
| + | m2=5; % cart 2 mass (kg) | ||
| + | x10=1; % cart 1 initial position (m) | ||
| + | x20=-1; % cart 2 initial position (m) | ||
| + | v10=0; % cart 1 initial velocity (m/s) | ||
| + | v20=0; % cart 2 initial velocity (m/s) | ||
| + | |||
| + | % Set time step stuff | ||
| + | simTime=10; % simulation time (s) | ||
| + | tStep=0.001; % simulation time step | ||
| + | iterations=simTime/tStep; | ||
| + | t=0:iterations; | ||
| + | |||
| + | % Pre-allocate variables for speed and add initial conditions | ||
| + | x1=zeros(iterations,1); | ||
| + | x1(1,:)=x10; | ||
| + | x2=zeros(iterations,1); | ||
| + | x2(1,:)=x20; | ||
| + | v1=zeros(iterations,1); | ||
| + | v1(1,:)=v10; | ||
| + | v2=zeros(iterations,1); | ||
| + | v2(1,:)=v20; | ||
| + | a1=zeros(iterations,1); | ||
| + | a1(1,:)=-(b1*v10-b2*(v20-v10)+k1*x10-k2*(x20-x10))/m1; | ||
| + | a2=zeros(iterations,1); | ||
| + | a2(1,:)=-(b2*(v20-v10)+k2*(x20-x10))/m2; | ||
| + | |||
| + | % Solve the ODE's with Euler's Method | ||
| + | for n=2:(iterations+1) | ||
| + | x1(n,:)=x1(n-1,:)+v1(n-1,:)*tStep; % cart 1 position | ||
| + | x2(n,:)=x2(n-1,:)+v2(n-1,:)*tStep; % cart 2 position | ||
| + | v1(n,:)=v1(n-1,:)+a1(n-1,:)*tStep; % cart 1 velocity | ||
| + | v2(n,:)=v2(n-1,:)+a2(n-1,:)*tStep; % cart 2 velocity | ||
| + | % Find cart accelerations | ||
| + | a1(n,:)=-(b1*v1(n,:)-b2*(v2(n,:)-v1(n,:))+k1*x1(n,:)-k2*(x2(n,:)-x1(n,:)))/m1; | ||
| + | a2(n,:)=-(b2*(v2(n,:)-v1(n,:))+k2*(x2(n,:)-x1(n,:)))/m2; | ||
| + | end | ||
| + | |||
| + | |||
| + | % Plot results | ||
| + | subplot(3,1,1) | ||
| + | hold on; | ||
| + | plot(t',x1,'r') | ||
| + | plot(t',x2,'m') | ||
| + | ylabel('Position (m)') | ||
| + | title('Position, Velocity, & Acceleration as a Function of Time') | ||
| + | legend('Cart 1','Cart 2') | ||
| + | subplot(3,1,2) | ||
| + | hold on; | ||
| + | plot(t',v1,'b') | ||
| + | plot(t',v2,'c') | ||
| + | ylabel('Velocity (m/s)') | ||
| + | legend('Cart 1','Cart 2') | ||
| + | subplot(3,1,3) | ||
| + | hold on; | ||
| + | plot(t',a1,'g') | ||
| + | plot(t',a2,'y') | ||
| + | ylabel('Acceleration (m/s^2)') | ||
| + | xlabel('time (iterations)') | ||
| + | legend('Cart 1','Cart 2') | ||
| + | |||
| + | toc | ||
| + | |||
| + | [[File:Artikelkeduaevi.jpg]] | ||
| + | |||
| + | Akan tetapi pada kasus ini, pembahasan yang dilakukan masih dengan Mass-Spring method. Untuk Finite Element Simplified (FES), akan diupdate pada kesempatan selanjutnya. | ||
| + | |||
| + | Source: https:// www.youtube.com/ watch?v=N524t6wdlcM&feature=youtu.be | ||
| + | |||
| + | =Tugas Artikel MS dan FES 2= | ||
| + | |||
| + | |||
| + | PENDAHULUAN | ||
| + | Sistem pemodelan yang digunakan dalam struktur bangunan ini adalah pemodelan tiga derajat kebebasan (3 DOF). Gambar 1 menunjukkan model struktur bangunan bertingkat yang ditandai dengan adanya perpindahan sebesar x2 dan x3 karena pengaruh beban input gaya eksitasi dari shaking table. Sedangkan untuk pemodelan matematis, diperoleh persamaan dari free body diagram sistem yang akan dianalisa. | ||
| + | |||
| + | |||
| + | [[File:FES1.png|500 px]] | ||
| + | |||
| + | |||
| + | ANALISA | ||
| + | |||
| + | |||
| + | [[File:FES2.png|500 px]] | ||
| + | |||
| + | |||
| + | Untuk free body diagram dan persamaan massa shaking table (M_1) adalah : | ||
| + | |||
| + | |||
| + | [[File:FES3.png|500 px]] | ||
| + | |||
| + | |||
| + | ∑▒〖Fx= M_1 ẍ_1 〗 | ||
| + | -M_1 ẍ_1 (t) - c_1 ẋ_1 (t)- c_(2 ) (ẋ_1- ẋ_2 )(t)- k_1 x_(1 ) (t)-k_2 (x_1- x_2) (t) = - mω^2 r cos〖ω t〗 | ||
| + | M_1 ẍ_1 (t)+ 〖(c〗_1+ c_2) ẋ_1 (t)+〖(k〗_1+k_2) x_(1 ) (t) -c_(2 ) ẋ_2 (t) -k_2 x_2 (t) = mω^2 r cos〖ω t〗 | ||
| + | |||
| + | |||
| + | [[File:FES4.png|500 px]] | ||
| + | |||
| + | |||
| + | ∑▒〖Fx= M_2 ẍ_2 〗 | ||
| + | -M_2 ẍ_2 (t)-c_(3 ) (ẋ_2- ẋ_3 )(t)+c_(2 ) (ẋ_1- ẋ_2)(t)-k_3 (x_2-x_3)(t) + k_2 (x_1-x_2)(t) = 0 | ||
| + | M_2 ẍ_2 (t)-c_(2 ) ẋ_1 (t)+〖(c〗_3+c_(2 )) ẋ_2 (t)-c_(3 ) ẋ_3 (t))- k_2 x_1 (t)+〖(k〗_3+k_2)x_2 (t)-k_3 x_3 (t)=0 | ||
| + | |||
| + | |||
| + | [[File:FES5.png|500 px]] | ||
| + | |||
| + | |||
| + | ∑▒〖Fx= M_3 ẍ_3 〗 | ||
| + | -M_3 ẍ_3 (t)+c_(3 ) (ẋ_2- ẋ_3 )(t)+k_3 (x_2-x_3)(t)= 0 | ||
| + | M_3 ẍ_3 (t)-c_(3 ) ẋ_2 (t)+c_(3 ) ẋ_3 (t)-k_3 x_2 (t)+〖k_3 x〗_3 (t)=0 | ||
| + | |||
| + | |||
| + | [[File:FES6.png|500 px]] | ||
| + | |||
| + | |||
| + | Setelah mendapatkan nilai parameter yang dibutuhkan untuk simulasi, Input yang digunakan yaitu input sinusoidal dengan frekuensi operasi 7 Hz atau 43,982 rad/s. | ||
| + | |||
| + | |||
| + | Untuk menyelesaikan persamaan gerak di atas maka dilakukan penyederhanaan persamaan menjadi 1 persamaan orde 6, dengan mengasumsikan x1 sebagai x, x2 sebagai y, dan x3 sebagai z, sehingga diperoleh persamaan, | ||
| + | z=(c_3 d/dt+k_3 )y/((m_3 d^2/〖dt〗^2 +c_3 d/dt+k_3 ) ) | ||
| + | |||
| + | |||
| + | Persamaan 4 disubtitusikan kepersamaan 2 sehingga didapatkan persamaan, | ||
| + | |||
| + | y=((c_2 m_3 d^3/〖dt〗^3 +(c_2 c_3+k_2 m_3)) d^2/〖dt〗^2 +((c_2 k_3+c_3 k_3 ) d/dt+k_2 k_3 ))/((m_2 m_3 d^4/〖dt〗^4 +(c_3 m_2+c_2 m_3+c_3 m_3 ) d^3/〖dt〗^3 +(k_3 m_2+k_2 m_3+k_3 m_3+c_2 c_3 ) d^2/〖dt〗^2 +(c_2 k_3+c_3 k_2 ) d/dt+k_2 k_3 ) ) | ||
| + | |||
| + | |||
| + | Persamaan 5 disubstitusi ke persamaan 1 dan mensubstitusi nilai c_1,c_2,c_3,k_1,k_2,k_3,m_1,m_2,m_3 sehingga didapatkan persamaan | ||
| + | |||
| + | mω^2 r cosωt=1,15 (d^6 x)/〖dt〗^6 +21,06 (d^5 x)/〖dt〗^5 +4153,74 (d^4 x)/〖dt〗^4 +42436,98 (d^3 x)/〖dt〗^3 +2,4.10^6 (d^2 x)/〖dt〗^2 +2,9.10^6 dx/dt+1,52.10^6 x | ||
| + | |||
| + | |||
| + | Untuk mencari nilai akar-akar dari persamaan di atas maka digunakan matlab untuk mempermudah perhitungan, | ||
| + | |||
| + | |||
| + | p=[1.154 21.059 4153.743 42436.977 2396974.157 2858796.484 151595214.4]; | ||
| + | r=roots(p) | ||
| + | r = | ||
| + | -3.6221 +52.7481i | ||
| + | -3.6221 -52.7481i | ||
| + | -5.5262 +24.9446i | ||
| + | -5.5262 -24.9446i | ||
| + | 0.0239 + 8.4846i | ||
| + | 0.0239 - 8.4846i | ||
| + | |||
| + | |||
| + | Maka didapatkan persamaan gerak berupa, | ||
| + | x=e^(-3,62t) (ASin(52,75t)+BCos(52,75t))+e^(-5,53t) (CSin(24,94t)+DCos(24,94t))+e^(0,024t) (ESin(8,48t)+FCos(8,48t))+GSin(43,982t)+HCos(43,982t) | ||
| + | |||
| + | |||
| + | Lalu dengan mengasumsikan nilai konstanta, | ||
| + | |||
| + | |||
| + | A=-0.0005 | ||
| + | B=0.0001 | ||
| + | C=0.0001 | ||
| + | D=-0.0002 | ||
| + | E=0.00032 | ||
| + | F=-0.009 | ||
| + | G=0.00008 | ||
| + | H=0.00001 | ||
| + | |||
| + | |||
| + | Maka dengan menggunakan software MATLAB dapat dibuat grafik posisi terhadap waktu. Berikut coding yang menjadi input dalam MATLAB: | ||
| + | |||
| + | |||
| + | syms x t A B C D E F | ||
| + | A=-0.0005 | ||
| + | B=0.0001 | ||
| + | C=0.0001 | ||
| + | D=-0.0002 | ||
| + | E=0.00032 | ||
| + | F=-0.009 | ||
| + | G=0.00008 | ||
| + | H=0.00001 | ||
| + | |||
| + | t=(1:100)/10 | ||
| + | x1 = exp(-3.62*t)*(A*sin(52.75*t) + B*cos(52.75*t)) + exp(5.53*t)*(C*sin(24.94*t) + D*cos(24.94*t)) + exp(0.024*t)*(E*sin(8.48*t) + F*cos(8.48*t)) + G*sin(43.982*t) + H*cos(43.982*t) | ||
| + | % Plot results | ||
| + | subplot(1,1,1) | ||
| + | hold on; | ||
| + | plot(t',x1,'r') | ||
| + | ylabel('Position (m)') | ||
| + | |||
| + | |||
| + | [[File:FES7.png|500 px]] | ||
| + | |||
| + | |||
| + | Grafik di atas menunjukan pengaruh getaran pada bagian bawah struktur pemodelan bangunan di mana perubahan arah gerak pada bagian bawah struktur membentuk pola sinusoidal yang menandakan adanya gerak bolak-balik pada struktur tersebut. | ||
| + | |||
| + | |||
| + | KESIMPULAN | ||
| + | Dalam permasalahan analisis gerak (perubahan arah, kecepatan dan percepatan) dapat dilakukan dengan metode lain berupa FES, namun pada artikel ini pemodelan FES belum dilakukan. Artikel ini hanya membahan mass-spring (MS) model yang terjadi pada suatu sistem pemodelan bangunan yang diberikan getaran. Sehingga dapat dilihat perilaku gerak bangunan sebagai respon dari adanya getaran yang diberikan. | ||
| + | |||
| + | |||
| + | REFERENSI | ||
| + | • Syaldiles Putri Indahdinata, Analisis Pengaruh Perubahan Cross Sectional Area Dan Posisi Peletakan Tuned Liquid Column Damper Terhadap Respon Dinamis Model Struktur Bangunan Bertingkat, Departemen Teknik Mesin FTI-ITS Surabaya, 2018. | ||
| + | |||
| + | |||
| + | =Diskusi Kelas= | ||
| + | |||
| + | |||
| + | Pertanyaan: | ||
| + | |||
| + | |||
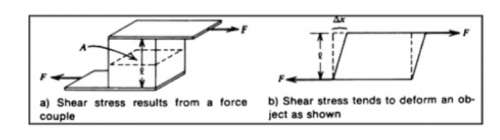
| + | Ketika nilai A dinaikan maka nilai F menjadi besar tetapi mengapa pressure loss turun ketika A semakin besar? | ||
| + | |||
| + | τ_xy A=F | ||
| + | |||
| + | ∆p= f ρ L/D V^2/2 | ||
| + | |||
| + | |||
| + | Jawab: | ||
| + | |||
| + | Dalam mekanik benda padat shear stress didefinisikan sebagai rasio antara gaya yang berkerja terhadap luasan yang dikenakan gaya tersebut, yang didefinisikan sebagai, | ||
| + | |||
| + | |||
| + | τ_xy=F/A | ||
| + | |||
| + | |||
| + | [[File:TK1.PNG|500 px]] | ||
| + | |||
| + | |||
| + | Ketika gaya diaplikasikan pada benda padat maka, benda padat mengalami deformasi atau bending namun dalam batas ketika gaya diberikan, hal ini berbeda dengan fluida, ketika fluida diberikan gaya maka fluida tersebut akan terdeformasi secara terus menerus, sehingga persamaan yang digunakan untuk menghitung tegangan geser pun berbeda, dalam mekanika fluida persamaan tegangan geser dapat dituliskan sebagai, | ||
| + | |||
| + | |||
| + | τ_xy=μ du/dy | ||
| + | |||
| + | |||
| + | [[File:TK2.PNG|300 px]] | ||
| + | |||
| + | |||
| + | di mana du/dy merupakan perubahan kecepatan terhadap perubahan jarak antara dua sisi plat. | ||
| + | |||
| + | Maka ketika nilai A (luasan) dalam pipa diperbesar maka akan menurunkan nilai u (kecepatan fluida) sesuai persamaan kontinuitas, | ||
| + | |||
| + | |||
| + | A_1 V_1=A_2 V_2 | ||
| + | |||
| + | |||
| + | Selain itu peningkatan A akan memperbesar nilai h (jarak antar 2 plat) | ||
| + | |||
| + | Sehingga akan menurunkan nilai τ_xy (shear stress) yang menyebabkan penurunan ∆p (pressure drop). | ||
| + | |||
| + | =UAS Komputasi Teknik= | ||
| + | |||
| + | [[File:UAS KompTek_page-0001.jpg|500 px]] | ||
| + | [[File:UAS_KompTek_page-0002.jpg|500 px]] | ||
| + | [[File:UAS_KompTek_page-0003.jpg|500 px]] | ||
| + | [[File:UAS_KompTek_page-0004.jpg|500 px]] | ||
| + | [[File:UAS_KompTek_page-0005.jpg|500 px]] | ||
Latest revision as of 19:30, 26 December 2021
Contents
Perkenalan Penulis
Nama : Kania Amelia Safitri
Prodi : Konversi Energi
Perkenalan penulis dengan komputasi teknik berawal dari kegiatan perkuliahan penulis saat menempuh gelar sarjana, penulis diajarkan bagaimana menggunakan beberapa software yang dapat membantu dalam menganalisis dan mengolah data, seperti matlab, minitab dan excel.
Pengetahuan Penulis tentang Komputasi Teknik
Semasa kuliah komputasi teknik digunakan untuk menyelesaikan permasalahan optimasi dalam bidang keteknikan dengan menggunakan matlab, serta untuk mempermudah analisa numerik dari suatu sebaran data di dalam excel, selain itu aplikasi minitab juga digunakan untuk menganalisis nilai statistik dari sebaran data yang dimiliki.
Matlab digunakan penulis untuk menunjukan nilai optimum dari suatu pemodelan matematika, dimana pemodelan matematika tersebut dirumuskan dari permasalahan yang ada di lapangan. Sebagai contoh, terdapat dua gudang penyimpanan kayu yang dapat dituliskan sebagai gudang A dan B dimana jarak gudang tersebut dengan tempat pemotongan masing-masing sejauh 10 km dan 8 km biaya pengantaran batang kayu perkilometer adalah $2, serta ongkos pemotongan kayu perbatang sebesar $12. Gudang A dapat menampung sekitar 200 batang kayu dan gudang B dapat menampung sekitar 125 batang kayu. Jika perhari hanya dapat dilakukan pemotongan sebanyak 300-310 batang kayu maka berapa biaya minimum yang harus dikeluarkan untuk mendapatkan hasil potongan kayu maksimum perbulannya?
Persoalan seperti di atas dapat diselesaikan dengan pemodelan matematika, lalu dilanjutkan dengan penggunan aplikasi mathlab, meskipun dapat dilakukan perhitungan manual namun penggunaan mathlab dapat membantu menyelesaikan persoalan tersebut dengan cepat.
Penulis menggunakan excel dalam proses pencarian nilai statistik suatu data atau mencari nilai dari suatu persamaan melalui suatu proses iterasi, selain ini excel juga digunakan penulis untuk mengolah data baik eksperimen maupun noneksperimen untuk membantu penulis dalam melihat tren yang terjadi, dengan membuat grafik dan trendline dari sebaran data yang dimiliki. Sebagai contoh, penulis memiliki data eksperimen dari pompa sentrifugal, dimana penulis mendapatkan nilai head dari pompa pada sisisuction dan discharge, lalu didapatkan data kenaikan head pompa. Data eksperimen yang ada dibandingkan dengan data yang tertulis pada katalog pompa, dengan bantuan excel penulis dapat membandingkan kedua data tersebut dengan mudah.
Penggunaan minitab sangat membantu dalam proses analisa statistik, cukup banyak tools dalam aplikasi minitab yang dapat digunakan untuk melakukan analisa statistik dengan cukup mudah, sebagai contoh untuk membandingkan suatu proses pembuatan suatu barang dengan bahan yang sama namun proses yang berbeda kita dapat melakukan analisa statistik untuk melihat sejauh apa perbedaan dari hasil yang didapatkan dalam proses tersebut, dengan minitab kita juga dapat mengetahui besar data error yang terjadi dalam suatu sistem produksi, dengan mengetahui sebaran data dan reability pada suatu proses produksi.
Gambaran di atas merupakan pengetahuan yang penulis dapatkan mengenai komputasi teknik, namun dengan berjalannya waktu penulis perlu melakukan review kembali mengenai pelajaran yang telah didapatkan, agar penulis dengan mudah mengaplikasikan kembali ilmu yang telah didapatkan. Penulis menilai kemampuan penulis berada pada taraf cukup dalam bidang komputasi teknik, besar harapan dengan adanya pembelajaran lebih lanjut mengenai komputasi teknik, penulis dapat mengembangkan kemampuan penulis menjadi lebih baik dari sebelumnya.
Draft Paper Komputasi Teknik
Studi Eksperimen Karakteristik Pompa Sentrifugal Single Stage dan Cussons Friction Loss Apparatus
ABSTRAK
Air menjadi kebutuhan primer bagi kehidupan manusia, karena kegunaannya yang penting maka dibangunlah sistem terintegrasi yang terdiri dari pompa dan pipa untuk mendistribusikan air. Fenomena rugi energi ditemukan pada proses pendistribusian air menggunakan pompa dan pipa, untuk mengetahui fenomena rugi energi yang terjadi maka dilakukan uji eksperimen pada suatu instalasi perpipaan. Laboratorium mekanika dan mesin fluida, memiliki alat uji eksperimen berupa CUSSONS friction loss in pipe apparatus dengan pompa sentrifugal single stage untuk mempelajari fenomena rugi energi yang terjadi pada instalasi perpipaan. Alat uji ini tersusun dari dua macam material pipa yaitu PVC dan acrylic, dengan variasi diameter pipa sebesar 0.75 dan 1.0inch, flow meters berupa venturi dan orifice¸ fitting perpipaan berupa elbow 45o, long radius elbow 90o, short radius elbow 90o, valve berupa ball valve dan pompa yang terhubung dengan NEWMAN electric motor yang memiliki daya sebesar 1.5 hp dan putaran motor sebesar 2850 RPM. Pressure drop pada instalasi perpipaan diukur menggunakan manometer raksa, kenaikan tekanan pompa diukur dengan pressure gauge, dan arus serta tegangan listrik motor pompa diukur menggunakan tang amper. Debit aliran instalasi divariasikan antara 10-55 l/min dengan kenaikan debit sebesar 5 l/min untuk pengambilan data pada pipa lurus line I, fitting dan ball valve, pada pipa lurus line II variasi debit hanya mencapai 40 l/min, sedangkan variasi debit aliran untuk flow meters adalah 10-30 l/min dengan kenaikan debit sebesar 2 l/min untuk orifice dan 4 l/min untuk venturi. Berdasarkan data hasil uji eksperimen didapatkan nilai loss coefficient 〖(K〗_l) untuk K_90= 0.58, untuk K_45= 0.38, K_BV= 0.62, dan K_LRE= 0.611. Kekasaran relatif (e/D) pada pipa line I= 0.0043 dan pada line II = 0.024. Nilai coefficient of discharge (C_d) pada flow meter jenis venturi C_v= 0.91 dan C_o= 0.72 pada debit maksimum. Efisiensi pompa (η_p) maksimum sebesar 27.1% pada saat head pompa=18.79 m. Validasi data dilakukan dengan menginput data yang telah didapatkan ke dalam software pipe flow expert sehingga didapatkan perbandingan hasil perhitungan secara manual dan software.
Kata Kunci—Pressure drop, fitting, flow meters, pompa.
PENDAHULUAN
DUNIA industri saat ini memiliki peranan penting dalam menjalankan roda kehidupan manusia, salah satu contohnya adalah industri pendistribusian fluida yang menggunakan sistem perpipaan, untuk mendapatkan sistem perpipaan yang efektif maka dibutuhkan data-data yang membantu dalam proses desain sistem perpipaan, seperti jenis fluida yang dialirkan, kapasitas aliran dan jarak yang ditempuh fluida, selain itu dibutuhkan pula estimasi dari data rugi energi yang terjadi di sepanjang aliran fluida karena rugi energi tidak mungkin dapat dihindari pada proses pendistribusian fluida. Salah satu penyebab rugi energi pada instalasi perpipaan adalah gesekan yang terjadi antara fluida yang mengalir dengan permukaan pipa, rugi energi jenis ini disebut dengan major losses, terdapat pula rugi energi yang terjadi akibat adanya pemasangan fitting, valve, dan flow meters rugi energi ni disebut dengan minor losses. Estimasi rugi energi yang terjadi pada instalasi perpipaan dapat membantu dalam mendapatkan pompa yang cocok dengan instalasi perpipaan. Melalui gambaran di atas penulis bermaksud melakukan eksperimen pada alat uji CUSSONS friction loss in pipe apparatus di laboratorium mekanika dan mesin fluida. Sebelumnya uji ekperimen untuk mengetahui fenomena yang terjadi pada instalasi perpipaan tersebut telah diuji oleh Dahmani [1] dan Sihombing [2], namun dalam pengujian yang telah dilakukan ditemukan kendala pada saat proses pembacaan data pada alat ukur manometer raksa dikarenakan perubahan tekanan yang terjadi pada pipa lurus line I cukup kecil, sehingga menurunkan akurasi data yang didapatkan. Setelah mengetahui kendala yang ada penulis ingin melakukan uji eksperimen dengan mengganti instalasi pada line I yang semula menggunakan diameter pipa sebesar 3/2inch menjadi pipa dengan diameter 1 inch. Hasil dari uji eksperimen ini kemudian akan dibandingkan dengan hasil uji eksperimen yang telah dilakukan oleh Dahmani [1] dan Sihombing [2] untuk melihat apakah terjadi perbaikan data yang dihasilkan setelah dilakukan pergantian peralatan pada alat uji eksperimen.
URAIAN PENELITIAN
A. Peralatan Uji Eksperimen
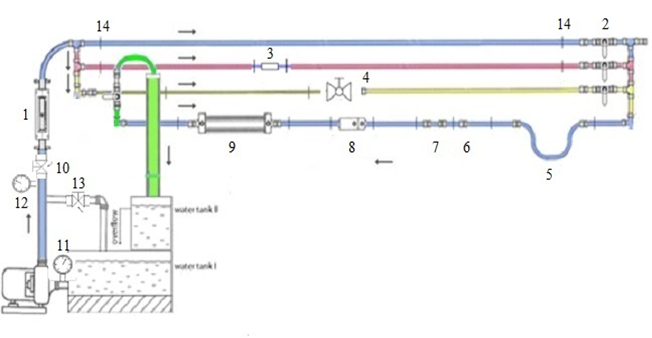
Evaluasi awal peralatan uji terintegrasi menjadi CUSSONS friction loss in pipe apparatus dan water circulating unit. CUSSONS friction loss in pipe apparatus terdiri dari empat line instalasi pipa dengan variasi diameter sebesar 1 inch dan 0.75 inch, material pipa yang digunakan berupa PVC dan acrylic, terdapat instalasi flow meters jenis venturi dan orifice, ball valve, serta fitting perpipaan berupa long radius elbow 90°, elbow 90°, dan elbow 45°. Water circulating unit terdiri dari pompa sentrifugal single stage, NEWMAN electric motor dan reservoir. Sekma peralatan uji dari CUSSONS friction loss in pipe apparatus ditunjukan oleh gambar. 1.
Gambar 1. Ilustrasi instalasi alat uji CUSSONS friction loss in pipe apparatus
Keterangan gambar 1:
1. Rotameter Fisher 2000
2. Gate Valve
3. Orifice
4. Ball valve
5. Long Radius Elbow 90º
6. Standard Elbow 90°
7. Elbow 45º
8. Venturi meter
9. Sudden Contraction dan Sudden Enlargement
10. Gate valve discharge
11. Pressure gauge suction
12. Pressure gauge discharge
13. Gate valve bypass
14. Pressure tap
Motor yang digunakan pada uji eksperimen ini adalah NEWMAN Electric Motor dengan spesifikasi daya sebesar 1.5 hp dan kecepatan putar sebesar 2850 RPM.
Peralatan alat ukur yang digunakan pada eksperimen ini berupa manometer raksa ilustrasi ditunjukkan pada gambar 3, pressure gauge, dan tang amper. Fungsi dari manometer raksa adalah untuk mengetahui perubahan tekanan yang terjadi pada pipa lurus, fitting, dan flowmeter dengan menghubungkan manometer raksa pada pressure tap. Selisih ketinggian pada muka air raksa menggambarkan besar perubahan tekanan yang terjadi. Perubahan tekanan yang terjadi dapat dihitung melalui persamaan 2.1.
Δp=(〖SG〗_Hg )ρgΔh , (2.1)
dimana: Δp = perubahan tekanan (Pa)
〖SG〗_Hg = specific gravity of Mercury = 13.6
ρ = massa jenis fluida (kg/m^3)
g = percepatan gravitasi (m/s^2)
Δh = selisih ketinggian air raksa (m).
Dengan mengetahui nilai pressure drop pada fitting, flow meters dan pipa lurus kita dapat menghitung nilai dari coefficient loss 〖(K〗_l), coefficient of discharge (C_d), dan faktor gesekan (f).
K_l=2 ∆p/(ρV ̅^2 ), (2.2)
C_d = (Q √(ρ(1- β^4)))/(A√2∆p) , (2.3)
f=2 D/L ∆p/(ρV ̅^2 ) , (2.4)
dimana:
K_l = loss coefficient (tak berdimensi)
f = faktor gesekan (tak berdimensi)
D = diameter pipa (m)
d = diameter leher pada flow meters (m)
β = d/D (tak berdimensi)
L = panjang pipa yang dilalui oleh fluida (m)
∆p = perbedaan tekanan (Pa)
ρ = massa jenis fluida (kg/m^3)
V ̅ = kecepatan rata-rata aliran fluida (m/s)
C_d = coefficient of discharge (tak berdimensi)
Q = kapasitas aliran fluida (m^3/s)
A = luasan leher pada flow meters (m^2).
Pressure gauge digunakan untuk mengukur perubahan tekanan yang terjadi pada sisi suction dan discharge pompa, dari data tersebut dapat diolah menjadi data head pompa 〖(H〗_p). Total H_p dihitung melalui persamaan 2.2.
H_p=(p_2- p_1)/γ+(V ̅_2^2- V ̅_1^2)/2g+z_2-z_1, (2.5)
dimana:
H_p = head pompa (m)
(p_2- p_1)/γ = selisih pressure head (m)
(V ̅_2^2- V ̅_1^2)/2g = selisih dynamic head (m)
z_2-z_1 = selisih static head (m).
Daya hidrolik pompa ((W) ̇_hp ) ditentukan setelah nilai head pompa 〖(H〗_p) didapatkan, berikut persamaan yang digunakan untuk menghitung daya hidrolik pada pompa.
W ̇_hp= γQH_p= ρgQH_p, (2.6)
dimana:
W ̇_hp = daya hidrolik pompa (Watt)
γ = berat jenis fluida (kg/m^2 s^2)
ρ = massa jenis fluida (kg/m^3)
g = percepatan gravitasi (m/s^2)
Q = kapasitas pompa (m^3/s)
H_p = head pompa (m).
Tang amper digunakan untuk mengetahui arus dan tegangan listrik yang mengalir pada motor pompa, dengan mengetahui nilai dari tegangan dan arus listrik pada motor pompa, kita dapat mengetahui nilai daya poros pompa daya poros pompa 〖(W ̇〗_sh).
W ̇_sh= η_m .W ̇_e (2.7)
dimana:
W ̇_sh = daya poros pompa (Watt)
η_m = efisiensi kerja motor (tak berdimensi)
W ̇_e = daya listrik (electrical power) (Watt).
Nilai efisiensi kerja motor pompa (η_m) pada rumusan diatas didapatkan dengan menggunakan persamaan 2.8.
η_m=(P_r×N)/W ̇_e , (2.8)
dimana:
P_r = daya motor pada name plate (Watt)
N = output persentase nilai daya (tak berdimensi)
Output persentase nilai daya merupakan perbandingan antara nilai arus (I) dan tegangan listrik (V) pada saat pompa dijalankan terhadap arus (I_r) dan tegangan listrik (V_r) yang tertera pada name plate motor.
N=I/I_r ×V/V_r ,
dimana:
I_r = arus listrik pada name plate (Amper)
V_r = tegangan listrik pada name plate (Volt)
I_ = arus listirk saat pompa dijalankan (Amper)
V_ = tegangan listrik saat pompa dijalanakan (Volt).
Sehingga, didapatkan nilai dari daya poros motor ((W) ̇_sh), setelah didapatkan W ̇_sh, efisiensi pompa 〖(η〗_p) dapat ditentukan. Efisiensi pompa 〖(η〗_p) merupakan perbandingan antara daya yang diberikan pompa kepada fluida terhadap daya yang diberikan motor listrik kepada pompa.
η_p= W ̇_hp/W ̇_sh , (2.9)
dimana:
η_p = efisiensi pompa (tak berdimensi)
W ̇_hp = daya hidrolik pompa (Watt)
W ̇_sh = daya poros pompa (Watt).
HASIL DAN ANALISA
Quiz Komputasi Teknik
Initial Thingking
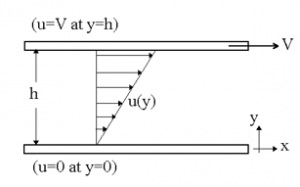
Sebuah pendulum bergerak dengan kondisi awal; u (kecepatan) sebesar 4 m/s, v (percepatan) sebesar 0 m/s, dan ω (frekuensi sudut) yang konstan sebesar 5 rad/s, untuk mengetahui gerak osilasi dari pendulum maka metode numerik digunakan untuk mempercepat dan mempermudah proses perhitungan, berikut persamaan yang digunakaan dalam metode numerik,
u^(n+1)= u^n+ (∆t v)^n
v^(n+1)= v^n- ∆t ω^2 u^n
∆t (perubahan waktu) diatur sebesar 0.05 s, lalu dengan memasukan nilai ω,u,v, dan ∆t yang telah diberikan sebelumnya dan dilakukan iterasi hingga detik ke 5 sehingga, akan didapatkan grafik osilasi yang akan ditunjukan pada grafik 1,2,3 dan 4.
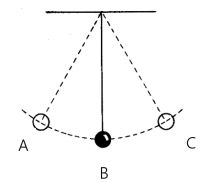
Pemodelan
Pendulum bergerak dari posisi B menuju ke A lalu berosilasi secara terus menerus (dengan mengasumsikan tidak adanya gaya gesekan yang terjadi di antara pendulum dengan udara). Secara analitikal nilai kecepatan dan percepatan pendulum dapat diketahui melalui persamaan;
u= ωA cos(ωt)
v= -ω^2 A sin(ωt)
dengan mengasumsikan nilai amplitudo A sebesar 1 maka, perumusan kecepatan dan percepatan menjadi;
u= ω cos(ωt)
v= -ω^2 sin(ωt)
Persamaan ini akan digunakan dalam proses verifikasi dari penggunaan metode numerik untuk mengitung besar kecepatan dan percepatan pada pendulum.
Perhitungan Numerik
Terdapat pada lampiran
Verifikasi dan Pemaknaan Hasil
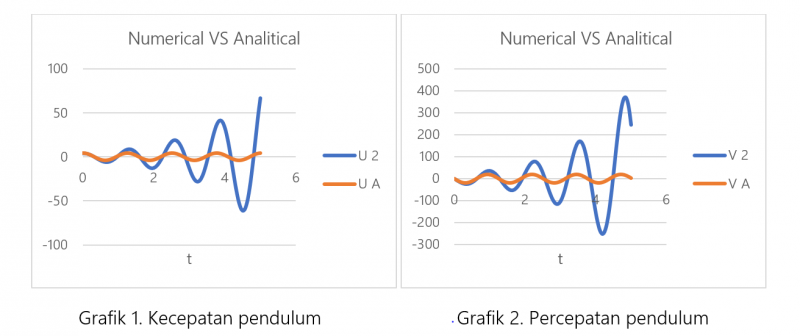
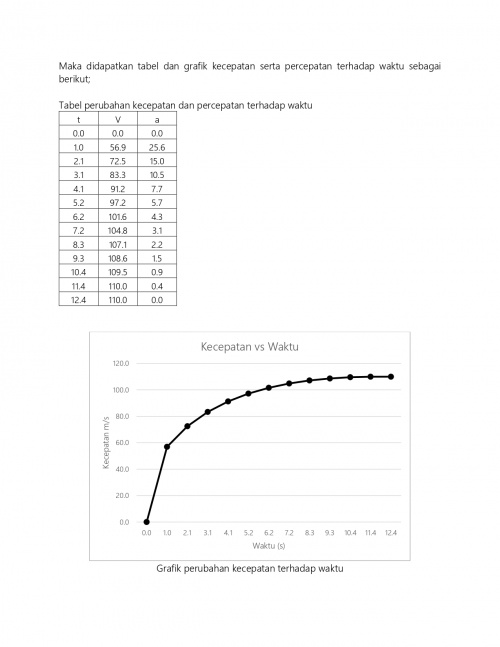
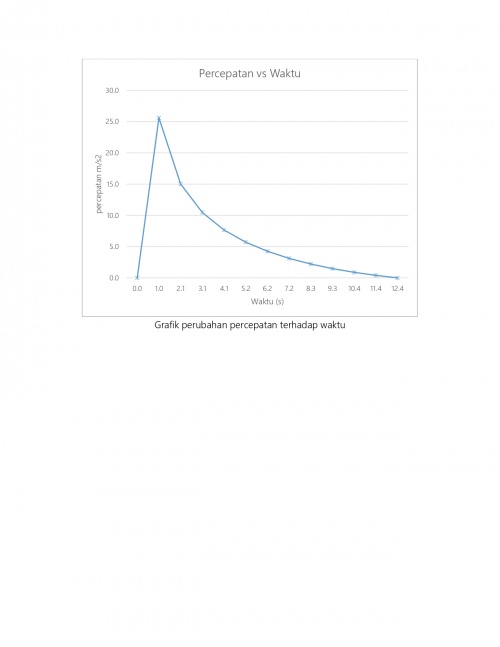
Proses verifikasi dilakukan dengan membandingkan data-data hasil numerik dengan data-data hasil analitikal berdasarkan hasil perhitungan menggunakan excel maka didapatkan grafik osilasi dari gerakkan yang dihasilkan oleh pendulum yang ditunjukkan oleh grafik 1 dan 2, dimana grafik 1 menunjukan kecepatan getaran pendulum sedangkan grafik 2 menunjukan percepatan getaran pendulum.
Grafik 1 dan 2 menunjukan perbedaan hasil antara data perhitungan metode numerik dengan analisis, data hasil perhitungan dengan menggunakan metode analisis ditunjukan oleh garis berwarna merah baik kecepatan maupun percepatan menunjukan trend osilasi yang stabil dari pergerakan pada 0 s hingga 5s, sedangkan untuk metode numerik menghasilkan trend yang tidak selaras dengan data hasil perhitungan analitik, sehingga dapat disimpulkan bahwa persamaan yang digunakan tidak terferifikasi, untuk itu diperlukan suatu persaamaan lain.
Penggunaan magic fix pada metode numerik
Dilakukanya modifikasi pada persamaan sebelumnya dengan mengganti nilai u^n pada persamaan v^(n+1)= v^n- ∆t ω^2 u^n dengan u^(n+1), sehingga persamaan dapat dituliskan kembali menjadi;
v^(n+1)= v^n- ∆t ω^2 u^(n+1)
dan untuk persamaan kecepatan getaran tetap digunakan persamaan
u^(n+1)= u^n+ (∆t v)^n
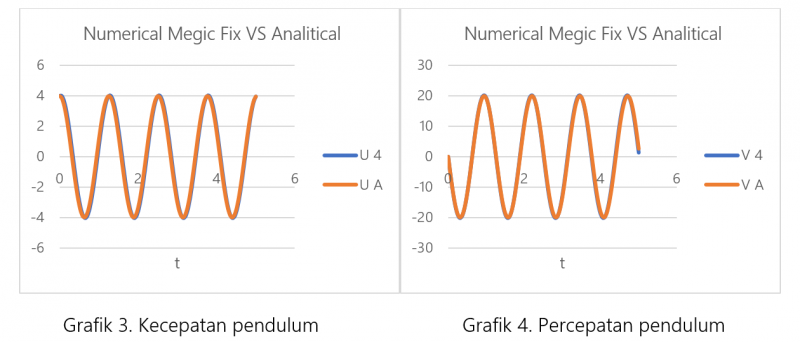
Sehingga, didapatkan grafik antara metode numerik dan analitikal untuk kecepatan dan percepatan sebagai berikut,
Terlihat pada grafik 3 dan 4 bahwasannya data-data hasil perhitungan dengan metode numerik memiliki kemiripan yang sangat tinggi dengan hasil analitik, dimana hasil keduanya saliang berdempetan sehingga dapat disimpulkan bahwasanya metode numerik yang dilakukan untuk menyelesaikan persoalaan ini terverifikasi.
Lampiran
Artikel Oscillating 1-D Dynamic System
Tugas Kelompok:
Kania Amelia Safitri (1906324113)
Evi Elisa Ambarita (1906324044)
Dieter Rahmadiawan (1906324031)
Chandra R.M. Simanjuntak (1906324012)
1. Pendahuluan
Artikel ini akan membahas penyelesaian permasalahan oscillating 1-D dynamic system pada system damping sesuai gambar di bawah. Pada system di bawah terdapat sebuah massa yang dihubungkan dengan 3 spring, dan 1 dashpot. System tersebut fix pada 2 boundary sisi kiri dan kanan.
Penyelesaian dari permasalahan tersebut akan dilakukan dengan 3 metode, yang kemudian akan dibandingkan hasil dari perhitungan pada tiap metode tersebut. Metode yang digunakan yaitu: analitikal, numerik, dan simulasi. Pada metode analitikal dilakukan tinjauan gaya aksi – reaksi pada free body diagram (FBD) yang muncul dari eksitasi yang diberikan. Kemudian untuk penyelesaian metode numerik akan dilakukan iterasi dengan bantuan software Microsoft Excel menggunakan Forward Euler. Sedangkan untuk proses simulasi akan dilakukan dengan bantuan software MATLAB.
2. Metode Penyelesaian
2.1 Metode Analitikal
Free Body Diagram (FBD)
Tinjauan Massa
Analisa FBD:
0-k_1 x-c_1 (dx/dt+dy/dt)-k_2 (x+y)=m (d^2 x)/(dt^2)
Tinjauan Titik (diantara c1, k2, dan k3)
Analisa FBD:
0-c_1(dx/dt+dy/dt)-k_2 (x+y)-k_3 y=0 (d^2 y)/(dt^2)
Diketahui: m=1kg c_1=1 N/m
k_1=1 N/m^2
k_2=2 N/m^2
k_3=3 N/m^2
dx/dt=x ̇
dy/dt=y ̇
(d^2 x)/(dt^2 )=x ̈
(d^2 y)/(dt^2 )=y ̈
Maka persamaan 1 dan 2 dapat dituliskaan kembali menjadi:
Persamaan 1,
0-x-(x ̇+y ̇ )-2 (x+y)=x ̈
-2y-y ̇=3x+x ̇+x ̈
Persamaan 2,
0-(x ̇+y ̇ )-2(x+y)-3y=0
-y ̇-5y=2x+x ̇
Penyelesaian
Asumsi
x ̇ =z subtitusi ke persamaan 3 dan 4 maka;
z ̇ =-(3x+2y+y+z)
y ̇ =-(2x+5y+z)
Karena pada persamaan 5 masih terdapat y ̇ maka subtitusi persamaan 6 ke persamaan 5, sehingga didapatkan nilai z ̇ sebagai berikut;
z ̇ =-x+3y
Penyelesaian menggunakan matrix;
Di mana nilai g_x (t), g_y (t), g_z (t)=0 (homogen)
sehingga
{λ^2 (λ+5)+0+((-1)(2)(-3))}-{(-1)(λ+5)+λ(-3)(1)+0}=0 λ^3+5λ^2+4λ+11=0
Maka didapatkan nilai λ sebesar
λ_1=-4.65
λ_2=-0.175±1.52i
Sehingga didapatkan persamaan
x_h=C_1 e^(-4.65t)+e^(-0.175t)(C_2sin[(1.52t)+C_3cos(1.52t)]
Jika diasumsikan nilai C_1,C_2,dan C_3 adalah 1, 2 dan 3 maka;
x_h=e^(-4.65t)+e^(-0.175t)[2sin(1.52t)+3cos(1.52t)]
Nilai x untuk t = 0 s, t = 1 s, dan t = 10 s adalah,
x_0= e^(-4.65(0))+e^(-0.175(0))(2sin(1.52(0))+3cos(1.52(0))
x_0=4 m
x_1= e^(-4.65(1))+ e^(-0.175(1))(2sin(1.52(1))+3cos(1.52(1))
x_1=1.81 m
x_10= e^(-4.65(10))+ e^(-0.175(10))(2sin(1.52(10))+3cos(1.52(10))
x_10=-0,29m
Mencari nilai y_h dengan mensubtitusi nilai x_h ke dalam persamaan
z ̇ =-x+3y, di mana nilai z ̇ = x ̈.
Mencari nilai x ̇ ;
x_h= e^(-4.65t)+e^(-0.175t)[2sin(1.52t)+3cos(1.52t)]
x ̇ =dx/dt=d/dt [e^(-4.65t)+e^(-0.175t){2sin(1.52t)+3cos(1.52t)}]
d/dt [e^(-4.65t)]= -4.65e^(-4.65t)
d/dt [e^(-0.175t) {2sin(1.52t)+3cos(1.52t)}]=-4.91e^(-0.175t)sin(1.52t)+2.515e^(-0.175t)cos(1.52t)
x ̇ =-4.65e^(-4.65t)-4.91e^(-0.175t)sin(1.52t)+2.515e^(-0.175t)cos(1.52t)
Nilai x ̇ untuk t = 0 s, t = 1 s, dan t = 10 s adalah
x ̇_0=-4.65e^0-4.91e^0 sin(0)+2.515e^0cos(0)
x ̇_0 =-2.135 m/s
x ̇_1=-4.65e^(-4.65(1))-4.91e^(-0.175(1))sin(1.52(1))+2.515e^(-0.175(1))cos(1.52(1))
x ̇_1 =-4.05 m/s
x ̇_10=-4.65e^(-4.65(10))-4.91e^(-0.175(10))sin(1.52(10))+2.515e^(-0.175(10))cos(1.52(10))
x ̇_10 =-0.8 m/s
Mencari nilai x ̈ ;
x ̈ =dx ̇ /dt=d/dt[-4.65e^(-4.65t)-4.91e^(-0.175t)sin(1.52t)+2.515e^(-0.175t)cos(1.52t)]
d/dt[4.65e^(-4.65t)]=-21.62e^(-4.65t)
d/dt[4.91e^(-0.175t)sin(1.52t)]=4.91(-0.175e^(-0.175t)sin(1.52t)+1.52e^(-0.175t)cos(1.52t)
d/dt [2.515e^(-0.175t)cos(1.52t)]=2.515(-0.175e^(-0.175t)cos(1.52t)-1.52e^(-0.175t)sin(1.52t))
x ̈ =21.62e^(-4.65t)-4.91(-0.175e^(-0.175t)sin(1.52t)+1.52e^(-0.175t) cos(1.52t)+2.515(-0.175e^(-0.175t)cos(1.52t)-1.52e^(-0.175t)sin(1.52t))
Persamaan x ̈ di atas dapat disederhanakan menjadi;
x ̈ _h=21.62e^(-4.65t)-2.96e^(-0.175t)sin(1.52t)-7.9e^(-0.175t)cos(1.52t)
Nilai x ̈ untuk t = 0 s, t = 1 s, dan t = 10 s adalah
x ̈ _0=21.62e^0-2.96e^0 sin(0)-7.9e^0 cos(0)
x ̈ _0=13.72 m/s^2
x ̈ _1=21.62e^(-4.65t)-2.96e^(-0.175t) sin(1.52t)-7.9e^(-0.175t)cos(1.52t)
x ̈ _1=-2.61 m/s^2
x ̈ _10=21.62e^(-4.65(10))-2.96e^(-0.175(10))sin(1.52(10)-7.9e^(-0.175(10))cos(1.52(10))
x ̈ _10=0.95 m/s^2
Mencari nilai y;
x ̈ =-x+3y
y =(x ̈ +x)/3
y_h =1/3 [21.62e^(-4.65t)-2.96e^(-0.175t)sin(1.52t)-7.9e^(-0.175t)cos(1.52t)+ e^(-4.65t)+ e^(-0.175t)(2sin(1.52t)+3 cos(1.52t))]
Persamaan y_h dapat disederhanakan menjadi;
y_h=1/3[22.62e^(-4.65t)-e^(-0.175t)(0.96sin(1.52t)+4.9cos(1.52t))]
Nilai y untuk t = 0 s, t = 1 s, dan t = 10 s adalah
y_0= 1/3 [22.62e^(-4.65(0))-e^(-0.175(0))(0.96 sin(0)+4.9 cos(0))]
y_0= 5.9 m
y_1= 1/3 [22.62e^(-4.65(1))- e^(-0.175(1)) (0.96 sin(1.52)+4.9 cos(1.52))]
y_1= -0.27 m
y_10= 1/3 [22.62e^(-4.65(10))- e^(-0.175(10)) (0.96 sin(15.2)+4.9 cos(15.2))]
y_10= -0.22 m
Mencari nilai y ̇ ;
y ̇ =dy/dt=d/dt {1/3 [22.62e^(-4.65t)- e^(-0.175t)(0.96sin(1.52t)+4.9cos(1.52t))]}
d/dt [22.62e^(-4.65t)]=-105.18e^(-4.65t)
d/dt [e^(-0.175t)(0.96 sin(1.52t)+4.9 cos(1.52t))]=-7.61e^(-0.175t)sin(1.52t)+0.6e^(-0.175t)cos(1.52t)
y ̇=1/3 [-105.18e^(-4.65t)+7.61e^(-0.175t)sin(1.52t)-0.6e^(-0.175t)cos(1.52t)]
Nilai y ̇ ketika t = 0 s, t = 1 s, dan t = 10 s adalah
y ̇_0=1/3 [-105.18e^0+7.61e^0sin(0)-0.6e^0cos(0)]
y ̇ _0= -35.26 m/s
y ̇ _1= 1/3 [-105.18e^(-4.65(1))+7.61e^(-0.175(1))sin(1.52(1))-0.6e^(-0.175(1)) cos(1.52(1))]
y ̇ _1=1.78 m/s
y ̇_10= 1/3 [-105.18e^(-4.65(10))+7.61e^(-0.175(10))sin(1.52(10))-0.6e^(-0.175(10))cos(1.52(10))]
y ̇ _10=0.24 m/s
2.2 Metode Numerik
Metode ini dilakukan dengan menggunakan software Microsoft Excel. Parameter input yang harus diketahui yaitu x pada t = 0 s, y pada t = 0 s, dan selisih penambahan waktu (∆t). Parameter input x dan y ini dapat juga disebut dengan initial condition. Lalu kemudian dilakukan iterasi sesuai dengan ∆t sampai waktu yang ditentukan. Nilai parameter input tersebut didapat dengan cara analitis seperti sudah disebut di atas, yaitu x_((t=0))=4 m; y_((t=0))=5.9 m; dan selisih waktu ∆t=0.1 second.
Seperti sudah disebutkan sebelumnya bahwa penyelesaiannya menggunakan Forward Euler, yaitu sebagai berikut:
x^(n+1)=x^n+x ̇^n.∆t
Dimana x ̇ pada t = 0 s menggunakan persamaan
y^(n+1)=y^n+y ̇^n.∆t
Dimana y ̇ menggunakan persamaan
x^(n+1)=x ̇^n+x ̈.∆t
Dimana x ̈=z ̇ menggunakan persamaan
2.3 Simulasi
Simulasi dilakukan dengan bantuan software MATLAB. Adapun agar simulasi dapat berjalan, maka perlu diberikan input coding pada software MATLAB yang isinya sebagai berikut.
% Calculates the position, velocity, and acceleration as a function of time
% of a system of carts connected by springs and dashpots. Euler's Method is
% used to solve the equations of motion numerically.
clear all; close all; clc;
tic
% Problem parameters
k1=1; % cart 1 spring constant (N/m)
k2=2; % cart 1 spring constant (N/m)
b1=1; % cart 1 viscous damping coefficient (kg/s)
m1=1; % cart 1 mass (kg)
k3=3; % cart 1 spring constant (N/m)
x10=4; % cart 1 initial position (m)
x20=5.9; % y movement initial position (m)
v10=-2.135; % cart 1 initial velocity (m/s)
v20=-35.36; % cart 2 initial velocity (m/s)
% Set time step stuff
simTime=60; % simulation time (s)
tStep=0.1; % simulation time step
iterations=simTime/tStep;
t=0:iterations;
% Pre-allocate variables for speed and add initial conditions
x1=zeros(iterations,1);
x1(1,:)=x10;
x2=zeros(iterations,1);
x2(1,:)=x20;
v1=zeros(iterations,1);
v1(1,:)=v10;
v2=zeros(iterations,1);
v2(1,:)=v20;
a1=zeros(iterations,1);
a1(1,:)=((0-(k1*x10)-b1*(v10+v20)-k2*(x20+x10))/m1);
% Solve the ODE's with Euler's Method
for n=2:(iterations+1)
x1(n,:)=x1(n-1,:)+v1(n-1,:)*tStep; % cart 1 position x2(n,:)=x2(n-1,:)+v2(n-1,:)*tStep; % cart 2 position v1(n,:)=v1(n-1,:)+a1(n-1,:)*tStep; % cart 1 velocity v2(n,:)=-(2*x1(n,:)+5*x2(n,:)+v1(n,:))
% Find cart accelerations
a1(n,:)=((0-k1*x1(n,:))-b1*(v1(n,:)+v2(n,:))-k2*(x2(n,:)+x1(n,:))/m1);
end
% Plot results
subplot(3,1,1)
hold on;
plot(t',x1,'r')
plot(t',x2,'m')
ylabel('Position (m)')
title('Position, Velocity, & Acceleration as a Function of Time')
legend('Pergerakan ke arah X','Pergerakan ke arah Y')
subplot(3,1,2)
hold on;
plot(t',v1,'b')
plot(t',v2,'c')
ylabel('Velocity (m/s)')
legend('Pergerakan ke arah X','Pergerakan ke arah Y')
subplot(3,1,3)
hold on;
plot(t',a1,'g')
ylabel('Acceleration (m/s^2)')
xlabel('time (1 = 0.01 detik)')
legend('Pergerakan ke arah X','Pergerakan ke arah Y')
toc
Grafik Hasil Perhitungan
Selanjutnya, untuk memverifikasi hasil numerik menggunakan metode euler yang dijelaskan diatas, digunakan metode Artificial Neural Networks (ANN) pada perangkat lunak matlab. Berikut sedikit pengenalan tentang ANN yang dapat kita temui dari beberapa sumber di internet. ANN adalah beberapa lapisan jaringan saraf (neural network) yang terhubung secara keseluruhan yang dapat dilihat dari gambar dibawah ini. Setiap node pada setiap lapisan terhubung ke setiap node dari lapisan selanjutnya. Jaringan dibuat lebih dalam dengan menambah jumlah lapisan tersembunyi (hidden layer).
Jika salah satu hidden layer atau node output diperbesar, maka akan ditemukan gambar dibawah ini
Node tertentu mengambil jumlah bobot dari inputnya, dan meneruskannya melalui fungsi aktivasi non-linear. Ini merupakan output dari node yang kemudian menjadi input dari node yang lain pada layer selanjutnya. Sinyal mengalir dari kiri ke kanan, dan output akhir dihitung dengan cara melakukan prosedur ini untuk semua node. Melatih jaringan saraf berarti mempelajari bobot yang terkait dengan semua edge.
Metode ANN ini digunakan untuk melatih data-data yang didapat dari numerik, dimana nilai posisi pada sumbu x dan y digunakan sebagai nilai input, dan nilai kecepatan pada sumbu x (u) dan sumbu y (v) yang merupakan hasil diferensial dari posisi digunakan sebagai nilai target. Data yang di training sebanyak 400 data.
Dengan demikian, diperoleh hasil yang dapat dilihat pada gambar diatas, dengan nilai R sebesar 0,99996 yang berarti data yang didapat dari metode Euler terverifikasi secara baik dengan persamaan yang dihasilkan dari metode ANN pada matlab.
Kesimpulan
Dari hasil yang sudah didapat untuk metode analitik, numerik, dan simulasi berikut beberapa hal yang dapat disimpulkan:
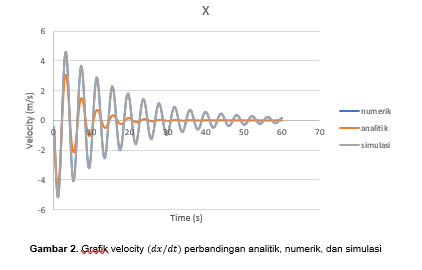
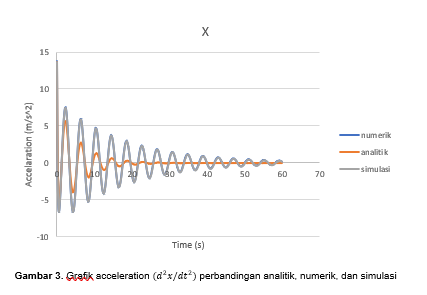
a) Hasil perhitungan numerik terhadap simulasi memiliki nilai yang berimpit. Hal ini dikarenakan, pada dasarnya simulasi yang dilakukan dengan MATLAB, menggunakan cara yang sama dengan numerik, hanya saja pada numerik persamaan-persamaannya harus dirubah menjadi 3 persamaan dengan orde 1. Sedangan pada simulasi, persamaan dari FBD langsung menjadi input pada MATLAB.
b) Hasil perhitungan numerik dan simulasi berbeda dengan metode analitik. Seperti sudah disebutkan pada materi perkuliahan sebelum ini, bahwa pada metode Forward Euler terdapat hal yang harus diperhatikan pada perkembangan amplitudonya.
c) Hasil metode forward euler telah terverifikasi dengan metode Artificial Neural Networks (ANN) yang dapat dilihat dari nilai R sebesar 0,99996 (mendekati 1) dari persamaan output metode ANN menggunakan software matlab.
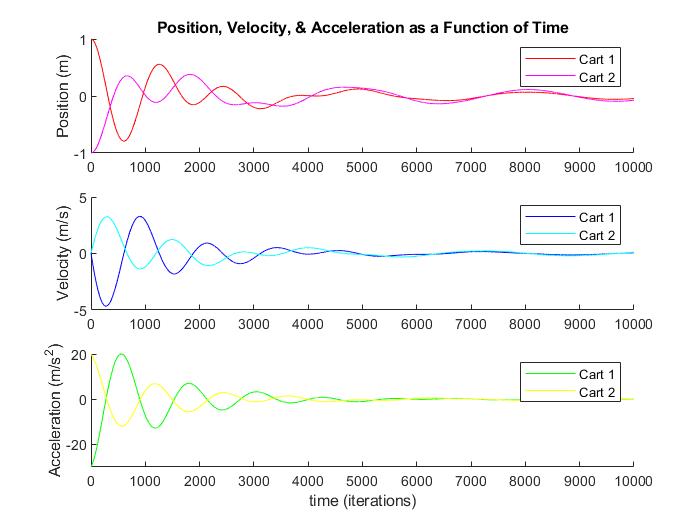
Tugas Artikel MS dan FES 1
Kasus ini menjelaskan sebuah sistem 2 cart spring-mass-damper. Persamaan gerak untuk system 2 degree of freedom yang digunakan adalah Newtonian mechanics dan diselesaikan secara numerik pada matlab.
% Calculates the position, velocity, and acceleration as a function of time % of a system of carts connected by springs and dashpots. Euler's Method is % used to solve the equations of motion numerically. clear all; close all; clc; tic % Problem parameters k1=50; % cart 1 spring constant (N/m) k2=50; % cart 2 spring constant (N/m) b1=3; % cart 1 viscous damping coefficient (kg/s) b2=3; % cart 2 viscous damping coefficient (kg/s) m1=5; % cart 1 mass (kg) m2=5; % cart 2 mass (kg) x10=1; % cart 1 initial position (m) x20=-1; % cart 2 initial position (m) v10=0; % cart 1 initial velocity (m/s) v20=0; % cart 2 initial velocity (m/s) % Set time step stuff simTime=10; % simulation time (s) tStep=0.001; % simulation time step iterations=simTime/tStep; t=0:iterations; % Pre-allocate variables for speed and add initial conditions x1=zeros(iterations,1); x1(1,:)=x10; x2=zeros(iterations,1); x2(1,:)=x20; v1=zeros(iterations,1); v1(1,:)=v10; v2=zeros(iterations,1); v2(1,:)=v20; a1=zeros(iterations,1); a1(1,:)=-(b1*v10-b2*(v20-v10)+k1*x10-k2*(x20-x10))/m1; a2=zeros(iterations,1); a2(1,:)=-(b2*(v20-v10)+k2*(x20-x10))/m2;
% Solve the ODE's with Euler's Method
for n=2:(iterations+1)
x1(n,:)=x1(n-1,:)+v1(n-1,:)*tStep; % cart 1 position
x2(n,:)=x2(n-1,:)+v2(n-1,:)*tStep; % cart 2 position
v1(n,:)=v1(n-1,:)+a1(n-1,:)*tStep; % cart 1 velocity
v2(n,:)=v2(n-1,:)+a2(n-1,:)*tStep; % cart 2 velocity
% Find cart accelerations
a1(n,:)=-(b1*v1(n,:)-b2*(v2(n,:)-v1(n,:))+k1*x1(n,:)-k2*(x2(n,:)-x1(n,:)))/m1;
a2(n,:)=-(b2*(v2(n,:)-v1(n,:))+k2*(x2(n,:)-x1(n,:)))/m2;
end
% Plot results
subplot(3,1,1)
hold on;
plot(t',x1,'r')
plot(t',x2,'m')
ylabel('Position (m)')
title('Position, Velocity, & Acceleration as a Function of Time')
legend('Cart 1','Cart 2')
subplot(3,1,2)
hold on;
plot(t',v1,'b')
plot(t',v2,'c')
ylabel('Velocity (m/s)')
legend('Cart 1','Cart 2')
subplot(3,1,3)
hold on;
plot(t',a1,'g')
plot(t',a2,'y')
ylabel('Acceleration (m/s^2)')
xlabel('time (iterations)')
legend('Cart 1','Cart 2')
toc
Akan tetapi pada kasus ini, pembahasan yang dilakukan masih dengan Mass-Spring method. Untuk Finite Element Simplified (FES), akan diupdate pada kesempatan selanjutnya.
Source: https:// www.youtube.com/ watch?v=N524t6wdlcM&feature=youtu.be
Tugas Artikel MS dan FES 2
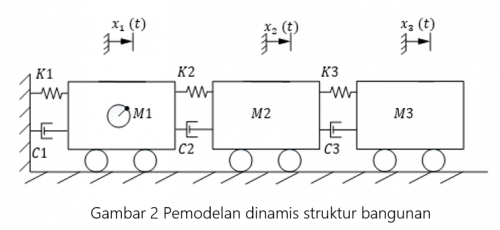
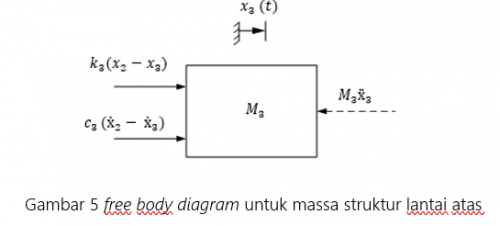
PENDAHULUAN Sistem pemodelan yang digunakan dalam struktur bangunan ini adalah pemodelan tiga derajat kebebasan (3 DOF). Gambar 1 menunjukkan model struktur bangunan bertingkat yang ditandai dengan adanya perpindahan sebesar x2 dan x3 karena pengaruh beban input gaya eksitasi dari shaking table. Sedangkan untuk pemodelan matematis, diperoleh persamaan dari free body diagram sistem yang akan dianalisa.
ANALISA
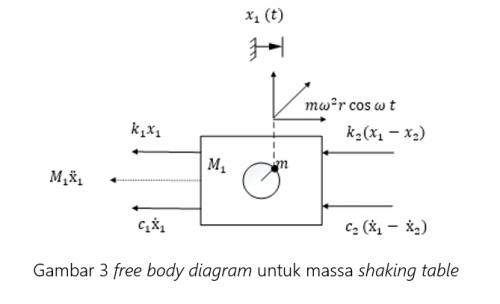
Untuk free body diagram dan persamaan massa shaking table (M_1) adalah :
∑▒〖Fx= M_1 ẍ_1 〗
-M_1 ẍ_1 (t) - c_1 ẋ_1 (t)- c_(2 ) (ẋ_1- ẋ_2 )(t)- k_1 x_(1 ) (t)-k_2 (x_1- x_2) (t) = - mω^2 r cos〖ω t〗
M_1 ẍ_1 (t)+ 〖(c〗_1+ c_2) ẋ_1 (t)+〖(k〗_1+k_2) x_(1 ) (t) -c_(2 ) ẋ_2 (t) -k_2 x_2 (t) = mω^2 r cos〖ω t〗
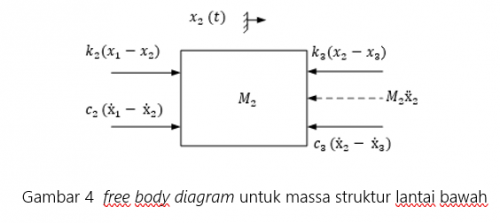
∑▒〖Fx= M_2 ẍ_2 〗
-M_2 ẍ_2 (t)-c_(3 ) (ẋ_2- ẋ_3 )(t)+c_(2 ) (ẋ_1- ẋ_2)(t)-k_3 (x_2-x_3)(t) + k_2 (x_1-x_2)(t) = 0
M_2 ẍ_2 (t)-c_(2 ) ẋ_1 (t)+〖(c〗_3+c_(2 )) ẋ_2 (t)-c_(3 ) ẋ_3 (t))- k_2 x_1 (t)+〖(k〗_3+k_2)x_2 (t)-k_3 x_3 (t)=0
∑▒〖Fx= M_3 ẍ_3 〗
-M_3 ẍ_3 (t)+c_(3 ) (ẋ_2- ẋ_3 )(t)+k_3 (x_2-x_3)(t)= 0
M_3 ẍ_3 (t)-c_(3 ) ẋ_2 (t)+c_(3 ) ẋ_3 (t)-k_3 x_2 (t)+〖k_3 x〗_3 (t)=0
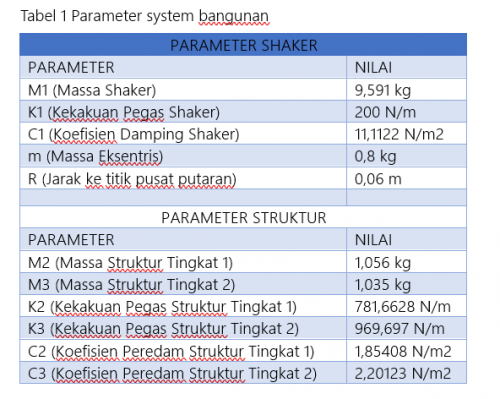
Setelah mendapatkan nilai parameter yang dibutuhkan untuk simulasi, Input yang digunakan yaitu input sinusoidal dengan frekuensi operasi 7 Hz atau 43,982 rad/s.
Untuk menyelesaikan persamaan gerak di atas maka dilakukan penyederhanaan persamaan menjadi 1 persamaan orde 6, dengan mengasumsikan x1 sebagai x, x2 sebagai y, dan x3 sebagai z, sehingga diperoleh persamaan,
z=(c_3 d/dt+k_3 )y/((m_3 d^2/〖dt〗^2 +c_3 d/dt+k_3 ) )
Persamaan 4 disubtitusikan kepersamaan 2 sehingga didapatkan persamaan,
y=((c_2 m_3 d^3/〖dt〗^3 +(c_2 c_3+k_2 m_3)) d^2/〖dt〗^2 +((c_2 k_3+c_3 k_3 ) d/dt+k_2 k_3 ))/((m_2 m_3 d^4/〖dt〗^4 +(c_3 m_2+c_2 m_3+c_3 m_3 ) d^3/〖dt〗^3 +(k_3 m_2+k_2 m_3+k_3 m_3+c_2 c_3 ) d^2/〖dt〗^2 +(c_2 k_3+c_3 k_2 ) d/dt+k_2 k_3 ) )
Persamaan 5 disubstitusi ke persamaan 1 dan mensubstitusi nilai c_1,c_2,c_3,k_1,k_2,k_3,m_1,m_2,m_3 sehingga didapatkan persamaan
mω^2 r cosωt=1,15 (d^6 x)/〖dt〗^6 +21,06 (d^5 x)/〖dt〗^5 +4153,74 (d^4 x)/〖dt〗^4 +42436,98 (d^3 x)/〖dt〗^3 +2,4.10^6 (d^2 x)/〖dt〗^2 +2,9.10^6 dx/dt+1,52.10^6 x
Untuk mencari nilai akar-akar dari persamaan di atas maka digunakan matlab untuk mempermudah perhitungan,
p=[1.154 21.059 4153.743 42436.977 2396974.157 2858796.484 151595214.4];
r=roots(p)
r =
-3.6221 +52.7481i -3.6221 -52.7481i -5.5262 +24.9446i -5.5262 -24.9446i 0.0239 + 8.4846i 0.0239 - 8.4846i
Maka didapatkan persamaan gerak berupa,
x=e^(-3,62t) (ASin(52,75t)+BCos(52,75t))+e^(-5,53t) (CSin(24,94t)+DCos(24,94t))+e^(0,024t) (ESin(8,48t)+FCos(8,48t))+GSin(43,982t)+HCos(43,982t)
Lalu dengan mengasumsikan nilai konstanta,
A=-0.0005
B=0.0001
C=0.0001
D=-0.0002
E=0.00032
F=-0.009
G=0.00008
H=0.00001
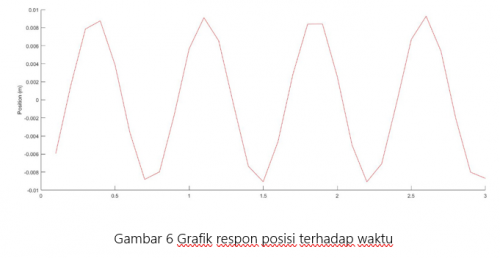
Maka dengan menggunakan software MATLAB dapat dibuat grafik posisi terhadap waktu. Berikut coding yang menjadi input dalam MATLAB:
syms x t A B C D E F
A=-0.0005
B=0.0001
C=0.0001
D=-0.0002
E=0.00032
F=-0.009
G=0.00008
H=0.00001
t=(1:100)/10 x1 = exp(-3.62*t)*(A*sin(52.75*t) + B*cos(52.75*t)) + exp(5.53*t)*(C*sin(24.94*t) + D*cos(24.94*t)) + exp(0.024*t)*(E*sin(8.48*t) + F*cos(8.48*t)) + G*sin(43.982*t) + H*cos(43.982*t) % Plot results subplot(1,1,1) hold on; plot(t',x1,'r') ylabel('Position (m)')
Grafik di atas menunjukan pengaruh getaran pada bagian bawah struktur pemodelan bangunan di mana perubahan arah gerak pada bagian bawah struktur membentuk pola sinusoidal yang menandakan adanya gerak bolak-balik pada struktur tersebut.
KESIMPULAN
Dalam permasalahan analisis gerak (perubahan arah, kecepatan dan percepatan) dapat dilakukan dengan metode lain berupa FES, namun pada artikel ini pemodelan FES belum dilakukan. Artikel ini hanya membahan mass-spring (MS) model yang terjadi pada suatu sistem pemodelan bangunan yang diberikan getaran. Sehingga dapat dilihat perilaku gerak bangunan sebagai respon dari adanya getaran yang diberikan.
REFERENSI
• Syaldiles Putri Indahdinata, Analisis Pengaruh Perubahan Cross Sectional Area Dan Posisi Peletakan Tuned Liquid Column Damper Terhadap Respon Dinamis Model Struktur Bangunan Bertingkat, Departemen Teknik Mesin FTI-ITS Surabaya, 2018.
Diskusi Kelas
Pertanyaan:
Ketika nilai A dinaikan maka nilai F menjadi besar tetapi mengapa pressure loss turun ketika A semakin besar?
τ_xy A=F
∆p= f ρ L/D V^2/2
Jawab:
Dalam mekanik benda padat shear stress didefinisikan sebagai rasio antara gaya yang berkerja terhadap luasan yang dikenakan gaya tersebut, yang didefinisikan sebagai,
τ_xy=F/A
Ketika gaya diaplikasikan pada benda padat maka, benda padat mengalami deformasi atau bending namun dalam batas ketika gaya diberikan, hal ini berbeda dengan fluida, ketika fluida diberikan gaya maka fluida tersebut akan terdeformasi secara terus menerus, sehingga persamaan yang digunakan untuk menghitung tegangan geser pun berbeda, dalam mekanika fluida persamaan tegangan geser dapat dituliskan sebagai,
τ_xy=μ du/dy
di mana du/dy merupakan perubahan kecepatan terhadap perubahan jarak antara dua sisi plat.
Maka ketika nilai A (luasan) dalam pipa diperbesar maka akan menurunkan nilai u (kecepatan fluida) sesuai persamaan kontinuitas,
A_1 V_1=A_2 V_2
Selain itu peningkatan A akan memperbesar nilai h (jarak antar 2 plat)
Sehingga akan menurunkan nilai τ_xy (shear stress) yang menyebabkan penurunan ∆p (pressure drop).