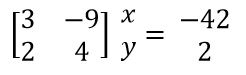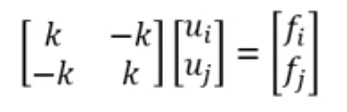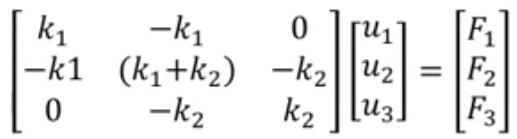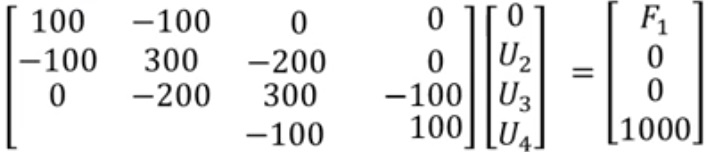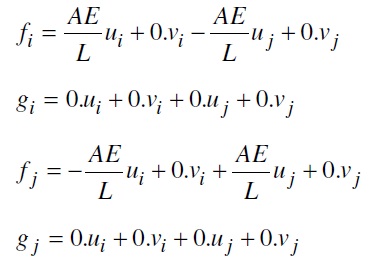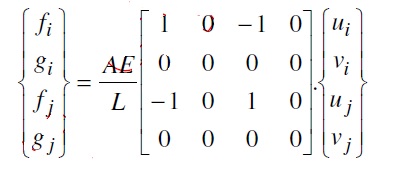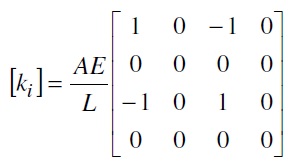Difference between revisions of "Ilham Akbar Abbas"
(→Pertemuan 5 Metode Numerik) |
|||
| (14 intermediate revisions by the same user not shown) | |||
| Line 215: | Line 215: | ||
4. menententukan gaya reaksi berdasarkan hasil yang di dapatkan | 4. menententukan gaya reaksi berdasarkan hasil yang di dapatkan | ||
| + | |||
| + | |||
| + | == Pertemuan 6 Metode Numerik == | ||
| + | |||
| + | 13 Maret 2019 | ||
| + | |||
| + | '''Resume''' | ||
| + | |||
| + | Pada hari ini kami mencoba melakukan perhitungan FEA pegas menggunakan eliminasi gauss yang nantinya akan dihitung menggunakan aplikasi python | ||
| + | |||
| + | contoh soal | ||
| + | |||
| + | [[File:pr1.jpg]] | ||
| + | |||
| + | Diketahui : | ||
| + | |||
| + | K1 = 100 N/mm | ||
| + | |||
| + | K2 = 200 N/mm | ||
| + | |||
| + | K3 = 100 N/mm | ||
| + | |||
| + | K4 = 1000 N | ||
| + | |||
| + | pertanyaanya ialah bagaimana cara mengetahui perpindahan atau displacement pada semua noda dan mengetahui reaction force pada noda 1. selanjutnya kita akan mengubah bentuk soal di atas menjadi bentuk matrix sperti di bahaw ini; | ||
| + | |||
| + | [[File:pr2.jpg]] | ||
| + | |||
| + | |||
| + | '''Tugas''' | ||
| + | |||
| + | Soal | ||
| + | |||
| + | [[File:Soal.jpg]] | ||
| + | |||
| + | Soal Tersebut dikerjakan menggunakan rumus pegas | ||
| + | |||
| + | F = K . Delta X | ||
| + | |||
| + | dimana K = (Modulus . Luas Permukaan) / Panjang | ||
| + | |||
| + | Flow Cahrt pengerjaan sebagai berikut | ||
| + | |||
| + | [[File:flow chart pengeerjaan.jpg]] | ||
| + | |||
| + | Pengaplikasian Perhitungan menggunakan Python | ||
| + | |||
| + | [[File:asdsafa]] | ||
| + | |||
| + | Link Vidio Pengaplikasian Perhitungan Gauss Jordan menggunakan Python : "https://youtu.be/JFEEFRb7dNA" | ||
| + | |||
| + | |||
| + | |||
| + | == Pertemuan 7 Metode Numerik == | ||
| + | |||
| + | '''Finite Element''' | ||
| + | |||
| + | FEM adalah singkatan dari Finite Element Method, dalam bahasa Indonesia disebut Metode Elemen Hingga. Konsep paling dasar FEM adalah, menyelesaikan suatu problem dengan cara membagi obyek analisa menjadi bagian-bagian kecil yang terhingga. Bagian-bagian kecil ini kemudian dianalisa dan hasilnya digabungkan kembali untuk mendapatkan penyelesaian untuk keseluruhan daerah. Kata “finite atau terhingga” digunakan untuk menekankan bahwa bagian-bagian kecil tersebut tidak tak terhingga, seperti yang lazim digunakan pada metode integral analitik. | ||
| + | |||
| + | Membagi bagian analisa menjadi bagian-bagian kecil disebut “discretizing atau diskritisasi”. Bagian-bagian kecil ini disebut elemen, yang terdiri dari titik-titik sudut (disebut nodal, atau node) dan daerah elemen yang terbentuk dari titik-titik tersebut. Membagi sebuah object menjadi bagian-bagian kecil secara fisika sebenarnya menuntun kita kepada pembuatan persamaan diferensial. Jadi secara lebih matematis, FEM didefinisikan sebagai teknik numerik untuk menyelesaikan problem yang dinyatakan dalam persamaan diferensial. Namun biasanya definisi FEM secara matematis memberikan kesan yang rumit yang sebenarnya tidak perlu. Oleh karena itu dalam pelajaran kita, pendekatan matematis tidak terlalu ditekankan. | ||
| + | |||
| + | Meski demikian, mengingat pentingnya, ilustrasi persamaan antara FEM dan diferensial-integral (kalkulus) akan kita bahas secara detail pada kesempatan berikutnya. | ||
| + | |||
| + | Untuk saat ini, yang perlu kita fahami lebih dahulu adalah gambaran besar cara kerja FEM. | ||
| + | |||
| + | Secara umum langkah-langkah dalam FEM bisa diringkas sebagai berikut: | ||
| + | |||
| + | 1. Membagi obyek analisa ke dalam elemen-element kecil. | ||
| + | |||
| + | 2. Melakukan modelisasi sederhana yang berlaku untuk setiap elemen. Misalnya dimodelkan sebagai pegas, di mana pegas ini sifatnya sederhana, yaitu tegangan berbanding lurus dengan perubahan bentuknya. | ||
| + | |||
| + | 3. Membuat formula sederhana untuk setiap element tersebut. Misalnya untuk pegas berlaku hukum f = k.x. Di mana k adalah konstanta pegas, dan x adalah pertambahan panjang pegas. Pada langkah ini kita akan memperoleh sebuah persamaan yang disebut “element stiffness matrix” atau matriks kekakuan elemen. | ||
| + | |||
| + | 4. Mengkombinasikan seluruh elemen dan membuat persamaan simultan yang mencakup semua variabel. Untuk elemen yang dimodelkan dengan pegas, mencakup f, k, dan x dari semua elemen.Biasanya pada langkah ini kita akan memperoleh sebuah persamaan yang disebut “global stiffness matrix” atau matriks kekakuan global. | ||
| + | |||
| + | [[File:FEM1.jpg]] | ||
| + | |||
| + | '''Kekakuan Rangka batang Bidang''' | ||
| + | |||
| + | Struktur plane truss merupakan suatu sistem struktur yang merupakan gabungan dari sejumlah elemen (batang) di mana pada setiap titik simpulnya dianggap berperilaku sebagai sendi dan setiap elemennya hanya dapat menerima gaya berupa gaya aksial (tarik ataupun tekan). | ||
| + | |||
| + | [[File:Fem2.jpg]] | ||
| + | |||
| + | Sumbu X-Y adalah sistem koordinat global struktur, yang nantinya diacu semua elemen. Sedangkan sumbu Z tegak lurus terhadap bidang gambar (mengarah pembaca) mengikuti kaidah tangan kanan, sehingga terbentuk sistem koordinat yang mengikuti right-handed rule. Sumbu x-y merupakan sistem koordinat lokal elemen, yang hanya berlaku untuk satu elemen tertentu saja, yang orientasinya disesuaikan dengan arah elemen yang bersangkutan. | ||
| + | |||
| + | Setiap elemen plane truss selalu memiliki dua nodal (titik simpul) ujung. Ujung awal elemen diberi notasi nodal i sedangkan ujung lainnya diberi notasi j. Pusat sumbu lokal elemen adalah nodal i , dan arah sumbu x lokal positif selalu dibuat dari nodal i ke nodal j dari elemen tersebut. | ||
| + | Sumbu y lokal dibuat tegak lurus sumbu x, sedangkan sumbu lokal arah z dibuat searah dengan sumbu Z global dan tegak lurus terhadap bidang struktur (bidang X-Y). | ||
| + | |||
| + | Persamaan hubungan antara aksi dan deformasi elemen dalam sistem koordinat lokal yang diperoleh berdasarkan prinsip superposisi dapat diuraikan sebagai berikut : | ||
| + | |||
| + | [[File:fem3.jpg]] | ||
| + | |||
| + | di mana : | ||
| + | |||
| + | x : sumbu batang | ||
| + | |||
| + | x, y : sistem koordinat lokal (elemen) | ||
| + | |||
| + | ui : displacement aksial pada titik nodal i | ||
| + | |||
| + | vi : displacement arah tegak lurus sumbu batang pada nodal i | ||
| + | |||
| + | fi : gaya aksial pada titik nodal i yang sesuai dengan ui | ||
| + | |||
| + | gi : gaya tegak lurus sumbu batang pada titik nodal i yang | ||
| + | sesuai dengan vi | ||
| + | |||
| + | Persamaan hubungan aksi-deformasi yang ditunjukkan Persamaan diatas dapat dinyatakan dalam bentuk matrix : | ||
| + | |||
| + | [[File:fem4.jpg]] | ||
| + | |||
| + | dengan : | ||
| + | |||
| + | A : Luas tampang batang | ||
| + | |||
| + | E : Modulus elastisitas batang | ||
| + | |||
| + | L : Panjang batang | ||
| + | |||
| + | Persamaan keseimbangan elemen dalam sistem koordinat lokal adalah | ||
| + | |||
| + | {fi}=[ki]{di} | ||
| + | |||
| + | di mana : | ||
| + | |||
| + | {fi} : vektor gaya dalam sistem koordinat lokal | ||
| + | |||
| + | [ki] : matrix kekakuan elemen plane truss dalam sistem koordinat lokal | ||
| + | |||
| + | {di} : vektor displacement dalam sistem koordinat lokal. | ||
| + | |||
| + | Subscript i menunjukkan nomor elemen yang bersangkutan | ||
| + | |||
| + | [[File:fem5.jpg]] | ||
| + | |||
| + | '''Transformasi Sumbu''' | ||
| + | |||
| + | Dalam analisis struktur yang dilakukan pada kebanyakan kasus, perlu dilakukan penyesuaian antara matrix kekakuan elemen struktur lokal (yang mengacu sumbu lokal secara individual) ke dalam matrix kekakuan elemen struktur global (mengacu pada sistem struktur global yang dianut semua elemen struktur. | ||
| + | |||
| + | Penyesuaian tersebut dapat dilakukan dengan memandang titik nodal awal i dan nodal akhir j dalam bidang X-Y (global) dari elemen mengalami perpindahan ke nodal i’ dan j’ dalam bidang x-y (lokal), sebagaimana diilustrasikan pada persamaan keseimbangan elemen dalam sistem koordinat lokal | ||
| + | |||
| + | [[File:femtugas.jpg]] | ||
| + | |||
| + | Berdasarkan tugas ditunjukkan perputaran sumbu Kartesian dari sumbu global X-Y menuju sumbu lokal x-y dengan kemiringan sudut a, sehingga dapat diperoleh Persamaan Transformasi Sumbu yang menunjukkan perubahan posisi suatu titik nodal dalam bentuk berikut : | ||
| + | |||
| + | x = X.cos a + Y.sin a | ||
| + | y = X.sin a + Y.cos a | ||
| + | |||
| + | Perhitungan yang dilakukan di python untuk mendapatkan hasil K elemen keseluruhan | ||
| + | |||
| + | [[File:fmpy.jpg]] | ||
| + | |||
| + | |||
| + | == Pertemuan 8 Metode Numerik (UTS) == | ||
Latest revision as of 04:13, 3 April 2019
Contents
Personal Data
Ilham Akbar Abbas
1506675213
Teknik Perkapalan
Departemen Teknik Mesin
Pertemuan 1 Metode Numerik
Rabu, 6 Februari 2019
Tugas 1
Pada hari ini, hari pertama kelas “metode numerik” kami berkenalan dengan seorang dosen yang bernama Bapak Ahmad Indra. Namun beliau sudah menyandang gelar Doktor dan juga beliau menyarankan kami untuk memanggil namanya dengan nama panggilan agar mungkin lebih akrab yaitu dari “Doktor Ahmad Indra” disingkat menjadi “DAI”.
Awal perbincangan dibuka dengan tujuan kelas itu sendiri, yaitu tujuan perkuliahan metode numerik. Dalam kelas ini tujuan dibagi dalam 2 garis besar, yang pertama adalah mahasiswa diharapkan dapat memahami konsep dan prinsip dari pelajaran metode numerik ini dan dapat menerapkanya. Lalu yang kedua ialah mahasiswa setelah mengambil kelas ini dapat menjadi orang yang lebih mengenal siapa dirinya secara pribadi. Pada poin pertama diturunkan lagi dalam beberapa poin, dan dijelaskan akan beberapa hal akan dipelajari kedepanya diantaranya Algoritma, penyelesaian persamaan-persamaan aljabar Linear, Diferensial & Integral, Optimasi, dan juga studi kasusnya. Lalu pada poin kedua ia lebih menekan pada hal yang sifatnya non akademis, yaitu mengenai cara mengenal diri dengan beberapa metode pendekatan yang nantinya akan ia berikan.
Pada Pembahasan kedua ia menjelaskan beberapa ilmu pengetahuan yang berkaitan dengan kuliah metode numerik. Yang pertama yaitu tentang filosofi Matematika, beliau mengatakan “Matematika dapat membantu dan juga dapat menyesatkan”. Ini sebenarnya sudah sangat jelas namun hanya beberapa orang yang dapat memahami ini, dikarenakan sifat dari matematika itu sendiri yang dianggap kebanyakan orang jelas dan realistis namun sebenarnya abstrak dan tidak realistis. Selalu ada angka diantara angka sehingga membuat matematika itu sendiri tidak memiliki batas atau infinity. Dikarenakannya matematika tidak memiliki batas dalam jumlah angka itu sendiri dalam jawaban membuat matematika irrelevant, namun para ahli matematika pendahulu membuat batasan-batasan dalam jawaban yang menggunakan metode matematika ini dan menjadikan matematika sebagai hal yang relevant.
Lalu pada pembahasan selanjutnya ia juga membahas tentang binary digit. Binary digit itu sendiri adalah sebuah sistem penulisan angka dengan menggunakan dua simbol yaitu 0 dan 1. Sistem bilangan ini merupakan dasar dari semua sistem bilangan berbasis digital. Dari sistem biner, kita dapat mengkonversinya ke sistem bilangan Oktal atau Hexadesimal. Sistem ini juga dapat kita sebut dengan istilah bit, atau Binary Digit. Pengelompokan biner dalam komputer selalu berjumlah 8, dengan istilah 1 Byte/bita. Dalam istilah komputer, 1 Byte = 8 bit. Kode-kode rancang bangun komputer. (Erika Kusumasari Rosit). Dalam sistem komunikasi digital modern, dimana data ditransmisikan dalam bentuk bit-bit biner, dibutuhkan sistem yang tahan terhadap noise yang terdapat di kanal transmisi sehingga data yang ditransmisikan tersebut dapat diterima dengan benar. Kesalahan dalam pengiriman atau penerimaan data merupakan permasalahan yang mendasar yang memberikan dampak yang sangat signifikan pada sistem komunikasi. Biner yang biasa dipakai itu ada 8 digit angka dan cuma berisikan angka 1 dan 0, tidak ada angka lainnya.
Lalu pada pembahasan terakhir ia juga membahas tentang apa itu GIGO (Garbage in, garbage out). GIGO merupakan istilah yang populer di pengolahan data, yaitu kualitas output merupakan hasil dari kualitas input. Jika sampah yang masuk maka sampah pula yang akan keluar dan sebaliknya. Maka dalam mengerjakan program tidak akan ada hasil yang sempurna apabila kita menggunakan data yang keliru.
Pertemuan 2 Metode Numerik
13 Februari 2019
Tugas 2
tentukan hasil dari x,y dengan menggunakan data yang diberikan a) 3x-9y=-42 b) 2x+4y=2 (nilai a,b,c,p,qdan r diasumsikan)
Jawab:
1) Diubah menjadi bentuk matrix
2) Dimisalkan menjadi
A x C = B
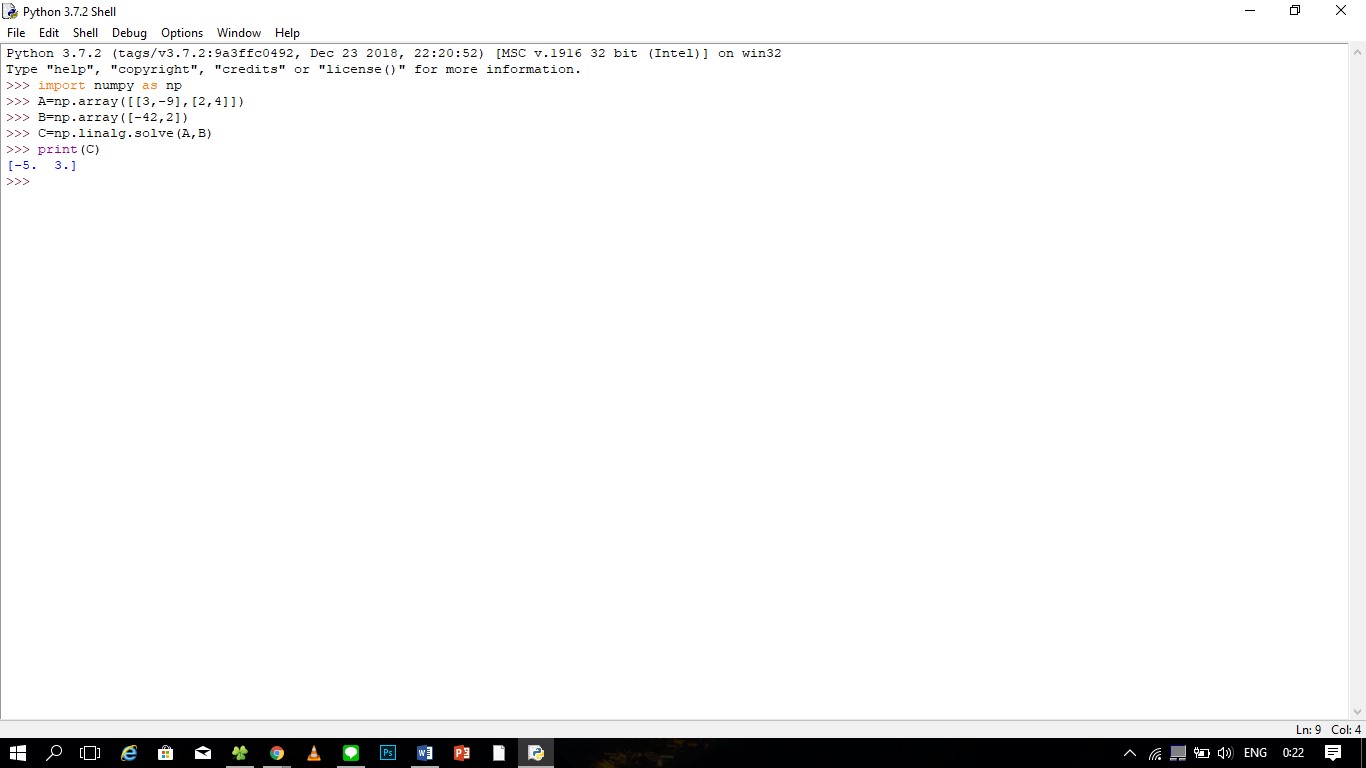
3) Diperlukan module python numpy
Untuk menambahkan module tersebut dapat ditambahkan melalui CMD yaitu dengan memasukkan command”python -m pip install numpy”.
4) Lalu masukan printah ,sebagaimana telah dilakukandi flowchart. 5) Dan ketik perintah "print C", maka akan keluar nilai dari x dan y
Berikut adalah Flow Chart pengerjaan
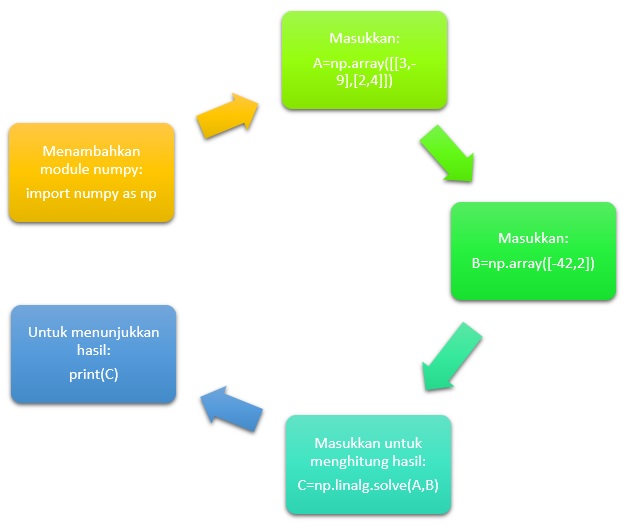
Pertemuan 3 Metode Numerik
20 Februari 2019
Resume
Pada hari ini kami belajar menggunakan aplikasi Python , aplikasi python itu sendiri ialah merupakan bahasa pemrograman tingkat tinggi, Python juga banyak digunakan untuk membuat berbagai macam program, seperti program CLI, GUI, Aplikasi Mobile, Web, IoT, Game, Program untuk Hacking, dan sebagainya. Python juga dikenal dengan bahasa pemrograman yang mudah dipelajari, karena strukturnya rapi dan mudah dipahami. kami diajari penggunaan aplikasi python untuk menyelesaikan matrix dengan jumlah yang besar nxn ,namun kita mempelajari terlebih dahulu matrix 3X3 menggunakan eleminasi Gauss yang dimana akan diubah menjadi menjadi matrix segitiga, untuk mempelajari dasar-dasar penggunaan aplikasi ini fungsi looping, dijalankan dalam batasan, maka harus diberi perintah in range , dan harus di ulang maka harus menggunakan perintah for, funsi if digunakan untuk mengetahui suatu hal yang di apabilakan.
contoh penggunaan bahasa:
untuk bentuk terakhir koefisien matrix L dan U
Algoritma untuk dekomposisi Doolittle dengan demikian identik dengan prosedur eliminasi Gauss, kecuali bahwa pada masing-masing λ disimpan dalam proporsi segitiga A paling rendah
for k in range(0,n-1):
for i in range(k+1,n):
if a[i,k] != 0.0:
lam = a[i,k]/a[k,k]
a[i,k+1:n] = a[i,k+1:n] - lam*a[k,k+1:n]
a[i,k] = lam
Tugas 3 membuat flow chart rumus yang diberikan beserta fungsi dari rumus python
Metode eliminasi gauss termasuk dalam metode penyelesaian persamaan linear dengan cara langsung. Inti dari metode ini adalah membawa persamaan kedalam bentuk matriks dan menyederhanakan matriks menjadi bentuk segitiga atas. Setelah mendapat bentuk matriks tersebut dilakukan subtitusi balik untuk mendapat nilai dari akar persamaan. Namun modern ini penyelesaian dapat diakuakan dengan cepat melalui aplikasi python dengan menggunakan rumus dibawah ini
keterangan:
n = jumlah baris atau kolom
i = baris ke
j = kolom
k = pivot
Langkah pengerjaan:
1. Masukkan library numpy dengan cara memasukkan import numpy as np.
2. Masukkan def gaussElimin(a,b): dimana def itu merupakan suatu fungsi, dan fungsi tersebut adalah eliminasi gauss dengan parameter a dan b. Baris berikutnya merupakan definisi dari n, di mana n tersebut adalah len(b) yang merupakan fungsi untuk mengembalikan angka atau objek berikut masuk ke fase eliminasi. hal yang pertama dimasukkan adalah fungsi range. Fungsi range ini berfungsi untuk menampilkan suatu list data, seperti yang dilihat untuk k range nya adalah (0,n-1)
3. Masukkan fungsi range untuk i dimana fungsi tersebut parameternya adalah (k+1,n) dimana dapat ditranslate sesudah kita mengetahui nilai k yang ingin dimasukkan. Dilanjutkan dengan memasukkan fungsi if dimana, if yaitu bila suatu kondisi tertentu tercapai maka apa yang harus dilakukan. Dengan fungsi ini kita bisa menjalankan suatu perintah dalam kondisi tertentu. Dimana perintah tersebut disini adalah a[i,k ] !=0.0: . setelah itu dilanjutkan dengan perhitungan lam dan perhitungan lainnya
4. Dilakukan fase substitusi balik, sehingga mendapatkan hasil sebagai berikut
Pertemuan 4 Metode Numerik
27 Februari 2019
Resume
Pada pertemuan kali ini Asisten Dosen kami yaitu bang Edo memberi tahu caramenginstal python dan membuat path untuk Numpy. Fungsi instalasi Numpy di CMD ini adalah untuk membuka beberapa fungsi pada IDLE Python.setelah itu kami diajarkan cara menginput matrix pada Python.
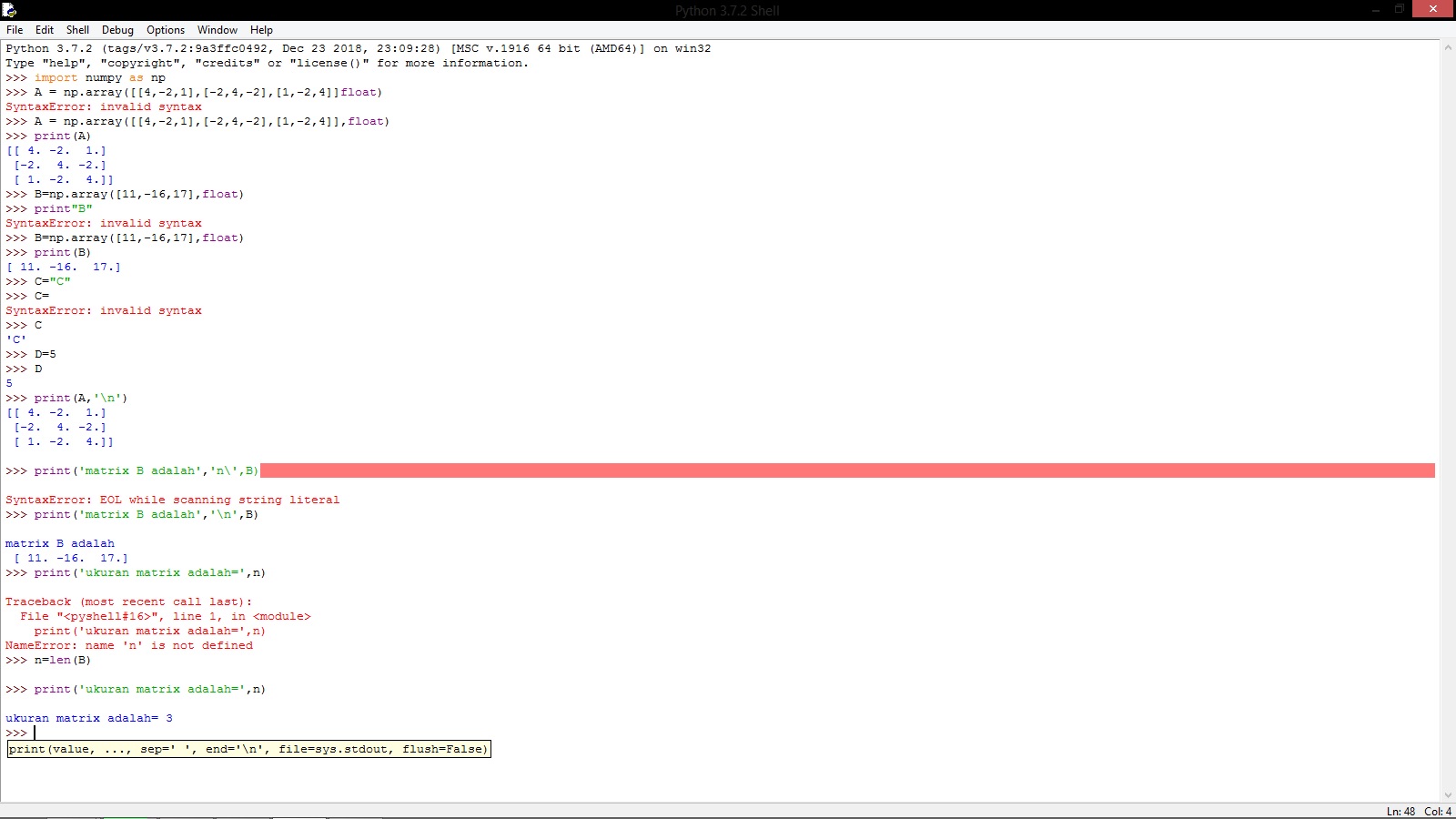
Tugas 3, Pertemuan 4
Cara Menghitung Matrix menggunakan Aplikasi Python dan di Upload ke Youtube
Link Vidio : https://youtu.be/y_dQi_bMvwE
Soal
Seorang pengusaha telah membangun sebuah kos-kosan. Ia ingin membangun kos dengan 3 lantai yaitu dengan 3 macam kamar,
1.kamar tanpa kamar mandi dalam sebanyak 9 unit kamar
2.kamar dengan kamar mandi dalam sebanyak 7 unit kamar
3.kamar dengan kamar mandi dalam + AC. Sebanyak 8 unit kamar
dengan kondisi kosan seperti berikut
1)Pada lantai pertama kamar tanpa kamar mandi dalam sebanyak 3 ruangan, kamar dengan kamar mandi dalam 3 ruangan dan kamar dengan kamar mandi dalam + AC sebanyak 2 ruangan. Sebulan pendapatan dari kamar tersebut sebesar Rp.150 juta.
2)Pada lantai kedua kamar tanpa kamar mandi dalam sebanyak 4 ruangan, kamar dengan kamar mandi dalam 2 ruangan dan kamar dengan kamar mandi dalam + AC sebanyak 3 ruangan. Sebulan pendapatan dari kamar tersebut sebesar Rp.200 juta.
3) Pada lantai ketiga kamar tanpa kamar mandi dalam sebanyak 2 ruangan, kamar dengan kamar mandi dalam 2 ruangan dan kamar dengan kamar mandi dalam + AC sebanyak 3 ruangan. Sebulan pendapatan dari kamar tersebut sebesar Rp.160 juta.
• Berapakah harga sewa dari masing masing perbulan kamar?
• Berapa lama Break Event Point(BEP) atau waktu balik modal?
Bila modal pembangunan sebesar 12.000.000.000 dengan biaya operasional sebesar RP.6.000.000 ( air, pajak, listrik,dll).
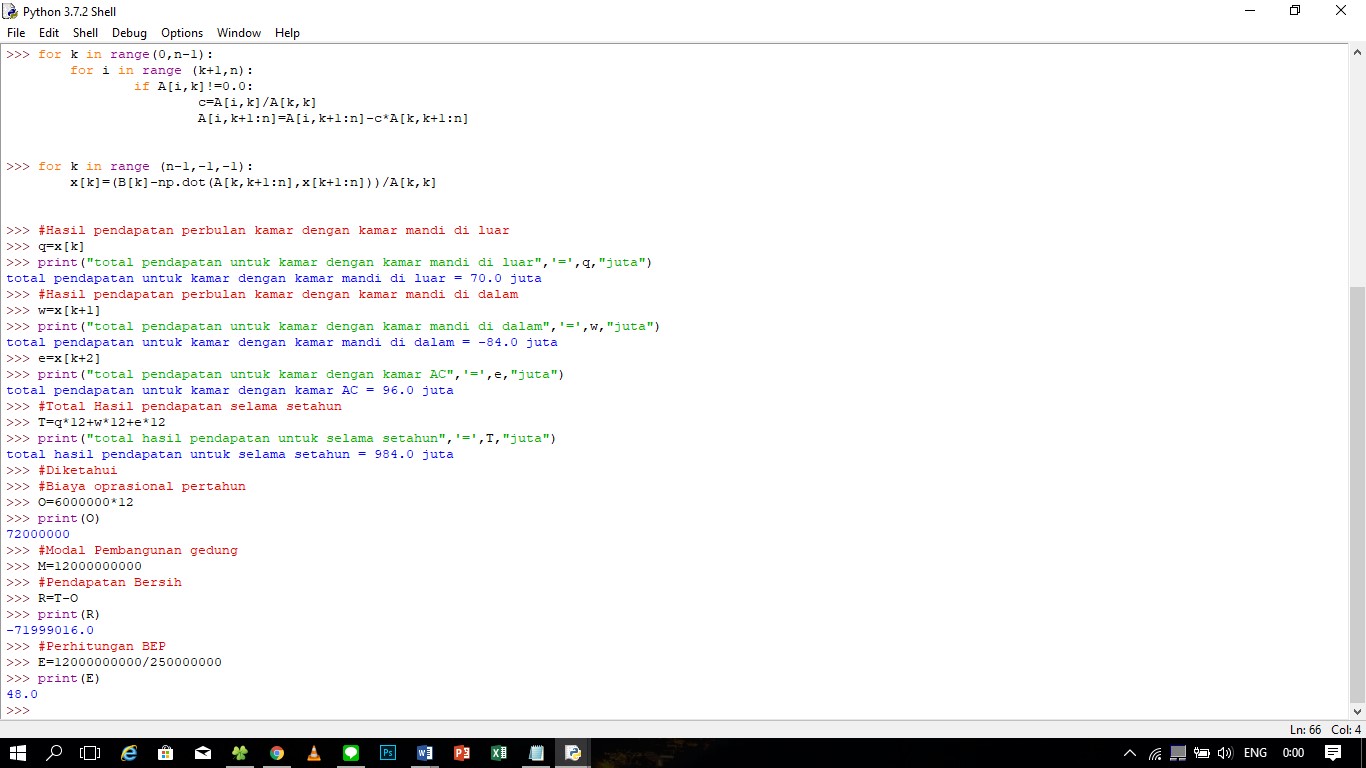
Jadi, dimasukanlah rumus pada Python sebagai berikut
Kesimpualan yang didapatkan adalah si Pengusaha akan mengalami balik modal pada bulan ke 48 atau pada tahun ke-2
Pertemuan 5 Metode Numerik
6 Maret 2019
Pengaplikasian perhitungan eliminasi gauss dappat digunakan perhitungan metode finite elemenet analysis (FEA) pegas. penghitungan tersebut dapat dilakukan dengan mengubah bentuk persamaan untuk perhitungan gaya pegas ke dalam bentuk matrix. berikut adalah perhitungannya
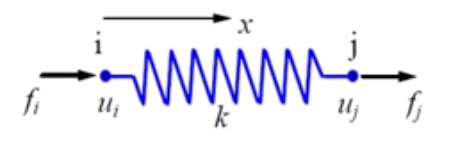
untuk penghitungan satu buah pegas
dimana :
x = arah gaya
u = perpindahan/ displacement
f = gaya
k = konstanta pegas
i = titik i
j = titik j
dapat diketahui bahwa dalam satu pegas memiliki dua node yaitu pada masing masing ujung pegas. anggap kedua node tersebut sebagai i dan j. untuk menghitung suatu FEA pegas kita dapat menghitung dengan menggunakan F= k . delta. dimana k adalah koefisien pegas dan delta adalah pengurangan displacement antara masing masing node ialah sma dengan
persamaan diubah kedalam bentuk matrix agar kita dapat menggunakan eliminasi gauss untuk enghitung FEA nya. hasil nya tersebut berupa gaya dari masing masing node
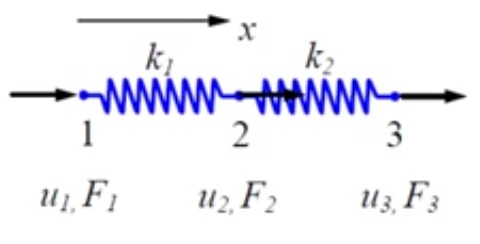
penghitungan itu juga dapat digunakan untuk menghitung pegas dalam bentuk rangkaian seri. contohnya anggap kita memiliki dua pegas yang dirangkai secara seri. dikarenakan pegas tersebut merupakan pegas seri, node yang dihasilkan sebanyak 3 buah, dimana menyebabkan terbentuknya matrix 3x3 pada saat perhitungan eliminasi gauss nya. selain itu juga displacementnya menjadi sebanyak 3 buah juga untuk masing masing node. sehingga dapat disimpulkan bahwa jumlah node sama dengan jumlah spring ditambah dengan satu
bentuk matrix berdasarkan persamaan nya
untuk penghitungannya terdapat beberapa tahap yaitu
1. menentukan matrix global stiffness
2. menentukan displacement pada node tetap adalah 0 atau tidak ada displacement sama sekali
3. menententukan displacement 1, 2, 3, ..., n dengan menggunakan eliminasi gauss
4. menententukan gaya reaksi berdasarkan hasil yang di dapatkan
Pertemuan 6 Metode Numerik
13 Maret 2019
Resume
Pada hari ini kami mencoba melakukan perhitungan FEA pegas menggunakan eliminasi gauss yang nantinya akan dihitung menggunakan aplikasi python
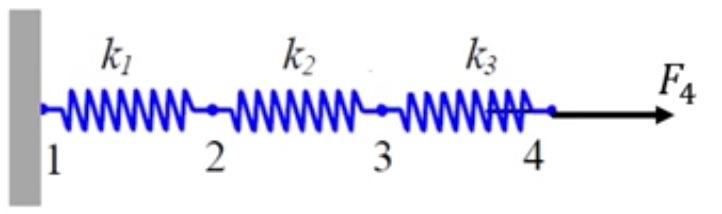
contoh soal
Diketahui :
K1 = 100 N/mm
K2 = 200 N/mm
K3 = 100 N/mm
K4 = 1000 N
pertanyaanya ialah bagaimana cara mengetahui perpindahan atau displacement pada semua noda dan mengetahui reaction force pada noda 1. selanjutnya kita akan mengubah bentuk soal di atas menjadi bentuk matrix sperti di bahaw ini;
Tugas
Soal
Soal Tersebut dikerjakan menggunakan rumus pegas
F = K . Delta X
dimana K = (Modulus . Luas Permukaan) / Panjang
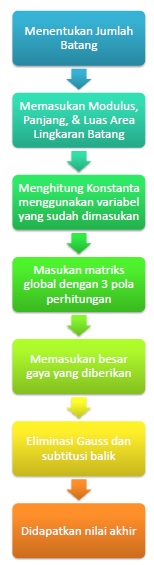
Flow Cahrt pengerjaan sebagai berikut
Pengaplikasian Perhitungan menggunakan Python
Link Vidio Pengaplikasian Perhitungan Gauss Jordan menggunakan Python : "https://youtu.be/JFEEFRb7dNA"
Pertemuan 7 Metode Numerik
Finite Element
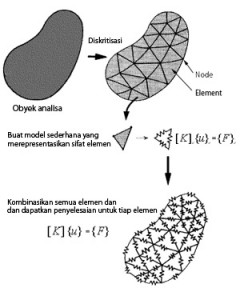
FEM adalah singkatan dari Finite Element Method, dalam bahasa Indonesia disebut Metode Elemen Hingga. Konsep paling dasar FEM adalah, menyelesaikan suatu problem dengan cara membagi obyek analisa menjadi bagian-bagian kecil yang terhingga. Bagian-bagian kecil ini kemudian dianalisa dan hasilnya digabungkan kembali untuk mendapatkan penyelesaian untuk keseluruhan daerah. Kata “finite atau terhingga” digunakan untuk menekankan bahwa bagian-bagian kecil tersebut tidak tak terhingga, seperti yang lazim digunakan pada metode integral analitik.
Membagi bagian analisa menjadi bagian-bagian kecil disebut “discretizing atau diskritisasi”. Bagian-bagian kecil ini disebut elemen, yang terdiri dari titik-titik sudut (disebut nodal, atau node) dan daerah elemen yang terbentuk dari titik-titik tersebut. Membagi sebuah object menjadi bagian-bagian kecil secara fisika sebenarnya menuntun kita kepada pembuatan persamaan diferensial. Jadi secara lebih matematis, FEM didefinisikan sebagai teknik numerik untuk menyelesaikan problem yang dinyatakan dalam persamaan diferensial. Namun biasanya definisi FEM secara matematis memberikan kesan yang rumit yang sebenarnya tidak perlu. Oleh karena itu dalam pelajaran kita, pendekatan matematis tidak terlalu ditekankan.
Meski demikian, mengingat pentingnya, ilustrasi persamaan antara FEM dan diferensial-integral (kalkulus) akan kita bahas secara detail pada kesempatan berikutnya.
Untuk saat ini, yang perlu kita fahami lebih dahulu adalah gambaran besar cara kerja FEM.
Secara umum langkah-langkah dalam FEM bisa diringkas sebagai berikut:
1. Membagi obyek analisa ke dalam elemen-element kecil.
2. Melakukan modelisasi sederhana yang berlaku untuk setiap elemen. Misalnya dimodelkan sebagai pegas, di mana pegas ini sifatnya sederhana, yaitu tegangan berbanding lurus dengan perubahan bentuknya.
3. Membuat formula sederhana untuk setiap element tersebut. Misalnya untuk pegas berlaku hukum f = k.x. Di mana k adalah konstanta pegas, dan x adalah pertambahan panjang pegas. Pada langkah ini kita akan memperoleh sebuah persamaan yang disebut “element stiffness matrix” atau matriks kekakuan elemen.
4. Mengkombinasikan seluruh elemen dan membuat persamaan simultan yang mencakup semua variabel. Untuk elemen yang dimodelkan dengan pegas, mencakup f, k, dan x dari semua elemen.Biasanya pada langkah ini kita akan memperoleh sebuah persamaan yang disebut “global stiffness matrix” atau matriks kekakuan global.
Kekakuan Rangka batang Bidang
Struktur plane truss merupakan suatu sistem struktur yang merupakan gabungan dari sejumlah elemen (batang) di mana pada setiap titik simpulnya dianggap berperilaku sebagai sendi dan setiap elemennya hanya dapat menerima gaya berupa gaya aksial (tarik ataupun tekan).
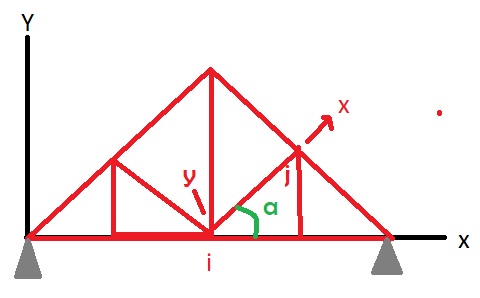
Sumbu X-Y adalah sistem koordinat global struktur, yang nantinya diacu semua elemen. Sedangkan sumbu Z tegak lurus terhadap bidang gambar (mengarah pembaca) mengikuti kaidah tangan kanan, sehingga terbentuk sistem koordinat yang mengikuti right-handed rule. Sumbu x-y merupakan sistem koordinat lokal elemen, yang hanya berlaku untuk satu elemen tertentu saja, yang orientasinya disesuaikan dengan arah elemen yang bersangkutan.
Setiap elemen plane truss selalu memiliki dua nodal (titik simpul) ujung. Ujung awal elemen diberi notasi nodal i sedangkan ujung lainnya diberi notasi j. Pusat sumbu lokal elemen adalah nodal i , dan arah sumbu x lokal positif selalu dibuat dari nodal i ke nodal j dari elemen tersebut. Sumbu y lokal dibuat tegak lurus sumbu x, sedangkan sumbu lokal arah z dibuat searah dengan sumbu Z global dan tegak lurus terhadap bidang struktur (bidang X-Y).
Persamaan hubungan antara aksi dan deformasi elemen dalam sistem koordinat lokal yang diperoleh berdasarkan prinsip superposisi dapat diuraikan sebagai berikut :
di mana :
x : sumbu batang
x, y : sistem koordinat lokal (elemen)
ui : displacement aksial pada titik nodal i
vi : displacement arah tegak lurus sumbu batang pada nodal i
fi : gaya aksial pada titik nodal i yang sesuai dengan ui
gi : gaya tegak lurus sumbu batang pada titik nodal i yang sesuai dengan vi
Persamaan hubungan aksi-deformasi yang ditunjukkan Persamaan diatas dapat dinyatakan dalam bentuk matrix :
dengan :
A : Luas tampang batang
E : Modulus elastisitas batang
L : Panjang batang
Persamaan keseimbangan elemen dalam sistem koordinat lokal adalah
{fi}=[ki]{di}
di mana :
{fi} : vektor gaya dalam sistem koordinat lokal
[ki] : matrix kekakuan elemen plane truss dalam sistem koordinat lokal
{di} : vektor displacement dalam sistem koordinat lokal.
Subscript i menunjukkan nomor elemen yang bersangkutan
Transformasi Sumbu
Dalam analisis struktur yang dilakukan pada kebanyakan kasus, perlu dilakukan penyesuaian antara matrix kekakuan elemen struktur lokal (yang mengacu sumbu lokal secara individual) ke dalam matrix kekakuan elemen struktur global (mengacu pada sistem struktur global yang dianut semua elemen struktur.
Penyesuaian tersebut dapat dilakukan dengan memandang titik nodal awal i dan nodal akhir j dalam bidang X-Y (global) dari elemen mengalami perpindahan ke nodal i’ dan j’ dalam bidang x-y (lokal), sebagaimana diilustrasikan pada persamaan keseimbangan elemen dalam sistem koordinat lokal
Berdasarkan tugas ditunjukkan perputaran sumbu Kartesian dari sumbu global X-Y menuju sumbu lokal x-y dengan kemiringan sudut a, sehingga dapat diperoleh Persamaan Transformasi Sumbu yang menunjukkan perubahan posisi suatu titik nodal dalam bentuk berikut :
x = X.cos a + Y.sin a y = X.sin a + Y.cos a
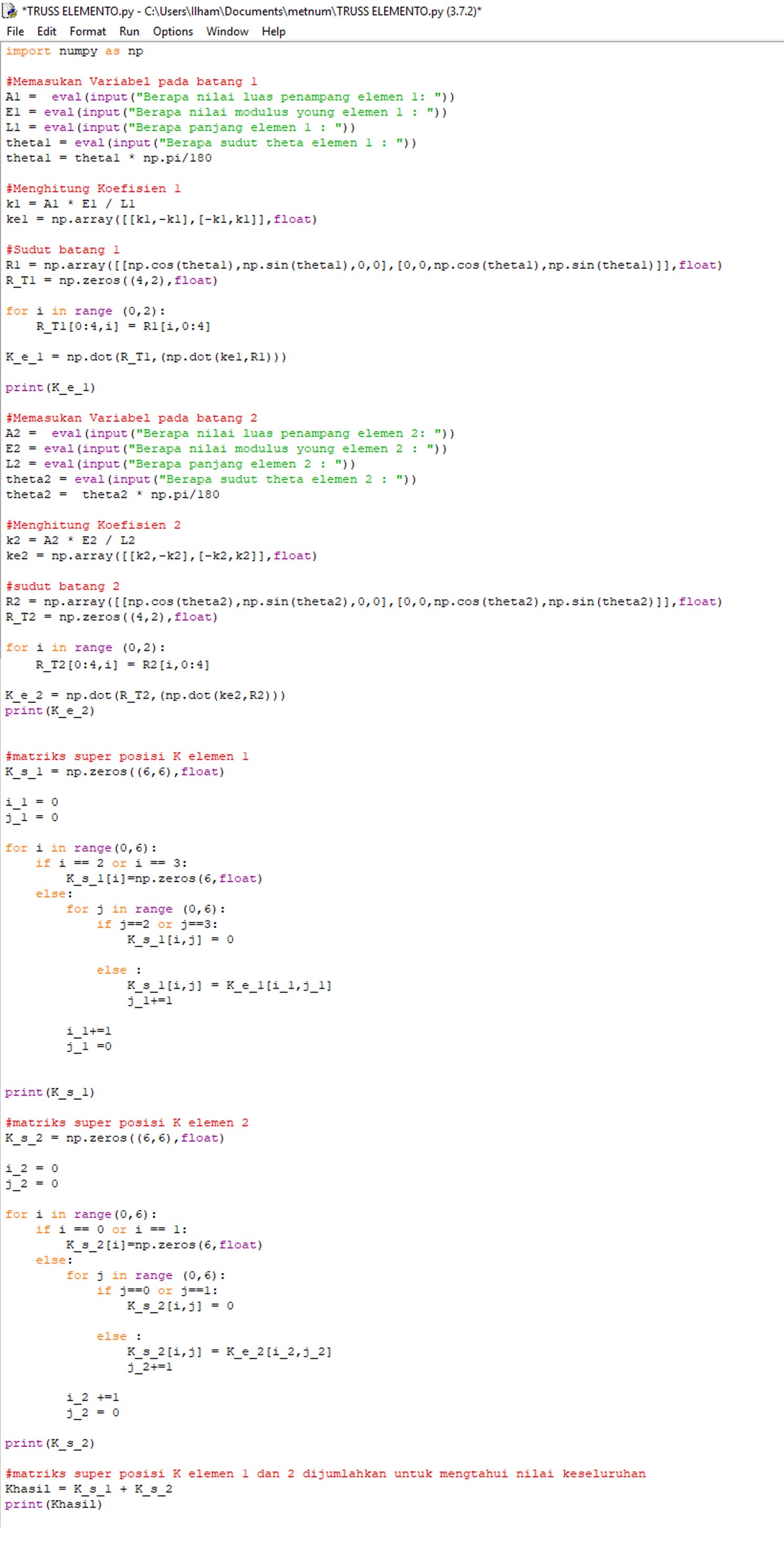
Perhitungan yang dilakukan di python untuk mendapatkan hasil K elemen keseluruhan