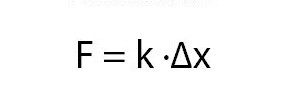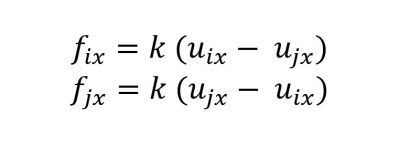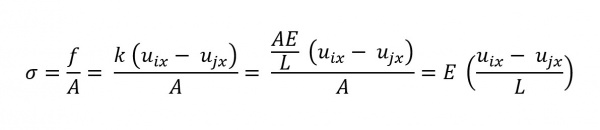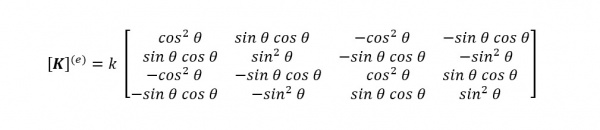Difference between revisions of "Metnum03-Ramandika Garindra Putra"
(→Tahap Pengerjaan) |
(→UAS) |
||
| (23 intermediate revisions by the same user not shown) | |||
| Line 21: | Line 21: | ||
Pertemuan ini membahas tentang program sederhana modelica untuk menghitung jumlah rata - rata angka. | Pertemuan ini membahas tentang program sederhana modelica untuk menghitung jumlah rata - rata angka. | ||
| + | |||
| + | |||
[[File:Matriks Aljabar.jpg]] | [[File:Matriks Aljabar.jpg]] | ||
== Tugas 2 == | == Tugas 2 == | ||
| Line 41: | Line 43: | ||
==Kuis== | ==Kuis== | ||
| − | [[File:Kuis Metnum Ramandika.jpg]] | + | [[File:Kuis Metnum Ramandika.jpg|300px]] |
| + | |||
'''1. Mendefinisikan Node & Elemen''' | '''1. Mendefinisikan Node & Elemen''' | ||
| − | [[File:Kuis Metnum Ramandika 1.jpg]] | + | [[File:Kuis Metnum Ramandika 1.jpg|400px]] |
| + | |||
| Line 55: | Line 59: | ||
a. Hukum Hooke | a. Hukum Hooke | ||
| − | [[File:Rumus Hukum Hooke.jpg]] | + | [[File:Rumus Hukum Hooke.jpg|300px]] |
b. Internal Force | b. Internal Force | ||
| − | [[File:Rumus Internal Force.jpg]] | + | [[File:Rumus Internal Force.jpg|400px]] |
c. Normal Stress | c. Normal Stress | ||
| − | [[File:Rumus Normal Stress.jpg]] | + | [[File:Rumus Normal Stress.jpg|600px]] |
'''3. Membuat Model Numerik''' | '''3. Membuat Model Numerik''' | ||
| Line 69: | Line 73: | ||
Untuk menentukan matriks kekakuan elemen dapat menggunakan Persamaan matriks berikut: | Untuk menentukan matriks kekakuan elemen dapat menggunakan Persamaan matriks berikut: | ||
| − | [[File:Matriks Model Numerik.jpg]] | + | [[File:Matriks Model Numerik.jpg|600px]] |
'''4. Menghitung Defleksi''' | '''4. Menghitung Defleksi''' | ||
| Line 122: | Line 126: | ||
'''2. Mengasumsikan problem (constraint, distribusi)''' | '''2. Mengasumsikan problem (constraint, distribusi)''' | ||
| + | |||
| + | |||
| + | a. Diasumsikan tidak ada bending karena bersifat truss | ||
| + | |||
| + | b. Beban terdistribusi pada node | ||
| + | |||
| + | c. Safety Factor = 2 | ||
| + | |||
| + | d. Batas displacement 0,001m sebelum terjadi buckling | ||
| + | |||
| + | e. Variabel bebas | ||
| + | |||
'''3. Mengasumsikan solusi problem (stress, displacement)''' | '''3. Mengasumsikan solusi problem (stress, displacement)''' | ||
| + | |||
| + | |||
| + | 1) Pilih material dengan 3 variasi, area , dan elastisitas material | ||
| + | |||
| + | 2) Buat 2 grafik perbandingan yang pertama grafik dengan material locked dan variasi area, lalu yg ke dua grafik dengan area locked dan variasi elastisitas | ||
| + | |||
| + | 3) Setelah itu kita hitung stress/cost | ||
| + | |||
'''4. Model numerik (untuk mencari stress)''' | '''4. Model numerik (untuk mencari stress)''' | ||
| + | |||
| + | |||
| + | model Trusses_3D_Tugas_Besar_Safety | ||
| + | |||
| + | //define initial variable | ||
| + | parameter Integer Points=size(P,1); //Number of Points | ||
| + | parameter Integer Trusses=size(C,1); //Number of Trusses | ||
| + | parameter Real Yield=215e6; //Yield Strength (Pa) | ||
| + | parameter Real Area=0.000224; //Area L Profile (Dimension=0.03, Thickness=0,004) (m2) | ||
| + | parameter Real Elas=193e9; //Elasticity SS 304 (Pa) | ||
| + | |||
| + | //define connection | ||
| + | parameter Integer C[:,2]=[1,5; | ||
| + | 2,6; | ||
| + | 3,7; | ||
| + | 4,8; | ||
| + | 5,6; //1st floor | ||
| + | 6,7; //1st floor | ||
| + | 7,8; //1st floor | ||
| + | 5,8; //1st floor | ||
| + | 5,9; | ||
| + | 6,10; | ||
| + | 7,11; | ||
| + | 8,12; | ||
| + | 9,10; //2nd floor | ||
| + | 10,11;//2nd floor | ||
| + | 11,12;//2nd floor | ||
| + | 9,12; //2nd floor | ||
| + | 9,13; | ||
| + | 10,14; | ||
| + | 11,15; | ||
| + | 12,16; | ||
| + | 13,14;//3rd floor | ||
| + | 14,15;//3rd floor | ||
| + | 15,16;//3rd floor | ||
| + | 13,16];//3rd floor | ||
| + | |||
| + | //define coordinates (please put orderly) | ||
| + | parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1 | ||
| + | -0.3,-0.375,0,1,1,1; //2 | ||
| + | -0.3,0.375,0,1,1,1; //3 | ||
| + | 0.3,0.375,0,1,1,1; //4 | ||
| + | |||
| + | 0.3,-0.375,0.6,0,0,0; //5 | ||
| + | -0.3,-0.375,0.6,0,0,0; //6 | ||
| + | -0.3,0.375,0.6,0,0,0; //7 | ||
| + | 0.3,0.375,0.6,0,0,0; //8 | ||
| + | |||
| + | 0.3,-0.375,1.2,0,0,0; //9 | ||
| + | -0.3,-0.375,1.2,0,0,0; //10 | ||
| + | -0.3,0.375,1.2,0,0,0; //11 | ||
| + | 0.3,0.375,1.2,0,0,0; //12 | ||
| + | |||
| + | 0.3,-0.375,1.8,0,0,0; //13 | ||
| + | -0.3,-0.375,1.8,0,0,0; //14 | ||
| + | -0.3,0.375,1.8,0,0,0; //15 | ||
| + | 0.3,0.375,1.8,0,0,0]; //16 | ||
| + | |||
| + | //define external force (please put orderly) | ||
| + | parameter Real F[Points*3]={0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,-500, | ||
| + | 0,0,-1000, | ||
| + | 0,0,-1000, | ||
| + | 0,0,-500}; | ||
| + | |||
| + | //solution | ||
| + | Real displacement[N], reaction[N]; | ||
| + | Real check[3]; | ||
| + | |||
| + | Real stress1[Trusses]; | ||
| + | Real safety[Trusses]; | ||
| + | Real dis[3]; | ||
| + | Real Str[3]; | ||
| + | |||
| + | protected | ||
| + | parameter Integer N=3*Points; | ||
| + | Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; | ||
| + | Real err=10e-10, ers=10e-4; | ||
| + | |||
| + | algorithm | ||
| + | //Creating Global Matrix | ||
| + | G:=id; | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | end for; | ||
| + | |||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | |||
| + | //Transforming to global matrix | ||
| + | g:=zeros(N,N); | ||
| + | for m,n in 1:3 loop | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n]; | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n]; | ||
| + | end for; | ||
| + | |||
| + | G_star:=G+g; | ||
| + | G:=G_star; | ||
| + | end for; | ||
| + | |||
| + | //Implementing boundary | ||
| + | for x in 1:Points loop | ||
| + | if P[x,4] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[(x*3)-2,a]:=0; | ||
| + | G[(x*3)-2,(x*3)-2]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x,5] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[(x*3)-1,a]:=0; | ||
| + | G[(x*3)-1,(x*3)-1]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x,6] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[x*3,a]:=0; | ||
| + | G[x*3,x*3]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | //Solving displacement | ||
| + | displacement:=Modelica.Math.Matrices.solve(G,F); | ||
| + | |||
| + | //Solving reaction | ||
| + | reaction:=(G_star*displacement)-F; | ||
| + | |||
| + | //Eliminating float error | ||
| + | for i in 1:N loop | ||
| + | reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; | ||
| + | displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i]; | ||
| + | end for; | ||
| + | |||
| + | //Checking Force | ||
| + | check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))}); | ||
| + | check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))}); | ||
| + | check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)}); | ||
| + | |||
| + | for i in 1:3 loop | ||
| + | check[i] := if abs(check[i])<=ers then 0 else check[i]; | ||
| + | end for; | ||
| + | |||
| + | //Calculating stress in each truss | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]); | ||
| + | end for; | ||
| + | |||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | |||
| + | Str:=(X*dis); | ||
| + | stress1[i]:=Modelica.Math.Vectors.length(Str); | ||
| + | end for; | ||
| + | |||
| + | //Safety factor | ||
| + | for i in 1:Trusses loop | ||
| + | if stress1[i]>0 then | ||
| + | safety[i]:=Yield/stress1[i]; | ||
| + | else | ||
| + | safety[i]:=0; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | end Trusses_3D_Tugas_Besar_Safety; | ||
| + | |||
'''5. Komputasi => mendapatkan data (data stress)''' | '''5. Komputasi => mendapatkan data (data stress)''' | ||
| Line 136: | Line 356: | ||
[[File:Material Lock.jpg|1000px|left]] | [[File:Material Lock.jpg|1000px|left]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | = UAS = | ||
| + | |||
| + | [[File:uas 1 rama.jpg]] | ||
| + | |||
| + | [[File:uas 2 rama.jpg]] | ||
| + | |||
| + | [[File:uas 3 rama.jpg]] | ||
| + | |||
| + | [[File:uas 4 rama.jpg]] | ||
| + | |||
| + | [[File:uas 5 rama.jpg]] | ||
| + | |||
| + | [[File:nomer 7 a.png]] | ||
| + | |||
| + | [[File:nomer 7 b.png]] | ||
| + | |||
| + | [[File:nomer 7 c.png]] | ||
| + | |||
| + | [[File:nomer 7 d.png]] | ||
Latest revision as of 18:04, 19 January 2021
Contents
Bio Data
Kelas Metode Numerik - 03
Nama : Ramandika Garindra
NPM : 1606907625
Program Studi : S1 Teknik Mesin Parallel
Kelas Metode Numerik
Pertemuan 1 (Senin, 9 November 2020)
Pada pertemuan pertama, Pak DAI menjelaskan terdapat empat penilaian utama dalam kelas Metode Numerik; (1) mengenal atau mengetahui progres pengetahuan; (2) mengerti konsep; (3) mampu membantu dalam memecahkan masalah dengan pemahaman tersebut di dunia keteknikan; (4) mendapat nilai tambah (moral value) dan lebih mengetahui diri sendiri.
Pembahasan selanjutnya mengenai arahan untuk meng-install software OpenModelica sebagai software yang digunakan dalam pelajaran Metode Numerik
Pertemuan 2 (Senin, 16 November 2020)
Pertemuan ini membahas tentang program sederhana modelica untuk menghitung jumlah rata - rata angka.
Tugas 2
Pertemuan 3 (Senin, 23 November 2020)
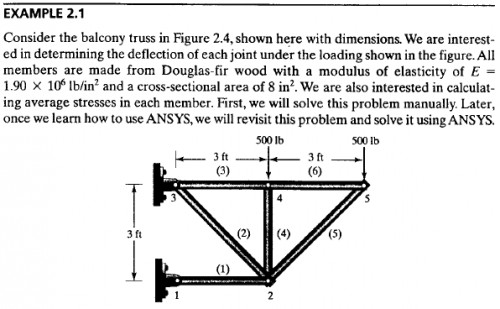
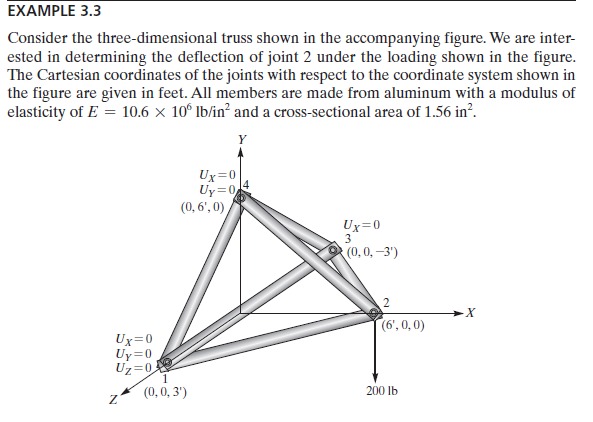
Pertemuan ke-3 membahas untuk membuktikan studi berdasarkan gambar soal 12.11.
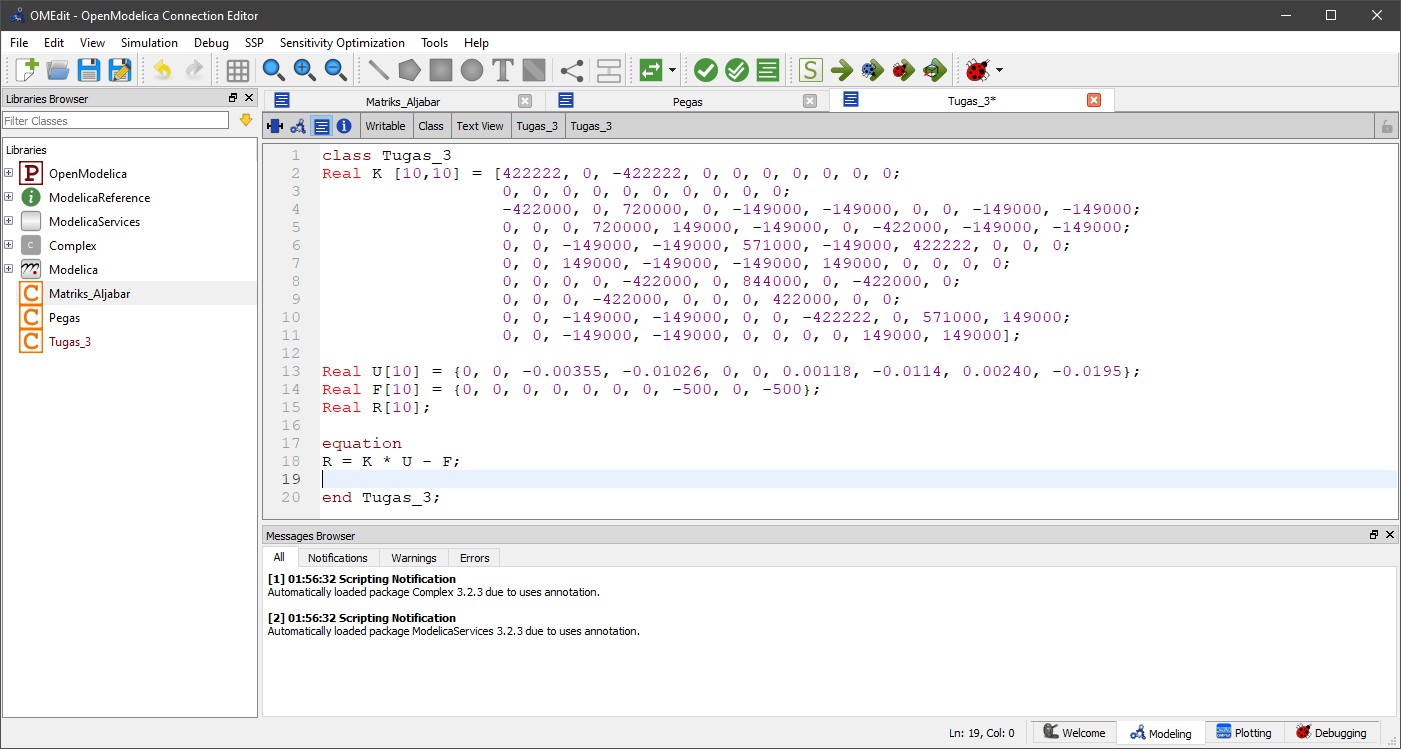
Tugas 3
Soal Pertemuan 3
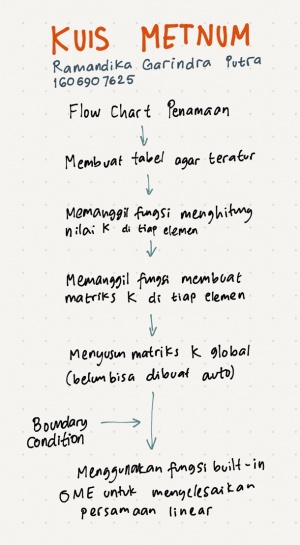
Kuis
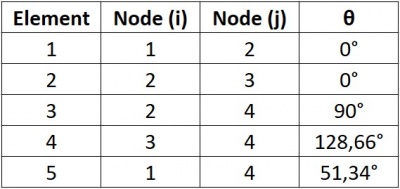
1. Mendefinisikan Node & Elemen
2. Membuat Model Matematika
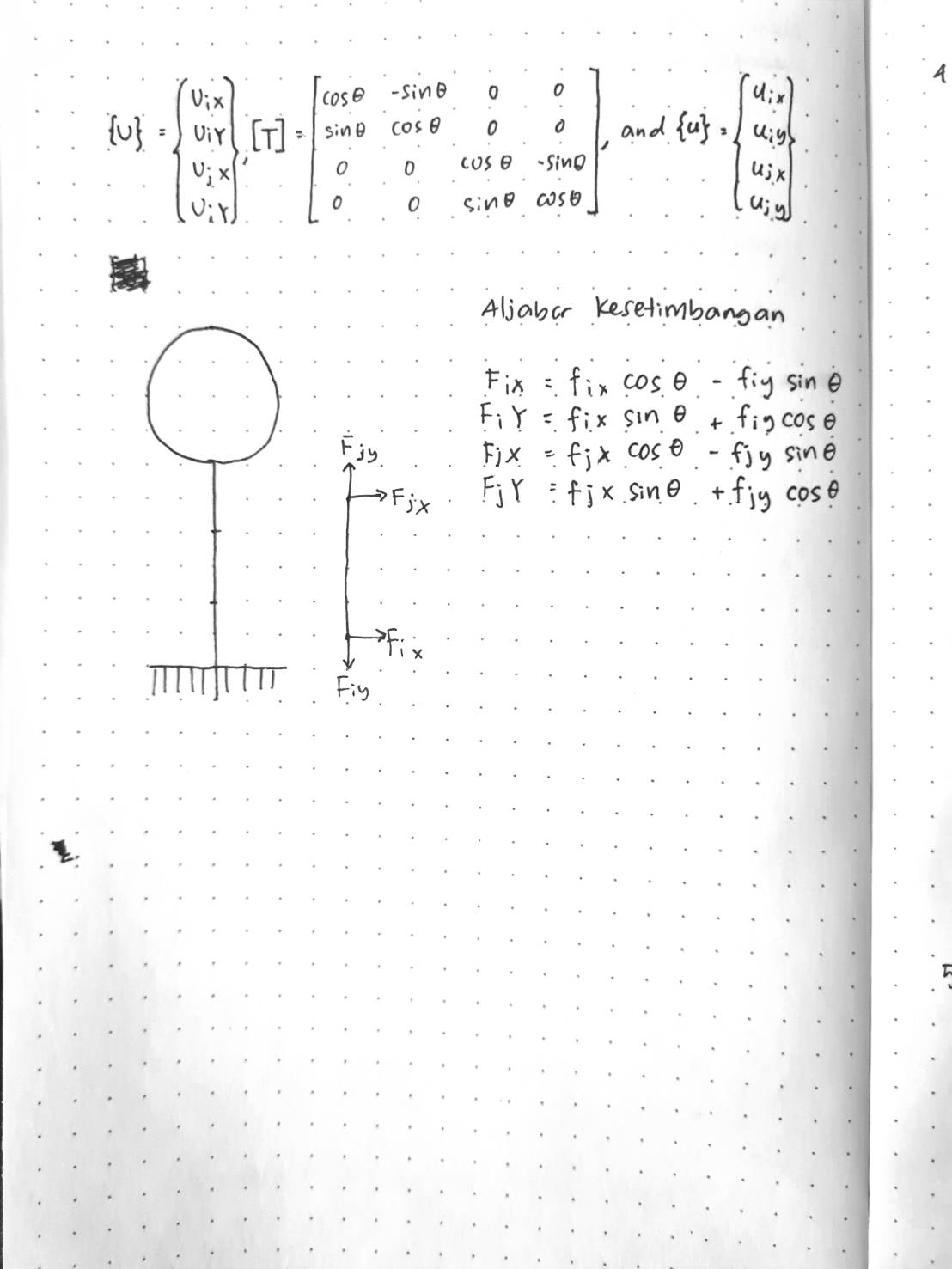
Mencari defleksi dari gambar yang tersedia menggunakan persamaan berikut:
a. Hukum Hooke
b. Internal Force
c. Normal Stress
3. Membuat Model Numerik
Untuk menentukan matriks kekakuan elemen dapat menggunakan Persamaan matriks berikut:
4. Menghitung Defleksi
Pertemuan 5 (Senin, 7 Desember 2020)
Pertemuan 6 (Senin, 14 Desember 2020), Muhasabah Pribadi
Pada pertemuan 6, Pak Dai mengarahkan kami semua untuk melakukan muhasabah pribadi. Berikut hasil muhasabah saya:
Pada pembelajaran metode numerik ini, saya selalu berusaha mengikuti pembelajaran di kelas pada setiap pertemuan. Tentang konsep statika struktur saya sudah cukup paham, karena saya juga sudah pernah mempelajari statika struktur pada semester semester sebelumnya.
Untuk pembelajaran programming menggunakan OpenModelica, saya merasa memang cukup sulit, karena saya belum pernah mempelajari basic programming, akan tetapi saya pernah membuat program menggunakan OpenCV Python, dan ternyata memang memiliki syntax yang cukup banyak berbeda, tetapi saya masih bisa mengikuti untuk mempelajari OpenModelica karena ada beberapa hal yang mirip.
Tugas Besar
Asumsi:
1. Variasi Stiffness terikat dengan variabel area. Memvariasikan Elastisitas tergolong sulit karena setiap material memiliki range yang tidak teratur dan dalam satu material yang sejenis (struktur biaya tetap) tidak terjadi perubahan nilai elastisitas yang berbanding lurus dengan perubahan biaya.
2. Beban akan terdistribusi hanya pada point penghubung (karena bersifat truss)
3. Safety factor bernilai 2.
4. Batas displacement 0,001 m sebelum buckling (pada kolom paling atas)
Tahap Pengerjaan
1. Mendefinisikan problem (node, elemen)
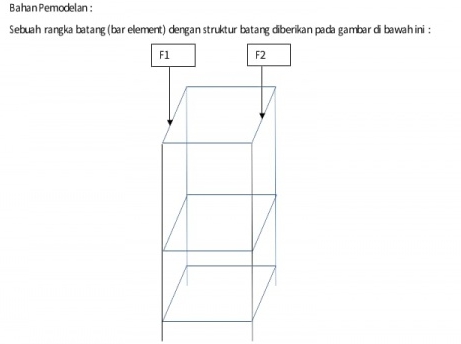
Pada soal yang diberikan, kami diminta untuk mencari optimalisasi pemilihan material untuk struktur tersebut. Material yang digunakan adalah besi siku (angle bar) yang akan menjadi sebuah produk seperti pada gambar. Kami harus membandingkan optimalisasi luas penampang dari berbagai material besi siku agar bisa didapatkan material yang paling efisien.
Dimensi dari struktur:
(p * l * t) = (0,6 m * 0,75 m * 1,8 m)
Di mana pada bagian atas terdapat dua gaya yang membebani, yaitu:
F1 = 2000 N
F2 = 1000 N
2. Mengasumsikan problem (constraint, distribusi)
a. Diasumsikan tidak ada bending karena bersifat truss
b. Beban terdistribusi pada node
c. Safety Factor = 2
d. Batas displacement 0,001m sebelum terjadi buckling
e. Variabel bebas
3. Mengasumsikan solusi problem (stress, displacement)
1) Pilih material dengan 3 variasi, area , dan elastisitas material
2) Buat 2 grafik perbandingan yang pertama grafik dengan material locked dan variasi area, lalu yg ke dua grafik dengan area locked dan variasi elastisitas
3) Setelah itu kita hitung stress/cost
4. Model numerik (untuk mencari stress)
model Trusses_3D_Tugas_Besar_Safety
//define initial variable parameter Integer Points=size(P,1); //Number of Points parameter Integer Trusses=size(C,1); //Number of Trusses parameter Real Yield=215e6; //Yield Strength (Pa) parameter Real Area=0.000224; //Area L Profile (Dimension=0.03, Thickness=0,004) (m2) parameter Real Elas=193e9; //Elasticity SS 304 (Pa)
//define connection parameter Integer C[:,2]=[1,5;
2,6;
3,7;
4,8;
5,6; //1st floor
6,7; //1st floor
7,8; //1st floor
5,8; //1st floor
5,9;
6,10;
7,11;
8,12;
9,10; //2nd floor
10,11;//2nd floor
11,12;//2nd floor
9,12; //2nd floor
9,13;
10,14;
11,15;
12,16;
13,14;//3rd floor
14,15;//3rd floor
15,16;//3rd floor
13,16];//3rd floor
//define coordinates (please put orderly) parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1
-0.3,-0.375,0,1,1,1; //2
-0.3,0.375,0,1,1,1; //3
0.3,0.375,0,1,1,1; //4
0.3,-0.375,0.6,0,0,0; //5
-0.3,-0.375,0.6,0,0,0; //6
-0.3,0.375,0.6,0,0,0; //7
0.3,0.375,0.6,0,0,0; //8
0.3,-0.375,1.2,0,0,0; //9
-0.3,-0.375,1.2,0,0,0; //10
-0.3,0.375,1.2,0,0,0; //11
0.3,0.375,1.2,0,0,0; //12
0.3,-0.375,1.8,0,0,0; //13
-0.3,-0.375,1.8,0,0,0; //14
-0.3,0.375,1.8,0,0,0; //15
0.3,0.375,1.8,0,0,0]; //16
//define external force (please put orderly) parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-500,
0,0,-1000,
0,0,-1000,
0,0,-500};
//solution Real displacement[N], reaction[N]; Real check[3];
Real stress1[Trusses]; Real safety[Trusses]; Real dis[3]; Real Str[3];
protected parameter Integer N=3*Points; Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; Real err=10e-10, ers=10e-4;
algorithm //Creating Global Matrix G:=id; for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g; G:=G_star;
end for;
//Implementing boundary for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for;
//Solving displacement displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction reaction:=(G_star*displacement)-F;
//Eliminating float error for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))}); check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))}); check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
//Calculating stress in each truss for i in 1:Trusses loop for j in 1:3 loop
q1[j]:=P[C[i,1],j]; q2[j]:=P[C[i,2],j]; dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor for i in 1:Trusses loop
if stress1[i]>0 then safety[i]:=Yield/stress1[i]; else safety[i]:=0; end if;
end for;
end Trusses_3D_Tugas_Besar_Safety;
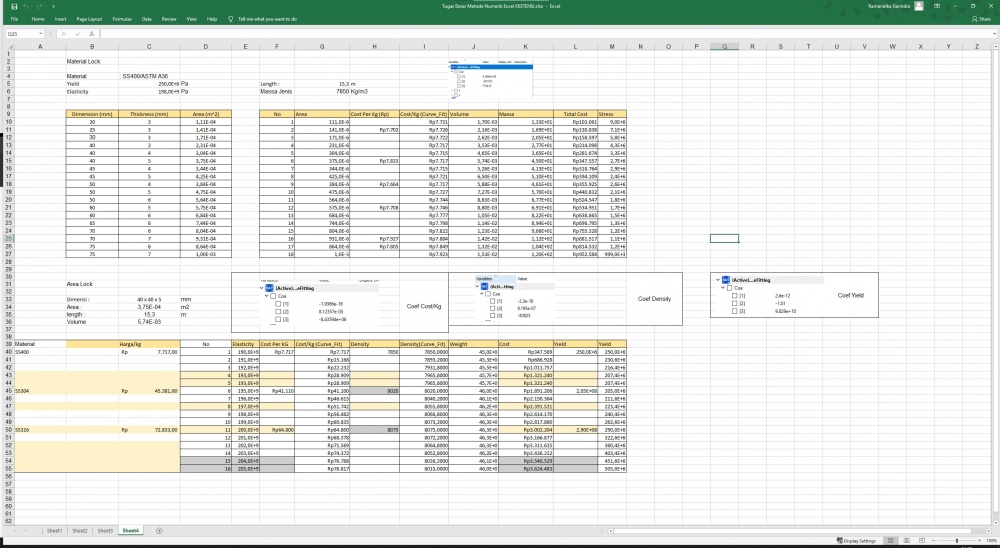
5. Komputasi => mendapatkan data (data stress)
6. Plotting => mencari stress setiap nilai E, dan cost untuk setiap nilai E
7. Optimasi => mencari titik temunya yang mendapatkan material optimum
Malam tadi saya dan teman teman mengadakan diskusi untuk membahas tentang pemilihan material, hingga didapatkan hasil sejauh ini seperti gambar berikut: