Difference between revisions of "Faris Muhammad Jihad - 1706064372"
(→Final Task (Tugas Besar CFD Application)) |
(→Final Task (Tugas Besar CFD Application)) |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 46: | Line 46: | ||
In fluids, two-phase flow is a flow of two phases with the same interfaces in a channel. This could happen in in single-component or multicomponent system, with the possible two-phase flow combinations being: solid-liquid, solid-gas, liquid-vapor, and a combination of the three possible combinations. The way the categorization of two-phase flows are labelled is through the superficial velocity in which the velocity of each phase in the system is used as the parameter. However, the implementation of Computational Fluid Dynamics for two-phase flows is not as common as for single-phase flows. This is due to the complications of two-phase interfaces with variant mass transfers that cause complex flows that are not easily predictable. | In fluids, two-phase flow is a flow of two phases with the same interfaces in a channel. This could happen in in single-component or multicomponent system, with the possible two-phase flow combinations being: solid-liquid, solid-gas, liquid-vapor, and a combination of the three possible combinations. The way the categorization of two-phase flows are labelled is through the superficial velocity in which the velocity of each phase in the system is used as the parameter. However, the implementation of Computational Fluid Dynamics for two-phase flows is not as common as for single-phase flows. This is due to the complications of two-phase interfaces with variant mass transfers that cause complex flows that are not easily predictable. | ||
| − | Currently in the field of Computational Fluid Dynamics, two-phase flow modelling is still ongoing. Several methods that have been proposed have their implementations regarding two-phase flows depending on their constraints and capabilities. In order to improve precision of the modelling of two-phase methods, the proposed methods must be understood, compared, and utilized correctly. This research paper compares those methods and concludes their best implementations. The methods that will be compared in this research paper for the modelling of two-phase flows are | + | Currently in the field of Computational Fluid Dynamics, two-phase flow modelling is still ongoing. Several methods that have been proposed have their implementations regarding two-phase flows depending on their constraints and capabilities. In order to improve precision of the modelling of two-phase methods, the proposed methods must be understood, compared, and utilized correctly. This research paper compares those methods and concludes their best implementations. The methods that will be compared in this research paper for the modelling of two-phase flows are the Volume of Fluid Method and the Level-Set Method. These two methods are compared because they are the most popular methods and have a longer history of being refined and implemented. |
For context, even though Computational Fluid Dynamics methods for two-phase flows are still under development and is not as accurate as single-phase flows, it is still a viable approach for engineering two-phase flow analyses. This is because it can predict detailed transient variations in individual phase velocities, void fractions, and corresponding temperatures, that cannot be done using other approaches. On top of that, it can also deal with heat transfer and pressure drop behaviors. | For context, even though Computational Fluid Dynamics methods for two-phase flows are still under development and is not as accurate as single-phase flows, it is still a viable approach for engineering two-phase flow analyses. This is because it can predict detailed transient variations in individual phase velocities, void fractions, and corresponding temperatures, that cannot be done using other approaches. On top of that, it can also deal with heat transfer and pressure drop behaviors. | ||
| Line 59: | Line 59: | ||
during each time step and describes accurately the location and shape of the free surface. It also allows enforcement of | during each time step and describes accurately the location and shape of the free surface. It also allows enforcement of | ||
the dynamic surface condition in the cells surrounding the interface. It is classified as one of the Eularien methods. | the dynamic surface condition in the cells surrounding the interface. It is classified as one of the Eularien methods. | ||
| + | |||
| + | [[File:VOF.jpg|400px|Image: 400 pixels]] | ||
In the VOF method, local grid refinements have to be done first for accurate results and then the equations of properties in the image below are used to solve a single momentum equation through the domain, and the attained velocity field is shared among the fluids. | In the VOF method, local grid refinements have to be done first for accurate results and then the equations of properties in the image below are used to solve a single momentum equation through the domain, and the attained velocity field is shared among the fluids. | ||
| − | [[File:VOF_method.JPG| | + | [[File:VOF_method.JPG|1000px|Image: 400 pixels]] |
Compared to the other methods, the VOF method is more computationally simpler since it only adds one more equation into the computation. It also has the capability of dealing with highly non-linear problems in which the free-surface experiences sharp topological changes. The VOF method is usually implemented for environmental cases such as the dam-break problem, sluice gate operation, internal waves, and surge propagation in a dry channel. | Compared to the other methods, the VOF method is more computationally simpler since it only adds one more equation into the computation. It also has the capability of dealing with highly non-linear problems in which the free-surface experiences sharp topological changes. The VOF method is usually implemented for environmental cases such as the dam-break problem, sluice gate operation, internal waves, and surge propagation in a dry channel. | ||
| Line 68: | Line 70: | ||
Level-set methods (LSM) | Level-set methods (LSM) | ||
| − | + | Since the VOF method is not optimal for computing curves and surfaces, the Level-set method (LSM) was proposed. The LSM utilizes level sets as a tool for the numerical analysis of surfaces and shapes. This method is not a Eulerien method, which gives it its advantage over other methods especially for surfaces and curves. This means that by using LSM, numerical computations of curves and surfaces on a Cartesian grid can be done without having to parameterize the object. | |
| + | |||
| + | [[File:LSM.JPG|400px|Image: 400 pixels]] | ||
| + | |||
| + | For computational fluid dynamics, the LSM has a specific slightly modified version called the Compact Level-set method (CompactLSM). This is a complement of the LSM that allows for more accurate and faster calculations of the interface equations. Below is the CompactLSM: | ||
| + | |||
| + | [[File:LSM_1.JPG|1000px|Image: 400 pixels]] | ||
| − | + | Due to the advantages of the LSM on implementing numerical computations for surfaces and shapes, it makes it easy for computing cases that change topology such as: when a shape splits in two, develops holes, or the reverse of these operations. This meant that LSM is useful for modeling time-varying objects. Some examples of this are an inflating airbag and a drop of oil in water. | |
| − | '''Discussion''' | + | '''Discussion and Conclusion''' |
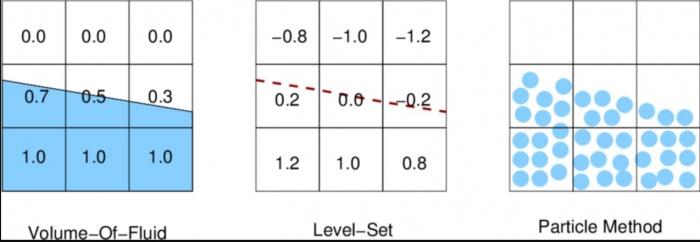
| − | In summary, the VOF method can be shortened into three parts: a scheme to locate the surface, an algorithm to track the surface as a sharp interface moving through a computational grid, and a means of applying boundary conditions at the surface. However, VOF method is not ideal when computing the curvature of the interface or any other smooth properties. The formulation of VOF in three space dimensions also resembles more the lines in a computer code than a rigorous mathematical method. Due to these reasons, the Level Set Method was proposed to deal with these shortfalls. | + | In summary, the VOF method can be shortened into three parts: a scheme to locate the surface, an algorithm to track the surface as a sharp interface moving through a computational grid, and a means of applying boundary conditions at the surface. However, VOF method is not ideal when computing the curvature of the interface or any other smooth properties. The formulation of VOF in three space dimensions also resembles more the lines in a computer code than a rigorous mathematical method. Due to these reasons, the Level Set Method (LSM) was proposed to deal with these shortfalls. The LSM in summary is that the front location is given as the zero level set of an auxiliary field defined over the domain of interest. Therefore, specific cases and parameters of the system must be determined before using one of these methods since they are used at different situations. |
| − | + | [[File:Visual_comparison.JPG|700px|Image: 400 pixels]] | |
'''Acknowledgement''' | '''Acknowledgement''' | ||
| Line 87: | Line 95: | ||
“Computational Fluid Dynamics in Two-Phase Flows.” Case.Edu, Case Western Reserve University, www.sciencedirect.com/topics/engineering/two-phase-flow. Accessed 20 Dec. 2020. | “Computational Fluid Dynamics in Two-Phase Flows.” Case.Edu, Case Western Reserve University, www.sciencedirect.com/topics/engineering/two-phase-flow. Accessed 20 Dec. 2020. | ||
| + | |||
| + | https://www.intechopen.com/books/numerical-simulation-from-brain-imaging-to-turbulent-flows/free-surface-flow-simulation-using-vof-method | ||
Bruce Stewart, H., & Wendroff, B. (1984). Two-phase flow: Models and methods. Journal of Computational Physics, 56(3), 363–409. | Bruce Stewart, H., & Wendroff, B. (1984). Two-phase flow: Models and methods. Journal of Computational Physics, 56(3), 363–409. | ||
| + | |||
| + | Katopodes, N. D. (2019). Volume of Fluid Method. Free-Surface Flow, 766–802. | ||
Latest revision as of 22:53, 16 January 2021
Contents
Profile
Name: Faris Muhammad Jihad
NPM: 1706064372
A mechanical engineering student at the Faculty of Engineering University of Indonesia. Attending the mechanical engineering international program since 2017, involvement of campus activities related to mechanical engineering are through the university robotics club and biomedical research group student assistant. Currently taking elective courses on Computational Fluid Dynamics (CFD) Application and Jet & Rocket Propulsion, whilst working on the last undergraduate assignment thesis with electro-mechanical research group for a thesis topic in robotics.
Study Summary
CFD Application
CFD Application, or more commonly referred to as Computational Fluid Dynamics is the branch of fluid mechanics that utilize numerical methods and data structures to simulate, analyze, and find solutions for fluid flow applications. Aside for the fundamentals of mathematics and physics, CFD requires the pre-requisites of programming, numerical methods, statistics & data, and fluid systems.
The latest development of CFD Application in the academic and industrial level implements this subject with softwares for simulation and data analysis. Amongst those softwares that is used in the CFD Application course in Mechanical Engineering University of Indonesia are CFDSOF and OpenModelica. Along with the usage of other softwares such as CAD from Solidworks or Autodesk Inventor in order to visually create the external environment of the fluid flow simulation.
This course is of importance for students heading towards many mechanical engineering branches since it is used in all industries that deal with thermo-fluid applications. Such as in the aerospace industry, automotive industry, manufacturing, and so on. Amongst those applications could be simulations for determining input of raw materials into a certain machine to optimize for efficiency, simulations for determining the airfoil of an airplane wing, and more.
CFD Application Tasks
Chapter 3
CHAPTER 3 TURBULENCE MODELLING - QUIZ 1 (Example 3.5):[1]
Chapter 4
CHAPTER 4 FINITE VOLUME METHOD FOR DIFFUSION PROBLEMS Simulation Assignment (Example 4.2 and 4.3):[2]
https://www.youtube.com/watch?v=AbvN-jlnxjU
Final Task (Tugas Besar CFD Application)
Title
Computational Fluid Dynamics Two-Phase Flow Modelling Methods: Literature Review
Introduction
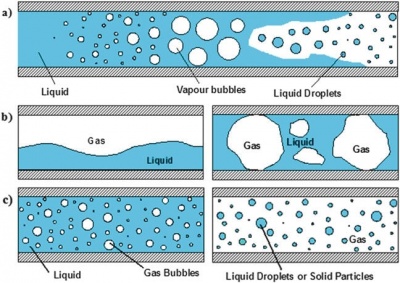
In fluids, two-phase flow is a flow of two phases with the same interfaces in a channel. This could happen in in single-component or multicomponent system, with the possible two-phase flow combinations being: solid-liquid, solid-gas, liquid-vapor, and a combination of the three possible combinations. The way the categorization of two-phase flows are labelled is through the superficial velocity in which the velocity of each phase in the system is used as the parameter. However, the implementation of Computational Fluid Dynamics for two-phase flows is not as common as for single-phase flows. This is due to the complications of two-phase interfaces with variant mass transfers that cause complex flows that are not easily predictable.
Currently in the field of Computational Fluid Dynamics, two-phase flow modelling is still ongoing. Several methods that have been proposed have their implementations regarding two-phase flows depending on their constraints and capabilities. In order to improve precision of the modelling of two-phase methods, the proposed methods must be understood, compared, and utilized correctly. This research paper compares those methods and concludes their best implementations. The methods that will be compared in this research paper for the modelling of two-phase flows are the Volume of Fluid Method and the Level-Set Method. These two methods are compared because they are the most popular methods and have a longer history of being refined and implemented.
For context, even though Computational Fluid Dynamics methods for two-phase flows are still under development and is not as accurate as single-phase flows, it is still a viable approach for engineering two-phase flow analyses. This is because it can predict detailed transient variations in individual phase velocities, void fractions, and corresponding temperatures, that cannot be done using other approaches. On top of that, it can also deal with heat transfer and pressure drop behaviors.
Methodology
Volume of fluid (VOF) method
In order to overcome the problem of low resolution for coarse computational grids, in 1981, Hirt and Nichols composed an interface tracking method called the Volume of fluid (VOF) method. The VOF method provides a simple technique for computing its movement during each time step and describes accurately the location and shape of the free surface. It also allows enforcement of the dynamic surface condition in the cells surrounding the interface. It is classified as one of the Eularien methods.
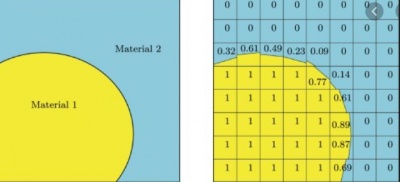
In the VOF method, local grid refinements have to be done first for accurate results and then the equations of properties in the image below are used to solve a single momentum equation through the domain, and the attained velocity field is shared among the fluids.
Compared to the other methods, the VOF method is more computationally simpler since it only adds one more equation into the computation. It also has the capability of dealing with highly non-linear problems in which the free-surface experiences sharp topological changes. The VOF method is usually implemented for environmental cases such as the dam-break problem, sluice gate operation, internal waves, and surge propagation in a dry channel.
Level-set methods (LSM)
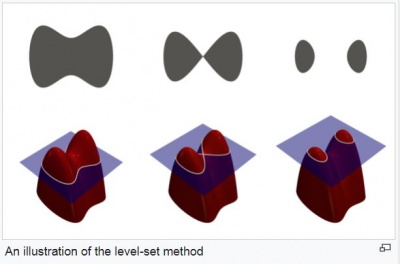
Since the VOF method is not optimal for computing curves and surfaces, the Level-set method (LSM) was proposed. The LSM utilizes level sets as a tool for the numerical analysis of surfaces and shapes. This method is not a Eulerien method, which gives it its advantage over other methods especially for surfaces and curves. This means that by using LSM, numerical computations of curves and surfaces on a Cartesian grid can be done without having to parameterize the object.
For computational fluid dynamics, the LSM has a specific slightly modified version called the Compact Level-set method (CompactLSM). This is a complement of the LSM that allows for more accurate and faster calculations of the interface equations. Below is the CompactLSM:
Due to the advantages of the LSM on implementing numerical computations for surfaces and shapes, it makes it easy for computing cases that change topology such as: when a shape splits in two, develops holes, or the reverse of these operations. This meant that LSM is useful for modeling time-varying objects. Some examples of this are an inflating airbag and a drop of oil in water.
Discussion and Conclusion
In summary, the VOF method can be shortened into three parts: a scheme to locate the surface, an algorithm to track the surface as a sharp interface moving through a computational grid, and a means of applying boundary conditions at the surface. However, VOF method is not ideal when computing the curvature of the interface or any other smooth properties. The formulation of VOF in three space dimensions also resembles more the lines in a computer code than a rigorous mathematical method. Due to these reasons, the Level Set Method (LSM) was proposed to deal with these shortfalls. The LSM in summary is that the front location is given as the zero level set of an auxiliary field defined over the domain of interest. Therefore, specific cases and parameters of the system must be determined before using one of these methods since they are used at different situations.
Acknowledgement
This research paper was written as a final project for the Application of Computational Fluid Dynamics course in the Mechanical Engineering Department, Faculty of Engineering, University of Indonesia. The author thanks Dr. Ahmad Indra as the advisor and lecturer of the research paper as well as the course, and also thanks the classmates for the educational discussions regarding the research paper and the course topics for the author's learning of the subject.
Reference
“Two-Phase Flow.” Sciencedirect.Com, ScienceDirect, www.sciencedirect.com/topics/engineering/two-phase-flow. Accessed 20 Dec. 2020.
“Computational Fluid Dynamics in Two-Phase Flows.” Case.Edu, Case Western Reserve University, www.sciencedirect.com/topics/engineering/two-phase-flow. Accessed 20 Dec. 2020.
Bruce Stewart, H., & Wendroff, B. (1984). Two-phase flow: Models and methods. Journal of Computational Physics, 56(3), 363–409.
Katopodes, N. D. (2019). Volume of Fluid Method. Free-Surface Flow, 766–802.