Difference between revisions of "Akmal Rayhansyah"
(→Ujian Akhir Semester) |
|||
| (47 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | |||
| + | == Perkenalan Singkat == | ||
| + | |||
Nama : Akmal Rayhansyah H. N. | Nama : Akmal Rayhansyah H. N. | ||
| Line 5: | Line 8: | ||
TTL : Bandung, 28 November 2000 | TTL : Bandung, 28 November 2000 | ||
| − | Halo, perkenalkan saya Akmal Rayhansyah. Teman-temanku biasa memanggil saya Akmal. Saya adalah seorang mahasiswa Teknik Mesin Universitas Indonesia angkatan 2019. | + | Halo, perkenalkan saya Akmal Rayhansyah. Teman-temanku biasa memanggil saya Akmal. Saya adalah seorang mahasiswa Teknik Mesin Universitas Indonesia angkatan 2019. Saya memilih jurusan teknik mesin karena saya memiliki ketertarikan di bidang permesinan terutama pada bidang manufaktur otomotif. Saat ini saya sedang berpartisipasi di tim Universitas Indonesia Super Milage Vehicle sebagai staf. Alasan mengapa saya berpartisipasi dalam tim tersebut adalah agar saya dapat gambaran mengenai ketertarikan saya dalam manufaktur otomotif tersebut. |
| + | |||
| + | == Metode Numerik == | ||
| + | Metode numerik itu sendiri merupakan suatu teknik penyelesaian permasalahan yang diformulasikan secara matematis dengan menggunakan operasi aritmatika. Metode ini digunakan disaat ada sebuah permasalahan matematis yang tidak bisa diselesaikan dengan metode analitik. Jikapun masalah tersebut terdapat penyelesaian secara analitik, proses penyelesaian tersebut akan sangat rumit dan memakan waktu yang cukup lama sehingga tidak efisien. | ||
| + | |||
| + | Adapun kelebihan dan kekurangan dalam menggunakan metode numerik, | ||
| + | |||
| + | Kelebihan : | ||
| + | |||
| + | 1. Mampu menyelesaikan persamaan diferensial non linier dan sangat kompleks | ||
| + | |||
| + | 2. Mampu menghasilkan nilai perkiraan atau pendekatan dari penyelesaian analitis sehingga penyelesaian tersebut mampu memuat nilai kesalahan | ||
| + | |||
| + | Kekuragan : | ||
| + | |||
| + | 1. Nilai yang didapat tidaklah eksak, melainkan berupa pendekatan | ||
| + | |||
| + | 2. Perhitungannya lama dan berulang-ulang apabila permasalahannya sangat kompleks | ||
| + | |||
| + | |||
| + | == Perkuliahan == | ||
| + | Sebelumnya, perkuliahan metode numerik difasilitasi oleh Bapak Dr. Ir. Engkos A. Kosasih, M.T. dari awal hingga Ujian Tengah Semester. Selama pengajaran oleh beliau, saya diajarkan beberapa topik metode numerik, yaitu | ||
| + | |||
| + | 1. Sistem Persamaan | ||
| + | |||
| + | 2. Pseudocode | ||
| + | |||
| + | 3. Turunan Numerik | ||
| + | |||
| + | 4. Metode Newton Rhapson, Secant, dan Bisection | ||
| + | |||
| + | 5. Regresi Linier | ||
| + | |||
| + | 6. Interpolasi | ||
| + | |||
| + | Setelah itu, pertemuan-pertemuan selanjutnya akan difasilitasi oleh Bapak Dr. Ir. Ahmad Indra S. | ||
| + | |||
| + | |||
| + | '''Minggu pertama (11 November 2020)''' | ||
| + | |||
| + | Pada minggu pertama ini, Bapak Dr. Ir. Ahmad Indra S. memberikan penjelasan terlebih dahulu mengenai apa itu metode numerik dan berbargai kegunaannya. Kemudian, beliau memperkenalkan saya kepada Wiki AIR (Ahmad Indra Research Group), salah satu media penerapan metode numerik milik beliau. Setelah itu saya juga diajarkan bagaimana cara mengakses dan menggunakan situs tersebut. Situs tersebut akan digunakan selama pembelajaran bersama beliau. | ||
| + | Kemudian, saya dan rekan sekelas berdiskusi dengan beliau mengenai apa saja kegunaan dan manfaat mempelajari metode numerik untuk kehidupan dan pekerjaan. Berikut merupakan esensi dalam mempelajari metode numerik, | ||
| + | |||
| + | 1. Memahami konsep dan prinsip dasar dalam metode numerik seperti algoritma, aljabar, persamaan diferensial, dan lain-lain | ||
| + | |||
| + | 2. Mengerti dalam menerapkan dan mengaplikasikan konsep metode numerik | ||
| + | |||
| + | 3. Mampu menerapkan dan mengaplikasikan metode numerik dalam persoalan teknik | ||
| + | |||
| + | 4. Menempuh 3 poin diatas dengan poin terpenting, yaitu adab | ||
| + | |||
| + | Setelah itu, saya juga mendapatkan pembelajaran mengenai gambaran dasar OpenModelica, sebuah program yang berfungsi untuk menyelesaikan permasalahan yang diberikan batasan oleh kita sendiri. | ||
| + | |||
| + | Tugas 1 | ||
| + | |||
| + | [[File:Tugas_1_operasistandar.mp4]] | ||
| + | |||
| + | |||
| + | '''Minggu kedua (18 November 2020)''' | ||
| + | |||
| + | Pada minggu kedua, Pak Dai memberikan ajaran tentang kehidupan kepada kita bahwa janganlah menjadi orang yang merugi, jadilah orang yang beruntung. Yang dimaksud dengan menjadi orang beruntung adalah jadilah orang yang mampu menjadi pribadi yang lebih baik seiring berjalannya waktu. | ||
| + | |||
| + | Setelah itu, kami diminta untuk mempresentasikan tugas yang dikerjakan oleh masing-masing di minggu sebelumnya dengan tujuan untuk menilai kemampuan para mahasiswa dalam memahami penggunaan aplikasi OpenModelica. | ||
| + | |||
| + | Kemudian Pak Dai memberikan materi pembelajaran baru, yaitu penggunaan ''class'' untuk memanggil sebuah ''function''. ''function'' yang bisa dipanggil kedalam beragam macamnya. | ||
| + | |||
| + | Tugas 2 | ||
| + | |||
| + | [[File:Tugas_2_operasipemanggilanfungsikelas.mp4]] | ||
| + | |||
| + | |||
| + | '''Minggu ketiga (25 November 2020)''' | ||
| + | |||
| + | Pada minggu ketiga, Pak Dai memberikan ajaran tentang cara menyelesaikan problema statistika struktur menggunakan OpenModelica. Berikut merupakan salah satuh contoh penyelesaian : | ||
| + | |||
| + | [[File:Contoh soal 3.1.jpg|center]] | ||
| + | |||
| + | Kemudian pseudocode-nya adalah sebagai berikut | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | style='border-style: none none solid solid;' | | ||
| + | |||
| + | model Trusses | ||
| + | |||
| + | parameter Integer N=10; //Global matrice = 2*points connected | ||
| + | parameter Real A=8; | ||
| + | parameter Real E=1.9e6; | ||
| + | Real G[N,N]; //global | ||
| + | Real Ginitial[N,N]; //global | ||
| + | Real Sol[N]; //global dispplacement | ||
| + | Real X[N]={0,0,0,0,0,0,0,-500,0,-500}; | ||
| + | Real R[N]; //global reaction force | ||
| + | Real SolMat[N,1]; | ||
| + | Real XMat[N,1]; | ||
| + | |||
| + | //boundary condition | ||
| + | Integer b1=1; | ||
| + | Integer b2=3; | ||
| + | |||
| + | //truss 1 | ||
| + | parameter Real X1=0; //degree between truss | ||
| + | Real k1=A*E/1; | ||
| + | Real K1[4,4]; //stiffness matrice | ||
| + | Integer p1a=1; | ||
| + | Integer p1b=2; | ||
| + | Real G1[N,N]; | ||
| + | |||
| + | //truss 2 | ||
| + | parameter Real X2=135; //degree between truss | ||
| + | Real k2=A*E/50.912; | ||
| + | Real K2[4,4]; //stiffness matrice | ||
| + | Integer p2a=2; | ||
| + | Integer p2b=3; | ||
| + | Real G2[N,N]; | ||
| + | |||
| + | //truss 3 | ||
| + | parameter Real X3=0; //degree between truss | ||
| + | Real k3=A*E/36; | ||
| + | Real K3[4,4]; //stiffness matrice | ||
| + | Integer p3a=3; | ||
| + | Integer p3b=4; | ||
| + | Real G3[N,N]; | ||
| + | |||
| + | //truss 4 | ||
| + | parameter Real X4=90; //degree between truss | ||
| + | Real k4=A*E/36; | ||
| + | Real K4[4,4]; //stiffness matrice | ||
| + | Integer p4a=2; | ||
| + | Integer p4b=4; | ||
| + | Real G4[N,N]; | ||
| + | |||
| + | //truss 5 | ||
| + | parameter Real X5=45; //degree between truss | ||
| + | Real k5=A*E/50.912; | ||
| + | Real K5[4,4]; //stiffness matrice | ||
| + | Integer p5a=2; | ||
| + | Integer p5b=5; | ||
| + | Real G5[N,N]; | ||
| + | |||
| + | //truss 6 | ||
| + | parameter Real X6=0; //degree between truss | ||
| + | Real k6=A*E/36; | ||
| + | Real K6[4,4]; //stiffness matrice | ||
| + | Integer p6a=4; | ||
| + | Integer p6b=5; | ||
| + | Real G6[N,N]; | ||
| + | |||
| + | /* | ||
| + | for each truss, please ensure pXa is lower then pXb (X represents truss element number) | ||
| + | */ | ||
| + | |||
| + | algorithm | ||
| + | |||
| + | //creating global matrice | ||
| + | K1:=Stiffness_Matrices(X1); | ||
| + | G1:=k1*Local_Global(K1,N,p1a,p1b); | ||
| + | |||
| + | K2:=Stiffness_Matrices(X2); | ||
| + | G2:=k2*Local_Global(K2,N,p2a,p2b); | ||
| + | |||
| + | K3:=Stiffness_Matrices(X3); | ||
| + | G3:=k3*Local_Global(K3,N,p3a,p3b); | ||
| + | |||
| + | K4:=Stiffness_Matrices(X4); | ||
| + | G4:=k4*Local_Global(K4,N,p4a,p4b); | ||
| + | |||
| + | K5:=Stiffness_Matrices(X5); | ||
| + | G5:=k5*Local_Global(K5,N,p5a,p5b); | ||
| + | |||
| + | K6:=Stiffness_Matrices(X6); | ||
| + | G6:=k6*Local_Global(K6,N,p6a,p6b); | ||
| + | |||
| + | G:=G1+G2+G3+G4+G5+G6; | ||
| + | Ginitial:=G; | ||
| + | |||
| + | //implementing boundary condition | ||
| + | for i in 1:N loop | ||
| + | G[2*b1-1,i]:=0; | ||
| + | G[2*b1,i]:=0; | ||
| + | G[2*b2-1,i]:=0; | ||
| + | G[2*b2,i]:=0; | ||
| + | end for; | ||
| + | |||
| + | G[2*b1-1,2*b1-1]:=1; | ||
| + | G[2*b1,2*b1]:=1; | ||
| + | G[2*b2-1,2*b2-1]:=1; | ||
| + | G[2*b2,2*b2]:=1; | ||
| + | |||
| + | //solving displacement | ||
| + | Sol:=Gauss_Jordan(N,G,X); | ||
| + | |||
| + | //solving reaction force | ||
| + | SolMat:=matrix(Sol); | ||
| + | XMat:=matrix(X); | ||
| + | R:=Reaction_Trusses(N,Ginitial,SolMat,XMat); | ||
| + | |||
| + | end trusses; | ||
| + | |} | ||
| + | |||
| + | Setelah mensimulasikan pseudocode diatas, berikut merupakan grafik hasil ''reaction'' dan ''displacement'' pada simulasi trusses diatas | ||
| + | |||
| + | [[File:grafik reaction contoh.png]] | ||
| + | grafik reaction | ||
| + | |||
| + | [[File:grafik displacement contoh.png]] | ||
| + | grafik displacement | ||
| + | |||
| + | Tugas 3, trusses 2(dua) dimensi | ||
| + | |||
| + | [[File:Soal truses.jpg|center]] | ||
| + | |||
| + | Persamaan | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | style='border-style: none none solid solid;' | | ||
| + | |||
| + | class trusses_week3 | ||
| + | |||
| + | parameter Integer N=8; //Global matrice = 2*points connected | ||
| + | parameter Real A=0.001; //Area m2 | ||
| + | parameter Real E=200e9; //Pa | ||
| + | Real G[N,N]; //global | ||
| + | Real Ginitial[N,N]; //global | ||
| + | Real Sol[N]; //global dispplacement | ||
| + | Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033}; | ||
| + | Real R[N]; //global reaction force | ||
| + | Real SolMat[N,1]; | ||
| + | Real XMat[N,1]; | ||
| + | |||
| + | //boundary condition | ||
| + | Integer b1=1; | ||
| + | Integer b2=3; | ||
| + | |||
| + | //truss 1 | ||
| + | parameter Real X1=0; //degree between truss | ||
| + | Real k1=A*E/1; | ||
| + | Real K1[4,4]; //stiffness matrice | ||
| + | Integer p1a=1; | ||
| + | Integer p1b=2; | ||
| + | Real G1[N,N]; | ||
| + | |||
| + | //truss 2 | ||
| + | parameter Real X2=0; //degree between truss | ||
| + | Real k2=A*E/1; | ||
| + | Real K2[4,4]; //stiffness matrice | ||
| + | Integer p2a=2; | ||
| + | Integer p2b=3; | ||
| + | Real G2[N,N]; | ||
| + | |||
| + | //truss 3 | ||
| + | parameter Real X3=90; //degree between truss | ||
| + | Real k3=A*E/1.25; | ||
| + | Real K3[4,4]; //stiffness matrice | ||
| + | Integer p3a=2; | ||
| + | Integer p3b=4; | ||
| + | Real G3[N,N]; | ||
| + | |||
| + | //truss 4 | ||
| + | parameter Real X4=90+38.6598; //degree between truss | ||
| + | Real k4=A*E/1.6; | ||
| + | Real K4[4,4]; //stiffness matrice | ||
| + | Integer p4a=1; | ||
| + | Integer p4b=4; | ||
| + | Real G4[N,N]; | ||
| + | |||
| + | //truss 5 | ||
| + | parameter Real X5=90-38.6598; //degree between truss | ||
| + | Real k5=A*E/1.6; | ||
| + | Real K5[4,4]; //stiffness matrice | ||
| + | Integer p5a=3; | ||
| + | Integer p5b=4; | ||
| + | Real G5[N,N]; | ||
| + | |||
| + | /* | ||
| + | for each truss, please ensure pXa is lower then pXb (X represents truss element number) | ||
| + | */ | ||
| + | |||
| + | algorithm | ||
| + | |||
| + | //creating global matrice | ||
| + | K1:=stiffness_matrices(X1); | ||
| + | G1:=k1*local_global(K1,N,p1a,p1b); | ||
| + | |||
| + | K2:=stiffness_matrices(X2); | ||
| + | G2:=k2*local_global(K2,N,p2a,p2b); | ||
| + | |||
| + | K3:=stiffness_matrices(X3); | ||
| + | G3:=k3*local_global(K3,N,p3a,p3b); | ||
| + | |||
| + | K4:=stiffness_matrices(X4); | ||
| + | G4:=k4*local_global(K4,N,p4a,p4b); | ||
| + | |||
| + | K5:=stiffness_matrices(X5); | ||
| + | G5:=k5*local_global(K5,N,p5a,p5b); | ||
| + | |||
| + | G:=G1+G2+G3+G4+G5; | ||
| + | Ginitial:=G; | ||
| + | |||
| + | //implementing boundary condition | ||
| + | for i in 1:N loop | ||
| + | G[2*b1-1,i]:=0; | ||
| + | G[2*b1,i]:=0; | ||
| + | G[2*b2-1,i]:=0; | ||
| + | G[2*b2,i]:=0; | ||
| + | end for; | ||
| + | |||
| + | G[2*b1-1,2*b1-1]:=1; | ||
| + | G[2*b1,2*b1]:=1; | ||
| + | G[2*b2-1,2*b2-1]:=1; | ||
| + | G[2*b2,2*b2]:=1; | ||
| + | |||
| + | //solving displacement | ||
| + | Sol:=gauss_jordan(N,G,X); | ||
| + | |||
| + | //solving reaction force | ||
| + | SolMat:=matrix(Sol); | ||
| + | XMat:=matrix(X); | ||
| + | R:=reaction_trusses(N,Ginitial,SolMat,XMat); | ||
| + | |||
| + | end trusses_week3; | ||
| + | |} | ||
| + | |||
| + | Fungsi Panggil | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | style='border-style: none none solid solid;' | | ||
| + | ''Matrice Transformation'' | ||
| + | |||
| + | function stiffness_matrices | ||
| + | |||
| + | input Real A; | ||
| + | Real Y; | ||
| + | output Real X[4,4]; | ||
| + | Real float_error = 10e-10; | ||
| + | |||
| + | final constant Real pi=2*Modelica.Math.asin(1.0); | ||
| + | |||
| + | algorithm | ||
| + | |||
| + | Y:=A/180*pi; | ||
| + | |||
| + | X:= | ||
| + | [(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,- | ||
| + | Modelica.Math.cos(Y)*Modelica.Math.sin(Y); | ||
| + | |||
| + | Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,- | ||
| + | Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2; | ||
| + | |||
| + | -(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y), | ||
| + | (Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y); | ||
| + | |||
| + | -Modelica.Math.cos(Y)*Modelica.Math.sin(Y),- | ||
| + | (Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2]; | ||
| + | |||
| + | for i in 1:4 loop | ||
| + | for j in 1:4 loop | ||
| + | if abs(X[i,j]) <= float_error then | ||
| + | X[i,j] := 0; | ||
| + | end if; | ||
| + | end for; | ||
| + | end for; | ||
| + | |||
| + | end stiffness_matrices; | ||
| + | |||
| + | | style="width: 20cm;"| | ||
| + | ''Global Element Matrice'' | ||
| + | |||
| + | function local_global | ||
| + | |||
| + | input Real Y[4,4]; | ||
| + | input Integer B; | ||
| + | input Integer p1; | ||
| + | input Integer p2; | ||
| + | output Real G[B,B]; | ||
| + | |||
| + | algorithm | ||
| + | |||
| + | for i in 1:B loop | ||
| + | for j in 1:B loop | ||
| + | G[i,j]:=0; | ||
| + | end for; | ||
| + | end for; | ||
| + | |||
| + | G[2*p1,2*p1]:=Y[2,2]; | ||
| + | G[2*p1-1,2*p1-1]:=Y[1,1]; | ||
| + | G[2*p1,2*p1-1]:=Y[2,1]; | ||
| + | G[2*p1-1,2*p1]:=Y[1,2]; | ||
| + | |||
| + | G[2*p2,2*p2]:=Y[4,4]; | ||
| + | G[2*p2-1,2*p2-1]:=Y[3,3]; | ||
| + | G[2*p2,2*p2-1]:=Y[4,3]; | ||
| + | G[2*p2-1,2*p2]:=Y[3,4]; | ||
| + | |||
| + | G[2*p2,2*p1]:=Y[4,2]; | ||
| + | G[2*p2-1,2*p1-1]:=Y[3,1]; | ||
| + | G[2*p2,2*p1-1]:=Y[4,1]; | ||
| + | G[2*p2-1,2*p1]:=Y[3,2]; | ||
| + | |||
| + | G[2*p1,2*p2]:=Y[2,4]; | ||
| + | G[2*p1-1,2*p2-1]:=Y[1,3]; | ||
| + | G[2*p1,2*p2-1]:=Y[2,3]; | ||
| + | G[2*p1-1,2*p2]:=Y[1,4]; | ||
| + | |||
| + | end local_global; | ||
| + | |||
| + | | style="width: 20cm;"| | ||
| + | ''Reaction Matrice Equation'' | ||
| + | |||
| + | function reaction_trusses | ||
| + | |||
| + | input Integer N; | ||
| + | input Real A[N,N]; | ||
| + | input Real B[N,1]; | ||
| + | input Real C[N,1]; | ||
| + | Real X[N,1]; | ||
| + | output Real Sol[N]; | ||
| + | Real float_error = 10e-10; | ||
| + | |||
| + | algorithm | ||
| + | X:=A*B-C; | ||
| + | |||
| + | for i in 1:N loop | ||
| + | if abs(X[i,1]) <= float_error then | ||
| + | X[i,1] := 0; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | for i in 1:N loop | ||
| + | Sol[i]:=X[i,1]; | ||
| + | end for; | ||
| + | |||
| + | end reaction_trusses; | ||
| + | |||
| + | | style="width: 20cm;"| | ||
| + | ''Gauss Jordan'' | ||
| + | |||
| + | function gauss_jordan | ||
| + | |||
| + | input Integer N; | ||
| + | input Real A[N,N]; | ||
| + | input Real B[N]; | ||
| + | output Real X[N]; | ||
| + | Real float_error = 10e-10; | ||
| + | |||
| + | algorithm | ||
| + | X:=Modelica.Math.Matrices.solve(A,B); | ||
| + | |||
| + | for i in 1:N loop | ||
| + | if abs(X[i]) <= float_error then | ||
| + | X[i] := 0; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | end gauss_jordan; | ||
| + | |||
| + | |} | ||
| + | |||
| + | [[File:grafik_displacement_tugas3.png]] | ||
| + | grafik displacement | ||
| + | |||
| + | [[File:grafik_reaction_tugas3.png]] | ||
| + | grafik reaction | ||
| + | |||
| + | '''Minggu keempat (2 Desember 2020)''' | ||
| + | |||
| + | Kuis flowchart | ||
| + | |||
| + | [[File:214733.jpg]] | ||
| + | |||
| + | Tugas 4, Trusses 3(tiga) dimensi | ||
| + | |||
| + | [[File:soal_tugas4_trusses3d.png|center]] | ||
| + | |||
| + | [[File:flowchart_tugas4_Akmal.jpg|403x599px]] | ||
| + | ''Flowchart'' penyelesaian | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | style='border-style: none none solid solid;' | | ||
| + | |||
| + | class Tugas_trusses3d | ||
| + | |||
| + | //define initial variable | ||
| + | parameter Integer Points=4; //Number of Points | ||
| + | parameter Integer Trusses=3; //Number of Trusses | ||
| + | parameter Real Area=0.0015; //Area | ||
| + | parameter Real Elas=70e9; //Elasticity | ||
| + | |||
| + | //define connection | ||
| + | parameter Integer C[Trusses,2]=[1,2; | ||
| + | 1,3; | ||
| + | 1,4]; | ||
| + | |||
| + | //define coordinates (please put orderly) | ||
| + | parameter Real P[Points,3]=[2,0,0; | ||
| + | 0,0,1.5; | ||
| + | 0,0,-1.5; | ||
| + | 0,1.5,0]; | ||
| + | |||
| + | //define external force (please put orderly) | ||
| + | parameter Real F[Points*3]={0,-5000,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0}; | ||
| + | |||
| + | //define boundary | ||
| + | parameter Integer b[:]={2,3,4}; | ||
| + | |||
| + | //solution | ||
| + | Real displacement[N], reaction[N]; | ||
| + | |||
| + | protected | ||
| + | parameter Integer N=3*Points; | ||
| + | Integer boundary[3*size(b,1)]=cat(1,(3*b).-2,(3*b).-1,3*b); | ||
| + | Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), err=10e-10, cx, cy, cz, L, E, | ||
| + | X[3,3]; | ||
| + | |||
| + | algorithm | ||
| + | //Creating Global Matrix | ||
| + | G:=id; | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | end for; | ||
| + | |||
| + | //Solving Constant | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | E:=Area*Elas/L; | ||
| + | |||
| + | //Solving Matrix | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=E*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | |||
| + | //Transforming to global matrix | ||
| + | g:=zeros(N,N); | ||
| + | for m,n in 1:3 loop | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n]; | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n]; | ||
| + | end for; | ||
| + | |||
| + | G_star:=G+g; | ||
| + | G:=G_star; | ||
| + | end for; | ||
| + | |||
| + | //Implementing boundary | ||
| + | for i in boundary loop | ||
| + | for j in 1:N loop | ||
| + | G[i,j]:=id[i,j]; | ||
| + | end for; | ||
| + | end for; | ||
| + | |||
| + | //Solving displacement | ||
| + | displacement:=Modelica.Math.Matrices.solve(G,F); | ||
| + | |||
| + | //Solving reaction | ||
| + | reaction:=(G_star*displacement)-F; | ||
| + | |||
| + | //Eliminating float error | ||
| + | for i in 1:N loop | ||
| + | reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; | ||
| + | displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i]; | ||
| + | end for; | ||
| + | |||
| + | end Tugas_trusses3d; | ||
| + | |} | ||
| + | |||
| + | [[File:reaction_trusses3d.png|800x421px]] | ||
| + | grafik reaction | ||
| + | |||
| + | [[File:displacement_trusses3d.png|800x421px]] | ||
| + | grafik displacement | ||
| + | |||
| + | '''Minggu Keenam (16 Desember 2020)''' | ||
| + | |||
| + | Pada pertemuan Metnum Rabu, 16 Desember 2020 kami diajarkan tentang optimasi menggunakan Open Modelica. Optimasi merupakan sebuah cara untuk mendapatkan nilai minimum atau maksimum dari suatu permasalahan. Terdapat beberapa aspek yang diperhatikan dalam melakukan optimasi yaitu fungsi objektif dan ada juga konstrain. Pada pertemuan ini Asisten Dosen Metode Numerik yaitu Bu Chandra memberikan tutorial atau mengajarkan cara untuk melakukan optimasi menggunakan metode Bracket. Pada metode "Bracket Optimization Using Golden Ratio" terdapat satu grafik yang mempunyai nilai f(x) global maks dan lokal maks serta terdapat f(x) global minimum dann lokal minimum. Pada pertemuan kali ini, Bu chandra mengajarkan hingga melakukan optimasi grafik tanpa sebuah konstrain. | ||
| + | |||
| + | Berikut merupakan coding open modelica yang diajarkan oleh Bu Chandra: | ||
| + | |||
| + | Fungsi panggil | ||
| + | |||
| + | function f_obj3 | ||
| + | import Modelica.Math; | ||
| + | input Real x; | ||
| + | output Real y; | ||
| + | algorithm | ||
| + | y:= 2*Math.sin(x)-x^2/10; | ||
| + | end f_obj3; | ||
| + | |||
| + | Setelah itu dibuat lah model optimasi sistem bracketnya: | ||
| + | |||
| + | model bracket_optimation3 | ||
| + | parameter Integer n=8; | ||
| + | Real x1[n]; | ||
| + | Real x2[n]; | ||
| + | Real xup; | ||
| + | Real xlow; | ||
| + | Real d; | ||
| + | Real f1[n]; | ||
| + | Real f2[n]; | ||
| + | Real xopt; | ||
| + | Real yopt; | ||
| + | algorithm | ||
| + | xup :=4; | ||
| + | xlow:=0; | ||
| + | for i in (1:n) loop | ||
| + | d:= (5^(1/2)-1)/2*(xup-xlow); | ||
| + | x1[i]:= xlow+d; | ||
| + | x2[i]:= xup-d; | ||
| + | f1[i]:= f_obj3(x1[i]); | ||
| + | f2[i]:= f_obj3(x2[i]); | ||
| + | if f1[i]>f2[i] then | ||
| + | xup:= xup; | ||
| + | xlow:= x2[i]; | ||
| + | xopt:= xup; | ||
| + | yopt:= f1[i]; | ||
| + | else | ||
| + | xlow:= xlow; | ||
| + | xup:= x1[i]; | ||
| + | xopt:= xup; | ||
| + | end if; | ||
| + | end for; | ||
| + | end bracket_optimation3; | ||
| + | |||
| + | |||
| + | == Tugas Besar == | ||
| + | |||
| + | '''Tujuan penyelesaian''' | ||
| + | |||
| + | Mencari harga pembuatan rangka truss sederhana yang optimal dengan memvariasikan dimensi dan elastisitas material | ||
| + | |||
| + | '''Problema (trusses)''' | ||
| + | |||
| + | [[File:Soal_tubes_Akmal.jpg]] | ||
| + | |||
| + | [[File:Profil_tubes_Akmal.jpg]] | ||
| + | |||
| + | '''Keterangan model''' | ||
| + | |||
| + | Asumsi : | ||
| + | 1. Beban akan terdistribusi hanya pada point penghubung (truss) | ||
| + | 2. Safety Factor minimal = 2 | ||
| + | 3. Batas displacement 0.001 m sebelum terjadinya buckling pada kolom paling atas | ||
| + | |||
| + | Constraint : | ||
| + | 1. Nodes pada lantai dasar fixed (1,2,3,4) | ||
| + | 2. Beban F1 dan F2 terdistribusi ke node sekitarnya | ||
| + | a. Node 13 & 16 = 1000 N | ||
| + | b. Node 14 & 15 = 500 N | ||
| + | |||
| + | '''Alur penyelesaian''' | ||
| + | |||
| + | 1. Mencari area paling optimum dengan membandingkan dimensi siku (Elastisitas tetap) | ||
| + | |||
| + | 2. Mencari material paling optimum dengan membandingkan berbagai material sesuai Elastisitas dan Yield strenght masing-masing (area tetap) | ||
| + | |||
| + | '''Mencari dan mengolah data''' | ||
| + | |||
| + | 1. Elastisitas tetap | ||
| + | |||
| + | [[File:Tabel elastisitas tetap.jpg]] | ||
| + | |||
| + | 2. Area tetap | ||
| + | |||
| + | [[File:Tabel area tetap.jpg]] | ||
| + | |||
| + | '''Pengerjaan''' | ||
| + | |||
| + | Pertama-tama, membuat kode model untuk mencari stress pada setiap variabel data | ||
| + | |||
| + | Model untuk mencari stress | ||
| + | |||
| + | class kuis_23desember | ||
| + | |||
| + | //initial variable | ||
| + | parameter Integer Points=16; //Jumlah Point | ||
| + | parameter Integer Trusses=24; //Jumlah Trusses | ||
| + | parameter Real Area=disesuaikan; //Area digunakan | ||
| + | parameter Real Elas=disesuaikan; //Elasticitas material | ||
| + | |||
| + | //define connection | ||
| + | parameter Integer C[Trusses,2]=[1,5; | ||
| + | 2,6; | ||
| + | 3,7; | ||
| + | 4,8; | ||
| + | 5,6; //lantai 1 | ||
| + | 6,7; //l1 | ||
| + | 7,8; //l1 | ||
| + | 5,8; //l1 | ||
| + | 5,9; | ||
| + | 6,10; | ||
| + | 7,11; | ||
| + | 8,12; | ||
| + | 9,10; //lantai 2 | ||
| + | 10,11;//l2 | ||
| + | 11,12;//l2 | ||
| + | 9,12; //l2 | ||
| + | 9,13; | ||
| + | 10,14; | ||
| + | 11,15; | ||
| + | 12,16; | ||
| + | 13,14;//lantai 3 | ||
| + | 14,15;//l3 | ||
| + | 15,16;//l3 | ||
| + | 13,16];//l3 | ||
| + | |||
| + | //define coordinates of connection | ||
| + | parameter Real P[Points,3]=[0.3,-0.375,0; //1 | ||
| + | -0.3,-0.375,0; //2 | ||
| + | -0.3,0.375,0; //3 | ||
| + | 0.3,0.375,0; //4 | ||
| + | 0.3,-0.375,0.6; //5 | ||
| + | -0.3,-0.375,0.6; //6 | ||
| + | -0.3,0.375,0.6; //7 | ||
| + | 0.3,0.375,0.6; //8 | ||
| + | 0.3,-0.375,1.2; //9 | ||
| + | -0.3,-0.375,1.2; //10 | ||
| + | -0.3,0.375,1.2; //11 | ||
| + | 0.3,0.375,1.2; //12 | ||
| + | 0.3,-0.375,1.8; //13 | ||
| + | -0.3,-0.375,1.8; //14 | ||
| + | -0.3,0.375,1.8; //15 | ||
| + | 0.3,0.375,1.8]; //16 | ||
| + | |||
| + | //define external force | ||
| + | parameter Real F[Points*3]={0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,-500, | ||
| + | 0,0,-1000, | ||
| + | 0,0,-1000, | ||
| + | 0,0,-500}; | ||
| + | |||
| + | //define boundary | ||
| + | parameter Integer b[:]={1,2,3,4}; | ||
| + | |||
| + | //solution | ||
| + | Real displacement[N], reaction[N]; | ||
| + | Real check[3]; | ||
| + | |||
| + | parameter Integer N=3*Points; | ||
| + | Integer boundary[3*size(b,1)]=cat(1,(3*b).-2,(3*b).-1,3*b); | ||
| + | Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; | ||
| + | Real err=10e-10; | ||
| + | Real ers=10e-4; | ||
| + | |||
| + | algorithm | ||
| + | //Creating Global Matrix | ||
| + | G:=id; | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | end for; | ||
| + | |||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | |||
| + | //Transforming to global matrix | ||
| + | g:=zeros(N,N); | ||
| + | for m,n in 1:3 loop | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n]; | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n]; | ||
| + | end for; | ||
| + | |||
| + | G_star:=G+g; | ||
| + | G:=G_star; | ||
| + | end for; | ||
| + | |||
| + | //Implementing boundary | ||
| + | for i in boundary loop | ||
| + | for j in 1:N loop | ||
| + | G[i,j]:=id[i,j]; | ||
| + | end for; | ||
| + | end for; | ||
| + | |||
| + | //Solving displacement | ||
| + | displacement:=Modelica.Math.Matrices.solve(G,F); | ||
| + | |||
| + | //Solving reaction | ||
| + | reaction:=(G_star*displacement)-F; | ||
| + | |||
| + | //Eliminating float error | ||
| + | for i in 1:N loop | ||
| + | reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; | ||
| + | displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i]; | ||
| + | end for; | ||
| + | |||
| + | //Checking Force | ||
| + | check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))}); | ||
| + | check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))}); | ||
| + | check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)}); | ||
| + | |||
| + | for i in 1:3 loop | ||
| + | check[i] := if abs(check[i])<=ers then 0 else check[i]; | ||
| + | end for; | ||
| + | |||
| + | end kuis_23desember | ||
| + | |||
| + | Setelah nilai stress diperoleh, nilai tersebut dimasukkan kedalam rumus Safety Factor yaitu yield strenght/stress sehingga diperoleh nilai Safety Factor | ||
| + | |||
| + | 1. Elastisitas tetap | ||
| + | |||
| + | [[File:Tabel hasil elastisitas tetap.jpg]] | ||
| + | |||
| + | 2. Area tetap | ||
| + | |||
| + | [[File:Tabel hasil area tetap.jpg]] | ||
| + | |||
| + | |||
| + | == Ujian Akhir Semester == | ||
| + | |||
| + | No.1 | ||
| + | [[File:no1Akmal.jpg|405x599px]] | ||
| + | |||
| + | No.2 | ||
| + | [[File:no2Akmal.jpg|699x599px]] | ||
| + | |||
| + | No.3 | ||
| + | [[File:no3Akmal.jpg|424x599px]] | ||
| + | |||
| + | No.4 | ||
| + | [[File:no4Akmal.jpg|796x599px]] | ||
| + | |||
| + | No.5 | ||
| + | [[File:no5Akmal.jpg|800x438px]] | ||
| + | |||
| + | No.6 | ||
| + | [[File:no6Akmal.jpg|800x185px]] | ||
| + | |||
| + | No.7 | ||
| + | [[File:no7Akmal.jpg]] | ||
| + | |||
| + | Coding-an untuk jawaban | ||
| + | class WaterTower_UAS | ||
| + | |||
| + | //define initial variable | ||
| + | parameter Integer Points = size(P, 1); | ||
| + | //Number of Points | ||
| + | parameter Integer Trusses = size(C, 1); | ||
| + | //Number of Trusses | ||
| + | parameter Real Yield = 503e6; | ||
| + | //Yield Strength (Pa) | ||
| + | parameter Real Area = 40; | ||
| + | //Area L Profile | ||
| + | parameter Real Elas = 71.7e9; | ||
| + | //Elasticity Al 6061 (Pa) | ||
| + | //define connection | ||
| + | parameter Integer C[:, 2] = [1, 2; 1, 3; 1, 4]; | ||
| + | //define coordinates (please put orderly) | ||
| + | parameter Real P[:, 6] = [0, 0, 0, 1, 1, 1; //1 | ||
| + | 6.5, 6.5, 36.5, 1, 1, 1; //2 | ||
| + | 6.5, 6.5, 36.5, 1, 1, 1; //3 | ||
| + | 6.5, 6.5, 36.5, 1, 1, 1]; //4 | ||
| + | //define external force (please put orderly) | ||
| + | parameter Real F[Points * 3] = {0,0,0,0,3708180,0,0,3708180,0,0,3708180,0}; | ||
| + | //solution | ||
| + | Real displacement[N], reaction[N]; | ||
| + | Real check[3]; | ||
| + | Real stress1[Trusses]; | ||
| + | Real safety[Trusses]; | ||
| + | Real dis[3]; | ||
| + | Real Str[3]; | ||
| + | protected | ||
| + | parameter Integer N = 3 * Points; | ||
| + | Real q1[3], q2[3], g[N, N], G[N, N], G_star[N, N], id[N, N] = identity(N), cx, cy, cz, L, X[3, 3]; | ||
| + | Real err = 10e-10, ers = 10e-4; | ||
| + | algorithm | ||
| + | //Creating Global Matrix | ||
| + | G := id; | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j] := P[C[i, 1], j]; | ||
| + | q2[j] := P[C[i, 2], j]; | ||
| + | end for; | ||
| + | L := Modelica.Math.Vectors.length(q2 - q1); | ||
| + | cx := (q2[1] - q1[1]) / L; | ||
| + | cy := (q2[2] - q1[2]) / L; | ||
| + | cz := (q2[3] - q1[3]) / L; | ||
| + | X := Area * Elas / L * [cx ^ 2, cx * cy, cx * cz; cy * cx, cy ^ 2, cy * cz; cz * cx, cz * cy, cz | ||
| + | ^ 2]; | ||
| + | g := zeros(N, N); | ||
| + | for m, n in 1:3 loop | ||
| + | g[3 * (C[i, 1] - 1) + m, 3 * (C[i, 1] - 1) + n] := X[m, n]; | ||
| + | g[3 * (C[i, 2] - 1) + m, 3 * (C[i, 2] - 1) + n] := X[m, n]; | ||
| + | g[3 * (C[i, 2] - 1) + m, 3 * (C[i, 1] - 1) + n] := -X[m, n]; | ||
| + | g[3 * (C[i, 1] - 1) + m, 3 * (C[i, 2] - 1) + n] := -X[m, n]; | ||
| + | end for; | ||
| + | G_star := G + g; | ||
| + | G := G_star; | ||
| + | end for; | ||
| + | //Solving Matrix | ||
| + | //Transforming to global matrix | ||
| + | //Implementing boundary | ||
| + | for x in 1:Points loop | ||
| + | if P[x, 4] <> 0 then | ||
| + | for a in 1:Points * 3 loop | ||
| + | G[x * 3 - 2, a] := 0; | ||
| + | G[x * 3 - 2, x * 3 - 2] := 1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x, 5] <> 0 then | ||
| + | for a in 1:Points * 3 loop | ||
| + | G[x * 3 - 1, a] := 0; | ||
| + | G[x * 3 - 1, x * 3 - 1] := 1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x, 6] <> 0 then | ||
| + | for a in 1:Points * 3 loop | ||
| + | G[x * 3, a] := 0; | ||
| + | G[x * 3, x * 3] := 1; | ||
| + | end for; | ||
| + | end if; | ||
| + | end for; | ||
| + | //Solving displacement | ||
| + | displacement := Modelica.Math.Matrices.solve(G, F); | ||
| + | //Solving reaction | ||
| + | reaction := G_star * displacement - F; | ||
| + | //Eliminating float error | ||
| + | for i in 1:N loop | ||
| + | reaction[i] := if abs(reaction[i]) <= err then 0 else reaction[i]; | ||
| + | displacement[i] := if abs(displacement[i]) <= err then 0 else displacement[i]; | ||
| + | end for; | ||
| + | //Checking Force | ||
| + | check[1] := sum({reaction[i] for i in 1:3:N - 2}) + sum({F[i] for i in 1:3:N - 2}); | ||
| + | check[2] := sum({reaction[i] for i in 2:3:N - 1}) + sum({F[i] for i in 2:3:N - 1}); | ||
| + | check[3] := sum({reaction[i] for i in 3:3:N}) + sum({F[i] for i in 3:3:N}); | ||
| + | for i in 1:3 loop | ||
| + | check[i] := if abs(check[i]) <= ers then 0 else check[i]; | ||
| + | end for; | ||
| + | //Calculating stress in each truss | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j] := P[C[i, 1], j]; | ||
| + | q2[j] := P[C[i, 2], j]; | ||
| + | dis[j] := abs(displacement[3 * (C[i, 1] - 1) + j] - displacement[3 * (C[i, 2] - 1) + j]); | ||
| + | end for; | ||
| + | L := Modelica.Math.Vectors.length(q2 - q1); | ||
| + | cx := (q2[1] - q1[1]) / L; | ||
| + | cy := (q2[2] - q1[2]) / L; | ||
| + | cz := (q2[3] - q1[3]) / L; | ||
| + | X := Elas / L * [cx ^ 2, cx * cy, cx * cz; cy * cx, cy ^ 2, cy * cz; cz * cx, cz * cy, cz ^ 2]; | ||
| + | Str := X * dis; | ||
| + | stress1[i] := Modelica.Math.Vectors.length(Str); | ||
| + | end for; | ||
| + | //Solving Matrix | ||
| + | //Safety factor | ||
| + | for i in 1:Trusses loop | ||
| + | if stress1[i] > 0 then | ||
| + | safety[i] := Yield / stress1[i]; | ||
| + | else | ||
| + | safety[i] := 0; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | end WaterTower_UAS; | ||
Latest revision as of 22:44, 14 January 2021
Perkenalan Singkat
Nama : Akmal Rayhansyah H. N.
NPM : 1906356361
TTL : Bandung, 28 November 2000
Halo, perkenalkan saya Akmal Rayhansyah. Teman-temanku biasa memanggil saya Akmal. Saya adalah seorang mahasiswa Teknik Mesin Universitas Indonesia angkatan 2019. Saya memilih jurusan teknik mesin karena saya memiliki ketertarikan di bidang permesinan terutama pada bidang manufaktur otomotif. Saat ini saya sedang berpartisipasi di tim Universitas Indonesia Super Milage Vehicle sebagai staf. Alasan mengapa saya berpartisipasi dalam tim tersebut adalah agar saya dapat gambaran mengenai ketertarikan saya dalam manufaktur otomotif tersebut.
Metode Numerik
Metode numerik itu sendiri merupakan suatu teknik penyelesaian permasalahan yang diformulasikan secara matematis dengan menggunakan operasi aritmatika. Metode ini digunakan disaat ada sebuah permasalahan matematis yang tidak bisa diselesaikan dengan metode analitik. Jikapun masalah tersebut terdapat penyelesaian secara analitik, proses penyelesaian tersebut akan sangat rumit dan memakan waktu yang cukup lama sehingga tidak efisien.
Adapun kelebihan dan kekurangan dalam menggunakan metode numerik,
Kelebihan :
1. Mampu menyelesaikan persamaan diferensial non linier dan sangat kompleks
2. Mampu menghasilkan nilai perkiraan atau pendekatan dari penyelesaian analitis sehingga penyelesaian tersebut mampu memuat nilai kesalahan
Kekuragan :
1. Nilai yang didapat tidaklah eksak, melainkan berupa pendekatan
2. Perhitungannya lama dan berulang-ulang apabila permasalahannya sangat kompleks
Perkuliahan
Sebelumnya, perkuliahan metode numerik difasilitasi oleh Bapak Dr. Ir. Engkos A. Kosasih, M.T. dari awal hingga Ujian Tengah Semester. Selama pengajaran oleh beliau, saya diajarkan beberapa topik metode numerik, yaitu
1. Sistem Persamaan
2. Pseudocode
3. Turunan Numerik
4. Metode Newton Rhapson, Secant, dan Bisection
5. Regresi Linier
6. Interpolasi
Setelah itu, pertemuan-pertemuan selanjutnya akan difasilitasi oleh Bapak Dr. Ir. Ahmad Indra S.
Minggu pertama (11 November 2020)
Pada minggu pertama ini, Bapak Dr. Ir. Ahmad Indra S. memberikan penjelasan terlebih dahulu mengenai apa itu metode numerik dan berbargai kegunaannya. Kemudian, beliau memperkenalkan saya kepada Wiki AIR (Ahmad Indra Research Group), salah satu media penerapan metode numerik milik beliau. Setelah itu saya juga diajarkan bagaimana cara mengakses dan menggunakan situs tersebut. Situs tersebut akan digunakan selama pembelajaran bersama beliau. Kemudian, saya dan rekan sekelas berdiskusi dengan beliau mengenai apa saja kegunaan dan manfaat mempelajari metode numerik untuk kehidupan dan pekerjaan. Berikut merupakan esensi dalam mempelajari metode numerik,
1. Memahami konsep dan prinsip dasar dalam metode numerik seperti algoritma, aljabar, persamaan diferensial, dan lain-lain
2. Mengerti dalam menerapkan dan mengaplikasikan konsep metode numerik
3. Mampu menerapkan dan mengaplikasikan metode numerik dalam persoalan teknik
4. Menempuh 3 poin diatas dengan poin terpenting, yaitu adab
Setelah itu, saya juga mendapatkan pembelajaran mengenai gambaran dasar OpenModelica, sebuah program yang berfungsi untuk menyelesaikan permasalahan yang diberikan batasan oleh kita sendiri.
Tugas 1
Minggu kedua (18 November 2020)
Pada minggu kedua, Pak Dai memberikan ajaran tentang kehidupan kepada kita bahwa janganlah menjadi orang yang merugi, jadilah orang yang beruntung. Yang dimaksud dengan menjadi orang beruntung adalah jadilah orang yang mampu menjadi pribadi yang lebih baik seiring berjalannya waktu.
Setelah itu, kami diminta untuk mempresentasikan tugas yang dikerjakan oleh masing-masing di minggu sebelumnya dengan tujuan untuk menilai kemampuan para mahasiswa dalam memahami penggunaan aplikasi OpenModelica.
Kemudian Pak Dai memberikan materi pembelajaran baru, yaitu penggunaan class untuk memanggil sebuah function. function yang bisa dipanggil kedalam beragam macamnya.
Tugas 2
Minggu ketiga (25 November 2020)
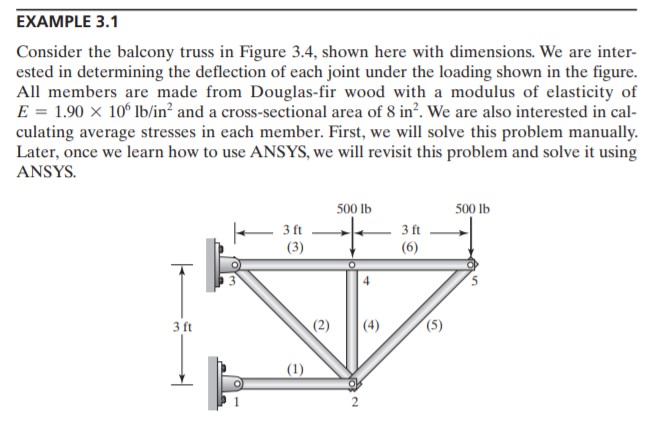
Pada minggu ketiga, Pak Dai memberikan ajaran tentang cara menyelesaikan problema statistika struktur menggunakan OpenModelica. Berikut merupakan salah satuh contoh penyelesaian :
Kemudian pseudocode-nya adalah sebagai berikut
|
model Trusses parameter Integer N=10; //Global matrice = 2*points connected
parameter Real A=8;
parameter Real E=1.9e6;
Real G[N,N]; //global
Real Ginitial[N,N]; //global
Real Sol[N]; //global dispplacement
Real X[N]={0,0,0,0,0,0,0,-500,0,-500};
Real R[N]; //global reaction force
Real SolMat[N,1];
Real XMat[N,1];
//boundary condition
Integer b1=1;
Integer b2=3;
//truss 1
parameter Real X1=0; //degree between truss
Real k1=A*E/1;
Real K1[4,4]; //stiffness matrice
Integer p1a=1;
Integer p1b=2;
Real G1[N,N];
//truss 2
parameter Real X2=135; //degree between truss
Real k2=A*E/50.912;
Real K2[4,4]; //stiffness matrice
Integer p2a=2;
Integer p2b=3;
Real G2[N,N];
//truss 3
parameter Real X3=0; //degree between truss
Real k3=A*E/36;
Real K3[4,4]; //stiffness matrice
Integer p3a=3;
Integer p3b=4;
Real G3[N,N];
//truss 4
parameter Real X4=90; //degree between truss
Real k4=A*E/36;
Real K4[4,4]; //stiffness matrice
Integer p4a=2;
Integer p4b=4;
Real G4[N,N];
//truss 5
parameter Real X5=45; //degree between truss
Real k5=A*E/50.912;
Real K5[4,4]; //stiffness matrice
Integer p5a=2;
Integer p5b=5;
Real G5[N,N];
//truss 6
parameter Real X6=0; //degree between truss
Real k6=A*E/36;
Real K6[4,4]; //stiffness matrice
Integer p6a=4;
Integer p6b=5;
Real G6[N,N];
/*
for each truss, please ensure pXa is lower then pXb (X represents truss element number)
*/
algorithm
//creating global matrice
K1:=Stiffness_Matrices(X1);
G1:=k1*Local_Global(K1,N,p1a,p1b);
K2:=Stiffness_Matrices(X2);
G2:=k2*Local_Global(K2,N,p2a,p2b);
K3:=Stiffness_Matrices(X3);
G3:=k3*Local_Global(K3,N,p3a,p3b);
K4:=Stiffness_Matrices(X4);
G4:=k4*Local_Global(K4,N,p4a,p4b);
K5:=Stiffness_Matrices(X5);
G5:=k5*Local_Global(K5,N,p5a,p5b);
K6:=Stiffness_Matrices(X6);
G6:=k6*Local_Global(K6,N,p6a,p6b);
G:=G1+G2+G3+G4+G5+G6;
Ginitial:=G;
//implementing boundary condition
for i in 1:N loop
G[2*b1-1,i]:=0;
G[2*b1,i]:=0;
G[2*b2-1,i]:=0;
G[2*b2,i]:=0;
end for;
G[2*b1-1,2*b1-1]:=1;
G[2*b1,2*b1]:=1;
G[2*b2-1,2*b2-1]:=1;
G[2*b2,2*b2]:=1;
//solving displacement
Sol:=Gauss_Jordan(N,G,X);
//solving reaction force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);
end trusses; |
Setelah mensimulasikan pseudocode diatas, berikut merupakan grafik hasil reaction dan displacement pada simulasi trusses diatas
grafik reaction
grafik displacement
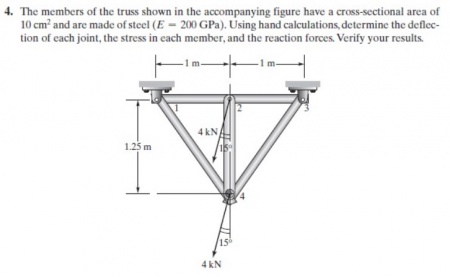
Tugas 3, trusses 2(dua) dimensi
Persamaan
|
class trusses_week3 parameter Integer N=8; //Global matrice = 2*points connected
parameter Real A=0.001; //Area m2
parameter Real E=200e9; //Pa
Real G[N,N]; //global
Real Ginitial[N,N]; //global
Real Sol[N]; //global dispplacement
Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033};
Real R[N]; //global reaction force
Real SolMat[N,1];
Real XMat[N,1];
//boundary condition
Integer b1=1;
Integer b2=3;
//truss 1
parameter Real X1=0; //degree between truss
Real k1=A*E/1;
Real K1[4,4]; //stiffness matrice
Integer p1a=1;
Integer p1b=2;
Real G1[N,N];
//truss 2
parameter Real X2=0; //degree between truss
Real k2=A*E/1;
Real K2[4,4]; //stiffness matrice
Integer p2a=2;
Integer p2b=3;
Real G2[N,N];
//truss 3
parameter Real X3=90; //degree between truss
Real k3=A*E/1.25;
Real K3[4,4]; //stiffness matrice
Integer p3a=2;
Integer p3b=4;
Real G3[N,N];
//truss 4
parameter Real X4=90+38.6598; //degree between truss
Real k4=A*E/1.6;
Real K4[4,4]; //stiffness matrice
Integer p4a=1;
Integer p4b=4;
Real G4[N,N];
//truss 5
parameter Real X5=90-38.6598; //degree between truss
Real k5=A*E/1.6;
Real K5[4,4]; //stiffness matrice
Integer p5a=3;
Integer p5b=4;
Real G5[N,N];
/*
for each truss, please ensure pXa is lower then pXb (X represents truss element number)
*/
algorithm
//creating global matrice
K1:=stiffness_matrices(X1);
G1:=k1*local_global(K1,N,p1a,p1b);
K2:=stiffness_matrices(X2);
G2:=k2*local_global(K2,N,p2a,p2b);
K3:=stiffness_matrices(X3);
G3:=k3*local_global(K3,N,p3a,p3b);
K4:=stiffness_matrices(X4);
G4:=k4*local_global(K4,N,p4a,p4b);
K5:=stiffness_matrices(X5);
G5:=k5*local_global(K5,N,p5a,p5b);
G:=G1+G2+G3+G4+G5;
Ginitial:=G;
//implementing boundary condition
for i in 1:N loop
G[2*b1-1,i]:=0;
G[2*b1,i]:=0;
G[2*b2-1,i]:=0;
G[2*b2,i]:=0;
end for;
G[2*b1-1,2*b1-1]:=1;
G[2*b1,2*b1]:=1;
G[2*b2-1,2*b2-1]:=1;
G[2*b2,2*b2]:=1;
//solving displacement
Sol:=gauss_jordan(N,G,X);
//solving reaction force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=reaction_trusses(N,Ginitial,SolMat,XMat);
end trusses_week3; |
Fungsi Panggil
|
Matrice Transformation function stiffness_matrices
input Real A;
Real Y;
output Real X[4,4];
Real float_error = 10e-10;
final constant Real pi=2*Modelica.Math.asin(1.0);
algorithm
Y:=A/180*pi;
X:=
[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,-
Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,-
Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2;
-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),
(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-
(Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2];
for i in 1:4 loop
for j in 1:4 loop
if abs(X[i,j]) <= float_error then
X[i,j] := 0;
end if;
end for;
end for;
end stiffness_matrices;
|
Global Element Matrice function local_global
input Real Y[4,4];
input Integer B;
input Integer p1;
input Integer p2;
output Real G[B,B];
algorithm
for i in 1:B loop
for j in 1:B loop
G[i,j]:=0;
end for;
end for;
G[2*p1,2*p1]:=Y[2,2];
G[2*p1-1,2*p1-1]:=Y[1,1];
G[2*p1,2*p1-1]:=Y[2,1];
G[2*p1-1,2*p1]:=Y[1,2];
G[2*p2,2*p2]:=Y[4,4];
G[2*p2-1,2*p2-1]:=Y[3,3];
G[2*p2,2*p2-1]:=Y[4,3];
G[2*p2-1,2*p2]:=Y[3,4];
G[2*p2,2*p1]:=Y[4,2];
G[2*p2-1,2*p1-1]:=Y[3,1];
G[2*p2,2*p1-1]:=Y[4,1];
G[2*p2-1,2*p1]:=Y[3,2];
G[2*p1,2*p2]:=Y[2,4];
G[2*p1-1,2*p2-1]:=Y[1,3];
G[2*p1,2*p2-1]:=Y[2,3];
G[2*p1-1,2*p2]:=Y[1,4];
end local_global;
|
Reaction Matrice Equation function reaction_trusses input Integer N; input Real A[N,N]; input Real B[N,1]; input Real C[N,1]; Real X[N,1]; output Real Sol[N]; Real float_error = 10e-10; algorithm X:=A*B-C; for i in 1:N loop if abs(X[i,1]) <= float_error then X[i,1] := 0; end if; end for; for i in 1:N loop Sol[i]:=X[i,1]; end for; end reaction_trusses; |
Gauss Jordan function gauss_jordan
input Integer N;
input Real A[N,N];
input Real B[N];
output Real X[N];
Real float_error = 10e-10;
algorithm
X:=Modelica.Math.Matrices.solve(A,B);
for i in 1:N loop
if abs(X[i]) <= float_error then
X[i] := 0;
end if;
end for;
end gauss_jordan;
|
grafik displacement
grafik reaction
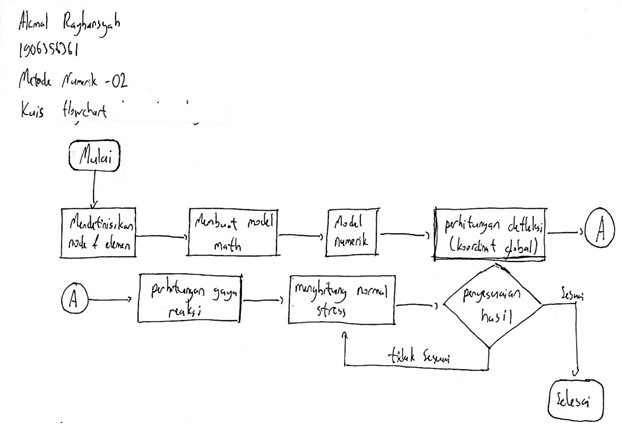
Minggu keempat (2 Desember 2020)
Kuis flowchart
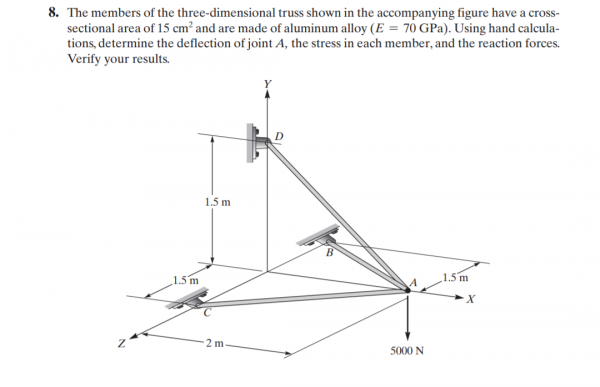
Tugas 4, Trusses 3(tiga) dimensi
Flowchart penyelesaian
|
class Tugas_trusses3d //define initial variable
parameter Integer Points=4; //Number of Points
parameter Integer Trusses=3; //Number of Trusses
parameter Real Area=0.0015; //Area
parameter Real Elas=70e9; //Elasticity
//define connection
parameter Integer C[Trusses,2]=[1,2;
1,3;
1,4];
//define coordinates (please put orderly)
parameter Real P[Points,3]=[2,0,0;
0,0,1.5;
0,0,-1.5;
0,1.5,0];
//define external force (please put orderly)
parameter Real F[Points*3]={0,-5000,0,
0,0,0,
0,0,0,
0,0,0};
//define boundary
parameter Integer b[:]={2,3,4};
//solution
Real displacement[N], reaction[N];
protected
parameter Integer N=3*Points;
Integer boundary[3*size(b,1)]=cat(1,(3*b).-2,(3*b).-1,3*b);
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), err=10e-10, cx, cy, cz, L, E,
X[3,3];
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Constant
L:=Modelica.Math.Vectors.length(q2-q1);
E:=Area*Elas/L;
//Solving Matrix
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=E*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary for i in boundary loop for j in 1:N loop G[i,j]:=id[i,j]; end for; end for; //Solving displacement displacement:=Modelica.Math.Matrices.solve(G,F); //Solving reaction reaction:=(G_star*displacement)-F; //Eliminating float error for i in 1:N loop reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i]; end for; end Tugas_trusses3d; |
grafik reaction
grafik displacement
Minggu Keenam (16 Desember 2020)
Pada pertemuan Metnum Rabu, 16 Desember 2020 kami diajarkan tentang optimasi menggunakan Open Modelica. Optimasi merupakan sebuah cara untuk mendapatkan nilai minimum atau maksimum dari suatu permasalahan. Terdapat beberapa aspek yang diperhatikan dalam melakukan optimasi yaitu fungsi objektif dan ada juga konstrain. Pada pertemuan ini Asisten Dosen Metode Numerik yaitu Bu Chandra memberikan tutorial atau mengajarkan cara untuk melakukan optimasi menggunakan metode Bracket. Pada metode "Bracket Optimization Using Golden Ratio" terdapat satu grafik yang mempunyai nilai f(x) global maks dan lokal maks serta terdapat f(x) global minimum dann lokal minimum. Pada pertemuan kali ini, Bu chandra mengajarkan hingga melakukan optimasi grafik tanpa sebuah konstrain.
Berikut merupakan coding open modelica yang diajarkan oleh Bu Chandra:
Fungsi panggil
function f_obj3 import Modelica.Math; input Real x; output Real y; algorithm y:= 2*Math.sin(x)-x^2/10; end f_obj3;
Setelah itu dibuat lah model optimasi sistem bracketnya:
model bracket_optimation3 parameter Integer n=8; Real x1[n]; Real x2[n]; Real xup; Real xlow; Real d; Real f1[n]; Real f2[n]; Real xopt; Real yopt; algorithm xup :=4; xlow:=0; for i in (1:n) loop d:= (5^(1/2)-1)/2*(xup-xlow); x1[i]:= xlow+d; x2[i]:= xup-d; f1[i]:= f_obj3(x1[i]); f2[i]:= f_obj3(x2[i]); if f1[i]>f2[i] then xup:= xup; xlow:= x2[i]; xopt:= xup; yopt:= f1[i]; else xlow:= xlow; xup:= x1[i]; xopt:= xup; end if; end for; end bracket_optimation3;
Tugas Besar
Tujuan penyelesaian
Mencari harga pembuatan rangka truss sederhana yang optimal dengan memvariasikan dimensi dan elastisitas material
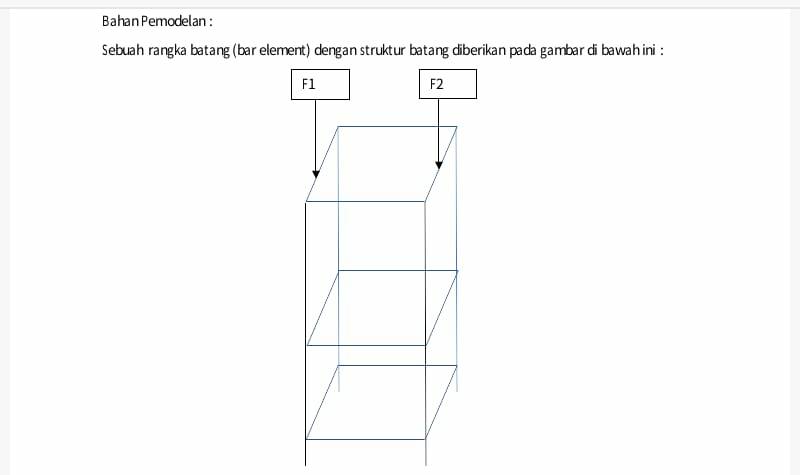
Problema (trusses)
Keterangan model
Asumsi : 1. Beban akan terdistribusi hanya pada point penghubung (truss) 2. Safety Factor minimal = 2 3. Batas displacement 0.001 m sebelum terjadinya buckling pada kolom paling atas
Constraint : 1. Nodes pada lantai dasar fixed (1,2,3,4) 2. Beban F1 dan F2 terdistribusi ke node sekitarnya a. Node 13 & 16 = 1000 N b. Node 14 & 15 = 500 N
Alur penyelesaian
1. Mencari area paling optimum dengan membandingkan dimensi siku (Elastisitas tetap)
2. Mencari material paling optimum dengan membandingkan berbagai material sesuai Elastisitas dan Yield strenght masing-masing (area tetap)
Mencari dan mengolah data
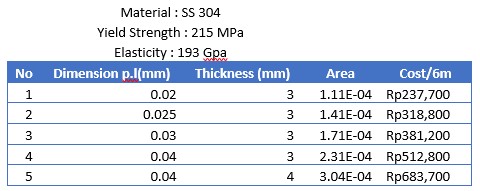
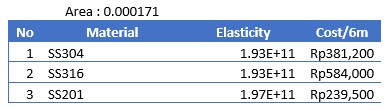
1. Elastisitas tetap
2. Area tetap
Pengerjaan
Pertama-tama, membuat kode model untuk mencari stress pada setiap variabel data
Model untuk mencari stress
class kuis_23desember
//initial variable
parameter Integer Points=16; //Jumlah Point
parameter Integer Trusses=24; //Jumlah Trusses
parameter Real Area=disesuaikan; //Area digunakan
parameter Real Elas=disesuaikan; //Elasticitas material
//define connection
parameter Integer C[Trusses,2]=[1,5;
2,6;
3,7;
4,8;
5,6; //lantai 1
6,7; //l1
7,8; //l1
5,8; //l1
5,9;
6,10;
7,11;
8,12;
9,10; //lantai 2
10,11;//l2
11,12;//l2
9,12; //l2
9,13;
10,14;
11,15;
12,16;
13,14;//lantai 3
14,15;//l3
15,16;//l3
13,16];//l3
//define coordinates of connection
parameter Real P[Points,3]=[0.3,-0.375,0; //1
-0.3,-0.375,0; //2
-0.3,0.375,0; //3
0.3,0.375,0; //4
0.3,-0.375,0.6; //5
-0.3,-0.375,0.6; //6
-0.3,0.375,0.6; //7
0.3,0.375,0.6; //8
0.3,-0.375,1.2; //9
-0.3,-0.375,1.2; //10
-0.3,0.375,1.2; //11
0.3,0.375,1.2; //12
0.3,-0.375,1.8; //13
-0.3,-0.375,1.8; //14
-0.3,0.375,1.8; //15
0.3,0.375,1.8]; //16
//define external force
parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-500,
0,0,-1000,
0,0,-1000,
0,0,-500};
//define boundary
parameter Integer b[:]={1,2,3,4};
//solution
Real displacement[N], reaction[N];
Real check[3];
parameter Integer N=3*Points;
Integer boundary[3*size(b,1)]=cat(1,(3*b).-2,(3*b).-1,3*b);
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
Real err=10e-10;
Real ers=10e-4;
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary
for i in boundary loop
for j in 1:N loop
G[i,j]:=id[i,j];
end for;
end for;
//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction
reaction:=(G_star*displacement)-F;
//Eliminating float error
for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
end kuis_23desember
Setelah nilai stress diperoleh, nilai tersebut dimasukkan kedalam rumus Safety Factor yaitu yield strenght/stress sehingga diperoleh nilai Safety Factor
1. Elastisitas tetap
2. Area tetap
Ujian Akhir Semester
No.1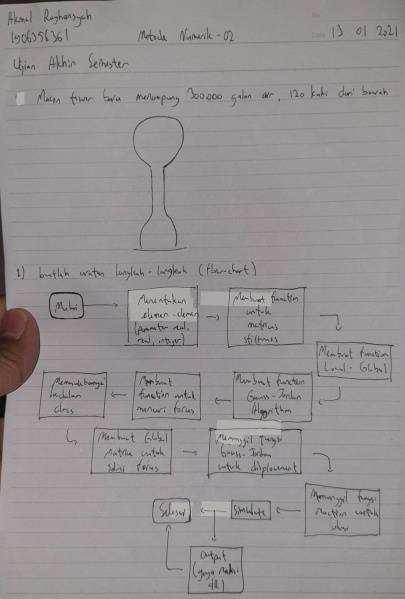
No.2
No.3
No.4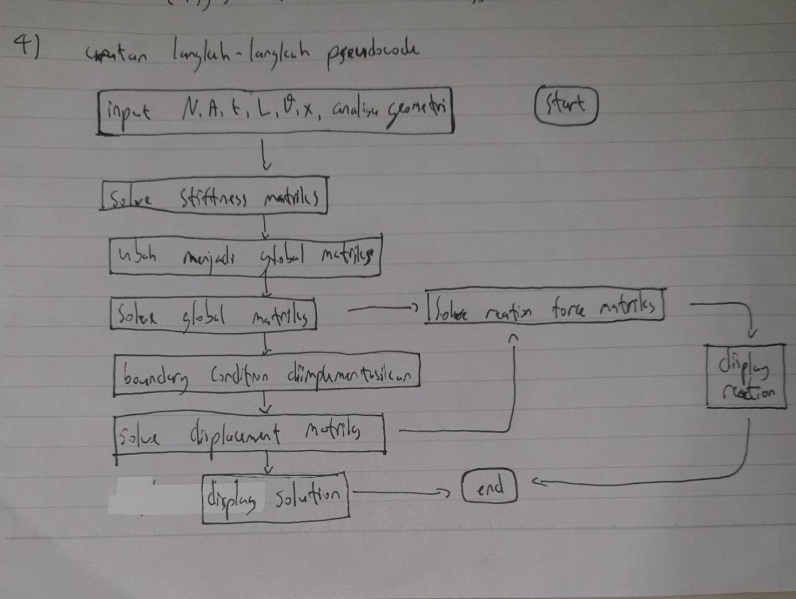
No.5
No.6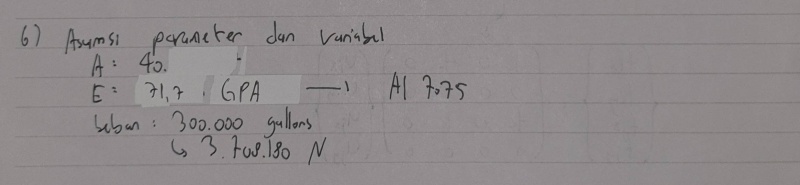
No.7
Coding-an untuk jawaban
class WaterTower_UAS
//define initial variable
parameter Integer Points = size(P, 1);
//Number of Points
parameter Integer Trusses = size(C, 1);
//Number of Trusses
parameter Real Yield = 503e6;
//Yield Strength (Pa)
parameter Real Area = 40;
//Area L Profile
parameter Real Elas = 71.7e9;
//Elasticity Al 6061 (Pa)
//define connection
parameter Integer C[:, 2] = [1, 2; 1, 3; 1, 4];
//define coordinates (please put orderly)
parameter Real P[:, 6] = [0, 0, 0, 1, 1, 1; //1
6.5, 6.5, 36.5, 1, 1, 1; //2
6.5, 6.5, 36.5, 1, 1, 1; //3
6.5, 6.5, 36.5, 1, 1, 1]; //4
//define external force (please put orderly)
parameter Real F[Points * 3] = {0,0,0,0,3708180,0,0,3708180,0,0,3708180,0};
//solution
Real displacement[N], reaction[N];
Real check[3];
Real stress1[Trusses];
Real safety[Trusses];
Real dis[3];
Real Str[3];
protected
parameter Integer N = 3 * Points;
Real q1[3], q2[3], g[N, N], G[N, N], G_star[N, N], id[N, N] = identity(N), cx, cy, cz, L, X[3, 3];
Real err = 10e-10, ers = 10e-4;
algorithm
//Creating Global Matrix
G := id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j] := P[C[i, 1], j];
q2[j] := P[C[i, 2], j];
end for;
L := Modelica.Math.Vectors.length(q2 - q1);
cx := (q2[1] - q1[1]) / L;
cy := (q2[2] - q1[2]) / L;
cz := (q2[3] - q1[3]) / L;
X := Area * Elas / L * [cx ^ 2, cx * cy, cx * cz; cy * cx, cy ^ 2, cy * cz; cz * cx, cz * cy, cz
^ 2];
g := zeros(N, N);
for m, n in 1:3 loop
g[3 * (C[i, 1] - 1) + m, 3 * (C[i, 1] - 1) + n] := X[m, n];
g[3 * (C[i, 2] - 1) + m, 3 * (C[i, 2] - 1) + n] := X[m, n];
g[3 * (C[i, 2] - 1) + m, 3 * (C[i, 1] - 1) + n] := -X[m, n];
g[3 * (C[i, 1] - 1) + m, 3 * (C[i, 2] - 1) + n] := -X[m, n];
end for;
G_star := G + g;
G := G_star;
end for;
//Solving Matrix
//Transforming to global matrix
//Implementing boundary
for x in 1:Points loop
if P[x, 4] <> 0 then
for a in 1:Points * 3 loop
G[x * 3 - 2, a] := 0;
G[x * 3 - 2, x * 3 - 2] := 1;
end for;
end if;
if P[x, 5] <> 0 then
for a in 1:Points * 3 loop
G[x * 3 - 1, a] := 0;
G[x * 3 - 1, x * 3 - 1] := 1;
end for;
end if;
if P[x, 6] <> 0 then
for a in 1:Points * 3 loop
G[x * 3, a] := 0;
G[x * 3, x * 3] := 1;
end for;
end if;
end for;
//Solving displacement
displacement := Modelica.Math.Matrices.solve(G, F);
//Solving reaction
reaction := G_star * displacement - F;
//Eliminating float error
for i in 1:N loop
reaction[i] := if abs(reaction[i]) <= err then 0 else reaction[i];
displacement[i] := if abs(displacement[i]) <= err then 0 else displacement[i];
end for;
//Checking Force
check[1] := sum({reaction[i] for i in 1:3:N - 2}) + sum({F[i] for i in 1:3:N - 2});
check[2] := sum({reaction[i] for i in 2:3:N - 1}) + sum({F[i] for i in 2:3:N - 1});
check[3] := sum({reaction[i] for i in 3:3:N}) + sum({F[i] for i in 3:3:N});
for i in 1:3 loop
check[i] := if abs(check[i]) <= ers then 0 else check[i];
end for;
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
q1[j] := P[C[i, 1], j];
q2[j] := P[C[i, 2], j];
dis[j] := abs(displacement[3 * (C[i, 1] - 1) + j] - displacement[3 * (C[i, 2] - 1) + j]);
end for;
L := Modelica.Math.Vectors.length(q2 - q1);
cx := (q2[1] - q1[1]) / L;
cy := (q2[2] - q1[2]) / L;
cz := (q2[3] - q1[3]) / L;
X := Elas / L * [cx ^ 2, cx * cy, cx * cz; cy * cx, cy ^ 2, cy * cz; cz * cx, cz * cy, cz ^ 2];
Str := X * dis;
stress1[i] := Modelica.Math.Vectors.length(Str);
end for;
//Solving Matrix
//Safety factor
for i in 1:Trusses loop
if stress1[i] > 0 then
safety[i] := Yield / stress1[i];
else
safety[i] := 0;
end if;
end for;
end WaterTower_UAS;