Difference between revisions of "Metnum03-Naufal Ihsan Kamal"
Nauflihsan (talk | contribs) |
Nauflihsan (talk | contribs) (→Jawaban UAS) |
||
| (7 intermediate revisions by 2 users not shown) | |||
| Line 145: | Line 145: | ||
== Pertemuan 5 (7 Desember 2020) == | == Pertemuan 5 (7 Desember 2020) == | ||
| + | |||
| + | == Pertemuan 6 (14 Desember 2020) == | ||
| + | |||
| + | Pada pertemuan kali ini,kami diminta untuk muhasabah diri sendiri terkait pembelajaran Metnum sampai saat ini,Berikut adalah hasil muhasabah saya: | ||
| + | |||
| + | Menurut saya,saya selalu berusaha untuk mengikuti pembelajaran Metnum disetiap pertemuan,untuk dasar-dasar terkait penggunaan software OpenModelica saya masih cukup paham.Kemudian untuk penggunaan OpenModelica dalam penyelesaian trus 2 Dimensi seperti contoh dibuku saya masih cukup paham terkait flowchartnya,hanya saja saya masih belum cukup paham terkait dengan materi yang terdapat pada akhir akhir pembelajaran kemarin,terutama penggunaan metode Looping dalam aplikasi trus 3 dimensi.Oleh karena itu disisa pertemuan Metnum ini saya masih berusaha untuk bisa mengerti terkait penggunaan metode Looping tersebut dikarenakan keterbatasan pengetahuan saya terkait coding codingnya. | ||
| + | |||
| + | == Aplikasi metode numerik dalam kasus optimisasi == | ||
| + | |||
| + | Hari ini kita belajar membuat struktur rangka seperti gambar yg dikirm di WA, | ||
| + | Dalam menyelesaikan persamaan ini kita jg hrus bisa membuat persm aljabar dan metode numeriknya | ||
| + | Tugas besarnya ialah mencari nilai optimal untuk meminimalkan biaya dan konstrainnya yaitu strukturnya mampu menahan beban dan reliable,caranya mnentukan gaya2 yang bekerja,lalu ada apa aja stressnya yg diizinkan yaitu setengah dari material allowence. | ||
| + | |||
| + | '''One-Dimensional Unconstrained Optimization''' | ||
| + | |||
| + | Optimasi adalah suatu cara untuk mendapatkan nilai max atau min dari suatu permasalahan. | ||
| + | |||
| + | Metode yang digunakan kali ini adalah gOLDEN rATIO Method | ||
| + | |||
| + | Langkah pertama adalah mengetahui penyelsaian matematis | ||
| + | Obejektif pertama adalah mencari nilai Fx Global Maximum | ||
| + | |||
| + | Langkah 2 kita melakkukan iterasi pertama nilai X thd calon nilai Fx Maksimum dengan batasan Xl dan Xu | ||
| + | |||
| + | Setelah kita dapat Xl dan Xu,kita masukan ke dalam persamaan untuk mencari X1 dan X2,lalu mengikuti aturan seperti yg tertera di gambar | ||
| + | |||
| + | Exercise kali ni kita menggunakan fungsi non-linier Fx=2sinx-x^2/10 | ||
| + | |||
| + | == Tugas Besar == | ||
| + | |||
| + | '''Tujuan''' | ||
| + | |||
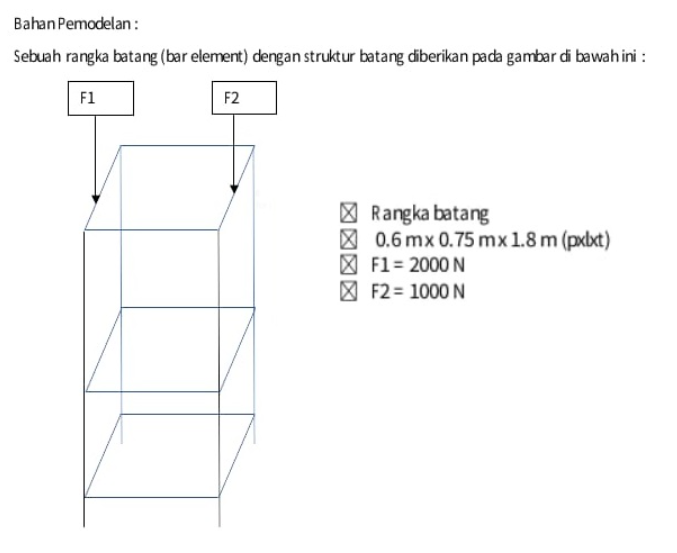
| + | Pada tugas besar kali ini kami diminta untuk mencari optimisasi desain untuk menekan biaya pada kasus yang diberikan. Optimisasi adalah suatu cara untuk mencari nilai ekstrim. | ||
| + | |||
| + | [[File:subet1.png]] | ||
| + | |||
| + | '''Constraint:''' | ||
| + | |||
| + | - Spesifikasi L (Panjang) dan geometri rangka truss | ||
| + | |||
| + | - Gaya beban terhadap struktur (1000 N dan 2000 N) | ||
| + | |||
| + | '''Asumsi:''' | ||
| + | |||
| + | - Diasumsikan tidak ada bending karena bersifat truss | ||
| + | |||
| + | - Beban terdistribusi pada node | ||
| + | |||
| + | - Safety Factor = 2 | ||
| + | |||
| + | - Batas displacement 0,001m sebelum terjadi buckling | ||
| + | |||
| + | - Variabel bebas | ||
| + | |||
| + | '''Metode Mengerjakan''' | ||
| + | |||
| + | 1. Pilih material dengan 3 variasi,area ,dan elastisitas material | ||
| + | |||
| + | 2. Buat 2 grafik perbandingan yang pertama grafik dengan material locked dan variasi area,lalu yg ke dua grafik dengan area locked dan variasi elastisitas | ||
| + | |||
| + | 3. Setelah itu kita hitung stress/cost | ||
| + | |||
| + | '''Data Material''' | ||
| + | |||
| + | [[File:subet2.png]] | ||
| + | |||
| + | '''Pembuatan Numerik''' | ||
| + | |||
| + | Koding Numerik ini dibuat untuk mencari nilai stress, safety factor,dan untuk mencari data untuk curve fitting | ||
| + | |||
| + | model Trusses_3D_Tugas_Besar_Safety | ||
| + | |||
| + | //define initial variable | ||
| + | parameter Integer Points=size(P,1); //Number of Points | ||
| + | parameter Integer Trusses=size(C,1); //Number of Trusses | ||
| + | parameter Real Yield=215e6; //Yield Strength (Pa) | ||
| + | parameter Real Area=0.000224; //Area L Profile (Dimension=0.03, Thickness=0,004) (m2) | ||
| + | parameter Real Elas=193e9; //Elasticity SS 304 (Pa) | ||
| + | |||
| + | //define connection | ||
| + | parameter Integer C[:,2]=[1,5; | ||
| + | 2,6; | ||
| + | 3,7; | ||
| + | 4,8; | ||
| + | 5,6; //1st floor | ||
| + | 6,7; //1st floor | ||
| + | 7,8; //1st floor | ||
| + | 5,8; //1st floor | ||
| + | 5,9; | ||
| + | 6,10; | ||
| + | 7,11; | ||
| + | 8,12; | ||
| + | 9,10; //2nd floor | ||
| + | 10,11;//2nd floor | ||
| + | 11,12;//2nd floor | ||
| + | 9,12; //2nd floor | ||
| + | 9,13; | ||
| + | 10,14; | ||
| + | 11,15; | ||
| + | 12,16; | ||
| + | 13,14;//3rd floor | ||
| + | 14,15;//3rd floor | ||
| + | 15,16;//3rd floor | ||
| + | 13,16];//3rd floor | ||
| + | |||
| + | //define coordinates (please put orderly) | ||
| + | parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1 | ||
| + | -0.3,-0.375,0,1,1,1; //2 | ||
| + | -0.3,0.375,0,1,1,1; //3 | ||
| + | 0.3,0.375,0,1,1,1; //4 | ||
| + | |||
| + | 0.3,-0.375,0.6,0,0,0; //5 | ||
| + | -0.3,-0.375,0.6,0,0,0; //6 | ||
| + | -0.3,0.375,0.6,0,0,0; //7 | ||
| + | 0.3,0.375,0.6,0,0,0; //8 | ||
| + | |||
| + | 0.3,-0.375,1.2,0,0,0; //9 | ||
| + | -0.3,-0.375,1.2,0,0,0; //10 | ||
| + | -0.3,0.375,1.2,0,0,0; //11 | ||
| + | 0.3,0.375,1.2,0,0,0; //12 | ||
| + | |||
| + | 0.3,-0.375,1.8,0,0,0; //13 | ||
| + | -0.3,-0.375,1.8,0,0,0; //14 | ||
| + | -0.3,0.375,1.8,0,0,0; //15 | ||
| + | 0.3,0.375,1.8,0,0,0]; //16 | ||
| + | |||
| + | //define external force (please put orderly) | ||
| + | parameter Real F[Points*3]={0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,-500, | ||
| + | 0,0,-1000, | ||
| + | 0,0,-1000, | ||
| + | 0,0,-500}; | ||
| + | |||
| + | //solution | ||
| + | Real displacement[N], reaction[N]; | ||
| + | Real check[3]; | ||
| + | |||
| + | Real stress1[Trusses]; | ||
| + | Real safety[Trusses]; | ||
| + | Real dis[3]; | ||
| + | Real Str[3]; | ||
| + | |||
| + | protected | ||
| + | parameter Integer N=3*Points; | ||
| + | Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; | ||
| + | Real err=10e-10, ers=10e-4; | ||
| + | |||
| + | algorithm | ||
| + | //Creating Global Matrix | ||
| + | G:=id; | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | end for; | ||
| + | |||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | |||
| + | //Transforming to global matrix | ||
| + | g:=zeros(N,N); | ||
| + | for m,n in 1:3 loop | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n]; | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n]; | ||
| + | end for; | ||
| + | |||
| + | G_star:=G+g; | ||
| + | G:=G_star; | ||
| + | end for; | ||
| + | |||
| + | //Implementing boundary | ||
| + | for x in 1:Points loop | ||
| + | if P[x,4] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[(x*3)-2,a]:=0; | ||
| + | G[(x*3)-2,(x*3)-2]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x,5] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[(x*3)-1,a]:=0; | ||
| + | G[(x*3)-1,(x*3)-1]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x,6] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[x*3,a]:=0; | ||
| + | G[x*3,x*3]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | //Solving displacement | ||
| + | displacement:=Modelica.Math.Matrices.solve(G,F); | ||
| + | |||
| + | //Solving reaction | ||
| + | reaction:=(G_star*displacement)-F; | ||
| + | |||
| + | //Eliminating float error | ||
| + | for i in 1:N loop | ||
| + | reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; | ||
| + | displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i]; | ||
| + | end for; | ||
| + | |||
| + | //Checking Force | ||
| + | check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))}); | ||
| + | check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))}); | ||
| + | check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)}); | ||
| + | |||
| + | for i in 1:3 loop | ||
| + | check[i] := if abs(check[i])<=ers then 0 else check[i]; | ||
| + | end for; | ||
| + | |||
| + | //Calculating stress in each truss | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]); | ||
| + | end for; | ||
| + | |||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | |||
| + | Str:=(X*dis); | ||
| + | stress1[i]:=Modelica.Math.Vectors.length(Str); | ||
| + | end for; | ||
| + | |||
| + | //Safety factor | ||
| + | for i in 1:Trusses loop | ||
| + | if stress1[i]>0 then | ||
| + | safety[i]:=Yield/stress1[i]; | ||
| + | else | ||
| + | safety[i]:=0; | ||
| + | end if; | ||
| + | end for; | ||
| + | |||
| + | end Trusses_3D_Tugas_Besar_Safety; | ||
| + | |||
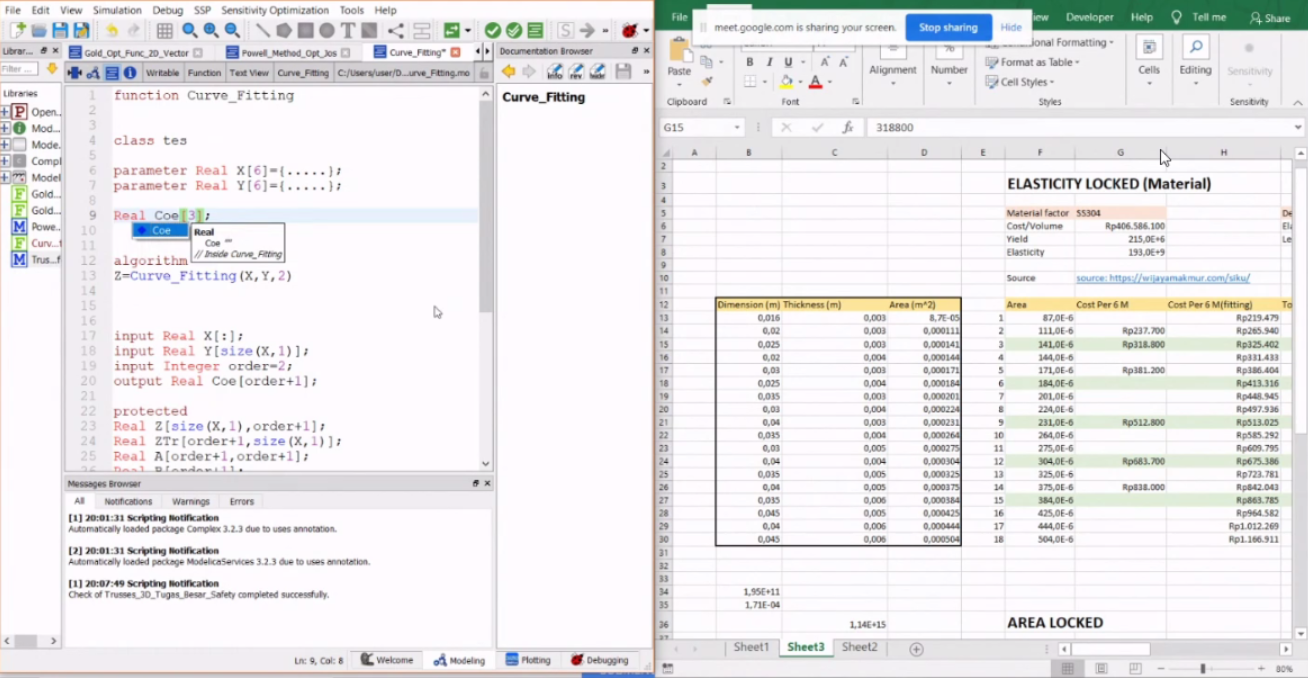
| + | '''Membuat Curve Fitting''' | ||
| + | |||
| + | Curve fitting digunakan untuk mencari nilai cost terhadap fungsi area/elastisitas | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | model callcurve | ||
| + | parameter Real [8] X={1.11e-4,1.41e-4,1.71e-4,2.31e-4,3.04e-4,3.75e-4,7.44e-4,8.64e-4}; | ||
| + | parameter Real [8] Y={273700 ,318800 ,381200 ,512800 ,683700 ,838000 ,1663100,1986400}; | ||
| + | Real [3] Coe; | ||
| + | algorithm | ||
| + | Coe:=Curve_Fitting(X,Y); | ||
| + | end callcurve; | ||
| + | |||
| + | |||
| + | function Curve_Fitting | ||
| + | input Real X[:]; | ||
| + | input Real Y[size(X,1)]; | ||
| + | input Integer order=2; | ||
| + | output Real Coe[order+1]; | ||
| + | protected | ||
| + | Real Z[size(X,1),order+1]; | ||
| + | Real ZTr[order+1,size(X,1)]; | ||
| + | Real A[order+1,order+1]; | ||
| + | Real B[order+1]; | ||
| + | algorithm | ||
| + | for i in 1:size(X,1) loop | ||
| + | for j in 1:(order+1) loop | ||
| + | Z[i,j]:=X[i]^(order+1-j); | ||
| + | end for; | ||
| + | end for; | ||
| + | ZTr:=transpose(Z); | ||
| + | A:=ZTr*Z; | ||
| + | B:=ZTr*Y; | ||
| + | Coe:=Modelica.Math.Matrices.solve(A,B); //Coe:=fill(2,size(Coe,1)); | ||
| + | end Curve_Fitting; | ||
| + | |||
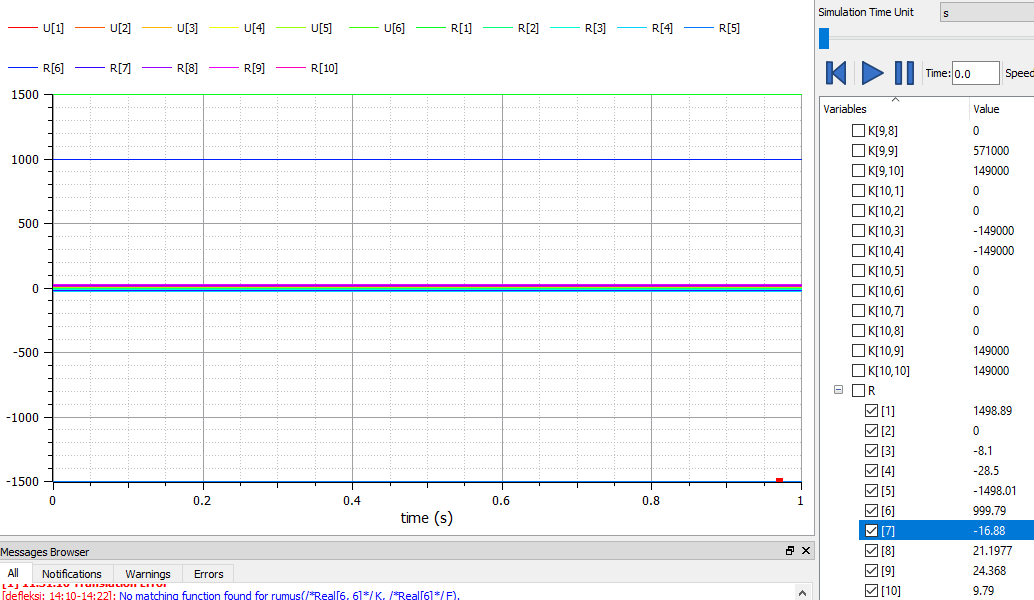
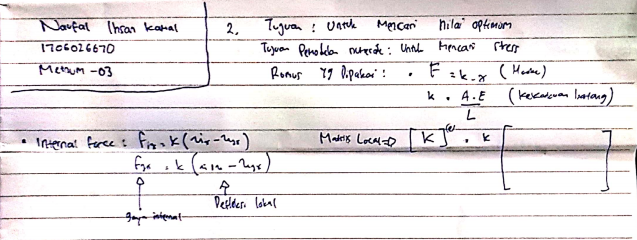
| + | == Jawaban UAS == | ||
| + | |||
| + | [[File:uasmetnum99.jpeg]] | ||
| + | |||
| + | [[File:uasmetnum100.png]] | ||
| + | |||
| + | [[File:uasmetnum101.png]] | ||
| + | |||
| + | [[File:uasmetnum102.png]] | ||
Latest revision as of 21:01, 14 January 2021
بِسْمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ
السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُهُ
Contents
- 1 BIODATA DIRI
- 2 Pertemuan 1 (19 November 2020)
- 3 Pertemuan 2 (16 November 2020)
- 4 TUGAS 2
- 5 Pertemuan 3 (23 November 2020)
- 6 Latihan 2.1
- 7 Pertemuan 4 (30 November 2020)
- 8 Pertemuan 5 (7 Desember 2020)
- 9 Pertemuan 6 (14 Desember 2020)
- 10 Aplikasi metode numerik dalam kasus optimisasi
- 11 Tugas Besar
- 12 Jawaban UAS
BIODATA DIRI
Nama : Naufal Ihsan Kamal
NPM : 1706026670
Program Studi : S1 Teknik Mesin Pararel Universitas Indonesia
Semoga sedikit ilmu yang saya sampaikan disini dapat memberi manfaat bagi kita semua
Pertemuan 1 (19 November 2020)
Sebelum memulai pertemuan pertama,kami menginstall sebuah aplikasi bernama OpenModelica yang memiliki fungsi untuk mensimulaikan suatu sistem yang didistribusikan dalam bentuk kode dan biner untuk penelitian.Dalam kuliah pertemuan kali ini Pak Dai menyebutkan bahwa ada 4 penilaian utama dari kelas Metnum ini,yaitu mengenal atau mengetahui progres pengetahuannya,mengerti Konsep,mampu membantu dalam memecahkan masalah dengan pemahaman tersebut di dunia keteknikan,dan yang terakhir mendapat nilai tambah (moral value) dan lebih mengetahui diri sendiri.
Pertemuan 2 (16 November 2020)
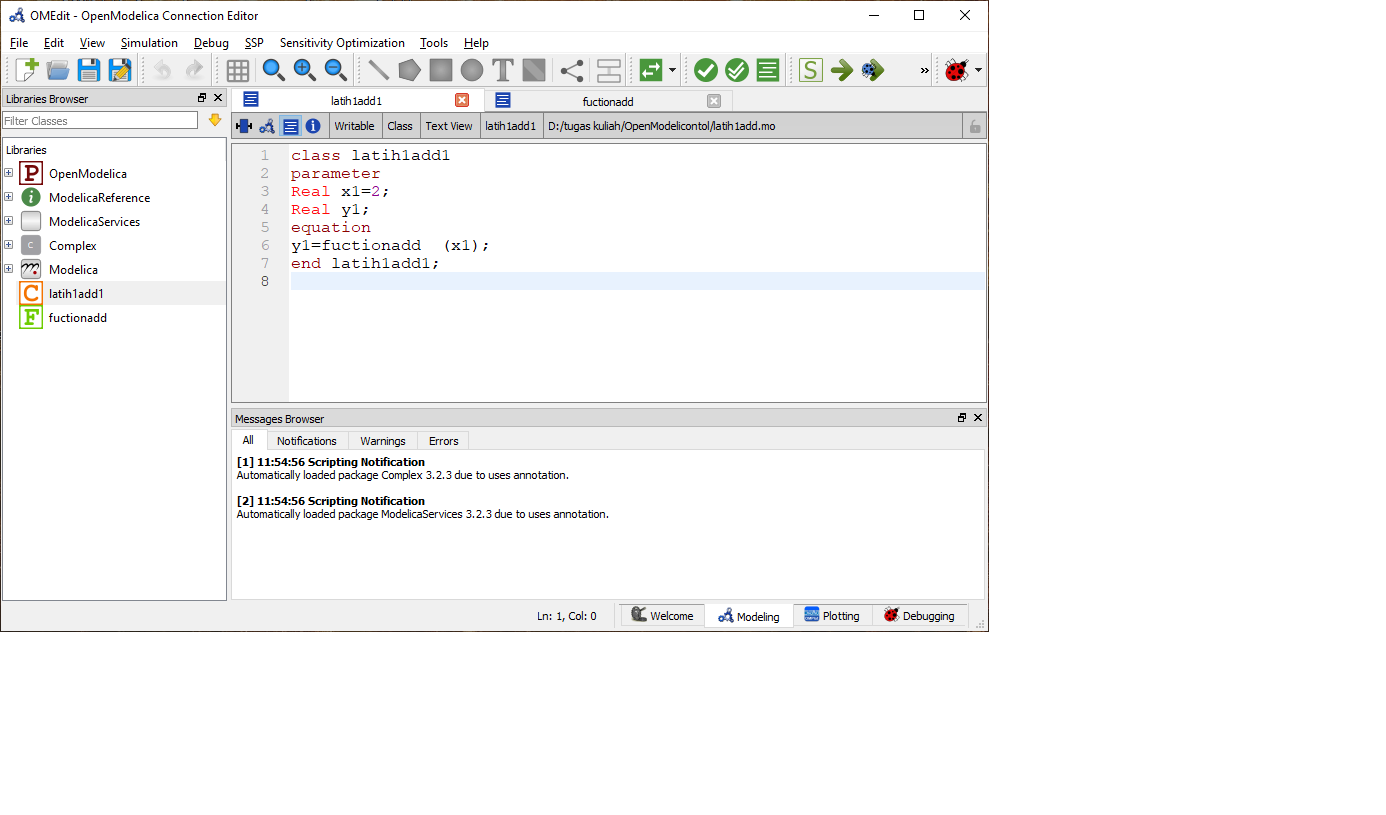
Pada pertemuan kedua kita belajar cara menggunakan function kedalam sebuah persamaan
pertama kita masukan numeric pada class seperti gambar dibawah ini
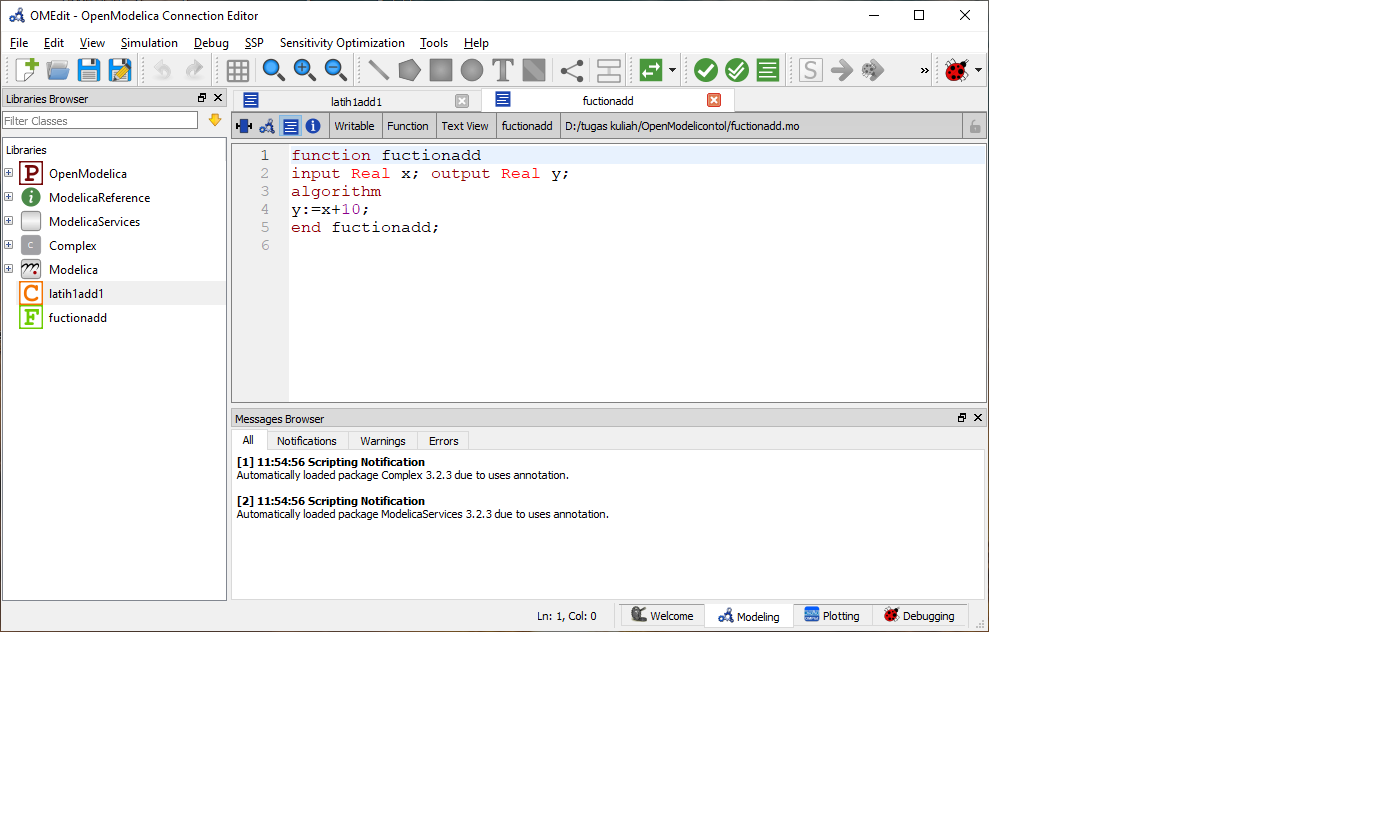
Lalu kita buat class baru dengan format function,kemudian masukan numeric seperti gambar dibawah ini
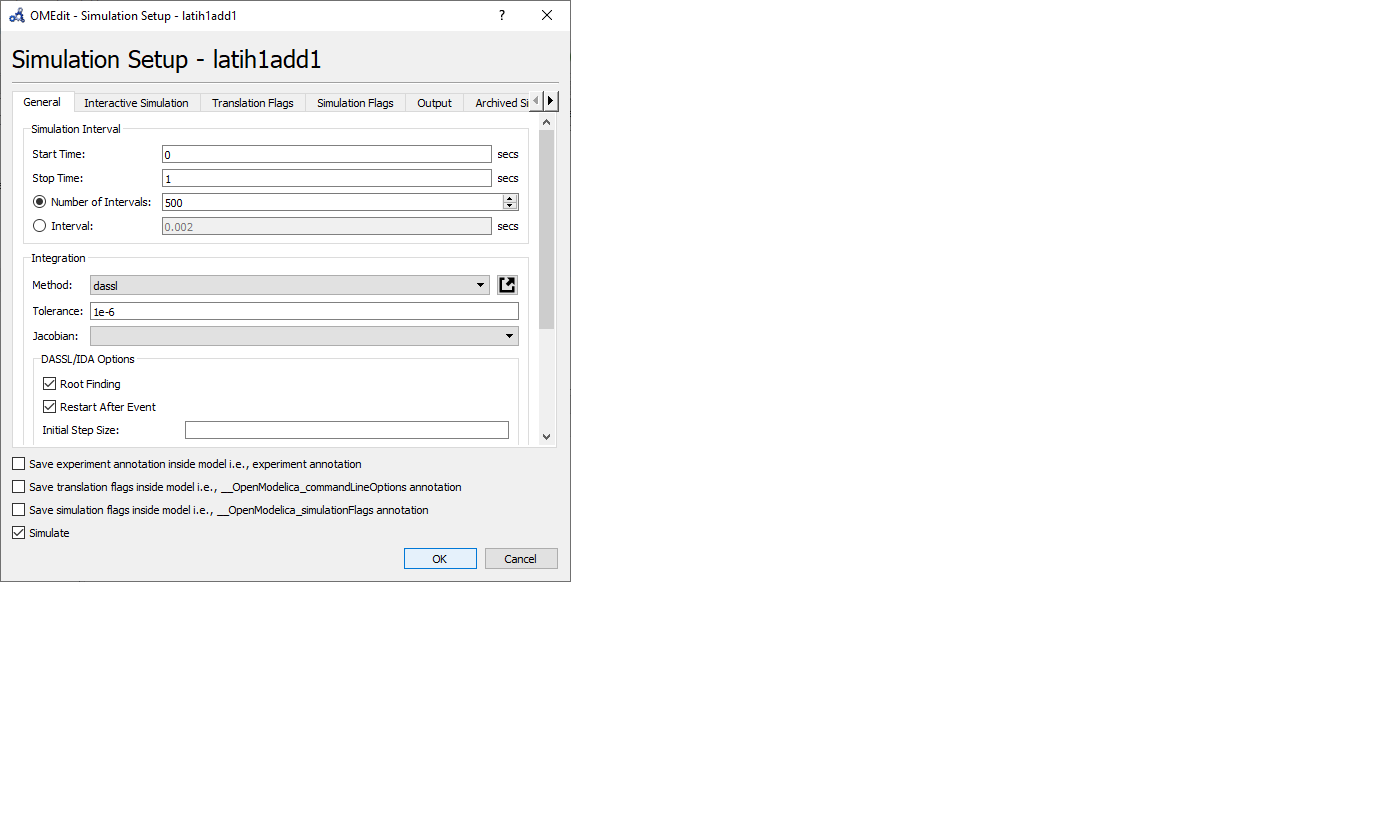
Setelah itu kita coba simulate dengar opsi seperti ini
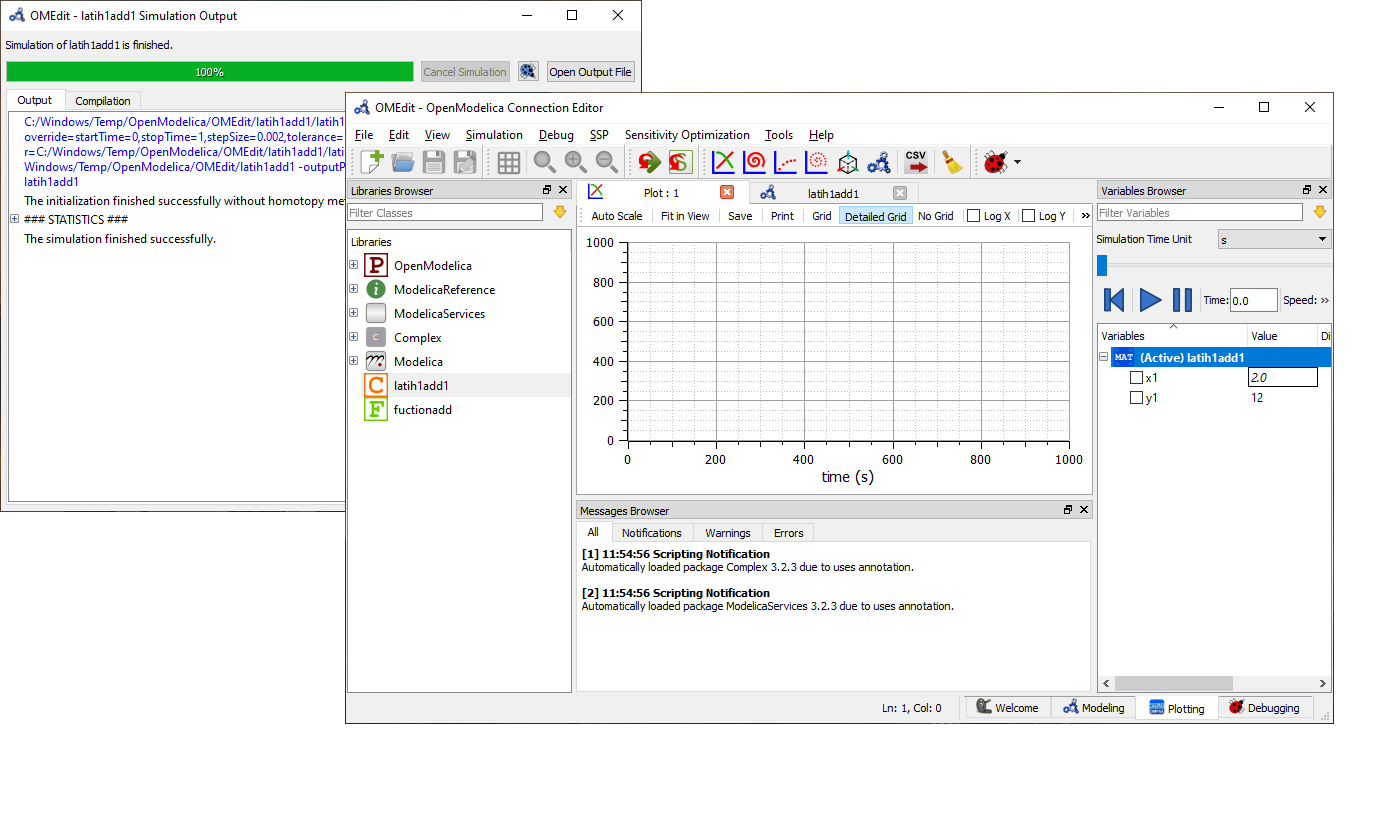
Dan kemudian kita bisa melihat hasilnya
TUGAS 2
Tugas kali ini kita membuat sebuah class untuk menyelesaikan persamaa2n aljabar simultan (metoda gauss elim, gauss seidel ataupun metoda lain).
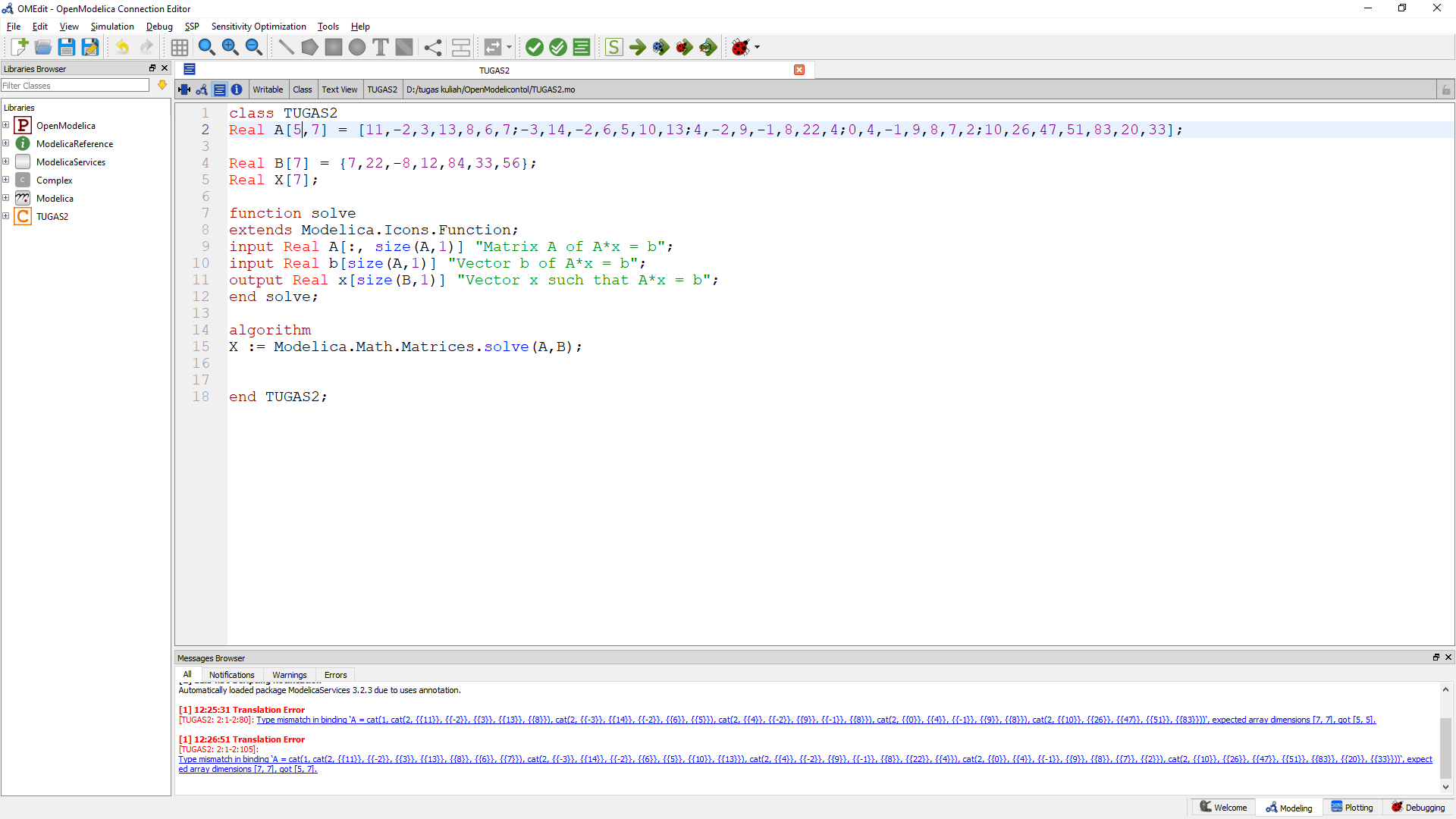
Saya menggunakan metode Gauss Elemination untuk menyelesaikan sebuah class bilangan Real A[5,7] = [11,-2,3,13,8,6,7;-3,14,-2,6,5,10,13;4,-2,9,-1,8,22,4;0,4,-1,9,8,7,2;10,26,47,51,83,20,33]
Lalu kita menggunakan Fungsi dan Algoritma seperti gambar dibawah ini
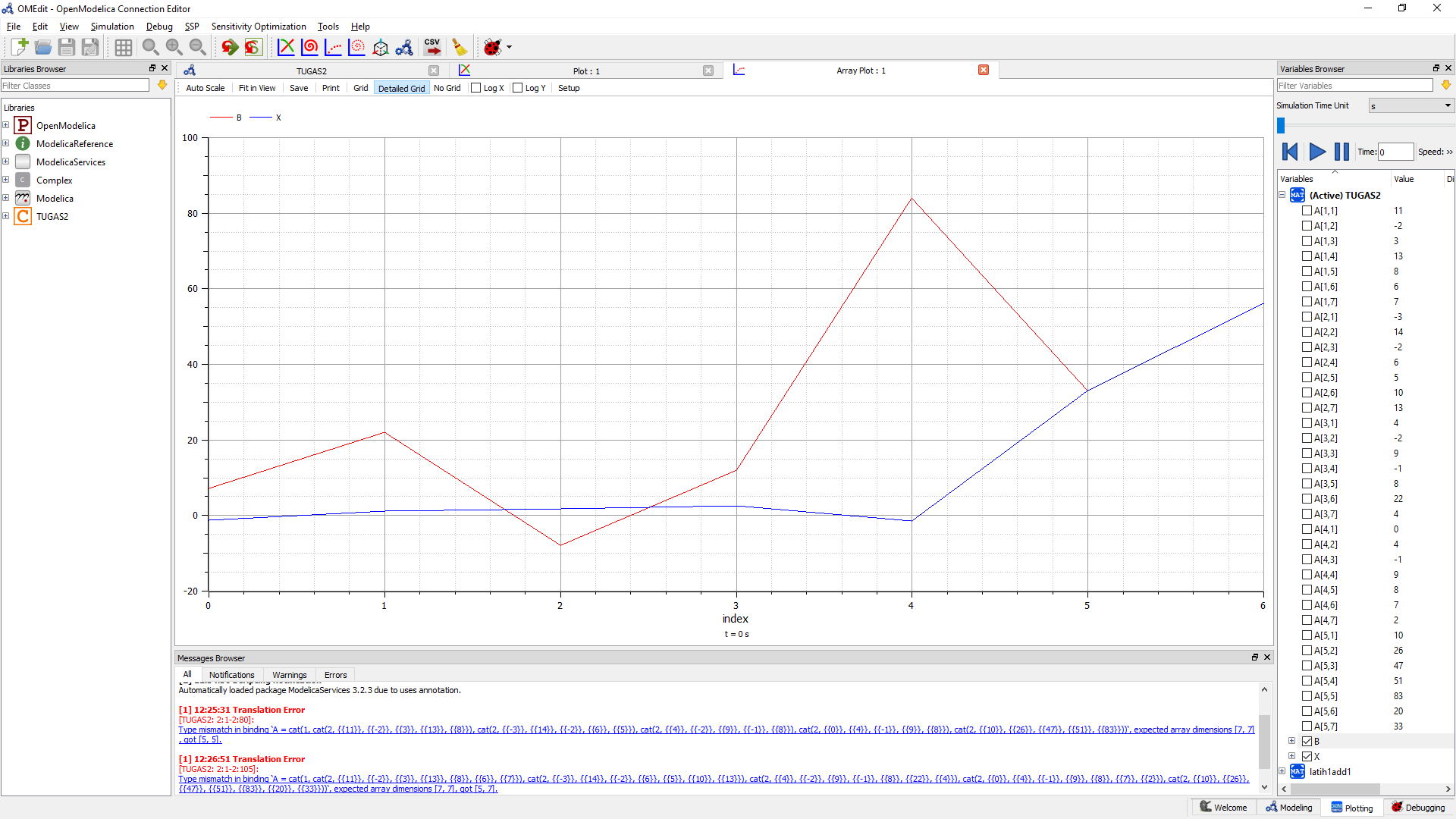
Setelah itu kita Simulate dan liat hasilnya
Pertemuan 3 (23 November 2020)
Pertemuan kali ini membahas tentang aplikasi metnum dalam permasalahan teknik.Contoh yang kita ambil yaitu bagaimana penyelesaian masalah teknik dalam Pegas-massa menggunakan OpenModelica

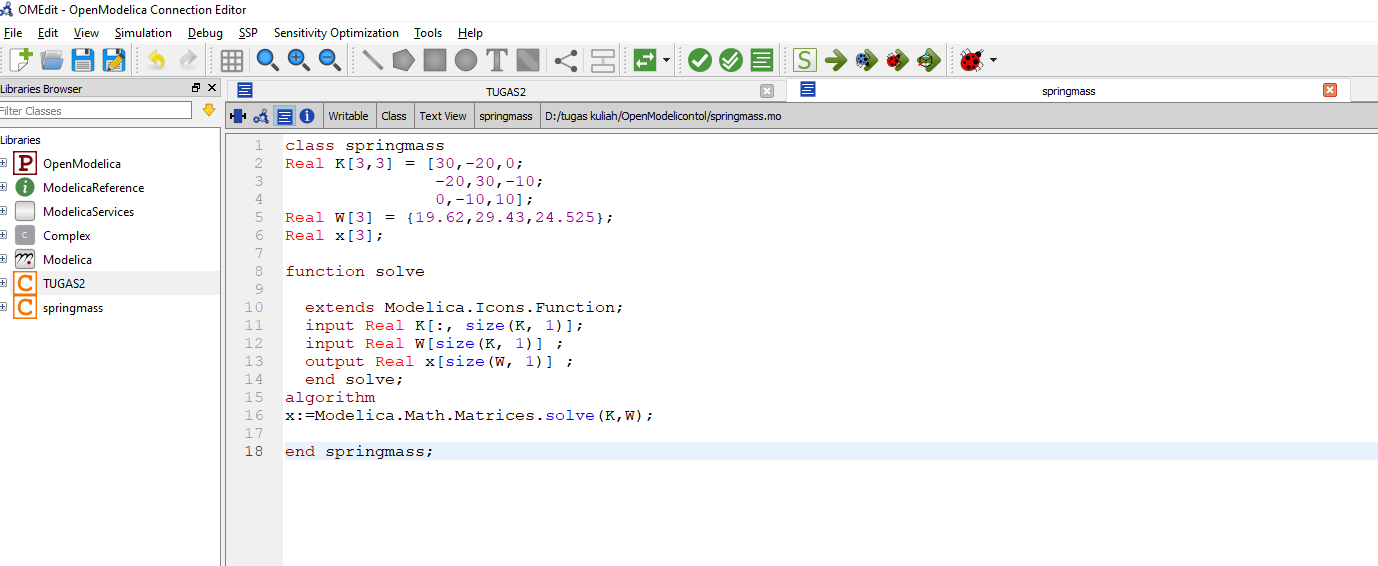
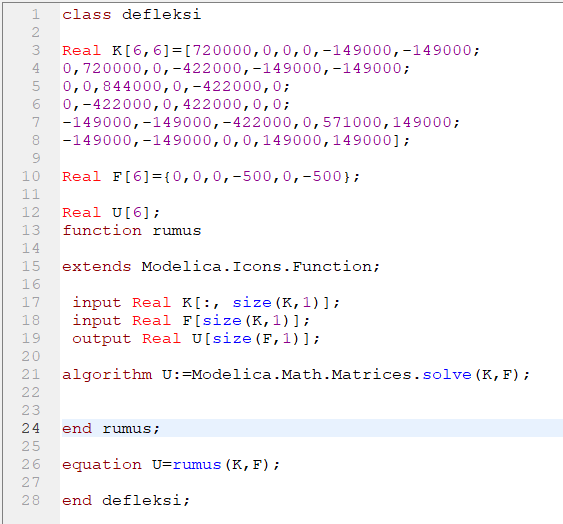
Pertama kita buat matriksnya dari persamaan yang ada kemudian kita masukan juga Fuction nya
extends Modelica.Icons.Function;
input Real K[:, size(K, 1)]; input Real W[size(K, 1)] ; output Real x[size(W, 1)] ;
Setelah itu kita masukan juga algoritma x:=Modelica.Math.Matrices.solve(K,W);
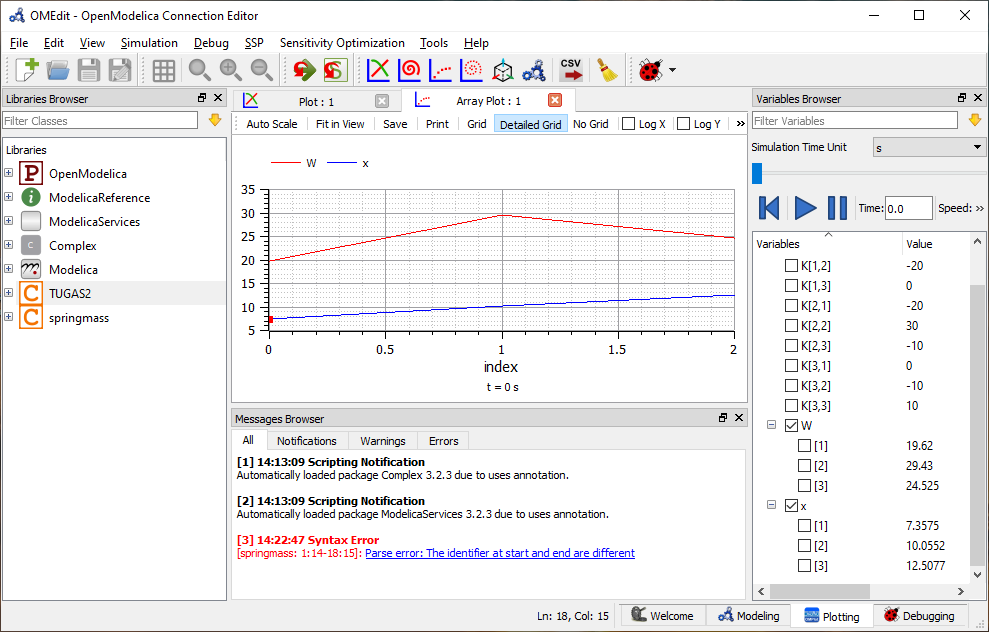
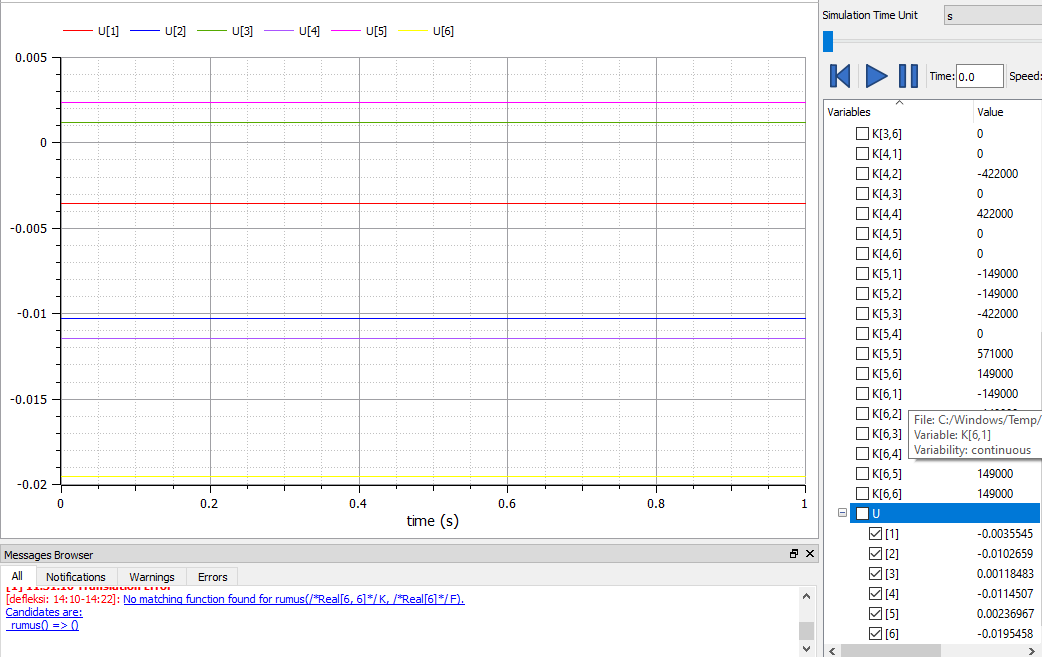
Setelah itu kita Simulate untuk melihat nilai X nya
Latihan 2.1
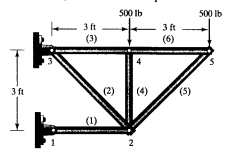
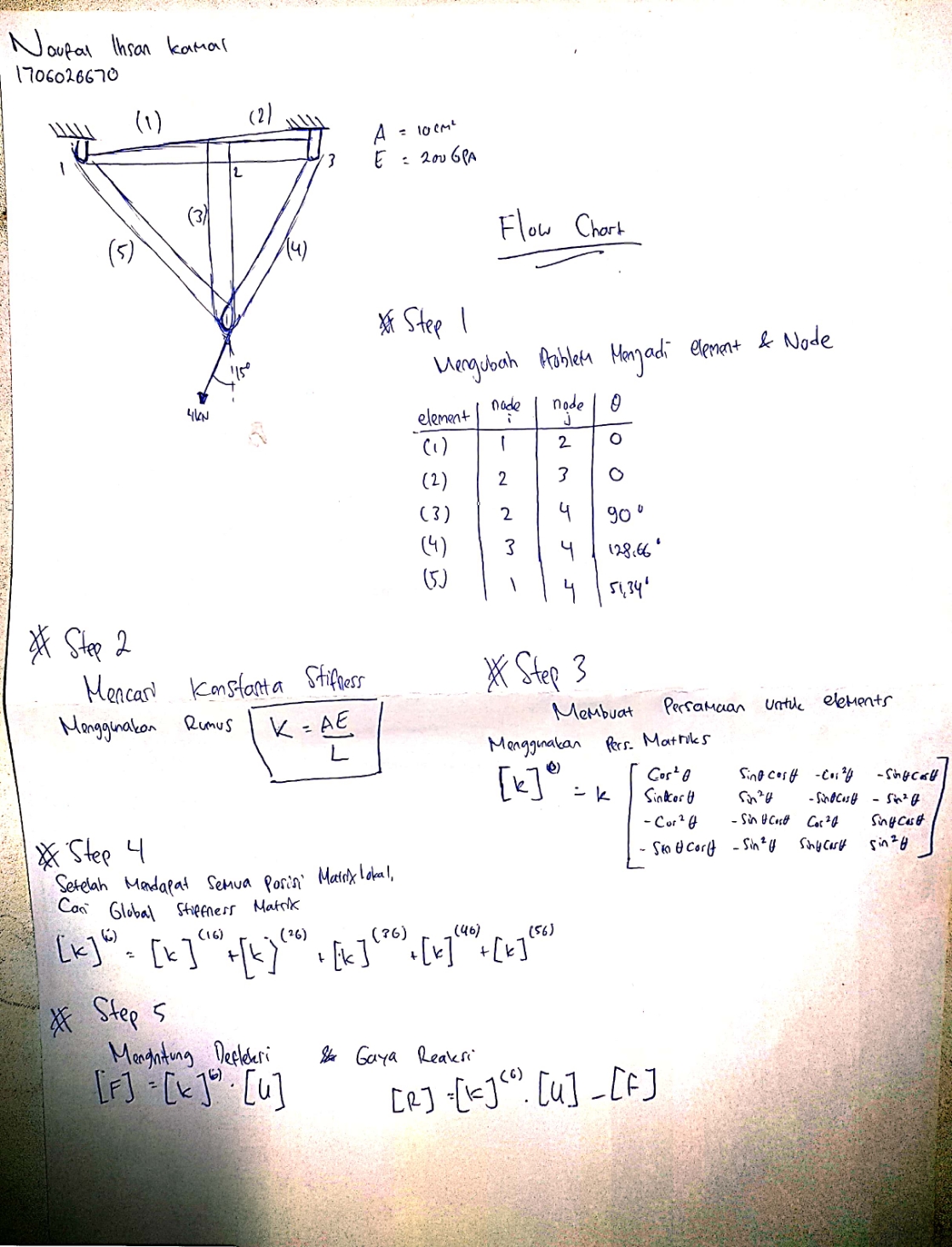
Latihan kali ini kita akan menganalisis Defleksi yang terjadi pada setiap Joint,Dengan mengikuti cara dibuku,kita akan mengerjakannya dalam beberapa step
1.Ubah Problem menjadi element dan node
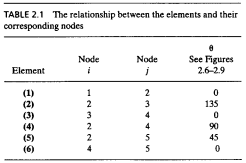
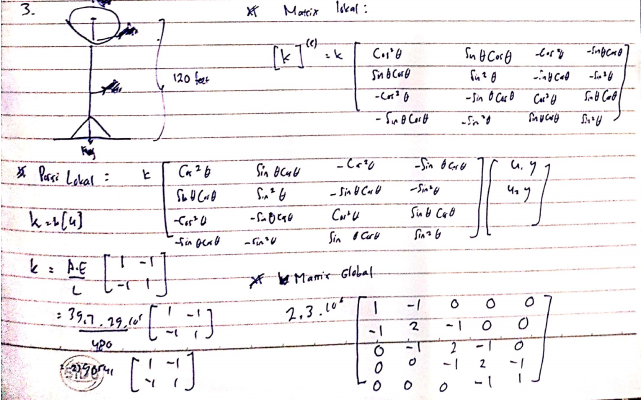
2.Stiffness Equation
Karena element 1,3,4,6 memiliki kesamaan panjang,cross-sectional area,dan modulus elasticity,maka kita bisa menggunakan persamaan yang sama,tetapi berbeda dengan element 2,5
3.Develop equations for elements
Karena elements 1,3,6 sejajar maka kita menggunakan sudut yang sama
Element 4 memiliki sudut berbeda yaitu 90,Element 2 memiliki sudut 135,dan Element 5 memiliki sudut 45
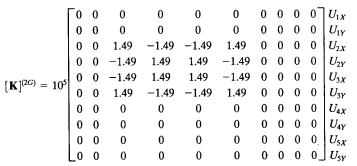
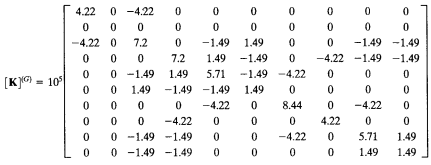
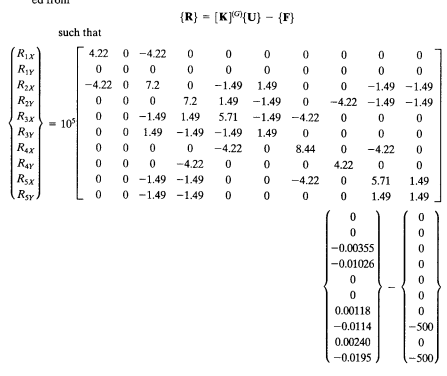
4.Assemble Elements
Global Stiffness Matrix
5.Boundery and Loads
Batas untuk node 1 dan 3 fixed,lalu pada node 4 dan 5 memiliki external loads
Hukum Hooke, F= k. x ,maka dalam persamaan matrix menjadi [F]=[K].[U]
6.Solusi menggunakan Modelica
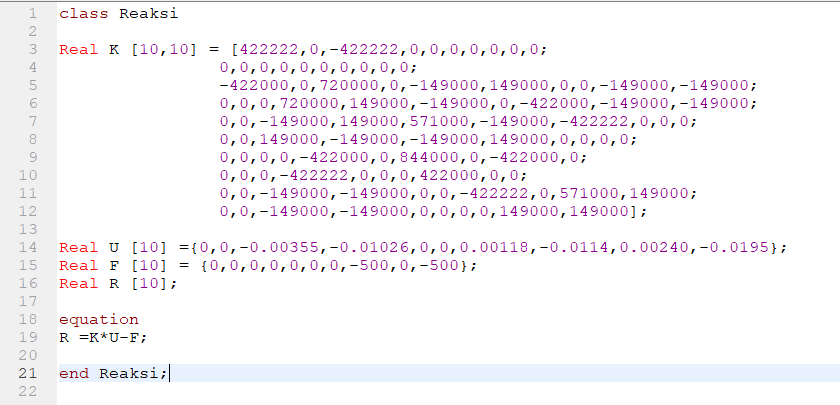
Gaya Reaksi
Kita bisa mencari gaya reaksi dengan memasukan rumus:
Setelah itu kita masukan kedalam Modelica dengan numeric,dan setelah itu kita bisa lihat hasilnya
Pertemuan 4 (30 November 2020)
Pada awal pertemuan,kita membahas tentang perbedaan antara Statis dengan Dinamis.Perbedaan paling utama pada 2 hal ini yaitu pada kondisi statis,beban tetap,tidak dipengaruhi oleh waktu.Sedangkan pada keadaan Dinamis,beban tidak tetap karena berubah terhadap waktu
Setelah itu kita Quiz dengan mengerjakan 2 soal lalu kami diminta untuk membuat flowchart pengerjaan nya,untuk soal pertamaa kurang lebih mirip seperti soal latihan 2.1
Pertemuan 5 (7 Desember 2020)
Pertemuan 6 (14 Desember 2020)
Pada pertemuan kali ini,kami diminta untuk muhasabah diri sendiri terkait pembelajaran Metnum sampai saat ini,Berikut adalah hasil muhasabah saya:
Menurut saya,saya selalu berusaha untuk mengikuti pembelajaran Metnum disetiap pertemuan,untuk dasar-dasar terkait penggunaan software OpenModelica saya masih cukup paham.Kemudian untuk penggunaan OpenModelica dalam penyelesaian trus 2 Dimensi seperti contoh dibuku saya masih cukup paham terkait flowchartnya,hanya saja saya masih belum cukup paham terkait dengan materi yang terdapat pada akhir akhir pembelajaran kemarin,terutama penggunaan metode Looping dalam aplikasi trus 3 dimensi.Oleh karena itu disisa pertemuan Metnum ini saya masih berusaha untuk bisa mengerti terkait penggunaan metode Looping tersebut dikarenakan keterbatasan pengetahuan saya terkait coding codingnya.
Aplikasi metode numerik dalam kasus optimisasi
Hari ini kita belajar membuat struktur rangka seperti gambar yg dikirm di WA, Dalam menyelesaikan persamaan ini kita jg hrus bisa membuat persm aljabar dan metode numeriknya Tugas besarnya ialah mencari nilai optimal untuk meminimalkan biaya dan konstrainnya yaitu strukturnya mampu menahan beban dan reliable,caranya mnentukan gaya2 yang bekerja,lalu ada apa aja stressnya yg diizinkan yaitu setengah dari material allowence.
One-Dimensional Unconstrained Optimization
Optimasi adalah suatu cara untuk mendapatkan nilai max atau min dari suatu permasalahan.
Metode yang digunakan kali ini adalah gOLDEN rATIO Method
Langkah pertama adalah mengetahui penyelsaian matematis Obejektif pertama adalah mencari nilai Fx Global Maximum
Langkah 2 kita melakkukan iterasi pertama nilai X thd calon nilai Fx Maksimum dengan batasan Xl dan Xu
Setelah kita dapat Xl dan Xu,kita masukan ke dalam persamaan untuk mencari X1 dan X2,lalu mengikuti aturan seperti yg tertera di gambar
Exercise kali ni kita menggunakan fungsi non-linier Fx=2sinx-x^2/10
Tugas Besar
Tujuan
Pada tugas besar kali ini kami diminta untuk mencari optimisasi desain untuk menekan biaya pada kasus yang diberikan. Optimisasi adalah suatu cara untuk mencari nilai ekstrim.
Constraint:
- Spesifikasi L (Panjang) dan geometri rangka truss
- Gaya beban terhadap struktur (1000 N dan 2000 N)
Asumsi:
- Diasumsikan tidak ada bending karena bersifat truss
- Beban terdistribusi pada node
- Safety Factor = 2
- Batas displacement 0,001m sebelum terjadi buckling
- Variabel bebas
Metode Mengerjakan
1. Pilih material dengan 3 variasi,area ,dan elastisitas material
2. Buat 2 grafik perbandingan yang pertama grafik dengan material locked dan variasi area,lalu yg ke dua grafik dengan area locked dan variasi elastisitas
3. Setelah itu kita hitung stress/cost
Data Material
Pembuatan Numerik
Koding Numerik ini dibuat untuk mencari nilai stress, safety factor,dan untuk mencari data untuk curve fitting
model Trusses_3D_Tugas_Besar_Safety
//define initial variable parameter Integer Points=size(P,1); //Number of Points parameter Integer Trusses=size(C,1); //Number of Trusses parameter Real Yield=215e6; //Yield Strength (Pa) parameter Real Area=0.000224; //Area L Profile (Dimension=0.03, Thickness=0,004) (m2) parameter Real Elas=193e9; //Elasticity SS 304 (Pa)
//define connection parameter Integer C[:,2]=[1,5;
2,6;
3,7;
4,8;
5,6; //1st floor
6,7; //1st floor
7,8; //1st floor
5,8; //1st floor
5,9;
6,10;
7,11;
8,12;
9,10; //2nd floor
10,11;//2nd floor
11,12;//2nd floor
9,12; //2nd floor
9,13;
10,14;
11,15;
12,16;
13,14;//3rd floor
14,15;//3rd floor
15,16;//3rd floor
13,16];//3rd floor
//define coordinates (please put orderly) parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1
-0.3,-0.375,0,1,1,1; //2
-0.3,0.375,0,1,1,1; //3
0.3,0.375,0,1,1,1; //4
0.3,-0.375,0.6,0,0,0; //5
-0.3,-0.375,0.6,0,0,0; //6
-0.3,0.375,0.6,0,0,0; //7
0.3,0.375,0.6,0,0,0; //8
0.3,-0.375,1.2,0,0,0; //9
-0.3,-0.375,1.2,0,0,0; //10
-0.3,0.375,1.2,0,0,0; //11
0.3,0.375,1.2,0,0,0; //12
0.3,-0.375,1.8,0,0,0; //13
-0.3,-0.375,1.8,0,0,0; //14
-0.3,0.375,1.8,0,0,0; //15
0.3,0.375,1.8,0,0,0]; //16
//define external force (please put orderly) parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-500,
0,0,-1000,
0,0,-1000,
0,0,-500};
//solution Real displacement[N], reaction[N]; Real check[3];
Real stress1[Trusses]; Real safety[Trusses]; Real dis[3]; Real Str[3];
protected parameter Integer N=3*Points; Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; Real err=10e-10, ers=10e-4;
algorithm //Creating Global Matrix G:=id; for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g; G:=G_star;
end for;
//Implementing boundary for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for;
//Solving displacement displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction reaction:=(G_star*displacement)-F;
//Eliminating float error for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))}); check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))}); check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
//Calculating stress in each truss for i in 1:Trusses loop for j in 1:3 loop
q1[j]:=P[C[i,1],j]; q2[j]:=P[C[i,2],j]; dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor for i in 1:Trusses loop
if stress1[i]>0 then safety[i]:=Yield/stress1[i]; else safety[i]:=0; end if;
end for;
end Trusses_3D_Tugas_Besar_Safety;
Membuat Curve Fitting
Curve fitting digunakan untuk mencari nilai cost terhadap fungsi area/elastisitas
model callcurve
parameter Real [8] X={1.11e-4,1.41e-4,1.71e-4,2.31e-4,3.04e-4,3.75e-4,7.44e-4,8.64e-4};
parameter Real [8] Y={273700 ,318800 ,381200 ,512800 ,683700 ,838000 ,1663100,1986400};
Real [3] Coe;
algorithm
Coe:=Curve_Fitting(X,Y);
end callcurve;
function Curve_Fitting
input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coe[order+1];
protected
Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1];
algorithm
for i in 1:size(X,1) loop for j in 1:(order+1) loop Z[i,j]:=X[i]^(order+1-j); end for; end for;
ZTr:=transpose(Z); A:=ZTr*Z; B:=ZTr*Y; Coe:=Modelica.Math.Matrices.solve(A,B); //Coe:=fill(2,size(Coe,1)); end Curve_Fitting;