Difference between revisions of "Muhammad Afif Rachmat"
Mafifrachmat (talk | contribs) (→Pertemuan Minggu 6) |
Mafifrachmat (talk | contribs) (→UAS) |
||
| (7 intermediate revisions by the same user not shown) | |||
| Line 608: | Line 608: | ||
| − | '''Tugas Besar | + | '''Tugas Besar''' |
[[File:600px-Soaltubes.jpeg|500px]] [[File:Soaltubes2.jpeg|500px]] | [[File:600px-Soaltubes.jpeg|500px]] [[File:Soaltubes2.jpeg|500px]] | ||
| Line 783: | Line 783: | ||
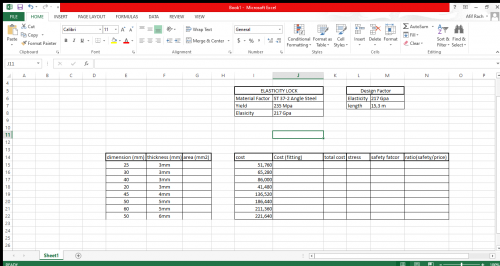
''Perhitungan harga '' | ''Perhitungan harga '' | ||
| − | + | Untuk menghitung harga dan bahan saya menggunakan bahan ST 37-2 Angle steel dimana dia merupakan low carbon steel yang biasa digunakan untuk bahan membuat rak etalase logam. Kemudian untuk harga saya mengacu pada link dibawah ini | |
| + | |||
| + | *http://www.pusatbesibaja.co.id/harga-besi-siku-profil-baja-distributor-pabrik-supplier-agen-jual-toko-produsen/ | ||
| + | *https://www.steel-sections.com/steelsections/st37-2-angle-steel.html | ||
| + | |||
| + | |||
| + | dari link diatas didapatkan beberapa data sebagai berikut | ||
| + | |||
| + | [[File:Q1.png|500px]] | ||
| + | |||
| + | |||
| + | data masih memiliki beberapa kekosongan. Untuk mengisinya, kita bisa menggunakan curve fitting pada aplikasi OpenModelica untuk melihat hasilnya. | ||
| + | Pada aplikasi OpenModelica kita menggunakan Fungsi sebagai berikut | ||
| + | |||
| + | function Curve_Fitting | ||
| + | input Real X[:]; | ||
| + | input Real Y[size(X,1)]; | ||
| + | input Integer order=2; | ||
| + | output Real Coef[order+1]; | ||
| + | |||
| + | protected | ||
| + | Real Z[size(X,1),order+1]; | ||
| + | Real ZTr[order+1,size(X,1)]; | ||
| + | Real A[order+1,order+1]; | ||
| + | Real B[order+1]; | ||
| + | |||
| + | algorithm | ||
| + | for i in 1:size(X,1) loop | ||
| + | for j in 1:(order+1) loop | ||
| + | Z[i,j]:=X[i]^(order+1-j); | ||
| + | end for; | ||
| + | end for; | ||
| + | ZTr:=transpose(Z); | ||
| + | |||
| + | A:=ZTr*Z; | ||
| + | B:=ZTr*Y; | ||
| + | Coef:=Modelica.Math.Matrices.solve(A,B); | ||
| + | |||
| + | end Curve_Fitting; | ||
| + | |||
| + | kemudian untuk memanggil fungsi tersebut kita membutuhkan model untuk bisa menjalankan fungsi Curve_Fitting. berikut adalah modelnya | ||
| + | |||
| + | model CurveFitting | ||
| + | parameter Real X[6]={0.000111, 0.000171, 0.000304, 0.000684, 0.000744, 0.000864}; | ||
| + | parameter Real Y[6]={179200, 239500, 429600, 963600, 1044800, 1428000}; | ||
| + | Real coef[3]; | ||
| + | |||
| + | equation | ||
| + | coef=FuncCurveFitting(X,Y,2); | ||
| + | end CurveFitting; | ||
| + | |||
| + | kemudian dari pengerjaan tersebut didapatkan hasil sebagai berikut | ||
| + | |||
| + | [[File:10Q.png|500px]] | ||
| + | |||
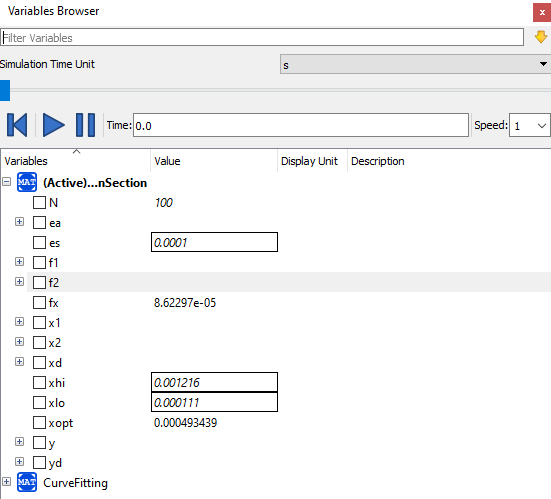
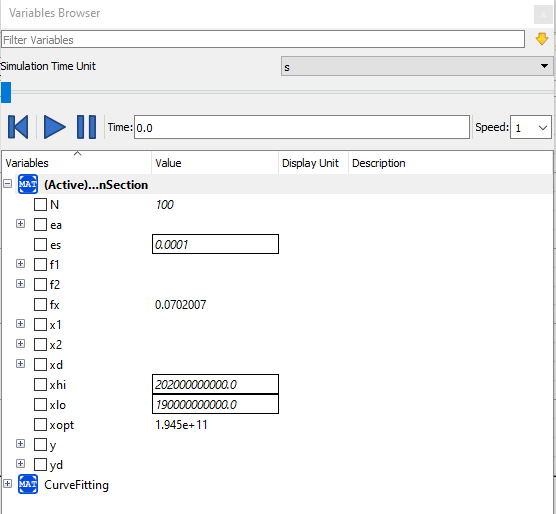
| + | setelah mendapatkan cukup data kita lanjutkan dengan mengoptimasi menggnakan metode golden section menggunakan OpenModelica berikut | ||
| + | |||
| + | |||
| + | model GoldenSection | ||
| + | parameter Real xd[:]={0.000111, 0.000141, 0.000171, 0.000231, 0.000291, 0.000304, 0.000384, 0.000684, 0.000575, 0.000744, 0.000864, 0.000725, | ||
| + | 0.001216}; | ||
| + | parameter Real yd[size(xd,1)]={6.29E-05, 7.24E-05, 7.96E-05, 8.86E-05, 9.26E-05, 9.30E-05, 9.32E-05, 8.02E-05, 8.58E-05, 7.72E-05, 7.15E-05, 7.82E- | ||
| + | 05, 5.79E-05}; | ||
| + | parameter Real xlo=0.000111; | ||
| + | parameter Real xhi=0.001216; | ||
| + | parameter Integer N=100; // maximum iteration | ||
| + | parameter Real es=0.0001; // maximum error | ||
| + | |||
| + | Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3]; | ||
| + | Real xopt, fx; | ||
| + | protected | ||
| + | Real d, xl, xu, xint, R=(5^(1/2)-1)/2; | ||
| + | |||
| + | algorithm | ||
| + | xl := xlo; | ||
| + | xu := xhi; | ||
| + | y := FuncCurveFitting(xd,yd); | ||
| + | |||
| + | for i in 1:N loop | ||
| + | d:= R*(xu-xl); | ||
| + | x1[i]:=xl+d; | ||
| + | x2[i]:=xu-d; | ||
| + | f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3]; | ||
| + | f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3]; | ||
| + | xint:=xu-xl; | ||
| + | |||
| + | if f1[i]>f2[i] then | ||
| + | xl:=x2[i]; | ||
| + | xopt:=x1[i]; | ||
| + | fx:=f1[i]; | ||
| + | else | ||
| + | xu:=x1[i]; | ||
| + | xopt:=x2[i]; | ||
| + | fx:=f2[i]; | ||
| + | end if; | ||
| + | ea[i]:=(1-R)*abs((xint)/xopt); | ||
| + | if ea[i]<es then | ||
| + | break; | ||
| + | end if; | ||
| + | end for; | ||
| + | end GoldenSection; | ||
| + | |||
| + | setelah disimulasikan, maka akan didapatkan hasil berupa Xopt yang merupakan nilai optimum. metode golden section harus dijalankan sebanyak 2 kali, yang pertama untuk material tetap, yang kedua untuk area tetap. code diatas merupakan golden section untuk material tetap. berikut hasil simulasi dari material tetap (gambar atas) dan area tetap (gambar bawah) | ||
| + | |||
| + | [[File:GoldenElas.PNG|800px|center|]] | ||
| + | |||
| + | [[File:GoldenArea.PNG|800px|center|]] | ||
| + | |||
| + | dan didapatkanlah hasil seperti diatas | ||
| + | |||
| + | ==== Kesimpulan ==== | ||
| + | |||
| + | dari hasil kalkulasi dan running di atas, didapatkan bahwa ruang area optimum adalah pada 1.945E+11 dan dimensi yang cukup mendekati area tersebut adalah pada 45x45 cm dan thickness 4mm. Adapun nilai elastisitas optimum yang didapatkan oleh golden section adalah 194.5E+9 dimana nilai tersebut masih dibawah nilai elastisitas ST 37-2 Angle steel sehingga dapa dikatakan material ST 37 ini cukup kuat dan relatif mrah untuk membuat rangka tersebut. | ||
| + | Jadi pilihan baja ST 37 adalah yang optimal untuk kualitas yang mumpuni dan harga yang terjangkau. | ||
| + | |||
| + | == UAS == | ||
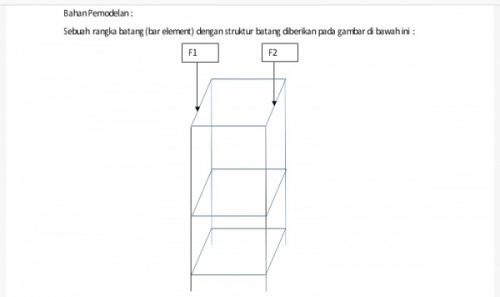
| + | Ujian Akhir Semester Metoda Numerik Semester Gasal 2021 | ||
| + | Perhatikan Water Tower dengan Reservoir berbentuk Bola pada Gambar diatas. Anda diminta untuk membuat pemodelan numerik untuk mengoptimalkan struktur Water Tower tersebut. | ||
| + | 1. Buatlah urutan langkah-langkah (prosedur) pemodelan numerik untuk optimasi struktur tersebut. | ||
| + | |||
| + | 2. Jelaskan tujuan pemodelan numerik soal no 1 diatas, hukum/dalil (fisika) yang dipakai dan asumsi-asumsi yang akan digunakan dalam perhitungan | ||
| + | |||
| + | 3. Untuk pemodelan numerik analisis strukturnya nya gunakan pendekatan 1D truss dgn membagi kolum (tiang) water tower kedalam 3 elemen (1D). | ||
| + | a). Susunlah persamaan aljabar kesetimbangan statik setiap elemen tsb. (matriks kesetimbangan lokal) | ||
| + | b) Matriks kesetimbangan global | ||
| + | |||
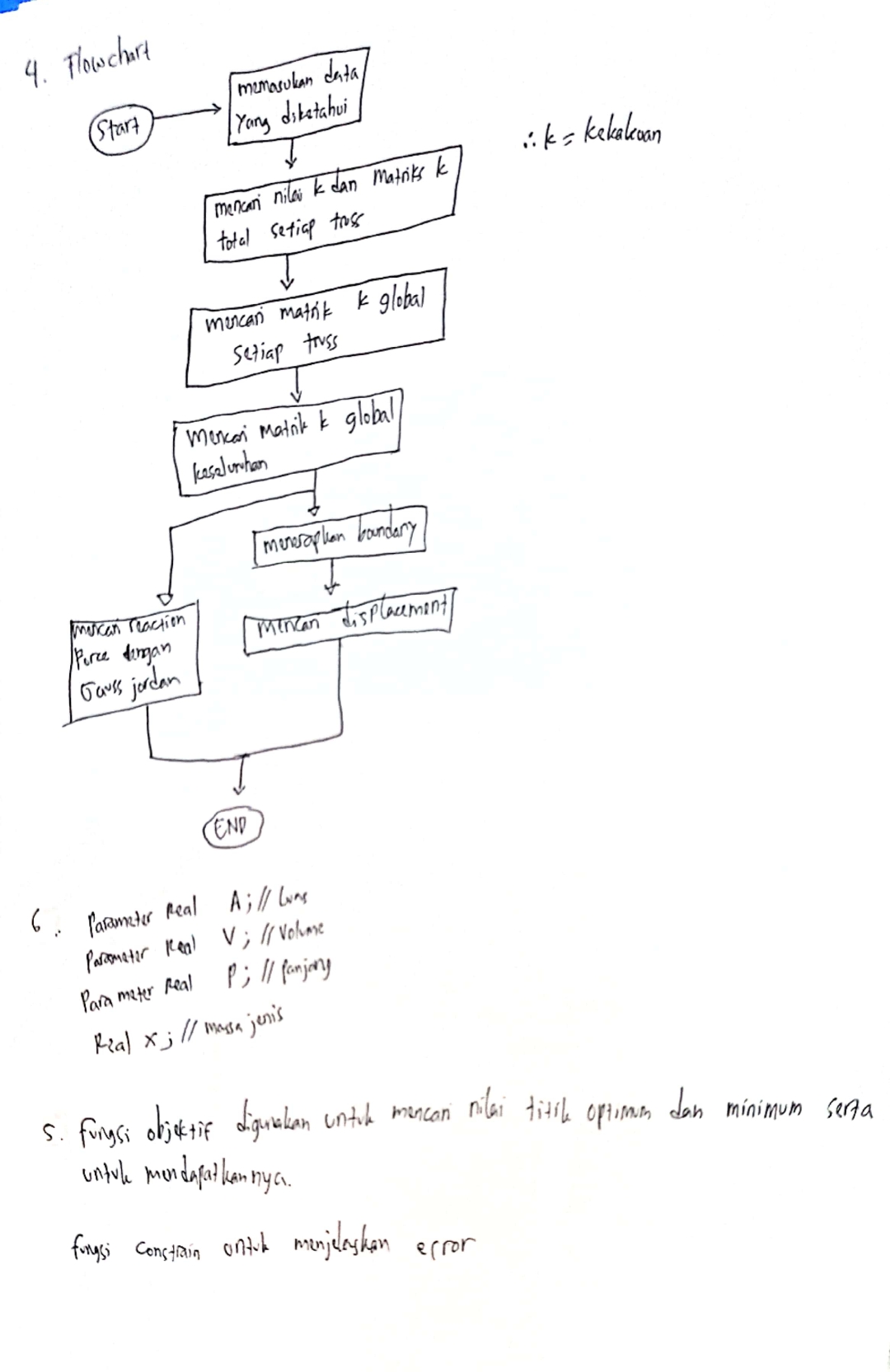
| + | 4. Susun urutan langkah-langkah (pseudocode) perhitungan matriks kesetimbangan global soal no 3 termasuk pengecekan kesalahan (verifikasi) perhitungannya | ||
| + | |||
| + | 5. Tulis dan jelaskan fungsi objektif dan constraint untuk optimasi struktur water tower tersebut | ||
| + | |||
| + | 6. Tuliskan asumsi nilai-nilai parameter dan variable untuk menghitung displacement, restraint dan stress utk model struktur water tower dgn 3 elemnt 1 D diatas | ||
| + | |||
| + | 7. Gunakan program modelica anda untuk menghitung displacement, restraint dan stress utk model struktur water tower dgn 3 element 1 D berdasarkan asumsi no 6 | ||
| + | |||
| + | '''JAWABAN''' | ||
| + | |||
| + | jawaban no 1 dan 2 berada di dalam satu lembar sebagai berikut | ||
| + | |||
| + | [[File:ASU2.jpg]] | ||
| + | |||
| + | jawaban untuk soal no 3 di lembar berikut | ||
| + | |||
| + | [[File:ASU3.jpg]] | ||
| + | |||
| + | Jawaban untuk soal no 4,5, dan 6 berada dalam satu lembar berikut | ||
| + | |||
| + | [[File:ASU4.jpg]] | ||
| + | |||
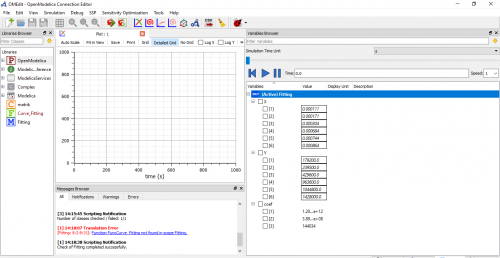
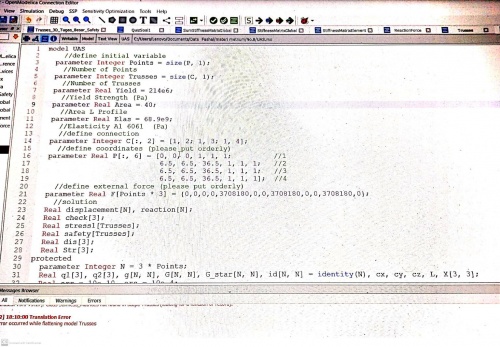
| + | untuk soal no 7 model yang dipakai pada Open modelica adalah sebagai berikut | ||
| + | |||
| + | [[File:622387.jpg|500px|center]] | ||
| + | |||
| + | [[File:622388.jpg|500px|center]] | ||
| + | |||
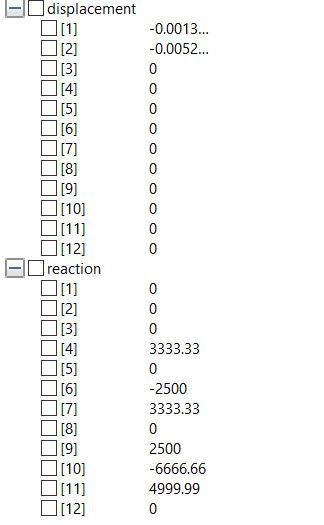
| + | dari model tersebut didapatkan hasil sebagai berikut | ||
| + | |||
| + | [[File:ASU5.jpg]] | ||
Latest revision as of 20:51, 14 January 2021
| Biodata | |
|---|---|

| |
| Nama | Muhammad Afif Rachmat |
| NPM | 1906356185 |
| Muhammad.afif92@ui.ac.id | |
| Youtube | https://www.youtube.com/watch?v=szu4bZKi0Vw |
Contents
Muhammad Afif Rachmat
Biodata Nama : Muhammad Afif Rachmat TTL : Lebak, 08 April 2001 Jurusan : Teknik Mesin Hobi : games, catur, outdoor
HALO! Perkenalkan nama saya Muhammad Afif Rachmat (NPM 1906356185) biasa dipanggil Afif. Saya Adalah mahasiswa Teknik Mesin angkatan 2019 dari Fakultas Teknik Universitas Indonesia. Seaya memiliki ketertarikan kepada bidang mesin karena saya ingin berinovasi dan berkreasi di bidang teknologi seperti Alm. B.J. Habibie. untuk itu saya memasuki jurusan mesin untuk mengejar cita-cits saya.
Materi Sebelum UTS
Sebelum UTS kami diajarkan oleh Bapak Engkos A. Kosasih, dan materi yang diajarkan diantaranya adalah:
- Deret Mclaurin & Deret Taylor, dengan metode forward, center, dan backward
- Bracketing Methods dan Open Methods, dimana bracketing methods meliputi graphical methods, bisection methods, dan false-position methods sedangkan open methods meliputi simple fixed-point iteration, newton-raphson methods, secant methods, dan brents methods
- Mencari nilai interpolasi dan regresi linier menggunakan matriks
Catatan Minggu Pertama (11 November 2020)
Tujuan Pembelajaran
- Memahami konsep dan prinsip dasar metode numerik
- Dapat menerapkan pemahaman yang didapatkan dalam mata kuliah Metode Numerik
- Mampu menerapkan pemahaman metode numerik dalam bidang keteknikan
- Membentuk kita menjadi orang yang lebih beradab
Manfaat Belajar bagi Diri Saya Sendiri
Menurut saya, pembelajaran adalah suatu proses untuk memahami peristiwa-peristiwa yang terjadi di sekitar kita. Saya merasakan bahwa dengan belajar, saya dapat lebih memahami tentang peristiwa-peristiwa yang terjadi di lingkungan saya, dan membantu saya untuk memecahkan permasalahan baru yang sebelumnya belum pernah saya temukan. Belajar juga dapat meningkatkan kepekaan sosial, kepedulian dan empati dalam diri saya.
Komputer dalam Metode Numerik
Komputer merupakan alat hitung yang sangat cepat, namun pada hakikatnya, komputer bersifat "dummy" dan mempunyai batasan-batasan hitungan yang tidak dapat dilewati. Apa artinya bagi diri saya adalah saya menyadari bahwa komputer merupakan alat hitung yang cepat, namun pada akhirnya semuanya bergantung kepada sang pengguna itu sendiri, sehingga kita harus bisa lebih percaya diri dan menyadari bahwa kemampuan kita bahkan lebih diatas komputer manapun.
Tugas Minggu Pertama
Dalam kesempatan kali ini saya membuat suatu video pembelajaran mengenai penggunaan aplikasi OpenModelica pada perhitungan gaya dalam Katrol Majemuk :
Catatan Minggu Kedua (18 N0vember 2020)
Pada Minggu kedua ini Mahasiswa harus sudah mengerjakan tugas yang diberikan oleh dosen dan bisa menjelaskannya .Sebelum memasuki materi pembelajaran metode numerik, Mahasiswa diminta mereview fungsi pembelajaran aljabar linear dan hubungannya dengan metode numerik. Kemudian, menceritakan pengalaman mempelajari aplikasi Open Modelica. Dan dari yang saya pelajari, aplikasi ini dibuat dengan tujuan bahasa pemodelan, bukan coding. Namun, ketika melakukan perhitungan, code yang ditulis harus dalam bahsa C++. Salah satu alasan pemilihan penggunaan aplikasi ini adalah karena Open Modelica dibuat open dan free, yang dimana semua orang boleh menggunakannya. Open Modelica mempunyai beberapa fitur, seperti membuat model, class, connector, expanable connector, record, function, dan lain-lain. Aplikasi ini object oriented, kita bisa membuat beberapa class fungsi dan class eksekusi, kemudian menggabungkannya ke dalam satu model, dengan pembelajaran hari dapat disebut sebagai sistem panggil.
Tugas Minggu Kedua
berikut adalah tugas untuk minggu kedua yaitu tentang class dan cara memanggil function.
Catatan Minggu Ketiga (25 November 2020)
Pada minggu ketiga ini kami diminta untuk membuat pseudocode untuk metode penyelesaian Gauss-Jordan. namun pada kelas, masih banyak mahasiswa termasuk saya yang sudah lupa dan tidak bisa membuat pseudocode untuk Gauss-Jordan. jadi untuk minggu ketiga ini mahasiswa harus melakukan latihan yang ada di buku finite element dan mencoba menyelesaikan persamaan pada 9.5 di OpenModelica.
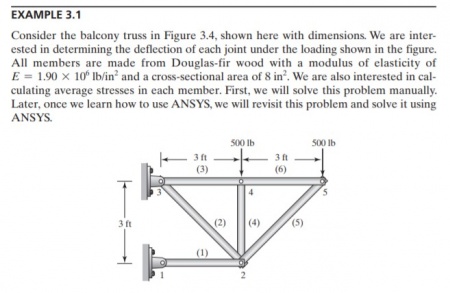
tugas tentang trusses
We can use Finete Element Method to solve this problem. We can make equation with numerical method use Open modelica.
|
Persamaan model Trusses
parameter Integer N=10; //Global matrice = 2*points connected
parameter Real A=8;
parameter Real E=1.9e6;
Real G[N,N]; //global
Real Ginitial[N,N]; //global
Real Sol[N]; //global dispplacement
Real X[N]={0,0,0,0,0,0,0,-500,0,-500};
Real R[N]; //global reaction force
Real SolMat[N,1];
Real XMat[N,1];
//boundary coundition
Integer b1=1;
Integer b2=3;
//truss 1
parameter Real X1=0; //degree between truss
Real k1=A*E/36;
Real K1[4,4]; //stiffness matrice
Integer p1a=1;
Integer p1b=2;
Real G1[N,N];
//truss 2
parameter Real X2=135; //degree between truss
Real k2=A*E/50.912;
Real K2[4,4]; //stiffness matrice
Integer p2a=2;
Integer p2b=3;
Real G2[N,N];
//truss 3
parameter Real X3=0; //degree between truss
Real k3=A*E/36;
Real K3[4,4]; //stiffness matrice
Integer p3a=3;
Integer p3b=4;
Real G3[N,N];
//truss 4
parameter Real X4=90; //degree between truss
Real k4=A*E/36;
Real K4[4,4]; //stiffness matrice
Integer p4a=2;
Integer p4b=4;
Real G4[N,N];
//truss 5
parameter Real X5=45; //degree between truss
Real k5=A*E/50.912;
Real K5[4,4]; //stiffness matrice
Integer p5a=2;
Integer p5b=5;
Real G5[N,N];
//truss 6
parameter Real X6=0; //degree between truss
Real k6=A*E/36;
Real K6[4,4]; //stiffness matrice
Integer p6a=4;
Integer p6b=5;
Real G6[N,N];
/*
for each truss, please ensure pXa is lower then pXb (X represents truss element number)
*/
algorithm
//creating global matrice
K1:=Stiffness_Matrices(X1);
G1:=k1*Local_Global(K1,N,p1a,p1b);
K2:=Stiffness_Matrices(X2);
G2:=k2*Local_Global(K2,N,p2a,p2b);
K3:=Stiffness_Matrices(X3);
G3:=k3*Local_Global(K3,N,p3a,p3b);
K4:=Stiffness_Matrices(X4);
G4:=k4*Local_Global(K4,N,p4a,p4b);
K5:=Stiffness_Matrices(X5);
G5:=k5*Local_Global(K5,N,p5a,p5b);
K6:=Stiffness_Matrices(X6);
G6:=k6*Local_Global(K6,N,p6a,p6b);
G:=G1+G2+G3+G4+G5+G6;
Ginitial:=G;
//implementing boundary condition
for i in 1:N loop
G[2*b1-1,i]:=0;
G[2*b1,i]:=0;
G[2*b2-1,i]:=0;
G[2*b2,i]:=0;
end for;
G[2*b1-1,2*b1-1]:=1;
G[2*b1,2*b1]:=1;
G[2*b2-1,2*b2-1]:=1;
G[2*b2,2*b2]:=1;
//solving displacement
Sol:=Gauss_Jordan(N,G,X);
//solving reaction force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);
end Trusses;
|
Stiffness Matricies
function Stiffness_Matrices
input Real A; Real Y; output Real X[4,4]; Real float_error = 10e-10; protected final constant Real pi=2*Modelica.Math.asin(1.0);
algorithm
Y:=A/180*pi; X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2;
-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2];
for i in 1:4 loop
for j in 1:4 loop
if abs(X[i,j]) <= float_error then
X[i,j] := 0;
end if;
end for;
end for;
end Stiffness_Matrices;
Trusses Problem 2 (Homework)
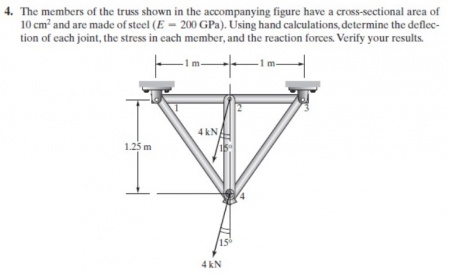
|
Persamaan class Trusses_HW
parameter Integer N=8; //Global matrice = 2*points connected
parameter Real A=0.001; //Area m2
parameter Real E=200e9; //Pa
Real G[N,N]; //global
Real Ginitial[N,N]; //global
Real Sol[N]; //global dispplacement
Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033};
Real R[N]; //global reaction force
Real SolMat[N,1];
Real XMat[N,1];
//boundary condition
Integer b1=1;
Integer b2=3;
//truss 1
parameter Real X1=0; //degree between truss
Real k1=A*E/1;
Real K1[4,4]; //stiffness matrice
Integer p1a=1;
Integer p1b=2;
Real G1[N,N];
//truss 2
parameter Real X2=0; //degree between truss
Real k2=A*E/1;
Real K2[4,4]; //stiffness matrice
Integer p2a=2;
Integer p2b=3;
Real G2[N,N];
//truss 3
parameter Real X3=90; //degree between truss
Real k3=A*E/1.25;
Real K3[4,4]; //stiffness matrice
Integer p3a=2;
Integer p3b=4;
Real G3[N,N];
//truss 4
parameter Real X4=90+38.6598; //degree between truss
Real k4=A*E/1.6;
Real K4[4,4]; //stiffness matrice
Integer p4a=1;
Integer p4b=4;
Real G4[N,N];
//truss 5
parameter Real X5=90-38.6598; //degree between truss
Real k5=A*E/1.6;
Real K5[4,4]; //stiffness matrice
Integer p5a=3;
Integer p5b=4;
Real G5[N,N];
/*
for each truss, please ensure pXa is lower then pXb (X represents truss element number)
*/
algorithm
//creating global matrice
K1:=Stiffness_Matrices(X1);
G1:=k1*Local_Global(K1,N,p1a,p1b);
K2:=Stiffness_Matrices(X2);
G2:=k2*Local_Global(K2,N,p2a,p2b);
K3:=Stiffness_Matrices(X3);
G3:=k3*Local_Global(K3,N,p3a,p3b);
K4:=Stiffness_Matrices(X4);
G4:=k4*Local_Global(K4,N,p4a,p4b);
K5:=Stiffness_Matrices(X5);
G5:=k5*Local_Global(K5,N,p5a,p5b);
G:=G1+G2+G3+G4+G5;
Ginitial:=G;
//implementing boundary condition
for i in 1:N loop
G[2*b1-1,i]:=0;
G[2*b1,i]:=0;
G[2*b2-1,i]:=0;
G[2*b2,i]:=0;
end for;
G[2*b1-1,2*b1-1]:=1;
G[2*b1,2*b1]:=1;
G[2*b2-1,2*b2-1]:=1;
G[2*b2,2*b2]:=1;
//solving displacement
Sol:=Gauss_Jordan(N,G,X);
//solving reaction force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);
end Trusses_HW;
|
Fungsi Panggil
|
Matrice Transformation function Stiffness_Matrices
input Real A;
Real Y;
output Real X[4,4];
Real float_error = 10e-10;
final constant Real pi=2*Modelica.Math.asin(1.0);
algorithm
Y:=A/180*pi;
X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2;
-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2];
for i in 1:4 loop
for j in 1:4 loop
if abs(X[i,j]) <= float_error then
X[i,j] := 0;
end if;
end for;
end for;
end Stiffness_Matrices;
|
Global Element Matrice function Local_Global
input Real Y[4,4];
input Integer B;
input Integer p1;
input Integer p2;
output Real G[B,B];
algorithm
for i in 1:B loop
for j in 1:B loop
G[i,j]:=0;
end for;
end for;
G[2*p1,2*p1]:=Y[2,2];
G[2*p1-1,2*p1-1]:=Y[1,1];
G[2*p1,2*p1-1]:=Y[2,1];
G[2*p1-1,2*p1]:=Y[1,2];
G[2*p2,2*p2]:=Y[4,4];
G[2*p2-1,2*p2-1]:=Y[3,3];
G[2*p2,2*p2-1]:=Y[4,3];
G[2*p2-1,2*p2]:=Y[3,4];
G[2*p2,2*p1]:=Y[4,2];
G[2*p2-1,2*p1-1]:=Y[3,1];
G[2*p2,2*p1-1]:=Y[4,1];
G[2*p2-1,2*p1]:=Y[3,2];
G[2*p1,2*p2]:=Y[2,4];
G[2*p1-1,2*p2-1]:=Y[1,3];
G[2*p1,2*p2-1]:=Y[2,3];
G[2*p1-1,2*p2]:=Y[1,4];
end Local_Global;
|
Gauss_Jordan function Gauss_Jordan input Integer N; input Real A[N,N]; input Real B[N]; output Real X[N]; Real float_error = 10e-10; algorithm X:=Modelica.Math.Matrices.solve(A,B); for i in 1:N loop
if abs(X[i]) <= float_error then
X[i] := 0;
end if;
end for;
end Gauss_Jordan; |
Reaction Matrice Equation function Reaction_Trusses input Integer N; input Real A[N,N]; input Real B[N,1]; input Real C[N,1]; Real X[N,1]; output Real Sol[N]; Real float_error = 10e-10; algorithm X:=A*B-C; for i in 1:N loop if abs(X[i,1]) <= float_error then X[i,1] := 0; end if; end for; for i in 1:N loop Sol[i]:=X[i,1]; end for; end Reaction_Trusses; |
Minggu Keempat (2 Desember 2020)
Pada pertemuan ke empat ini mahasiswa harus melaporkan hasil pekerjaan rmah yang diberikan selama seminggu terakhir untuk di koreksi. pada pertengahan kelas didapati bahwa model pseudocode yang paling baik adalah yang josiah dan ka Hikaru. kemudian mahasiswa harus mengkaji ulang dan mengevaluasi pekerjaan rumah untuk menjadi seperti josiah atau ka Hikaru. dan di akhir pertemuah, diberikan Quiz untuk membuat diagram kelas dan flowchart dari modelica yang sudah diprogram oleh josiah. ditambah dengan PR 4 untuk membuat flowchart dan diagram kelas pada soal trusses yang diberikan.
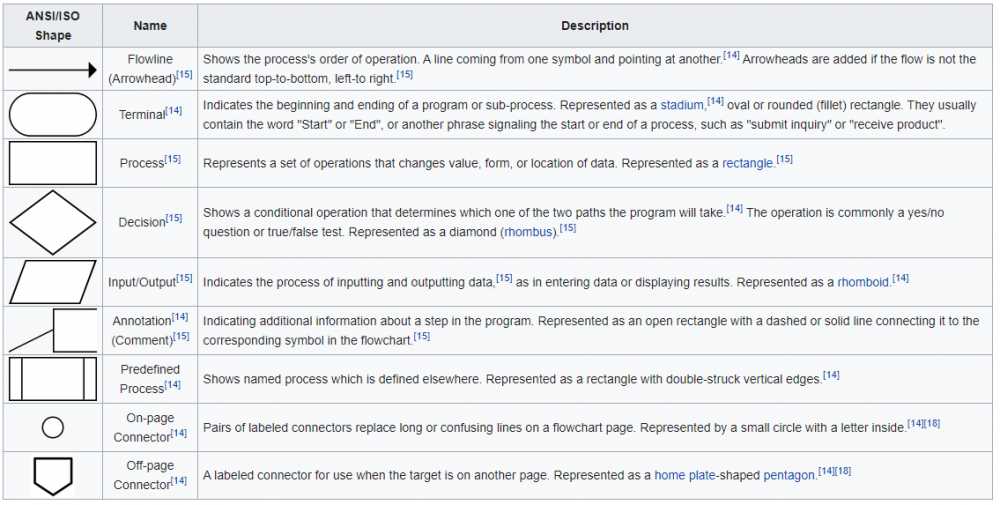
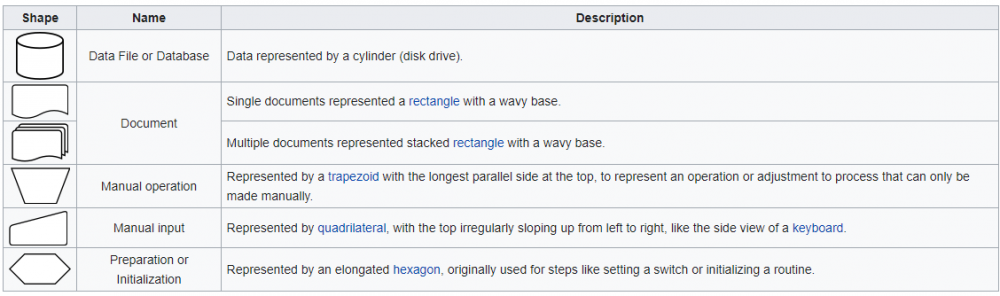
flowchart adalah alur pengerjaan atau sebuah peta konsep untuk mempermudah penjelasan mengenai penyelesaian suatu sistem. Didalam flowchart terdapat diagram kelas untuk melambangkan apa yang harus dilakukan atau yang terjadi kepada sistem tersebut selama berada di bagian itu. berikut adalah jenis-jenis diagram kelas untuk melambangkan suatu kerja.
Quiz Flowchart and Diagram Class
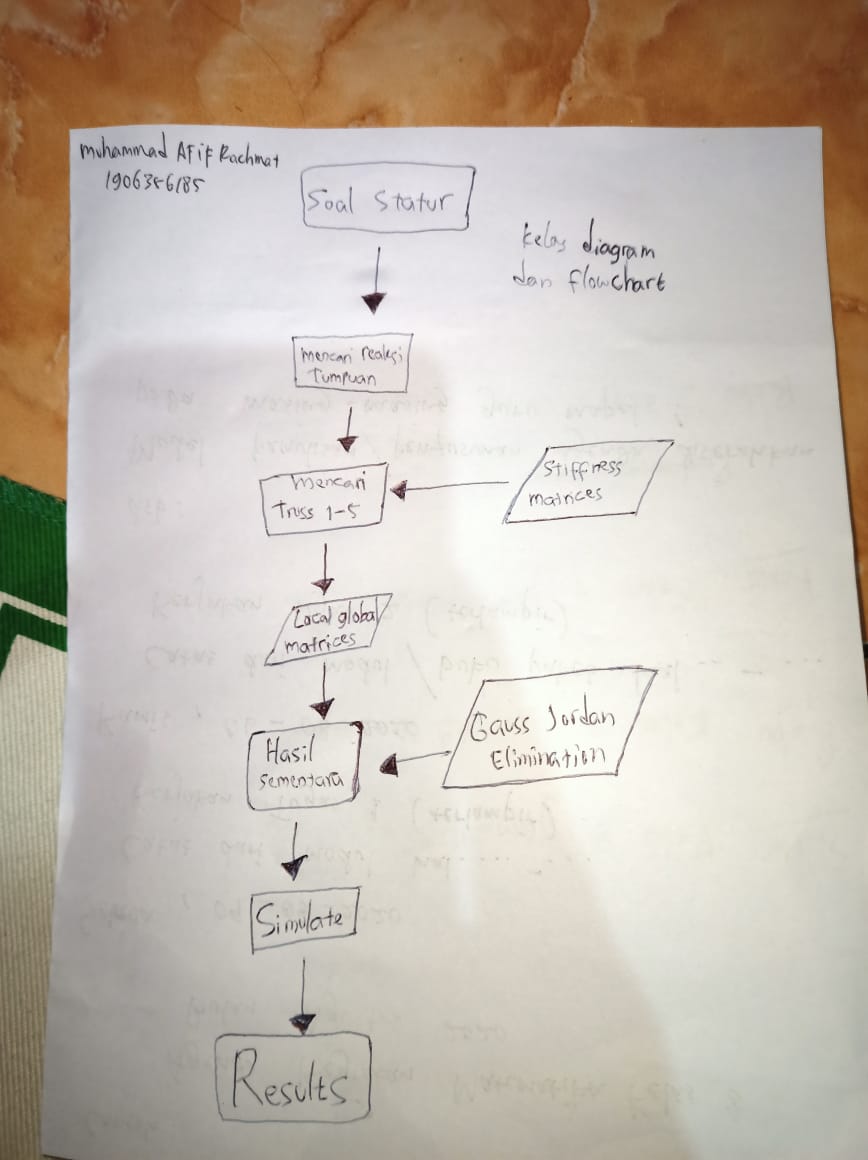
Pada Quiz pertama saya mencoba membuat flowchart dan diagram class sendiri untuk menaksir alur pengerjaan modelica josiah, berikut adalah hasil yang saya buat sendiri berdasarkan perkiraan saya:
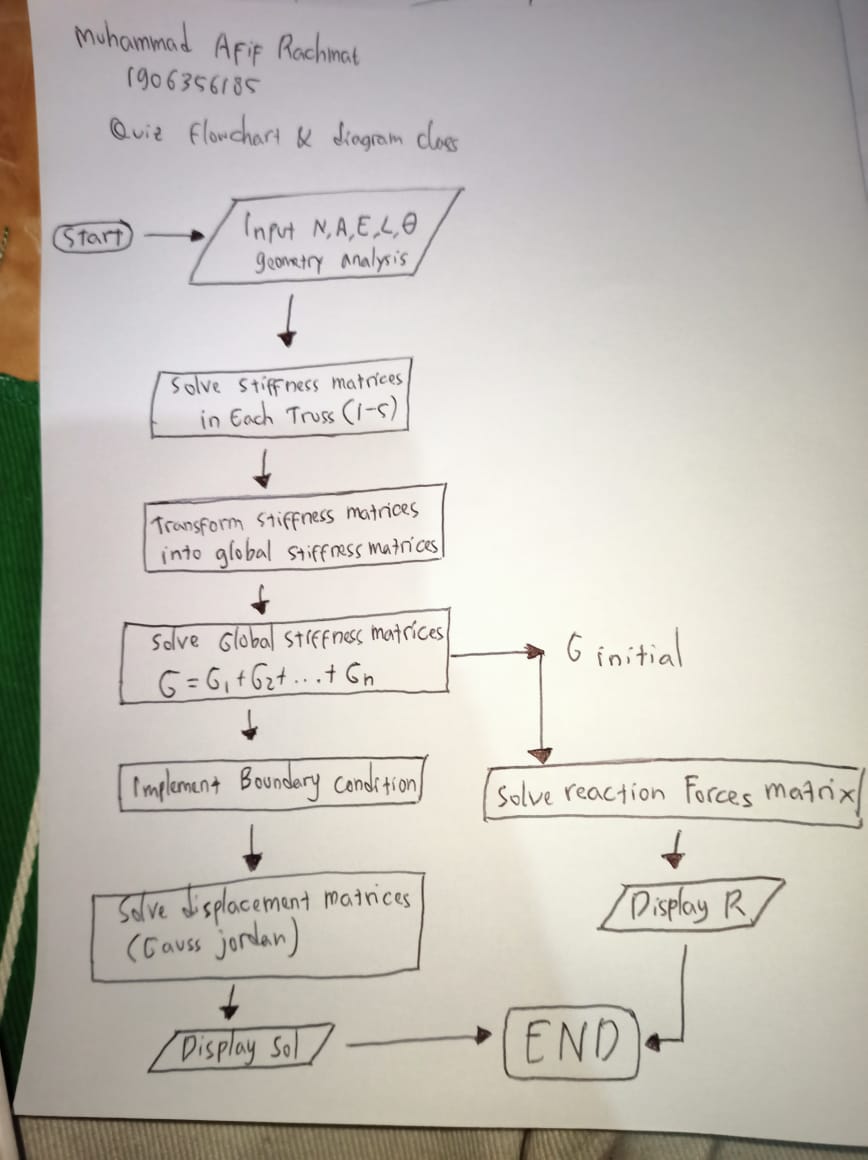
Kemudian Setelah beberapa saat berdiskusi, akhirnya diperlihatkan bahwa flowchart josiah lebih baik dan lebih lengkap. sehingga semua mahasiswa harus merevisi hasil pengerjaannya masing-masing agar menjadi seperti josiah. berikut adalah flowchart hasil revisi saya berdasarkan flowchart josiah.
Tugas Minggu keempat
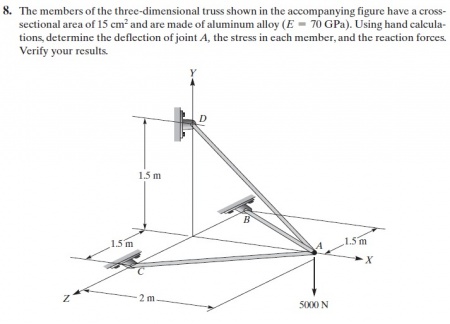
Pada pr kali ini kami ditugaskan untuk membuat coding dari OpenModelica untuk menyelesaikan soal dibawah dan jga membuat flowchart dan diagram kelas untuk alur pengerjaan soal tersebut.
pada gambar dapat diketahui bahwa: Luas Cross-sectional Area = 15 cm^2, E = 70 GPa, Banyak Truss = 3, Banyak Point = 4
Dan berikut adalah flowchart dan diagram class untuk alur penyelesaiannya
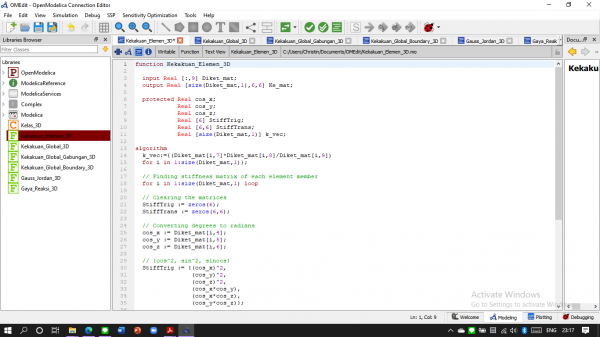
Dibawah ini adalah coding untuk soal 3d trusses berdasarkan dari saudara Ahmad Mohammad Fahmi dari kelas metode numerik 03 :
bentuk Operasi OpenModelica untuk membuat fungsi Kekakuan elemen
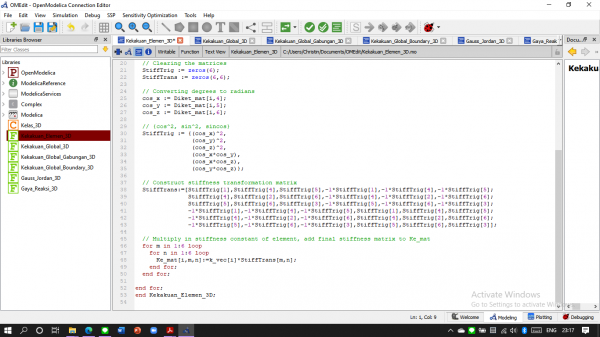
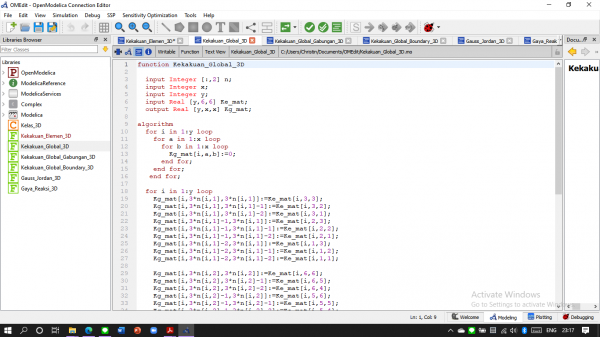
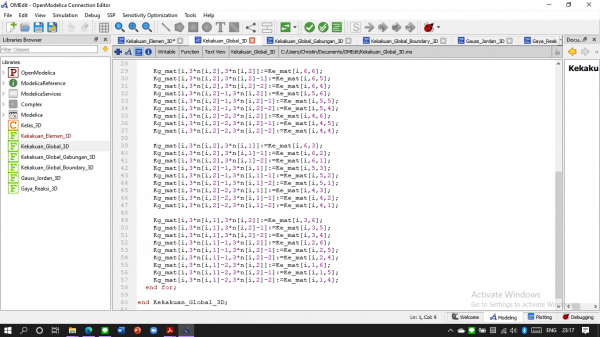
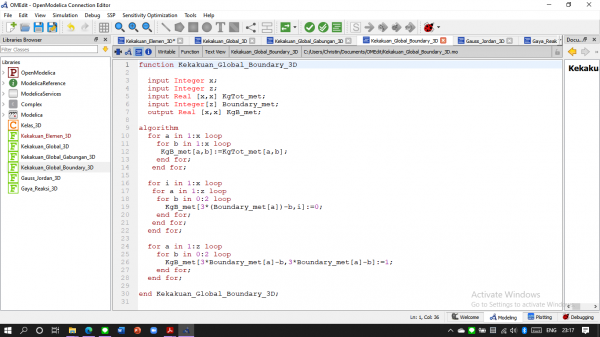
Kemudian membuat fungsi Kekakuan Global
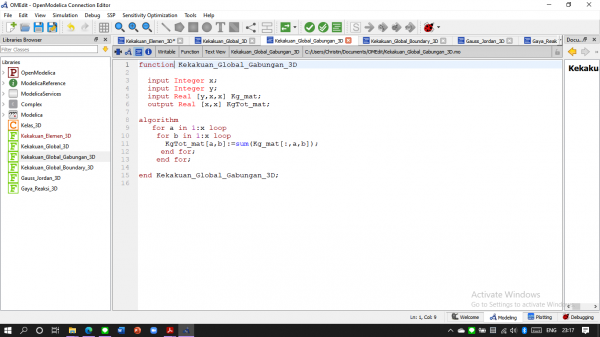
Setelah itu berdasarkan hasil penjumlahan kekakuan per elemen dibuatlah fungsi Kekakuan Global Gabungan
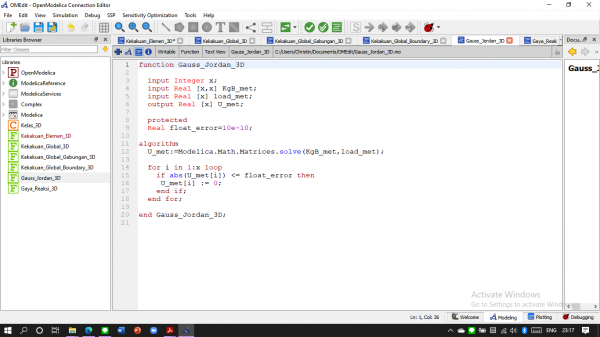
Selanjutnya membuat fungsi Gauss Jordan
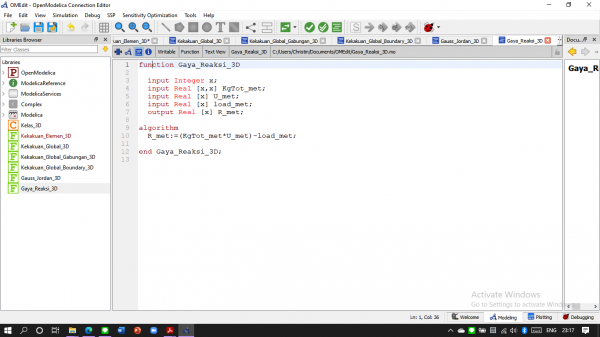
kemudian membuat fungi Gaya Reaksi
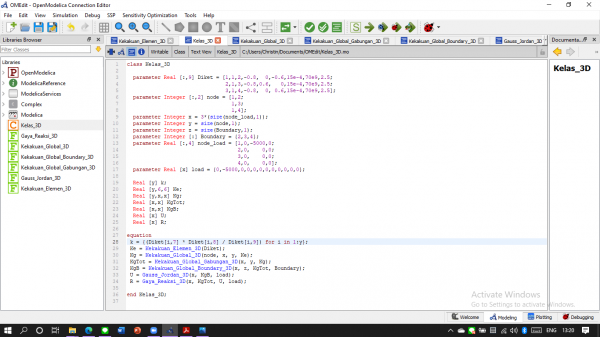
Membuat Kelas Pemanggil
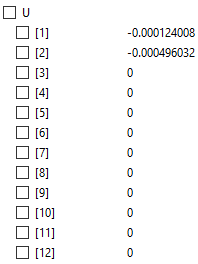
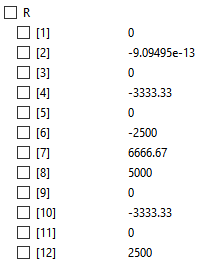
Setelah itu didapatlah hasil untuk U (defleksi) dan R (gaya reaksi)
Aplikasi metode numerik dalam kasus optimisasi
Pertemuan Minggu 5 : Kelas Pengganti
Pada pertemuan kelas pengganti ini, kami mereview ulang hal apa saja yang sudah adad pada pertemuan sebelumnya. Pada kelas ini kami juga diajarkan kembali tentang sistem trusses menggunakan software open modelica. Pak Dai sebagai dosen metnum juga mengajarkan tentang pelajaran-pelajaran hidup. Beliau banyak memberikan nasihat-nasihat kebaikan pada kehidupan seperti manusia yang harus selalu berserah diri kepada Allah SWt. Beliau juga mengajarkan kita untuk muhasabah diri dengan memberi penilaian kepada diri sendiri tentang kemampuan penguasaan materi trusses menggunakan Open Modelica.
Pertemuan Minggu 6
Pada pertemuan kali ini kami diajarkan tentang optimasi menggunakan Open Modelica. Optimasi sendiri adalah sebuah cara untuk mendapatkan nilai minimum atau maksimum dari suatu permasalahan. Terdapat beberapa aspek yang diperhatikan dalam melakukan optimasi yaitu fungsi objektif dan ada juga konstrain. Pada kali ini Asisten Dosen yaitu Bu Chandra memberikan tutorial untuk melakukan optimasi menggunakan metode Bracket. Pada metode "Bracket Optimization Using Golden Ratio" terdapat satu graik yang mempunyai nilai f(x) global maks dan lokal maks serta terdapat f(x) global minimum dann lokal minimum. Pada pertemuan kali ini, Bu chandra mengajarkan sampai melakukan optimasi grafik tanpa sebuah konstrain.
Selanjutkan Bu Chandra mengajarkan langsung, dengan menggunakan Software Open MOdelica. Kita dapat membuat sebuah fungsi pada awalnya:
Fungsi panggil
function f_obj3 import Modelica.Math; input Real x; output Real y; algorithm y:= 2*Math.sin(x)-x^2/10; end f_obj3;
setelah itu kita dapat membuat model optimasi sistem bracket sesuai yang diajarkan
model bracket_optimation3 parameter Integer n=8; Real x1[n]; Real x2[n]; Real xup; Real xlow; Real d; Real f1[n]; Real f2[n]; Real xopt; Real yopt; algorithm xup :=4; xlow:=0; for i in (1:n) loop d:= (5^(1/2)-1)/2*(xup-xlow); x1[i]:= xlow+d; x2[i]:= xup-d; f1[i]:= f_obj3(x1[i]); f2[i]:= f_obj3(x2[i]); if f1[i]>f2[i] then xup:= xup; xlow:= x2[i]; xopt:= xup; yopt:= f1[i]; else xlow:= xlow; xup:= x1[i]; xopt:= xup; end if; end for; end bracket_optimation3;
Tugas Besar
Pada tugas besar kali ini kita akan mendesign suatu rangka dengan cost yang yang serendah mungkin tetapi dengan kualitas yang optimum. Terdapat beberapa variabel yang diperhatikan diantaranya :
- 1. Harga material
- 2. Jenis material
- 3. Luas Cross Section
- 4. Penampang yang digunakan
Setelah itu kita akan melakukan optimasi dan membentuk kurva efisiensi harga dengan curve fitting menggunakan Metode numerik.
Pada tugas besar trusses kali ini saya menggunakan asumsi:
- Area=0.000141
- Material yang digunakan adalah aluminium dengan Modulus elastisitas E = 70e9 N / m2
|
Trusses Modelling model Trusses_3D_Manual
//define initial variable
parameter Integer Points=16; //Number of Points
parameter Integer Trusses=24; //Number of Trusses
parameter Real Area=0.000141; //Area
parameter Real Elas=1; //Elasticity (equals to one in order to determine the displacement limit)
//define connection
parameter Integer C[Trusses,2]=[1,5;
2,6;
3,7;
4,8;
5,6; //1st floor
6,7; //1st floor
7,8; //1st floor
5,8; //1st floor
5,9;
6,10;
7,11;
8,12;
9,10; //2nd floor
10,11;//2nd floor
11,12;//2nd floor
9,12; //2nd floor
9,13;
10,14;
11,15;
12,16;
13,14;//3rd floor
14,15;//3rd floor
15,16;//3rd floor
13,16];//3rd floor
//define coordinates (please put orderly)
parameter Real P[Points,3]=[0.3,-0.375,0; //1
-0.3,-0.375,0; //2
-0.3,0.375,0; //3
0.3,0.375,0; //4
0.3,-0.375,0.6; //5
-0.3,-0.375,0.6; //6
-0.3,0.375,0.6; //7
0.3,0.375,0.6; //8
0.3,-0.375,1.2; //9
-0.3,-0.375,1.2; //10
-0.3,0.375,1.2; //11
0.3,0.375,1.2; //12
0.3,-0.375,1.8; //13
-0.3,-0.375,1.8; //14
-0.3,0.375,1.8; //15
0.3,0.375,1.8]; //16
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-500,
0,0,-1000,
0,0,-1000,
0,0,-500};
//define boundary
parameter Integer b[:]={1,2,3,4};
//solution
Real displacement[N], reaction[N];
Real check[3];
parameter Integer N=3*Points;
Integer boundary[3*size(b,1)]=cat(1,(3*b).-2,(3*b).-1,3*b);
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
Real err=10e-10;
Real ers=10e-4;
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary
for i in boundary loop
for j in 1:N loop
G[i,j]:=id[i,j];
end for;
end for;
//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction
reaction:=(G_star*displacement)-F;
//Eliminating float error
for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
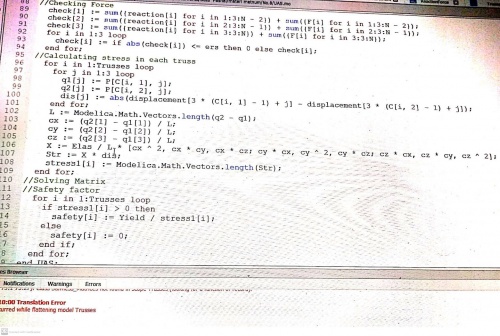
end Trusses_3D_Manual;
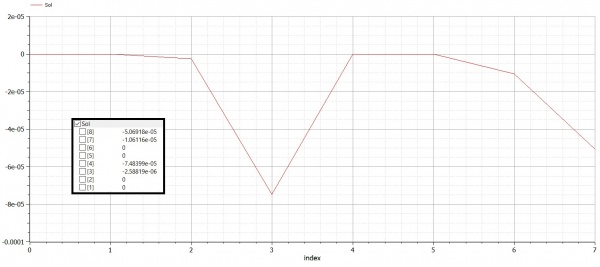
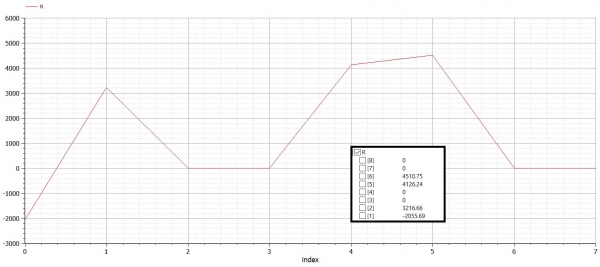
Berikut Reaction dan displacement yang terjadi
Untuk menghitung harga dan bahan saya menggunakan bahan ST 37-2 Angle steel dimana dia merupakan low carbon steel yang biasa digunakan untuk bahan membuat rak etalase logam. Kemudian untuk harga saya mengacu pada link dibawah ini
function Curve_Fitting input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coef[order+1]; protected Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1]; algorithm for i in 1:size(X,1) loop
for j in 1:(order+1) loop
Z[i,j]:=X[i]^(order+1-j);
end for;
end for;
ZTr:=transpose(Z);
A:=ZTr*Z; B:=ZTr*Y; Coef:=Modelica.Math.Matrices.solve(A,B); end Curve_Fitting; kemudian untuk memanggil fungsi tersebut kita membutuhkan model untuk bisa menjalankan fungsi Curve_Fitting. berikut adalah modelnya model CurveFitting parameter Real X[6]={0.000111, 0.000171, 0.000304, 0.000684, 0.000744, 0.000864};
parameter Real Y[6]={179200, 239500, 429600, 963600, 1044800, 1428000};
Real coef[3];
equation coef=FuncCurveFitting(X,Y,2); end CurveFitting; kemudian dari pengerjaan tersebut didapatkan hasil sebagai berikut setelah mendapatkan cukup data kita lanjutkan dengan mengoptimasi menggnakan metode golden section menggunakan OpenModelica berikut
parameter Real xd[:]={0.000111, 0.000141, 0.000171, 0.000231, 0.000291, 0.000304, 0.000384, 0.000684, 0.000575, 0.000744, 0.000864, 0.000725,
0.001216};
parameter Real yd[size(xd,1)]={6.29E-05, 7.24E-05, 7.96E-05, 8.86E-05, 9.26E-05, 9.30E-05, 9.32E-05, 8.02E-05, 8.58E-05, 7.72E-05, 7.15E-05, 7.82E-
05, 5.79E-05};
parameter Real xlo=0.000111;
parameter Real xhi=0.001216;
parameter Integer N=100; // maximum iteration
parameter Real es=0.0001; // maximum error
Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3]; Real xopt, fx; protected Real d, xl, xu, xint, R=(5^(1/2)-1)/2; algorithm xl := xlo;
xu := xhi;
y := FuncCurveFitting(xd,yd);
for i in 1:N loop
d:= R*(xu-xl);
x1[i]:=xl+d;
x2[i]:=xu-d;
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
xint:=xu-xl;
if f1[i]>f2[i] then
xl:=x2[i];
xopt:=x1[i];
fx:=f1[i];
else
xu:=x1[i];
xopt:=x2[i];
fx:=f2[i];
end if;
ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
break;
end if;
end for;
end GoldenSection; setelah disimulasikan, maka akan didapatkan hasil berupa Xopt yang merupakan nilai optimum. metode golden section harus dijalankan sebanyak 2 kali, yang pertama untuk material tetap, yang kedua untuk area tetap. code diatas merupakan golden section untuk material tetap. berikut hasil simulasi dari material tetap (gambar atas) dan area tetap (gambar bawah) dan didapatkanlah hasil seperti diatas Kesimpulandari hasil kalkulasi dan running di atas, didapatkan bahwa ruang area optimum adalah pada 1.945E+11 dan dimensi yang cukup mendekati area tersebut adalah pada 45x45 cm dan thickness 4mm. Adapun nilai elastisitas optimum yang didapatkan oleh golden section adalah 194.5E+9 dimana nilai tersebut masih dibawah nilai elastisitas ST 37-2 Angle steel sehingga dapa dikatakan material ST 37 ini cukup kuat dan relatif mrah untuk membuat rangka tersebut. Jadi pilihan baja ST 37 adalah yang optimal untuk kualitas yang mumpuni dan harga yang terjangkau. UASUjian Akhir Semester Metoda Numerik Semester Gasal 2021 Perhatikan Water Tower dengan Reservoir berbentuk Bola pada Gambar diatas. Anda diminta untuk membuat pemodelan numerik untuk mengoptimalkan struktur Water Tower tersebut. 1. Buatlah urutan langkah-langkah (prosedur) pemodelan numerik untuk optimasi struktur tersebut. 2. Jelaskan tujuan pemodelan numerik soal no 1 diatas, hukum/dalil (fisika) yang dipakai dan asumsi-asumsi yang akan digunakan dalam perhitungan 3. Untuk pemodelan numerik analisis strukturnya nya gunakan pendekatan 1D truss dgn membagi kolum (tiang) water tower kedalam 3 elemen (1D). a). Susunlah persamaan aljabar kesetimbangan statik setiap elemen tsb. (matriks kesetimbangan lokal) b) Matriks kesetimbangan global 4. Susun urutan langkah-langkah (pseudocode) perhitungan matriks kesetimbangan global soal no 3 termasuk pengecekan kesalahan (verifikasi) perhitungannya 5. Tulis dan jelaskan fungsi objektif dan constraint untuk optimasi struktur water tower tersebut 6. Tuliskan asumsi nilai-nilai parameter dan variable untuk menghitung displacement, restraint dan stress utk model struktur water tower dgn 3 elemnt 1 D diatas 7. Gunakan program modelica anda untuk menghitung displacement, restraint dan stress utk model struktur water tower dgn 3 element 1 D berdasarkan asumsi no 6 JAWABAN jawaban no 1 dan 2 berada di dalam satu lembar sebagai berikut jawaban untuk soal no 3 di lembar berikut Jawaban untuk soal no 4,5, dan 6 berada dalam satu lembar berikut untuk soal no 7 model yang dipakai pada Open modelica adalah sebagai berikut dari model tersebut didapatkan hasil sebagai berikut |