Difference between revisions of "Metnum03-Kevan Jeremy Igorio"
(Created page with "== BIODATA DIRI == 200px|thumb|left|Foto Diri Nama : Kevan Jeremy Igorio NPM : 1806233266 Program Studi : S1 Teknik Mesin...") |
(→Jawaban Uas) |
||
| (52 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
== BIODATA DIRI == | == BIODATA DIRI == | ||
| − | [[File:4ADC9F12-F585-4AFD-B5B1-47AB425D255B.jpg| | + | [[File:4ADC9F12-F585-4AFD-B5B1-47AB425D255B.jpg|100px|thumb|left|Foto Diri]] |
Nama : Kevan Jeremy Igorio | Nama : Kevan Jeremy Igorio | ||
| Line 7: | Line 7: | ||
Program Studi : S1 Teknik Mesin Pararel Universitas Indonesia | Program Studi : S1 Teknik Mesin Pararel Universitas Indonesia | ||
| + | |||
| + | == Metode Numerik 03 - 2020 == | ||
| + | |||
| + | == Pertemuan 1 (9 November 2020) == | ||
| + | |||
| + | Pada pertemuan ini pak Dai menyampaikan 4 penilaian utama dari kelas Metode Numerik | ||
| + | |||
| + | * Mengenal atau mengetahui progres pengetahuannya | ||
| + | * Mengerti Konsep | ||
| + | * Mampu membantu dalam memecahkan masalah dengan pemahaman tersebut di dunia keteknikan | ||
| + | * Mendapat nilai tambah (moral value) dan lebih mengetahui diri sendiri | ||
| + | |||
| + | Lalu, pada pertemuan 1 ini saya juga akan membahas mengenai '''Materi Metode Numerik Sebelum UTS''' dan '''OpenModelica''' | ||
| + | |||
| + | |||
| + | '''Materi Metode Numerik Sebelum UTS''' | ||
| + | |||
| + | Secara garis besar Metode Numerik memiliki beberapa cakupan bahasan, yaitu : | ||
| + | |||
| + | * Mencari akar - akar | ||
| + | * Regresi linear | ||
| + | * Turunan Numerik | ||
| + | |||
| + | Cakupan bahasan pertama, mencari akar - akar, terdiri dari dua metode yaitu ''Open Methods'' dan ''Closed Methods (Bracketing Methods).'' Pada Closed Methods digunakan batas batasan yang terdiri dari batas atas dan batas bawah. Terdapat 3 metode yang dipelajari, yaitu : Graphical Methods, Bisection Methods, dan False-Position Methods. Lalu untuk Open Methods terdapat 3 metode yang dipelajari, yaitu : Fixed-Point Iteration, Newton-Rapshon, dan Secant Method. | ||
| + | |||
| + | Regresi linear adalah sebuah pendekatan untuk memodelkan hubungan antara variabel terikat Y dan satu atau lebih variabel bebas yang disebut X. Salah satu kegunaan dari regresi linear adalah untuk melakukan prediksi berdasarkan data-data yang telah dimiliki sebelumnya. Regresi liner memiliki persamaan | ||
| + | |||
| + | '''Y = a + bx''' | ||
| + | |||
| + | Sebelum UTS, saya juga mempelajari mengenai Turunan Numerik. Terdapat 3 metode yaitu, Forward, Backward, dan juga Central. | ||
| + | |||
| + | |||
| + | '''OpenModelica''' | ||
| + | |||
| + | == Pertemuan 2 (16 November 2020) == | ||
| + | |||
| + | Pada pertemuan ini, kami diminta untuk membahas kembali apa yang telah kami pelajari tentang OpenModelica. Lalu kami membuat simulasi untuk menghitung rata-rata dari 5 angka. | ||
| + | |||
| + | Berikut merupakan algoritma yang saya buat untuk penjumlahan angka | ||
| + | |||
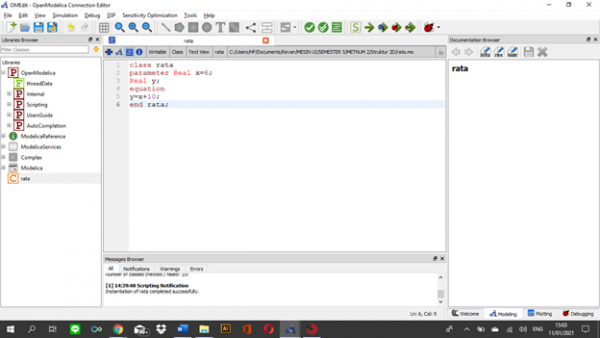
| + | [[File:Cdngp2kevan.png|600px|center]] | ||
| + | |||
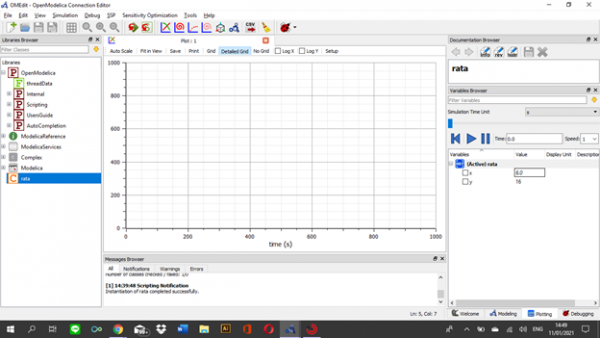
| + | Setelah itu dapat dilihat grafik input dan hasil sebagai berikut, dengan nilai input x=6 didapatkan hasil y=16. | ||
| + | |||
| + | [[File:GrafikT2Kevan.png|600px|center]] | ||
| + | |||
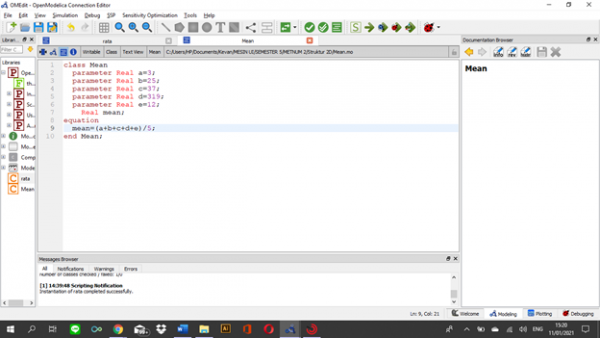
| + | Untuk menghitung rata-rata 5 angka, saya menggunakan algoritma sebagai berikut | ||
| + | |||
| + | [[File:Cdngmeankevan.png|600px|center]] | ||
| + | |||
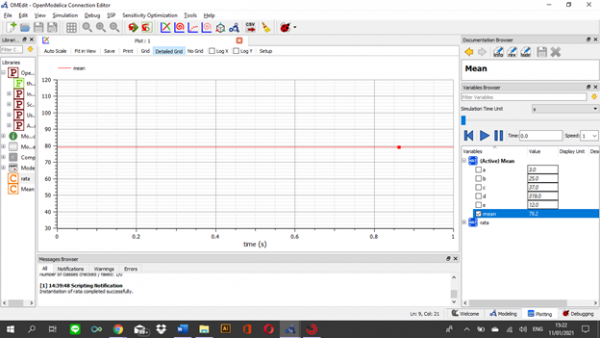
| + | Dengan input nilai 3, 25, 37, 319, dan 12 didapatkan hasil mean 79.2 seperti pada grafik dibawah ini. | ||
| + | |||
| + | [[File:Hasilcdngmeankevan.png|600px|center]] | ||
| + | |||
| + | == Tugas Pertemuan 2 == | ||
| + | |||
| + | Setelah pertemuan, Pak Dai memberikan tugas kepada kami untuk membuat simulasi modelica mengenai perhitungan aljabar simultan seperti Gauss elimination, Gauss Seidel, dsb. | ||
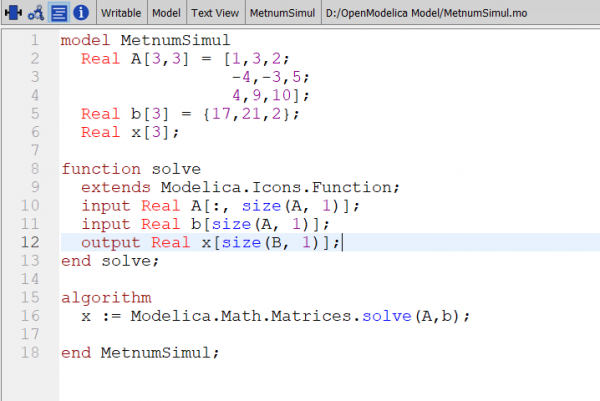
| + | Untuk tugas kali ini, saya menggunakan OpenModelica untuk menyelesaikan sistem persamaan linier dengan menggunakan metode Gauss elimination. Metode Gauss melibatkan perubahan bentuk sistem persamaan menjadi bentuk matrix. berikut adalah coding yang sudah saya buat: | ||
| + | |||
| + | [[File:metnum_simul.png|600px|center]] | ||
| + | |||
| + | Saya melakukan penyelesaian dari 3 persamaan linier dengan 3 variabel. | ||
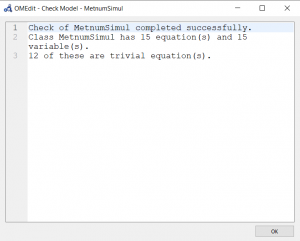
| + | Setelah membuat coding, saya mengecek coding yang telah saya buat | ||
| + | |||
| + | [[File:check_simul.png|300px|center]] | ||
| + | |||
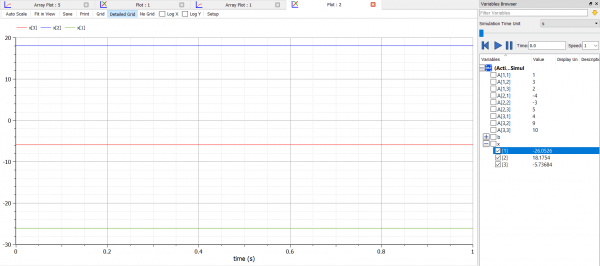
| + | setelah mengecek coding, saya menjalankan simulasi tersebut dan melakukan plotting dari hasil simulasi tersebut | ||
| + | |||
| + | [[File:hasil_simul.png|600px|center]] | ||
| + | |||
| + | Dapat dilihat dari hasil plotting bahwa terdapat 3 garis yang menyatakan penyelesaian pada ketiga sistem persamaan yang ingin diselesaikan. | ||
| + | |||
| + | == Pertemuan 3 == | ||
| + | |||
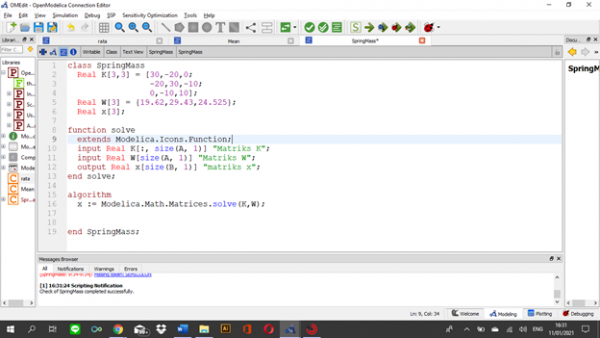
| + | Pada pertemuan hari ini, Pak Dai menjelaskan mengenai aplikasi metode numerik pada permasalahan teknik. Salah satu permasalahan teknik yang dibahas adalah permasalahan sistem pegas-massa. Lalu pak Dai meminta kami untuk memahami permasalahan pada Figure 12.11 pada e-book Metode Numerik. Dengan mengubah sistem menjadi bentuk matrix, kita mendapatkan bentuk matrix dari sistem tersebut sebagai berikut: | ||
| + | |||
| + | persamaan matrix tersebut dapat diselesaikan dengan metode eliminasi gauss. Lalu saya membuat coding di OpenModelica sebagai berikut | ||
| + | |||
| + | |||
| + | [[File:Pertemuan3cdngKevan.png|600px|center]] | ||
| + | |||
| + | |||
| + | setelah melakukan melakukan pengecekan dan tidak ada masalah, saya melakukan simulasi untuk menemukan nilai x1,x2, dan x3 dari persamaan matriks tersebut. Setelah melakukan simulasi, saya melakukan plotting untuk melihat hasil yang ditemukan | ||
| + | |||
| + | |||
| + | [[File:Prtmn3hslcdngkevan.png|600px|center]] | ||
| + | |||
| + | dapat dilihat bahwa nilai x1 = 7.3575; x2 = 10.0552; x3 = 12.5077, sesuai dengan hasil yang ada di buku Metode Numerik. | ||
| + | |||
| + | == Pertemuan 4 == | ||
| + | |||
| + | QUIZ | ||
| + | |||
| + | |||
| + | == Pertemuan 5 == | ||
| + | |||
| + | Pada pertemuan ini kami membahas quiz yang diberikan minggu lalu dengan mempelajari algoritma yang sudah dibuat dan juga flowchartnya. Pertama-tama teman saya Edward Joshua membantu menjelaskan mengenai langkah pengerjaan soal yang diberikan, kemudian dibantu pula oleh Ahmad Muhammad Fahmi untuk menjelaskan algoritma yang sudah dia buat. | ||
| + | |||
| + | Pada algoritma yang sudah dibuat oleh teman saya, dia menggunakan sistem looping untuk penyelasaian soal quiz yang telah diberikan dengan parameter input A (Luas Permukaan), E (Modulus Elastisitas), node, dan load. | ||
| + | |||
| + | TUGAS PERTEMUAN 5 | ||
| + | |||
| + | 1. Mempelajari codingan 3D Fahmi | ||
| + | |||
| + | 2. Mengaplikasikan pada soal Example 3.3 | ||
| + | |||
| + | 3. Memberikan masukan atas codingan Fahmi | ||
| + | |||
| + | |||
| + | == Pertemuan 6 == | ||
| + | |||
| + | Pada pertemuan hari ini, Pak Dai meminta kami untuk melakukan muhasabah terhadap hasil pembelajaran kami selama kelas Metode Numerik bersama Pak Dai. Berikut adalah muhasabah saya: | ||
| + | |||
| + | Saya kesulitan untuk dapat mengikuti kelas setelah UTS dikarenakan kondisi kesehatan saya yang menyebabkan saya harus absen di beberapa kelas yang diadakan. Namun saya sudah mencoba sebisa mungkin untuk melengkapi wiki dan juga membuat codingan seperti yang sudah teman - tean saya lakukan. | ||
| + | |||
| + | |||
| + | == Pertemuan 7 == | ||
| + | |||
| + | Pada pertemuan hari ini, Pak Dai menjelaskan mengenai tugas besar Metode Numerik yaitu Aplikasi Metode Numerik dalam Optimasi Desain Struktur Rangka Sederhana. Secara garis besar yang dicari adalah material yang tepat dan murah untuk rangka sederhana. Setelah itu kami melakukan praktik optimasi bersama Asisten Dosen, Bu Candra. | ||
| + | |||
| + | Praktik yang dilakukan adalah Bracket Optimization Using Golden Ratio Method. Misalkan terdapat suatu fungsi yang memiliki nilai fungsi maksimum global dan lokal serta fungsi minimum global dan lokal. | ||
| + | |||
| + | == Tugas Besar == | ||
| + | |||
| + | |||
| + | Pada tugas besar ini kami diminta utuk melakukan optimisasi pemilihan material dan luas penampang trusses untuk rangka seperti gambar dibawah ini | ||
| + | |||
| + | |||
| + | [[File:Truss rangka.png|600px|center]] | ||
| + | |||
| + | |||
| + | '''ASUMSI''' | ||
| + | |||
| + | 1. Beban akan terdistribusi hanya pada node (karena bersifat trusses). | ||
| + | |||
| + | 2. Safety factor minimal bernilai 2. | ||
| + | |||
| + | 3. Batas displacement 0,001 m sebelum buckling (pada truss paling atas). | ||
| + | |||
| + | 4. Ketinggian trusses pada tiap lantai sama yaitu 0,6 m. | ||
| + | |||
| + | |||
| + | |||
| + | '''METODOLOGI''' | ||
| + | |||
| + | |||
| + | '''I. ELASTICITY LOCKED''' | ||
| + | |||
| + | 1. Mencari data yield strength dan elasticity dari material yang dipilih | ||
| + | |||
| + | 2. Mencari harga truss sesuai dengan material. | ||
| + | |||
| + | 3. Menghitung nilai safety factor. | ||
| + | |||
| + | 4. Membuat rasio (efficiency) dari safety factor dengan total cost. | ||
| + | |||
| + | 5. Membuat persamaan (mencari Coe) antara rasio dengan area menggunakan curve-fitting. | ||
| + | |||
| + | 6. Melakukan optimasi menggunakan metode golden section. | ||
| + | |||
| + | |||
| + | '''II. AREA LOCKED''' | ||
| + | |||
| + | 1. Mendefinisikan luas penampang yang sama untuk seluruh variasi material | ||
| + | |||
| + | 2. Mencari harga untuk 3 jenis variasi material. | ||
| + | |||
| + | 3. Menghitung nilai ''safety factor'' pada 3 variasi truss. | ||
| + | |||
| + | 4. Membuat rasio antara ''safety factor'' dengan ''total cost''. | ||
| + | |||
| + | 5. Membuat persamaan (mencari Coe) antara rasio dengan area menggunakan curve-fitting. | ||
| + | |||
| + | 6. Melakukan optimasi menggunakan metode golden section | ||
| + | |||
| + | |||
| + | |||
| + | '''ELASTICITY LOCKED''' | ||
| + | |||
| + | |||
| + | [[File:SS 304.png|400px|left]] | ||
| + | |||
| + | |||
| + | [[File:Areaelasticity lockeed.png|400px|left]] | ||
| + | |||
| + | sumber: https://wijayamakmur.com/siku/ | ||
| + | |||
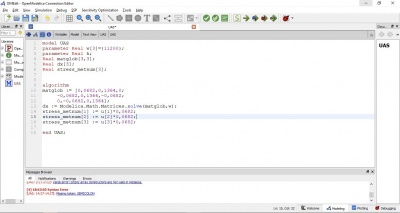
| + | ==Jawaban Uas== | ||
| + | |||
| + | [[File:IMG 2621.jpeg|400px|left]] | ||
| + | |||
| + | |||
| + | [[File:IMG 2620.jpg|400px|left]] | ||
| + | |||
| + | |||
| + | [[File:2C5982D5-F372-4A85-BBA4-DF81A29B30D6.jpeg|400px|left]] | ||
Latest revision as of 19:52, 14 January 2021
Contents
BIODATA DIRI
Nama : Kevan Jeremy Igorio
NPM : 1806233266
Program Studi : S1 Teknik Mesin Pararel Universitas Indonesia
Metode Numerik 03 - 2020
Pertemuan 1 (9 November 2020)
Pada pertemuan ini pak Dai menyampaikan 4 penilaian utama dari kelas Metode Numerik
- Mengenal atau mengetahui progres pengetahuannya
- Mengerti Konsep
- Mampu membantu dalam memecahkan masalah dengan pemahaman tersebut di dunia keteknikan
- Mendapat nilai tambah (moral value) dan lebih mengetahui diri sendiri
Lalu, pada pertemuan 1 ini saya juga akan membahas mengenai Materi Metode Numerik Sebelum UTS dan OpenModelica
Materi Metode Numerik Sebelum UTS
Secara garis besar Metode Numerik memiliki beberapa cakupan bahasan, yaitu :
- Mencari akar - akar
- Regresi linear
- Turunan Numerik
Cakupan bahasan pertama, mencari akar - akar, terdiri dari dua metode yaitu Open Methods dan Closed Methods (Bracketing Methods). Pada Closed Methods digunakan batas batasan yang terdiri dari batas atas dan batas bawah. Terdapat 3 metode yang dipelajari, yaitu : Graphical Methods, Bisection Methods, dan False-Position Methods. Lalu untuk Open Methods terdapat 3 metode yang dipelajari, yaitu : Fixed-Point Iteration, Newton-Rapshon, dan Secant Method.
Regresi linear adalah sebuah pendekatan untuk memodelkan hubungan antara variabel terikat Y dan satu atau lebih variabel bebas yang disebut X. Salah satu kegunaan dari regresi linear adalah untuk melakukan prediksi berdasarkan data-data yang telah dimiliki sebelumnya. Regresi liner memiliki persamaan
Y = a + bx
Sebelum UTS, saya juga mempelajari mengenai Turunan Numerik. Terdapat 3 metode yaitu, Forward, Backward, dan juga Central.
OpenModelica
Pertemuan 2 (16 November 2020)
Pada pertemuan ini, kami diminta untuk membahas kembali apa yang telah kami pelajari tentang OpenModelica. Lalu kami membuat simulasi untuk menghitung rata-rata dari 5 angka.
Berikut merupakan algoritma yang saya buat untuk penjumlahan angka
Setelah itu dapat dilihat grafik input dan hasil sebagai berikut, dengan nilai input x=6 didapatkan hasil y=16.
Untuk menghitung rata-rata 5 angka, saya menggunakan algoritma sebagai berikut
Dengan input nilai 3, 25, 37, 319, dan 12 didapatkan hasil mean 79.2 seperti pada grafik dibawah ini.
Tugas Pertemuan 2
Setelah pertemuan, Pak Dai memberikan tugas kepada kami untuk membuat simulasi modelica mengenai perhitungan aljabar simultan seperti Gauss elimination, Gauss Seidel, dsb. Untuk tugas kali ini, saya menggunakan OpenModelica untuk menyelesaikan sistem persamaan linier dengan menggunakan metode Gauss elimination. Metode Gauss melibatkan perubahan bentuk sistem persamaan menjadi bentuk matrix. berikut adalah coding yang sudah saya buat:
Saya melakukan penyelesaian dari 3 persamaan linier dengan 3 variabel. Setelah membuat coding, saya mengecek coding yang telah saya buat
setelah mengecek coding, saya menjalankan simulasi tersebut dan melakukan plotting dari hasil simulasi tersebut
Dapat dilihat dari hasil plotting bahwa terdapat 3 garis yang menyatakan penyelesaian pada ketiga sistem persamaan yang ingin diselesaikan.
Pertemuan 3
Pada pertemuan hari ini, Pak Dai menjelaskan mengenai aplikasi metode numerik pada permasalahan teknik. Salah satu permasalahan teknik yang dibahas adalah permasalahan sistem pegas-massa. Lalu pak Dai meminta kami untuk memahami permasalahan pada Figure 12.11 pada e-book Metode Numerik. Dengan mengubah sistem menjadi bentuk matrix, kita mendapatkan bentuk matrix dari sistem tersebut sebagai berikut:
persamaan matrix tersebut dapat diselesaikan dengan metode eliminasi gauss. Lalu saya membuat coding di OpenModelica sebagai berikut
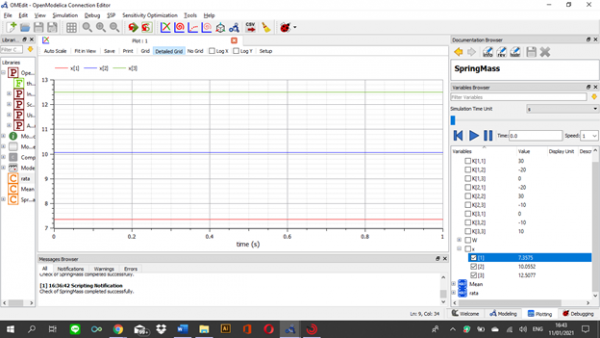
setelah melakukan melakukan pengecekan dan tidak ada masalah, saya melakukan simulasi untuk menemukan nilai x1,x2, dan x3 dari persamaan matriks tersebut. Setelah melakukan simulasi, saya melakukan plotting untuk melihat hasil yang ditemukan
dapat dilihat bahwa nilai x1 = 7.3575; x2 = 10.0552; x3 = 12.5077, sesuai dengan hasil yang ada di buku Metode Numerik.
Pertemuan 4
QUIZ
Pertemuan 5
Pada pertemuan ini kami membahas quiz yang diberikan minggu lalu dengan mempelajari algoritma yang sudah dibuat dan juga flowchartnya. Pertama-tama teman saya Edward Joshua membantu menjelaskan mengenai langkah pengerjaan soal yang diberikan, kemudian dibantu pula oleh Ahmad Muhammad Fahmi untuk menjelaskan algoritma yang sudah dia buat.
Pada algoritma yang sudah dibuat oleh teman saya, dia menggunakan sistem looping untuk penyelasaian soal quiz yang telah diberikan dengan parameter input A (Luas Permukaan), E (Modulus Elastisitas), node, dan load.
TUGAS PERTEMUAN 5
1. Mempelajari codingan 3D Fahmi
2. Mengaplikasikan pada soal Example 3.3
3. Memberikan masukan atas codingan Fahmi
Pertemuan 6
Pada pertemuan hari ini, Pak Dai meminta kami untuk melakukan muhasabah terhadap hasil pembelajaran kami selama kelas Metode Numerik bersama Pak Dai. Berikut adalah muhasabah saya:
Saya kesulitan untuk dapat mengikuti kelas setelah UTS dikarenakan kondisi kesehatan saya yang menyebabkan saya harus absen di beberapa kelas yang diadakan. Namun saya sudah mencoba sebisa mungkin untuk melengkapi wiki dan juga membuat codingan seperti yang sudah teman - tean saya lakukan.
Pertemuan 7
Pada pertemuan hari ini, Pak Dai menjelaskan mengenai tugas besar Metode Numerik yaitu Aplikasi Metode Numerik dalam Optimasi Desain Struktur Rangka Sederhana. Secara garis besar yang dicari adalah material yang tepat dan murah untuk rangka sederhana. Setelah itu kami melakukan praktik optimasi bersama Asisten Dosen, Bu Candra.
Praktik yang dilakukan adalah Bracket Optimization Using Golden Ratio Method. Misalkan terdapat suatu fungsi yang memiliki nilai fungsi maksimum global dan lokal serta fungsi minimum global dan lokal.
Tugas Besar
Pada tugas besar ini kami diminta utuk melakukan optimisasi pemilihan material dan luas penampang trusses untuk rangka seperti gambar dibawah ini
ASUMSI
1. Beban akan terdistribusi hanya pada node (karena bersifat trusses).
2. Safety factor minimal bernilai 2.
3. Batas displacement 0,001 m sebelum buckling (pada truss paling atas).
4. Ketinggian trusses pada tiap lantai sama yaitu 0,6 m.
METODOLOGI
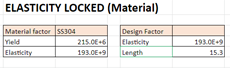
I. ELASTICITY LOCKED
1. Mencari data yield strength dan elasticity dari material yang dipilih
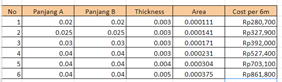
2. Mencari harga truss sesuai dengan material.
3. Menghitung nilai safety factor.
4. Membuat rasio (efficiency) dari safety factor dengan total cost.
5. Membuat persamaan (mencari Coe) antara rasio dengan area menggunakan curve-fitting.
6. Melakukan optimasi menggunakan metode golden section.
II. AREA LOCKED
1. Mendefinisikan luas penampang yang sama untuk seluruh variasi material
2. Mencari harga untuk 3 jenis variasi material.
3. Menghitung nilai safety factor pada 3 variasi truss.
4. Membuat rasio antara safety factor dengan total cost.
5. Membuat persamaan (mencari Coe) antara rasio dengan area menggunakan curve-fitting.
6. Melakukan optimasi menggunakan metode golden section
ELASTICITY LOCKED
sumber: https://wijayamakmur.com/siku/
Jawaban Uas