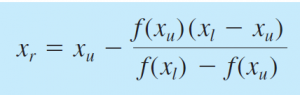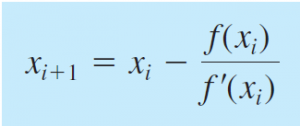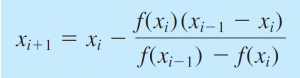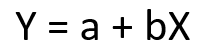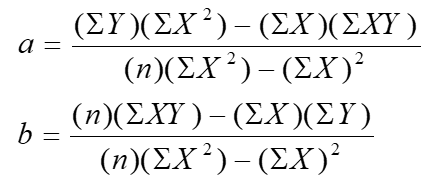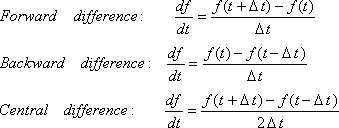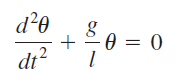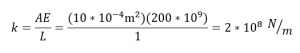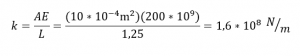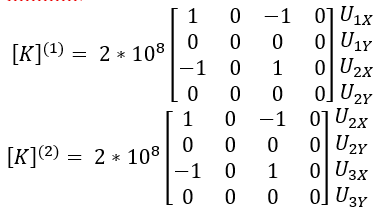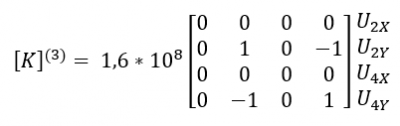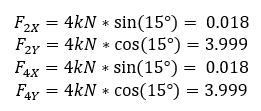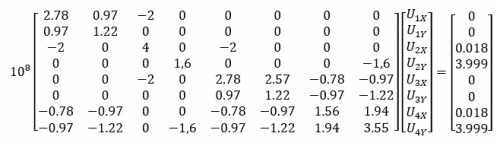Difference between revisions of "Metnum03-Samuel Sitompul"
(→JAWABAN UJIAN AKHIR SEMESTER) |
|||
| (20 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | '''Biodata''' | |
Nama: Samuel Albert B C H Sitompul | Nama: Samuel Albert B C H Sitompul | ||
| Line 8: | Line 8: | ||
| − | + | = Pertemuan Minggu Pertama Metode Numerik 03 (9 November 2020) = | |
| + | Metode Numerik adalah salah satu mata kuliah yang sangat banyak penerapannya dalam dunia keteknikan. Mata kuliah ini salah satu mata kuliah yang cukup menarik karena penerapannya sangat luas dan bermanfaat. Sejauh ini yang telah saya pelajari sebelum UTS mencakup 3 materi besar yaitu mencari akar-akar, regresi linier, dan turunan numerik. | ||
| + | '''1. Mencari Akar-Akar''' | ||
| + | Pada materi ini, saya mempelajari metode-metode untuk mencari akar secara numerik. Beberapa metode yang saya pelajari adalah metode pencarian akar menggunakan Closed methods (Bracketing Method) dan Open Methods. | ||
| + | {|class="wikitable" | ||
| + | |''Metode Closed Methods'' merupakan metode pencarian akar-akar dengan menggunakan batas atas dan batas bawah untuk mencari akar dan mengukur persentasi error yang didapat untuk mendapat tingkat akurasi dari iterasi. Metode yang saya pelajari ada 3 yaitu Graphical Methods, Bisection Methods, dan False-Position Methods. | ||
| − | == Pertemuan Minggu Kedua Metode Numerik 03 (16 November 2020) | + | '''Graphical Methods''' |
| + | |||
| + | Sebuah metode sederhana yang menggunakan grafik untuk memperkirakan akar-akar suatu fungsi. Metode ini dilakukan dengan melakukan plotting dari suatu fungsi ke dalam bentuk grafik. | ||
| + | |||
| + | '''Bisection Methods''' | ||
| + | |||
| + | Metode ini merupakan salah satu jenis metode incremental search method yang menggunakan batas atas dan batas bawah untuk mempersempit area pencarian akar-akar. | ||
| + | |||
| + | '''False-Position Methods''' | ||
| + | |||
| + | [[File:Rumus-false-position.png|thumb|300px|style="float:right;"|Rumus ''False Position Method'']] | ||
| + | |||
| + | Metode ini sangat mirip dengan metode Bisection. Hal yang membedakan metode False-Position dengan Bisection adalah penentuan titik tengah dari batas-batas yang ditentukan. Penentuan titik tengah dari False-Position Method menggunakan persamaan berikut. | ||
| + | |} | ||
| + | |||
| + | {|class="wikitable" | ||
| + | |''Metode Open Methods'' merupakan metode pencarian yang hanya menggunakan 1 titik untuk menemukan akar-akar. Metode ini dapat menggunakan turunan suatu fungsi untuk menentukan titik pengujian baru yang semakin dekat dengan nilai akar-akar yang diinginakn. Metode yang saya pelajari ada 3 yaitu Fixed-Point Iteration, Newton-Rapshon, dan Secant Method | ||
| + | |||
| + | '''Fixed-Point Iteration''' | ||
| + | |||
| + | Metode ini disebut juga metode iterasi sederhana, adalah metode yang memisahkan x dengan sebagian x yang lain sehingga diperoleh: x=g(x) | ||
| + | |||
| + | '''Newton-Raphson''' [[File:Rumus-newton-raphson.png|thumb|300px|style="float:left;"|Rumus ''Newton Rapshon'']] | ||
| + | |||
| + | Metode ini menggunakan satu titik awal dan mendekatinya dengan memperhatikan slope atau gradien pada titik tersebut. Slop atau gradien didapatkan dengan melakukan turunan dari fungsi tersebut. Persamaan untuk Newton-Raphson adalah sebagai berikut: | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | '''Secant Method''' | ||
| + | |||
| + | Metode ini merupakan metode modifikasi Newton-Raphson dimana metode Newton-Raphson tidak digunakan (karena f'(x) sulit ditemukan atau tidak mungkin ditemukan). Persaman untuk metode Secant adalah sebagai berikut | ||
| + | |||
| + | [[File:Rumus-secant.png|thumb|300px|style="float:left;"|Rumus ''Secant'']] | ||
| + | |||
| + | |} | ||
| + | |||
| + | '''2. Regresi Linier''' | ||
| + | |||
| + | regresi linear adalah sebuah pendekatan untuk memodelkan hubungan antara variable terikat Y dan satu atau lebih variable bebas yang disebut X. Salah satu kegunaan dari regresi linear adalah untuk melakukan prediksi berdasarkan data-data yang telah dimiliki sebelumnya. Hubungan di antara variable-variabel tersebut disebut sebagai model regresi linear. | ||
| + | |||
| + | Persamaan umum Regresi Linier adalah sebagai berikut: | ||
| + | |||
| + | [[File:Rumus-regresi-linier-umum.png]] | ||
| + | |||
| + | dimana: | ||
| + | |||
| + | [[File:konstanta-regresi-linier.png]] | ||
| + | |||
| + | '''3. Turunan Numerik''' | ||
| + | |||
| + | Turunan Numerik adalah menentukan hampiran nilai turunan fungsi f yang diberikan dalam bentuk tabel. Terdapat 3 pendekatan dalam menghitung turunan numerik: | ||
| + | |||
| + | [[File:numerical-difference-approx.png]] | ||
| + | |||
| + | ==Tugas Pertemuan 1: OpenModelica== | ||
| + | |||
| + | Setelah pertemuan 1, pak Dai meminta kami untuk mempelajari OpenModelica | ||
| + | |||
| + | Untuk mempelajari OpenModelica, saya menggunakan referensi/tutorial dari YouTube dengan tautan berikut: | ||
| + | |||
| + | https://www.youtube.com/watch?v=SW5Eclf1tRs | ||
| + | |||
| + | https://www.youtube.com/watch?v=m0Ahs8fEN28&t=519s&ab_channel=NSTUFACE | ||
| + | |||
| + | Dari video-video tersebut saya diperkenalkan mengenai interface OpenModelica untuk pemula. Saya juga mempelajari bahwa OpenModelica menggunakan bahasa program Modelica untuk penggunaannya. Bahasa ini mirip dengan bahasa pemograman lain seperti python. Kelebihan yang saya lihat dari OpenModelica ini adalah program ini memiliki tools yang membantu mempermudah kita untuk membuat sistem dalam bentuk grafis atau skema. Model-model ini dapat kita aplikasikan dalam kehidupan nyata seperti membuat sistem elektrikal, magnetik, fluida, perpindahan panas, dsb. | ||
| + | |||
| + | Dalam konteks Metode Numerik, saya mempelajari bahwa OpenModelica dapat membantu kita dalam menyelesaikan permasalahan-permasalahan dalam mata kuliah Metode Numerik dan memvisualisasikan penyelesaian tersebut dalam bentuk grafik, salah satunya adalah penyelesaian Persamaan Diferensial Biasa atau ODE. | ||
| + | |||
| + | Contoh penyelesaian permasalahan ODE menggunakan OpenModelica adalah persamaan pendulum, yang didefinisikan sebagai berikut: | ||
| + | |||
| + | [[File:persamaan-pendulum.png|300px|center]] | ||
| + | |||
| + | Dengan menggunakan referensi dari tautan kedua, saya membuat bahasa pemograman untuk menyelesaikan persamaan pendulum tersebut. | ||
| + | |||
| + | model pendulum | ||
| + | Real y "variable state"; | ||
| + | Real x; | ||
| + | parameter Real L=1 "pendulum length"; | ||
| + | constant Real g=9.80665; | ||
| + | initial equation | ||
| + | y=9 "initial value"; | ||
| + | equation | ||
| + | x=der(y); | ||
| + | der(x)+(g/L)*(y)=0 "differential equation"; | ||
| + | annotation(experiment(StartTime = 0, StopTime = 100)); | ||
| + | end pendulum; | ||
| + | |||
| + | |||
| + | Penyelesaian dari persamaan tersebut digambarkan dalam bentuk grafik sebagai berikut | ||
| + | |||
| + | [[File:pendulum-solution-om.png|600px|Hasil Plotting]] | ||
| + | |||
| + | Dari grafik tersebut dapat dilihat bahwa seiring berjalannya waktu, pendulum melakukan osilasi. Namun dapat dilihat bahwa pendulum tersebut tidak kembali ketitik semula seiring berjalannya waktu. | ||
| + | |||
| + | Dari pembelajaran ini, saya mempelajari bahwa OpenModelica merupakan tools yang berguna dalam pelajaran Metode Numerik. | ||
| + | |||
| + | |||
| + | |||
| + | = Pertemuan Minggu Kedua Metode Numerik 03 (16 November 2020) = | ||
Pada pertemuan kedua kali ini, Kami diminta oleh Pak Dai untuk menunjukkan pemahaman kami mengenai tugas minggu lalu, yaitu mempelajari OpenModelica. Lalu kami melakukan simulasi dengan membuat program sederhana didalam OpenModelica untuk menjumlahkan 10 angka pada variabel. | Pada pertemuan kedua kali ini, Kami diminta oleh Pak Dai untuk menunjukkan pemahaman kami mengenai tugas minggu lalu, yaitu mempelajari OpenModelica. Lalu kami melakukan simulasi dengan membuat program sederhana didalam OpenModelica untuk menjumlahkan 10 angka pada variabel. | ||
| Line 32: | Line 138: | ||
| − | + | = Pertemuan Minggu Ketiga Metode Numerik 03 (23 November 2020) = | |
| − | Di pertemuan hari ini, Pak Dai menjelaskan tentang aplikasi metode numerik untuk permasalahan-permasalahan teknik. Salah satunya adalah permasalahan sistem pegas-massa. | + | Di pertemuan hari ini, Pak Dai menjelaskan tentang aplikasi metode numerik untuk permasalahan-permasalahan teknik. Salah satunya adalah permasalahan sistem pegas-massa. |
| + | Lalu pak Dai meminta kami untuk memahami permasalahan pada Figure 12.11 pada e-book Metode Numerik. Dengan mengubah sistem menjadi bentuk matrix, kita mendapatkan bentuk matrix dari sistem tersebut sebagai berikut: | ||
| + | [[File:spring-mass-model.png|600px|center]] | ||
| + | ==Tugas Pertemuan 3== | ||
Setelah kelas, Pak Dai memberikan tugas untuk menyelesaikan soal berikut: | Setelah kelas, Pak Dai memberikan tugas untuk menyelesaikan soal berikut: | ||
[[File:soalpr.jpeg|500px|center]] | [[File:soalpr.jpeg|500px|center]] | ||
| + | alur berpikir untuk menyelesaikan masalah : | ||
| + | |||
| + | '''1. Mengubah problem menjadi node dan elemen''' | ||
| + | |||
| + | '''2. Menentukan nilai Konstanta kekakuan/stiffness constant dari elemen''' | ||
| + | |||
| + | '''3. Menyusun dan menggabungkan matriks elemen-elemen''' | ||
| + | |||
| + | '''4. Menyusun dan menggabungkan matriks elemen-elemen''' | ||
| + | |||
| + | '''5. Menerapkan kondisi batas dan beban''' | ||
| + | |||
| + | '''6. Tahap pencarian solusi''' | ||
| + | |||
| + | '''7. Mendapatkan nilai gaya reaksi''' | ||
| + | |||
| + | '''8. Mendapatkan gaya Internal dan Normal Stress''' | ||
Untuk menyelesaikan soal ini perlu dilakukan pengelompokan menjadi node dan elemen seperti pada tabel berikut: | Untuk menyelesaikan soal ini perlu dilakukan pengelompokan menjadi node dan elemen seperti pada tabel berikut: | ||
| Line 62: | Line 188: | ||
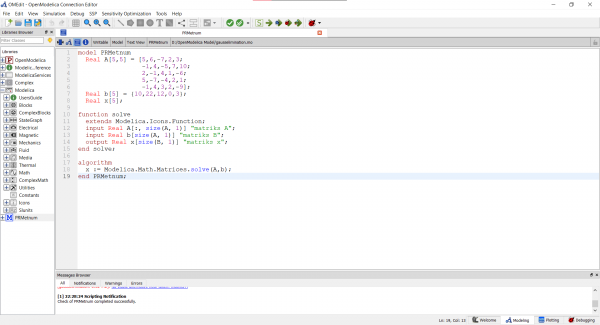
Persamaan diatas kemudian diselesaikan dengan OpenModelica, berikut saya lampirkan coding yang saya buat | Persamaan diatas kemudian diselesaikan dengan OpenModelica, berikut saya lampirkan coding yang saya buat | ||
| − | [[File:Defleksicoding.png| | + | [[File:Defleksicoding.png|500px|center]] |
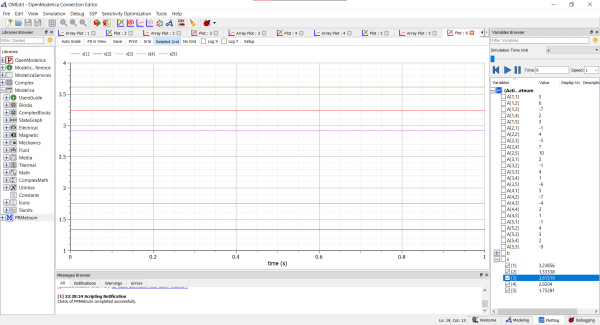
setelah melakukan pengecekan dan simulasi, saya melakukan plotting. berikut hasil plotting simulasi tersebut. | setelah melakukan pengecekan dan simulasi, saya melakukan plotting. berikut hasil plotting simulasi tersebut. | ||
| − | [[File:Defleksiplot.png| | + | [[File:Defleksiplot.png|500px|center]] |
hasil dapat dilihat pada panel di bagian kanan bawah gambar. | hasil dapat dilihat pada panel di bagian kanan bawah gambar. | ||
| Line 81: | Line 207: | ||
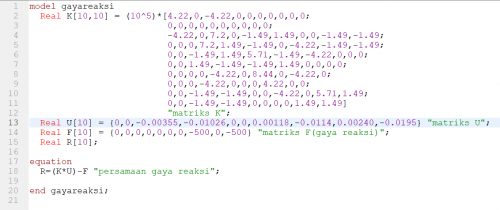
Persamaan diatas dapat diselesaikan oleh openmodelica. berikut adalah coding yang saya buat | Persamaan diatas dapat diselesaikan oleh openmodelica. berikut adalah coding yang saya buat | ||
| − | [[File:Gayareaksicoding.png| | + | [[File:Gayareaksicoding.png|500px|center]] |
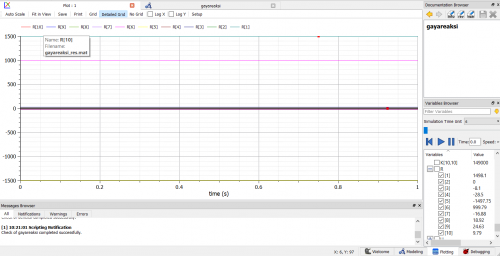
hasil simulasi tersebut di plot sebagai berikut: | hasil simulasi tersebut di plot sebagai berikut: | ||
| − | [[File:Gayareaksiplot.png| | + | [[File:Gayareaksiplot.png|500px|center]] |
nilai R tiap node dapat dilihat di bagian kanan bawah gambar | nilai R tiap node dapat dilihat di bagian kanan bawah gambar | ||
| − | = | + | = PErtemuan Minggu Keempat (30 November 2020) = |
| + | |||
| + | ==Quiz 1== | ||
Pada pertemuan minggu ke IV hari ini, Pak Dai mengadakan kuis untuk menguji kemampuan inidvidu kami, para peserta diberikan 2 buah soal kuis dan diminta untuk menuliskan flowchartynya. Berikut merupakan kedua soal kuisnya. | Pada pertemuan minggu ke IV hari ini, Pak Dai mengadakan kuis untuk menguji kemampuan inidvidu kami, para peserta diberikan 2 buah soal kuis dan diminta untuk menuliskan flowchartynya. Berikut merupakan kedua soal kuisnya. | ||
| − | [[File:Soal 1 Quiz_Samuel Sitompul.jpg]] | + | [[File:Soal 1 Quiz_Samuel Sitompul.jpg |center]] |
| − | [[File:Soal 2 Quiz _Samuel Sitompul.jpg]] | + | [[File:Soal 2 Quiz _Samuel Sitompul.jpg|center]] |
dan berikut merupakan tampilan flowchart pengerjaan sebagai jawaban soal kuis tersebut yang telah saya buat. Mengingat alur pengerjaan kedua soal tersebut hampir sama, maka tampilan flowchart tersebut merepresentasikan keduanya. | dan berikut merupakan tampilan flowchart pengerjaan sebagai jawaban soal kuis tersebut yang telah saya buat. Mengingat alur pengerjaan kedua soal tersebut hampir sama, maka tampilan flowchart tersebut merepresentasikan keduanya. | ||
| − | [[File:Quiz 1_Metnum_Samuel Sitompul.jpg]] | + | [[File:Quiz 1_Metnum_Samuel Sitompul.jpg|500 px|center]] |
| − | + | ==Tugas soal no. 4 == | |
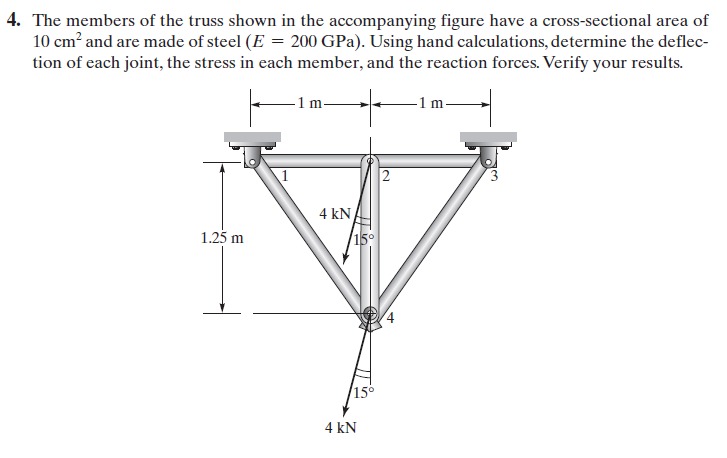
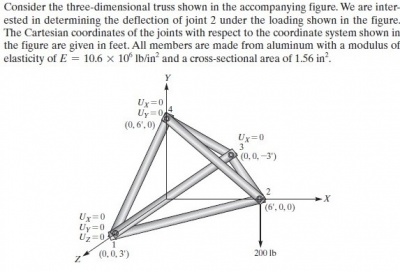
Soal no.4 | Soal no.4 | ||
| − | untuk soal | + | {|class="wikitable" |
| + | | '''Soal No.4''' || | ||
| + | |||
| + | {| class="mw-collapsible mw-collapsed wikitable" | ||
| + | ! '''1. Mengubah problem menjadi node dan elemen''' | ||
| + | |- | ||
| + | | [[File:Element-Table-Problem4.png |400px|center]] | ||
| + | |} | ||
| + | |||
| + | {| class="mw-collapsible mw-collapsed wikitable" | ||
| + | ! '''2. Menentukan nilai Konstanta kekakuan/stiffness constant dari elemen''' | ||
| + | |- | ||
| + | | Elemen 1,2 || [[File:Element12-problem4.png |300px]] | ||
| + | |- | ||
| + | | Elemen 3 || [[File:Element3-problem4.png |300px]] | ||
| + | |- | ||
| + | | Elemen 4,5 || [[File:Element45-problem4.png |300px]] | ||
| + | |} | ||
| + | |||
| + | {| class="mw-collapsible mw-collapsed wikitable" | ||
| + | ! '''4. Menyusun dan menggabungkan matriks elemen-elemen''' | ||
| + | |- | ||
| + | | '''Elemen''' || '''Local Matrix''' || '''Global Matrix''' | ||
| + | |- | ||
| + | | Elemen 1,2 || [[File:Localmatrix-element12.png |400px]] || [[File:Globalmatrix-element12.png |400px]] | ||
| + | |- | ||
| + | | Elemen 3 || [[File:Localmatrix-element3.png |400px]] || [[File:Globalmatrix-element3.png |400px]] | ||
| + | |- | ||
| + | | Elemen 4,5 || [[File:Localmatrix-element45.png |400px]] || [[File:Globalmatrix-element45.png |400px]] | ||
| + | |} | ||
| + | |||
| + | {| class="mw-collapsible mw-collapsed wikitable" | ||
| + | ! '''4. Menyusun dan menggabungkan matriks elemen-elemen''' | ||
| + | |- | ||
| + | | [[File:Matrixglobal-sum.png |400px]] | ||
| + | |} | ||
| + | |||
| + | {| class="mw-collapsible mw-collapsed wikitable" | ||
| + | ! '''5. Menerapkan kondisi batas dan beban''' | ||
| + | |- | ||
| + | | Kondisi batas untuk node 1, dan 3 adalah fixed | ||
| + | |- | ||
| + | | External force pada node 2 dan 4 || [[File:Externalforce-problem4.png|400px]] | ||
| + | |- | ||
| + | |Dengan menerapkan Hukum Hooke, F= k. x, maka dalam persamaan matrix menjadi [F]=[K].[U]. Didapat || [[File:Solving-equation-problem4.png|500px|center]] | ||
| + | |} | ||
| + | |||
| + | {| class="mw-collapsible mw-collapsed wikitable" | ||
| + | ! '''6. Tahap pencarian solusi''' | ||
| + | |- | ||
| + | | [[File:Solving-equation-simplified-problem4.png |500px|center]] | ||
| + | |- | ||
| + | | Persamaan matriks diatas dapat diselesaikan dengan OpenModelica, berikut adalah pemograman yang saya buat || [[File:Gauss-elimination-problem4.png|600px|center]] | ||
| + | |- | ||
| + | | setelah melakukan pengecekan dan simulasi, saya melakukan plotting terhadap hasil simulasi. berikut hasilnya: || | ||
| + | [[File:Plot-problem4.png|600px|center]] | ||
| + | |} | ||
| + | |||
| + | |} | ||
| + | |||
| + | terdapat permasalahan pada software openmodelica yang belum bisa saya temui pemecahannya, sehingga tidak dapat menyelesaikan solusi dari persamaan tersebut. | ||
| + | |||
| + | =Pertemuan Minggu Kelima (7 Desember 2020)= | ||
| + | |||
| + | pemanfaatan fungsi input automatis unutk mengurangi kesalahan input manual, berikut beberapa gambaran alur proses coding. ==>oleh edward josua, melihat codingnya josiah. | ||
| + | |||
| + | * banyak digunakan fungsi panggil dalam algoritma ini, diantaranya unutk mencari kekakuan , mencari matriks reaksi, serta untuk eliminasi gauss jordan, sehingga fungsi lebih simpel | ||
| + | |||
| + | * kemudain algoritma terdiri dari matriks lokal kemudian di gunakan fungsi stiffness yang dapat menjumlahkan matriks global , lokal. sehingga didaptkan jumlah matriks global. kemudain diterapkan booundary condition, boundary condition sebagai parameter untuk loop function | ||
| + | |||
| + | * kemudian digunakan fungsi gauss jordan untuk menenutkan defleksi, hasil komputasi di bentuk dalam matriks defleksi, kemudain dimasukan kedalamfunsi reaction trusses sehingga didapatkan solusi. | ||
| + | |||
| + | Dari penjelasan Ahmad Mohammad Fahmi, | ||
| + | [[File:Flowchart-samuel sitompul.png|400px]] | ||
| + | |||
| + | gambar berikut menunjukan kembali alur proses pemikiran coding dari tugas trusses ini. | ||
| + | |||
| + | *fahmi menjelaskan juga dengan class yang sesuai akan mempermudah penyusunan coding karena akan di gunakan banyak proses looping untuk menghitung nilai defleksinya. | ||
| + | |||
| + | Kesimpulan tugas, | ||
| + | *menerapkan yang di coding oleh fahmi,kemudian menambahkan coding utnuk mengecek hasi sigam Fx Fy Fz, sehingga hasil lebih akurat(perhitungan coding tidak salah). | ||
| + | |||
| + | *menggunakan contoh soal dari pak dai yang di kirim di whatsapp; | ||
| + | |||
| + | *Mengupdate dan menulis di wiki, kemudian memberikan masukan untuk menyempurnakan coding tersebut. | ||
| + | == Tugas 05 == | ||
| + | [[File:Metnum Tugas5 samuel Model.jpg|400px]] | ||
| + | - '''Fungsi Matriks Elemen (Stiffness Matrix Element)''' | ||
| + | function StiffnessMatrixElement | ||
| + | input Real [:,6] inisiasi_mat; | ||
| + | output Real [size(inisiasi_mat,1),6,6] Ke_mat; | ||
| + | protected | ||
| + | Real cos_x; | ||
| + | Real cos_y; | ||
| + | Real [6] StiffTrig; | ||
| + | Real [6,6] StiffTrans; | ||
| + | Real [size(inisiasi_mat,1)] k_vec; | ||
| + | algorithm | ||
| + | L := {(sqrt(inisiasi_mat[i,2]^2 + inisiasi_mat[i,3]^2 + inisiasi_mat[i,4]^2)) for i in 1:size(inisiasi_mat,1)}; | ||
| + | k_vec := {(inisiasi_mat[i,5] * inisiasi_mat[i,6] / L[i]) for i in 1:size(inisiasi_mat,1)}; | ||
| + | for i in 1:size(inisiasi_mat,1) loop | ||
| + | StiffTrig := zeros(6); | ||
| + | StiffTrans := zeros(6,6); | ||
| + | cos_x := inisiasi_mat[i,2]/L[i]; | ||
| + | cos_y := inisiasi_mat[i,3]/L[i]; | ||
| + | cos_z := inisiasi_mat[i,4]/L[i]; | ||
| + | StiffTrig := {(cos_x)^2, | ||
| + | (cos_y)^2, | ||
| + | (cos_z)^2, | ||
| + | (cos_x*cos_y), | ||
| + | (cos_x*cos_z), | ||
| + | (cos_y*cos_z)}; | ||
| + | StiffTrans := [ StiffTrig[1], StiffTrig[4], StiffTrig[5], -1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5]; | ||
| + | StiffTrig[4], StiffTrig[2], StiffTrig[6], -1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6]; | ||
| + | StiffTrig[5], StiffTrig[6], StiffTrig[3], -1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3]; | ||
| + | -1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5], StiffTrig[1], StiffTrig[4], StiffTrig[5]; | ||
| + | -1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6], StiffTrig[4], StiffTrig[2], StiffTrig[6]; | ||
| + | -1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3], StiffTrig[5], StiffTrig[6], StiffTrig[3]]; | ||
| + | for m in 1:6 loop | ||
| + | for n in 1:6 loop | ||
| + | Ke_mat[i,m,n] := k_vec[i] * StiffTrans[m,n]; | ||
| + | end for; | ||
| + | end for; | ||
| + | end for; | ||
| + | end StiffnessMatrixElement; | ||
| + | |||
| + | - '''Stiffness Matrix Global''' | ||
| + | function StiffnessMatrixGlobal | ||
| + | input Integer [:,2] n; | ||
| + | input Integer x; | ||
| + | input Integer y; | ||
| + | input Real [y,6,6] Ke_mat; | ||
| + | output Real [y,x,x] Kg_mat; | ||
| + | algorithm | ||
| + | Kg_mat:=zero(size(ke_mat,1),3*x,3*x); | ||
| + | for i in 1:size(Ke_mat,1) loop | ||
| + | Kg_mat[i,3*n[i,1],3*n[i,1]]:=Ke_mat[i,3,3]; | ||
| + | Kg_mat[i,3*n[i,1],3*n[i,1]-1]:=Ke_mat[i,3,2]; | ||
| + | Kg_mat[i,3*n[i,1],3*n[i,1]-2]:=Ke_mat[i,3,1]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,1]]:=Ke_mat[i,2,3]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,1]-1]:=Ke_mat[i,2,2]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,1]-2]:=Ke_mat[i,2,1]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,1]]:=Ke_mat[i,1,3]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,1]-1]:=Ke_mat[i,1,2]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,1]-2]:=Ke_mat[i,1,1]; | ||
| + | Kg_mat[i,3*n[i,2],3*n[i,2]]:=Ke_mat[i,6,6]; | ||
| + | Kg_mat[i,3*n[i,2],3*n[i,2]-1]:=Ke_mat[i,6,5]; | ||
| + | Kg_mat[i,3*n[i,2],3*n[i,2]-2]:=Ke_mat[i,6,4]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,2]]:=Ke_mat[i,5,6]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,2]-1]:=Ke_mat[i,5,5]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,2]-2]:=Ke_mat[i,5,4]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,2]]:=Ke_mat[i,4,6]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,2]-1]:=Ke_mat[i,4,5]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,2]-2]:=Ke_mat[i,4,4]; | ||
| + | Kg_mat[i,3*n[i,2],3*n[i,1]]:=Ke_mat[i,6,3]; | ||
| + | Kg_mat[i,3*n[i,2],3*n[i,1]-1]:=Ke_mat[i,6,2]; | ||
| + | Kg_mat[i,3*n[i,2],3*n[i,1]-2]:=Ke_mat[i,6,1]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,1]]:=Ke_mat[i,5,3]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,1]-1]:=Ke_mat[i,5,2]; | ||
| + | Kg_mat[i,3*n[i,2]-1,3*n[i,1]-2]:=Ke_mat[i,5,1]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,1]]:=Ke_mat[i,4,3]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,1]-1]:=Ke_mat[i,4,2]; | ||
| + | Kg_mat[i,3*n[i,2]-2,3*n[i,1]-2]:=Ke_mat[i,4,1]; | ||
| + | Kg_mat[i,3*n[i,1],3*n[i,2]]:=Ke_mat[i,3,6]; | ||
| + | Kg_mat[i,3*n[i,1],3*n[i,2]-1]:=Ke_mat[i,3,5]; | ||
| + | Kg_mat[i,3*n[i,1],3*n[i,2]-2]:=Ke_mat[i,3,4]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,2]]:=Ke_mat[i,2,6]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,2]-1]:=Ke_mat[i,2,5]; | ||
| + | Kg_mat[i,3*n[i,1]-1,3*n[i,2]-2]:=Ke_mat[i,2,4]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,2]]:=Ke_mat[i,1,6]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,2]-1]:=Ke_mat[i,1,5]; | ||
| + | Kg_mat[i,3*n[i,1]-2,3*n[i,2]-2]:=Ke_mat[i,1,4]; | ||
| + | end for; | ||
| + | end StiffnessMatrixGlobal; | ||
| + | |||
| + | - '''Sum of Stiffness Matrix Global''' | ||
| + | function SumStiffnessMatrixGlobal | ||
| + | input Real [:,:,:] Kg_mat; | ||
| + | output Real [size(Kg_mat,2),size(Kg_mat,2)] KgTot_mat; | ||
| + | algorithm | ||
| + | for a in 1:size(Kg_mat,2) loop | ||
| + | for b in 1:size(Kg_mat,2) loop | ||
| + | KgTot_mat[a,b] := sum(Kg_mat [:,a,b]); | ||
| + | end for; | ||
| + | end for; | ||
| + | end SumStiffnessMatrixGlobal; | ||
| + | |||
| + | - '''Implement Boundary Condition''' | ||
| + | function BoundaryStiffnessMatrixGlobal | ||
| + | input Real [:,:] KgTot_met; | ||
| + | input Integer[:] Boundary_xyz; | ||
| + | input Integer[:] Boundary_xy; | ||
| + | input Integer[:] Boundary_xz; | ||
| + | input Integer[:] Boundary_yz; | ||
| + | input Integer[:] Boundary_x; | ||
| + | input Integer[:] Boundary_y; | ||
| + | input Integer[:] Boundary_z; | ||
| + | output Real [size(KgTot_met,1),size(KgTot_met,1)] KgB_met; | ||
| + | algorithm | ||
| + | for a in 1:size(KgTot_met,1) loop | ||
| + | for b in 1:size(KgTot_met,1) loop | ||
| + | KgB_met[a,b] := KgTot_met [a,b]; | ||
| + | end for; | ||
| + | end for; | ||
| + | if Boundary_xyz[1] <> 0 then | ||
| + | for i in 1:size(KgTot_met,1) loop | ||
| + | for a in 1:size(Boundary_xyz,1) loop | ||
| + | for b in 0:2 loop | ||
| + | KgB_met[3*(Boundary_xyz[a])-b,i]:=0; | ||
| + | KgB_met[3*Boundary_xyz[a]-b,3*Boundary_xyz[a]-b]:=1; | ||
| + | end for; | ||
| + | end for; | ||
| + | end for; | ||
| + | end if; | ||
| + | if Boundary_xy[1] <> 0 then | ||
| + | for i in 1:size(KgTot_met,1) loop | ||
| + | for a in 1:size(Boundary_xy,1) loop | ||
| + | for b in 1:2 loop | ||
| + | KgB_met[3*(Boundary_xy[a])-b,i]:=0; | ||
| + | KgB_met[3*Boundary_xy[a]-b,3*Boundary_xy[a]-b]:=1; | ||
| + | end for; | ||
| + | end for; | ||
| + | end for; | ||
| + | end if; | ||
| + | if Boundary_xz[1] <> 0 then | ||
| + | for i in 1:size(KgTot_met,1) loop | ||
| + | for a in 1:size(Boundary_xz,1) loop | ||
| + | for b in 0:2:2 loop | ||
| + | KgB_met[3*(Boundary_xz[a])-b,i]:=0; | ||
| + | KgB_met[3*Boundary_xz[a]-b,3*Boundary_xz[a]-b]:=1; | ||
| + | end for; | ||
| + | end for; | ||
| + | end for; | ||
| + | end if; | ||
| + | if Boundary_yz[1] <> 0 then | ||
| + | for i in 1:size(KgTot_met,1) loop | ||
| + | for a in 1:size(Boundary_yz,1) loop | ||
| + | for b in 0:1 loop | ||
| + | KgB_met[3*(Boundary_yz[a])-b,i]:=0; | ||
| + | KgB_met[3*Boundary_yz[a]-b,3*Boundary_yz[a]-b]:=1; | ||
| + | end for; | ||
| + | end for; | ||
| + | end for; | ||
| + | end if; | ||
| + | if Boundary_x[1] <> 0 then | ||
| + | for i in 1:size(KgTot_met,1) loop | ||
| + | for a in 1:size(Boundary_x,1) loop | ||
| + | KgB_met[3*(Boundary_x[a])-2,i]:=0; | ||
| + | KgB_met[3*Boundary_x[a]-2,3*Boundary_x[a]-2]:=1; | ||
| + | end for; | ||
| + | end for; | ||
| + | end if; | ||
| + | if Boundary_y[1] <> 0 then | ||
| + | for i in 1:size(KgTot_met,1) loop | ||
| + | for a in 1:size(Boundary_y,1) loop | ||
| + | KgB_met[3*(Boundary_y[a])-1,i]:=0; | ||
| + | KgB_met[3*Boundary_y[a]-1,3*Boundary_y[a]-1]:=1; | ||
| + | end for; | ||
| + | end for; | ||
| + | end if; | ||
| + | if Boundary_z[1] <> 0 then | ||
| + | for i in 1:size(KgTot_met,1) loop | ||
| + | for a in 1:size(Boundary_z,1) loop | ||
| + | KgB_met[3*Boundary_z[a],i]:=0; | ||
| + | KgB_met[3*Boundary_z[a],3*Boundary_z[a]]:=1; | ||
| + | end for; | ||
| + | end for; | ||
| + | end if; | ||
| + | end BoundaryStiffnessMatrixGlobal; | ||
| + | |||
| + | - '''Gauss-Jordan''' | ||
| + | function GaussJordan | ||
| + | input Real [:,:] KgB_met; | ||
| + | input Real [size(KgB_met,1)] load_met; | ||
| + | output Real [size(KgB_met,1)] U_met; | ||
| + | protected | ||
| + | Real float_error = 10e-10; | ||
| + | algorithm | ||
| + | U_met:=Modelica.Math.Matrices.solve(KgB_met,load_met); | ||
| + | for i in 1:size(KgB_met,1) loop | ||
| + | if abs(U_met[i]) <= float_error then | ||
| + | U_met[i] := 0; | ||
| + | end if; | ||
| + | end for; | ||
| + | end GaussJordan; | ||
| + | |||
| + | - '''Reaction Force''' | ||
| + | function ReactionForce | ||
| + | input Integer x; | ||
| + | input Real [:,:] KgTot_met; | ||
| + | input Real [size(KgTot_met,1)] U_met; | ||
| + | input Real [size(KgTot_met,1)] load_met; | ||
| + | output Real [x] R_met; | ||
| + | protected Real float_error = 10e-10; | ||
| + | algorithm | ||
| + | R_met := (KgTot_met*U_met)-load_met; | ||
| + | for t in 1:size(KgTot_met,1) loop | ||
| + | if abs(R_met[t]) <= float_error then | ||
| + | R_met[t] := 0; | ||
| + | end if; | ||
| + | end for; | ||
| + | end ReactionForce; | ||
| + | |||
| + | - '''Pengecekan kesetimbangan gaya''' (resultan gaya = 0) | ||
| + | function CheckForce | ||
| + | input Real [:] load; | ||
| + | input Real [size(load,1)] R; | ||
| + | output Real [3] F; | ||
| + | protected Real float_error = 10e-10; | ||
| + | protected | ||
| + | Real load_x; | ||
| + | Real load_y; | ||
| + | Real load_z; | ||
| + | Real R_x; | ||
| + | Real R_y; | ||
| + | Real R_z; | ||
| + | algorithm | ||
| + | load_x := sum({load[i] for i in 1:3:(size(load,1)-2)}); | ||
| + | load_y := sum({load[i] for i in 2:3:(size(load,1)-1)}); | ||
| + | load_z := sum({load[i] for i in 3:3:size(load,1)}); | ||
| + | R_x := sum({R[i] for i in 1:3:(size(load,1)-2)}); | ||
| + | R_y := sum({R[i] for i in 2:3:(size(load,1)-1)}); | ||
| + | R_z := sum({R[i] for i in 3:3:size(load,1)}); | ||
| + | F[1] := load_x + R_x; | ||
| + | F[2] := load_y + R_y; | ||
| + | F[3] := load_z + R_z; | ||
| + | for i in 1:3 loop | ||
| + | if abs(F[i]) <= float_error then | ||
| + | F[i] := 0; | ||
| + | end if; | ||
| + | end for; | ||
| + | end CheckForce; | ||
| + | |||
| + | = Pertemuan Minggu Keenam (14 Desember 2020), Muhasabah Pribadi = | ||
| + | pada pertemuan ini pak dai memberikan arahan kepada para mahasiswa tentang nilai pribadi masing-masing, dimana pada masa seperti ini orang -orang selalu mempentingkan nilai yang didapat deibandingkan ilmu yang dimiliki. | ||
| + | |||
| + | *Muhasabah* | ||
| + | |||
| + | saya melihat dalam diri saya selama waktu pembelajaran Kuliah Metode Numerik saya selalu mengikuti Konsep berpikir dan alur/ flowchart dalam menyelesaikan sebuah masalah, pada mata kuilah ini materi atau konsep dasar sudah saya pahami dan mengerti seperti tentang truss, konsep statika struktur dari truss dapat saya mangerti. | ||
| + | |||
| + | Namun Karena basic coding saya kurang saya belum begitu bisa untuk menerjemahkan hasil pemikiran saya tersebut dalam bentuk coding, kemudian hal-hal seperti konsep berpikir looping sudah bisa saya pahami sebgainnya namun masih dikarenakan kurangnya basic coding menyebabjan saya kurang bisa menginrtpretasikan pemikiran saya tesebut ke dalam bentuk coding. | ||
| + | |||
| + | = Tugas Besar Metode Numerik = | ||
| + | |||
| + | ==Soal== | ||
| + | |||
| + | [[File:Tugas Besar Metnum Geometri Jos.jpg|center]] | ||
| + | |||
| + | ==Tujuan== | ||
| + | |||
| + | Melakukan optimasi rangka truss sederhana untuk mencari harga optimum dengan memvariasi dimensi dan elastisitas material | ||
| + | |||
| + | ==Metodologi== | ||
| + | |||
| + | Menentukan Material paling optimum | ||
| + | |||
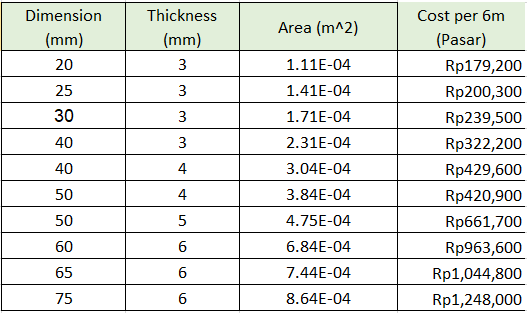
| + | Mencari harga untuk 6 ukuran batang dengan material yang sama yaitu SS304. | ||
| + | Mengitung nilai safety factor pada 6 ukuran batang dengan coding awal. | ||
| + | Membuat rasio antara safety factor dengan harga total. | ||
| + | Membuat persamaan antara rasio (safe/harga) dengan area dengan metode curve fitting. | ||
| + | Melakukan optimasi menggunakan metode golden section. | ||
| + | Untuk area penampang yang sama: | ||
| + | |||
| + | Mencari harga untuk 4 jenis material dengan area penampang yang sama yaitu 171 mm^2. | ||
| + | Mengitung nilai safety factor pada 4 jenis batang dengan coding awal. | ||
| + | Membuat rasio antara safety factor dengan harga total. | ||
| + | Membuat persamaan antara rasio (safe/harga) dengan jenis material dengan metode curve fitting. | ||
| + | Melakukan optimasi menggunakan metode golden section. | ||
| + | |||
| + | ==Penyelesaian== | ||
| + | '''1. Mendefinisikan Problem''' | ||
| + | |||
| + | Untuk dapat menyelesaikan permasalahan soal, perlu didefinisikan node dan elemen pada soal | ||
| + | |||
| + | [[File:Rangka siku definition.png|400px|center]] | ||
| + | |||
| + | '''2. Membuat asumsi dan constraint pada problem''' | ||
| + | |||
| + | Asumsi: | ||
| + | - Diasumsikan tidak ada bending karena bersifat truss | ||
| + | - Safety Factor = 2 | ||
| + | |||
| + | Constraint | ||
| + | - Node 1,2,3,4 (lantai dasar) fixed | ||
| + | - Node 13 & 16 = 1000; Node 14 & 15 = 500N | ||
| + | |||
| + | '''3. Metodologi''' | ||
| + | |||
| + | Pertama diuji coba untuk jenis material yang sama, lalu mencari area paling optimum untuk setiap jenis material | ||
| + | |||
| + | Kemudian uji coba untuk area penampang yang sama, lalu mencari material paling optimum untuk setiap area | ||
| + | |||
| − | + | '''4. Mencari Data Material''' | |
| − | + | - Material SS304 | |
| − | + | [[File:Tabel ss304.png]] | |
| − | + | - Material SS201 | |
| − | + | [[File:Tabel ss201.png]] | |
| − | |||
| − | + | '''5. Membuat model numerik''' | |
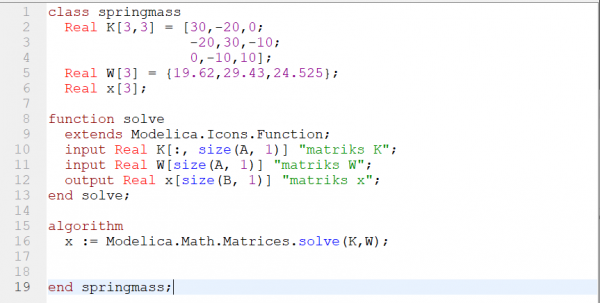
| − | + | Program Numerik ini dibuat untuk mencari nilai stress, safety factor, serta membantu dalam melakukan curve fitting | |
| − | + | model Tugas_Besar_Samuel | |
| − | - | + | //define initial variable |
| + | parameter Integer Points=size(P,1); //Number of Points | ||
| + | parameter Integer Trusses=size(C,1); //Number of Trusses | ||
| + | parameter Real Yield= (nilai yield) ; //Yield Strength Material(Pa) | ||
| + | parameter Real Area= (nilai area) ; //Luas Siku (Dimension=30x30x3mm) | ||
| + | parameter Real Elas= (nilai elastisitas) ; //Elasticity Material (Pa) | ||
| + | //define connection | ||
| + | parameter Integer C[:,2]=[ 1,5; // (1) | ||
| + | 2,6; // (2) | ||
| + | 3,7; // (3) | ||
| + | 4,8; // (4) | ||
| + | 5,6; // (5) | ||
| + | 6,7; // (6) | ||
| + | 7,8; // (7) | ||
| + | 5,8; // (8) | ||
| + | 5,9; // (9) | ||
| + | 6,10; // (10) | ||
| + | 7,11; // (11) | ||
| + | 8,12; // (12) | ||
| + | 9,10; // (13) | ||
| + | 10,11;// (14) | ||
| + | 11,12;// (15) | ||
| + | 9,12; // (16) | ||
| + | 9,13; // (17) | ||
| + | 10,14;// (18) | ||
| + | 11,15;// (19) | ||
| + | 12,16;// (20) | ||
| + | 13,14;// (21) | ||
| + | 14,15;// (22) | ||
| + | 15,16;// (23) | ||
| + | 13,16];//(24) | ||
| + | //define coordinates (please put orderly) | ||
| + | parameter Real P[:,6]=[ 0 ,0 ,0,1,1,1; //node 1 | ||
| + | 0.75,0 ,0,1,1,1; //node 2 | ||
| + | 0.75,0.6,0,1,1,1; //node 3 | ||
| + | 0 ,0.6,0,1,1,1; //node 4 | ||
| + | |||
| + | 0 ,0 ,0.3,0,0,0; //node 5 | ||
| + | 0.75,0 ,0.3,0,0,0; //node 6 | ||
| + | 0.75,0.6,0.3,0,0,0; //node 7 | ||
| + | 0 ,0.6,0.3,0,0,0; //node 8 | ||
| + | |||
| + | 0 ,0 ,1.05,0,0,0; //node 9 | ||
| + | 0.75,0 ,1.05,0,0,0; //node 10 | ||
| + | 0.75,0.6,1.05,0,0,0; //node 11 | ||
| + | 0 ,0.6,1.05,0,0,0; //node 12 | ||
| + | |||
| + | 0 ,0 ,1.8,0,0,0; //node 13 | ||
| + | 0.75,0 ,1.8,0,0,0; //node 14 | ||
| + | 0.75,0.6,1.8,0,0,0; //node 15 | ||
| + | 0 ,0.6,1.8,0,0,0]; //node 16 | ||
| + | |||
| + | //define external force (please put orderly) | ||
| + | parameter Real F[Points*3]={0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,0, | ||
| + | 0,0,-1000, | ||
| + | 0,0,-500, | ||
| + | 0,0,-500, | ||
| + | 0,0,-1000}; | ||
| + | //solution | ||
| + | Real displacement[N], reaction[N]; | ||
| + | Real check[3]; | ||
| + | Real stress1[Trusses]; | ||
| + | Real safety[Trusses]; | ||
| + | Real dis[3]; | ||
| + | Real Str[3]; | ||
| + | protected | ||
| + | parameter Integer N=3*Points; | ||
| + | Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; | ||
| + | Real err=10e-15, ers=10e-8; | ||
| + | algorithm | ||
| + | //Creating Global Matrix | ||
| + | G:=id; | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | end for; | ||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | //Transforming to global matrix | ||
| + | g:=zeros(N,N); | ||
| + | for m,n in 1:3 loop | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n]; | ||
| + | g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n]; | ||
| + | g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n]; | ||
| + | end for; | ||
| + | G_star:=G+g; | ||
| + | G:=G_star; | ||
| + | end for; | ||
| + | //Implementing boundary | ||
| + | for x in 1:Points loop | ||
| + | if P[x,4] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[(x*3)-2,a]:=0; | ||
| + | G[(x*3)-2,(x*3)-2]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x,5] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[(x*3)-1,a]:=0; | ||
| + | G[(x*3)-1,(x*3)-1]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | if P[x,6] <> 0 then | ||
| + | for a in 1:Points*3 loop | ||
| + | G[x*3,a]:=0; | ||
| + | G[x*3,x*3]:=1; | ||
| + | end for; | ||
| + | end if; | ||
| + | end for; | ||
| + | //Solving displacement | ||
| + | displacement:=Modelica.Math.Matrices.solve(G,F); | ||
| + | //Solving reaction | ||
| + | reaction:=(G_star*displacement)-F; | ||
| + | //Eliminating float error | ||
| + | for i in 1:N loop | ||
| + | reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; | ||
| + | displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i]; | ||
| + | end for; | ||
| + | //Checking Force | ||
| + | check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))}); | ||
| + | check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))}); | ||
| + | check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)}); | ||
| + | for i in 1:3 loop | ||
| + | check[i] := if abs(check[i])<=ers then 0 else check[i]; | ||
| + | end for; | ||
| + | //Calculating stress in each truss | ||
| + | for i in 1:Trusses loop | ||
| + | for j in 1:3 loop | ||
| + | q1[j]:=P[C[i,1],j]; | ||
| + | q2[j]:=P[C[i,2],j]; | ||
| + | dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]); | ||
| + | end for; | ||
| + | //Solving Matrix | ||
| + | L:=Modelica.Math.Vectors.length(q2-q1); | ||
| + | cx:=(q2[1]-q1[1])/L; | ||
| + | cy:=(q2[2]-q1[2])/L; | ||
| + | cz:=(q2[3]-q1[3])/L; | ||
| + | X:=(Elas/L)*[cx^2,cx*cy,cx*cz; | ||
| + | cy*cx,cy^2,cy*cz; | ||
| + | cz*cx,cz*cy,cz^2]; | ||
| + | Str:=(X*dis); | ||
| + | stress1[i]:=Modelica.Math.Vectors.length(Str); | ||
| + | end for; | ||
| + | //Safety factor | ||
| + | for i in 1:Trusses loop | ||
| + | if stress1[i]>0 then | ||
| + | safety[i]:=Yield/stress1[i]; | ||
| + | else | ||
| + | safety[i]:=0; | ||
| + | end if; | ||
| + | end for; | ||
| + | end Tugas_Besar_Samuel; | ||
| − | |||
| − | + | = JAWABAN UJIAN AKHIR SEMESTER = | |
| + | * Jawaban 1 dan 2 | ||
| − | [[File: | + | [[File:WhatsApp_Image_2021-01-13_at_4.51.09_PM.jpeg|400px]] |
| − | + | * Jawaban 1 s/d 3 | |
| − | [[File: | + | [[File:WhatsApp_Image_2021-01-13_at_5.15.10_PM.jpeg|400px]] |
| − | + | * Jawaban 1 s/d 6 | |
| − | [[File: | + | [[File:WhatsApp_Image_2021-01-13_at_5.31.02_PM.jpeg|400px]] |
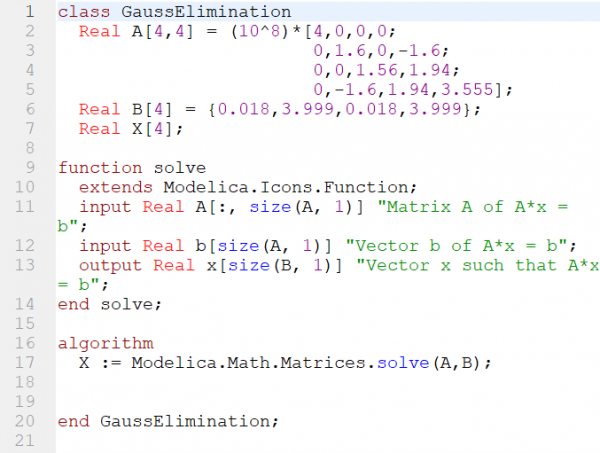
| − | + | Kemudian untuk soalno 7 jawaban dalam bentuk coding di open modelica sebagai berikut, | |
| − | + | | '''Main Function''' | |
| − | + | model SoalNo7_samuel | |
| + | //initiation= [ elemen#, theta, A, E, L] | ||
| + | parameter Real [:,5] initiation= [1, 0, 2.011e-4, 1.9e11, 1; //isi sesuai data | ||
| + | 2, 0, 2.011e-4, 1.9e11, 1; | ||
| + | 3, 45, 2.011e-4, 1.9e11, 1; | ||
| + | 4, 135, 2.011e-4, 1.9e11, 1]; | ||
| + | //node = [ i, j] | ||
| + | parameter Integer [3,2] node = [1, 2; //isi sesuai data | ||
| + | 2, 3; | ||
| + | 1, 4, | ||
| + | 2, 4, | ||
| + | 3, 4]; | ||
| + | //jumlah node | ||
| + | parameter Integer n = 4; //isi sesuai data | ||
| + | //titik node boundary | ||
| + | parameter Integer [:] Boundary = {3,4}; //isi sesuai data | ||
| − | [[ | + | //load = [ F1x, F1y, F2x,F2y,F3x,F3y,F4x,F4y] |
| + | parameter Real [2*n] load = { 0, 1135562, 0, 0, 0, 0, 0, 0}; //isi sesuai data | ||
| + | Real [size(inisiasi,1)] k; | ||
| + | Real [size(inisiasi,1),4,4] Ke; | ||
| + | Real [size(inisiasi,1),2*n,2*n] Kg; | ||
| + | Real [2*n,2*n] KgTot; | ||
| + | Real [2*n,2*n] KgB; | ||
| + | Real [2*n] U; | ||
| + | Real [2*n] R; | ||
| + | //check force | ||
| + | Real [2] F; | ||
| + | equation | ||
| + | k = {(initiation[i,3] * initiation[i,4] / initiation[i,5]) for i in 1:size(initiation,1)}; | ||
| + | Ke = StiffnessMatrixElement(initiation); | ||
| + | Kg = StiffnessMatrixGlobal(n, node, Ke); | ||
| + | KgTot = SumStiffnessMatrixGlobal(Kg); | ||
| + | KgB = BoundaryStiffnessMatrixGlobal(KgTot, Boundary); | ||
| + | U = GaussJordan(KgB, load); | ||
| + | R = ReactionForce(KgTot, U, load); | ||
| + | end SoalNo7_samuel; | ||
| − | + | Kemudian di bentuk juga fungsi panggil yaitu | |
| − | + | function MatrixElementStiffness_samuel | |
| + | input Real [:,5] initiation_mat; | ||
| + | output Real [size(initiation_mat,1),4,4] Ke_mat; | ||
| + | protected | ||
| + | Real theta; | ||
| + | Real [3] StiffTrig; | ||
| + | Real [4,4] StiffTrans; | ||
| + | Real [size(initiation_mat,1)] k_vec; | ||
| + | Real float_error = 10e-10; | ||
| + | algorithm | ||
| + | k_vec := {(initiation_mat[i,3] * initiation_mat[i,4] / initiation_mat[i,5]) for i in 1:size(initiationi_mat,1)}; | ||
| + | // Finding stiffness matrix of each element member | ||
| + | for i in 1:size(initiation_mat,1) loop | ||
| + | // Clearing the matrices | ||
| + | StiffTrig := zeros(3); | ||
| + | StiffTrans := zeros(4,4); | ||
| + | // Converting degrees to radians | ||
| + | theta := Modelica.SIunits.Conversions.from_deg(initiation_mat[i,2]); | ||
| + | // {cos^2, sin^2, sincos} | ||
| + | StiffTrig := {(Modelica.Math.cos(theta))^2, | ||
| + | (Modelica.Math.sin(theta))^2, | ||
| + | (Modelica.Math.sin(theta)*Modelica.Math.cos(theta))}; | ||
| + | // Handle float error elements in StiffTrig | ||
| + | for t in 1:size(StiffTrig,1) loop | ||
| + | if abs(StiffTrig[t]) <= float_error then | ||
| + | StiffTrig[t] := 0; | ||
| + | end if; | ||
| + | end for; | ||
| + | // Construct stiffness transformation matrix | ||
| + | StiffTrans := [ StiffTrig[1], StiffTrig[3], -1*StiffTrig[1], -1*StiffTrig[3]; | ||
| + | StiffTrig[3], StiffTrig[2], -1*StiffTrig[3], -1*StiffTrig[2]; | ||
| + | -1*StiffTrig[1], -1*StiffTrig[3], StiffTrig[1], StiffTrig[3]; | ||
| + | -1*StiffTrig[3], -1*StiffTrig[2], StiffTrig[3], StiffTrig[2]]; | ||
| + | // Multiply in stiffness constant of element, add final stiffness matrix to Ke_mat | ||
| + | for m in 1:4 loop | ||
| + | for n in 1:4 loop | ||
| + | Ke_mat[i,m,n] := k_vec[i] * StiffTrans[m,n]; | ||
| + | end for; | ||
| + | end for; | ||
| + | end for; | ||
| + | end MatrixElementStiffness_samuel | ||
| − | + | Kemudian di masukan ke functon matrix global stifness, | |
| − | + | function MatrixGlobalStriffness_samuel | |
| + | input Integer x; | ||
| + | input Integer [:,2] n; | ||
| + | input Real [:,4,4] Ke_mat; | ||
| + | output Real [size(Ke_mat,1),2*x,2*x] Kg_mat; | ||
| + | algorithm | ||
| + | Kg_mat := zeros(size(Ke_mat,1),2*x,2*x); | ||
| + | for i in 1:size(Ke_mat,1) loop | ||
| + | Kg_mat[i,2*n[i,1],2*n[i,1]]:=Ke_mat[i,2,2]; | ||
| + | Kg_mat[i,2*n[i,1]-1,2*n[i,1]-1]:=Ke_mat[i,1,1]; | ||
| + | Kg_mat[i,2*n[i,1],2*n[i,1]-1]:=Ke_mat[i,2,1]; | ||
| + | Kg_mat[i,2*n[i,1]-1,2*n[i,1]]:=Ke_mat[i,1,2]; | ||
| + | Kg_mat[i,2*n[i,2],2*n[i,2]]:=Ke_mat[i,4,4]; | ||
| + | Kg_mat[i,2*n[i,2]-1,2*n[i,2]-1]:=Ke_mat[i,3,3]; | ||
| + | Kg_mat[i,2*n[i,2],2*n[i,2]-1]:=Ke_mat[i,4,3]; | ||
| + | Kg_mat[i,2*n[i,2]-1,2*n[i,2]]:=Ke_mat[i,3,4]; | ||
| + | Kg_mat[i,2*n[i,2],2*n[i,1]]:=Ke_mat[i,4,2]; | ||
| + | Kg_mat[i,2*n[i,2]-1,2*n[i,1]-1]:=Ke_mat[i,3,1]; | ||
| + | Kg_mat[i,2*n[i,2],2*n[i,1]-1]:=Ke_mat[i,4,1]; | ||
| + | Kg_mat[i,2*n[i,2]-1,2*n[i,1]]:=Ke_mat[i,3,2]; | ||
| + | Kg_mat[i,2*n[i,1],2*n[i,2]]:=Ke_mat[i,2,4]; | ||
| + | Kg_mat[i,2*n[i,1]-1,2*n[i,2]-1]:=Ke_mat[i,1,3]; | ||
| + | Kg_mat[i,2*n[i,1],2*n[i,2]-1]:=Ke_mat[i,2,3]; | ||
| + | Kg_mat[i,2*n[i,1]-1,2*n[i,2]]:=Ke_mat[i,1,4]; | ||
| + | end for; | ||
| + | end MatrixGlobalStiffness_samuel; | ||
| − | dengan | + | hasil matrix global ini kemudian akan di jumlahkan dengan fungsi berikut, |
| − | [[ | + | function MatrixGlobalStiffnessSum_samuel |
| + | input Real [:,:,:] Kg_mat; | ||
| + | output Real [size(Kg_mat,2),size(Kg_mat,2)] KgTot_mat; | ||
| + | algorithm | ||
| + | for a in 1:size(Kg_mat,2) loop | ||
| + | for b in 1:size(Kg_mat,2) loop | ||
| + | KgTot_mat[a,b] := sum(Kg_mat [:,a,b]); | ||
| + | end for; | ||
| + | end for; | ||
| + | end MatrixGlobalStiffnessSum_samuel; | ||
| − | + | setelah selesai disusun function untuk mengimput boundary condition untuk mencari defleksi, | |
| − | [[ | + | function MatrixGlobalStiffnessBoundaryCond_samuel |
| + | input Real [:,:] KgTot_met; | ||
| + | input Integer[:] Boundary_met; | ||
| + | output Real [size(KgTot_met,1),size(KgTot_met,1)] KgB_met; | ||
| + | algorithm | ||
| + | for a in 1:size(KgTot_met,1) loop | ||
| + | for b in 1:size(KgTot_met,1) loop | ||
| + | KgB_met[a,b] := KgTot_met[a,b]; | ||
| + | end for; | ||
| + | end for; | ||
| + | for i in 1:size(KgTot_met,1) loop | ||
| + | for a in 1:size(Boundary_met,1) loop | ||
| + | for b in 0:1 loop | ||
| + | KgB_met[2*(Boundary_met[a])-b,i]:=0; | ||
| + | KgB_met[2*Boundary_met[a]-b,2*Boundary_met[a]-b]:=1; | ||
| + | end for; | ||
| + | end for; | ||
| + | end for; | ||
| + | end MatrixGlobalStiffnessBoundaryCond_samuel; | ||
| − | + | digunakan function gauss jordan sehingga dapat dilihat sebagai berikut, | |
| − | [[ | + | function GaussJordan_samuel |
| + | input Real [:,:] KgB_met; | ||
| + | input Real [size(KgB_met,1)] load_met; | ||
| + | output Real [size(KgB_met,1)] U_met; | ||
| + | protected | ||
| + | Real float_error = 10e-10; | ||
| + | algorithm | ||
| + | U_met:=Modelica.Math.Matrices.solve(KgB_met,load_met); | ||
| + | for i in 1:size(KgB_met,1) loop | ||
| + | if abs(U_met[i]) <= float_error then | ||
| + | U_met[i] := 0; | ||
| + | end if; | ||
| + | end for; | ||
| + | end GaussJordan_samuel; | ||
| − | + | untuk menentukan reaction force digunakan function berikut, | |
| − | + | function ReactionForce_samuel | |
| + | input Real [:,:] KgTot_met; | ||
| + | input Real [size(KgTot_met,1)] U_met; | ||
| + | input Real [size(KgTot_met,1)] load_met; | ||
| + | output Real [size(KgTot_met,1)] R_met; | ||
| + | protected Real float_error = 10e-10; | ||
| + | algorithm | ||
| + | R_met := KgTot_met*U_met-load_met; | ||
| + | for t in 1:size(KgTot_met,1) loop | ||
| + | if abs(R_met[t]) <= float_error then | ||
| + | R_met[t] := 0; | ||
| + | end if; | ||
| + | end for; | ||
| + | end ReactionForce_samuel; | ||
Latest revision as of 13:35, 14 January 2021
Biodata
Nama: Samuel Albert B C H Sitompul
NPM : 1606907556
Hobi: Membaca Buku
Contents
- 1 Pertemuan Minggu Pertama Metode Numerik 03 (9 November 2020)
- 2 Pertemuan Minggu Kedua Metode Numerik 03 (16 November 2020)
- 3 Pertemuan Minggu Ketiga Metode Numerik 03 (23 November 2020)
- 4 PErtemuan Minggu Keempat (30 November 2020)
- 5 Pertemuan Minggu Kelima (7 Desember 2020)
- 6 Pertemuan Minggu Keenam (14 Desember 2020), Muhasabah Pribadi
- 7 Tugas Besar Metode Numerik
- 8 JAWABAN UJIAN AKHIR SEMESTER
Pertemuan Minggu Pertama Metode Numerik 03 (9 November 2020)
Metode Numerik adalah salah satu mata kuliah yang sangat banyak penerapannya dalam dunia keteknikan. Mata kuliah ini salah satu mata kuliah yang cukup menarik karena penerapannya sangat luas dan bermanfaat. Sejauh ini yang telah saya pelajari sebelum UTS mencakup 3 materi besar yaitu mencari akar-akar, regresi linier, dan turunan numerik.
1. Mencari Akar-Akar
Pada materi ini, saya mempelajari metode-metode untuk mencari akar secara numerik. Beberapa metode yang saya pelajari adalah metode pencarian akar menggunakan Closed methods (Bracketing Method) dan Open Methods.
| Metode Closed Methods merupakan metode pencarian akar-akar dengan menggunakan batas atas dan batas bawah untuk mencari akar dan mengukur persentasi error yang didapat untuk mendapat tingkat akurasi dari iterasi. Metode yang saya pelajari ada 3 yaitu Graphical Methods, Bisection Methods, dan False-Position Methods.
Graphical Methods Sebuah metode sederhana yang menggunakan grafik untuk memperkirakan akar-akar suatu fungsi. Metode ini dilakukan dengan melakukan plotting dari suatu fungsi ke dalam bentuk grafik. Bisection Methods Metode ini merupakan salah satu jenis metode incremental search method yang menggunakan batas atas dan batas bawah untuk mempersempit area pencarian akar-akar. False-Position Methods Metode ini sangat mirip dengan metode Bisection. Hal yang membedakan metode False-Position dengan Bisection adalah penentuan titik tengah dari batas-batas yang ditentukan. Penentuan titik tengah dari False-Position Method menggunakan persamaan berikut. |
| Metode Open Methods merupakan metode pencarian yang hanya menggunakan 1 titik untuk menemukan akar-akar. Metode ini dapat menggunakan turunan suatu fungsi untuk menentukan titik pengujian baru yang semakin dekat dengan nilai akar-akar yang diinginakn. Metode yang saya pelajari ada 3 yaitu Fixed-Point Iteration, Newton-Rapshon, dan Secant Method
Fixed-Point Iteration Metode ini disebut juga metode iterasi sederhana, adalah metode yang memisahkan x dengan sebagian x yang lain sehingga diperoleh: x=g(x) Newton-RaphsonMetode ini menggunakan satu titik awal dan mendekatinya dengan memperhatikan slope atau gradien pada titik tersebut. Slop atau gradien didapatkan dengan melakukan turunan dari fungsi tersebut. Persamaan untuk Newton-Raphson adalah sebagai berikut:
Metode ini merupakan metode modifikasi Newton-Raphson dimana metode Newton-Raphson tidak digunakan (karena f'(x) sulit ditemukan atau tidak mungkin ditemukan). Persaman untuk metode Secant adalah sebagai berikut |
2. Regresi Linier
regresi linear adalah sebuah pendekatan untuk memodelkan hubungan antara variable terikat Y dan satu atau lebih variable bebas yang disebut X. Salah satu kegunaan dari regresi linear adalah untuk melakukan prediksi berdasarkan data-data yang telah dimiliki sebelumnya. Hubungan di antara variable-variabel tersebut disebut sebagai model regresi linear.
Persamaan umum Regresi Linier adalah sebagai berikut:
dimana:
3. Turunan Numerik
Turunan Numerik adalah menentukan hampiran nilai turunan fungsi f yang diberikan dalam bentuk tabel. Terdapat 3 pendekatan dalam menghitung turunan numerik:
Tugas Pertemuan 1: OpenModelica
Setelah pertemuan 1, pak Dai meminta kami untuk mempelajari OpenModelica
Untuk mempelajari OpenModelica, saya menggunakan referensi/tutorial dari YouTube dengan tautan berikut:
https://www.youtube.com/watch?v=SW5Eclf1tRs
https://www.youtube.com/watch?v=m0Ahs8fEN28&t=519s&ab_channel=NSTUFACE
Dari video-video tersebut saya diperkenalkan mengenai interface OpenModelica untuk pemula. Saya juga mempelajari bahwa OpenModelica menggunakan bahasa program Modelica untuk penggunaannya. Bahasa ini mirip dengan bahasa pemograman lain seperti python. Kelebihan yang saya lihat dari OpenModelica ini adalah program ini memiliki tools yang membantu mempermudah kita untuk membuat sistem dalam bentuk grafis atau skema. Model-model ini dapat kita aplikasikan dalam kehidupan nyata seperti membuat sistem elektrikal, magnetik, fluida, perpindahan panas, dsb.
Dalam konteks Metode Numerik, saya mempelajari bahwa OpenModelica dapat membantu kita dalam menyelesaikan permasalahan-permasalahan dalam mata kuliah Metode Numerik dan memvisualisasikan penyelesaian tersebut dalam bentuk grafik, salah satunya adalah penyelesaian Persamaan Diferensial Biasa atau ODE.
Contoh penyelesaian permasalahan ODE menggunakan OpenModelica adalah persamaan pendulum, yang didefinisikan sebagai berikut:
Dengan menggunakan referensi dari tautan kedua, saya membuat bahasa pemograman untuk menyelesaikan persamaan pendulum tersebut.
model pendulum Real y "variable state"; Real x; parameter Real L=1 "pendulum length"; constant Real g=9.80665; initial equation y=9 "initial value"; equation x=der(y); der(x)+(g/L)*(y)=0 "differential equation"; annotation(experiment(StartTime = 0, StopTime = 100)); end pendulum;
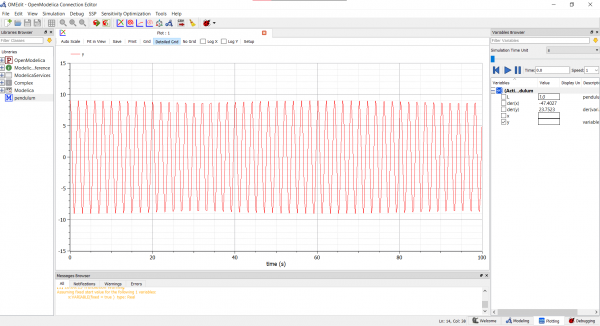
Penyelesaian dari persamaan tersebut digambarkan dalam bentuk grafik sebagai berikut
Dari grafik tersebut dapat dilihat bahwa seiring berjalannya waktu, pendulum melakukan osilasi. Namun dapat dilihat bahwa pendulum tersebut tidak kembali ketitik semula seiring berjalannya waktu.
Dari pembelajaran ini, saya mempelajari bahwa OpenModelica merupakan tools yang berguna dalam pelajaran Metode Numerik.
Pertemuan Minggu Kedua Metode Numerik 03 (16 November 2020)
Pada pertemuan kedua kali ini, Kami diminta oleh Pak Dai untuk menunjukkan pemahaman kami mengenai tugas minggu lalu, yaitu mempelajari OpenModelica. Lalu kami melakukan simulasi dengan membuat program sederhana didalam OpenModelica untuk menjumlahkan 10 angka pada variabel.
Setelah kelas, Pak Dai memberikan tugas kepada kita untuk membuat simulasi untuk menyelesaikan persamaan aljabar simultan (bisa metode eliminasi gauss, metode gauss seidel, dsb.) Berikut adalah hasil percobaan saya untuk menyelesaikan sistem persamaan aljabar. Untuk simulasi ini, saya menggunakan metode eliminasi gauss untuk menyelesaikan permasalahan aljabar simultan.
Metode eliminasi gauss merupakan salah satu metode dalam menyelesaikan sebuah sistem persamaan dengan mengubah sistem persamaan tersebut kedalam bentuk matrix. Setelah diubah, lalu matrix yang berisi angka dipindah-ruaskan lalu diselesaikan sehingga didapat nilai-nilai dari variabel yang kita cari.
Berikut adalah model simulasi yang saya buat:
Saya mencoba menyelesaikan 5 sistem persamaan linier dengan metode eliminasi gauss dengan perintah "Modelica.Math.Matrices.solve(A,b)". Setelah melakukan pengecekan model, saya menjalankan simulasi dan melakukan plotting seusai simulasi. Berikut adalah hasil plotting tersebut:
dapat dilihat bahwa tiap garis menunjukkan penyelesaian dari sistem persamaan tersebut. Terdapat 5 solusi dari 5 sistem persamaan dengan 5 variabel
Pertemuan Minggu Ketiga Metode Numerik 03 (23 November 2020)
Di pertemuan hari ini, Pak Dai menjelaskan tentang aplikasi metode numerik untuk permasalahan-permasalahan teknik. Salah satunya adalah permasalahan sistem pegas-massa. Lalu pak Dai meminta kami untuk memahami permasalahan pada Figure 12.11 pada e-book Metode Numerik. Dengan mengubah sistem menjadi bentuk matrix, kita mendapatkan bentuk matrix dari sistem tersebut sebagai berikut:
Tugas Pertemuan 3
Setelah kelas, Pak Dai memberikan tugas untuk menyelesaikan soal berikut:
alur berpikir untuk menyelesaikan masalah :
1. Mengubah problem menjadi node dan elemen
2. Menentukan nilai Konstanta kekakuan/stiffness constant dari elemen
3. Menyusun dan menggabungkan matriks elemen-elemen
4. Menyusun dan menggabungkan matriks elemen-elemen
5. Menerapkan kondisi batas dan beban
6. Tahap pencarian solusi
7. Mendapatkan nilai gaya reaksi
8. Mendapatkan gaya Internal dan Normal Stress
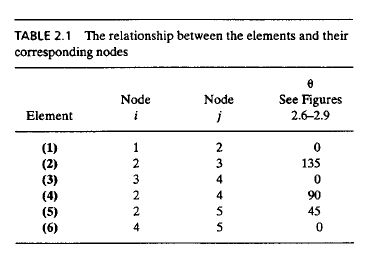
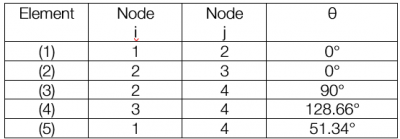
Untuk menyelesaikan soal ini perlu dilakukan pengelompokan menjadi node dan elemen seperti pada tabel berikut:
lalu perlu dilakukan perhitungan nilai kekakuan pada elemen. Untuk elemen 1,3,5, dan 6 nilai kekakuannya adalah 4,22 x 10^5 lb/in. sedangkan untuk elemen 2, dan 4 nilai kekakuannya adalah 2,98 x 10^5 lb/in.
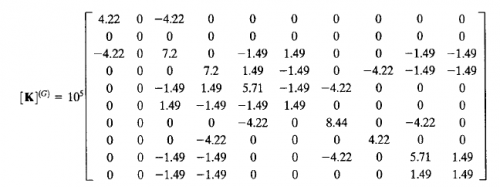
setelah itu perlu dilakukan analisis kekakuan pada tiap elemen dalam matriks koordinat global, kemudian dijumlahkan untuk mendapatkan K global. berikut adalah hasil penjumlahan dari nilai kekakuan tiap elemen:
disederhanakan menjadi
setelah mendapat matriks kekakuan, diterapkan kondisi batas dan beban. Untuk node 1 dan 3 adalah fixed, maka U1X=0, U1Y=0, U3X=0, U3Y=0 dan beban diberikan pada node 4 dan 5 sebesar F4Y= -500lb dan F5Y= -500lb
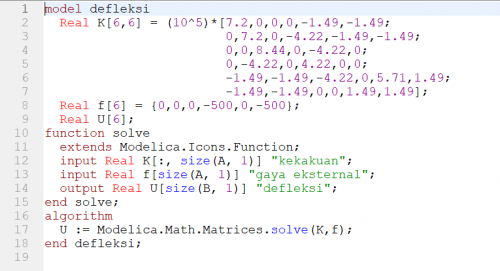
dengan menggunakan Hukum Hooke yaitu F=k.x, maka didapatkan persamaan defleksi menjadi
Persamaan diatas kemudian diselesaikan dengan OpenModelica, berikut saya lampirkan coding yang saya buat
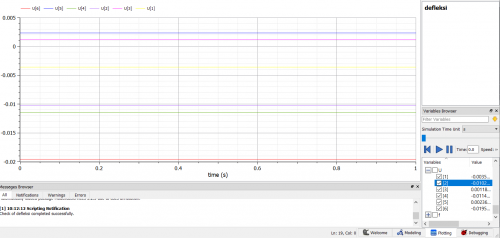
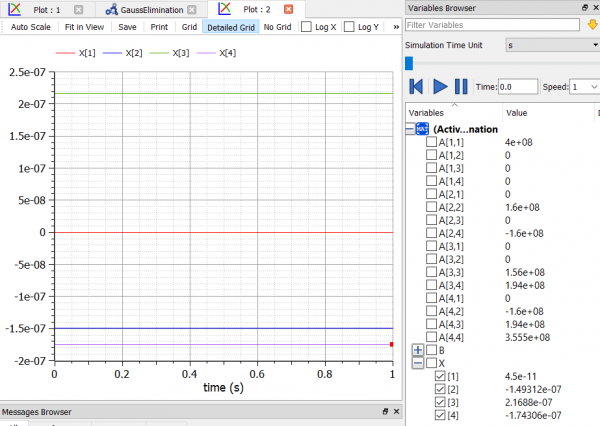
setelah melakukan pengecekan dan simulasi, saya melakukan plotting. berikut hasil plotting simulasi tersebut.
hasil dapat dilihat pada panel di bagian kanan bawah gambar.
Untuk mendapatkan gaya reaksi, persamaannya adalah:
{R}=[K].{U}-{F}
diterapkan matriks-matriks yang sudah diketahui, didapat:
Persamaan diatas dapat diselesaikan oleh openmodelica. berikut adalah coding yang saya buat
hasil simulasi tersebut di plot sebagai berikut:
nilai R tiap node dapat dilihat di bagian kanan bawah gambar
PErtemuan Minggu Keempat (30 November 2020)
Quiz 1
Pada pertemuan minggu ke IV hari ini, Pak Dai mengadakan kuis untuk menguji kemampuan inidvidu kami, para peserta diberikan 2 buah soal kuis dan diminta untuk menuliskan flowchartynya. Berikut merupakan kedua soal kuisnya.
dan berikut merupakan tampilan flowchart pengerjaan sebagai jawaban soal kuis tersebut yang telah saya buat. Mengingat alur pengerjaan kedua soal tersebut hampir sama, maka tampilan flowchart tersebut merepresentasikan keduanya.
Tugas soal no. 4
Soal no.4
terdapat permasalahan pada software openmodelica yang belum bisa saya temui pemecahannya, sehingga tidak dapat menyelesaikan solusi dari persamaan tersebut.
Pertemuan Minggu Kelima (7 Desember 2020)
pemanfaatan fungsi input automatis unutk mengurangi kesalahan input manual, berikut beberapa gambaran alur proses coding. ==>oleh edward josua, melihat codingnya josiah.
- banyak digunakan fungsi panggil dalam algoritma ini, diantaranya unutk mencari kekakuan , mencari matriks reaksi, serta untuk eliminasi gauss jordan, sehingga fungsi lebih simpel
- kemudain algoritma terdiri dari matriks lokal kemudian di gunakan fungsi stiffness yang dapat menjumlahkan matriks global , lokal. sehingga didaptkan jumlah matriks global. kemudain diterapkan booundary condition, boundary condition sebagai parameter untuk loop function
- kemudian digunakan fungsi gauss jordan untuk menenutkan defleksi, hasil komputasi di bentuk dalam matriks defleksi, kemudain dimasukan kedalamfunsi reaction trusses sehingga didapatkan solusi.
Dari penjelasan Ahmad Mohammad Fahmi,
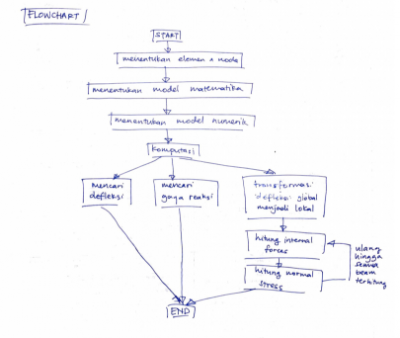
gambar berikut menunjukan kembali alur proses pemikiran coding dari tugas trusses ini.
- fahmi menjelaskan juga dengan class yang sesuai akan mempermudah penyusunan coding karena akan di gunakan banyak proses looping untuk menghitung nilai defleksinya.
Kesimpulan tugas,
- menerapkan yang di coding oleh fahmi,kemudian menambahkan coding utnuk mengecek hasi sigam Fx Fy Fz, sehingga hasil lebih akurat(perhitungan coding tidak salah).
- menggunakan contoh soal dari pak dai yang di kirim di whatsapp;
- Mengupdate dan menulis di wiki, kemudian memberikan masukan untuk menyempurnakan coding tersebut.
Tugas 05
 - Fungsi Matriks Elemen (Stiffness Matrix Element)
- Fungsi Matriks Elemen (Stiffness Matrix Element)
function StiffnessMatrixElement
input Real [:,6] inisiasi_mat;
output Real [size(inisiasi_mat,1),6,6] Ke_mat;
protected
Real cos_x;
Real cos_y;
Real [6] StiffTrig;
Real [6,6] StiffTrans;
Real [size(inisiasi_mat,1)] k_vec;
algorithm
L := {(sqrt(inisiasi_mat[i,2]^2 + inisiasi_mat[i,3]^2 + inisiasi_mat[i,4]^2)) for i in 1:size(inisiasi_mat,1)};
k_vec := {(inisiasi_mat[i,5] * inisiasi_mat[i,6] / L[i]) for i in 1:size(inisiasi_mat,1)};
for i in 1:size(inisiasi_mat,1) loop
StiffTrig := zeros(6);
StiffTrans := zeros(6,6);
cos_x := inisiasi_mat[i,2]/L[i];
cos_y := inisiasi_mat[i,3]/L[i];
cos_z := inisiasi_mat[i,4]/L[i];
StiffTrig := {(cos_x)^2,
(cos_y)^2,
(cos_z)^2,
(cos_x*cos_y),
(cos_x*cos_z),
(cos_y*cos_z)};
StiffTrans := [ StiffTrig[1], StiffTrig[4], StiffTrig[5], -1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5];
StiffTrig[4], StiffTrig[2], StiffTrig[6], -1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6];
StiffTrig[5], StiffTrig[6], StiffTrig[3], -1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3];
-1*StiffTrig[1], -1*StiffTrig[4], -1*StiffTrig[5], StiffTrig[1], StiffTrig[4], StiffTrig[5];
-1*StiffTrig[4], -1*StiffTrig[2], -1*StiffTrig[6], StiffTrig[4], StiffTrig[2], StiffTrig[6];
-1*StiffTrig[5], -1*StiffTrig[6], -1*StiffTrig[3], StiffTrig[5], StiffTrig[6], StiffTrig[3]];
for m in 1:6 loop
for n in 1:6 loop
Ke_mat[i,m,n] := k_vec[i] * StiffTrans[m,n];
end for;
end for;
end for;
end StiffnessMatrixElement;
- Stiffness Matrix Global
function StiffnessMatrixGlobal
input Integer [:,2] n;
input Integer x;
input Integer y;
input Real [y,6,6] Ke_mat;
output Real [y,x,x] Kg_mat;
algorithm
Kg_mat:=zero(size(ke_mat,1),3*x,3*x);
for i in 1:size(Ke_mat,1) loop
Kg_mat[i,3*n[i,1],3*n[i,1]]:=Ke_mat[i,3,3];
Kg_mat[i,3*n[i,1],3*n[i,1]-1]:=Ke_mat[i,3,2];
Kg_mat[i,3*n[i,1],3*n[i,1]-2]:=Ke_mat[i,3,1];
Kg_mat[i,3*n[i,1]-1,3*n[i,1]]:=Ke_mat[i,2,3];
Kg_mat[i,3*n[i,1]-1,3*n[i,1]-1]:=Ke_mat[i,2,2];
Kg_mat[i,3*n[i,1]-1,3*n[i,1]-2]:=Ke_mat[i,2,1];
Kg_mat[i,3*n[i,1]-2,3*n[i,1]]:=Ke_mat[i,1,3];
Kg_mat[i,3*n[i,1]-2,3*n[i,1]-1]:=Ke_mat[i,1,2];
Kg_mat[i,3*n[i,1]-2,3*n[i,1]-2]:=Ke_mat[i,1,1];
Kg_mat[i,3*n[i,2],3*n[i,2]]:=Ke_mat[i,6,6];
Kg_mat[i,3*n[i,2],3*n[i,2]-1]:=Ke_mat[i,6,5];
Kg_mat[i,3*n[i,2],3*n[i,2]-2]:=Ke_mat[i,6,4];
Kg_mat[i,3*n[i,2]-1,3*n[i,2]]:=Ke_mat[i,5,6];
Kg_mat[i,3*n[i,2]-1,3*n[i,2]-1]:=Ke_mat[i,5,5];
Kg_mat[i,3*n[i,2]-1,3*n[i,2]-2]:=Ke_mat[i,5,4];
Kg_mat[i,3*n[i,2]-2,3*n[i,2]]:=Ke_mat[i,4,6];
Kg_mat[i,3*n[i,2]-2,3*n[i,2]-1]:=Ke_mat[i,4,5];
Kg_mat[i,3*n[i,2]-2,3*n[i,2]-2]:=Ke_mat[i,4,4];
Kg_mat[i,3*n[i,2],3*n[i,1]]:=Ke_mat[i,6,3];
Kg_mat[i,3*n[i,2],3*n[i,1]-1]:=Ke_mat[i,6,2];
Kg_mat[i,3*n[i,2],3*n[i,1]-2]:=Ke_mat[i,6,1];
Kg_mat[i,3*n[i,2]-1,3*n[i,1]]:=Ke_mat[i,5,3];
Kg_mat[i,3*n[i,2]-1,3*n[i,1]-1]:=Ke_mat[i,5,2];
Kg_mat[i,3*n[i,2]-1,3*n[i,1]-2]:=Ke_mat[i,5,1];
Kg_mat[i,3*n[i,2]-2,3*n[i,1]]:=Ke_mat[i,4,3];
Kg_mat[i,3*n[i,2]-2,3*n[i,1]-1]:=Ke_mat[i,4,2];
Kg_mat[i,3*n[i,2]-2,3*n[i,1]-2]:=Ke_mat[i,4,1];
Kg_mat[i,3*n[i,1],3*n[i,2]]:=Ke_mat[i,3,6];
Kg_mat[i,3*n[i,1],3*n[i,2]-1]:=Ke_mat[i,3,5];
Kg_mat[i,3*n[i,1],3*n[i,2]-2]:=Ke_mat[i,3,4];
Kg_mat[i,3*n[i,1]-1,3*n[i,2]]:=Ke_mat[i,2,6];
Kg_mat[i,3*n[i,1]-1,3*n[i,2]-1]:=Ke_mat[i,2,5];
Kg_mat[i,3*n[i,1]-1,3*n[i,2]-2]:=Ke_mat[i,2,4];
Kg_mat[i,3*n[i,1]-2,3*n[i,2]]:=Ke_mat[i,1,6];
Kg_mat[i,3*n[i,1]-2,3*n[i,2]-1]:=Ke_mat[i,1,5];
Kg_mat[i,3*n[i,1]-2,3*n[i,2]-2]:=Ke_mat[i,1,4];
end for;
end StiffnessMatrixGlobal;
- Sum of Stiffness Matrix Global
function SumStiffnessMatrixGlobal
input Real [:,:,:] Kg_mat;
output Real [size(Kg_mat,2),size(Kg_mat,2)] KgTot_mat;
algorithm
for a in 1:size(Kg_mat,2) loop
for b in 1:size(Kg_mat,2) loop
KgTot_mat[a,b] := sum(Kg_mat [:,a,b]);
end for;
end for;
end SumStiffnessMatrixGlobal;
- Implement Boundary Condition
function BoundaryStiffnessMatrixGlobal
input Real [:,:] KgTot_met;
input Integer[:] Boundary_xyz;
input Integer[:] Boundary_xy;
input Integer[:] Boundary_xz;
input Integer[:] Boundary_yz;
input Integer[:] Boundary_x;
input Integer[:] Boundary_y;
input Integer[:] Boundary_z;
output Real [size(KgTot_met,1),size(KgTot_met,1)] KgB_met;
algorithm
for a in 1:size(KgTot_met,1) loop
for b in 1:size(KgTot_met,1) loop
KgB_met[a,b] := KgTot_met [a,b];
end for;
end for;
if Boundary_xyz[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_xyz,1) loop
for b in 0:2 loop
KgB_met[3*(Boundary_xyz[a])-b,i]:=0;
KgB_met[3*Boundary_xyz[a]-b,3*Boundary_xyz[a]-b]:=1;
end for;
end for;
end for;
end if;
if Boundary_xy[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_xy,1) loop
for b in 1:2 loop
KgB_met[3*(Boundary_xy[a])-b,i]:=0;
KgB_met[3*Boundary_xy[a]-b,3*Boundary_xy[a]-b]:=1;
end for;
end for;
end for;
end if;
if Boundary_xz[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_xz,1) loop
for b in 0:2:2 loop
KgB_met[3*(Boundary_xz[a])-b,i]:=0;
KgB_met[3*Boundary_xz[a]-b,3*Boundary_xz[a]-b]:=1;
end for;
end for;
end for;
end if;
if Boundary_yz[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_yz,1) loop
for b in 0:1 loop
KgB_met[3*(Boundary_yz[a])-b,i]:=0;
KgB_met[3*Boundary_yz[a]-b,3*Boundary_yz[a]-b]:=1;
end for;
end for;
end for;
end if;
if Boundary_x[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_x,1) loop
KgB_met[3*(Boundary_x[a])-2,i]:=0;
KgB_met[3*Boundary_x[a]-2,3*Boundary_x[a]-2]:=1;
end for;
end for;
end if;
if Boundary_y[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_y,1) loop
KgB_met[3*(Boundary_y[a])-1,i]:=0;
KgB_met[3*Boundary_y[a]-1,3*Boundary_y[a]-1]:=1;
end for;
end for;
end if;
if Boundary_z[1] <> 0 then
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_z,1) loop
KgB_met[3*Boundary_z[a],i]:=0;
KgB_met[3*Boundary_z[a],3*Boundary_z[a]]:=1;
end for;
end for;
end if;
end BoundaryStiffnessMatrixGlobal;
- Gauss-Jordan
function GaussJordan
input Real [:,:] KgB_met;
input Real [size(KgB_met,1)] load_met;
output Real [size(KgB_met,1)] U_met;
protected
Real float_error = 10e-10;
algorithm
U_met:=Modelica.Math.Matrices.solve(KgB_met,load_met);
for i in 1:size(KgB_met,1) loop
if abs(U_met[i]) <= float_error then
U_met[i] := 0;
end if;
end for;
end GaussJordan;
- Reaction Force
function ReactionForce
input Integer x;
input Real [:,:] KgTot_met;
input Real [size(KgTot_met,1)] U_met;
input Real [size(KgTot_met,1)] load_met;
output Real [x] R_met;
protected Real float_error = 10e-10;
algorithm
R_met := (KgTot_met*U_met)-load_met;
for t in 1:size(KgTot_met,1) loop
if abs(R_met[t]) <= float_error then
R_met[t] := 0;
end if;
end for;
end ReactionForce;
- Pengecekan kesetimbangan gaya (resultan gaya = 0)
function CheckForce
input Real [:] load;
input Real [size(load,1)] R;
output Real [3] F;
protected Real float_error = 10e-10;
protected
Real load_x;
Real load_y;
Real load_z;
Real R_x;
Real R_y;
Real R_z;
algorithm
load_x := sum({load[i] for i in 1:3:(size(load,1)-2)});
load_y := sum({load[i] for i in 2:3:(size(load,1)-1)});
load_z := sum({load[i] for i in 3:3:size(load,1)});
R_x := sum({R[i] for i in 1:3:(size(load,1)-2)});
R_y := sum({R[i] for i in 2:3:(size(load,1)-1)});
R_z := sum({R[i] for i in 3:3:size(load,1)});
F[1] := load_x + R_x;
F[2] := load_y + R_y;
F[3] := load_z + R_z;
for i in 1:3 loop
if abs(F[i]) <= float_error then
F[i] := 0;
end if;
end for;
end CheckForce;
Pertemuan Minggu Keenam (14 Desember 2020), Muhasabah Pribadi
pada pertemuan ini pak dai memberikan arahan kepada para mahasiswa tentang nilai pribadi masing-masing, dimana pada masa seperti ini orang -orang selalu mempentingkan nilai yang didapat deibandingkan ilmu yang dimiliki.
- Muhasabah*
saya melihat dalam diri saya selama waktu pembelajaran Kuliah Metode Numerik saya selalu mengikuti Konsep berpikir dan alur/ flowchart dalam menyelesaikan sebuah masalah, pada mata kuilah ini materi atau konsep dasar sudah saya pahami dan mengerti seperti tentang truss, konsep statika struktur dari truss dapat saya mangerti.
Namun Karena basic coding saya kurang saya belum begitu bisa untuk menerjemahkan hasil pemikiran saya tersebut dalam bentuk coding, kemudian hal-hal seperti konsep berpikir looping sudah bisa saya pahami sebgainnya namun masih dikarenakan kurangnya basic coding menyebabjan saya kurang bisa menginrtpretasikan pemikiran saya tesebut ke dalam bentuk coding.
Tugas Besar Metode Numerik
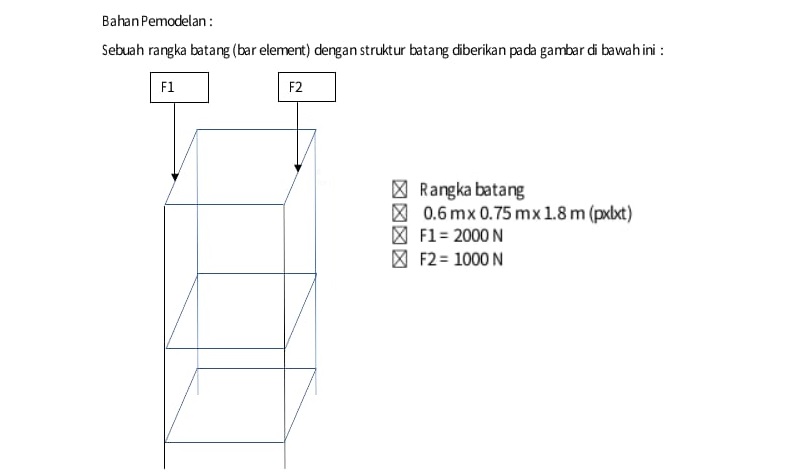
Soal
Tujuan
Melakukan optimasi rangka truss sederhana untuk mencari harga optimum dengan memvariasi dimensi dan elastisitas material
Metodologi
Menentukan Material paling optimum
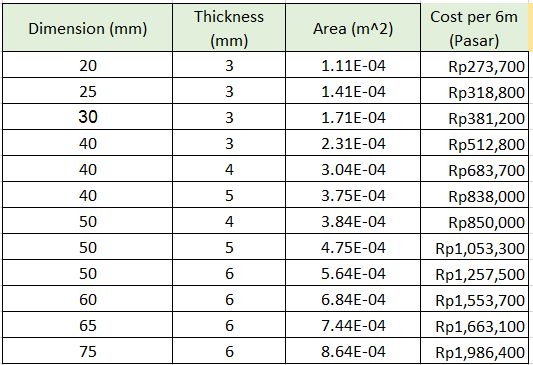
Mencari harga untuk 6 ukuran batang dengan material yang sama yaitu SS304. Mengitung nilai safety factor pada 6 ukuran batang dengan coding awal. Membuat rasio antara safety factor dengan harga total. Membuat persamaan antara rasio (safe/harga) dengan area dengan metode curve fitting. Melakukan optimasi menggunakan metode golden section. Untuk area penampang yang sama:
Mencari harga untuk 4 jenis material dengan area penampang yang sama yaitu 171 mm^2. Mengitung nilai safety factor pada 4 jenis batang dengan coding awal. Membuat rasio antara safety factor dengan harga total. Membuat persamaan antara rasio (safe/harga) dengan jenis material dengan metode curve fitting. Melakukan optimasi menggunakan metode golden section.
Penyelesaian
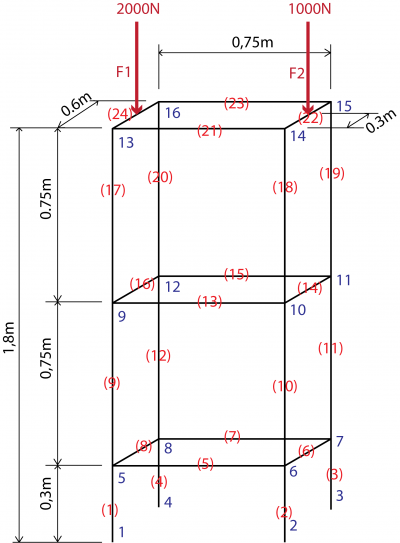
1. Mendefinisikan Problem
Untuk dapat menyelesaikan permasalahan soal, perlu didefinisikan node dan elemen pada soal
2. Membuat asumsi dan constraint pada problem
Asumsi: - Diasumsikan tidak ada bending karena bersifat truss - Safety Factor = 2
Constraint - Node 1,2,3,4 (lantai dasar) fixed - Node 13 & 16 = 1000; Node 14 & 15 = 500N
3. Metodologi
Pertama diuji coba untuk jenis material yang sama, lalu mencari area paling optimum untuk setiap jenis material
Kemudian uji coba untuk area penampang yang sama, lalu mencari material paling optimum untuk setiap area
4. Mencari Data Material
- Material SS304
- Material SS201
5. Membuat model numerik
Program Numerik ini dibuat untuk mencari nilai stress, safety factor, serta membantu dalam melakukan curve fitting
model Tugas_Besar_Samuel
//define initial variable
parameter Integer Points=size(P,1); //Number of Points
parameter Integer Trusses=size(C,1); //Number of Trusses
parameter Real Yield= (nilai yield) ; //Yield Strength Material(Pa)
parameter Real Area= (nilai area) ; //Luas Siku (Dimension=30x30x3mm)
parameter Real Elas= (nilai elastisitas) ; //Elasticity Material (Pa)
//define connection
parameter Integer C[:,2]=[ 1,5; // (1)
2,6; // (2)
3,7; // (3)
4,8; // (4)
5,6; // (5)
6,7; // (6)
7,8; // (7)
5,8; // (8)
5,9; // (9)
6,10; // (10)
7,11; // (11)
8,12; // (12)
9,10; // (13)
10,11;// (14)
11,12;// (15)
9,12; // (16)
9,13; // (17)
10,14;// (18)
11,15;// (19)
12,16;// (20)
13,14;// (21)
14,15;// (22)
15,16;// (23)
13,16];//(24)
//define coordinates (please put orderly)
parameter Real P[:,6]=[ 0 ,0 ,0,1,1,1; //node 1
0.75,0 ,0,1,1,1; //node 2
0.75,0.6,0,1,1,1; //node 3
0 ,0.6,0,1,1,1; //node 4
0 ,0 ,0.3,0,0,0; //node 5
0.75,0 ,0.3,0,0,0; //node 6
0.75,0.6,0.3,0,0,0; //node 7
0 ,0.6,0.3,0,0,0; //node 8
0 ,0 ,1.05,0,0,0; //node 9
0.75,0 ,1.05,0,0,0; //node 10
0.75,0.6,1.05,0,0,0; //node 11
0 ,0.6,1.05,0,0,0; //node 12
0 ,0 ,1.8,0,0,0; //node 13
0.75,0 ,1.8,0,0,0; //node 14
0.75,0.6,1.8,0,0,0; //node 15
0 ,0.6,1.8,0,0,0]; //node 16
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-1000,
0,0,-500,
0,0,-500,
0,0,-1000};
//solution
Real displacement[N], reaction[N];
Real check[3];
Real stress1[Trusses];
Real safety[Trusses];
Real dis[3];
Real Str[3];
protected
parameter Integer N=3*Points;
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
Real err=10e-15, ers=10e-8;
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary
for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for;
//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction
reaction:=(G_star*displacement)-F;
//Eliminating float error
for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor
for i in 1:Trusses loop
if stress1[i]>0 then
safety[i]:=Yield/stress1[i];
else
safety[i]:=0;
end if;
end for;
end Tugas_Besar_Samuel;
JAWABAN UJIAN AKHIR SEMESTER
- Jawaban 1 dan 2
- Jawaban 1 s/d 3
- Jawaban 1 s/d 6
Kemudian untuk soalno 7 jawaban dalam bentuk coding di open modelica sebagai berikut,
| Main Function
model SoalNo7_samuel
//initiation= [ elemen#, theta, A, E, L]
parameter Real [:,5] initiation= [1, 0, 2.011e-4, 1.9e11, 1; //isi sesuai data
2, 0, 2.011e-4, 1.9e11, 1;
3, 45, 2.011e-4, 1.9e11, 1;
4, 135, 2.011e-4, 1.9e11, 1];
//node = [ i, j]
parameter Integer [3,2] node = [1, 2; //isi sesuai data
2, 3;
1, 4,
2, 4,
3, 4];
//jumlah node
parameter Integer n = 4; //isi sesuai data
//titik node boundary
parameter Integer [:] Boundary = {3,4}; //isi sesuai data
//load = [ F1x, F1y, F2x,F2y,F3x,F3y,F4x,F4y]
parameter Real [2*n] load = { 0, 1135562, 0, 0, 0, 0, 0, 0}; //isi sesuai data
Real [size(inisiasi,1)] k;
Real [size(inisiasi,1),4,4] Ke;
Real [size(inisiasi,1),2*n,2*n] Kg;
Real [2*n,2*n] KgTot;
Real [2*n,2*n] KgB;
Real [2*n] U;
Real [2*n] R;
//check force
Real [2] F;
equation
k = {(initiation[i,3] * initiation[i,4] / initiation[i,5]) for i in 1:size(initiation,1)};
Ke = StiffnessMatrixElement(initiation);
Kg = StiffnessMatrixGlobal(n, node, Ke);
KgTot = SumStiffnessMatrixGlobal(Kg);
KgB = BoundaryStiffnessMatrixGlobal(KgTot, Boundary);
U = GaussJordan(KgB, load);
R = ReactionForce(KgTot, U, load);
end SoalNo7_samuel;
Kemudian di bentuk juga fungsi panggil yaitu
function MatrixElementStiffness_samuel
input Real [:,5] initiation_mat;
output Real [size(initiation_mat,1),4,4] Ke_mat;
protected
Real theta;
Real [3] StiffTrig;
Real [4,4] StiffTrans;
Real [size(initiation_mat,1)] k_vec;
Real float_error = 10e-10;
algorithm
k_vec := {(initiation_mat[i,3] * initiation_mat[i,4] / initiation_mat[i,5]) for i in 1:size(initiationi_mat,1)};
// Finding stiffness matrix of each element member
for i in 1:size(initiation_mat,1) loop
// Clearing the matrices
StiffTrig := zeros(3);
StiffTrans := zeros(4,4);
// Converting degrees to radians
theta := Modelica.SIunits.Conversions.from_deg(initiation_mat[i,2]);
// {cos^2, sin^2, sincos}
StiffTrig := {(Modelica.Math.cos(theta))^2,
(Modelica.Math.sin(theta))^2,
(Modelica.Math.sin(theta)*Modelica.Math.cos(theta))};
// Handle float error elements in StiffTrig
for t in 1:size(StiffTrig,1) loop
if abs(StiffTrig[t]) <= float_error then
StiffTrig[t] := 0;
end if;
end for;
// Construct stiffness transformation matrix
StiffTrans := [ StiffTrig[1], StiffTrig[3], -1*StiffTrig[1], -1*StiffTrig[3];
StiffTrig[3], StiffTrig[2], -1*StiffTrig[3], -1*StiffTrig[2];
-1*StiffTrig[1], -1*StiffTrig[3], StiffTrig[1], StiffTrig[3];
-1*StiffTrig[3], -1*StiffTrig[2], StiffTrig[3], StiffTrig[2]];
// Multiply in stiffness constant of element, add final stiffness matrix to Ke_mat
for m in 1:4 loop
for n in 1:4 loop
Ke_mat[i,m,n] := k_vec[i] * StiffTrans[m,n];
end for;
end for;
end for;
end MatrixElementStiffness_samuel
Kemudian di masukan ke functon matrix global stifness,
function MatrixGlobalStriffness_samuel input Integer x; input Integer [:,2] n; input Real [:,4,4] Ke_mat; output Real [size(Ke_mat,1),2*x,2*x] Kg_mat; algorithm Kg_mat := zeros(size(Ke_mat,1),2*x,2*x); for i in 1:size(Ke_mat,1) loop Kg_mat[i,2*n[i,1],2*n[i,1]]:=Ke_mat[i,2,2]; Kg_mat[i,2*n[i,1]-1,2*n[i,1]-1]:=Ke_mat[i,1,1]; Kg_mat[i,2*n[i,1],2*n[i,1]-1]:=Ke_mat[i,2,1]; Kg_mat[i,2*n[i,1]-1,2*n[i,1]]:=Ke_mat[i,1,2]; Kg_mat[i,2*n[i,2],2*n[i,2]]:=Ke_mat[i,4,4]; Kg_mat[i,2*n[i,2]-1,2*n[i,2]-1]:=Ke_mat[i,3,3]; Kg_mat[i,2*n[i,2],2*n[i,2]-1]:=Ke_mat[i,4,3]; Kg_mat[i,2*n[i,2]-1,2*n[i,2]]:=Ke_mat[i,3,4]; Kg_mat[i,2*n[i,2],2*n[i,1]]:=Ke_mat[i,4,2]; Kg_mat[i,2*n[i,2]-1,2*n[i,1]-1]:=Ke_mat[i,3,1]; Kg_mat[i,2*n[i,2],2*n[i,1]-1]:=Ke_mat[i,4,1]; Kg_mat[i,2*n[i,2]-1,2*n[i,1]]:=Ke_mat[i,3,2]; Kg_mat[i,2*n[i,1],2*n[i,2]]:=Ke_mat[i,2,4]; Kg_mat[i,2*n[i,1]-1,2*n[i,2]-1]:=Ke_mat[i,1,3]; Kg_mat[i,2*n[i,1],2*n[i,2]-1]:=Ke_mat[i,2,3]; Kg_mat[i,2*n[i,1]-1,2*n[i,2]]:=Ke_mat[i,1,4]; end for; end MatrixGlobalStiffness_samuel;
hasil matrix global ini kemudian akan di jumlahkan dengan fungsi berikut,
function MatrixGlobalStiffnessSum_samuel
input Real [:,:,:] Kg_mat;
output Real [size(Kg_mat,2),size(Kg_mat,2)] KgTot_mat;
algorithm
for a in 1:size(Kg_mat,2) loop
for b in 1:size(Kg_mat,2) loop
KgTot_mat[a,b] := sum(Kg_mat [:,a,b]);
end for;
end for;
end MatrixGlobalStiffnessSum_samuel;
setelah selesai disusun function untuk mengimput boundary condition untuk mencari defleksi,
function MatrixGlobalStiffnessBoundaryCond_samuel
input Real [:,:] KgTot_met;
input Integer[:] Boundary_met;
output Real [size(KgTot_met,1),size(KgTot_met,1)] KgB_met;
algorithm
for a in 1:size(KgTot_met,1) loop
for b in 1:size(KgTot_met,1) loop
KgB_met[a,b] := KgTot_met[a,b];
end for;
end for;
for i in 1:size(KgTot_met,1) loop
for a in 1:size(Boundary_met,1) loop
for b in 0:1 loop
KgB_met[2*(Boundary_met[a])-b,i]:=0;
KgB_met[2*Boundary_met[a]-b,2*Boundary_met[a]-b]:=1;
end for;
end for;
end for;
end MatrixGlobalStiffnessBoundaryCond_samuel;
digunakan function gauss jordan sehingga dapat dilihat sebagai berikut,
function GaussJordan_samuel
input Real [:,:] KgB_met;
input Real [size(KgB_met,1)] load_met;
output Real [size(KgB_met,1)] U_met;
protected
Real float_error = 10e-10;
algorithm
U_met:=Modelica.Math.Matrices.solve(KgB_met,load_met);
for i in 1:size(KgB_met,1) loop
if abs(U_met[i]) <= float_error then
U_met[i] := 0;
end if;
end for;
end GaussJordan_samuel;
untuk menentukan reaction force digunakan function berikut,
function ReactionForce_samuel
input Real [:,:] KgTot_met;
input Real [size(KgTot_met,1)] U_met;
input Real [size(KgTot_met,1)] load_met;
output Real [size(KgTot_met,1)] R_met;
protected Real float_error = 10e-10;
algorithm
R_met := KgTot_met*U_met-load_met;
for t in 1:size(KgTot_met,1) loop
if abs(R_met[t]) <= float_error then
R_met[t] := 0;
end if;
end for;
end ReactionForce_samuel;