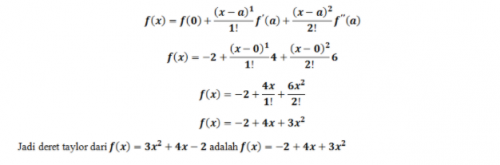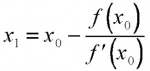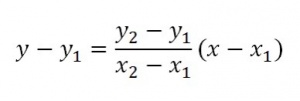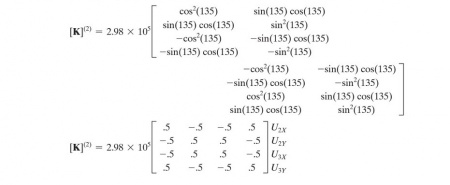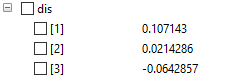Difference between revisions of "Metnum03 Luthfi Aldianta"

From ccitonlinewiki
Jump to: navigation, search
 
(28 intermediate revisions by the same user not shown)
Line 386: Line 386:
 
Kemudian menentukan jenis material apa yang digunakan, seperi stainless steel, kemudian identifikasi dimensi yang digunakan, biaya yang dikeluarkan, spesifikasi, dan perbandingan dari material lain. Kemudian dijelaskan gambaran optimasi dari contoh sistem fluida berupa pompa, dimana terdapat parameter seperti head, pump efficiency, capacity dan horsepower. Dimana apabila terdapat suatu sistem, maka berapa head dan capacity yang optimum dari suatu sistem yang digunakan. Sehingga diakhir didapatkan peak efficiency point dari sistem pompa dan pompa yang tersedia.
 
Kemudian menentukan jenis material apa yang digunakan, seperi stainless steel, kemudian identifikasi dimensi yang digunakan, biaya yang dikeluarkan, spesifikasi, dan perbandingan dari material lain. Kemudian dijelaskan gambaran optimasi dari contoh sistem fluida berupa pompa, dimana terdapat parameter seperti head, pump efficiency, capacity dan horsepower. Dimana apabila terdapat suatu sistem, maka berapa head dan capacity yang optimum dari suatu sistem yang digunakan. Sehingga diakhir didapatkan peak efficiency point dari sistem pompa dan pompa yang tersedia.
  
 +
Dengan Grafik sebagai berikut.
 +
 +
[[File:Grafik pompa.jpg|400px|center]]
  
 
Berikutnya dijelaskan praktik optimasi sistem truss oleh Bu Chandra, lebih jelas mengenai inisiasi dari optimasi. Kasus yang diberikan adalah One Dimensional Unconstrained Optimization. Optimasi sendiri adalah cara untuk mendapatkan nilai maksimum atau minimum dari suatu permasalahan. Metode yang digunakan adalah Bracket Optimization Using Golden Ratio Method. Optimasi fungsi non linear, dan objektifnya adalah mendapatkan nilai f(x) maksimum atau minimum. Kemudian dalam penerapannya dapat menggunakan persamaan sebagai berikut,
 
Berikutnya dijelaskan praktik optimasi sistem truss oleh Bu Chandra, lebih jelas mengenai inisiasi dari optimasi. Kasus yang diberikan adalah One Dimensional Unconstrained Optimization. Optimasi sendiri adalah cara untuk mendapatkan nilai maksimum atau minimum dari suatu permasalahan. Metode yang digunakan adalah Bracket Optimization Using Golden Ratio Method. Optimasi fungsi non linear, dan objektifnya adalah mendapatkan nilai f(x) maksimum atau minimum. Kemudian dalam penerapannya dapat menggunakan persamaan sebagai berikut,
Line 403: Line 406:
  
 
Exercise, f(x) = 2sinx - x^2/10, untuk menentukan f(x) maksimumnya, kemudian batasan - batasan dari persamaannya.
 
Exercise, f(x) = 2sinx - x^2/10, untuk menentukan f(x) maksimumnya, kemudian batasan - batasan dari persamaannya.
 +
 +
Berikut adalah syntax yang digunakan untuk function dan model dari exercise tersebut.
 +
 +
'''function'''
 +
 +
function function_obj
 +
import Modelica.Math;
 +
input Real x;
 +
output Real y;
 +
 +
algorithm
 +
y:= 2*Math.sin(x)-x^2/10;
 +
end function_obj;
 +
 +
'''model'''
 +
 +
model bracket_optimation
 +
parameter Integer n=8;
 +
Real x1[n];
 +
Real x2[n];
 +
Real xup;
 +
Real xlow;
 +
Real d;
 +
Real f1[n];
 +
Real f2[n];
 +
Real xopt;
 +
Real yopt;
 +
 +
algorithm
 +
xup  :=4;
 +
xlow :=0;
 +
 +
for i in (1:n) loop
 +
  d:= (5^(1/2)-1)/2*(xup-xlow);
 +
  x1[i]:= xlow+d;
 +
  x2[i]:= xup+d;
 +
  f1[i]:= function_obj(x1[i]);
 +
  f2[i]:= function_obj(x2[i]);
 +
 
 +
  if f1[i]>f2[i] then
 +
  xup:= xup;
 +
  xlow:= x2[i];
 +
  xopt:= xup;
 +
  yopt:= f1[i];
 +
 
 +
  else
 +
  xlow:= xlow;
 +
  xup:= x1[i];
 +
  xopt:= xup;
 +
 
 +
  end if;
 +
end for;
 +
 
 +
end bracket_optimation;
 +
 +
Berikut hasil dari simulasi yang dilakukan
 +
 +
[[File:Hasil simulasi luthfi.png|450px|center]]
 +
 +
[[File:Screenshot 2020-12-21 144146.png|450px|center]]
 +
 +
 +
Sekian materi penjelasan pada pertemuan hari ini, kurang lebihnya mohon maaf, Wassalamualaikum Wr. Wb.
 +
 +
 +
== Tugas Besar Metode Numerik ==
 +
 +
Pada tugas besar yang diberikan, yaitu melakukan optimisasi dari struktur truss. Berikut adalah pemodelan yang diberikan untuk dilakukan analisa optimisasi, beserta beberapa parameter yang diketahui.
 +
 +
 +
[[File:Struktur luthfi 1.jpeg|450px|center]]
 +
 +
 +
[[File:Struktur luthfi 2.jpeg|250px|]]
 +
 +
 +
'''[Metodologi]'''
 +
 +
Berdasarkan pemodelan yang diberikan, mahasiswa dapat melakukan variasi dalam parameter,
 +
 +
- Material
 +
 +
- Luas permukaan truss
 +
 +
Kemudian dapat dilakukan asumsi untuk melakukan perhitungan,
 +
 +
- Nilai berdasarkan elastisitas dari material yang digunakan
 +
 +
- Beban terdistribusi di node - node
 +
 +
- Nilai safety factor 2
 +
 +
- Batas displacement yang diasumsikan 0,001 m
 +
 +
 +
'''[Data yang Digunakan]'''
 +
 +
'''1. Elasticity Locked'''
 +
 +
[[File:Data elasticity luthfi 2.png|500px|]]
 +
 +
[[File:Data elasticity luthfi 3.png|100px|]]
 +
 +
[[File:Data elasticity luthfi 1.png|250px|]]
 +
 +
Sumber Referensi :
 +
 +
https://www.theworldmaterial.com/aisi-316-ss316-stainless-steel-properties-composition/
 +
 +
https://wijayamakmur.com/siku/
 +
 +
'''2. Area Locked'''
 +
 +
[[File:Data area luthfi 1.png|450px|]]
 +
 +
[[File:Data area luthfi 2.png|200px|]]
 +
 +
[[File:Data area luthfi 3.png|400px|]]
 +
 +
Sumber Referensi :
 +
 +
https://xinfurui.en.made-in-china.com/product/xscETKAJvYWj/China-Ss-316-Stainless-Steel-Plate-Price-Per-Kg.html
 +
 +
https://www.alibaba.com/product-detail/ms-hot-rolled-hr-carbon-ss400_60775324090.html?
 +
spm=a2700.pc_countrysearch.main07.10.23ee37eeiROfIt
 +
 +
https://www.indiamart.com/proddetail/s355-structural-steel-plate-19015855997.html
 +
 +
https://www.tokopedia.com/kingsteelid
 +
 +
 +
'''[Coding yang Digunakan]'''
 +
 +
 +
'''Syntax untuk perhitungan : displacement, reaction force, stress, dan safety factor'''
 +
 +
model Tugas_besar_3D_trusses
 +
//define initial variable
 +
  parameter Integer Points=16; //Number of Points
 +
  parameter Integer Trusses=24; //Number of Trusses
 +
  parameter Real Area= 0,000171; //Area L Profile (Dimension=0.03, Thickness=0,003)
 +
  parameter Real Elas= 193e9 ; //Elasticity for Stainless Steel 316
 +
//define connection
 +
  parameter Integer C[Trusses,2]=[1,5;
 +
                                2,6;
 +
                                3,7;
 +
                                4,8;
 +
                                5,6;  //1st floor
 +
                                6,7;  //1st floor
 +
                                7,8;  //1st floor
 +
                                5,8;  //1st floor
 +
                                5,9;
 +
                                6,10;
 +
                                7,11;
 +
                                8,12;
 +
                                9,10; //2nd floor
 +
                                10,11;//2nd floor
 +
                                11,12;//2nd floor
 +
                                9,12; //2nd floor
 +
                                9,13;
 +
                                10,14;
 +
                                11,15;
 +
                                12,16;
 +
                                13,14;//3rd floor
 +
                                14,15;//3rd floor
 +
                                15,16;//3rd floor
 +
                                13,16];//3rd floor                                                           
 +
//define coordinates (please put orderly)
 +
  parameter Real P[Points,3]=[0.3,-0.375,0;    //1
 +
                            -0.3,-0.375,0;    //2
 +
                            -0.3,0.375,0;    //3
 +
                            0.3,0.375,0;      //4
 +
                            0.3,-0.375,0.6;  //5
 +
                            -0.3,-0.375,0.6;  //6
 +
                            -0.3,0.375,0.6;  //7
 +
                            0.3,0.375,0.6;    //8
 +
                            0.3,-0.375,1.2;  //9
 +
                            -0.3,-0.375,1.2;  //10 
 +
                            -0.3,0.375,1.2;  //11
 +
                            0.3,0.375,1.2;    //12
 +
                            0.3,-0.375,1.8;  //13
 +
                            -0.3,-0.375,1.8;  //14
 +
                            -0.3,0.375,1.8;  //15
 +
                            0.3,0.375,1.8];  //16                           
 +
//define external force (please put orderly)
 +
  parameter Real F[Points*3]={0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,-500,
 +
                            0,0,-1000,
 +
                            0,0,-1000,
 +
                            0,0,-500};
 +
//define boundary
 +
  parameter Integer b[:]={1,2,3,4};
 +
//solution
 +
  Real displacement[N], reaction[N];
 +
  Real check[3];
 +
  parameter Integer N=3*Points;
 +
  Integer boundary[3*size(b,1)]=cat(1,(3*b).-2,(3*b).-1,3*b);
 +
  Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
 +
  Real err=10e-10;
 +
  Real ers=10e-4;
 +
algorithm
 +
//Creating Global Matrix
 +
G:=id;
 +
for i in 1:Trusses loop
 +
for j in 1:3 loop
 +
  q1[j]:=P[C[i,1],j];
 +
  q2[j]:=P[C[i,2],j];
 +
end for;   
 +
  //Solving Matrix
 +
  L:=Modelica.Math.Vectors.length(q2-q1);
 +
  cx:=(q2[1]-q1[1])/L;
 +
  cy:=(q2[2]-q1[2])/L;
 +
  cz:=(q2[3]-q1[3])/L;
 +
  X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
 +
                    cy*cx,cy^2,cy*cz;
 +
                    cz*cx,cz*cy,cz^2];
 +
  //Transforming to global matrix
 +
  g:=zeros(N,N);
 +
  for m,n in 1:3 loop
 +
    g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
 +
    g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
 +
    g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
 +
    g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
 +
  end for; 
 +
  G_star:=G+g;
 +
  G:=G_star;
 +
end for;
 +
//Implementing boundary
 +
  for i in boundary loop
 +
  for j in 1:N loop
 +
  G[i,j]:=id[i,j];
 +
end for;
 +
end for;
 +
//Solving displacement
 +
  displacement:=Modelica.Math.Matrices.solve(G,F);
 +
//Solving reaction
 +
  reaction:=(G_star*displacement)-F;
 +
//Eliminating float error
 +
  for i in 1:N loop
 +
  reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
 +
  displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
 +
end for;
 +
//Checking Force
 +
  check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
 +
  check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
 +
  check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
 +
  for i in 1:3 loop
 +
  check[i] := if abs(check[i])<=ers then 0 else check[i];
 +
end for;
 +
end Tugas_besar_3D_trusses;
 +
 +
'''Syntax untuk curve fitting'''
 +
 +
function curve_fitting
 +
  input Real X[:];
 +
  input Real Y[size(X,1)];
 +
  input Integer order=2;
 +
  output Real Coe[order+1];
 +
protected
 +
  Real Z[size(X,1),order+1];
 +
  Real ZTr[order+1,size(X,1)];
 +
  Real A[order+1,order+1];
 +
  Real B[order+1];
 +
  algorithm
 +
  for i in 1:size(X,1) loop
 +
  for j in 1:(order+1) loop
 +
  Z[i,j]:=X[i]^(order+1-j);
 +
end for;
 +
end for;
 +
  ZTr:=transpose(Z);
 +
  A:=ZTr*Z;
 +
  B:=ZTr*Y;
 +
  Coe:=Modelica.Math.Matrices.solve(A,B);
 +
end curve_fitting;
 +
 +
'''[Hasil Pergitungan]'''
 +
 +
'''1. Elasticity Locked'''
 +
 +
[[File:Hasil elasticity luthfi 1.png|800px|]]
 +
 +
[[File:Hasil elasticity luthfi 3.png|200px|]]
 +
 +
[[File:Locked luthfi 1.png|400px|]]
 +
 +
Berdasarkan hasil cost dan ratio dari simulasi pada material dengan parameter berupa material locked atau elasticity locked dan area di variasikan, didapatkan hasil optimasi pada material SS316 yaitu pada dimensi 50 x 50 x 5 mm. Dimana pada ratio kekakuannya paling tinggi, dan harga yang masih relevan dibanding area lain.
 +
 +
'''2. Area Locked'''
 +
 +
[[File:Hasil data luthfi 1.png|1300px|]]
 +
 +
[[File:Hasil area luthfi 1.1.png|650px|]]
 +
 +
[[File:Locked luthfi 2.png|400px|]]
 +
 +
Berdasarkan hasil dari simulasi untuk parameter area locked dan elasticity divariasikan, diketahui hasil grafik untuk optimasinya. Hasil optimasi yang didapatkan yaitu pada material SS304 untuk ukuran 30 x 30 x 3 mm.
 +
 +
Terima kasih atas perhatiannya, kurang lebihnya mohon maaf, sekian dari penulis. Wassalamualaikum Wr. Wb.
 +
 +
 +
== Ujian Akhir Semester - Metode Numerik 03 ==
 +
 +
Assalamualaikum Wr. Wb. dalam pengerjaan soal - soal yang telah diberikan oleh Pak Dai setelah dilakukan pengerjaan di kertas dilakukan pelengkapan jawaban diwiki masing - masing. Berikut lampiran jawaban dari penulis untuk soal yang diberikan.
 +
 +
[[File:Jawaban no 1 luthfi.jpg|400px|]]
 +
 +
Penjelasan No. 1
 +
 +
Pada soal no 1 tersebut, diberikan penjelasan mengenai pemodelan dari struktur yang optimum untuk diaplikasikan pada beban berupa water tank dengan variabel 300.000 galon dan dengan ketinggian 120 feet dari permukaan. Berikut adalah penjelasan mengenail prosedut untuk optimasi struktur yang digunakan.
 +
 +
• Melakukan identifikasi untuk jumlah batang yang akan digunakan, sehingga menghasilkan jumlah node – node dan juga parameter apa saja yang akan digunakan seperti luas permukaan area, modulus young, panjang batang.
 +
 +
• Berdasarkan parameter yang telah diketahui sebelumnya, dapat dilakukan perhitungan pada rumusan untuk mencari nilai dari k (kekakuan), dengan persamaan k = A x E / L
 +
 +
• Melakukan identifikasi untuk parameter dx dan dy pada setiap batang sehingga dapat diinput ke matriks lokal, untuk masing – masing batang yang digunakan.
 +
 +
• Matriks lokal yang telah didapatkan untuk setiap batang dari struktur, diinput ke matriks global. Tetapi dalam persamaan matriks yang terpisah. Sehingga tahapan selanjutnya dapat digabung dan dijumlahkan matriks lokal menjadi matriks global secara utuh.
 +
 +
• Setelah ditentukan matriks global yang digunakan, dapat dilakukan eliminasi dari boundary pada node di matriks yang tidak terpengaruh oleh gaya luar.
 +
 +
• Selanjutnya matriks global yang telah disederhanakan dilakukan perhitungan untuk mencari defleksi, dengan persamaan yaitu {U} = [T] {u}
 +
 +
• Kemudian dapat dilakukan perhitungan untuk reaction force dengan persamaan, R = K x U – F
 +
 +
Langkah optimasi sendiri dapat dilakukan sebagai berikut,
 +
 +
• Menvariasikan pada 2 tipe parameter, yaitu untuk elasticity locked dan area locked
 +
 +
• Penerapan untuk kedua tipe tersebut serupa, tetapi untuk variabel yang dirubah yaitu material pada area locked dan area pada elasticity locked
 +
 +
• Setelah didapatkan data terkait variasi dari parameter, dapat dilakukan curve fitting untuk didapatkan data yang akan di lihat hasil optimasinya
 +
 +
• Data lain yang digunakan adalah ratio, yaitu perbandingan stiffness dengan cost dari material sebagai parameter optimasi.
 +
 +
• Setelah itu dapat dilakukan analisa optimasi dari grafik yang didapatkan berdasarkan data yang dihasilkan.
 +
 +
 +
[[File:Jawaban no 2 luthfi.jpg|400px|]]
 +
 +
Penjelasan No. 2
 +
 +
Pada soal nomor 2 yang telah diberikan oleh Pak Dai, ditanyakan mengenai tujuan pemodelan numerik dari soal no 1, hokum fisika apa saja yang terkait, dan asumsi apa saja yang digunakan. Berikut beberapa penjelasan tambahan dari jawaban yang telah dibuat oleh penulis.
 +
 +
• Tujuan pemodelan numerik,
 +
 +
Pada beberapa poin yang telah dicantumkan seperti menentukan material dan area yang divariasikan sebagai contohnya, hal ini digunakan karena dalam optimasi perlu dilakukan perbandingan berdasarkan parameter material yang digunakan dan ukuran area yang digunakan terhadap gaya luar yang diberikan. Sehingga ouputnya material dan area yang digunakan lebih optimum baik dari kekuatan material atau cost yang dikeluarkan.
 +
 +
• Hukum fisika yang digunakan
 +
Hukum – hukum fisika pada pemodelan tersebut, pada umumnya melibatkan utamanya hukum hooked, karena hukum tersebut berkaitan langsung dengan gaya luar, konstanta kekakuan, dan juga displacement. Dimana ketiga variabel tersebut digunakan dalam perhitungan optimasi batang yang dipakai. Beberapa rumusan lain seperti yield strength, modulus elastis, yang juga digunakan sebagai parameter perhitungan pada optimasi.
 +
 +
• Asumsi – asumsi yang digunakan
 +
Beberapa asumsi yang digunakan untuk menyederhanakan dalam perhitungan optimasi dari batang. Berikut beberapa asumsi seperti node – node yang terdistribusi, kemudian terdapat asumsi untuk safety factor yang digunakan, dan batas displacement dari gaya luar yang dikenakan pada batang.
 +
 +
 +
[[File:Jawaban no 3- luthfi.jpg|400px|]]
 +
 +
Penjelasan No. 3
 +
 +
Pada nomor 3 yaitu mengenai penjelasan pemodelan dengan matriks lokal dan global. Dimana untuk matriks lokal didapatkan dari batang - batang yang digunakan pada struktur water tank, matriks yang digunakan berdasarkan turunan dari U1x, U1y, U2x, U2y karena pada pemodelan menggunakan dua axis yaitu x dan y. Matriks lokal yang telah didapatkan untuk dx dan dy dicari sudutnya untuk diinput ke matriks lokal.
 +
 +
Selanjutnya dalam penerapan matriks global didapatkan dari masing - masing matriks lokal kemudian dijumlahkan sehingga didapatkan matriks global keseluruhan dari batang - batang yang digunakan. Matriks global juga dapat disederhanakan dengan mengeliminasi node - node berdasarkan boundary yang digunakan untuk perhitungan selanjutnya mencari reaction force dan displacement.
 +
 +
[[File:Jawaban no 4 - 6 luthfi.jpg|400px|]]
 +
 +
Penjelasan No. 4 - 6
 +
 +
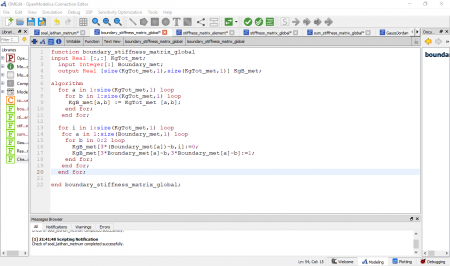
Pada soal yang diberikan untuk no.4 berdasarkan flowchart untuk pseudocode dari optimisasi tahapan awal memasuka data yang diketahui, kemudian membuat matriks elemen lokal, membuat matriks elemen global, mengaplikasikan boundary, kemudian di gauss, output displacement, kemudian reaction force dihitung, dan terakhir check force. Pada no 5, mengenai fungsi objective dan constrain yang digunakan pada node - node dari struktur. Kemudian no 6 berisi asumsi yang akan digunakan dalam menghitung pemodelan di openmodelica.
 +
 +
Berikut asumsi yang digunakan, setelah pengecekan kembali,
 +
 +
- L untuk masing - masing batang = 10 m
 +
 +
- A = 0,0001 m2 (material SS316 untuk ukuran 20 x 20 x 3 mm)
 +
 +
- E = 200 GPa
 +
 +
[[File:Jawaban no 7 luthfi.jpg|400px|]]
 +
 +
Hasil stress, displacement.
 +
 +
• displacement : didapatkan hasil displacement simulasi yaitu 0.107143, 0.0214286, dan -0.0642857
 +
 +
• stress : diketahui berdasarkan simulasi didapatkan stress pada setiap batang yaitu 214286, 425871, dan -128571
 +
 +
 +
------------------------------------------------------------------------------------------------------------------------------------------
 +
 +
 +
Berikut adalah parameter dan asumsi yang digunakan untuk soal no. 7
 +
 +
- L diasumsikan untuk setiap batang = 10 m
 +
 +
- Batang truss menggunakan material SS316 (E = 200,0E+9 dan yield = 290,0E+6)
 +
 +
- Luas area pada truss = 0,0001 m2
 +
 +
- Asumsi beban = 400 N
 +
 +
 +
model UAS_Metnum_Luthfi_Aldianta
 +
  parameter Real w[3]={30000,0,-30000};//beban dan gaya reaksi terhadap node 3 (-) dan node 1 (+)
 +
  //asumsi dari elemen yang digunakan//
 +
  parameter Real a = 0.0001;//luas penampang
 +
  parameter Real e = 200e9;// modulus elastis
 +
  parameter Real l = 10;// panjang batang
 +
  //parameter dicari
 +
  Real k;//kekakuan
 +
  Real mglobal[3,3];//matriks global
 +
  Real dis[3];//displacement
 +
  Real stress_a[3];//stress yang dialami
 +
algorithm
 +
  //persamaan nilai kekakuan//
 +
  k := a*e/l;
 +
  //persamaan matriks global//
 +
  mglobal := [k,2*k,0;
 +
          -k,2*k,-k;
 +
            0,-k,2*k];
 +
  //displacement dengan metode gauss-jordan//
 +
  dis := Modelica.Math.Matrices.solve(mglobal,w);
 +
  //mecari stress pada tiap elemen//
 +
  stress_a[1] := dis[1]*k;
 +
  stress_a[2] := dis[2]*k;
 +
  stress_a[3] := dis[3]*k;
 +
  end UAS_Metnum_Luthfi_Aldianta;
 +
 +
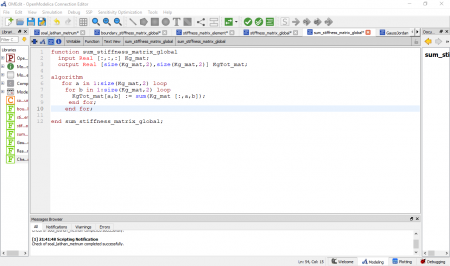
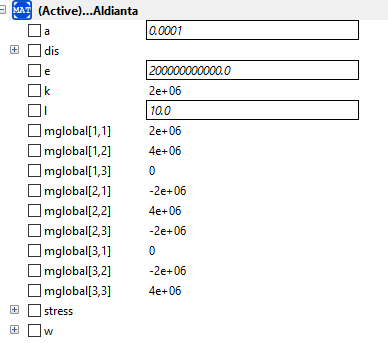
Hasil simulasi sebagai berikut.
 +
 +
[[File:Hasil simluthfi 1.png|400px|]][[File:Hasil simluthfi 2.png|300px|]][[File:Hasil simluthfi 3.png|250px|]]

Latest revision as of 01:22, 14 January 2021

بِسْمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ

السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُ

Luthfi Aldianta.Mahasiswa S1 Teknik Mesin.Fakultas Teknik Universitas Indonesia


BIODATA DIRI

Nama : Luthfi Aldianta

NPM : 1806181804

Program studi : Teknik Mesin

Tempat Tanggal Lahir : Medan 22 April 2000

Pertemuan Metode Numerik 1 : 9 November 2020

Assalamualaikum Wr. Wb. Pada pertemuan hari ini Pak Dai memberikan arahan dalam sistem pembelajaran menggunakan tools Air.eng.ui.ac.id sebagai media belajar. Kemudian Pak Dai memberikan gambaran mengenai 4 poin penting dalam berlangsungnya kegiatan belajar khususnya mata kuliah metode numerik. Pertama adalah memahami kembali konsep - konsep metode numerik yang telah dipelajari di perkuliahan sebelum UTS, dimana outuputnya dapat dituliskan kembali di page masing - masing mahasiswa dan sebagai pengingat kembali materi tersebut. Kedua yaitu dari materi yang telah dipelajari kembali, dapat melakukan pengerjaan soal - soal atau perhitungan - perhitungan untuk lebih menguasai konsep materi. Ketiga adalah mengaplikasikan metode numerik pada persoalan - persoalan yang berkaitan dengan teknik mesin sebagai outputnya. Dan terakhir yaitu, nilai tambah bagi diri sendiri, dimana sebagai tolak ukur sudah sejauh apa menguasai materi metode numerik dan peningkatan pengetahuan yang telah dikuasai.

Materi sebelum UTS Mata Kuliah Metode Numerik

Berdasarkan pemahaman yang penulis dapat dari perkuliahan sebelum UTS yaitu mengenai deret Mclaurin dan deret Taylor, deret Mclaurin sendiri adalah fungsi f(x) yang memiliki turunan f'(x), f"(x), f"'(x), dan seterusnya yang kontinu. Kemudian diekpansi kedalam deret Taylor. Deret Taylor ini yang akan menghasilkan nilai dari turunan berdasarkan deret Mclaurin. Contoh penggunaannya pada perhitungan seperti sin x, cos x, log x, dan lainnya. Berikut contoh soal dan penyelesaian deret Mclaurin dan deret Taylor.

Contoh luthfi 1.png
Contoh luthfi 2.png

Materi lain yaitu metode Newton - Rhapson, dimana metode ini untuk mencari akar suatu fungsi f(x) dengan pendekatan satu titik, dimana fungsi f(x) mempunyai turunan. Metode ini menggunakan pendekatan satu titik sebagai titik awal. Semakin dekat titik awal yang kita pilih, maka semakin cepat konvergen ke akarnya.

Metnum luthfi 3.jpg

Kemudian terdapat materi mengenai Regresi, interpolasi, dam materi lain yang berkaitan. Materi Regresi adalah metode dalam statistika untuk menentukan hubungan antar variabel satu dengan variabel lain. Fungsinya yaitu untuk mendapatkan kurva sebagai wakil data dari kumpulan data, dimana kurva dapat berbentuk garis linear. Interpolasi adalah perkiraan nilai titik data yang terletak diantara titik - titik data yang sudah diketahui dengan asumsi titik data tersebut dilewati suatu fungsi kurva tertentu. Fungsinya adalah mendapatkan nilai diantara dua titik data.

Metnum luthfi 2.jpg

Terdapat juga materi mengenai turunan numerik dan turunan parsial. Turunan numerik yaitu menurunkan suatu fungsi denga menggunakan tabel atau software yang menggunakan konsep perhitungan yang sama dengan teori. Sedangkan turunan parsial adalah perubahan nilai suatu fungsi yang memiliki 2 variabel atau lebih secara sebagian atau tidak keseluruhan. Seperti f(z) = f(x.y), ketika kita menurunkan x maka y dianggap sebagai konstanta atau bisa disebut mencari turunan parsial z terhadap x.

Metnum luthfi 1.jpg



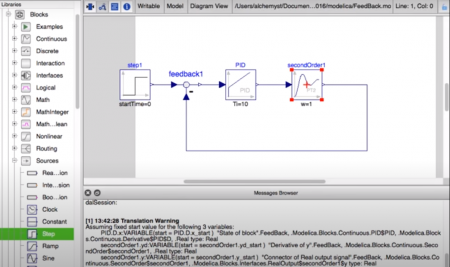
Pada tutorial yang penulis pelajari mengenai software Open Modelica, yaitu mengenai Simulasi sebuah feedback control system dengan referensi sebagai berikut.

https://youtu.be/Dw66ODbMS2A

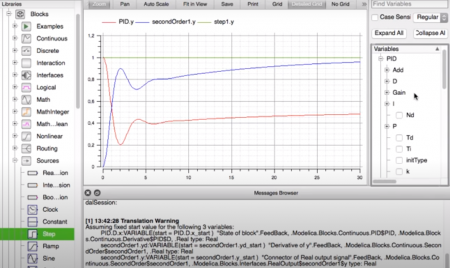
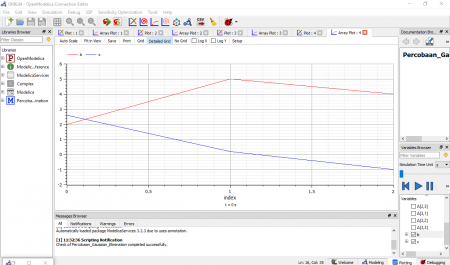
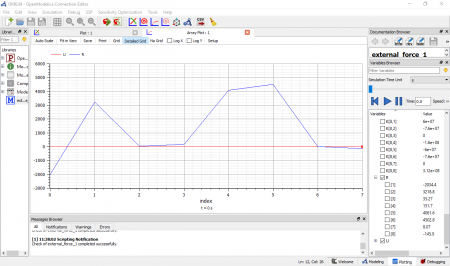
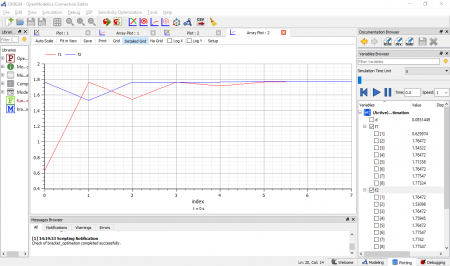
Tahap awal dalam simulasi yaitu melakukan pembuatan model untuk disimulasikan. Simulasi menggunakan sistem linear, dimana menggunakan simple second order system sebagai target untuk kontrol. Kemudian menggunakan PID control dimana pada Open modelica menggunakan tool continous. Selanjutnya memasukan blok ke area simulasi untuk PID control dan simple second order system. Berikutnya dengan menggunakan menu math digunakan tool feedback ke area simulasi, dan digunakan menu source berupa tool step, kemudian dikoneksikan untuk keseluruhan sistem. Cara dalam melakukan koneksi yaitu dengan melakukan drag untuk keselurah blok dan tools yang ada, membuat sistem menjadi closed loop. Berikut hasil dari sitem yang akan disimulasikan.

Feedback control system

Tahap selanjutnya memasukan nilai parameter. Mengatur parameter untuk blok PID, kemudian second order block. Sistem menggunakan underdamped dengan nilai damping <1. Langkah setelahnya yaitu mengecek sistem dari perhitungan dimana didapatkan 22 persamaan dan 22 variabel. Simulasi dilakukan dengan menggunakan 30 interval. Kemudian saat melakukan simulasi file harus disimpan pada area yang ada, sebagai hasil data yang didapatkan. Pada hasil output data dari grafik kita dapat mendapatkan variabel seperti U dan y untuk contohnya. Padah hasil akhir simulasi yang didapat kita juga dapat mengubah parameter untuk mendapatkan variasi yang kita tentukan dan hasil simulasi hanya tinggal dilakukan kembali. Berikut hasil simulasi yang dihasilkan.

Data hasil simulasi


Tutorial Hasil Pembelajaran Open Modelica

Berdasarkan tugas metode numerik yang diberikan oleh Pak Dai, yaitu mengenai membuat tutorial video dalam mempelajari software Open Modelica. Berikut penulis lampirkan link video hasil pembelajaran tersebut.

https://youtu.be/aqxLHM2Qd8w

Demikian hasil pembelajaran pada pertemuan pertama metode numerik dari penulis.

Wassalamualaikum Wr. Wb.

Pertemuan Metode Numerik 2 : 16 November 2020

Assalamualaikum Wr. Wb. pada kegiatan pembelajaran mata kuliah metode numerik hari ini. Pak Dai mengawali dengan mereview tugas yang diberikan pada pertemuan minggu lalu. Review tersebut mengenai software Open Modelica dan perhitungan yang masing - masing mahasiswa lakukan, dimana penulis menjelaskan mengenai sistem circuit sederhana. Terdapat dua resistor yaitu berupa 10 ohm dan 100 ohm pada parameternya. Kemudian terdapat voltage sebesar 220 v, kapasitor 0.01 F, dan Induktor 0.1 H. Hasil dari sistem tersebut didapatkan 39 persamaan dan 39 variabel. Berdasarkan hasil simulasi didapatkan plotting grafik dengan perubahan terhadap waktu, untuk masing - masing parameter yang dikerjakan.

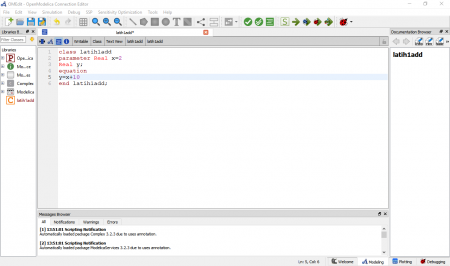
Selanjutnya pertemuan hari ini, Pak Dai memberikan materi untuk membuat program menghitung rata - rata dari data. Berikut adalah lampiran dari tutorial yang diberikan oleh Pak Dai.

Dibuat menggunakan bahasa pemrograman untuk perhitungan yang akan digunakan. Pada percobaan pertama menghitung nilai x untuk persamaan y = x+10, kemudian mendapat nilai y.

Lat 1 luthfi.png

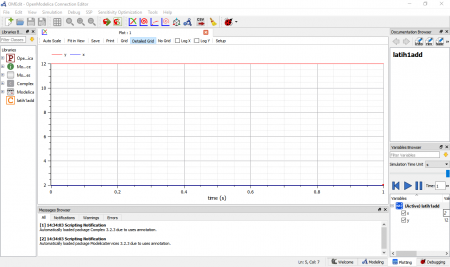
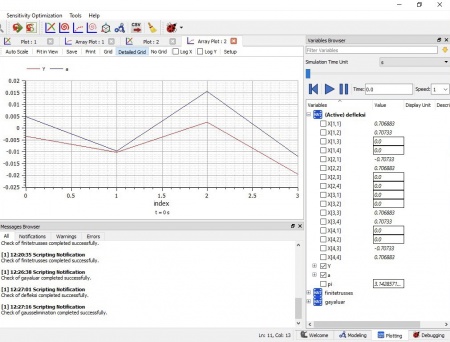
Berikut adalah hasil simulasi yang dilakukan, dimana terdapat grafik dari hasil persaman apabila x = 2 maka y = 12, begitu pun untuk contoh x yang berbeda maka nilai y akan mengikuti dengan dijumlah 10.

Lat 2 luthfi.png

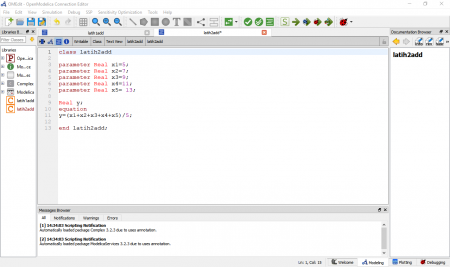
Berikutnya adalah mencoba perhitungan untuk menentukan rata - rata dari kelompok data yang ada.

Lat 3 luthfi.png

Kemudian terdapat hasil simulasi dari perhitungan untuk nilai dari masing - masing data dan hasil dari rata - rata yang didapatkan.

Lat 4 luthfi.png



Pada hari ini, Pak Dai memberikan tugas mengenai perhitungan aljabar simultan. Aljabar simultan sendiri adalah penyelesaian matematik yang melibatkan kekompleksan yang sangat rumit sehingga memerlukan cara penyelesaian yang membuatnya sederhana dengan menggunakan tools yang ada, seperti komputer dengan program visual basic, matlab, atau lainnya.


Beberapa metode yang dapat diterapkan pada aljabar simultan seperti,

1. Metode Eliminasi Gauss

2. Metode Crammer

3. Metode Gauss Seidel

4. Metode Gauss-Jordan


Berikut adalah hasil percobaan tugas penulis mengenai aljabar simultan dengan metode eliminasi Gauss. Penulis menggunakan referensi yang ada pada website openmodelica sebagai berikut.

link : https://build.openmodelica.org/Documentation/Modelica.Math.Matrices.solve.html

Dengan menggunakan persamaan, 

                                                        X1 + 2X2 + X3 = 2
                                                       3X1 +  X2 + 3x3 = 5
                                                       2X1 -  X2 +  x3 = 4

Didapatkan percobaan sebagai berikut.

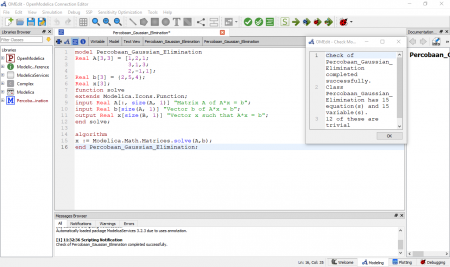
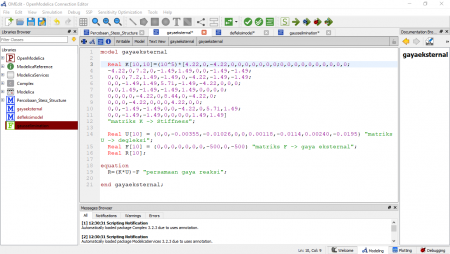
Langkah yang dilakukan adalah membuat model dengan nama yang kita tentukan, kemudian memasukan matriks sesuai persamaan. Penulis menggunakan persamaan matriks 3x3 untuk real A, kemudian menentukan hasilnya untuk real b, dan real x sebagai jumlah nilai x yang dicari. Kemudian memerintahkan perhitungan matriks, untuk A bagian dari A*x = b, dan b bagian dari A*x = b. Begitu pun dengan outputnya x, yaitu bagian dari A*x = b. Untuk extends menggunakan Modelica.Icons.Function. Selanjutnya algorithm menggunakan Modelica.Math.Matrices.solve(A,b)

Luthfi 1 simulasi.png

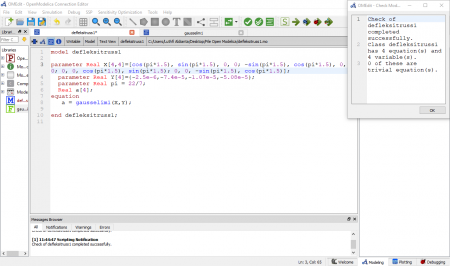
Kemudian setelah selesai menuliskan perhitungan untuk aljabar simultan yang digunakan, dilakukan check model. Terlihat setelah melakukan check model, terdapat 15 persamaan dan 15 variabel. Kemudian terdapat 12 trivial equation. Selanjutnya dilakukan running untuk model tersebut.

Luthfi 2 simulasi.png

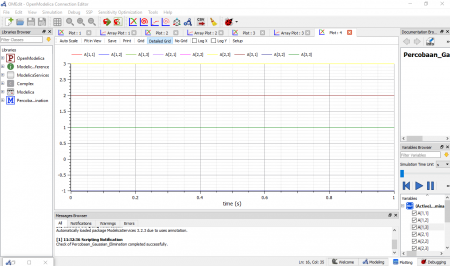
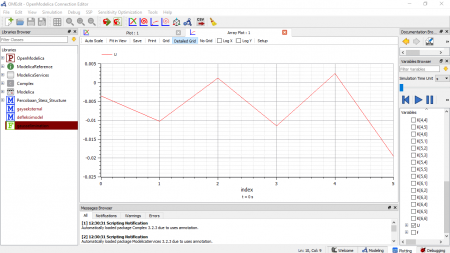
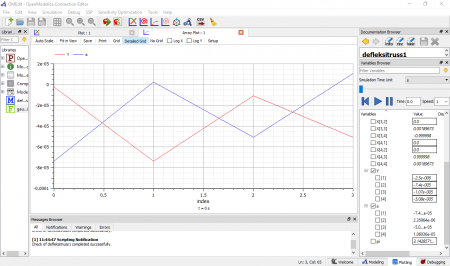
Berikut adalah hasil plotting dari simulasi untuk variabel persamaan kuadrat, untuk masing - masing baris dan kolom pada matriks.

Luthfi 3 simulasi.png

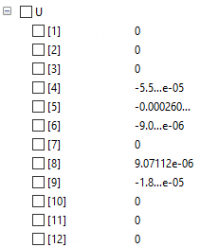
Kemudian berikut adalah hasil dari nilai x1, x2, dan x3 dari hasil simulasi gauss elimination, dengan hasil yaitu x1 = 2.6, x2 = 0.2, dan x3 = -1

Luthfi 4 simulasi.png

Sekian materi pembelajaran pada pertemuan 2 dari penulis, kurang lebihnya mohon maaf. Terima kasih, Wassalamualaikum Wr. Wb.


Pertemuan Metode Numerik 3 : 23 November 2020

Assalamualaikum Wr. Wb. Pada pertemuan hari ini, pak Dai memberikan penjelasan mengenai aplikasi metode numerik pada persoalan teknik. Terbagi ke dalam beberapa tahap yaitu

1. Masalah Teknik, pada tahap ini membuat gambaran mengenai permasalahan yang ada seperti membuat sketsa, rincian parameter yang diketahui, dan metode apa yang harus digunakan.

2. Analisa Masalah, tahap ini tentunya telah mengetahui variabel apa saja yan ada dan variabel atau persamaan apa yang akan dicari.

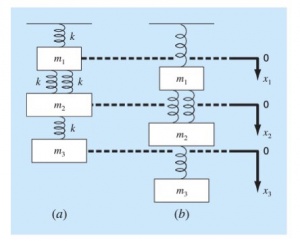
3. Model Matematis, pada tahap ini membuat model matematika dari variabel atau persamaan yang ada, pada contoh yang digunakan yaitu mengubah persamaan pada aplikasi pegas massa menjadi matriks untuk dicari hasil perhitungannya.

4. Model Numerik, menggunakan bahasa pemrograman untuk menyelesaikan matriks yang telah dibuat, contohnya yaitu menggunakan aljabar simultan pada openmodelica untuk mencari plotting hasil perhitungannya.

5. Komputer, menggunakan software untuk menyelesaikan perhitungan dapat berupa openmodelica, matlab, phyton, dan lainnya.

6. Solusi, tahap ini adalah hasil dari simulasi model yang telah dibuat, sehingga terdapat hasil perhitungan yang dicari, dapat berupa grafik apabila menggunakan openmodelica.

Luthfi 1 pegas massa.png



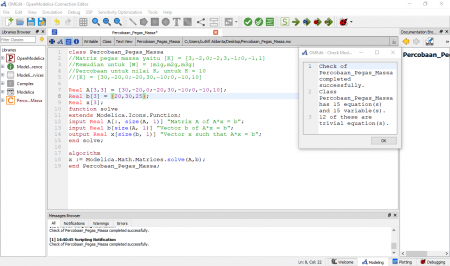
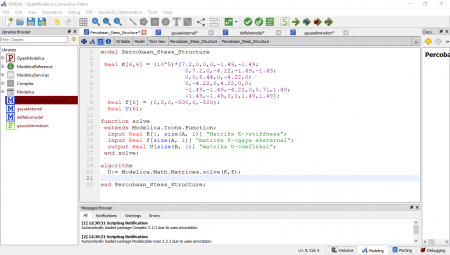
Berikutnya diberikan tugas untuk menyelesaikan permasalahan teknik pada pegas massa, dan berikut adalah hasil dari pembuatan class yang dibuat oleh penulis. Penulis menggunakan matriks 3x3 sesuai permasalahan yang ada, penulis mengunakan asumsi nilai k yaitu 10N/m untuk disubtitusi ke persamaan. Selanjutnya menggunakan salah satu metode aljabar simultan yaitu gauss elimination. Berikut lampiran yang terlihat, dimana terdapat 15 persamaan dan 15 variabe. Kemudian 12 trivial equation.

Luthfi 1 tugas.jpg

Berikut adalah soal yang diberikan mengenai pegas massa yang diberikan oleh pak Dai dengan variabel berat dan dx dari pegas massa.

Luthfi 2 pegas massa.png

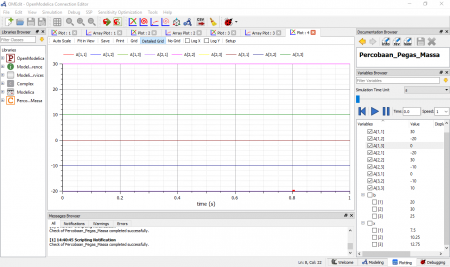
Berikut adalah hasil plotting untuk setiap variabel pada matriks 3x3

Luthfi 3 pegas massa.png

Selanjutnya yaitu hasil plotting untuk mendapatkan gaya yanh dicari untuk x1, x2, dan x3. Berikut adalah hasilnya, dimana x1 = 7.5 N, x2 = 10.25N, dan x3 = 12.75 N.

Luthfi 4 pegas massa.png

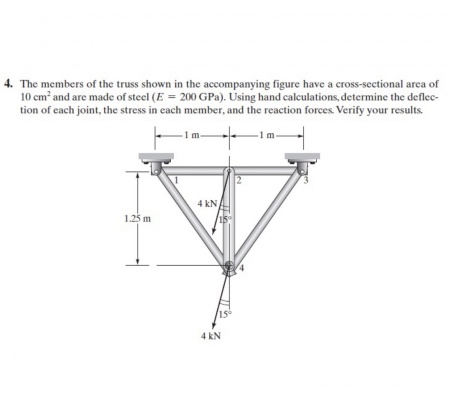
Pada hari ini Pak Dai memberikan tugas dari permasalahan teknik, mengenai statika struktur dari pin yang terdapat pada rangkaian struktur. Dengan membuat persamaan dari struktur tersebut kemudian dipindahkan ke matriks sehingga didapat perhitungan untuk menentukan stress rata - rata pada setiap pin.

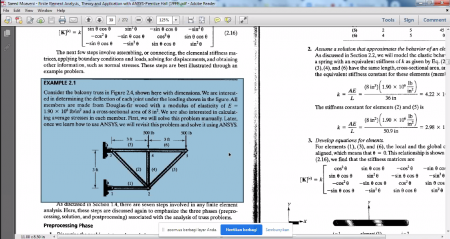
Luthfi 5 pegas massa.png

Berikut adalah pembahasan secara teori dengan perhitungannya berdasarkan soal mengenai truss yang diberikan. Pada soal tersebut menggunakan 6 persamaan pada batang yang terdapat pada struktur, dengan telah diketahui e untuk modulus elastisitas, cross section area, dan panjang batang.

Luthfi 9 tugas.jpg

Kemudian dari persamaan tersebut dibuat matrix dengan bentuk 4x4 dan disubstitusi untuk tetta atau sudut yang dimiliki oleh masing - masing batang. Untuk yang pertama adalah 0 sebagai berikut. Kemudian untuk sudut 135 derajat.

Luthfi 2 tugas.jpg

Selanjutnya dengan menggunakan global matrix untuk setiap elemen yang tersedia, dikalikan dengan nilai k yang telah didapatkan dari perhitungan persamaan K = A.E/L untuk L1 dan L2

Luthfi 3 tugas.jpg

Tahap ini adalah menggabungkan data - data elemen yang sebelumnya terdapat pada matrix untuk K1+K2+K3 dan seterusnya.

Luthfi 5 tugas.jpg

Berikutnya mengukur parameter untuk batasan kondisi dan load dari persamaan pada matrix yang digunakan.

Luthfi 6 tugas.jpg

Setelah diketahui nilai U1X, U1Y dan seterusnya dengan menggunakan persamaan, 

                                                             {R} ={K}^(G){U} - {F}
Luthfi 7 tugas.jpg

Terakhir dari data matrix yang didapatkan diperoleh reaction force dari masing - masing batang.

Luthfi 8 tugas.jpg


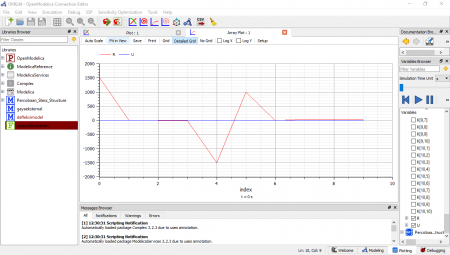
Berikut adalah hasil simulasi dari openmodelica yang penulis lakukan.

Persamaan 1 luthfi.png
Hasil simulasi luthfi 1.png
Persamaan 2 luthfi.png
Hasil simulasi luthfi 2.png
Persamaan 3 luthfi.png
Hasil simulasi luthfi 3.jpg
Persamaan 4 luthfi.png

Sekian untuk materi dari pertemuan 3 mata kuliah metode numerik, kurang lebihnya mohon maaf. Wassalamualaikum Wr. Wb.

Pertemuan Metode Numerik 4 : 30 November 2020

Pada hari ini pak Dai memulai dengan materi perbedaan statis dan dinamis, dimana statis adalah perubahan dari variabel benda yang di perhitungkan, tetapi benda diam. Kemudian dinamis adalah perubahan dari variabel benda yang diperhitungkan tetapi benda bergerak bersamaan dari perhitungan yang dilakukan. Kemudian hari ini Pak Dai menjelaskan konsep dari tugas pertemuan sebelumya mengenai truss dari suatu struktur. Pada penjelasan tersebut yaitu bagaimana menerapkan masalah teknik, analisa masalah, model matematis, model numerik, komputter, dan solusi. Dimana untuk soal sebelumnya tahapannya yaitu menentukan node - node pada struktur batang, menentukan nilai K dari perhitungan K=E.A/L, kemudian menentukan matriks lokal untuk setiap node, menentukan matriks global dari penjumlahan matriks lokal, melakukan operasi matriks untuk mendapatkan nilai defleksi dan nilai reaction force sebagai outputnya.

Pada pertemuan hari ini pak Dai juga memberikan penjelasan mengenai prosedut dalam menyelesaikan suatu permasalahan teknik dengan openmodelica, dimana tools tersebut hanya sebagai alat bantu dan mahasiswa diharuskan memahami konsep dasar terlebih dahulu untuk menyelesaikan kasus - kasus permasalahan teknik, sehingga software open modelica dapat digunakan secara efektif dan bukan untuk mempersulit pengerjaan persoalan - persoalan. Selanjutnya pada pertemuan hari ini pak Dai memberikan arahan berupa mengerjakan soal quiz yang diberikan untuk dikerjakan sesuai dengan metode yang dilakukan ketika latihan.

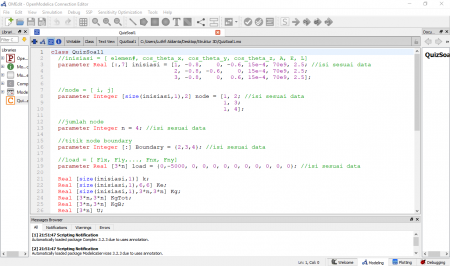
Berikut adalah soal quiz yang diberikan oleh Pak Dai.

Soal quiz luthfi 2.jpg
Soal quiz luthfi 1.jpg



Berikut adalah flow chart yang penulis kerjakan untuk di quiz yang diberikan mengenai struktur dari soal untuk 2 dimensi dan 3 dimensi yang diberikan oleh Pak Dai.

Flow chart 2.jpg

dengan parameter yang diketahui yaitu e untuk modulus elastis dan A untuk luas permukaan, kemudian dilakukan perhitungan untuk nilai K dari masing - masing batang. Selanjutnya dilakukan perhitungan dalam matrix untuk 2 dimensi atau 3 dimensi. Perhitungan matrix dilanjutkan dengan untuk mencari defleksi dan mencari gaya reaksi dari truss structure.

Flow chart 1.jpg

Pembahasan Soal Quiz No. 4

Pada tahapan mengenai pembahasan soal quiz no 1, dimana menentukan node – node berupa variable i dan j, kemudian variabel θ. Diketahui dari struktur truss tersebut memiliki lima bentuk node. Kemudian dalam menentukan nilai K terdapat parameter yang telah diketahui yaitu luas permukaan (A) = 10^-3m2 lalu modulus elastisitas (E) = 200GPa dan juga panjang batang untuk 3 variasi yaitu untuk 1m, 1,25m, dan 1,6m. Setelah menentukan nilai K, proses selanjutnya dapat dilakukan perhitungan untuk mendapatkan matriks local dari node – node yang ada, kemudian dilanjutkan dengan melakukan penjumlahan matriks lokal dengan output adalah matriks global. Berdasarkan matriks global yang didapatkan, penulis dapat melakukan operasi perhitungan dengan menggunakan openmodelica dengan mempertimbangkan boundary dari struktur batang yang ada.

Percobaantruss 1 luthfi 1.png

Pada node 1 dan 3 karena batang fix dan tidak terdapat gaya luar yang mengenainya maka dalam perhitungan untuk menentukan nilai defleksi, dilakukan hanya pada U2x, U2y, U4x, dan U4y. Kemudian setelah diketahui untuk matriks yang digunakan, memasukan variabel gaya luar berdasarkan parameter dari soal. Berikut adalah text view untuk syntax dari penjelasan sebelumnya dengan hasil check model mendapatkan 24 variabel dan 24 equation. Terdapat pula 20 trivial equation.

Percobaantruss 1 luthfi 2.png

Setelah itu penulis melakukan simulasi untuk mengetahui nilai U yang dicari dari pemodelan matriks yang digunakan, terlihat terdapat 4 nilai untuk nilau U dengan plotting sebagai berikut yang didapatkan.


Selanjutnya adalah melakukan perhitungan untuk mendapatkan nilai dari reaction force pada truss struktur. Pada syntax yang digunakan adalah dengan menggunakan matriks global keseluruhan, kemudian menggunakan parameter U yang telah diketahui sebelumnya, dan parameter F yang diketahui di soal.


Persamaannya sendiri untuk mencari reaction force yaitu R=(K*U)-F, berikut adalah hasil lampiran untuk syntax yang digunakan. Berdasarkan chech model didapatkan 88 equation dan 88 variabel. Kemudian terdapat 80 trivial equation.

Percobaantruss 1 luthfi 3.png

Hasil yang didapatkan dari simulasi untuk reaction force sebagai berikut.

Percobaantruss 1 luthfi 4.png

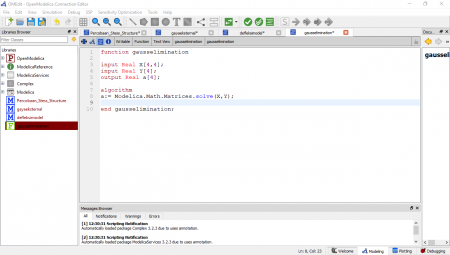
Kemudian berikut adalah syntax yang digunakan dalam mencari displacement dari salah satu node, dengan memasukan fungsi gauss elimination juga sebagai equation yang digunakan. Berikut lampiran untuk mencari displacement pada salah satu node.

Percobaantruss 1 luthfi 5.png
Percobaantruss 1 luthfi 6.png

Berikut adalah syntax function gauss elimination yang digunakan dalam equation displacement.

Persamaan 4 luthfi.png


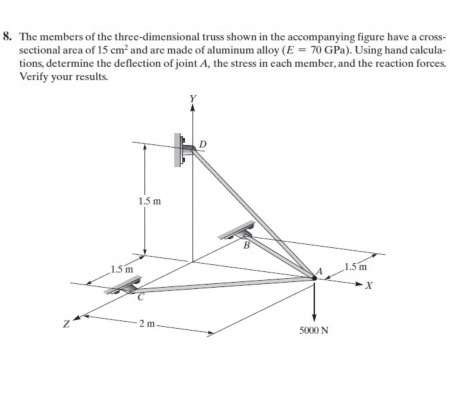
Pembahasan Soal Quiz No. 8

Berikut hasil percobaan untuk soal quiz no 8.

Q1 luthfi 1.pngQ1 luthfi 2.png

Q1 luthfi 3.pngQ1 luthfi 4.png

Q1 luthfi 5.pngQ1 luthfi 9.png

Pertemuan Metode Numerik 5 : 7 Desember 2020

Assalamualaikum Wr. Wb. Pada pertemuan hari ini Pak Dai memberikan kesempatan bagi mahasiswa yang telah mengerjakan kuis untuk menjelaskan flow chart dan juga hasil dari pengerjaan yang dilakukan. Pada kesempatan tersebut Ahmad Mohammad Fahmi yang telah berhasil menyelesaikan soal quiz yang diberikan, menjelaskan hasil pengerjaanya. Berdasarkan dari pembahasan tersebut, Ahmad Mohammad Fahmi menggunakan sistem looping untuk perhitungan dengan banyak data.

Penjelasan yang penulis pahami, dalam menyelesaikan soal quiz yang diberikan, Ahmad Mohammad membuat class untuk parameter - parameter soal yang ada, baik itu dari variabel yang diketahui seperti node, A, E, dan load. Kemudian parameter yang perlu dihitung terlebih dahulu seperti l, kemudian menggunakan loop untuk mencari nilai K dari masing - masing elemen.

Setelah menggunakan class, Ahmad Mohammad menggunakan function untuk membuat matriks lokal, matriks global, penjumlahan matriks global, boundary condition dari matriks, gauss jordan, reaction force, dan check force. Berdasarkan fungsi - fungsi tersebut, nantinya akan diinput ke dalam class sebagai langkah akhir untuk check model dan melakukan simulasi.

Pembahasan mengenai function seperti matriks lokal, dimana untuk soal no 4 menggunakan matriks berdimensi 4x4 dan untuk soal no 8 menggunakan matriks 6x6. Kemudian dari function matriks global dilakukan input dari matriks lokal berdasarkan node - node dari matriks. Kemudian function penjumlahan matriks global, sehingga didapatkan matriks secara keseluruhan, function boundary condition dimana menjadikan perhitungan matriks hanya pada boundary condition atau node tumpuan dari truss, dan beberapa function lain seperti gauss jordan untuk mendapatkan hasil U, R untuk reaction force, dan checkforce sebagai function untuk mengecek perhitungan sudah setimbang.



1. Pembahasan Hasil Belajar Coding Ahmad Mohammad Fahmi

Tahap awal Memasukan parameter apa saja yang digunakan, pada kasus yang diberikan, diketahui terdapat node - node, cross section area, modulus elastitas, dan panjang dari sumbu x, y, z. Kemudian dari elemen yang diketahui dibuat matriks untuk memasukan variabel - variabel yang ada. Disini Ahmad menggunakan kolom tak hingga (:) dan 5 baris untuk soal no 4 dan 7 baris untuk soal no 8. Kemudian menggunakan parameter integer, yang dimaksudkan untuk memasukan node - node dari elemen, untuk soal no 4 jumlah i, j pada node adalah 5. Kemudian no 8 jumlah node i, j adalah 3.

Tahap selanjutnya memasukan boundary apa saja yang digunakan, untuk soal no 4 adalah node 1 dan 3, untuk soal no 8 adalah node 2,3, dan 4. Kemudian memasukan load yang diberikan pada node, di soal no 4 terdapat 2 load yaitu -1035.28 N, -3863.70N. Selanjutnya di soal no 8 terdapat 1 load yaitu -5000N. Load tersebut dimasukan pada axis yang searah pada gaya batang. Kemudian memasukan parameter real apa saja yang digunakan untuk function dan looping nantinya. Sebagai berikut.

Real [size(inisiasi,1)] k;

Real [size(inisiasi,1),6,6] Ke;

Real [size(inisiasi,1),3*n,3*n] Kg;

Real [3*n,3*n] KgTot;

Real [3*n,3*n] KgB;

Real [3*n] U;

Real [3*n] R;

//check force

Real [3] F;

Kemudian memasukan persamaan untuk menghitung nilai K, dari persamaan tersebut digunakan loop untuk setiap batang yang digunakan. Stiffness matrix element, dimana pada function ini digunakan parameter yang telah diletakkan di class, untuk di panggil dan dibuat matrix lokal berdasarkan jenis truss yang digunakan. Untuk soal no 4 menggunakan matriks dengan stifftrig cos^theta, sin^2theta, dan sin theta * cos theta. Berikunya untuk soal no 8 (cos_x)^2, (cos_y)^2, (cos_z)^2, (cos_x*cos_y), (cos_x*cos_z), dan (cos_y*cos_z). Kemudian setelah dimasukan untuk matriks element tersebut, dilanjutkan untuk matriks global, yaitu terdapat semua nilai yang ada pada matriks lokal. Kemudian dengan function GaussJordan untuk mendapat nilai defleksi (U), function gaya reaksi (R), dan function check force. Setelah itu, function dimasukan ke dalam class yang digunakan di awal, kemudian check model dan melakukan simulasi, diketahui dari check model mendapat hasil sebagai berikut. Sebagai contoh untuk soal no 8, didapatkan variabel dan equation 858. Kemudian setelah dilakukan simulasi didapatkan untuk masing - masing nilai U dan R yang menjadi output dari soal truss tersebut untuk no 4 dan 8.

2. Tugas Berikutnya yaitu mengerjakan exercise 3.3 dari coding Ahmad Mohammad Fahmi, berikut adalah soal yang diberikan.

Soal 3.3 luthfi.jpg

Berikut adalah pembahasan soal latihan 3.3.

Dimana terlihat dari syntax yang digunakan, untuk parameter dan equation yang dimasukan. Terlihat juga terdapat variabel dan equation yang didapatkan telah setimbang.

Metnum 3.3 luthfi 1.pngMetnum 3.3 luthfi 2.png

Metnum 3.3 luthfi 3.pngMetnum 3.3 luthfi 4.pngMetnum 3.3 luthfi 5.png

Metnum 3.3 luthfi 6.pngMetnum 3.3 luthfi 7.pngMetnum 3.3 luthfi 8.png


3. Masukan atas codingan Ahmad Mohammad Fahmi

Berdasarkan hasil codingan yang dilakukan oleh Ahmad Mohammad sudah baik, dimana dalam latihan soal mengenai truss pada pertemuan sebelum - sebelumnya memasukan data pada matriks dan dilakukan perhitungan secara manual pada software openmodelica secara keseluruhan. Tetapi untuk beberapa contoh terakhir yang diberikan, Ahmad Mohammad telah menggunakan loop, sehingga data yang perhitungannya banyak dapat dilakukan secara otomatis oleh software dengan menerapkan batasan - batasan pada perhitungan, contohnya seperti batas kolom pada matriks inisiasi yang dihitung.

Kemudian selain dengan menggunakan loop, Ahmad Mohammad juga menggunakan class dan fucntion, dimana dari bentuk perhitungannya terlihat lebih rapi, dibandingkan dengan menggunakan 1 class atau 1 model dengan perhitungan functionya di satu tempat. Kemudian dari sistem class dan function yang dibuat oleh Ahmad Mohammad, juga memberikan kemudahan dalam variasi soal yang ada nantinya, contohnya seperti soal 2D atau 3D, yaitu yang perlu dirubah dari class dan function tidak perlu keseluruhan, hanya terbatas pada variabel apa saja yang diketahui. Kemudian yang berubah lagi adalah boundary condition yang terdapat pada node - node.

Selajutnya untuk hasil coding dari no 3.3 yang dikerjakan juga menerapkan sistem yang sama, dimana soal yan dibahas mengenai truss 3D, tetapi disini terdapat beberapa perubahan yang cukup signifikan pada beberapa bagian di class dan function, walaupun menerapkan cara yang sama pada pengerjaannya, terdapat beberapa bentuk boundary, parameter real yang menggunakan persamaan yang berbeda jika dibandingkan dengan soal no 8, juga dengan istilah - istilah yang digunakan baik pada parameter ataupu equation dan algorithm yang belum dijelaskan, mungkin dapat digunakan sebagai masukan kedepannya, tetapi secara keseluruhan sudah baik dan perhitungan juga benar untuk output yang dihasilkan, baik itu defleksi, reacion force, dan penjumlahan untuk gaya - gayanya.


Pertemuan Metode Numerik 6 : 14 Desember 2020

Assalamualaikum Wr. Wb.


Pada pertemuan kali ini, Pak Dai memberikan arahan bagi masing - masing mahasiswa untuk melakukan muhasabah diri mengenai materi pembelajaran mata kuliah metode numerik. Mahasiswa diharapkan menilai diri sendiri sesuai pemahaman dan konsep yang telah dipahami. Berikutnya berdasarkan muhasabah diri tersebut dan nilai yang diberikan mahasiswa masing - masing dari pemahaman belajar, Pak Dai kemudian memberikan kesempatan kepada mahasiswa untuk menerangkan beberapa materi yang dipahami. Sebagai konfirmasi untuk nilai yang diberikan pada muhasabah diri.

Kemudian pembelajaran dilanjutkan dengan pemaparan materi oleh Christo mengenai pemahaman dari alur berfikir mengenai soal - soal yang telah diberikan, kemudian di jelaskan kedalam software Openmodelica, mengenai bagaimana mengidentifikasi parameter apa saja dari soal yang diketahui, membentuk model dari soal yang diberikan, melakukan perhitungan dari model soal seperti melibatkan function apa saja yang digunakan. Selain itu, pemaparan juga dijelaskan oleh Josiah Enrico dan Ahmad Mohammad sebagai perbandingan dari alur pengerjaan soal - soal yang telah diberikan.


Sekian penjelasan pada pertemuan kali ini, kurang lebihnya mohon maaf. Wassalamualaikum Wr. Wb.

Pertemuan Metode Numerik 7 : 21 Desember 2020

Assalamualaikum Wr. Wb

Pada pertemuan hari ini dijelaskan mengenai optimasi dari truss, dimana dalam penjelasannya pada truss terdapat 3 displacement yaitu sumbu yz, tetta, dan r. Pembuatan pemodelan dari persamaannya, boundary conditionnnya, dan dalam codingannya. Penerapan dari tugas besar ini adalah untuk menekan biaya dalam desain yang digunakan. Kemudian dari optimisasi ini ditujukan untuk mencari gaya, kesetimbangan gaya : untuk mengecek perhitungan, stress, kekuatan material. Kekuatan material harus lebih kuat, dan stress dari beban yang diberikan tidak boleh melebihi 1/2 dari kekuatan material.


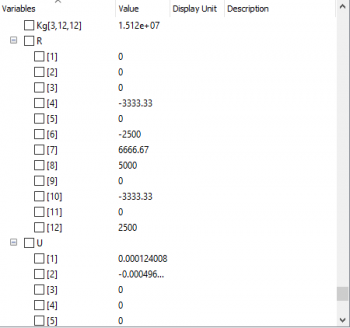
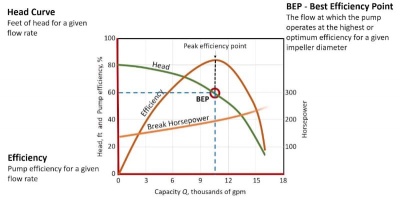
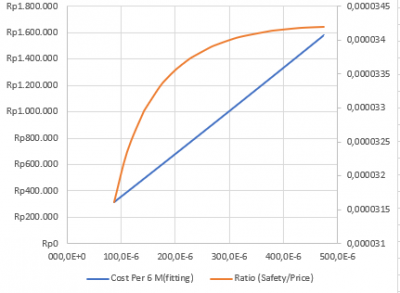
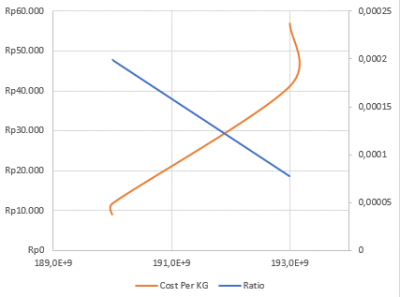
Kemudian menentukan jenis material apa yang digunakan, seperi stainless steel, kemudian identifikasi dimensi yang digunakan, biaya yang dikeluarkan, spesifikasi, dan perbandingan dari material lain. Kemudian dijelaskan gambaran optimasi dari contoh sistem fluida berupa pompa, dimana terdapat parameter seperti head, pump efficiency, capacity dan horsepower. Dimana apabila terdapat suatu sistem, maka berapa head dan capacity yang optimum dari suatu sistem yang digunakan. Sehingga diakhir didapatkan peak efficiency point dari sistem pompa dan pompa yang tersedia.

Dengan Grafik sebagai berikut.

Grafik pompa.jpg

Berikutnya dijelaskan praktik optimasi sistem truss oleh Bu Chandra, lebih jelas mengenai inisiasi dari optimasi. Kasus yang diberikan adalah One Dimensional Unconstrained Optimization. Optimasi sendiri adalah cara untuk mendapatkan nilai maksimum atau minimum dari suatu permasalahan. Metode yang digunakan adalah Bracket Optimization Using Golden Ratio Method. Optimasi fungsi non linear, dan objektifnya adalah mendapatkan nilai f(x) maksimum atau minimum. Kemudian dalam penerapannya dapat menggunakan persamaan sebagai berikut,

d = akar5 - 1/2 x (xu-xl)

x1 = x1 + d

x2 = xu - d

dengan syarat sebagai berikut.

- f(x1)>f(x2), maka domain sebelah kiri x2 dapat dieliminasi xL = x2 untuk iterasi berikutnya xu = xu lama.

- f(x2)>f(x1), domain x disebelah kanan x1 dapar dieliminasi xu = x1 untuk iterasi berikutnya xL = xL lama.


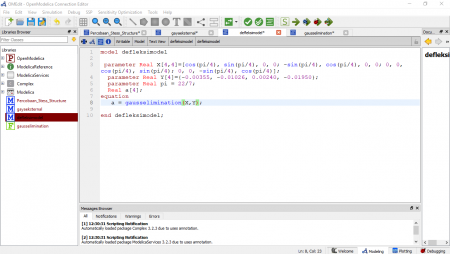
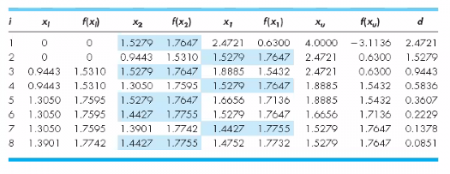
Exercise, f(x) = 2sinx - x^2/10, untuk menentukan f(x) maksimumnya, kemudian batasan - batasan dari persamaannya.

Berikut adalah syntax yang digunakan untuk function dan model dari exercise tersebut.

function 

function function_obj
import Modelica.Math;
input Real x;
output Real y;

algorithm
y:= 2*Math.sin(x)-x^2/10;
end function_obj;

model

model bracket_optimation parameter Integer n=8; Real x1[n]; Real x2[n]; Real xup; Real xlow; Real d; Real f1[n]; Real f2[n]; Real xopt; Real yopt;

algorithm xup  :=4; xlow :=0;

for i in (1:n) loop 

 d:= (5^(1/2)-1)/2*(xup-xlow);
 x1[i]:= xlow+d;
 x2[i]:= xup+d;
 f1[i]:= function_obj(x1[i]);
 f2[i]:= function_obj(x2[i]);
 
 if f1[i]>f2[i] then
 xup:= xup;
 xlow:= x2[i];
 xopt:= xup;
 yopt:= f1[i];
 
 else
 xlow:= xlow;
 xup:= x1[i];
 xopt:= xup;
 
 end if;
end for;
 
end bracket_optimation;

Berikut hasil dari simulasi yang dilakukan

Hasil simulasi luthfi.png
Screenshot 2020-12-21 144146.png


Sekian materi penjelasan pada pertemuan hari ini, kurang lebihnya mohon maaf, Wassalamualaikum Wr. Wb.


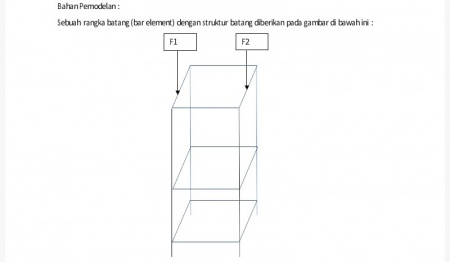
Tugas Besar Metode Numerik

Pada tugas besar yang diberikan, yaitu melakukan optimisasi dari struktur truss. Berikut adalah pemodelan yang diberikan untuk dilakukan analisa optimisasi, beserta beberapa parameter yang diketahui.


Struktur luthfi 1.jpeg


Struktur luthfi 2.jpeg


[Metodologi]

Berdasarkan pemodelan yang diberikan, mahasiswa dapat melakukan variasi dalam parameter,

- Material

- Luas permukaan truss

Kemudian dapat dilakukan asumsi untuk melakukan perhitungan,

- Nilai berdasarkan elastisitas dari material yang digunakan

- Beban terdistribusi di node - node

- Nilai safety factor 2

- Batas displacement yang diasumsikan 0,001 m


[Data yang Digunakan]

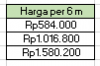
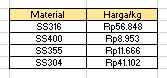
1. Elasticity Locked

Data elasticity luthfi 2.png

Data elasticity luthfi 3.png

Data elasticity luthfi 1.png

Sumber Referensi :

https://www.theworldmaterial.com/aisi-316-ss316-stainless-steel-properties-composition/

https://wijayamakmur.com/siku/

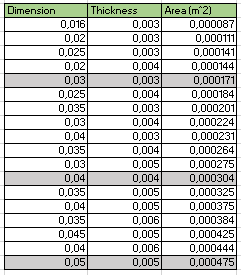
2. Area Locked

Data area luthfi 1.png

Data area luthfi 2.png

Data area luthfi 3.png

Sumber Referensi :

https://xinfurui.en.made-in-china.com/product/xscETKAJvYWj/China-Ss-316-Stainless-Steel-Plate-Price-Per-Kg.html

https://www.alibaba.com/product-detail/ms-hot-rolled-hr-carbon-ss400_60775324090.html? spm=a2700.pc_countrysearch.main07.10.23ee37eeiROfIt

https://www.indiamart.com/proddetail/s355-structural-steel-plate-19015855997.html

https://www.tokopedia.com/kingsteelid


[Coding yang Digunakan]


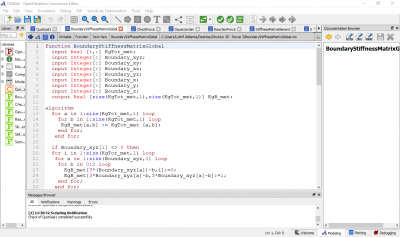
Syntax untuk perhitungan : displacement, reaction force, stress, dan safety factor 

model Tugas_besar_3D_trusses
//define initial variable
 parameter Integer Points=16; //Number of Points
 parameter Integer Trusses=24; //Number of Trusses
 parameter Real Area= 0,000171; //Area L Profile (Dimension=0.03, Thickness=0,003)
 parameter Real Elas= 193e9 ; //Elasticity for Stainless Steel 316
//define connection
 parameter Integer C[Trusses,2]=[1,5; 
                               2,6;
                               3,7;
                               4,8;
                               5,6;  //1st floor
                               6,7;  //1st floor
                               7,8;  //1st floor
                               5,8;  //1st floor
                               5,9;
                               6,10;
                               7,11;
                               8,12;
                               9,10; //2nd floor
                               10,11;//2nd floor 
                               11,12;//2nd floor
                               9,12; //2nd floor
                               9,13;
                               10,14;
                               11,15;
                               12,16;
                               13,14;//3rd floor
                               14,15;//3rd floor
                               15,16;//3rd floor
                               13,16];//3rd floor                                                             
//define coordinates (please put orderly)
 parameter Real P[Points,3]=[0.3,-0.375,0;     //1
                           -0.3,-0.375,0;    //2
                           -0.3,0.375,0;     //3
                           0.3,0.375,0;      //4
                           0.3,-0.375,0.6;   //5
                           -0.3,-0.375,0.6;  //6
                           -0.3,0.375,0.6;   //7
                           0.3,0.375,0.6;    //8
                           0.3,-0.375,1.2;   //9
                           -0.3,-0.375,1.2;  //10  
                           -0.3,0.375,1.2;   //11
                           0.3,0.375,1.2;    //12
                           0.3,-0.375,1.8;   //13
                           -0.3,-0.375,1.8;  //14
                           -0.3,0.375,1.8;   //15
                           0.3,0.375,1.8];   //16                            
//define external force (please put orderly)
 parameter Real F[Points*3]={0,0,0,
                           0,0,0, 
                           0,0,0, 
                           0,0,0, 
                           0,0,0, 
                           0,0,0, 
                           0,0,0, 
                           0,0,0, 
                           0,0,0, 
                           0,0,0, 
                           0,0,0, 
                           0,0,0, 
                           0,0,-500, 
                           0,0,-1000, 
                           0,0,-1000, 
                           0,0,-500};
//define boundary
 parameter Integer b[:]={1,2,3,4};
//solution
 Real displacement[N], reaction[N];
 Real check[3];
 parameter Integer N=3*Points;
 Integer boundary[3*size(b,1)]=cat(1,(3*b).-2,(3*b).-1,3*b);
 Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
 Real err=10e-10;
 Real ers=10e-4;
algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
for j in 1:3 loop
 q1[j]:=P[C[i,1],j];
 q2[j]:=P[C[i,2],j];
end for;     
  //Solving Matrix
  L:=Modelica.Math.Vectors.length(q2-q1);
  cx:=(q2[1]-q1[1])/L;
  cy:=(q2[2]-q1[2])/L;
  cz:=(q2[3]-q1[3])/L; 
  X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
                    cy*cx,cy^2,cy*cz;
                    cz*cx,cz*cy,cz^2];
 //Transforming to global matrix
  g:=zeros(N,N); 
  for m,n in 1:3 loop
    g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
    g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
    g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
    g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
  end for;  
 G_star:=G+g;
 G:=G_star;
end for;
//Implementing boundary
 for i in boundary loop
 for j in 1:N loop
 G[i,j]:=id[i,j];
end for;
end for;
//Solving displacement
 displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction
 reaction:=(G_star*displacement)-F;
//Eliminating float error
 for i in 1:N loop
 reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
 displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for; 
//Checking Force
 check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
 check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
 check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
 for i in 1:3 loop
 check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
end Tugas_besar_3D_trusses;

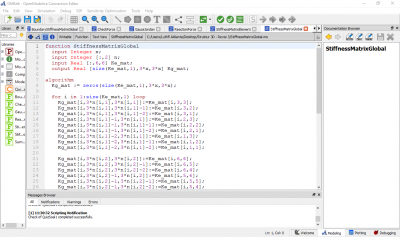
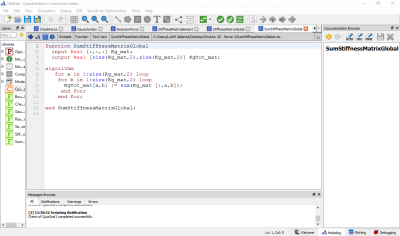
Syntax untuk curve fitting 

function curve_fitting
 input Real X[:];
 input Real Y[size(X,1)];
 input Integer order=2;
 output Real Coe[order+1];
protected
 Real Z[size(X,1),order+1];
 Real ZTr[order+1,size(X,1)];
 Real A[order+1,order+1];
 Real B[order+1];
  algorithm
 for i in 1:size(X,1) loop
 for j in 1:(order+1) loop
 Z[i,j]:=X[i]^(order+1-j);
end for;
end for;
 ZTr:=transpose(Z);
 A:=ZTr*Z;
 B:=ZTr*Y;
 Coe:=Modelica.Math.Matrices.solve(A,B);
end curve_fitting;

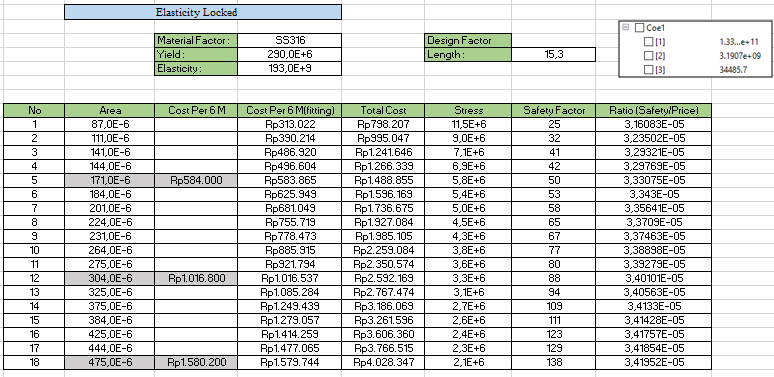
[Hasil Pergitungan]

1. Elasticity Locked

Hasil elasticity luthfi 1.png

Hasil elasticity luthfi 3.png

Locked luthfi 1.png

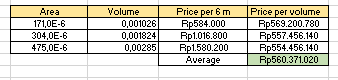
Berdasarkan hasil cost dan ratio dari simulasi pada material dengan parameter berupa material locked atau elasticity locked dan area di variasikan, didapatkan hasil optimasi pada material SS316 yaitu pada dimensi 50 x 50 x 5 mm. Dimana pada ratio kekakuannya paling tinggi, dan harga yang masih relevan dibanding area lain.

2. Area Locked

Hasil data luthfi 1.png

Hasil area luthfi 1.1.png

Locked luthfi 2.png

Berdasarkan hasil dari simulasi untuk parameter area locked dan elasticity divariasikan, diketahui hasil grafik untuk optimasinya. Hasil optimasi yang didapatkan yaitu pada material SS304 untuk ukuran 30 x 30 x 3 mm.

Terima kasih atas perhatiannya, kurang lebihnya mohon maaf, sekian dari penulis. Wassalamualaikum Wr. Wb.


Ujian Akhir Semester - Metode Numerik 03

Assalamualaikum Wr. Wb. dalam pengerjaan soal - soal yang telah diberikan oleh Pak Dai setelah dilakukan pengerjaan di kertas dilakukan pelengkapan jawaban diwiki masing - masing. Berikut lampiran jawaban dari penulis untuk soal yang diberikan.

Jawaban no 1 luthfi.jpg

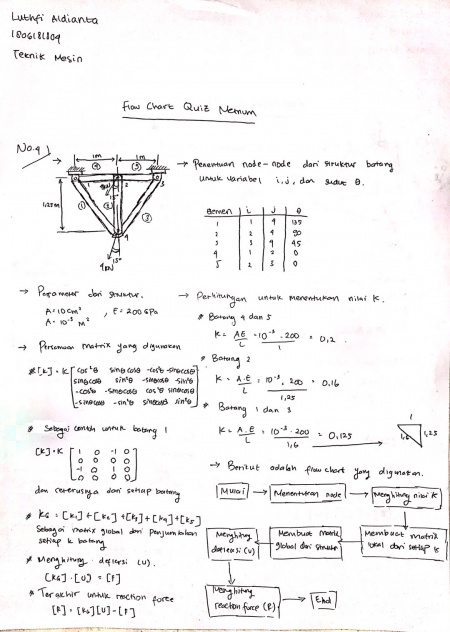
Penjelasan No. 1

Pada soal no 1 tersebut, diberikan penjelasan mengenai pemodelan dari struktur yang optimum untuk diaplikasikan pada beban berupa water tank dengan variabel 300.000 galon dan dengan ketinggian 120 feet dari permukaan. Berikut adalah penjelasan mengenail prosedut untuk optimasi struktur yang digunakan.

• Melakukan identifikasi untuk jumlah batang yang akan digunakan, sehingga menghasilkan jumlah node – node dan juga parameter apa saja yang akan digunakan seperti luas permukaan area, modulus young, panjang batang.

• Berdasarkan parameter yang telah diketahui sebelumnya, dapat dilakukan perhitungan pada rumusan untuk mencari nilai dari k (kekakuan), dengan persamaan k = A x E / L

• Melakukan identifikasi untuk parameter dx dan dy pada setiap batang sehingga dapat diinput ke matriks lokal, untuk masing – masing batang yang digunakan.

• Matriks lokal yang telah didapatkan untuk setiap batang dari struktur, diinput ke matriks global. Tetapi dalam persamaan matriks yang terpisah. Sehingga tahapan selanjutnya dapat digabung dan dijumlahkan matriks lokal menjadi matriks global secara utuh.

• Setelah ditentukan matriks global yang digunakan, dapat dilakukan eliminasi dari boundary pada node di matriks yang tidak terpengaruh oleh gaya luar.

• Selanjutnya matriks global yang telah disederhanakan dilakukan perhitungan untuk mencari defleksi, dengan persamaan yaitu {U} = [T] {u}

• Kemudian dapat dilakukan perhitungan untuk reaction force dengan persamaan, R = K x U – F

Langkah optimasi sendiri dapat dilakukan sebagai berikut,

• Menvariasikan pada 2 tipe parameter, yaitu untuk elasticity locked dan area locked

• Penerapan untuk kedua tipe tersebut serupa, tetapi untuk variabel yang dirubah yaitu material pada area locked dan area pada elasticity locked

• Setelah didapatkan data terkait variasi dari parameter, dapat dilakukan curve fitting untuk didapatkan data yang akan di lihat hasil optimasinya

• Data lain yang digunakan adalah ratio, yaitu perbandingan stiffness dengan cost dari material sebagai parameter optimasi.

• Setelah itu dapat dilakukan analisa optimasi dari grafik yang didapatkan berdasarkan data yang dihasilkan.


Jawaban no 2 luthfi.jpg

Penjelasan No. 2

Pada soal nomor 2 yang telah diberikan oleh Pak Dai, ditanyakan mengenai tujuan pemodelan numerik dari soal no 1, hokum fisika apa saja yang terkait, dan asumsi apa saja yang digunakan. Berikut beberapa penjelasan tambahan dari jawaban yang telah dibuat oleh penulis.

• Tujuan pemodelan numerik,

Pada beberapa poin yang telah dicantumkan seperti menentukan material dan area yang divariasikan sebagai contohnya, hal ini digunakan karena dalam optimasi perlu dilakukan perbandingan berdasarkan parameter material yang digunakan dan ukuran area yang digunakan terhadap gaya luar yang diberikan. Sehingga ouputnya material dan area yang digunakan lebih optimum baik dari kekuatan material atau cost yang dikeluarkan.

• Hukum fisika yang digunakan Hukum – hukum fisika pada pemodelan tersebut, pada umumnya melibatkan utamanya hukum hooked, karena hukum tersebut berkaitan langsung dengan gaya luar, konstanta kekakuan, dan juga displacement. Dimana ketiga variabel tersebut digunakan dalam perhitungan optimasi batang yang dipakai. Beberapa rumusan lain seperti yield strength, modulus elastis, yang juga digunakan sebagai parameter perhitungan pada optimasi.

• Asumsi – asumsi yang digunakan Beberapa asumsi yang digunakan untuk menyederhanakan dalam perhitungan optimasi dari batang. Berikut beberapa asumsi seperti node – node yang terdistribusi, kemudian terdapat asumsi untuk safety factor yang digunakan, dan batas displacement dari gaya luar yang dikenakan pada batang.


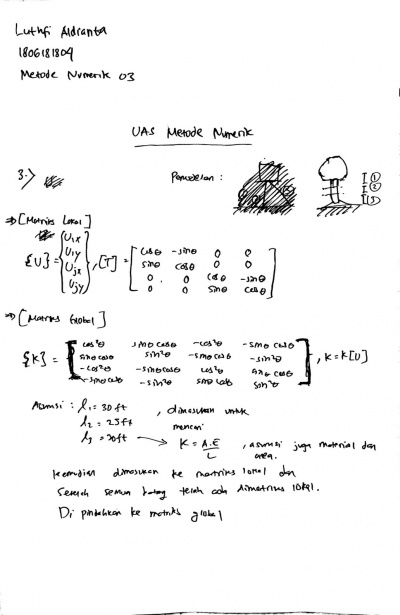
Jawaban no 3- luthfi.jpg

Penjelasan No. 3

Pada nomor 3 yaitu mengenai penjelasan pemodelan dengan matriks lokal dan global. Dimana untuk matriks lokal didapatkan dari batang - batang yang digunakan pada struktur water tank, matriks yang digunakan berdasarkan turunan dari U1x, U1y, U2x, U2y karena pada pemodelan menggunakan dua axis yaitu x dan y. Matriks lokal yang telah didapatkan untuk dx dan dy dicari sudutnya untuk diinput ke matriks lokal.

Selanjutnya dalam penerapan matriks global didapatkan dari masing - masing matriks lokal kemudian dijumlahkan sehingga didapatkan matriks global keseluruhan dari batang - batang yang digunakan. Matriks global juga dapat disederhanakan dengan mengeliminasi node - node berdasarkan boundary yang digunakan untuk perhitungan selanjutnya mencari reaction force dan displacement.

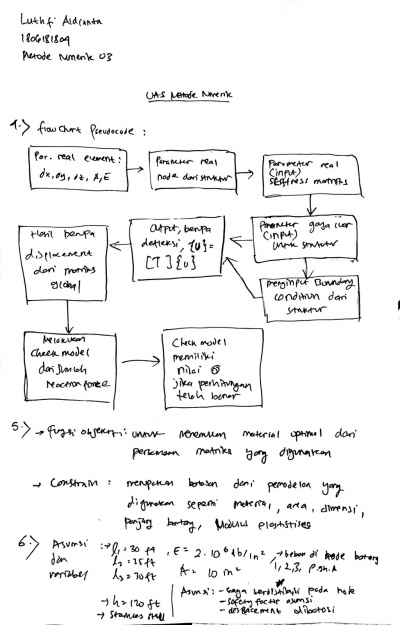
Jawaban no 4 - 6 luthfi.jpg

Penjelasan No. 4 - 6

Pada soal yang diberikan untuk no.4 berdasarkan flowchart untuk pseudocode dari optimisasi tahapan awal memasuka data yang diketahui, kemudian membuat matriks elemen lokal, membuat matriks elemen global, mengaplikasikan boundary, kemudian di gauss, output displacement, kemudian reaction force dihitung, dan terakhir check force. Pada no 5, mengenai fungsi objective dan constrain yang digunakan pada node - node dari struktur. Kemudian no 6 berisi asumsi yang akan digunakan dalam menghitung pemodelan di openmodelica.

Berikut asumsi yang digunakan, setelah pengecekan kembali,

- L untuk masing - masing batang = 10 m

- A = 0,0001 m2 (material SS316 untuk ukuran 20 x 20 x 3 mm)

- E = 200 GPa

Jawaban no 7 luthfi.jpg

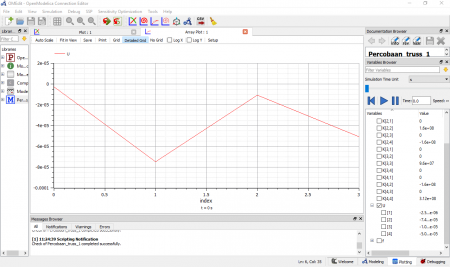
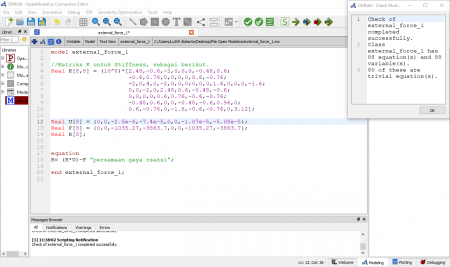
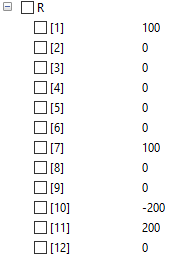
Hasil stress, displacement.

• displacement : didapatkan hasil displacement simulasi yaitu 0.107143, 0.0214286, dan -0.0642857

• stress : diketahui berdasarkan simulasi didapatkan stress pada setiap batang yaitu 214286, 425871, dan -128571



Berikut adalah parameter dan asumsi yang digunakan untuk soal no. 7

- L diasumsikan untuk setiap batang = 10 m

- Batang truss menggunakan material SS316 (E = 200,0E+9 dan yield = 290,0E+6)

- Luas area pada truss = 0,0001 m2

- Asumsi beban = 400 N 


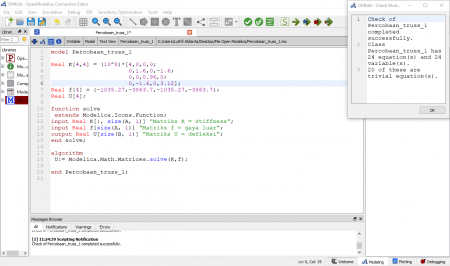
model UAS_Metnum_Luthfi_Aldianta
 parameter Real w[3]={30000,0,-30000};//beban dan gaya reaksi terhadap node 3 (-) dan node 1 (+)
 //asumsi dari elemen yang digunakan//
 parameter Real a = 0.0001;//luas penampang
 parameter Real e = 200e9;// modulus elastis
 parameter Real l = 10;// panjang batang
 //parameter dicari
 Real k;//kekakuan 
 Real mglobal[3,3];//matriks global
 Real dis[3];//displacement
 Real stress_a[3];//stress yang dialami
algorithm
 //persamaan nilai kekakuan//
 k := a*e/l;
 //persamaan matriks global//
 mglobal := [k,2*k,0;
          -k,2*k,-k;
           0,-k,2*k];
 //displacement dengan metode gauss-jordan//
 dis := Modelica.Math.Matrices.solve(mglobal,w);
 //mecari stress pada tiap elemen//
 stress_a[1] := dis[1]*k;
 stress_a[2] := dis[2]*k;
 stress_a[3] := dis[3]*k;
  end UAS_Metnum_Luthfi_Aldianta;

Hasil simulasi sebagai berikut.

Hasil simluthfi 1.pngHasil simluthfi 2.pngHasil simluthfi 3.png

Retrieved from "http://air.eng.ui.ac.id/index.php?title=Metnum03_Luthfi_Aldianta&oldid=55574"