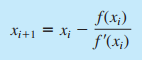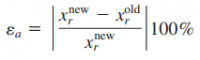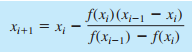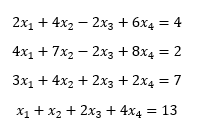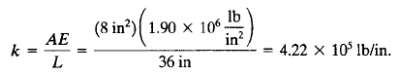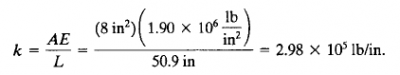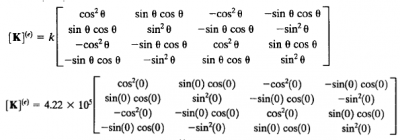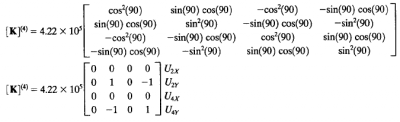Difference between revisions of "Metnum03 Ikhsanul Fikri Fakhrurrozi"

From ccitonlinewiki
Jump to: navigation, search
(→‎Pertemuan ketujuh)
(→‎JAWABAN UAS)
 
(26 intermediate revisions by the same user not shown)
Line 493: Line 493:
  
 
- Beban akan terdistribusi hanya pada point penghubung (karena bersifat truss)
 
- Beban akan terdistribusi hanya pada point penghubung (karena bersifat truss)
 +
 +
'''Material Lock'''
 +
 +
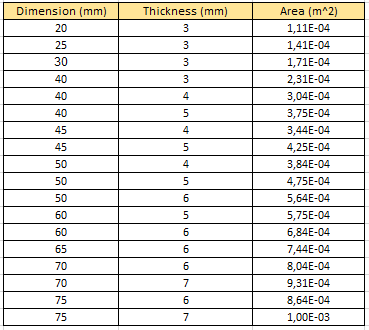
Pada bagian material lock data yang akan diambil berdasarkan pada satu material yang sama dengan variasi area. Saya menggunakan material ASTM A36 berprofil siku dengan modulus elastisitas sebesar 200 Gpa dan variasi area sebagai berikut :
 +
 +
[[File:varmat1_iff.PNG|centre|600px]]
 +
 +
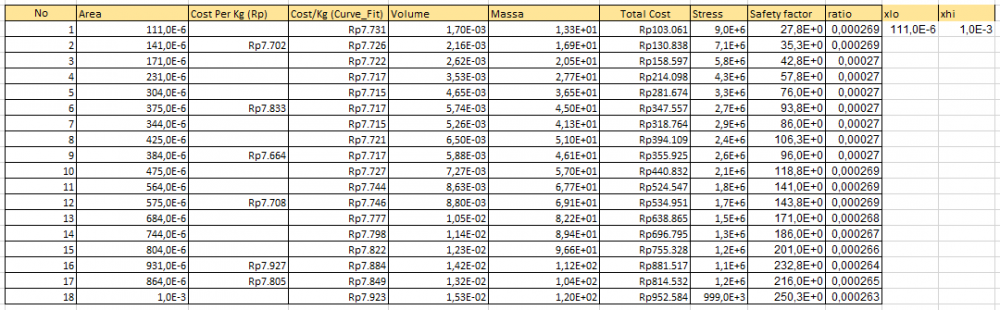
Kemudian hal berikutnya yang dilakukan adalah menentukan harga dari 6 sampel dengan variasi area tersebut kemudian dilakukan cutve fitting terhadap harga-harga sampel tersebut sehingga diketahui harga-harga per Kg dan nilai tegangan pada setiap variasi area.
 +
Sehingga didapatkan hasil curve fitting yang dituliskan pada excel sebagai berikut :
 +
 +
[[File:matbaru_iff.PNG|centre|1000px]]
 +
 +
Kemudian nilai stress didapatkan dari nilai stress maksimum yang didapatkan dari simulasi openmodelica.
 +
 +
Berikut adalah coding untuk mecari nilai stress maksimum dan curve fitting untuk menentukan harga.
 +
 +
 +
 +
 +
 +
'''Model Trusses'''
 +
 +
model Trusses_3D_Tugas_Besar_Safety
 +
 +
//define initial variable
 +
 +
parameter Integer Points=size(P,1); //Number of Points
 +
 +
parameter Integer Trusses=size(C,1);//Number of Trusses
 +
 +
parameter Real Yield=250e6; //Yield Strength (Pa) Material ASTM A36
 +
 +
parameter Real Area=3.75E-04; //Area L Profile (0.04 x 0.04 x 0.005) (m2)
 +
 +
parameter Real Elas=2e11; //Elasticity ASTM A36 (Pa)
 +
//define connection parameter
 +
Integer C[:,2]= [1,5;
 +
                2,6;
 +
                3,7;
 +
                4,8;
 +
                5,6;  //1st floor
 +
                6,7;  //1st floor
 +
                7,8;  //1st floor
 +
                5,8;  //1st floor
 +
                5,9;
 +
                6,10;
 +
                7,11;
 +
                8,12;
 +
                9,10; //2nd floor
 +
                10,11;//2nd floor
 +
                11,12;//2nd floor
 +
                9,12; //2nd floor
 +
                9,13;
 +
                10,14;
 +
                11,15;
 +
                12,16;
 +
                13,14;//3rd floor
 +
                14,15;//3rd floor
 +
                15,16;//3rd floor
 +
                13,16];//3rd floor                                                       
 +
//define coordinates (please put orderly)                 
 +
       
 +
parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1
 +
                          -0.3,-0.375,0,1,1,1;    //2
 +
                          -0.3,0.375,0,1,1,1;    //3
 +
                          0.3,0.375,0,1,1,1;      //4
 +
                         
 +
                          0.3,-0.375,0.6,0,0,0;  //5
 +
                          -0.3,-0.375,0.6,0,0,0;  //6
 +
                          -0.3,0.375,0.6,0,0,0;  //7
 +
                          0.3,0.375,0.6,0,0,0;    //8
 +
                         
 +
                          0.3,-0.375,1.2,0,0,0;  //9
 +
                          -0.3,-0.375,1.2,0,0,0;  //10 
 +
                          -0.3,0.375,1.2,0,0,0;  //11
 +
                          0.3,0.375,1.2,0,0,0;    //12
 +
                         
 +
                          0.3,-0.375,1.8,0,0,0;  //13
 +
                          -0.3,-0.375,1.8,0,0,0;  //14
 +
                          -0.3,0.375,1.8,0,0,0;  //15
 +
                          0.3,0.375,1.8,0,0,0];  //16                     
 +
//define external force (please put orderly) parameter Real F[Points*3]=
 +
                          {0,0,0,
 +
                          0,0,0,
 +
                          0,0,0,
 +
                          0,0,0,
 +
                          0,0,0,
 +
                          0,0,0,
 +
                          0,0,0,
 +
                          0,0,0,
 +
                          0,0,0,
 +
                          0,0,0,
 +
                          0,0,0,
 +
                          0,0,0,
 +
                          0,0,-500,
 +
                          0,0,-1000,
 +
                          0,0,-1000,
 +
                          0,0,-500};
 +
//solution Real displacement[N], reaction[N]; 
 +
                     
 +
Real check[3];
 +
 +
Real stress1[Trusses];
 +
 +
Real safety[Trusses];
 +
 +
Real dis[3]; Real Str[3];
 +
 +
protected parameter Integer N=3*Points;
 +
 +
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
 +
Real err=10e-10, ers=10e-6;
 +
 +
 +
algorithm //Creating Global Matrix G:=id;
 +
 +
for i in 1:Trusses loop
 +
for j in 1:3 loop
 +
  q1[j]:=P[C[i,1],j];
 +
  q2[j]:=P[C[i,2],j];
 +
end for;
 +
     
 +
  //Solving Matrix
 +
  L:=Modelica.Math.Vectors.length(q2-q1);
 +
  cx:=(q2[1]-q1[1])/L;
 +
  cy:=(q2[2]-q1[2])/L;
 +
  cz:=(q2[3]-q1[3])/L;
 +
  X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
 +
                    cy*cx,cy^2,cy*cz;
 +
                    cz*cx,cz*cy,cz^2];
 +
 +
  //Transforming to global matrix
 +
  g:=zeros(N,N);
 +
  for m,n in 1:3 loop
 +
    g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
 +
    g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
 +
    g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
 +
    g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
 +
  end for; 
 +
 +
G_star:=G+g;
 +
 +
G:=G_star;
 +
 +
end for;
 +
//Implementing boundary for x in 1:Points loop
 +
if P[x,4] <> 0 then
 +
  for a in 1:Points*3 loop
 +
    G[(x*3)-2,a]:=0;
 +
    G[(x*3)-2,(x*3)-2]:=1;
 +
  end for;
 +
end if;
 +
if P[x,5] <> 0 then
 +
  for a in 1:Points*3 loop
 +
    G[(x*3)-1,a]:=0;
 +
    G[(x*3)-1,(x*3)-1]:=1;
 +
  end for;
 +
end if;
 +
if P[x,6] <> 0 then
 +
  for a in 1:Points*3 loop
 +
    G[x*3,a]:=0;
 +
    G[x*3,x*3]:=1;
 +
  end for;
 +
end if;
 +
 +
end for;
 +
//Solving displacement displacement:=Modelica.Math.Matrices.solve(G,F);
 +
 +
//Solving reaction reaction:=(G_star*displacement)-F;
 +
 +
//Eliminating float error for i in 1:N loop
 +
 +
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
 +
 +
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
 +
 +
end for;
 +
 +
//Checking Force check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
 +
 +
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
 +
 +
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
 +
 +
for i in 1:3 loop
 +
 +
check[i] := if abs(check[i])<=ers then 0 else check[i];
 +
 +
end for;
 +
 +
//Calculating stress in each truss for i in 1:Trusses loop
 +
 +
for j in 1:3 loop
 +
 +
  q1[j]:=P[C[i,1],j];
 +
  q2[j]:=P[C[i,2],j];
 +
  dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
 +
end for;   
 +
  //Solving Matrix
 +
  L:=Modelica.Math.Vectors.length(q2-q1);
 +
  cx:=(q2[1]-q1[1])/L;
 +
  cy:=(q2[2]-q1[2])/L;
 +
  cz:=(q2[3]-q1[3])/L;
 +
  X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
 +
                cy*cx,cy^2,cy*cz;
 +
                cz*cx,cz*cy,cz^2];
 +
 
 +
  Str:=(X*dis);
 +
  stress1[i]:=Modelica.Math.Vectors.length(Str);
 +
 +
end for;
 +
 +
//Safety factor for i in 1:Trusses loop
 +
 +
if stress1[i]>0 then
 +
  safety[i]:=Yield/stress1[i];
 +
else
 +
  safety[i]:=0;
 +
end if;
 +
end for;
 +
 +
end Trusses_3D_Tugas_Besar_Safety;
 +
 +
 +
 +
 +
'''Model Curve Fitting'''
 +
 +
model CurveFitting
 +
 +
parameter Real X[6]={141e-6,375e-6,384e-6,575e-6,931e-6,864e-6};
 +
 +
parameter Real Y[6]={7702,7833,7664,7708,7927,7805};
 +
 +
Real Coe[3];
 +
 +
algorithm
 +
Coe:=Curve_Fitting(X,Y,2);
 +
 +
end CurveFitting;
 +
 
 +
 +
'''Function Curve Fitting'''
 +
 +
function Curve_Fitting
 +
 +
input Real X[:];
 +
input Real Y[size(X,1)];
 +
input Integer order=2;
 +
output Real Coe[order+1];
 +
 +
protected
 +
Real Z[size(X,1),order+1];
 +
Real ZTr[order+1,size(X,1)];
 +
Real A[order+1,order+1];
 +
Real B[order+1];
 +
 +
algorithm
 +
 +
for i in 1:size(X,1) loop
 +
for j in 1:(order+1) loop
 +
Z[i,j]:=X[i]^(order+1-j);
 +
end for;
 +
end for;
 +
ZTr:=transpose(Z);
 +
 +
A:=ZTr*Z;
 +
B:=ZTr*Y;
 +
Coe:=Modelica.Math.Matrices.solve(A,B);
 +
 +
end Curve_Fitting;
 +
 +
 +
 +
 +
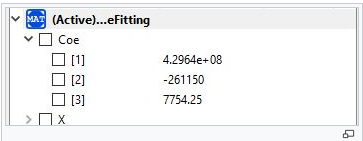
Sehingga didapatkan hasil curve fitting yang dituliskan pada excel sebagai berikut :
 +
 +
[[File:varmathasilcoe01_iff.PNG|centre|400px]]
 +
 +
 +
 +
'''Area Lock'''
 +
 +
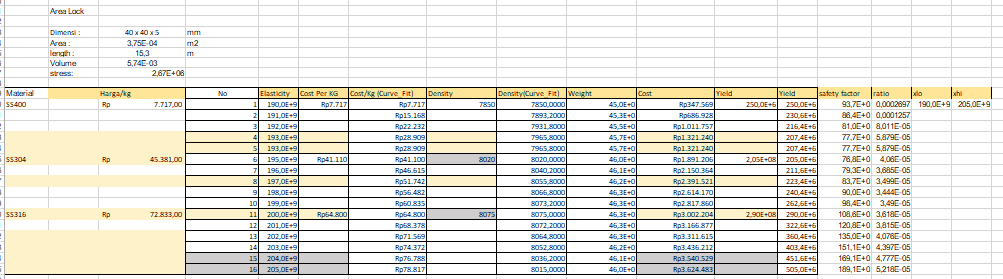
Pada bagian area lock saya mengambil satu luas area dengan spesifikasi berikut : 
 +
 +
Dimensi = 40 x 40 x 5 mm
 +
 +
Area = 3,75E-4 m2
 +
 +
L= 15.3 m
 +
 +
V = 5,74E-3
 +
 +
hal ini dilakukan secara acak untuk di lock dengan variasi 3 material yang berbeda, yaitu stainless steel 304 dan 316 dan ASTM A36. Kemudian dilakukan curve fitting pada bagian cost per kg, density dan yield sehingga didapatkan harga-harga dan nilai tegangan maksimal dari material-material tersebut.
 +
 +
Berikut adalah hasil yang diperoleh :
 +
 +
[[File:datbar02_iff.PNG|centre]]
 +
 +
Berikut adalah coding untuk curve fitting cost
 +
 +
[[File:codingcf01_iff.PNG|centre|600px]]
 +
 +
Berikut hasilnya
 +
 +
[[File: hasil01_iff.PNG|centre|400px]]
 +
 +
Berikut adalah coding untuk curve fitting density
 +
 +
[[File:codingcf02_iff.PNG|centre|600px]]
 +
 +
Berikut hasilnya
 +
 +
[[File: hasilcf02_iff.PNG|centre|400px]]
 +
 +
Berikut adalah coding untuk curve fitting yield
 +
 +
[[File:codingcf03_iff.PNG|centre|600px]]
 +
 +
Berikut hasilnya
 +
 +
[[File:hasilcf03_iff.PNG|centre|400px]]
 +
 +
 +
'''Optimasi'''
 +
 +
Nilai luas area penampang optimum untuk material SS400 adalah 0,00011 m^2 atau untuk ukuran yang ada di pasaran ukuran optimumnya adalah batang L dengan lebar 20mm dan tebal 3mm.
 +
 +
[[File:hasilopt_iff.PNG|centre|400px]]
 +
 +
 +
Material optimum yang digunakan dengan luas area 40x40x5mm adalah material dengan nilai modulus elastisitas 190018000000 N/m^2 dengan material yang mendekati adalah ss400.
 +
 +
[[File:hasilopt2_iff.PNG|centre|400px]]
 +
 +
 +
Untuk cost yang dibutuhkan dalam struktur ini adalah Rp 103.061
 +
 +
 +
Coding yang digunakan dalam optimasi ini adalah sebagai berikut :
 +
 +
 +
model opt2
 +
parameter Real xd[:]={//area atau elastisitas//};
 +
parameter Real yd[size(xd,1)]={//ratio//};
 +
parameter Real xlo=190e9;
 +
parameter Real xhi=205e9;
 +
parameter Integer N=18; // maximum iteration
 +
parameter Real es=0.0001; // maximum error
 +
Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3];
 +
Real xopt,  fx;
 +
protected
 +
Real d, xl, xu, xint, R=(5^(1/2)-1)/2;
 +
 +
algorithm
 +
xl := xlo;
 +
xu := xhi;
 +
y  := Curve_Fitting(xd,yd);
 +
 +
for i in 1:N loop
 +
d:= R*(xu-xl);
 +
x1[i]:=xl+d;
 +
x2[i]:=xu-d;
 +
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
 +
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
 +
xint:=xu-xl;
 +
 +
if f1[i]>f2[i] then
 +
  xl:=x2[i];
 +
  xopt:=x1[i];
 +
  fx:=f1[i];
 +
  else
 +
    xu:=x1[i];
 +
    xopt:=x2[i];
 +
    fx:=f2[i];
 +
end if;
 +
 +
ea[i]:=(1-R)*abs((xint)/xopt);
 +
if ea[i]<es then
 +
  break;
 +
end if;
 +
end for;
 +
 +
end opt2;
 +
 +
 +
 +
== '''JAWABAN UAS''' ==
 +
 +
 +
[[File:uas1_iff.jpeg|centre|600px]]
 +
 +
[[File:uas2_iff.jpeg|centre|600px]]
 +
 +
[[File:uas3_iff.jpeg|centre|600px]]
 +
 +
[[File:uas4_iff.jpeg|centre|600px]]
 +
 +
[[File:uas5_iff.PNG|centre|600px]]

Latest revision as of 18:19, 13 January 2021

Alhamdulillah, segala puji bagi Allah SWT dan sholawat serta salam kepada Nabi Muhammad SAW, Perkenalkan nama saya Fikri, informasi singkat saya dapat dilihat sebagai berikut :

FOTO 100 kb.jpeg

Nama : Ikhsanul Fikri Fakhrurrozi

Email : ifikrifakhrurrozi97@gmail.com








Pertemuan Pasca UTS

Pertemuan Pertama

Hari, Tanggal : Senin 9 November 2020 Oleh : Dr. Ahmad Indra


Pada pertemuan pertama Pak Dai memberikan PR, sebagai berikut :

1. apa saja yang sudah dipelajari di metode numerik?

2. Buatlah video tentang aplikasi Open Modelica.


Metode bisection

Metode bisection merupakan salah satu metode incremental search yang mana interval dari dua titik x dibagi dua sehingga mendapatkan nilai x lagi. Berikut adalah langkah-langkah metode bisection :

• Lakukan tembakan pada dua titik terendah (xi) dan titik tertinggi (xu). • Kemudian carilah xr dengan menjumlahkan antara xi dan xu kemudian hasil dari penjumlahan tersebut dibagi dua. • Lakukan evaluasi sebagai berikut :

Jika f(xl) f(xr) < 0, akar persamaan terletak di sub interval terendah. Jadi, atur xu = xr kemudian kembali ke langkah 2.

Jika f(xl) f(xr) > 0, akar persamaan terletak di sub interval tertinggi. Jadi, atur xi = xr kemudian kembali ke langkah 2.

Jika f(xl) f(xr) = 0, akar persamaan sama dengan xr. Sehingga hentikan perhitungan.

Metode Newton-Raphson

Metode newton-raphson dapat diwakili dengan formula berikut :

NR formula.PNG

Kemudian aplikasi dari metode Newton-Raphson adalah sebagai berikut :


NR ex.PNG


Perhitungan nilai persentase error antara nilai akhir dan nilai awal adalah selisih antara nilai awal dan nilai akhir dibagi dengan nilai akhir kemudian hasilnya dikalikan 100 untuk mendapatkan persentase dari nilai errornya.

Error formula.PNG

Metode Sekan

Metode sekan dapat diwakili dengan formula berikut :

Sekann formula.PNG

Aplikasinya dapat dilihat pada contoh soal berikut :


Sekan formula.PNG


Kemudian untuk aplikasi penggunaan openmodelica saya berikan penjelasannya dalam bentuk video dengan link berikut ini :

Aplikasi Least Square Fit Regression pada Openmodelica


Pertemuan Kedua

Hari, Tanggal : Senin 16 November 2020 Oleh : Dr. Ahmad Indra


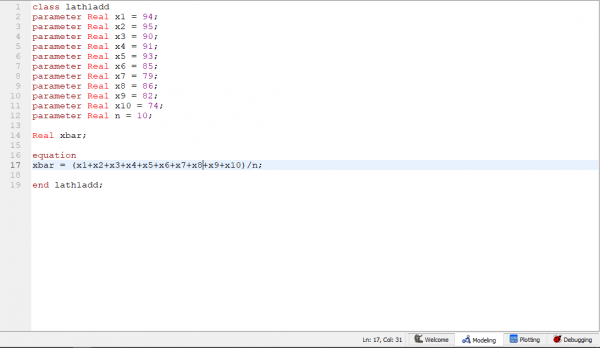
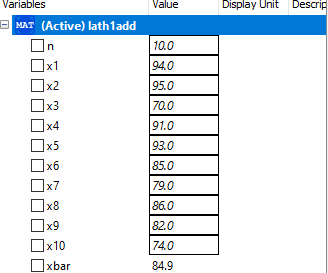
Pada pertemuan hari ini pak Dai mengevaluasi hasil belaja mahasiswa terkait dengan penggunaan aplikasi openmodelica. Kemudian mahasiswa diminta untuk membuat coding sederhana terkait nilai rata-rata 10 sample. Berikut saya lampirkan hasil coding dan simulasinya.


coding


hasil


PR Aljabar Simultan dengan Openmodelica

Kemudian pada hari ini juga pak Dai memberikan PR kepada mahasiswa berupa aplikasi penyelesaian problem aljabar simultan baik itu menggunakan metode gauss elimination, gauss-seidell, dll. Kemudian saya menggunakan persamaan berikut ini dalam menyelesaikan problem aljabar simultan menggunakan gauss elimination :


persamaan aljabar


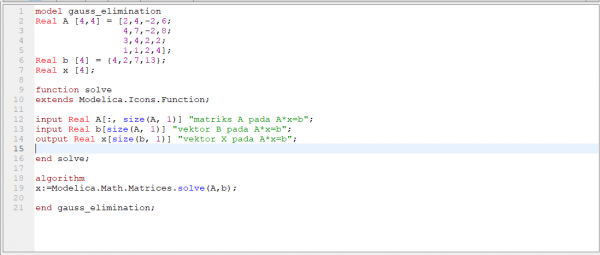
kemudian saya menyelesaikan persamaan aljabar tersebut dengan menggunakan metode gauss elimination di software openmodelica. berikut adalah hasil codingnya :


coding


Pada coding ini saya menggunakan fasilitas library pada openmodelica yaitu "Modelica.Math.Matrices.solve(A,b)" untuk menyelesaikan problem aljabar tersebut. Kemudian hasil dari coding tersebut adalah sebagai berikut :


persamaan aljabar


Hasil dari gauss elimination tersebut adalah x1 = -41, x2 = 26, x3 = 12, x4 = 1.


Pertemuan Ketiga

Hari, Tanggal : Senin 23 November 2020 Oleh : Dr. Ahmad Indra


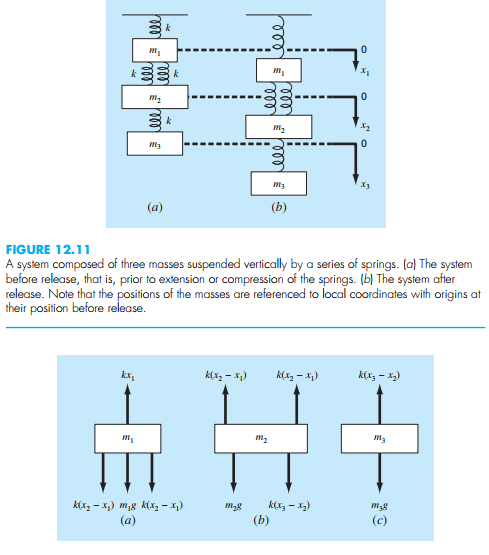
Pada hari ini pak Dai membahas tentang respon dan displacement dari permasalahan berupa rangkaian pegas, kemudian dilakukan pembuktian terhadap perhitungan tersebut.


Pegas iff.PNG


1. massa 1 


  2k(x2-x1)+(m1*g)-(k*x1) = m1*(d^2x1/dt^2) ---> karena tidak ada percepatan searah sumbu x maka d^2x1/dt^2 = 0,

  Sehingga 3kx1-3kx2 = m1*g.


2. massa 2 


  2(m2*g+[k(x3-x2)]-2k(x2-x1) = 0

  3kx2-2kx1-kx3 = m2*g.


3. massa 3 


  m3*g-k(x3-x2) = 0

  kx3-kx2 = m3*g.



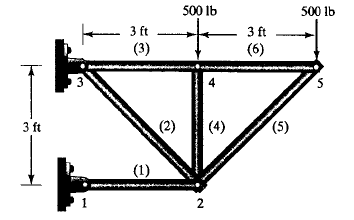
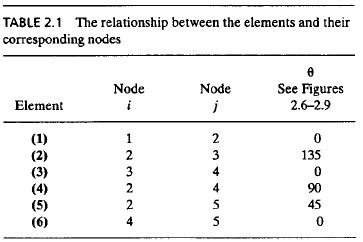
PR Defleksi dan Gaya Reaksi

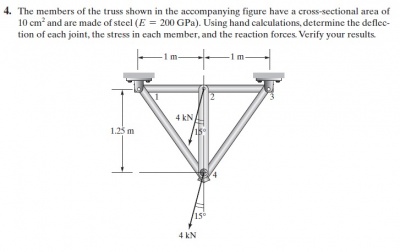
Pak Dai memberikan PR terkait dengan pemahaman materi dan aplikasi pada openmodelica. Berikut adalah soal yang diberi diberikan oleh pak Dai dan penyelesaiannya secara manual.


Def iff.PNG


Dari gambar diatas akan dicari defleksi dan gaya reaksi di tiap elemennya. Berikut adalah langkah-langkah penyelesaiannya,


1. Menentukan node i dan j (karena 2D) pada setiap elemen


Node iff.PNG


2. Tentukan nilai konstanta kekakuan/stiffness constant dari elemen 

  - Elemen 1,3,4,6
Elemen1 iff.PNG


  - Elemen 2,5


Elemen2 iff.PNG


3. Membuat persamaan elemen-elemen 

  -Elemen 1,3,6
   Karena orientasi elemen 1,3,6 searah dengan sumbu X global, maka koordinat local sejajar dengan koordinat global
   Sehingga persamaan matrix umum untuk kekakuan batangnya adalah


Mat1 iff.PNG


   [K] adalah matrix untuk kekakuan k, dan (e) adalah elemen yang akan dianalisa

   Masukkan nilai K pada elemen 1,3,6


Mat136 iff.PNG


    Kemudian matriks globalnya adalah,


Kg136 iff.PNG


  - Elemen 4


Elemen4 iff.PNG


    Lalu matriks globalnya adalah


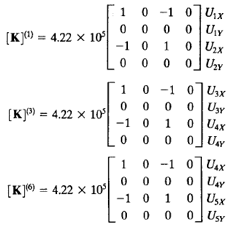
Elemen4g iff.PNG


   - Elemen 2,5


Elemen25 iff.PNG


     Lalu matriks globalnya adalah


Elemen25next iff.PNG


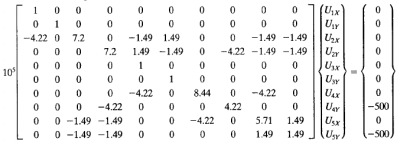
4. Kemudian gabungkan matriks-matriks dari elemen-elemen yang ada sehingga didapatkan,


Kg24 iff.PNG


5. Kemudian terapkan kondisi batas yang ada pada node 1 dan 3 sehingga diperoleh U1x = 0, U1y = 0, U3x = 0, U3y = 0. Lalu terapkan pembebanan yang ada pada node 4 dan 5 sebesar -500lb pada F4y dan F5y.


Dengan menerapkan Hukum Hooke F= k.x, maka dalam persamaan matrix menjadi [F]=[K(G)].[U¬(e)], sehingga didapatkan:


Hookem iff.PNG


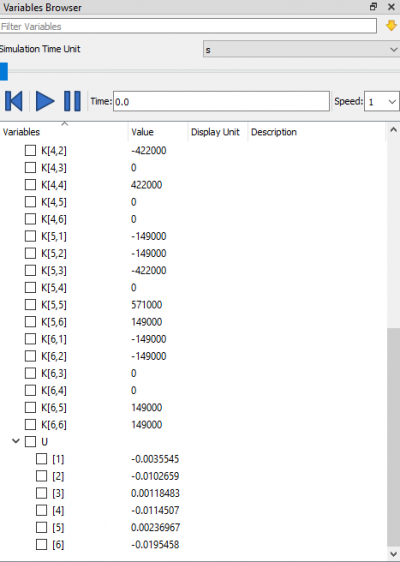
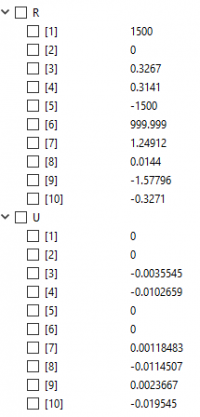
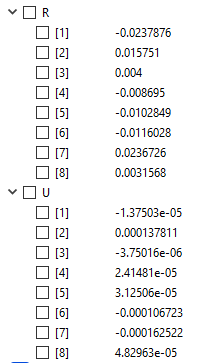
karena U1x, U1y, U3x dan U3y = 0 maka matriksnya dapat disederhanakan dari 10 x 10 menjadi 6 x 6 dengan eliminasi gauss. Kemudian saya melakukan perhitungan di openmodelica sehingga hasilnya sama dengan yang ada di buku.


Mat6.PNG


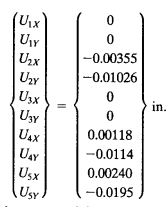
6. Berikut solusi yang saya dapatkan dibuku dan openmodelica.


Mat6book iff.PNG


Mat6ome.PNG


7. Mencari nilai Gaya Reaksi 

 Dengan menerapkan Matriks [K], {U} dan {F}, maka


R iff.PNG


Kemudian saya mencari penyelesaiannya di openmodelica sehingga didapatkan


Solusiakhirn iff.PNG


Pertemuan Keempat

Hari, Tanggal : Senin 30 November 2020 Oleh : Dr. Ahmad Indra

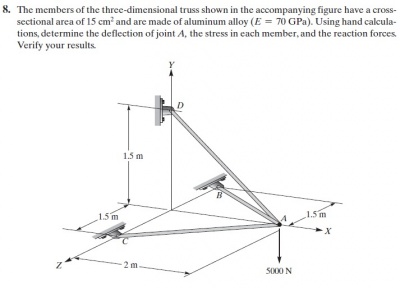
QUIZ Defleksi dan Gaya Reaksi

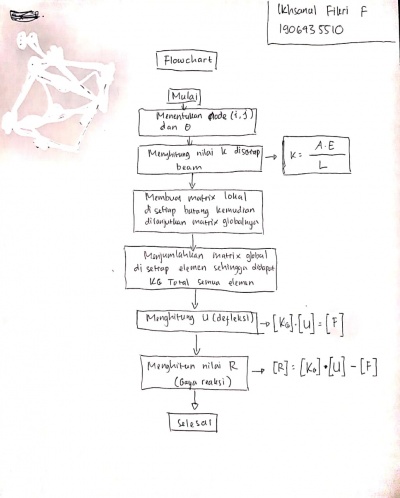
Pada hari ini pak Dai memberikan quiz sebagai berikut,


Soal1 iff.JPEG


Soal2 iff.JPEG


Pada hari ini pak Dai meminta kami untuk memberikan flowchart dalam menyelesaikan soal-soal diatas. Berikut adalah flowchartnya,


Fcn iff.JPEG


PR Defleksi dan Gaya Reaksi II

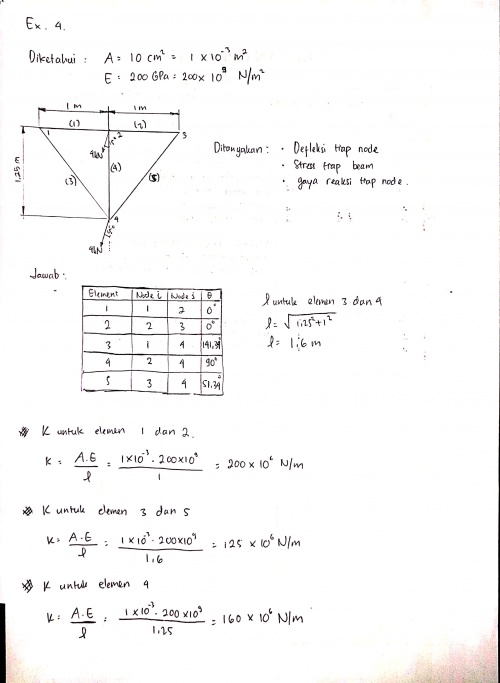
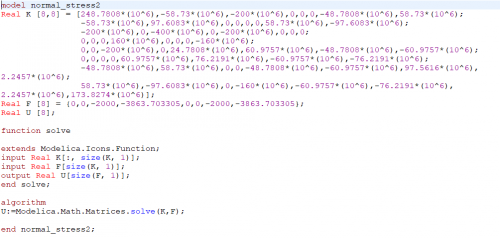
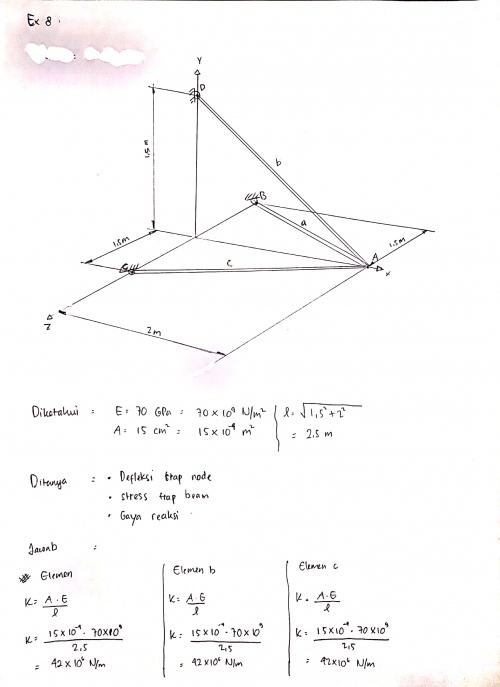
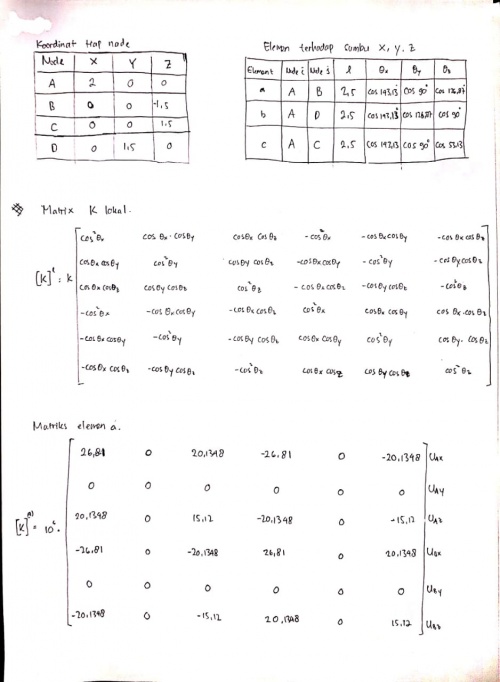
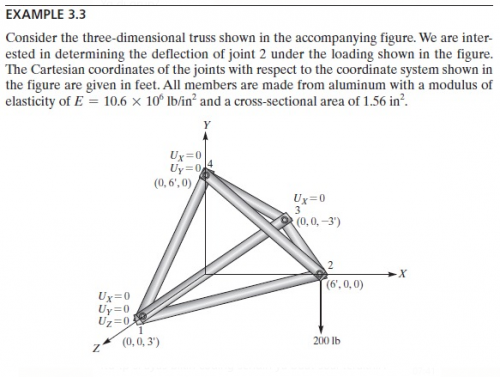
Pada hari ini saya sudah mengerjakan PR Defleksi dan Gaya Reaksi berdasarkan soal quiz minggu lalu. Saya melakukan perhitungan secara manual dan dengan menggunakan program. Perhitungan manual yang saya kerjakan hanya sampai menentukan matriks global semua elemen kemudian dilanjutkan perhitungan nilai defleksi dan gaya reaksi menggunakan openmodelica. berikut adalah perhitungan manual dan dengan openmodelica untuk ex 4 dan 8.

Perhitungan manual ex.4


Manual01 iff.JPEG


Manual012n iff.JPEG


Manual0123 iff.JPEG


Hasil ex.4

Hasilex4 iff.PNG

Coding ex.4

Coding1ex4 iff.PNG
Coding2ex4 iff.PNG


Perhitungan manual ex.8


Manual11 iff.JPEG


Manual112 iff.JPEG


Manual1123 iff.JPEG


Hasil ex.8

500px

Coding ex.8

500px


Pertemuan kelima

Hari, Tanggal : Senin 7 Desember 2020 Oleh : Dr. Ahmad Indra


Pada pertemuan hari ini kami membahas terkait dengna kasus pada kuis yang diberikan sebelumnya. Kami mempelajari bagaimana menyelesaikan kasus dengan menggunakan openmodelica dalam penyelesaian kasus tersebut. Kemudian teman kami fahmi menjelaskan beberapa hal yang dibahas dari koding hasil pengerjaannya. Berikut adalah hal-hal yang dijelaskan,

1. Bagaimana cara melakukan proses looping

2. Bagaimana membuat data dalam bentuk array

3. Apa itu protected

4. Dan pengerjaan secara keseluruhan mengenai koding yang telah dikerjaan

Kemudian Pak Dai memberikan kami tugas untuk memahami program yang dibuat oleh fahmi kemudian memberikan masukan terkait kodingnya serta mengerjakan kasus selanjutnya menggunakan koding tersebut.


Tugas 05 3D

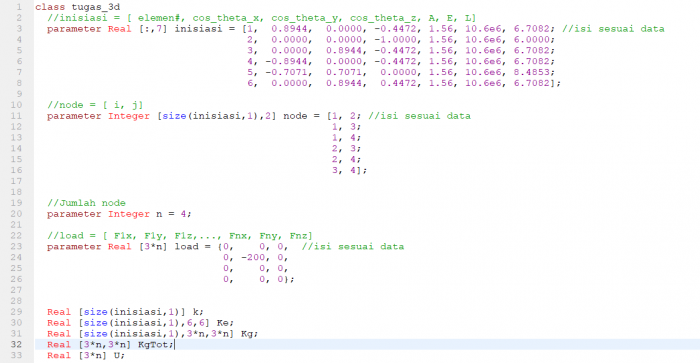
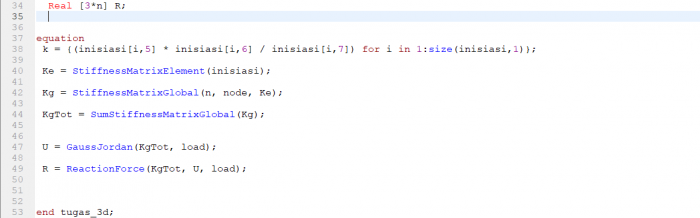
Berikut adalah tugas baru yang diberikan oleh pak Dai.

Capture1 iff.PNG

Berikut adalah penyelesaiannya,

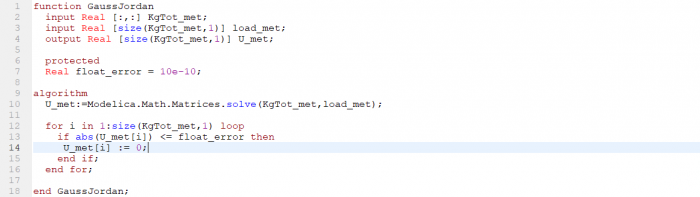
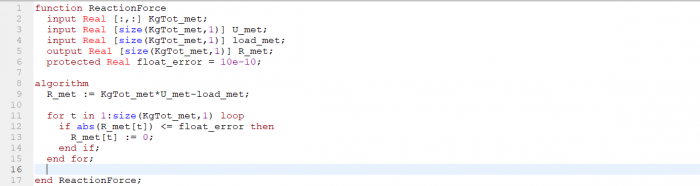
1. Membuat class yang nantinya digunakan untuk memanggil fungsi-fungsi untuk menyelesaikan persoalan.

Class1 iff.PNG
Class2 iff.PNG

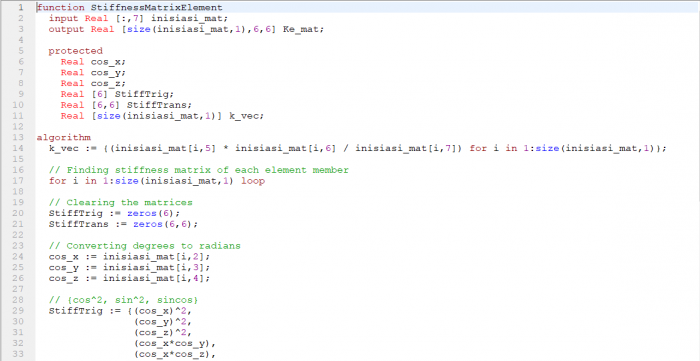
2. Membuat Fungsi Matriks untuk K lokal pada setiap elemen.

Func1 iff.PNG
Func2 iff.PNG

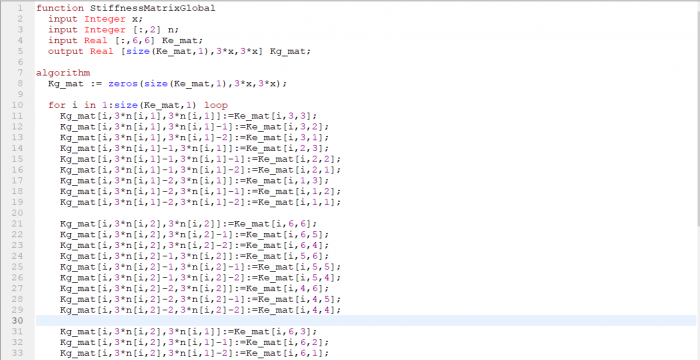
3. Membuat fungsi matriks untuk K global pada setiap elemen

Func3 iff.PNG
Func4 iff.PNG

4. Menjumlahkan Matriks K Global semua elemen yang ada.

Func5 iff.PNG

5. Membuat fungsi U dengan gauss jordan U = Kg*U

Func6 iff.PNG

6. Membuat fungsi untuk gaya reaksi

Func7 iff.PNG

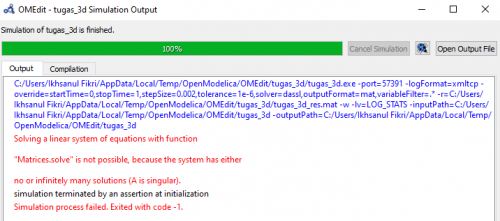
Namun setelah saya simulasi ternyata hasil perhitungannya error

Error iff.PNG


Pertemuan keenam

Hari, Tanggal : Senin 14 Desember 2020 Oleh : Dr. Ahmad Indra

Pada pertemuan ini pak Dai meminta kami untuk muhasabah diri. Kami diminta untuk memberikan nilai pada diri kami sendiri terkait pemmahaman kami terhadap metode numerik. Kemudian beberapa teman kami dipanggil untuk ditanya terkait pemahaman kami terhadap metode numerik. Pemahaman tersebut termasuk pada perhitungan matematis kasus trusses dan juga coding yang dibuat


Pertemuan ketujuh

Hari, Tanggal : Senin 21 Desember 2020 Oleh : Dr. Ahmad Indra dan Bu Candra


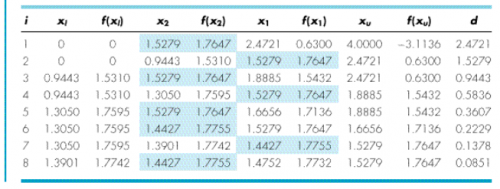
Pada hari ini pak Dai memberikan pemaparan terkait tugas besar. Kemudian pak Dai memberi arahan kepada bu Candra untuk mengajari kami terkait optimisasi. Optimisasi adalah suatu cara untuk mendapatkan nilai maksimum atau minimum dari suatu permasalahan. Dalam optimisasi tersebut harus ada fungsi objektif dan ada konstrain/batasan/interval. Kemudian kami melakukan simulasi pengerjaan soal di buku chapra. berikut adalah soal beserta penyelesaian yang ada di buku,


Soal1op iff.PNG


Komparasi iff.PNG


kemudian kami melakukan coding dengan fungsi objektif dan modelnya,

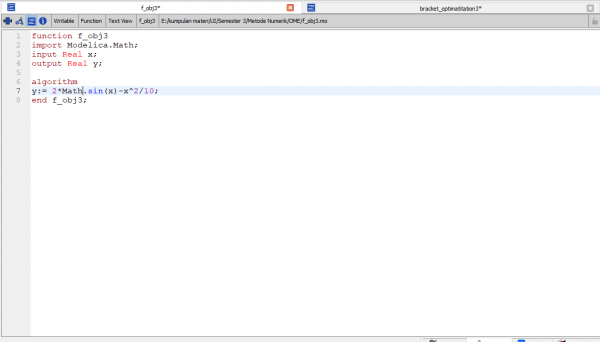
1. coding fungsi

Fungsiop iff.PNG


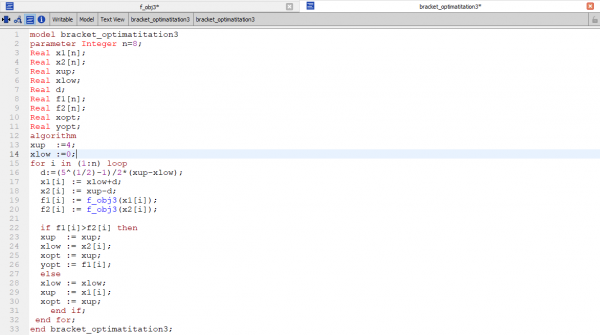
2. coding model

Modelop iff.PNG


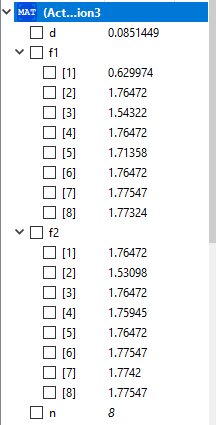
kemudian berikut adalah hasilnya,

Hasilop1 iff.PNG


Hasil2op1 iff.PNG


TUGAS BESAR

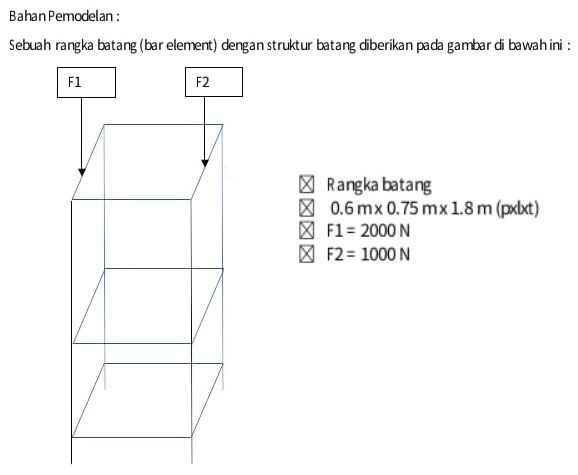
Pada tugas besar ini kami diminta untuk menentukan cost sebagai dengan variasi area dan material. Berikut adalah rangkaian trusses yang dijadikan sebagai objek kasus.

Soaltubes iff.PNG


Constraint:

- Spesifikasi L (Panjang) dan geometri rangka truss

- Gaya beban terhadap struktur (1000 N dan 2000 N)

Asumsi:

- Variasi Stiffness terikat dengan variabel area. Memvariasikan Elastisitas tergolong sulit karena setiap material memiliki range yang tidak teratur dan dalam satu material yang sejenis (struktur biaya tetap) tidak terjadi perubahan nilai elastisitas yang berbanding lurus dengan perubahan biaya.

- Beban akan terdistribusi hanya pada point penghubung (karena bersifat truss)

Material Lock

Pada bagian material lock data yang akan diambil berdasarkan pada satu material yang sama dengan variasi area. Saya menggunakan material ASTM A36 berprofil siku dengan modulus elastisitas sebesar 200 Gpa dan variasi area sebagai berikut :

Varmat1 iff.PNG

Kemudian hal berikutnya yang dilakukan adalah menentukan harga dari 6 sampel dengan variasi area tersebut kemudian dilakukan cutve fitting terhadap harga-harga sampel tersebut sehingga diketahui harga-harga per Kg dan nilai tegangan pada setiap variasi area. Sehingga didapatkan hasil curve fitting yang dituliskan pada excel sebagai berikut :

Matbaru iff.PNG

Kemudian nilai stress didapatkan dari nilai stress maksimum yang didapatkan dari simulasi openmodelica.

Berikut adalah coding untuk mecari nilai stress maksimum dan curve fitting untuk menentukan harga.



Model Trusses

model Trusses_3D_Tugas_Besar_Safety

//define initial variable

parameter Integer Points=size(P,1); //Number of Points

parameter Integer Trusses=size(C,1);//Number of Trusses

parameter Real Yield=250e6; //Yield Strength (Pa) Material ASTM A36

parameter Real Area=3.75E-04; //Area L Profile (0.04 x 0.04 x 0.005) (m2)

parameter Real Elas=2e11; //Elasticity ASTM A36 (Pa) //define connection parameter Integer C[:,2]= [1,5; 

                2,6;
                3,7;
                4,8;
                5,6;  //1st floor
                6,7;  //1st floor
                7,8;  //1st floor
                5,8;  //1st floor
                5,9;
                6,10;
                7,11;
                8,12;
                9,10; //2nd floor
                10,11;//2nd floor 
                11,12;//2nd floor
                9,12; //2nd floor
                9,13;
                10,14;
                11,15;
                12,16;
                13,14;//3rd floor
                14,15;//3rd floor
                15,16;//3rd floor
                13,16];//3rd floor

//define coordinates (please put orderly)

parameter Real P[:,6]=[0.3,-0.375,0,1,1,1; //1 

                          -0.3,-0.375,0,1,1,1;    //2
                          -0.3,0.375,0,1,1,1;     //3
                          0.3,0.375,0,1,1,1;      //4
                          
                          0.3,-0.375,0.6,0,0,0;   //5
                          -0.3,-0.375,0.6,0,0,0;  //6
                          -0.3,0.375,0.6,0,0,0;   //7
                          0.3,0.375,0.6,0,0,0;    //8
                          
                          0.3,-0.375,1.2,0,0,0;   //9
                          -0.3,-0.375,1.2,0,0,0;  //10  
                          -0.3,0.375,1.2,0,0,0;   //11
                          0.3,0.375,1.2,0,0,0;    //12
                          
                          0.3,-0.375,1.8,0,0,0;   //13
                          -0.3,-0.375,1.8,0,0,0;  //14
                          -0.3,0.375,1.8,0,0,0;   //15
                          0.3,0.375,1.8,0,0,0];   //16

//define external force (please put orderly) parameter Real F[Points*3]= 

                         {0,0,0,
                          0,0,0, 
                          0,0,0, 
                          0,0,0, 
                          0,0,0, 
                          0,0,0, 
                          0,0,0, 
                          0,0,0, 
                          0,0,0, 
                          0,0,0, 
                          0,0,0, 
                          0,0,0, 
                          0,0,-500, 
                          0,0,-1000, 
                          0,0,-1000, 
                          0,0,-500};

//solution Real displacement[N], reaction[N];

Real check[3];

Real stress1[Trusses];

Real safety[Trusses];

Real dis[3]; Real Str[3];

protected parameter Integer N=3*Points;

Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; Real err=10e-10, ers=10e-6;


algorithm //Creating Global Matrix G:=id;

for i in 1:Trusses loop for j in 1:3 loop 

 q1[j]:=P[C[i,1],j];
 q2[j]:=P[C[i,2],j];

end for; 

  //Solving Matrix
  L:=Modelica.Math.Vectors.length(q2-q1);
  cx:=(q2[1]-q1[1])/L;
  cy:=(q2[2]-q1[2])/L;
  cz:=(q2[3]-q1[3])/L; 
  X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
                    cy*cx,cy^2,cy*cz;
                    cz*cx,cz*cy,cz^2];

  //Transforming to global matrix
  g:=zeros(N,N); 
  for m,n in 1:3 loop
    g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
    g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
    g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
    g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
  end for;

G_star:=G+g;

G:=G_star;

end for; //Implementing boundary for x in 1:Points loop 

if P[x,4] <> 0 then
  for a in 1:Points*3 loop
    G[(x*3)-2,a]:=0;
    G[(x*3)-2,(x*3)-2]:=1;
  end for;
end if;
if P[x,5] <> 0 then
  for a in 1:Points*3 loop
    G[(x*3)-1,a]:=0;
    G[(x*3)-1,(x*3)-1]:=1;
  end for;
end if;
if P[x,6] <> 0 then
  for a in 1:Points*3 loop
    G[x*3,a]:=0;
    G[x*3,x*3]:=1;
  end for;
end if;

end for; //Solving displacement displacement:=Modelica.Math.Matrices.solve(G,F);

//Solving reaction reaction:=(G_star*displacement)-F;

//Eliminating float error for i in 1:N loop

reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];

displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];

end for;

//Checking Force check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});

check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});

check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});

for i in 1:3 loop 

check[i] := if abs(check[i])<=ers then 0 else check[i];

end for;

//Calculating stress in each truss for i in 1:Trusses loop

for j in 1:3 loop 

 q1[j]:=P[C[i,1],j];
 q2[j]:=P[C[i,2],j];
 dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);

end for; 

  //Solving Matrix
  L:=Modelica.Math.Vectors.length(q2-q1);
  cx:=(q2[1]-q1[1])/L;
  cy:=(q2[2]-q1[2])/L;
  cz:=(q2[3]-q1[3])/L; 
  X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
               cy*cx,cy^2,cy*cz;
               cz*cx,cz*cy,cz^2];
  
  Str:=(X*dis);
  stress1[i]:=Modelica.Math.Vectors.length(Str);

end for;

//Safety factor for i in 1:Trusses loop 

if stress1[i]>0 then
  safety[i]:=Yield/stress1[i];
else
  safety[i]:=0;
end if;

end for;

end Trusses_3D_Tugas_Besar_Safety;



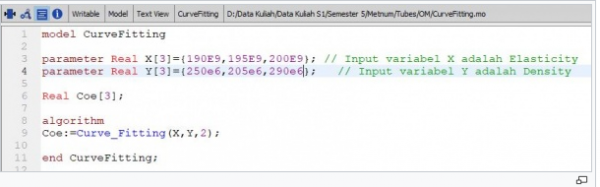
Model Curve Fitting

model CurveFitting

parameter Real X[6]={141e-6,375e-6,384e-6,575e-6,931e-6,864e-6};

parameter Real Y[6]={7702,7833,7664,7708,7927,7805};

Real Coe[3];

algorithm Coe:=Curve_Fitting(X,Y,2);

end CurveFitting;


Function Curve Fitting

function Curve_Fitting

input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coe[order+1];

protected Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1];

algorithm

for i in 1:size(X,1) loop 

for j in 1:(order+1) loop
Z[i,j]:=X[i]^(order+1-j);
end for;

end for; ZTr:=transpose(Z);

A:=ZTr*Z; B:=ZTr*Y; Coe:=Modelica.Math.Matrices.solve(A,B);

end Curve_Fitting;



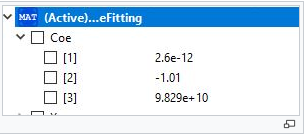
Sehingga didapatkan hasil curve fitting yang dituliskan pada excel sebagai berikut :

Varmathasilcoe01 iff.PNG


Area Lock

Pada bagian area lock saya mengambil satu luas area dengan spesifikasi berikut :

Dimensi = 40 x 40 x 5 mm

Area = 3,75E-4 m2

L= 15.3 m

V = 5,74E-3

hal ini dilakukan secara acak untuk di lock dengan variasi 3 material yang berbeda, yaitu stainless steel 304 dan 316 dan ASTM A36. Kemudian dilakukan curve fitting pada bagian cost per kg, density dan yield sehingga didapatkan harga-harga dan nilai tegangan maksimal dari material-material tersebut.

Berikut adalah hasil yang diperoleh :

Datbar02 iff.PNG

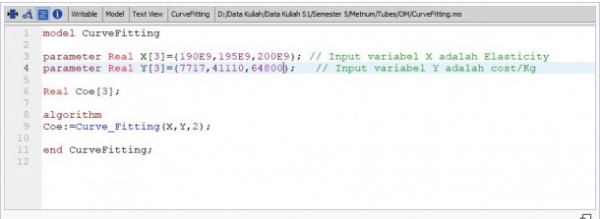
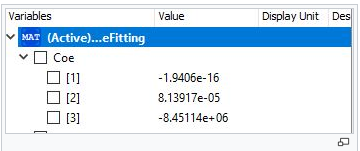
Berikut adalah coding untuk curve fitting cost

Codingcf01 iff.PNG

Berikut hasilnya

Hasil01 iff.PNG

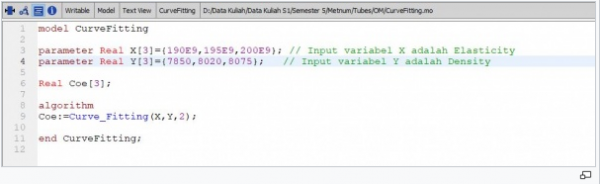
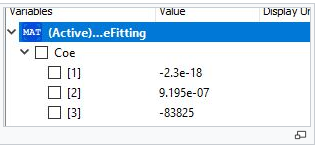
Berikut adalah coding untuk curve fitting density

Codingcf02 iff.PNG

Berikut hasilnya

Hasilcf02 iff.PNG

Berikut adalah coding untuk curve fitting yield

Codingcf03 iff.PNG

Berikut hasilnya

Hasilcf03 iff.PNG


Optimasi

Nilai luas area penampang optimum untuk material SS400 adalah 0,00011 m^2 atau untuk ukuran yang ada di pasaran ukuran optimumnya adalah batang L dengan lebar 20mm dan tebal 3mm.

Hasilopt iff.PNG


Material optimum yang digunakan dengan luas area 40x40x5mm adalah material dengan nilai modulus elastisitas 190018000000 N/m^2 dengan material yang mendekati adalah ss400.

Hasilopt2 iff.PNG


Untuk cost yang dibutuhkan dalam struktur ini adalah Rp 103.061


Coding yang digunakan dalam optimasi ini adalah sebagai berikut :


model opt2 parameter Real xd[:]={//area atau elastisitas//}; parameter Real yd[size(xd,1)]={//ratio//}; parameter Real xlo=190e9; parameter Real xhi=205e9; parameter Integer N=18; // maximum iteration parameter Real es=0.0001; // maximum error Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3]; Real xopt, fx; protected Real d, xl, xu, xint, R=(5^(1/2)-1)/2;

algorithm xl := xlo; xu := xhi; y  := Curve_Fitting(xd,yd);

for i in 1:N loop 

d:= R*(xu-xl);
x1[i]:=xl+d;
x2[i]:=xu-d;
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
xint:=xu-xl;

if f1[i]>f2[i] then
  xl:=x2[i];
  xopt:=x1[i];
  fx:=f1[i];
  else
    xu:=x1[i];
    xopt:=x2[i];
    fx:=f2[i];
end if;

ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
  break;
end if;

end for;

end opt2;


JAWABAN UAS

Uas1 iff.jpeg
Uas2 iff.jpeg
Uas3 iff.jpeg
Uas4 iff.jpeg
Uas5 iff.PNG
Retrieved from "http://air.eng.ui.ac.id/index.php?title=Metnum03_Ikhsanul_Fikri_Fakhrurrozi&oldid=55231"