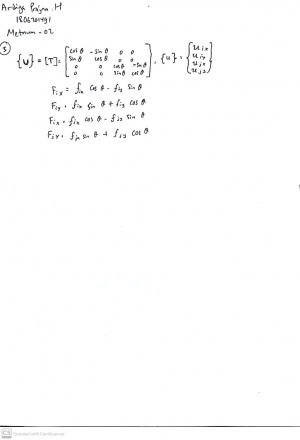Difference between revisions of "Ardiya Prajna Hardianto"

From ccitonlinewiki
Jump to: navigation, search
(→‎UAS)
 
(23 intermediate revisions by the same user not shown)
Line 66: Line 66:
 
== '''Tugas Minggu 3''' ==
 
== '''Tugas Minggu 3''' ==
  
−
Berikut 2 contoh penggunaan aplikasi Modelica untuk menyelesaikan perhitungan displacement dan reaction force pada trusses:
+
Penggunaan aplikasi Modelica untuk menyelesaikan perhitungan displacement dan reaction force pada trusses:
  
−
'''Trusses Problem 1 (Example 3.1)'''
+
'''Trusses Problem 1'''
  
−
[[File:Example 3.1 Arya.jpg|700px|thumb|right]]
+
[[File:Example 3.1 Arya.jpg|700px|center|thumb]]
−
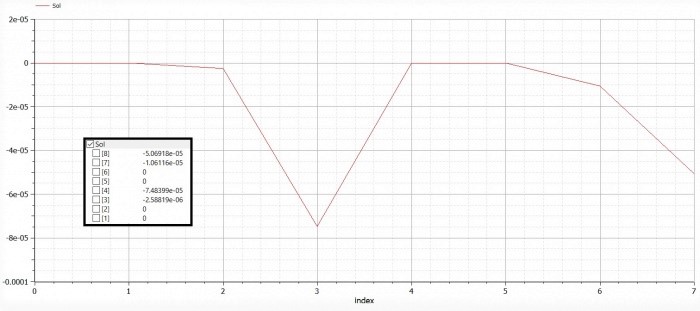
[[File:Trusses 1 Displacement Arya.jpg|700px|thumb|right|Grafik Displacement]]
+
[[File:Trusses 1 Displacement Arya.jpg|700px|thumb|center|Grafik Displacement]]
−
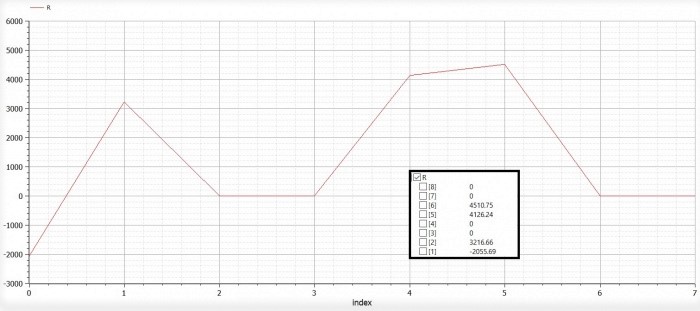
[[File:Trusses 1 Reaction Arya.jpg|700px|thumb|right|Grafik Reaction Forces]]
+
[[File:Trusses 1 Reaction Arya.jpg|700px|thumb|center|Grafik Reaction Forces]]
 
{| class="wikitable"
 
{| class="wikitable"
 
|-
 
|-
Line 196: Line 196:
  
  
−
'''Trusses Problem 2 (Homework)'''
+
'''Trusses Problem 2 (PR)'''
 
[[File:Tugas 3 Arya.jpg|700px|thumb|center]]
 
[[File:Tugas 3 Arya.jpg|700px|thumb|center]]
−
[[File:Trusses 2 Displacement Aryaa.jpg|700px|thumb|center|Grafik Displacement]]
+
[[File:Trusses 2 Displacements Arya.jpg|700px|thumb|center|Grafik Displacement]]
 
[[File:Trusses 2 Reaction Arya.jpg|700px|thumb|center|Grafik Reaction Forces]]
 
[[File:Trusses 2 Reaction Arya.jpg|700px|thumb|center|Grafik Reaction Forces]]
 
{| class="wikitable"
 
{| class="wikitable"
Line 415: Line 415:
  
 
|}
 
|}
 +
 +
== '''Minggu 4''' ==
 +
'''Quiz class diagram and flowchart:'''
 +
 +
[[File:Tugas 3 Arya.jpg|700px]]
 +
[[File:Quiz metnum ardiya.jpg|700px]]
 +
 +
== '''Minggu 6''' ==
 +
 +
Pada pertemuan minggu ke-6, kami diajarkan mengenai optimasi dengan menggunakan aplikasi OpenModelica. Optimasi merupakan cara untuk mendapatkan nilai minimum atau maksimum dari suatu permasalahan.  Terdapat beberapa aspek yang diperhatikan dalam melakukan optimasi yaitu fungsi objektif dan ada juga konstrain. Pada kali ini Asisten Dosen yaitu Bu Chandra memberikan tutorial untuk melakukan optimasi menggunakan metode Bracket. Pada metode "Bracket Optimization Using Golden Ratio" terdapat satu graik yang mempunyai nilai f(x) global maks dan lokal maks serta terdapat f(x) global minimum dann lokal minimum. Pada pertemuan kali ini, Bu chandra mengajarkan sampai melakukan optimasi grafik tanpa sebuah konstrain.
 +
 +
Berikutnya kami diberikan contoh penggunaan optimasi pada OpenModelica sebagai berikut
 +
 +
Fungsi panggil
 +
function f_obj3
 +
import Modelica.Math;
 +
input Real x;
 +
output Real y;
 +
algorithm
 +
y:= 2*Math.sin(x)-x^2/10;
 +
end f_obj3;
 +
 +
setelah itu kita dapat membuat model optimasi sistem bracket sesuai yang diajarkan
 +
 +
model bracket_optimation3
 +
parameter Integer n=8;
 +
Real x1[n];
 +
Real x2[n];
 +
Real xup;
 +
Real xlow;
 +
Real d;
 +
Real f1[n];
 +
Real f2[n];
 +
Real xopt;
 +
Real yopt;
 +
algorithm
 +
xup :=4;
 +
xlow:=0;
 +
for i in (1:n) loop
 +
  d:= (5^(1/2)-1)/2*(xup-xlow);
 +
  x1[i]:= xlow+d;
 +
  x2[i]:= xup-d;
 +
  f1[i]:= f_obj3(x1[i]);
 +
  f2[i]:= f_obj3(x2[i]);
 +
  if f1[i]>f2[i] then
 +
  xup:= xup;
 +
  xlow:= x2[i];
 +
  xopt:= xup;
 +
  yopt:= f1[i];
 +
  else
 +
  xlow:= xlow;
 +
  xup:= x1[i];
 +
  xopt:= xup;
 +
  end if;
 +
  end for;
 +
end bracket_optimation3;
 +
 +
== '''Tugas Besar: Aplikasi Numerik dalam Optimasi Design Struktur Rangka Sederhana''' ==
 +
 +
[[File:600px-Soaltubes.jpeg|500px]]  [[File:Soaltubes2.jpeg|500px]]
 +
 +
Pada tugas besar kali ini kita akan mendesign suatu rangka dengan cost yang yang serendah mungkin tetapi dengan kualitas yang optimum. Terdapat beberapa variabel yang diperhatikan diantaranya :
 +
*1. Harga material
 +
*2. Jenis  material
 +
*3. Luas Cross Section
 +
*4. Penampang yang digunakan
 +
Setelah itu kita akan melakukan optimasi dan membentuk kurva efisiensi harga dengan curve fitting menggunakan Metode numerik.
 +
 +
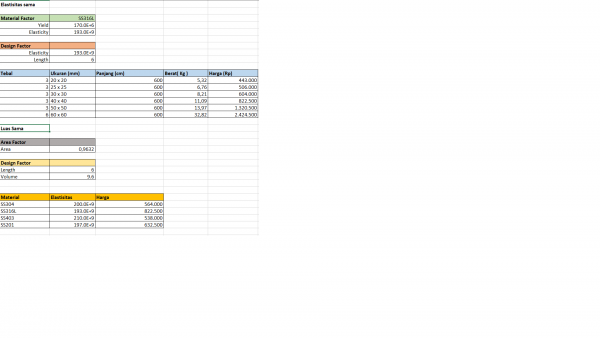
'''Data'''
 +
 +
[[File:Data_tubes.png|600px|center]]
 +
 +
'''Program'''
 +
 +
Program penghitungan pada Displacement,Reaction Force,Stress dan Safety Factor
 +
 +
model Tugas_Besar_Ardiya
 +
 +
//define initial variable
 +
parameter Integer Points=size(P,1); //Number of Points
 +
parameter Integer Trusses=size(C,1); //Number of Trusses
 +
parameter Real Yield=170e6; //Yield Strength (Pa)
 +
parameter Real Area=0.09632;  //Area L Profile (Dimension=0.04, Thickness=0,003) (m2)
 +
parameter Real Elas=193e9;    //Elasticity SS 316L  (Pa)
 +
 +
//define connection
 +
parameter Integer C[:,2]=[1,5;
 +
                          2,6;
 +
                          3,7;
 +
                          4,8;
 +
                          5,6;  //1st floor
 +
                          6,7;  //1st floor
 +
                          7,8;  //1st floor
 +
                          5,8;  //1st floor
 +
                          5,9;
 +
                          6,10;
 +
                          7,11;
 +
                          8,12;
 +
                          9,10; //2nd floor
 +
                          10,11;//2nd floor
 +
                          11,12;//2nd floor
 +
                          9,12; //2nd floor
 +
                          9,13;
 +
                          10,14;
 +
                          11,15;
 +
                          12,16;
 +
                          13,14;//3rd floor
 +
                          14,15;//3rd floor
 +
                          15,16;//3rd floor
 +
                          13,16];//3rd floor
 +
                                                             
 +
//define coordinates (please put orderly)
 +
parameter Real P[:,6]=[0.3,-0.375,0,1,1,1;    //1
 +
                        -0.3,-0.375,0,1,1,1;    //2
 +
                        -0.3,0.375,0,1,1,1;    //3
 +
                        0.3,0.375,0,1,1,1;      //4
 +
                         
 +
                        0.3,-0.375,0.6,0,0,0;  //5
 +
                        -0.3,-0.375,0.6,0,0,0;  //6
 +
                        -0.3,0.375,0.6,0,0,0;  //7
 +
                        0.3,0.375,0.6,0,0,0;    //8
 +
                           
 +
                        0.3,-0.375,1.2,0,0,0;  //9
 +
                        -0.3,-0.375,1.2,0,0,0;  //10 
 +
                        -0.3,0.375,1.2,0,0,0;  //11
 +
                        0.3,0.375,1.2,0,0,0;    //12
 +
                           
 +
                        0.3,-0.375,1.8,0,0,0;  //13
 +
                        -0.3,-0.375,1.8,0,0,0;  //14
 +
                        -0.3,0.375,1.8,0,0,0;  //15
 +
                        0.3,0.375,1.8,0,0,0];  //16
 +
                         
 +
//define external force (please put orderly)
 +
parameter Real F[Points*3]={0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,0,
 +
                            0,0,-500,
 +
                            0,0,-1000,
 +
                            0,0,-1000,
 +
                            0,0,-500};
 +
 +
//solution
 +
Real displacement[N], reaction[N];
 +
Real check[3];
 +
 +
Real stress1[Trusses];
 +
Real safety[Trusses];
 +
Real dis[3];
 +
Real Str[3];
 +
 
 +
protected
 +
parameter Integer N=3*Points;
 +
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
 +
Real err=10e-10, ers=10e-4;
 +
 +
algorithm
 +
//Creating Global Matrix
 +
G:=id;
 +
for i in 1:Trusses loop
 +
  for j in 1:3 loop
 +
  q1[j]:=P[C[i,1],j];
 +
  q2[j]:=P[C[i,2],j];
 +
  end for;
 +
     
 +
    //Solving Matrix
 +
    L:=Modelica.Math.Vectors.length(q2-q1);
 +
    cx:=(q2[1]-q1[1])/L;
 +
    cy:=(q2[2]-q1[2])/L;
 +
    cz:=(q2[3]-q1[3])/L;
 +
    X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
 +
                      cy*cx,cy^2,cy*cz;
 +
                      cz*cx,cz*cy,cz^2];
 +
 +
  //Transforming to global matrix
 +
  g:=zeros(N,N);
 +
  for m,n in 1:3 loop
 +
    g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
 +
    g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
 +
    g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
 +
    g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
 +
  end for; 
 +
 +
G_star:=G+g;
 +
G:=G_star;
 +
end for;
 +
 +
//Implementing boundary
 +
for x in 1:Points loop
 +
if P[x,4] <> 0 then
 +
  for a in 1:Points*3 loop
 +
    G[(x*3)-2,a]:=0;
 +
    G[(x*3)-2,(x*3)-2]:=1;
 +
  end for;
 +
end if;
 +
if P[x,5] <> 0 then
 +
  for a in 1:Points*3 loop
 +
    G[(x*3)-1,a]:=0;
 +
    G[(x*3)-1,(x*3)-1]:=1;
 +
  end for;
 +
end if;
 +
if P[x,6] <> 0 then
 +
  for a in 1:Points*3 loop
 +
    G[x*3,a]:=0;
 +
    G[x*3,x*3]:=1;
 +
  end for;
 +
end if;
 +
end for;
 +
 +
//Solving displacement
 +
displacement:=Modelica.Math.Matrices.solve(G,F);
 +
 +
//Solving reaction
 +
reaction:=(G_star*displacement)-F;
 +
 +
//Eliminating float error
 +
for i in 1:N loop
 +
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
 +
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
 +
end for;
 +
 +
//Checking Force
 +
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
 +
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
 +
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
 +
 
 +
for i in 1:3 loop
 +
check[i] := if abs(check[i])<=ers then 0 else check[i];
 +
end for;
 +
 +
//Calculating stress in each truss
 +
for i in 1:Trusses loop
 +
for j in 1:3 loop
 +
  q1[j]:=P[C[i,1],j];
 +
  q2[j]:=P[C[i,2],j];
 +
  dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
 +
end for;
 +
     
 +
  //Solving Matrix
 +
  L:=Modelica.Math.Vectors.length(q2-q1);
 +
  cx:=(q2[1]-q1[1])/L;
 +
  cy:=(q2[2]-q1[2])/L;
 +
  cz:=(q2[3]-q1[3])/L;
 +
  X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
 +
                cy*cx,cy^2,cy*cz;
 +
                cz*cx,cz*cy,cz^2];
 +
 
 +
  Str:=(X*dis);
 +
  stress1[i]:=Modelica.Math.Vectors.length(Str);
 +
end for;
 +
 +
//Safety factor
 +
for i in 1:Trusses loop
 +
if stress1[i]>0 then
 +
  safety[i]:=Yield/stress1[i];
 +
else
 +
  safety[i]:=0;
 +
end if;
 +
end for;
 +
 +
end Tugas_Besar_Ardiya;
 +
 +
Curve Fitting
 +
 +
function Kurva
 +
 +
input Real X[:];
 +
input Real Y[size(X,1)];
 +
input Integer order=2;
 +
output Real Coe[order+1];
 +
 +
protected
 +
Real Z[size(X,1),order+1];
 +
Real ZTr[order+1,size(X,1)];
 +
Real A[order+1,order+1];
 +
Real B[order+1];
 +
 +
algorithm
 +
 +
for i in 1:size(X,1) loop
 +
for j in 1:(order+1) loop
 +
Z[i,j]:=X[i]^(order+1-j);
 +
end for;
 +
end for;
 +
ZTr:=transpose(Z);
 +
 +
A:=ZTr*Z;
 +
B:=ZTr*Y;
 +
Coe:=Modelica.Math.Matrices.solve(A,B);
 +
 +
end Kurva;
 +
 +
Gold Optimization
 +
 +
model Gold_Opt
 +
 +
parameter Real xd[:];
 +
parameter Real yd[size(xd,1)];
 +
parameter Real xlo=64e-6;
 +
parameter Real xhi=215e-6;
 +
parameter Integer N=10; // maximum iteration
 +
parameter Real es=0.0001; // maximum error
 +
 +
Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3];
 +
Real xopt,  fx;
 +
protected
 +
Real d, xl, xu, xint, R=(5^(1/2)-1)/2;
 +
 +
algorithm
 +
xl := xlo;
 +
xu := xhi;
 +
y  := Kurva(xd,yd);
 +
 
 +
for i in 1:N loop
 +
  d:= R*(xu-xl);
 +
  x1[i]:=xl+d;
 +
  x2[i]:=xu-d;
 +
  f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
 +
  f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
 +
  xint:=xu-xl;
 +
 +
if f1[i]>f2[i] then
 +
  xl:=x2[i];
 +
  xopt:=x1[i];
 +
  fx:=f1[i];
 +
  else
 +
    xu:=x1[i];
 +
    xopt:=x2[i];
 +
    fx:=f2[i];
 +
end if;
 +
 +
ea[i]:=(1-R)*abs((xint)/xopt);
 +
if ea[i]<es then
 +
  break;
 +
end if;
 +
end for;
 +
 +
end Gold_Opt;
 +
 +
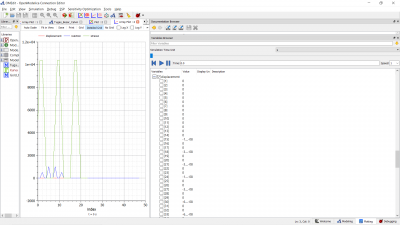
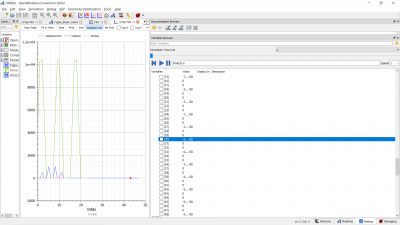
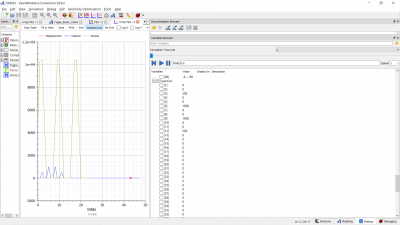
'''Hasil'''
 +
 +
[[File:Dis1.png|400px|left]]
 +
[[File:Dis 2.png|400px|left]]
 +
[[File:React1.png|400px|left]]
 +
[[File:Safety.png|400px|left]]
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
'''Kesimpulan'''
 +
Dengan penggunaan luas area sebsar 171 mm^2 atau material siku 40x40 dengan thickness 3mm, maka material yang paling optimal untuk digunakan adalah material dengan tingkat elastisitas sebesar 193 GPa
 +
 +
Material yang terletak dalam range elastisitas ini adalah material SS316L dengan tingkat elasitisas sama dengan nilai optimal yaitu 193 GPa.
 +
 +
== '''UAS''' ==
 +
[[File:UAS Ardiya no 1.jpg|300px]]
 +
[[File:UAS Ardiya no 2.jpg|300px]]
 +
[[File:UAS Ardiya no 3.jpg|300px]]
 +
[[File:UAS Ardiya no 4.jpg|300px]]
 +
[[File:UAS Ardiya no 5.jpg|300px]]

Latest revision as of 18:10, 13 January 2021

بِسْمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ

Assalamualaikum wr. wb.

Biodata

Ardiya Prajna Hardianto

Nama  : Ardiya Prajna Hardianto

NPM  : 1806201491

TTL  : Jakarta, 19 April 2000

Tempat Tinggal: Bekasi

Saya adalah mahasiswa FTUI angkatan 2018 jurusan Teknik Mesin.

Saya memilih jurusan Teknik Mesin karena saya ingin tahu lebih dalam tentang dunia Mechanical Engineering dan segala ilmu pendukungnya.


Metode Numerik

Metode numerik merupakan teknik penyelesaian permsalahan yang diformulasikan secara matematis dengan menggunakan operasi hitungan (aritmatik) yaitu operasi tambah, kurang, kali, dan bagi. Metode ini digunakan karena banyak permasalahan matematis tidak dapat diselesaikan menggunakan metode analitik.

Pada kelas MetNum 02 semester ganjil 2020/2021 sampai dengan UTS, perkuliahan diisi oleh Bapak Dr. Ir. Engkos A. Kosasih, M.T. Dimana kita membahas materi seperti:

- Regresi Linear

- Sistem Persamaan dengan metode Newton Rhapson, Sekan, dan Biseksi

- Interpolasi

- Deret Taylor dan McClaurin

- Pseudocode

- Turunan Numerik


Review Minggu 1

Untuk pertemuan pertama saya mempelajari cara menggunakan OpenModelica dimulai dari persamaan yang cukup sederhana, OpenModelica sendiri merupakan aplikasi penghitungan permodelan yang lumayan kompleks, sehingga OpenModelica itu sendiri sangat membantu saat menyelesaikan permodelan masalah mulai dari yang cukup mudah sampai ke cukup kompleks.

Tugas Minggu 1

https://www.youtube.com/watch?v=GhtBMIlO70w

Review Minggu 2

Pada kegiatan pembelajaran mata kuliah metode numerik hari ini. Bapak Ahmad Indra mengawali dengan mereview tugas yang diberikan pada pertemuan minggu lalu. Review tersebut mengenai software Open Modelica dan perhitungan yang masing - masing mahasiswa lakukan.

Review Minggu 3

Pada awal-awal Pak Dai memaparkan tiga aplikasi metode numerik yang sering digunakan dalam menyelesaikan permasalahan teknik, pertama ada Computation Fluid Dynamics (CFD), lalu Finite Element Analysis, dan Metode Stokastik. CFD dan FEA berbasis ilmu fisika, kemudian metode stokastik berbasis data dan statistik. Ada lima langkah yang Pak Dai paparkan dalam mengaplikasikan metode numerik ke permasalahan teknik :

Riset masalah tekniknya terlebih dahulu Menganalisis masalah (mendefinisikan variabel yang mau dicari dan mencari parameter fisikanya) Membuat model matematika Membuat model numerik Setelah itu cari penyelesaian dengan bantuan komputer untuk mendapatkan output yang diinginkan Agar Kami bisa lebih paham tentang dasar-dasar metode numerik, Pak Dai menyuruh Kami untuk mencoba membuat fungsi untuk menyelesaikan Persamaan 9.12 di buku Numerical Methods for Engineers 7th Edition oleh Chapra dengan cara apapun (misalnya eliminasi gauss). Kedua, Kami disuru latihan menyelesaikan sistem persamaan dengan membuat fungsi penyelesaian dengan cara pseudocode 9.4 untuk menjawab soal 9.5 yang ada di buku yang sama juga. Latihan yang kedua ini dimaksudkan agar Kami paham dalam penggunaan array dalam penggunaan OpenModelica, yang dimana array ini dapat memudahkan mengumpulkan himpunan penyelesaian.

Tugas Minggu 3

Penggunaan aplikasi Modelica untuk menyelesaikan perhitungan displacement dan reaction force pada trusses:

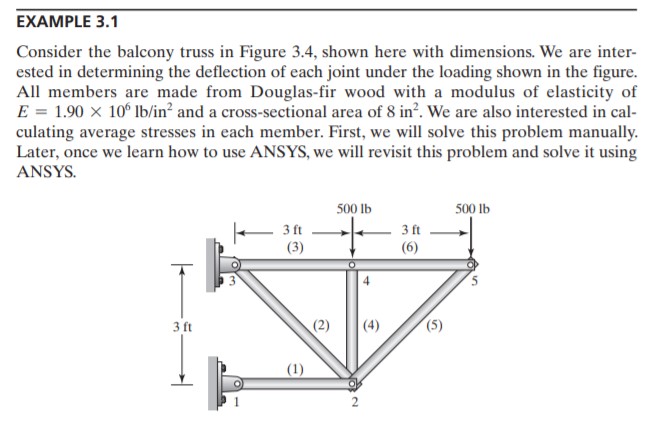
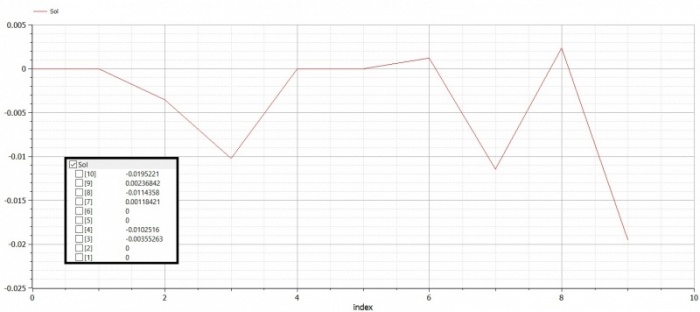
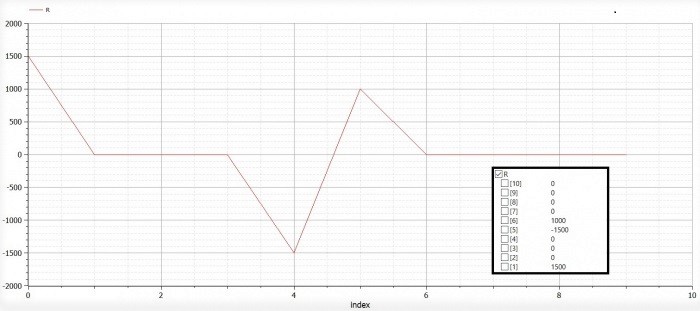
Trusses Problem 1

Example 3.1 Arya.jpg
Grafik Displacement
Grafik Reaction Forces

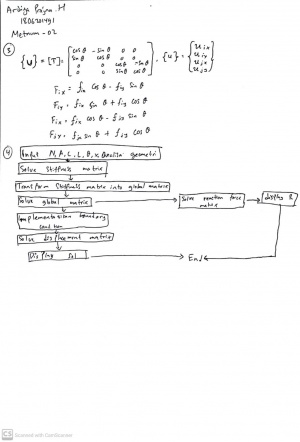
Persamaan 

model Trusses

parameter Integer N=10; //Global matrice = 2*points connected
parameter Real A=8;
parameter Real E=1.9e6;
Real G[N,N]; //global
Real Ginitial[N,N]; //global
Real Sol[N]; //global dispplacement
Real X[N]={0,0,0,0,0,0,0,-500,0,-500};
Real R[N]; //global reaction force
Real SolMat[N,1];
Real XMat[N,1];

//boundary coundition
Integer b1=1;
Integer b2=3;

//truss 1
parameter Real X1=0; //degree between truss
Real k1=A*E/36;
Real K1[4,4]; //stiffness matrice
Integer p1a=1;
Integer p1b=2;
Real G1[N,N];

//truss 2
parameter Real X2=135; //degree between truss
Real k2=A*E/50.912;
Real K2[4,4]; //stiffness matrice
Integer p2a=2;
Integer p2b=3;
Real G2[N,N];

//truss 3
parameter Real X3=0; //degree between truss
Real k3=A*E/36;
Real K3[4,4]; //stiffness matrice
Integer p3a=3;
Integer p3b=4;
Real G3[N,N];

//truss 4
parameter Real X4=90; //degree between truss
Real k4=A*E/36;
Real K4[4,4]; //stiffness matrice
Integer p4a=2;
Integer p4b=4;
Real G4[N,N];

//truss 5
parameter Real X5=45; //degree between truss
Real k5=A*E/50.912;
Real K5[4,4]; //stiffness matrice
Integer p5a=2;
Integer p5b=5;
Real G5[N,N];

//truss 6
parameter Real X6=0; //degree between truss
Real k6=A*E/36;
Real K6[4,4]; //stiffness matrice
Integer p6a=4;
Integer p6b=5;
Real G6[N,N];

/*
for each truss, please ensure pXa is lower then pXb (X represents truss element number)
*/

algorithm

//creating global matrice
K1:=Stiffness_Matrices(X1);
G1:=k1*Local_Global(K1,N,p1a,p1b);

K2:=Stiffness_Matrices(X2);
G2:=k2*Local_Global(K2,N,p2a,p2b);

K3:=Stiffness_Matrices(X3);
G3:=k3*Local_Global(K3,N,p3a,p3b);

K4:=Stiffness_Matrices(X4);
G4:=k4*Local_Global(K4,N,p4a,p4b);

K5:=Stiffness_Matrices(X5);
G5:=k5*Local_Global(K5,N,p5a,p5b);

K6:=Stiffness_Matrices(X6);
G6:=k6*Local_Global(K6,N,p6a,p6b);

G:=G1+G2+G3+G4+G5+G6;
Ginitial:=G;

//implementing boundary condition
for i in 1:N loop
 G[2*b1-1,i]:=0;
 G[2*b1,i]:=0;
 G[2*b2-1,i]:=0;
 G[2*b2,i]:=0;
end for;

G[2*b1-1,2*b1-1]:=1;
G[2*b1,2*b1]:=1;
G[2*b2-1,2*b2-1]:=1;
G[2*b2,2*b2]:=1;

//solving displacement
Sol:=Gauss_Jordan(N,G,X);

//solving reaction force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);

end Trusses;


Trusses Problem 2 (PR)

Tugas 3 Arya.jpg
Grafik Displacement
Grafik Reaction Forces

Persamaan 

class Trusses_HW

parameter Integer N=8; //Global matrice = 2*points connected
parameter Real A=0.001; //Area m2
parameter Real E=200e9; //Pa
Real G[N,N]; //global
Real Ginitial[N,N]; //global
Real Sol[N]; //global dispplacement
Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033};
Real R[N]; //global reaction force
Real SolMat[N,1];
Real XMat[N,1];

//boundary condition
Integer b1=1;
Integer b2=3;

//truss 1
parameter Real X1=0; //degree between truss
Real k1=A*E/1;
Real K1[4,4]; //stiffness matrice
Integer p1a=1;
Integer p1b=2;
Real G1[N,N];

//truss 2
parameter Real X2=0; //degree between truss
Real k2=A*E/1;
Real K2[4,4]; //stiffness matrice
Integer p2a=2;
Integer p2b=3;
Real G2[N,N];

//truss 3
parameter Real X3=90; //degree between truss
Real k3=A*E/1.25;
Real K3[4,4]; //stiffness matrice
Integer p3a=2;
Integer p3b=4;
Real G3[N,N];

//truss 4
parameter Real X4=90+38.6598; //degree between truss
Real k4=A*E/1.6;
Real K4[4,4]; //stiffness matrice
Integer p4a=1;
Integer p4b=4;
Real G4[N,N];

//truss 5
parameter Real X5=90-38.6598; //degree between truss
Real k5=A*E/1.6;
Real K5[4,4]; //stiffness matrice
Integer p5a=3;
Integer p5b=4;
Real G5[N,N];

/*
for each truss, please ensure pXa is lower then pXb (X represents truss element number)
*/

algorithm

//creating global matrice
K1:=Stiffness_Matrices(X1);
G1:=k1*Local_Global(K1,N,p1a,p1b);

K2:=Stiffness_Matrices(X2);
G2:=k2*Local_Global(K2,N,p2a,p2b);

K3:=Stiffness_Matrices(X3);
G3:=k3*Local_Global(K3,N,p3a,p3b);

K4:=Stiffness_Matrices(X4);
G4:=k4*Local_Global(K4,N,p4a,p4b);

K5:=Stiffness_Matrices(X5);
G5:=k5*Local_Global(K5,N,p5a,p5b);

G:=G1+G2+G3+G4+G5;
Ginitial:=G;

//implementing boundary condition
for i in 1:N loop
 G[2*b1-1,i]:=0;
 G[2*b1,i]:=0;
 G[2*b2-1,i]:=0;
 G[2*b2,i]:=0;
end for;

G[2*b1-1,2*b1-1]:=1;
G[2*b1,2*b1]:=1;
G[2*b2-1,2*b2-1]:=1;
G[2*b2,2*b2]:=1;

//solving displacement
Sol:=Gauss_Jordan(N,G,X);

//solving reaction force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);

end Trusses_HW;

Fungsi Panggil

Matrice Transformation 

function Stiffness_Matrices
input Real A;
Real Y;
output Real X[4,4];
Real float_error = 10e-10;

final constant Real pi=2*Modelica.Math.asin(1.0);

algorithm

Y:=A/180*pi;
    
X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y);

Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2;

-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y);

-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2];

for i in 1:4 loop
 for j in 1:4 loop
   if abs(X[i,j]) <= float_error then
     X[i,j] := 0;
   end if;
 end for;
end for;

end Stiffness_Matrices;

Global Element Matrice 

function Local_Global
input Real Y[4,4];
input Integer B;
input Integer p1;
input Integer p2;
output Real G[B,B];

algorithm

for i in 1:B loop
 for j in 1:B loop
     G[i,j]:=0;
 end for;
end for;

G[2*p1,2*p1]:=Y[2,2];
G[2*p1-1,2*p1-1]:=Y[1,1];
G[2*p1,2*p1-1]:=Y[2,1];
G[2*p1-1,2*p1]:=Y[1,2];

G[2*p2,2*p2]:=Y[4,4];
G[2*p2-1,2*p2-1]:=Y[3,3];
G[2*p2,2*p2-1]:=Y[4,3];
G[2*p2-1,2*p2]:=Y[3,4];

G[2*p2,2*p1]:=Y[4,2];
G[2*p2-1,2*p1-1]:=Y[3,1];
G[2*p2,2*p1-1]:=Y[4,1];
G[2*p2-1,2*p1]:=Y[3,2];

G[2*p1,2*p2]:=Y[2,4];
G[2*p1-1,2*p2-1]:=Y[1,3];
G[2*p1,2*p2-1]:=Y[2,3];
G[2*p1-1,2*p2]:=Y[1,4];

end Local_Global;

Reaction Matrice Equation 

function Reaction_Trusses
input Integer N;
input Real A[N,N];
input Real B[N,1];
input Real C[N,1];
Real X[N,1];
output Real Sol[N];
Real float_error = 10e-10;

algorithm
X:=A*B-C;

for i in 1:N loop
 if abs(X[i,1]) <= float_error then
   X[i,1] := 0;
 end if;
end for;

for i in 1:N loop
 Sol[i]:=X[i,1];
end for;

end Reaction_Trusses;

Minggu 4

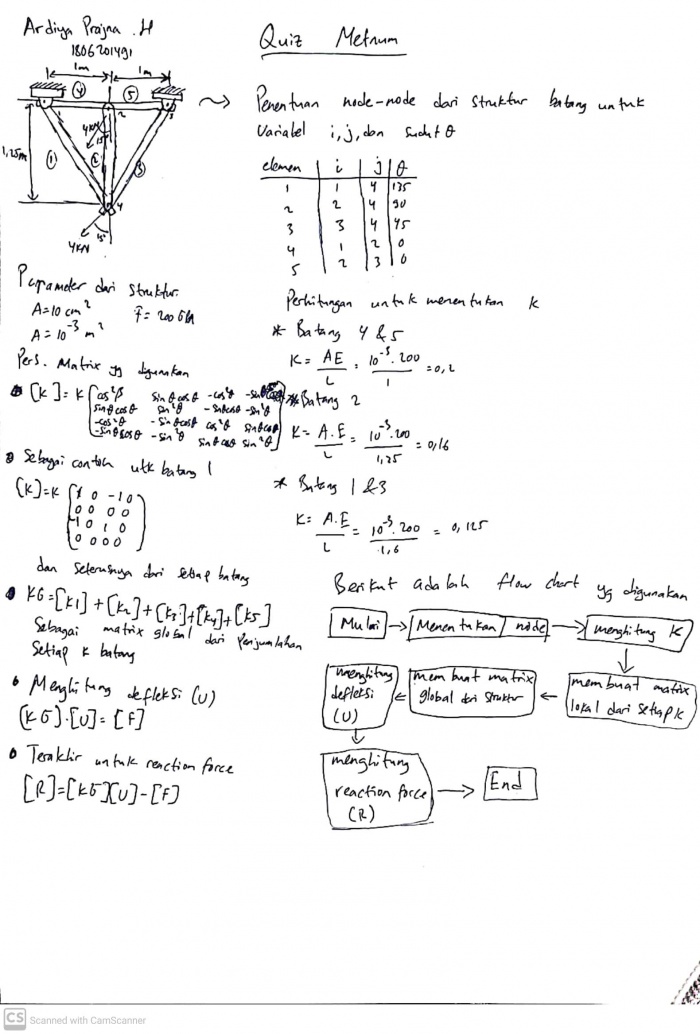
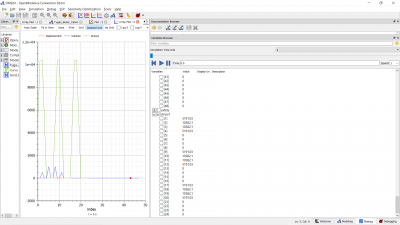
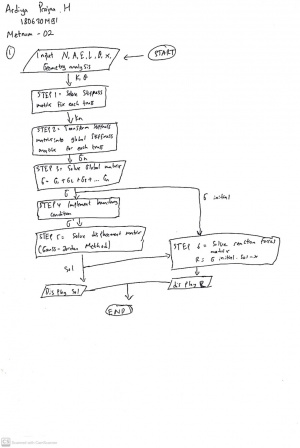
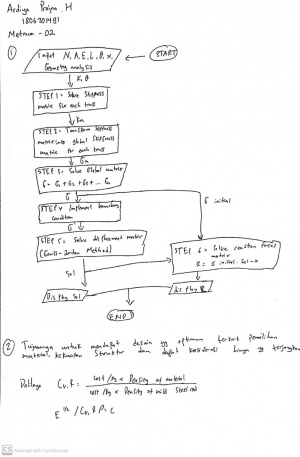
Quiz class diagram and flowchart:

Tugas 3 Arya.jpg Quiz metnum ardiya.jpg

Minggu 6

Pada pertemuan minggu ke-6, kami diajarkan mengenai optimasi dengan menggunakan aplikasi OpenModelica. Optimasi merupakan cara untuk mendapatkan nilai minimum atau maksimum dari suatu permasalahan. Terdapat beberapa aspek yang diperhatikan dalam melakukan optimasi yaitu fungsi objektif dan ada juga konstrain. Pada kali ini Asisten Dosen yaitu Bu Chandra memberikan tutorial untuk melakukan optimasi menggunakan metode Bracket. Pada metode "Bracket Optimization Using Golden Ratio" terdapat satu graik yang mempunyai nilai f(x) global maks dan lokal maks serta terdapat f(x) global minimum dann lokal minimum. Pada pertemuan kali ini, Bu chandra mengajarkan sampai melakukan optimasi grafik tanpa sebuah konstrain.

Berikutnya kami diberikan contoh penggunaan optimasi pada OpenModelica sebagai berikut

Fungsi panggil 

function f_obj3
import Modelica.Math;
input Real x;
output Real y;
algorithm
y:= 2*Math.sin(x)-x^2/10;
end f_obj3;

setelah itu kita dapat membuat model optimasi sistem bracket sesuai yang diajarkan 

model bracket_optimation3
parameter Integer n=8;
Real x1[n];
Real x2[n];
Real xup;
Real xlow;
Real d;
Real f1[n];
Real f2[n];
Real xopt;
Real yopt;
algorithm
xup :=4;
xlow:=0;
for i in (1:n) loop
  d:= (5^(1/2)-1)/2*(xup-xlow);
  x1[i]:= xlow+d;
  x2[i]:= xup-d;
  f1[i]:= f_obj3(x1[i]);
  f2[i]:= f_obj3(x2[i]);
  if f1[i]>f2[i] then
  xup:= xup;
  xlow:= x2[i];
  xopt:= xup;
  yopt:= f1[i];
  else
  xlow:= xlow;
  xup:= x1[i];
  xopt:= xup;
  end if;
  end for;
end bracket_optimation3;

Tugas Besar: Aplikasi Numerik dalam Optimasi Design Struktur Rangka Sederhana

600px-Soaltubes.jpeg Soaltubes2.jpeg

Pada tugas besar kali ini kita akan mendesign suatu rangka dengan cost yang yang serendah mungkin tetapi dengan kualitas yang optimum. Terdapat beberapa variabel yang diperhatikan diantaranya :

  • 1. Harga material
  • 2. Jenis material
  • 3. Luas Cross Section
  • 4. Penampang yang digunakan

Setelah itu kita akan melakukan optimasi dan membentuk kurva efisiensi harga dengan curve fitting menggunakan Metode numerik.

Data

Data tubes.png

Program

Program penghitungan pada Displacement,Reaction Force,Stress dan Safety Factor

model Tugas_Besar_Ardiya 

//define initial variable
parameter Integer Points=size(P,1); //Number of Points
parameter Integer Trusses=size(C,1); //Number of Trusses
parameter Real Yield=170e6; //Yield Strength (Pa)
parameter Real Area=0.09632;   //Area L Profile (Dimension=0.04, Thickness=0,003) (m2)
parameter Real Elas=193e9;     //Elasticity SS 316L  (Pa)

//define connection
parameter Integer C[:,2]=[1,5; 
                          2,6;
                          3,7;
                          4,8;
                          5,6;  //1st floor
                          6,7;  //1st floor
                          7,8;  //1st floor
                          5,8;  //1st floor
                          5,9;
                         6,10;
                         7,11;
                         8,12;
                         9,10; //2nd floor
                         10,11;//2nd floor 
                         11,12;//2nd floor
                          9,12; //2nd floor
                          9,13;
                         10,14;
                         11,15;
                         12,16;
                         13,14;//3rd floor
                         14,15;//3rd floor
                         15,16;//3rd floor
                         13,16];//3rd floor
                                                             
//define coordinates (please put orderly)
parameter Real P[:,6]=[0.3,-0.375,0,1,1,1;     //1
                       -0.3,-0.375,0,1,1,1;    //2
                       -0.3,0.375,0,1,1,1;     //3
                       0.3,0.375,0,1,1,1;      //4
                          
                       0.3,-0.375,0.6,0,0,0;   //5
                       -0.3,-0.375,0.6,0,0,0;  //6
                       -0.3,0.375,0.6,0,0,0;   //7
                       0.3,0.375,0.6,0,0,0;    //8
                           
                       0.3,-0.375,1.2,0,0,0;   //9
                       -0.3,-0.375,1.2,0,0,0;  //10  
                       -0.3,0.375,1.2,0,0,0;   //11
                       0.3,0.375,1.2,0,0,0;    //12
                           
                       0.3,-0.375,1.8,0,0,0;   //13
                       -0.3,-0.375,1.8,0,0,0;  //14
                       -0.3,0.375,1.8,0,0,0;   //15
                        0.3,0.375,1.8,0,0,0];   //16
                          
//define external force (please put orderly)
parameter Real F[Points*3]={0,0,0,
                            0,0,0, 
                            0,0,0, 
                            0,0,0, 
                            0,0,0, 
                            0,0,0, 
                            0,0,0, 
                            0,0,0, 
                            0,0,0, 
                            0,0,0, 
                            0,0,0, 
                            0,0,0, 
                            0,0,-500, 
                            0,0,-1000, 
                            0,0,-1000, 
                            0,0,-500}; 

//solution
Real displacement[N], reaction[N];
Real check[3]; 

Real stress1[Trusses];
Real safety[Trusses];
Real dis[3];
Real Str[3];
 
protected
parameter Integer N=3*Points;
Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3];
Real err=10e-10, ers=10e-4; 

algorithm
//Creating Global Matrix
G:=id;
for i in 1:Trusses loop
 for j in 1:3 loop
  q1[j]:=P[C[i,1],j];
  q2[j]:=P[C[i,2],j];
 end for;
      
   //Solving Matrix
   L:=Modelica.Math.Vectors.length(q2-q1);
   cx:=(q2[1]-q1[1])/L;
   cy:=(q2[2]-q1[2])/L;
   cz:=(q2[3]-q1[3])/L; 
   X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
                     cy*cx,cy^2,cy*cz;
                     cz*cx,cz*cy,cz^2]; 

  //Transforming to global matrix
  g:=zeros(N,N); 
  for m,n in 1:3 loop
    g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
    g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
    g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
    g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
  end for;  

G_star:=G+g;
G:=G_star;
end for;

//Implementing boundary
for x in 1:Points loop
if P[x,4] <> 0 then
  for a in 1:Points*3 loop
    G[(x*3)-2,a]:=0;
    G[(x*3)-2,(x*3)-2]:=1;
  end for;
end if;
if P[x,5] <> 0 then
  for a in 1:Points*3 loop
    G[(x*3)-1,a]:=0;
    G[(x*3)-1,(x*3)-1]:=1;
  end for;
end if;
if P[x,6] <> 0 then
  for a in 1:Points*3 loop
    G[x*3,a]:=0;
    G[x*3,x*3]:=1;
  end for;
end if;
end for;

//Solving displacement
displacement:=Modelica.Math.Matrices.solve(G,F);

//Solving reaction
reaction:=(G_star*displacement)-F;

//Eliminating float error
for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i];
displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;

//Checking Force
check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))});
check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))});
check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
 
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;

//Calculating stress in each truss
for i in 1:Trusses loop
for j in 1:3 loop
 q1[j]:=P[C[i,1],j];
 q2[j]:=P[C[i,2],j];
 dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
     
  //Solving Matrix
  L:=Modelica.Math.Vectors.length(q2-q1);
  cx:=(q2[1]-q1[1])/L;
  cy:=(q2[2]-q1[2])/L;
  cz:=(q2[3]-q1[3])/L; 
  X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
               cy*cx,cy^2,cy*cz;
               cz*cx,cz*cy,cz^2];
  
  Str:=(X*dis);
  stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;

//Safety factor
for i in 1:Trusses loop
if stress1[i]>0 then
  safety[i]:=Yield/stress1[i];
else
  safety[i]:=0;
end if; 
end for;

end Tugas_Besar_Ardiya;

Curve Fitting

function Kurva

input Real X[:];
input Real Y[size(X,1)];
input Integer order=2;
output Real Coe[order+1];

protected
Real Z[size(X,1),order+1];
Real ZTr[order+1,size(X,1)];
Real A[order+1,order+1];
Real B[order+1];

algorithm

for i in 1:size(X,1) loop
for j in 1:(order+1) loop
Z[i,j]:=X[i]^(order+1-j);
end for;
end for;
ZTr:=transpose(Z);

A:=ZTr*Z;
B:=ZTr*Y;
Coe:=Modelica.Math.Matrices.solve(A,B);

end Kurva;

Gold Optimization

model Gold_Opt

parameter Real xd[:];
parameter Real yd[size(xd,1)];
parameter Real xlo=64e-6;
parameter Real xhi=215e-6; 
parameter Integer N=10; // maximum iteration
parameter Real es=0.0001; // maximum error

Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3];
Real xopt,  fx;
protected
Real d, xl, xu, xint, R=(5^(1/2)-1)/2; 

algorithm
xl := xlo; 
xu := xhi;
y  := Kurva(xd,yd);
 
for i in 1:N loop
 d:= R*(xu-xl);
 x1[i]:=xl+d;
 x2[i]:=xu-d;
 f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
 f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
 xint:=xu-xl;

if f1[i]>f2[i] then
  xl:=x2[i];
  xopt:=x1[i];
  fx:=f1[i];
  else
    xu:=x1[i];
    xopt:=x2[i];
    fx:=f2[i];
end if;

ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
  break;
end if;
end for;

end Gold_Opt;

Hasil

Dis1.png
Dis 2.png
React1.png
Safety.png


































Kesimpulan Dengan penggunaan luas area sebsar 171 mm^2 atau material siku 40x40 dengan thickness 3mm, maka material yang paling optimal untuk digunakan adalah material dengan tingkat elastisitas sebesar 193 GPa

Material yang terletak dalam range elastisitas ini adalah material SS316L dengan tingkat elasitisas sama dengan nilai optimal yaitu 193 GPa.

UAS

UAS Ardiya no 1.jpg UAS Ardiya no 2.jpg UAS Ardiya no 3.jpg UAS Ardiya no 4.jpg UAS Ardiya no 5.jpg

Retrieved from "http://air.eng.ui.ac.id/index.php?title=Ardiya_Prajna_Hardianto&oldid=55196"