Difference between revisions of "Raihan Tsaqif A"
(→TUGAS BESAR METODE NUMERIK) |
(→TUGAS BESAR METODE NUMERIK) |
||
| Line 230: | Line 230: | ||
end CurveFitting; | end CurveFitting; | ||
| + | |||
| + | |||
| + | |||
| + | *Optimasi | ||
| + | model OptimasiRangka | ||
| + | |||
| + | parameter Real xd[:]={111e-6,141e-6,171e-6,231e-6,304e-6}; | ||
| + | parameter Real yd[size(xd,1)]={7.25e-5,7.83e-5,8.15e-5,8.31e-5,9.08e-5}; | ||
| + | parameter Real xlo=111e-6; | ||
| + | parameter Real xhi=425e-6; | ||
| + | parameter Integer N=10; // maximum iteration | ||
| + | parameter Real es=0.0001; // maximum error | ||
| + | |||
| + | Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3]; | ||
| + | Real xopt, fx; | ||
| + | protected | ||
| + | Real d, xl, xu, xint, R=(5^(1/2)-1)/2; | ||
| + | |||
| + | algorithm | ||
| + | xl := xlo; | ||
| + | xu := xhi; | ||
| + | y := Curve_Fitting(xd,yd); | ||
| + | |||
| + | for i in 1:N loop | ||
| + | d:= R*(xu-xl); | ||
| + | x1[i]:=xl+d; | ||
| + | x2[i]:=xu-d; | ||
| + | f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3]; | ||
| + | f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3]; | ||
| + | xint:=xu-xl; | ||
| + | |||
| + | if f1[i]>f2[i] then | ||
| + | xl:=x2[i]; | ||
| + | xopt:=x1[i]; | ||
| + | fx:=f1[i]; | ||
| + | else | ||
| + | xu:=x1[i]; | ||
| + | xopt:=x2[i]; | ||
| + | fx:=f2[i]; | ||
| + | end if; | ||
| + | |||
| + | ea[i]:=(1-R)*abs((xint)/xopt); | ||
| + | if ea[i]<es then | ||
| + | break; | ||
| + | end if; | ||
| + | end for; | ||
| + | end OptimasiRangka | ||
Revision as of 15:59, 6 January 2021
Biodata
Nama : Raihan Tsaqif A
NPM : 1906379176
TTL : Semarang, 8 Oktober 2001
Hobi : Belajar
Saya adalah mahasiswa teknik mesin angkatan 2019, saya tertarik mengambil jurusan teknik mesin karena saya melihat bahwa di seluruh dunia ini semua bekerja dengan mesin. Mesin tidak hanya sesuatu yang melakukan pembakaran akan tetapi sebuah mekanisme pada suatu benda juga bisa disebut mesin sehingga dapat disimpulkan bahwa jurusan ini memiliki cakupan ilmu teknik yang sangat luas. Tujuan saya dalam mengikuti mata kuliah ini adalah untuk menjadi insan yang berguna untuk lingkungan sekitar dan dapat mendobrak perkembangan teknologi di Indonesia.
Tugas Metode Numerik
Pada tugas kali ini saya menggunakan aplikasi modelica dalam menentukan perubahan momentum tiap satuan waktu atau sebutan lainnya adalah gaya. Oleh karena itu saya lampirkan video sebagai berikut, sehingga harapannya dapat memberikan penjelasan juga kepada yang lainnya.
QUIZ METNUM
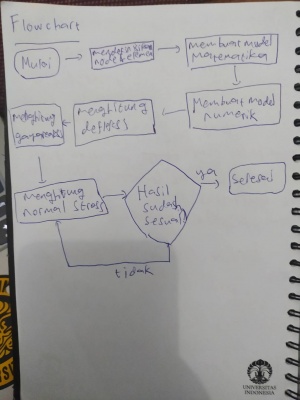
Flowchart
Pada quiz kali ini saya akan melampirkan langkah pengerjaan melalui flowchart
TUGAS BESAR METODE NUMERIK
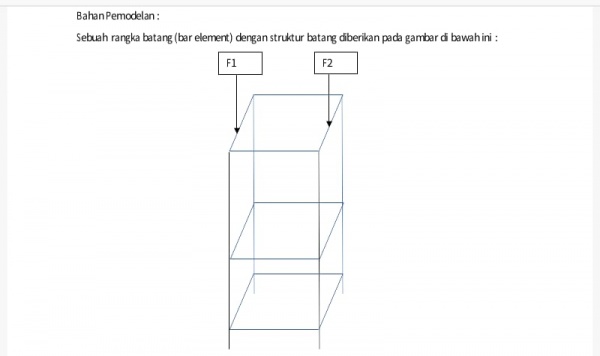
Dalam tugas besar ini kami diminta untuk mendesain rangka sesuai yang tertera dibawah dengan menggunakan rangka yang optimal dan cost yang minimum
Adapun Hal yang Harus Diperhitungkan sebagai Plotting
a. Harga material di dapat dari nilai optimum defleksi dan cross section
b. Material (Elastisitas properti)
c. Area Cross Section Truss (L profile/truss siku), luas cross section sebagai X
d. Defleksi sebagai Y
class contohkuis
//define initial variable parameter Integer Points=16; //Number of Points parameter Integer Trusses=24; //Number of Trusses parameter Real Area=0.000141; //Area (0.025m 'l' x 0.003m 'thickness') parameter Real Elas=68.9e9; //Elasticity Aluminium 6063
//define connection parameter Integer C[Trusses,2]=[1,5;
2,6;
3,7;
4,8;
5,6; //1st floor
6,7; //1st floor
7,8; //1st floor
5,8; //1st floor
5,9;
6,10;
7,11;
8,12;
9,10; //2nd floor
10,11;//2nd floor
11,12;//2nd floor
9,12; //2nd floor
9,13;
10,14;
11,15;
12,16;
13,14;//3rd floor
14,15;//3rd floor
15,16;//3rd floor
13,16];//3rd floor
//define coordinates (please put orderly) parameter Real P[Points,3]=[0.3,-0.375,0; //1
-0.3,-0.375,0; //2
-0.3,0.375,0; //3
0.3,0.375,0; //4
0.3,-0.375,0.6; //5
-0.3,-0.375,0.6; //6
-0.3,0.375,0.6; //7
0.3,0.375,0.6; //8
0.3,-0.375,1.2; //9
-0.3,-0.375,1.2; //10
-0.3,0.375,1.2; //11
0.3,0.375,1.2; //12
0.3,-0.375,1.8; //13
-0.3,-0.375,1.8; //14
-0.3,0.375,1.8; //15
0.3,0.375,1.8]; //16
//define external force (please put orderly) parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-500,
0,0,-1000,
0,0,-1000,
0,0,-500};
//define boundary parameter Integer b[:]={1,2,3,4};
//solution Real displacement[N], reaction[N]; Real check[3];
parameter Integer N=3*Points; Integer boundary[3*size(b,1)]=cat(1,(3*b).-2,(3*b).-1,3*b); Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; Real err=10e-10; Real ers=10e-4;
algorithm //Creating Global Matrix G:=id; for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary for i in boundary loop
for j in 1:N loop G[i,j]:=id[i,j]; end for;
end for;
//Solving displacement displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction reaction:=(G_star*displacement)-F;
//Eliminating float error for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))}); check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in (2:3:(N-1))}); check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for; end contohkuis;
Selanjutnya saya menampilkan pengolahan data yang saya lakukan di excel setelah melakukan riset material yang tersedia pada market
- Curve Fitting
function CurveFitting
input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coe[order+1];
protected Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1];
algorithm
for i in 1:size(X,1) loop
for j in 1:(order+1) loop Z[i,j]:=X[i]^(order+1-j); end for;
end for; ZTr:=transpose(Z);
A:=ZTr*Z; B:=ZTr*Y; Coe:=Modelica.Math.Matrices.solve(A,B);
end CurveFitting;
- Optimasi
model OptimasiRangka
parameter Real xd[:]={111e-6,141e-6,171e-6,231e-6,304e-6}; parameter Real yd[size(xd,1)]={7.25e-5,7.83e-5,8.15e-5,8.31e-5,9.08e-5}; parameter Real xlo=111e-6; parameter Real xhi=425e-6; parameter Integer N=10; // maximum iteration parameter Real es=0.0001; // maximum error
Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3]; Real xopt, fx; protected Real d, xl, xu, xint, R=(5^(1/2)-1)/2;
algorithm xl := xlo; xu := xhi; y := Curve_Fitting(xd,yd);
for i in 1:N loop
d:= R*(xu-xl);
x1[i]:=xl+d;
x2[i]:=xu-d;
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
xint:=xu-xl;
if f1[i]>f2[i] then
xl:=x2[i];
xopt:=x1[i];
fx:=f1[i];
else
xu:=x1[i];
xopt:=x2[i];
fx:=f2[i];
end if;
ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
break;
end if;
end for; end OptimasiRangka