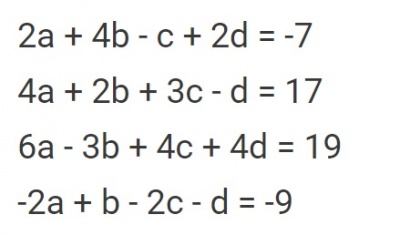Difference between revisions of "Abraham Mahendiartha Putra"
(→Tugas Besar Metode Numerik) |
(→Minggu 7 (Rabu, 24 December 2020)) |
||
| Line 722: | Line 722: | ||
Data kemudian dilakukan optimasi dan mendapatkan hasil sebagai berikut : | Data kemudian dilakukan optimasi dan mendapatkan hasil sebagai berikut : | ||
| + | |||
| + | [[File:AreaLocked Optimation.png|350px|center]] | ||
| + | |||
| + | '''Kesimpulan''' | ||
| + | |||
| + | Dengan penggunaan luas area sebsar 171 mm^2 atau material siku 30x30 dengan thickness 3mm, maka material yang paling optimal untuk digunakan adalah material dengan tingkat elastisitas sebesar 69,5 GPa atau sebesar 69,5 x 10^9 Pa. | ||
| + | |||
| + | Material yang terletak dalam range elastisitas ini adalah material AL 6060 dengan tingkat elasitisas sama dengan nilai optimal yaitu 69.5 GPa. | ||
Revision as of 15:11, 6 January 2021
Biodata Diri
Nama : Abraham Mahendiartha Putra
NPM : 1806201390
TTL : Jakarta, 25 Mei 2000
Hobi : Bersepeda
Saya adalah mahasiswa FTUI angkatan 2018 dari jurusan Teknik Mesin dan saya adalah salah satu ciptaan terbaik dari Tuhan Yang Maha Esa, karena pada prinsipnya Tuhan Yang Maha Esa itu mendesain manusia dengan sebaik-baiknya makhluk.
Saya merupakan mahasiswa dari Universitas Indonesia dengan jurusan Teknik Mesin. Saya selalu termotivasi untuk mengembangkan kemampuan saya baik secara akademik maupun non akademik, dengan cara metode pembelajaran baik di dalam maupun diluar universitas. Saya berharap saya dapat menjadi orang yang dapat membantu bagi sekitar saya di masa depan.
Contents
- 1 Biodata Diri
- 2 Tujuan Pembelajaran
- 3 Mata Kuliah Metode Numerik
- 3.1 Minggu 1 (Rabu, 11 November 2020)
- 3.2 Minggu 2 (Rabu, 18 November 2020)
- 3.3 Minggu 3 (Rabu, 25 November 2020)
- 3.4 Minggu 3 (Rabu, 2 December 2020)
- 3.5 Minggu 4 (Rabu, 9 December 2020)
- 3.6 Minggu 5 (Senin, 14 Decmber 2020)
- 3.7 Minggu 6 (Rabu, 16 December 2020)
- 3.8 Minggu 7 (Rabu, 24 December 2020)
Tujuan Pembelajaran
Tujuan dari pembelajaran metode numerik ini adalah :
- 1. Membuat saya paham konsep dengan dengan baik tentang dasar-dasar dari metode numerik. Jika tidak dapat memahami konsep dengan baik maka tidak dapat mengerti.
- 2. Memampukan saya memahami konsep didalam sebuah model numerik.
- 3. Memampukan saya dalam mengerjakan soal teknik dengan ilmu numerik.
- 4. Sebagai nilai tambah bagi saya agar menjadi manusia yang beradab seperti pada Sila ke-2 Pancasila.
Mata Kuliah Metode Numerik
Selama pelajaran metode numerik sebelum uts ini, saya belajar tentang adanya error atau kesalahan di dalam metode numerik, serta saya juga belajar tentang banyaknya pendekatan aproksimasi dalam menentukan sebuah faktor-faktor sebuah persamaan. Cara-cara yang digunakan cukup banyak, dengan salah satunya adalah Newton-Rhapson, Bisection, serta secant method. Selain hal tersebut saya juga diajarkan metode interpolasi yang mana metode ini dapat membantu saya dalam menentukan sebuah angka diantara 2 buah data.
Pada diskusi pembelajaran Rabu 11 November 2020, saya belajar bahwa sebagai manusia saya memang sering merasa saya mengerti dan paham banyak hal. Namun diatas semua itu, saya harus mengetahui limitasi serta harus tau bahwa Tuhan adalah yang paling mengerti dan paling tau di dunia ini. Saya diberikan sebuah contoh pemahaman dengan menghitung nilai 1/0 dimana nilai tersebut tidak dapat di definisikan oleh manusia, tapi nilai tersebut hanya diketahui oleh Tuhan karena pada akhirnya Tuhan adalah Yang Maha Esa.
Minggu 1 (Rabu, 11 November 2020)
Tugas 1
Pada minggu pertama ini, setiap mahasiswa diminta untuk melihat dan mempraktikan tentang tutorial atau dasar Open Modellica dari youtube. Kemudian kami juga diharapkan untuk mengupload video tutorial singkat. Berikut ini adalah video basic tutorial dari saya untuk penghitungan defleksi statik pada Open Modellica
Minggu 2 (Rabu, 18 November 2020)
Pada minggu kedua ini, kelas kami diminta untuk mereview dan menunjukan apa yang telah kami pelajari dari minggu pertama kemarin, serta apa yang telah kami pelajari dirumah pada aplikasi Open Modellica. Dalam kelas minggu 2, saya menunjukan apa yang telah saya buat pada Pak Dai dan Asisten. Selain itu, pada minggu ke 2 ini saya diajari apa alasan pemilihan penggunaan Open Modellica oleh Pak Dai, dimana Open Modellica bukanlah merupakah aplikasi programming namun aplikasi ini lebih terfokuskan untuk modelling dan perhitungan, sehingga hal ini yang menyebabkan penghitungan pada Open Modellica menjadi lama karena bahasa yang kita tulis pada Open Modellica akan di translate terlebih dahulu dalam bahasa C++ kemudian akan di proses kembali menjadi data-data perhitungan.
Dalam minggu kedua ini, kami juga mempelajari ilmu baru yaitu tentang class panggil dari file function. Dimana contoh fungsi yang kita buat adalah sebagai berikut :
FungsiTambahX1
function FungsiTambahX1 input Real x; output Real y; algorithm y:=x+10; end FungsiTambahX1;
Kemudian, kami membuat kelas untuk memanggil file fungsi yang telah kami buat diatas :
Panggil
class Panggil parameter Real x1=5; Real hasil10tambahx1; equation hasil10tambahx1=FungsiTambahX1(x1);
Dengan menggunakan file panggil diatas, nilai input x1 dapat didapatkan berdasarkan nilai yang diketik pada kelas panggil dan nilai input akan masuk terhadap function yang dipanggil oleh kelas panggil.
Tugas 2
Pada minggu ini, kami diberikan tugas kedua untuk membuat fungsi panggil seperti yang dicontohkan dalam perkelasan Metode Numerik pekan 2, dengan menggunakan persamaan algebra simultan dan variabel array. Dalam algebra simultan, ada beberapa variabel yang harus dicari valuenya dan variabel array adalah adalah variabel yang memiliki beberapa data nilai di dalamnya.
Dalam tugas ini saya akan membuat 4 persamaan sederhana dengan 4 nilai variabel yang nilainya harus dicari. Soal dari tugas 2 ini adalah sebagai berikut :
Kemudian, saya membuat file seperti berikut ini untuk menghitung persamaan berikut:
GaussFunction
function GaussFunction input Real A[4,4]; input Real B[4]; output Real R[4]; algorithm R:=Modelica.Math.Matrices.solve(A,B); end GaussFunction;
GaussJordan
class GaussJordan
parameter Real A[4,4]=[2,4,-1,2;4,2,3,-1;6,-3,4,4;-2,1,-2,-1];
parameter Real B[4]={-7,17,19,-9};
Real X[4];
equation
X=GaussFunction(A,B);
end GaussJordan;
Dengan menggunakan perhitungan diatas ini, maka didapatkan hasil sebagai berikut di Open Modellica, yang mana perhitungan ini saya bandingkan langsung dengan solusi manual yang diberikan oleh sebuah website. Hasil ini menunjukan bahwa hasil perhitungan jika data yang dimasukan adalah sama, maka tidak mungkin memiliki hasil yang berbeda.

Selain itu saya juga membuat sebuah video untuk menunjukan hasil yang telah saya buat dan cara memasukan data jika bentuk matriks yang diberikan adalah berbeda, serta bagaimana cara menangani jika ada error yang terjadi dalam proses pengerjaan.
Minggu 3 (Rabu, 25 November 2020)
Pada minggu ketiga ini, kami mempelajari tentang cara-cara penyelesaian lain pada open Modellica. Yang difokuskan pada minggu ini adalah penggunaan array dalam penggunaan Open Modellica, dimana array adalah kumpulan himpunan penyelesaian. Didalam array penting adanya penggunaan pembatasan itterasi dengan menggunakan parameter integer. Selain itu, Pak Dai juga mengajak kami agar mencoba membuat pseudocode saya sendiri tanpa menggunakan fungsi yang digunakan oleh OpenModellica. Dalam proses ini, saya juga dibantu jelaskan oleh teman saya yaitu Christo tentang pseudocode GaussJordan yang telah ia buat, yang bentuknya adalah berikut ini :
GaussJordan.mo
function GaussJordan
input Real [:,:] A;
output Real [:,:] B;
protected // untuk local variable
Integer h = 1; //pivot row
Integer k = 1; //pivot coloumn
Integer m = size(A,1); //Number of row
Integer n = size(A,2); //Number of column
Integer c = 0;
Integer max_row; // Row index of max number in pivot column
Real [:] pivot_column;
Real [:] pivot_row;
Real [:,:] temp_array;
Real r;
Real float_error = 10e-10;
algorithm
//fungsi input A dan output B
B := A;
while h <= m and k <= n loop
for i in 1 : m loop
for j in 1 : n loop
if abs(B[i,j]) <= float_error then
B[i,j] := 0;
end if;
end for;
end for;
//Finding pivot
pivot_column:= {B[i,h] for i in h:m};
//Mencari baris terbawah yang mempunyai nilai pivot tertinggi
c:=h-1;
for element in pivot_column loop
c:= c+1;
if abs(element)== max(abs(pivot_column)) then
max_row :=c;
end if;
end for;
//Jika tidak ada pivot di kolom ini, pindah ke kolom selanjutnya
if B[max_row,k] == 0 then
k:=k+1;
else
// tukar row h - max_row
temp_array := B;
temp_array[h] := B[max_row];
temp_array[max_row] := B[h];
B:= temp_array;
//devide pivot row by pivot number
B[h] := B[h]/B[h,k];
for i in (h+1) :m loop
r := B[i,k]/B[h,k];
B[i,k]:=0;
for j in (k+1) : n loop
B[i,j] := B[i,j]-B[h,j] * r;
end for;
end for;
//move ke pivot kolom dan row selanjutnya
h := h+1;
k := k+1;
end if;
end while;
// proses dari kanan atas
h :=m;
k :=n;
while h >=1 and k>=1 loop
//dealing with error
for i in 1:m loop
for j in 1:n loop
if abs(B[i,j]) <=float_error then
B[i,j]:=0;
end if;
end for;
end for;
//finding pivot
pivot_row := {B[h,i] for i in 1:k};
//Get position index k of pivot
c := 0;
for element in pivot_row loop
c := c+1;
if element <> 0 then
break;
end if;
end for;
k:= c;
// no pivot in this row, move to next row
if B[h,k] == 0 then
h:= h-1;
else
//perform row operatation
for i in 1:(h-1) loop
r := B[i,k];
B[i] := B[i] - B[h] *r;
end for;
//move to next pivot row dan column
h:=h+1;
k:=k+1;
end if;
end while;
end GaussJordan;
Tugas 4
Pada hari ini kamu juga diberi tugas untuk menerapkan Pseudocode mathlab dari Figure 9.4 yang ada di buku terhadap open modellica. Dimana pseudocode untuk tugas ini yang telah saya buat adalah sebagai berikut :
PseudoCode Truss
PR_Truss
class PR_Truss
parameter Integer N=8; //Bentuk matriks berapa x berapa
parameter Real A=0.001;
parameter Real E=200e9;
Real KG[N,N];
Real KGinitial[N,N];
Real Sol[N];
Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033};
Real R[N];
Real SolMat[N,1];
Real XMat[N,1];
Real L1=1;
Real L2=1;
Real L3=1.6;
Real L4=1.25;
Real L5=1.6;
Real Tetha1=degtorad(0);//Data dari Chegg
Real Tetha2=degtorad(0);//Data dari Chegg
Real Tetha3=degtorad(231.34);//Data dari Chegg
Real Tetha4=degtorad(270);//Data dari Chegg
Real Tetha5=degtorad(308.66);//Data dari Chegg
//Boundary
Integer b1=1;
Integer b2=3;
//Truss 1
Real X1=Tetha1;
Real k1=A*E/L1;
Real K1[4,4];
Integer p1o=1;
Integer p1i=2;
Real KG1[N,N];
//Truss 2
Real X2=Tetha2;
Real k2=A*E/L2;
Real K2[4,4];
Integer p2o=2;
Integer p2i=3;
Real KG2[N,N];
//Truss 3
Real X3=Tetha3;
Real k3=A*E/L3;
Real K3[4,4];
Integer p3o=2;
Integer p3i=4;
Real KG3[N,N];
//Truss 4
Real X4=Tetha4;
Real k4=A*E/L4;
Real K4[4,4];
Integer p4o=1;
Integer p4i=4;
Real KG4[N,N];
//Truss 5
Real X5=Tetha5;
Real k5=A*E/L5;
Real K5[4,4];
Integer p5o=3;
Integer p5i=4;
Real KG5[N,N];
algorithm
//Pembuatan K Global
K1:=Stiffness_Matrices(X1);
KG1:=k1*Local_Global(K1,N,p1o,p1i);
K2:=Stiffness_Matrices(X2);
KG2:=k2*Local_Global(K2,N,p2o,p2i);
K3:=Stiffness_Matrices(X3);
KG3:=k3*Local_Global(K3,N,p3o,p3i);
K4:=Stiffness_Matrices(X4);
KG4:=k4*Local_Global(K4,N,p4o,p4i);
K5:=Stiffness_Matrices(X5);
KG5:=k5*Local_Global(K5,N,p5o,p5i);
KG:=KG1+KG2+KG3+KG4+KG5;
KGinitial:=KG;
//Implementing Boundary
for i in 1:N loop
KG[2*b1-1,i]:=0;
KG[2*b1,i]:=0;
KG[2*b2-1,i]:=0;
KG[2*b2,i]:=0;
end for;
KG[2*b1-1,2*b1-1]:=1;
KG[2*b1,2*b1]:=1;
KG[2*b2-1,2*b2-1]:=1;
KG[2*b2,2*b2]:=1;
//Solving Displacement
Sol:=Gauss_Jordan(N,KG,X);
//Solving Reaction Force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaction_Trusses(N,KGinitial,SolMat,XMat);
end PR_Truss;
PseudoCode Panggil
degtorad
function degtorad input Real deg; output Real rad; protected constant Real pi = 3.14; algorithm rad:=deg*pi/180; end degtorad;
Stiffness_Matrices
function Stiffness_Matrices
input Real A;
output Real X[4,4];
protected
Real Y;
Real float_error = 10e-10;
final constant Real pi=2*Modelica.Math.asin(1.0);
algorithm
Y:=A;
X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,-
Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-
(Modelica.Math.sin(Y))^2;
-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),
(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),
(Modelica.Math.sin(Y))^2];
for i in 1:4 loop
for j in 1:4 loop
if abs(X[i,j]) <= float_error then
X[i,j] := 0;
end if;
end for;
end for;
end Stiffness_Matrices;
Local_Global
function Local_Global input Real Y[4,4]; input Integer B; input Integer p1; input Integer p2; output Real G[B,B]; algorithm for i in 1:B loop for j in 1:B loop G[i,j]:=0; end for; end for; G[2*p1,2*p1]:=Y[2,2]; G[2*p1-1,2*p1-1]:=Y[1,1]; G[2*p1,2*p1-1]:=Y[2,1]; G[2*p1-1,2*p1]:=Y[1,2]; G[2*p2,2*p2]:=Y[4,4]; G[2*p2-1,2*p2-1]:=Y[3,3]; G[2*p2,2*p2-1]:=Y[4,3]; G[2*p2-1,2*p2]:=Y[3,4]; G[2*p2,2*p1]:=Y[4,2]; G[2*p2-1,2*p1-1]:=Y[3,1]; G[2*p2,2*p1-1]:=Y[4,1]; G[2*p2-1,2*p1]:=Y[3,2]; G[2*p1,2*p2]:=Y[2,4]; G[2*p1-1,2*p2-1]:=Y[1,3]; G[2*p1,2*p2-1]:=Y[2,3]; G[2*p1-1,2*p2]:=Y[1,4]; end Local_Global;
Reaction_Trusses
function Reaction_Trusses input Integer N; input Real A[N,N]; input Real B[N,1]; input Real C[N,1]; output Real Sol[N]; protected Real X[N,1]; Real float_error = 10e-10; algorithm X:=A*B-C; for i in 1:N loop if abs(X[i,1]) <= float_error then X[i,1] := 0; end if; end for; for i in 1:N loop Sol[i]:=X[i,1]; end for; end Reaction_Trusses;
Gauss_Jordan
function Gauss_Jordan input Integer N; input Real A[N,N]; input Real B[N]; output Real X[N]; protected Real float_error = 10e-10; algorithm X:=Modelica.Math.Matrices.solve(A,B); for i in 1:N loop if abs(X[i]) <= float_error then X[i] := 0; end if; end for; end Gauss_Jordan;
Minggu 3 (Rabu, 2 December 2020)
Buatlah Diagram Class dan Flowchart untuk coding dari Josiah Enrico.
Quiz 1
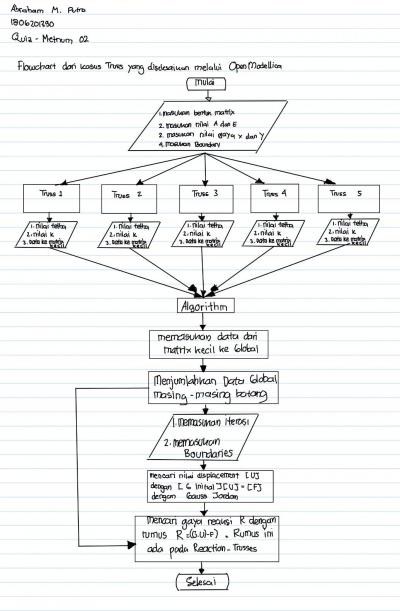
Flow chart yang buat berdasarkan flowchart tersebut yang dapat saya mengerti adalah sebagai berikut :
Serta untuk ClassDiagram yang dapat saya mengerti adalah sebagai berikut:
Minggu 4 (Rabu, 9 December 2020)
Buatlah coding dan pelajari openmodellica dari Fahmi atau Josiah Enrico
Tugas 4
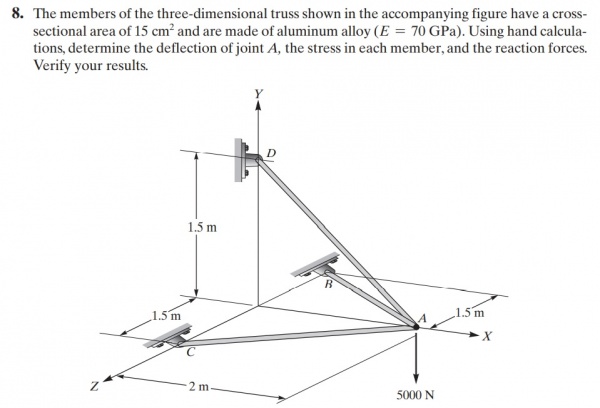
Soal No.8
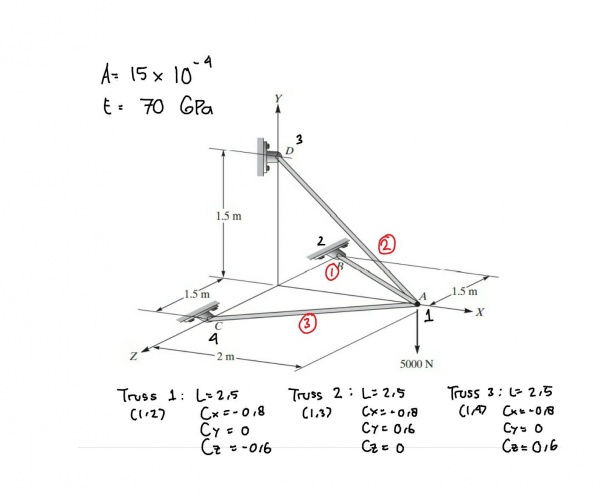
Dimana sebelom dikerjakan, diperlukan pembuatan FBD dari soal tersebut sebagai berikut :
Serta penulisan data pada matrix akan sebagai berikut :
Data : [{Truss} , {Node1} , {Node2}, {Cx} , {Cy} , {Cz} , {A} , {E} , {L}]
dan local akan sebagai berikut :
Local : [{Node} , {Fx} , {Fy} , {Fz}]
Dengan referensi coding untuk 3D truss tersebut berdasarkan referensi dari Ahmad Mohammad Fahmi,
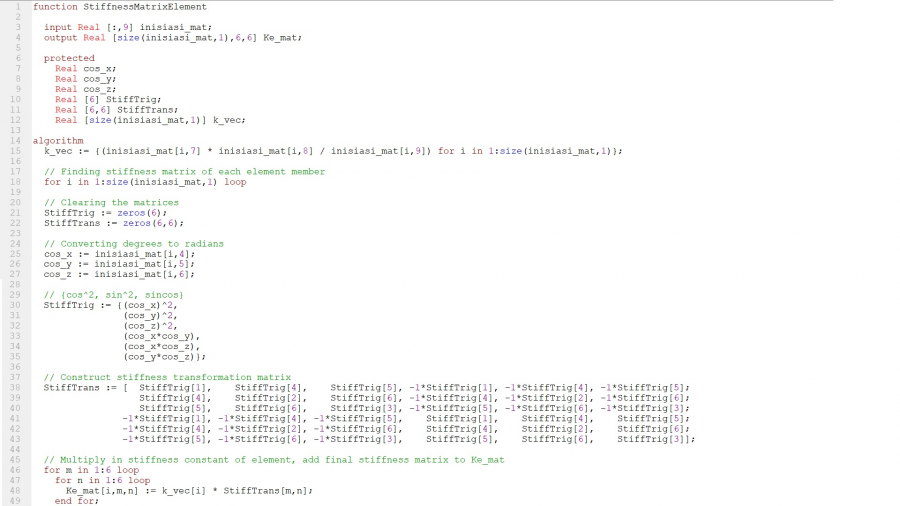
Maka step pertama yang dilakukan adalah membuat Stiffness Matrix Element, dimana proses ini dilakukan untuk menentukan nilai per matrix kecil (per truss)
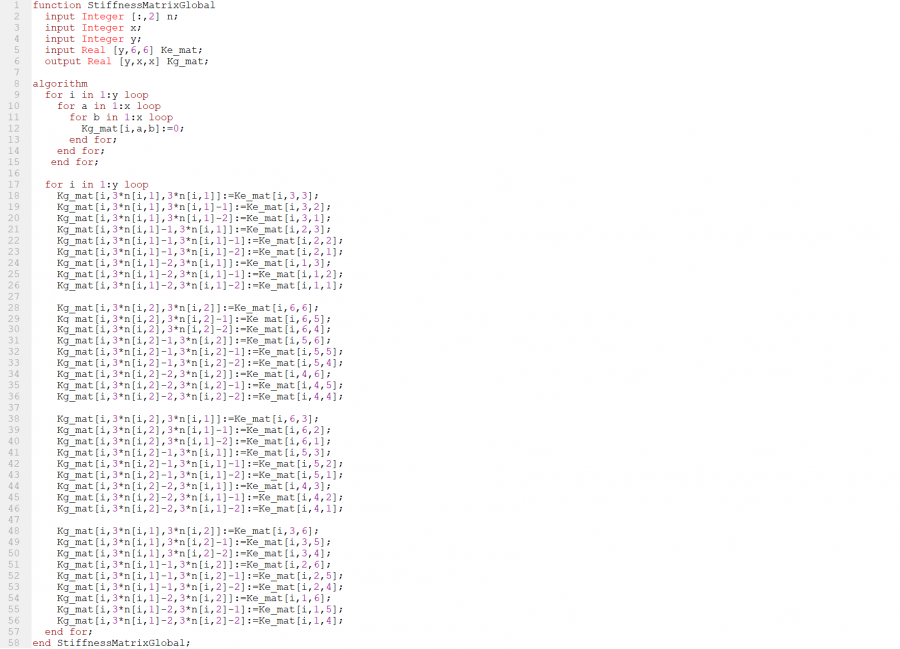
Kemudian step kedua yang dilakukan adalah membuat Stiffness Matrix Global, dimana pembuatan ini dilakukan untuk membuat format dari matrix global dan untuk menyatukan data dari matrix elemen yang ada
Kemudian matrix global dari setiap elemen akan dijumlahkan dengan fungsi :
Setelah itu diperlukan membuat boundaries untuk perhitungan loop nantinya
Lalu matrix akan diselesaikan perhitungannya menggunakan Gauss Jordan yang telah dibuat yaitu :
Dan untuk melihat reaction dari persoalannya maka digunakan function sebagai berikut :
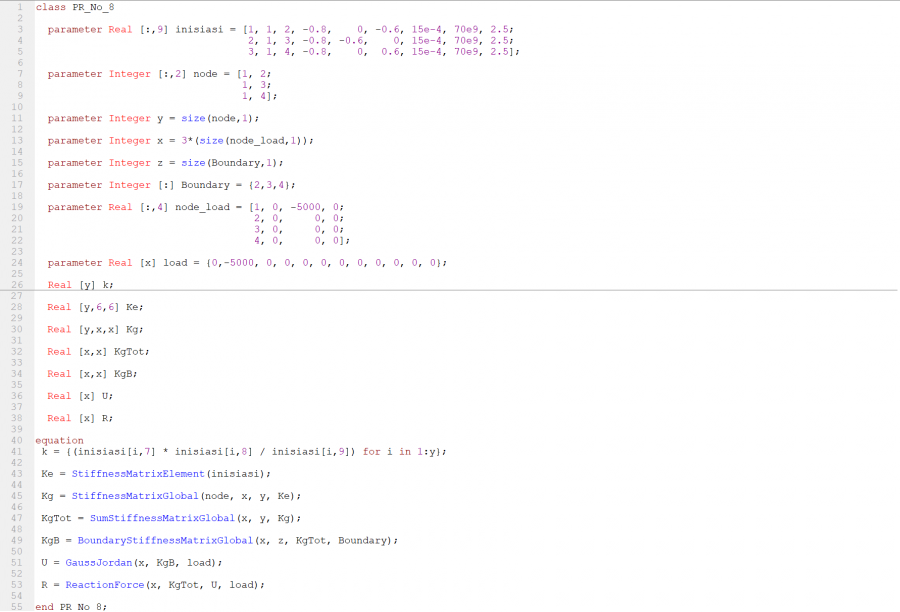
Serta yang terakhir adalah dibuat Class untuk memanggil semua fungsi yang dibuat dan melihat hasil dari U dan R
Terakhir, akan dilakukan proses simulate yang akan menghasilkan 2 data yang dicari
Nilai U (Displacement)Nilai R (Reaction Force)
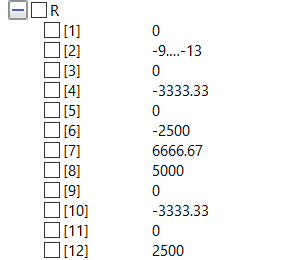
Untuk membantu menjelaskan, maka telah saya buat video singkat untuk persoalan tersebut :
Minggu 5 (Senin, 14 Decmber 2020)
Pada minggu ke 5 ini, dilakukan sebuah pertemuan kelas pengganti. Seharusnya, pertemuan ke-5 ini diadakan pada Rabu 9 December 2020 namun diakibatkan adanya PILKADA di Indonesia yang mengakibatkan libur nasional, maka pertemuan ini diadakan di Senin 14 December 2020 ini. Dalam minggu ini kami diajarkan untuk melakukan muhasabah dan melakukan self-assessment terhadap kemampuan kami masing-masing secara sejujurnya. Kami dalam mengisi nilai harus mengetahui batasan kami masing-masing dalam ilmu yang telah kami pelajari serta harus dapat menjelaskan apa yang telah kami pelajari untuk menunjukan bukti pembelajaran yang telah kami lakukan.
Minggu 6 (Rabu, 16 December 2020)
Pada minggu ke 6 ini, sebelum dimulainya perkuliahan kami diberikan materi terlebih dahulu tentang optimasi sebuah sistem dengan menggunakan Open Modellica. Materi ini dijelaskan melalui sebuah video oleh Bu Candra tentang penjelasan suatu kasus optimasi serta pseudocode dari kasus tersebut. Sebuah sistem adalah kumpulan komponen yang tersusun dan bekerja sama untuk mencapai suatu tujuan. Optimasi sendiri adalah mencari nilai terbaik atau paling efisien dari suatu sistem.
Sebelum perkuliahan dimulai, kami diajak untuk mencoba sendiri dan melakukan diskusi bersama teman perkuliahan. Pseudocode dari OpenModellica saya adalah seperti berikut:
FungsiObjek.mo
function FungsiObjek input Real x; output Real y; algorithm y:= 2*Modelica.Math.sin(x)-x^2/10; end FungsiObjek;
Dimana fungsi ini akan menjadi sebuah fungsi yang ada dipanggil dengan file jenis model.
GoldenMethod.mo
model GoldenMethod
parameter Integer n = 8;
Real x1[n];
Real x2[n];
Real xup;
Real xlow;
Real f1[n];
Real f2[n];
Real xopt;
Real yopt;
Real d;
algorithm
xup := 4;
xlow := 0;
for i in 1:n loop
d:=((5^(1/2)-1)/2) * (xup-xlow);
x1[i] := xlow+d;
x2[i] := xup-d;
f1[i] := FungsiObjek(x1[i]);
f2[i] := FungsiObjek(x2[i]);
if f1[i]>f2[i] then
xup := xup;
xlow := x2[i];
xopt := xup;
yopt := f1[i];
else
xlow :=xlow;
xup := x1[i];
xopt := xup;
end if;
end for;
end GoldenMethod;
Pada kelas model ini, digunakan untuk memanggil fungsi yang telah dibuat terlebih dahulu
Minggu 7 (Rabu, 24 December 2020)
Pada minggu ke-7 ini, kami diberikan quiz untuk menghitung data dari Truss 3D yang diperoleh soal yang diberikan.
Tugas Besar Metode Numerik
Latar Belakang
Optimasi merupakan salah satu kunci dalam proses desain suatu benda untuk mencapai hasil yang paling optimal. Dengan menggunakan optimasi, maka kualitas suatu benda dan harga suatu benda dapat disesuaikan dan dapat cari titik paling efektifnya yang sesuai dengan target yang diinginkan dengan cost serendah-rendahnya.
Tujuan
Dengan menggunakan optimasi ini, maka mahasiswa dapat mendesain benda sesuai dengan ketentuan yang diberikan namun memiliki harga yang paling murah serta memiliki kemampuan yang sama atau melebihi dari target penggunaan.
Ilustrasi Soal
Data Diketahui
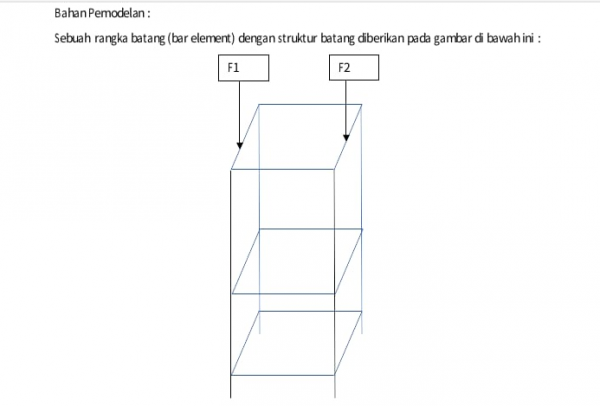
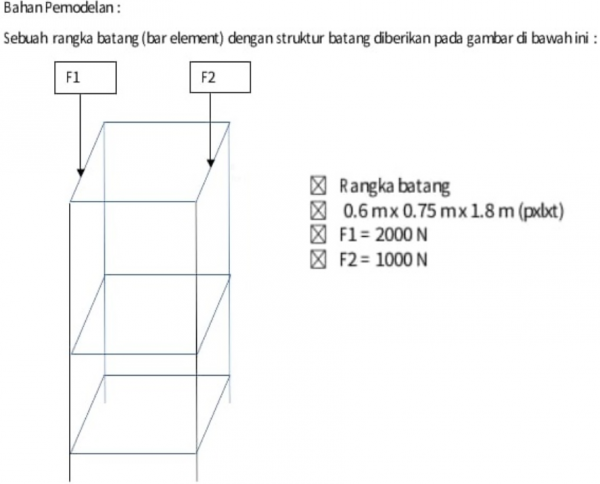
Jenis Konstruksi : Rangka batang dengan struktur batang
•Dimensi rangka batang (PxLxT) : 0.6 m x 0.75 m x 1.8 m
•F1 = 2000N (Ditengah-tengah bar)
•F2 = 1000N (Ditengah-tengah bar)
Ketentuan
•Mengoptimasi agar mendapatkan harga termurah dengan faktor berubah kekuatan dan area
Asumsi yang Digunakan
• Tidak terjadi lendutan pada konstruksi
• Beban terdistribusi rata antara dua node
• Lantai dasar bersifat fix
Metodologi Pengerjaan
Dalam proses pengerjaan tugas besar ini, dibuat codingan sesuai dengan model yang ada serta menggunakan codingan ini untuk mengoptimasi agar mendapat material dengan harga serta ukuran yang paling cocok.
Dalam tugas besar ini saya mengasumsikan bahwa nilai cross-sectional area dari truss sebagai variabel bebasnya serta nilai yang dicari sebagai harga-nya.
Untuk penghitungan dalam tugas optimasi ini, saya menggunakan material dengan spesifikasi sebagai berikut :
•Jenis Material : Alumunium 6063 •Ultimate Tensile Strength : 241 MPa •Tensile Yield Strength : 214 MPa •Shear Strength : 152 MPa •Modulus of Elasticity : 68.9 GPa •Shear Modulus : 25.8 GPa
Optimasi
Dalam proses mengoptimasi data, dilakukan 2 metode pendekatan :
1. Jenis Material yang digunakan telah ditentukan dengan Al 6063 dan luas besi siku divariasikan.
2. Luas Penampang yang digunakan adalah 0.000171 m^2 dan akan dicari material yang optimal.
Dalam proses pengolahan data untuk optimasi, maka dicari terlebih dahulu total harga, safety factor, serta rasio safety factor terhadap cost, yang kemudian akan diolah dengan curve fitting.
1. Elasticity Locked
Data excel dibawah ini adalah data yang digunakan :
Data kemudian dilakukan optimasi dan mendapatkan hasil sebagai berikut :
Kesimpulan Berdasarkan optimasi yang telah dilakukan, maka paling ideal untuk luas penampang rangka dengan material Al 6063 adalah 0,000089 m^2 atau 89 mm^2
2. Area Locked
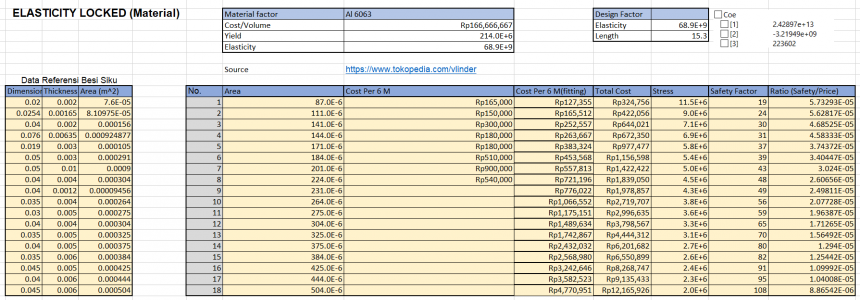
Data excel dibawah ini adalah data yang digunakan :
Data kemudian dilakukan optimasi dan mendapatkan hasil sebagai berikut :
Kesimpulan
Dengan penggunaan luas area sebsar 171 mm^2 atau material siku 30x30 dengan thickness 3mm, maka material yang paling optimal untuk digunakan adalah material dengan tingkat elastisitas sebesar 69,5 GPa atau sebesar 69,5 x 10^9 Pa.
Material yang terletak dalam range elastisitas ini adalah material AL 6060 dengan tingkat elasitisas sama dengan nilai optimal yaitu 69.5 GPa.