Difference between revisions of "Metnum03-Laksita Aji Safitri"
| Line 749: | Line 749: | ||
Menghitung safty factor dan rasio | Menghitung safty factor dan rasio | ||
| − | [[File:rasiogold1.jpg|centre| | + | [[File:rasiogold1.jpg|centre|700px]] |
kemudian,Memilih material yang paling optimal dengan menggunakan kodingan seperti berikut: | kemudian,Memilih material yang paling optimal dengan menggunakan kodingan seperti berikut: | ||
| Line 878: | Line 878: | ||
Menghitung safty factor dan rasio | Menghitung safty factor dan rasio | ||
| − | [[File:rasiogold2.jpg|centre| | + | [[File:rasiogold2.jpg|centre|700px]] |
kemudian,Memilih material yang paling optimal dengan menggunakan kodingan seperti berikut: | kemudian,Memilih material yang paling optimal dengan menggunakan kodingan seperti berikut: | ||
| Line 929: | Line 929: | ||
[[File:hasilopt.gold2.jpg|centre|700px]] | [[File:hasilopt.gold2.jpg|centre|700px]] | ||
| + | |||
| + | jadi dapat diambil kesimpulan,dari perhitungan yang di dapat dari optimasi maupun perhitungan, kita dapat menggunakan material SS400/A36 dengan dimensi 40x40x4 | ||
Revision as of 22:50, 4 January 2021
ASSALAMU'ALAIKUM WR.WB
Contents
- 1 BIODATA DIRI
- 2 Pertemuan 1 Metode Numerik 03 (Senin,9 November 2020)
- 3 Tugas 1
- 4 Pertemuan 2 Metode Numerik 03 (Senin,16 November 2020)
- 5 Tugas 2
- 6 Pertemuan 3 Metode Numerik 03 (Senin,23 November 2020)
- 7 Tugas 3
- 8 Pertemuan 4 Metode Numerik 03 (Senin,30 November 2020)
- 9 Quis 2
- 10 Tugas 4 (Quis 2)
- 11 Pertemuan 5 Metode Numerik 03 (Senin,7 Desember 2020)
- 12 Tugas 5
- 13 Pertemuan 6 Metode Numerik 03 (Senin,14 Desember 2020)
- 14 Pertemuan 7 Metode Numerik 03 (Senin,21 Desember 2020)
- 15 TUBES
BIODATA DIRI
Nama : LAKSITA AJI SAFITRI
NPM : 1906435523
Agama : Islam
Program studi : S1-Teknik Mesin
Pertemuan 1 Metode Numerik 03 (Senin,9 November 2020)
Untuk pembelajaran sebelum pasca UTS kita telah mengenal beberapa metode dalam numerik, yaitu
1. Deret Taylor dan Derer Mclaurin
merupakan representasi dari fungsi matematika sebagai jumlah tak hingga dari suku-suku yang nilainya dihitung dari turunan fungsi tersebut disuatu titik.deret ini dapat dianggap sebagai limit polinomial taylor.bila deret tersebut terpusat pada titik 0 atau a=0, maka deret tersebut dapat diartikan sebagai deret mclaurin atau deret taylor baku. nilai Rn(x) merupakan tangkisan errror yang mana jika kita menentukan turunan hingga turunan ke 4, maka turunan ke 5 dan seterusnya merupakan error
deret tailor dan deret mclaurin ini sagat bermanfaat dalam metode numerik untuk menghitung atau menghampiri nilai -nilai fungsi yang susah dihitungsecara manual seperti nilai sinx,cosx,ln(x+1) dll
2. Open Methode
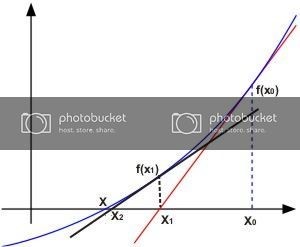
a. Newton-Raphson Method
Metode Newton-Raphson adalah metode pencarian akar suatu fungsi f(x) dengan pendekatan satu titik, dimana fungsi f(x mempunyai turunan. Metode ini dianggap lebih
mudah dari Metode Bagi-Dua (Bisection Method) karena metode ini menggunakan pendekatan satu titik sebagai titik awal. Semakin dekat titik awal yang kita pilih
dengan akar sebenarnya, maka semakin cepat konvergen ke akarnya.
Prosedur Metode Newton :
menentukan x_0 sebagai titik awal, kemudian menarik garis lurus (misal garis l) yang menyinggung titik f(x_0). Hal ini berakibat garis l memotong sumbu-x di titik
x_1. Setelah itu diulangi langkah sebelumnya tapi sekarang x_1 dianggap sebagai titik awalnya. Dari mengulang langkah-langkah sebelumnya akan mendapatkan x_2,
x_3, ..... x_n dengan x_n yang diperoleh adalah bilangan riil yang merupakan akar atau mendekati akar yang sebenarnya.
Perhatikan gambar diatas untuk menurunkan rumus Metode Newton-Raphson:
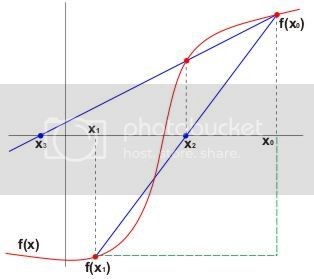
b.Secant Method
Pada Metode Newton-Raphson memerlukan syarat wajib yaitu fungsi f(x) harus memiliki turunan f'(x). Sehingga syarat wajib ini dianggap sulit karena tidak semua
fungsi bisa dengan mudah mencari turunannya. Oleh karena itu muncul ide dari yaitu mencari persamaan yang ekivalen dengan rumus turunan fungsi. Ide ini lebih
dikenal dengan nama Metode Secant. Ide dari metode ini yaitu menggunakan gradien garis yang melalui titik (x_0, f(x_0)) dan (x_1, f(x_1)). Perhatikan gambar
dibawah ini.
Prosedur Metode Secant :
Ambil dua titik awal, misal x_0 dan x_1. Ingat bahwa pengambilan titik awal tidak disyaratkan alias pengambilan secara sebarang. Setelah itu hitung x_2 menggunakan rumus diatas. Kemudian pada iterasi selanjutnya ambil x_1 dan x_2 sebagai titik awal dan hitung x_3. Kemudian ambil x_2 dan x_3 sebagai titik awal dan hitung x_4. Begitu seterusnya sampai iterasi yang diingankan atau sampai mencapai error yang cukup kecil.
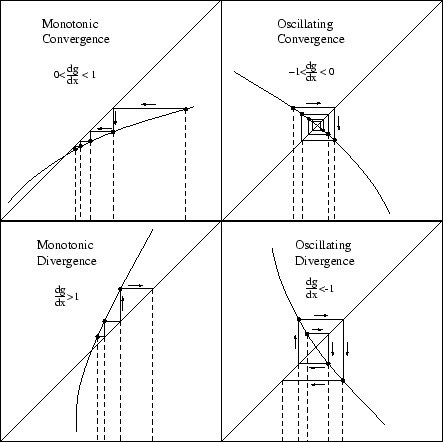
c.Simple fixed point
Metode Titik Tetap adalah suatu metode pencarian akar suatu fungsi f(x) secara sederhana dengan menggunakan satu titik awal. Perlu diketahui bahwa fungsi f(x) yang ingin dicari hampiran akarnya harus konvergen. Misal x adalah Fixed Point (Titik Tetap) fungsi f(x) bila g(x) = x dan f(x) = 0.
Prosedur Metode Titik Tetap
Misal f(x) adalah fungsi yang konvergen dengan f(x) = 0, maka untuk mencari nilai akarnya atau hampiran akarnya kita terlebih dahulu mengubah kedalam bentuk x = g(x). Kemudian tentukan nilai titik awal, misal x1. Setelah itu disubstitusikan titik awalnya ke persamaan g(x) sedemikian sehingga g(x1) = x2, setelah itu titik x2 yang diperoleh substitusikan lagi ke g(x) sedemikian sehingga g(x2) = x3. Jadi apabila ditulis iterasinya akan menjadi
x1 (penetuan titik awal)
x2 = g(x1) (iterasi pertama)
x3 = g(x2) (iterasi kedua)
........
xn = g(xn-1) (iterasi ke-n)
Seperti rumus iterasi lain, maka kesalahan aproksimasinya:
Iterasi ini akan berhenti jika x = g(x) dan f(x) = 0 atau sudah mencapai nilai error yang cukup kecil (|xn – xn-1| < ἐ).
3. Bracketing method
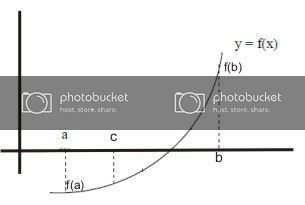
a.bisection method
Metode Bagi-Dua adalah algoritma pencarian akar pada sebuah interval. Interval tersebut membagi dua bagian, lalu memilih dari dua bagian ini dipilih bagian mana yang mengandung akar dan bagian yang tidak mengandung akar dibuang. Hal ini dilakukan berulang-ulang hingga diperoleh akar persamaan atau mendekati akar persamaan. Metode ini berlaku ketika ingin memecahkan persamaan f(x)=0 dengan f(x) merupakan fungsi kontinyu.
Prosedur Metode Bagi-Dua :
Misal dijamin bahwa f(x) adalah fungsi kontinyu pada interval [a, b] dan f(a)f(b) < 0. Ini artinya bahwa f(x) paling tidak harus memiliki akar pada interval [a, b]. Kemudian definisikan titik tengah pada interval [a, b] yaitu c = {a+b}/{2}. Dari sini kita memperoleh dua subinterval yaitu [a, c] dan [c, b]. Setelah itu, cek apakah f(a)f(c) < 0 atau f(b)f(c) < 0 ? Jika f(a)f(c) < 0 maka b = c (artinya titik b digantikan oleh titik c yang berfungsi sebagai titik b pada iterasi berikutnya), jika tidak maka a = c. Dari iterasi pertama kita memperoleh interval [a, b] yang baru dan titik tengah c yang baru. Kemudian lakukan pengecekan lagi seperti sebelumnya sampai memperoleh error yang cukup kecil.
b.false position method
alternatif perbaikan dari metode interval bagi-dua (bisection method) yang kurang efisien.Kekurangan metode bagi-dua adalah dalam membagi selang mulai dari xlower
sampai xupper menjadi bagian yang sama; besaran f(xl) dan f(xu) tidak diperhitungkan, misalnya f(xl) apakah lebih dekat ke nol atau ke f(xu).
Untuk aplikasi pada matakuliah metode numerik, kita menggunakan aplikasi OpenModelica. yang mana aplikasi ini merupakan perangkat lunak permodelan dan simuasi open source yang ditujukan untuk penggunaan industri dan akademik.Pengembangan jangka panjangnya didukung oleh organisasi nirlaba-Open Source Modelica Consotium (OSMC).
Tujuan dengan upaya OpenModelica adalah untuk menciptakan lingkungan permodelan,kompilasi dan simulasi open source modelica yang komprehensif berdasarkan perangkat lunak bebas yang didistribusikan dalam bentuk kode sumber dan biner untuk penelitian, pengajaran dan penggunaan industri.
Website: http://openmodelica.org/
Tugas 1
Pengaplikasian deret mclaurin dengan menggunakan OpenModelica
youtube: https://www.youtube.com/watch?v=jCt1Vy0FRp4
Pertemuan 2 Metode Numerik 03 (Senin,16 November 2020)
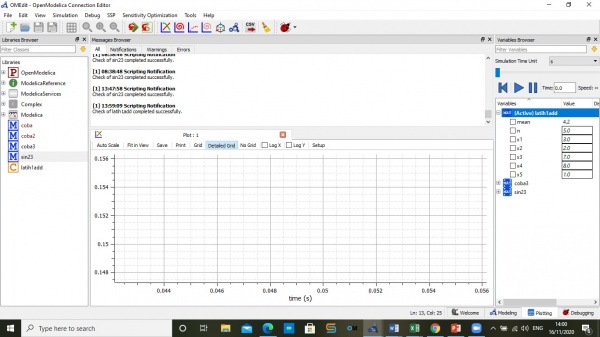
Paada minggu ini saya belajar tentang cara mengkoding dengan menggunakan aplikasi modeica untu menghitung nilai mean dan membuat koding untuk mengitung nilai y1 menggunakan Specialization function dan class, berikut hasil pembelajaran yang telah disampaikan
1.Latihan membuat koding mean dengan jumlah data 10 dengan menggunakan openmodelica
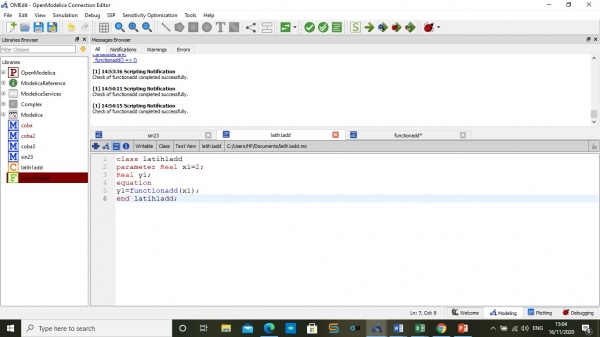
2.Latihan membuat koding untuk mencari nilai y1 menggunakan menggunakan Specialization function dan class
Tugas 2
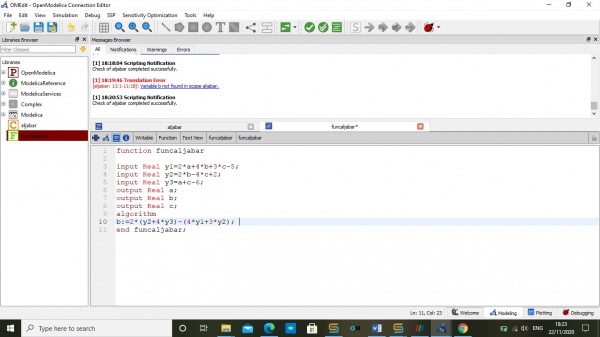
1.Latihan membuat koding untuk mencari nilai a,b dan c pada 3 persamaan menggunakan Specialization function dan class
1. f(x)= 2a+4b+3c-5
2. f(x)= 2b-4c+2
3. f(x)= a+c-6
I. Kita membuat fuction equation untuk menyelesaikan persamaan diatas
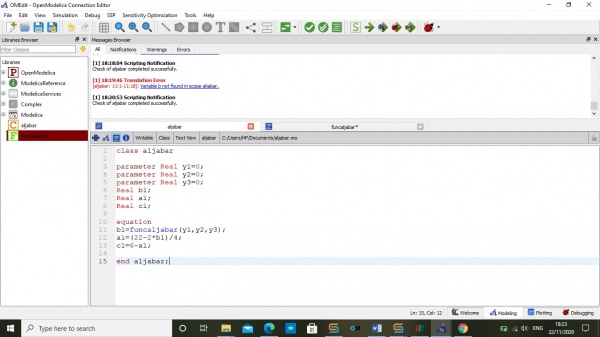
II. Kita membuat class dengan memanggil equation pada koding function
III. Hasil Perhitungan a,b dan c
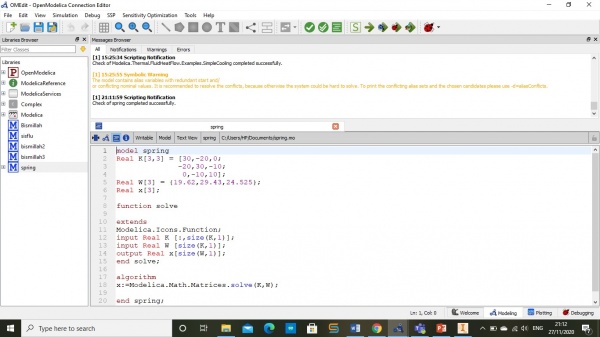
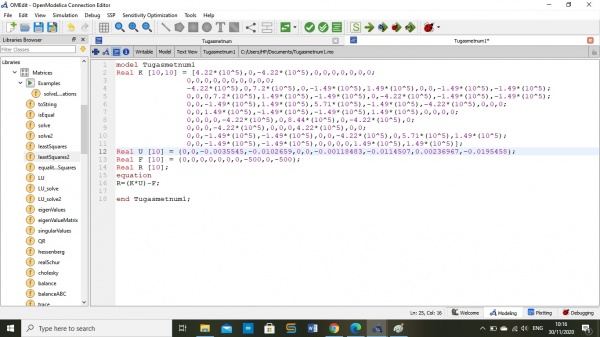
2.Latihan membuat koding untuk mencari nilai X1,X2 dan X3 pada 3 persamaan menggunakan Perintah library pda modelica (Modelica.Math.Mactrices.solve(A,b)
I. Menentukan soal yang akan kita gunakan
disini terdapat 3 persamaan aljabar simultan yang akan diselesaikan dengan metode Gauss Elimination dengan mengubah soal tersebut kedalam matriks.
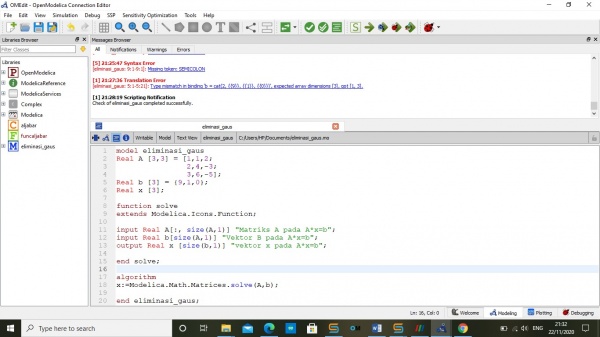
II. Membuat koding penyelesaian dengan eliminasi gaus
setelah mengubah soal menjadi matriksm kemudian kita akan membuat kodingan seperti pada gambar berikut:
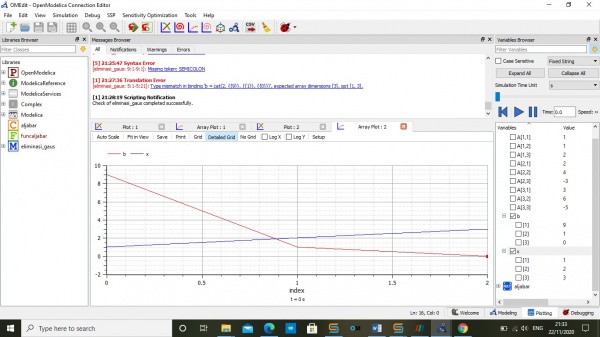
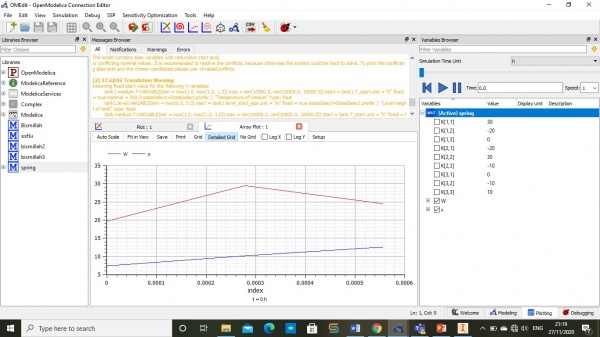
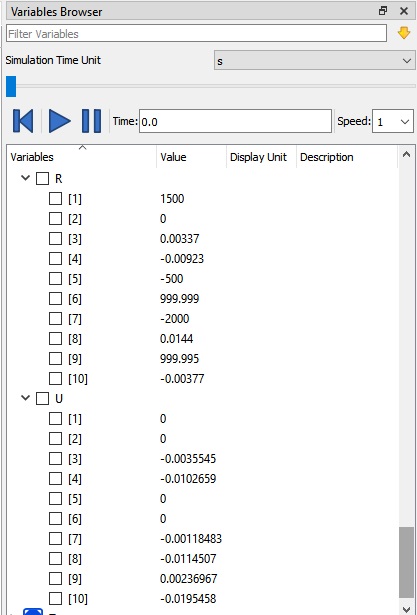
III. Hasil matriks
dari hasil kodingan yang telah aplikasikan, maka akan menemukan hasilkan nilai dari X1,x2 dan x3 yaitu
x1=1,
x2=2
x3=3
Pertemuan 3 Metode Numerik 03 (Senin,23 November 2020)
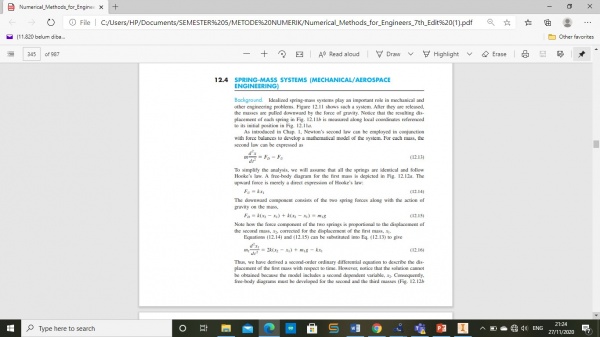
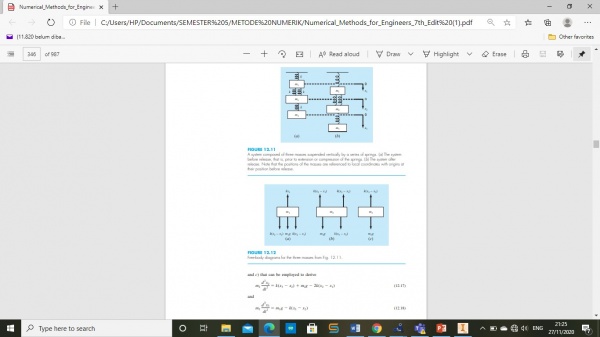
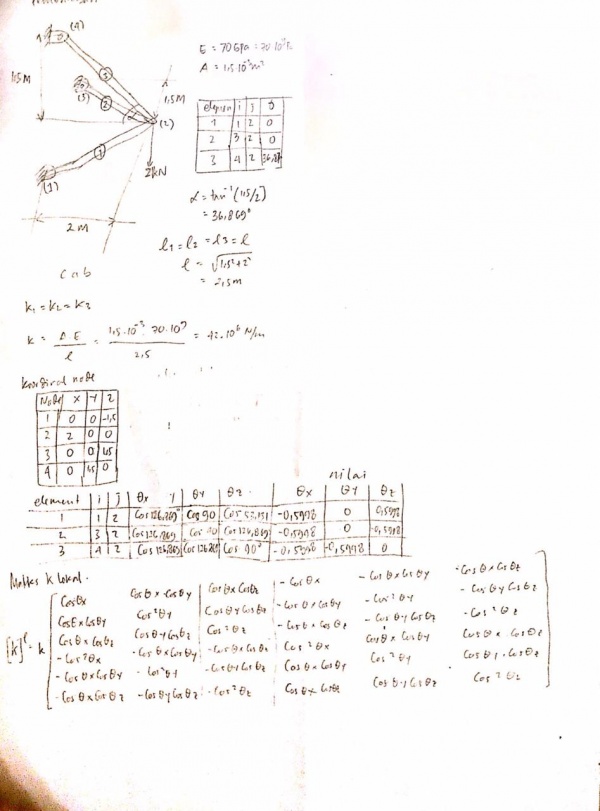
Pada hari ini kami diminta untuk mempelajari respon dan displacement dari soal pegas yang ada di buku hal 327 dan membuktikan perhitungan tsb. untuk soal nya yaitu:
dengan pengaplikasian Openmodelica kita dapat mengetahui nilai displacementnya:
Tugas 3
Menggunakan metode matriks untuk menghitung deflekdi yang ada pada rangkaian berikut:
Hasil kodingan yang di buat yaitu,
Pertemuan 4 Metode Numerik 03 (Senin,30 November 2020)
Quis 2
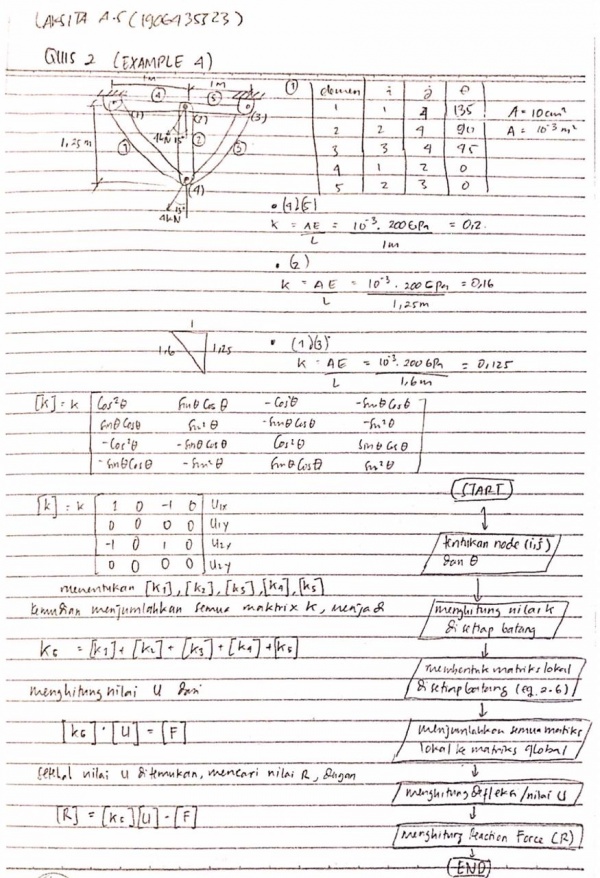
Pada hari ini, kami diberikan quis yang berisikan soal berikut,
lalu untuk langkah pertama kami membuat flowchart yaang akan dipergunakan untuk perhitungan di openmodelica
Tugas 4 (Quis 2)
Melakukan perhitungan secra manual untuk penyelesaian dari soal quiz 2
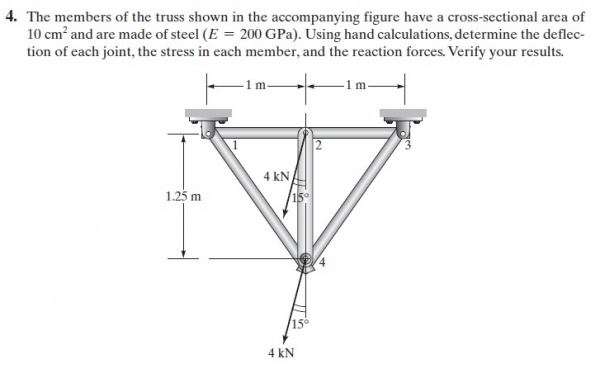
1. SOAL 2D
Penyelesaian:
Hasil kodinng
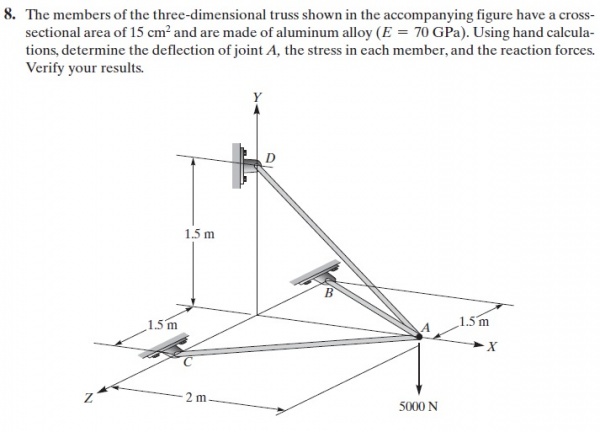
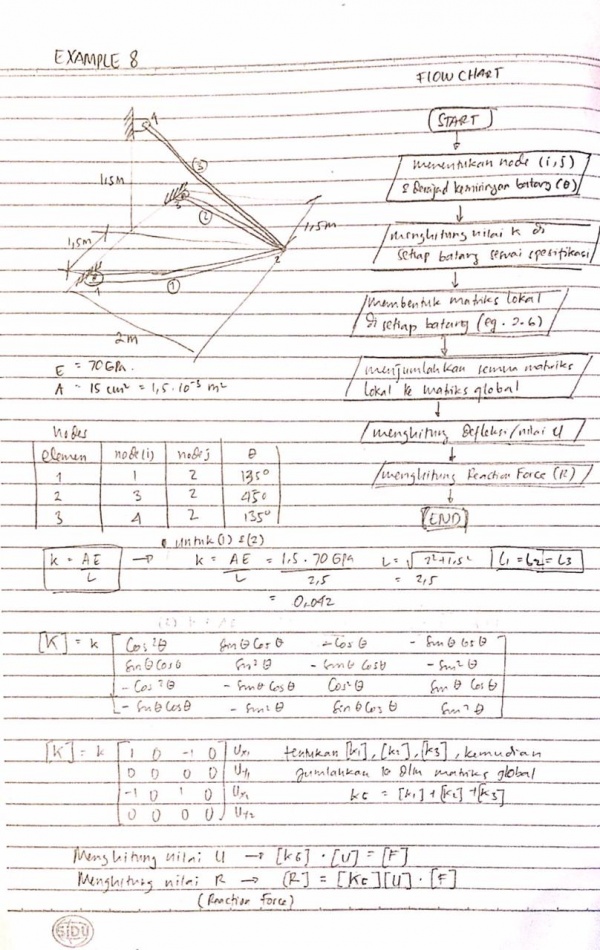
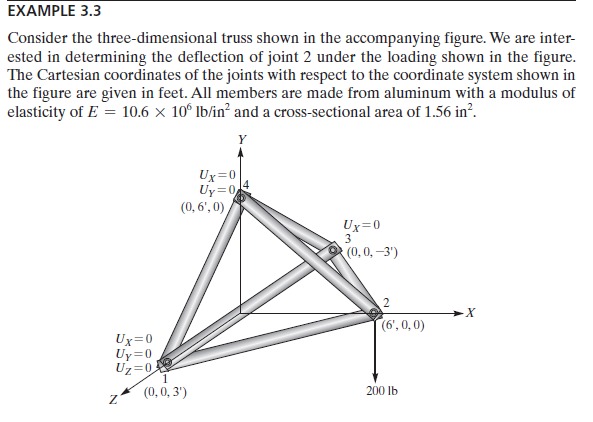
SOAL 3D
penyelesaian:
Pertemuan 5 Metode Numerik 03 (Senin,7 Desember 2020)
Pembahasan Quiz 2. Jadi, dari pengerjaan soal kuis 2, terdapat beberapa koreksi mengenai hasil koding yang saya buat. yaitu sebagai berikut:
Soal 2D
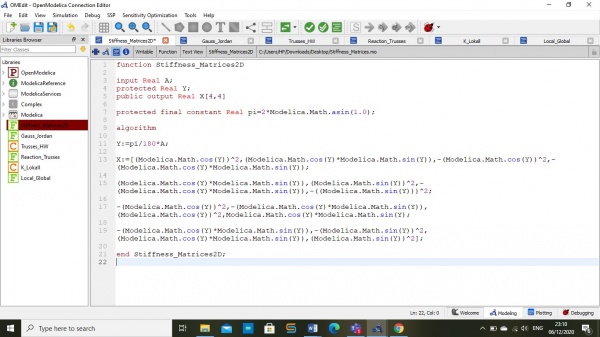
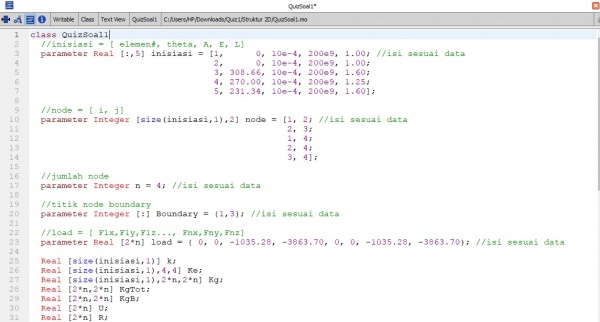
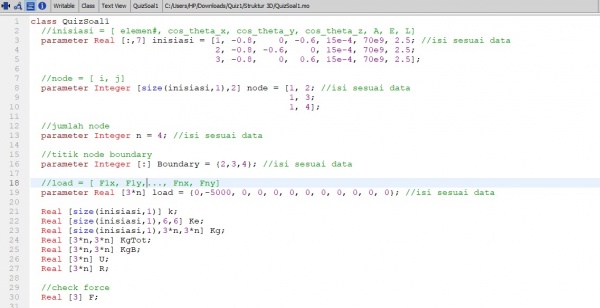
pada soal diatas kita akan menyelesaikan soal tersebut degan 1 class dan 7 Function. yang mana fuction tersebut digunakan untuk mempermudah proses perhitungnan, yag akan terpanggil ketika file function disebut dalam class.
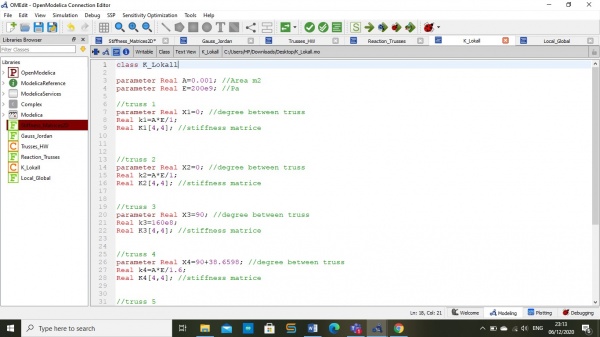
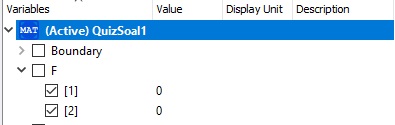
1. Membuat Class dengan memasukan beberapa fuction yang akan digunakan. class ini berfungsi untuk me-list data input,output maupun fuction yag akan kita gunakan.
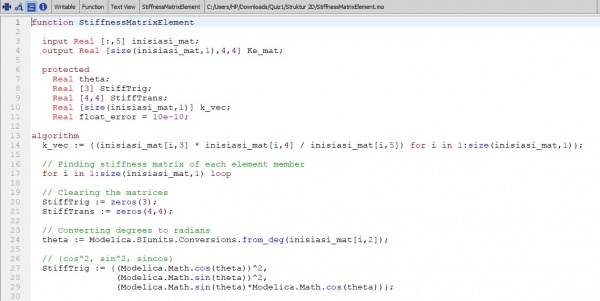
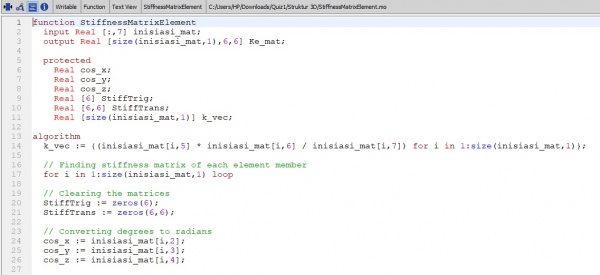
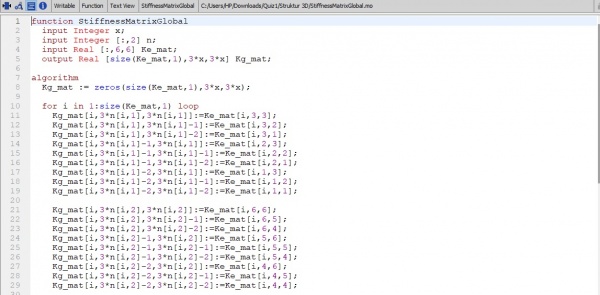
2. membuat fuction K atau matriks nilai K lokal per elemen/ batang
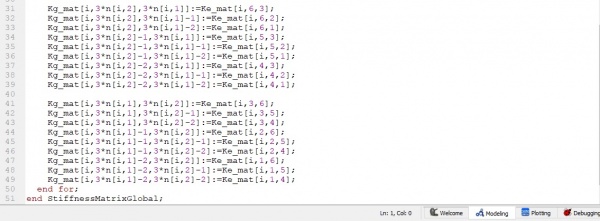
3. Setelah membuat fuction Ke lokal, maka akan dirubah menjadi Kg atau k global
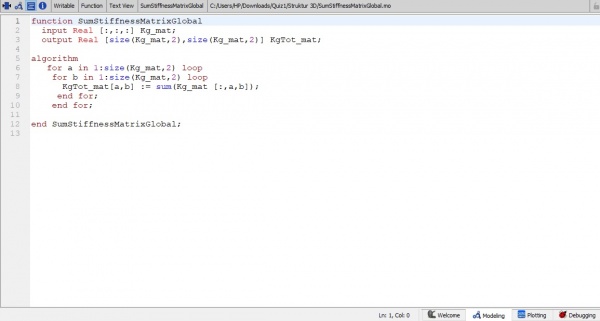
4. Setelah merubah menjadi k globa maka k global tersebut akan di tambahkan sebagai total Kglobal. Rumusnya yaitu SumKg= Kg1+Kg2+Kg3+Kg4+Kg5
5. Setelah Kg digabungkan maka dilakukan boundary pada setiap batang sesuai dengan node yang terhubung
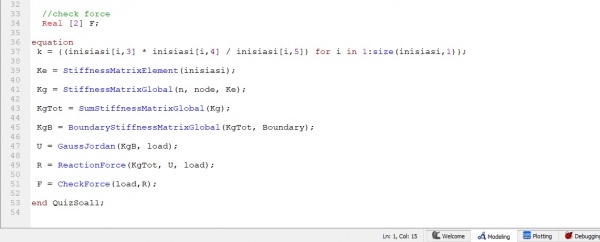
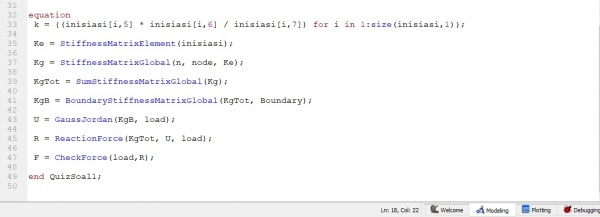
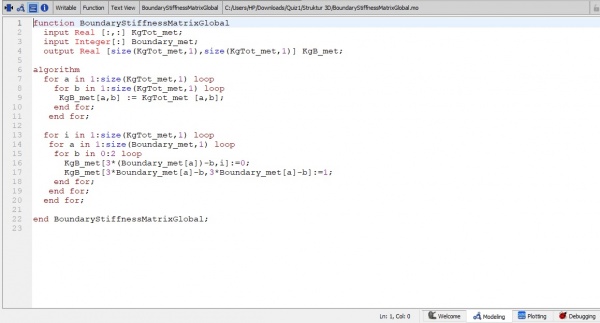
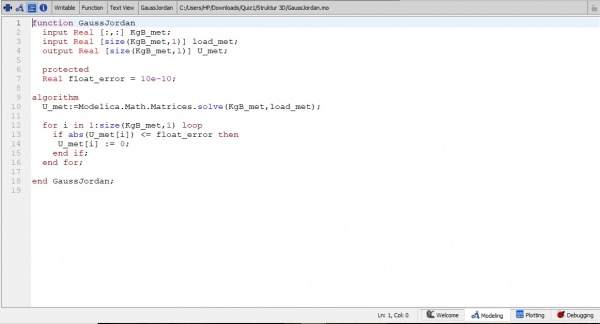
6.setelah dilakukan boundary di setiap batangnya, maka dilakukna penyederhanaan melalui gaus jordan
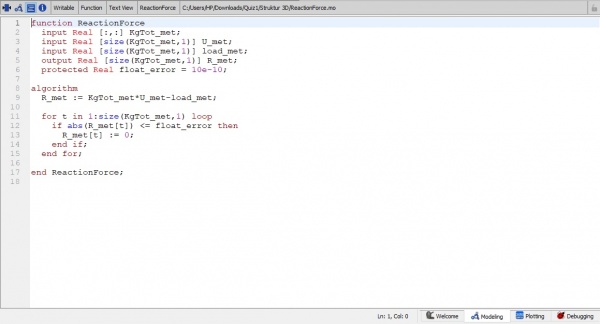
7. setelah dilakukan gauss jordan maka kita bisa meghitung Reaction Force dari matriks yang kita dapatkan
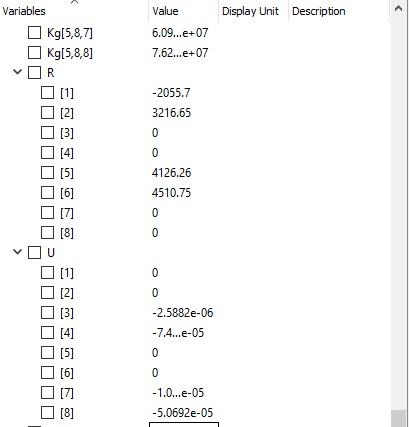
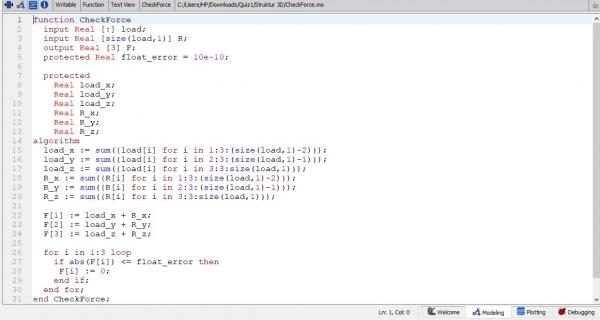
8. dari hasil reaction force yang kita hitung, maka kita akan melihat hasil dari reactin force, apakah sudah seimbang atau belum (F=0)
9. Hasil koding perhitungan
Soal 3D
pada soal diatas kita akan menyelesaikan soal tersebut degan 1 class dan 7 Function. yang mana fuction tersebut digunakan untuk mempermudah proses perhitungnan, yag akan terpanggil ketika file function disebut dalam class.
1. Membuat Class dengan memasukan beberapa fuction yang akan digunakan. class ini berfungsi untuk me-list data input,output maupun fuction yag akan kita gunakan.
2. membuat fuction K atau matriks nilai K lokal per elemen/ batang
3. Setelah membuat fuction Ke lokal, maka akan dirubah menjadi Kg atau k global
4. Setelah merubah menjadi k globa maka k global tersebut akan di tambahkan sebagai total Kglobal. Rumusnya yaitu SumKg= Kg1+Kg2+Kg3+Kg4+Kg5
5. Setelah Kg digabungkan maka dilakukan boundary pada setiap batang sesuai dengan node yang terhubung
6.setelah dilakukan boundary di setiap batangnya, maka dilakukna penyederhanaan melalui gaus jordan
7. setelah dilakukan gauss jordan maka kita bisa meghitung Reaction Force dari matriks yang kita dapatkan
8. dari hasil reaction force yang kita hitung, maka kita akan melihat hasil dari reactin force, apakah sudah seimbang atau belum (F=0)
9. Hasil koding perhitungan
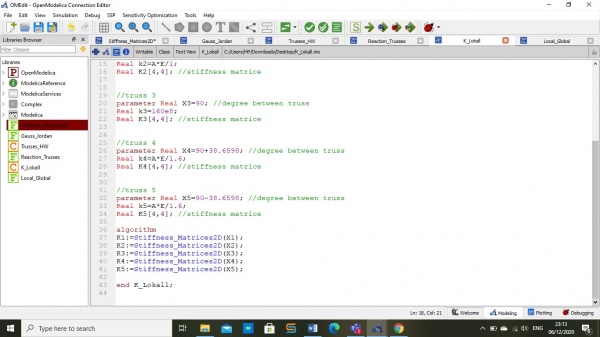
Tugas 5
Soal
Penyelesaian:
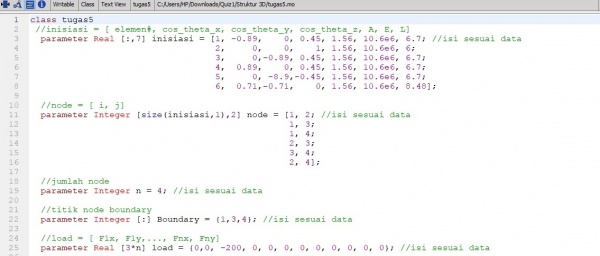
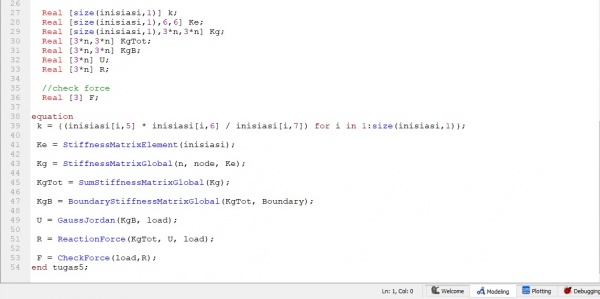
pada soal diatas kita akan menyelesaikan soal tersebut degan 1 class dan 7 Function. yang mana fuction tersebut digunakan untuk mempermudah proses perhitungnan, yag akan terpanggil ketika file function disebut dalam class.
1. Membuat Class dengan memasukan beberapa fuction yang akan digunakan. class ini berfungsi untuk me-list data input,output maupun fuction yag akan kita gunakan.
2. membuat fuction K atau matriks nilai K lokal per elemen/ batang
3. Setelah membuat fuction Ke lokal, maka akan dirubah menjadi Kg atau k global
4. Setelah merubah menjadi k globa maka k global tersebut akan di tambahkan sebagai total Kglobal. Rumusnya yaitu SumKg= Kg1+Kg2+Kg3+Kg4+Kg5
5. Setelah Kg digabungkan maka dilakukan boundary pada setiap batang sesuai dengan node yang terhubung
6.setelah dilakukan boundary di setiap batangnya, maka dilakukna penyederhanaan melalui gaus jordan
7. setelah dilakukan gauss jordan maka kita bisa meghitung Reaction Force dari matriks yang kita dapatkan
8. dari hasil reaction force yang kita hitung, maka kita akan melihat hasil dari reactin force, apakah sudah seimbang atau belum (F=0)
9. Hasil koding perhitungan
Pertemuan 6 Metode Numerik 03 (Senin,14 Desember 2020)
pada pertemuan ini, kami diminta untuk mereview pembelajaran selama paska UTS mengenai penggunaan aplikasi modelica. dan disini kami dijelaskan dari beberapa koding. yaitu untuk pembahasan menggunakan 1 model ataupun menggunakan 1class 7 fuction.
Pertemuan 7 Metode Numerik 03 (Senin,21 Desember 2020)
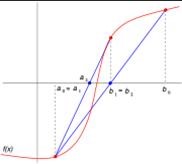
pada materi hari ini ita mempeljari one-dimensional unconstrained optimization yangn digunakan untuk menentukan niali maksimum atau minimum dari suatu permasalahan, disini terdapay fungsi objektif dan konstrain. namunn pada pembahasan kali ini menjelaskan tentang optimasi fungsi grafik tanpa konstrain. Metode yang kami lakukan yaitu Bracked Optimization Using Golden Ratio method. jadi pada metode ini terdapat suatu grafik fungsi yang memiliki nilai F(X) global max dan lokal max, serta F(X) min Global dan min lokal.
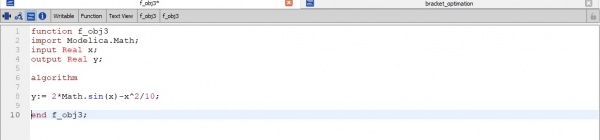
Contoh: F(x)= 2*sin(x)-x^2/10
Penyelesaian dengan open modelica:
1.Membuat 1 fuction optimasi
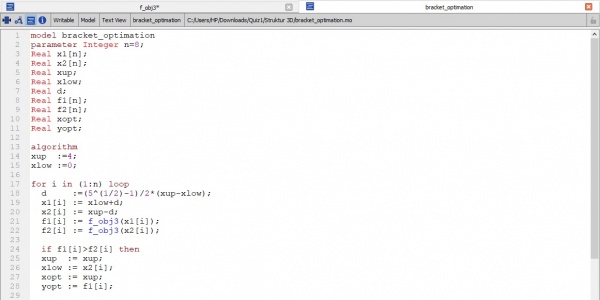
2. Membuat 1 model optimasi
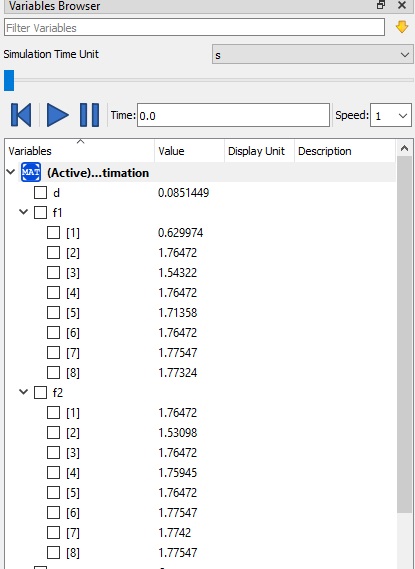
3. Mensimulasikan hasil koding
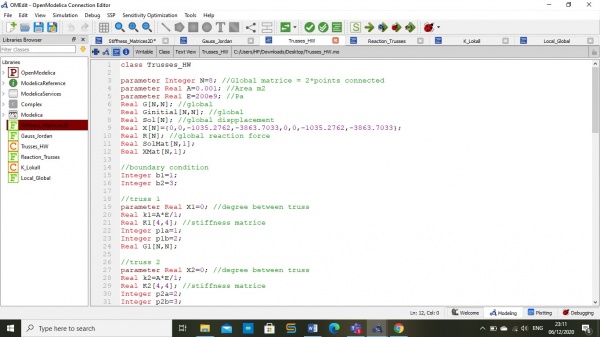
TUBES
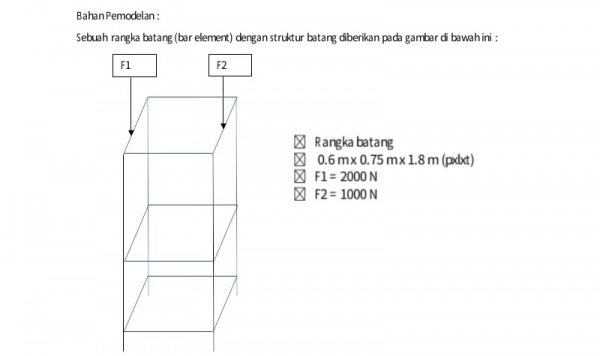
Membuat koding dan menghitung BEP yang effisien untuk membuat rangka dengan kekuatan beban sesuai dengan ketentuan, yaitu 1000N dan 2000N. dimana akan di sesuaikan dengan material yang akan saya pilih untuk dapat menahan beban tersebut. Untuk ketentuannnya yaitu:
Asumsi yang digunakan untuk melakukan perhitungan ini antara lain:
1. Variasi Stiffness terikat dengan variabel area pada material yang akan digunakan.Karena kan sulit jika memvariasikan elastisitas,dimana setiap material memiliki range yang tidak teratur dan dalam satu material yang sejenis (struktur biaya tetap) tidak terjadi perubahan nilai elastisitas yang berbanding lurus dengan perubahan biaya.
2. Dimensi material mengukuti standar ukuran material yang dipilih
3. Beban akan terdistribusi hanya pada node / point penghubung (karena bersifat trusses).
4. Terdapat 2 perhitungan yaitu dengan material lock dan area lock.
1.Material Lock
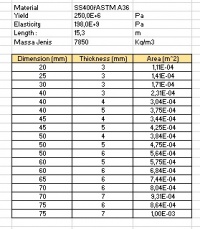
Material Lock merupakan pengambilan data dengan material yang sama dan memvariasikan luas areanya. Pada material lock ini saya menggunakan material ASTM A36/SS400 yang berprofil siku. dimana data yang saya ambil sebagau berikut: .
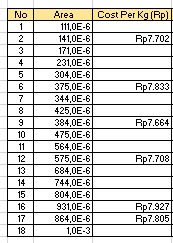
Kemudian memberikan beberapa sample dengan variasi area dan harga.
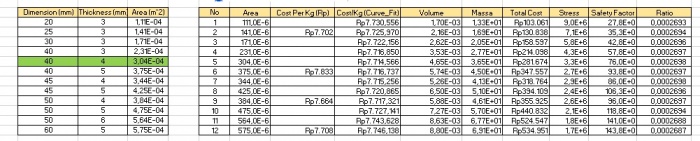
Selanjutnya kita mencari massa, nilai tegangan dan harga per kg memalui pengkodingan curve fitting.Sehingga didapatkan hasil curve fitting yang dituliskan pada excel sebagai berikut :
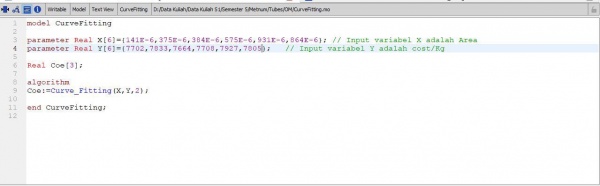
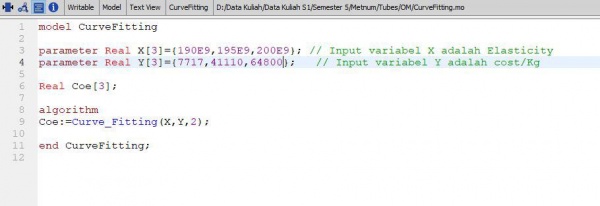
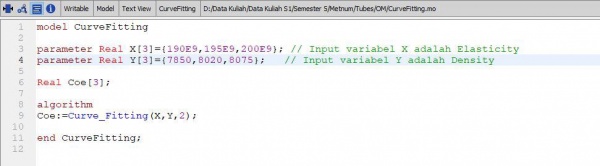
A. Koding curve
function
function Curve_Fitting input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coe[order+1]; protected Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1]; algorithm for i in 1:size(X,1) loop for j in 1:(order+1) loop Z[i,j]:=X[i]^(order+1-j); end for; end for; ZTr:=transpose(Z); A:=ZTr*Z; B:=ZTr*Y; Coe:=Modelica.Math.Matrices.solve(A,B); //Coe:=fill(2,size(Coe,1)); end Curve_Fitting; /* for i in 1:3 loop for j in 1:Points loop R[j]:=reaction[3*(j-1)+i]; end for; Sur[i]:=sum(R); end for; */
model
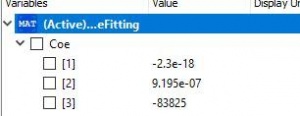
hasil curve fitting
B.Hasil Excle
bisa kita lihat, akan terhitung secara otomatis harga di excel dengan menginput data hasil kodingan curve fitting.
Kemudian nilai stress didapatkan dari nilai stress max yang didapatkan dari simulasi openmodelica.Berikut adalah coding untuk mecari nilai stress maksimum untuk menentukan harga:
Model Trusses
model Trusses_3D_Tugas_Besar_Safety
//define initial variable
parameter Integer Points=size(P,1); //Number of Points
parameter Integer Trusses=size(C,1);//Number of Trusses
parameter Real Yield=250e6; //Yield Strength (Pa) Material ASTM A36/ss400
parameter Real Area=3.75E-04; //Area L Profile (0.04 x 0.04 x 0.005) (m2)
parameter Real Elas=1.98e11; //Elasticity ASTM A36 (Pa)
//define connection parameter
Integer C[:,2]= [1,5;
2,6;
3,7;
4,8;
5,6; //1st floor
6,7; //1st floor
7,8; //1st floor
5,8; //1st floor
5,9;
6,10;
7,11;
8,12;
9,10; //2nd floor
10,11;//2nd floor
11,12;//2nd floor
9,12; //2nd floor
9,13;
10,14;
11,15;
12,16;
13,14;//3rd floor
14,15;//3rd floor
15,16;//3rd floor
13,16];//3rd floor
//define coordinates (please put orderly) parameter Real P[:,6]=
[0.3,-0.375,0,1,1,1; //1
-0.3,-0.375,0,1,1,1; //2
-0.3,0.375,0,1,1,1; //3
0.3,0.375,0,1,1,1; //4
0.3,-0.375,0.6,0,0,0; //5
-0.3,-0.375,0.6,0,0,0; //6
-0.3,0.375,0.6,0,0,0; //7
0.3,0.375,0.6,0,0,0; //8
0.3,-0.375,1.2,0,0,0; //9
-0.3,-0.375,1.2,0,0,0; //10
-0.3,0.375,1.2,0,0,0; //11
0.3,0.375,1.2,0,0,0; //12
0.3,-0.375,1.8,0,0,0; //13
-0.3,-0.375,1.8,0,0,0; //14
-0.3,0.375,1.8,0,0,0; //15
0.3,0.375,1.8,0,0,0]; //16
//define external force (please put orderly) parameter Real F[Points*3]={0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,0,
0,0,-500,
0,0,-1000,
0,0,-1000,
0,0,-500};
//solution Real displacement[N], reaction[N]; Real check[3];
Real stress1[Trusses]; Real safety[Trusses]; Real dis[3]; Real Str[3];
protected parameter Integer N=3*Points; Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), cx, cy, cz, L, X[3,3]; Real err=10e-10, ers=10e-6;
algorithm //Creating Global Matrix G:=id; for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g; G:=G_star;
end for;
//Implementing boundary for x in 1:Points loop
if P[x,4] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-2,a]:=0;
G[(x*3)-2,(x*3)-2]:=1;
end for;
end if;
if P[x,5] <> 0 then
for a in 1:Points*3 loop
G[(x*3)-1,a]:=0;
G[(x*3)-1,(x*3)-1]:=1;
end for;
end if;
if P[x,6] <> 0 then
for a in 1:Points*3 loop
G[x*3,a]:=0;
G[x*3,x*3]:=1;
end for;
end if;
end for;
//Solving displacement displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction reaction:=(G_star*displacement)-F;
//Eliminating float error for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for;
//Checking Force check[1]:=sum({reaction[i] for i in (1:3:(N-2))})+sum({F[i] for i in (1:3:(N-2))}); check[2]:=sum({reaction[i] for i in (2:3:(N-1))})+sum({F[i] for i in
(2:3:(N-1))}); check[3]:=sum({reaction[i] for i in (3:3:N)})+sum({F[i] for i in (3:3:N)});
for i in 1:3 loop
check[i] := if abs(check[i])<=ers then 0 else check[i];
end for;
//Calculating stress in each truss for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
dis[j]:=abs(displacement[3*(C[i,1]-1)+j]-displacement[3*(C[i,2]-1)+j]);
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
Str:=(X*dis);
stress1[i]:=Modelica.Math.Vectors.length(Str);
end for;
//Safety factor for i in 1:Trusses loop
if stress1[i]>0 then
safety[i]:=Yield/stress1[i];
else
safety[i]:=0;
end if;
end for;
end Trusses_3D_Tugas_Besar_Safety;
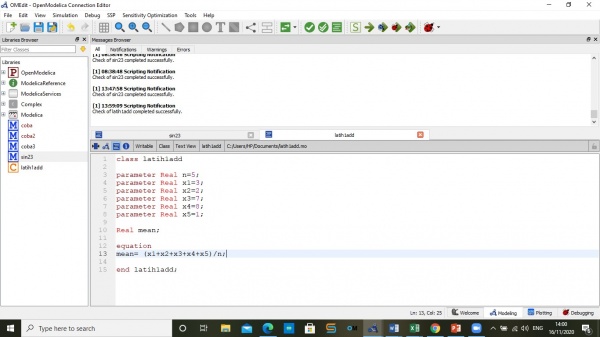
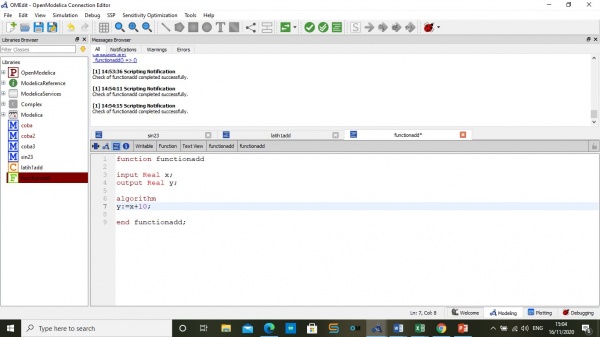
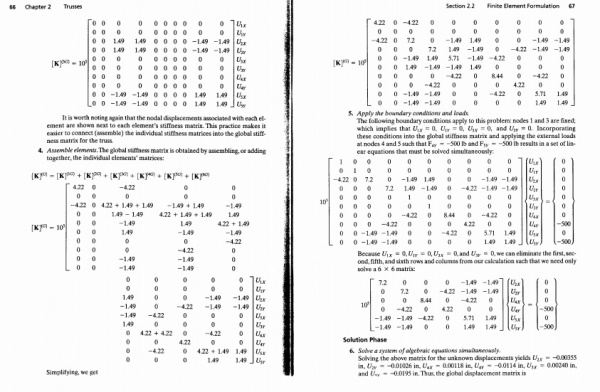
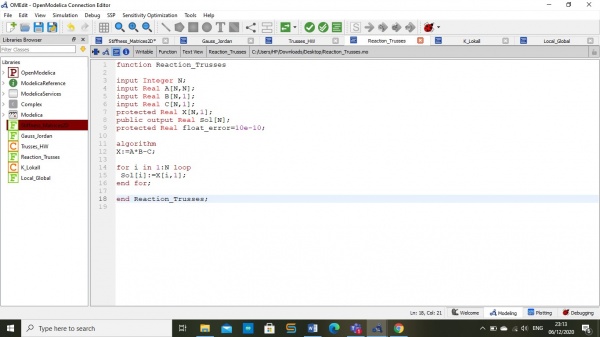
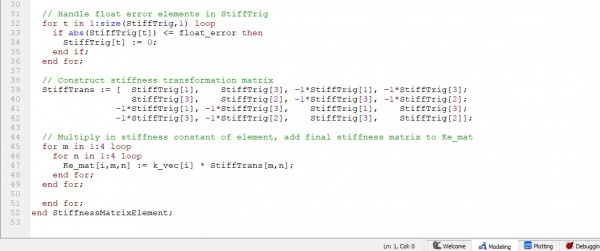
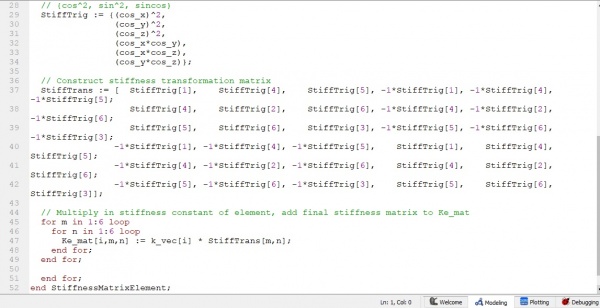
Menghitung safty factor dan rasio
kemudian,Memilih material yang paling optimal dengan menggunakan kodingan seperti berikut:
Opt.Gold
model Opt_Gold
parameter Real xd[:]={1110E-6,1410E-6,1710E-6,2310E-6,3040E-6,3750E-6,3440E-6,4250E-6,3840E-6,4750E-6,5640E-6,5750E-6};
parameter Real yd[size(xd,1)]={ 0.0002693,0.0002694,0.0002696,0.0002697,0.0002698,0.0002697,0.0002698,0.0002696,0.0002697,0.0002694,0.0002688,0.0002687};
parameter Real xlo=1110E-6;
parameter Real xhi=5750E-6;
parameter Integer N=100; // maximum iteration
parameter Real es=0.0001; // maximum error
Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3];
Real xopt, fx;
protected
Real d, xl, xu, xint, R=(5^(1/2)-1)/2;
algorithm
xl := xlo;
xu := xhi;
y := curve_fitting(xd,yd);
for i in 1:N loop
d:= R*(xu-xl);
x1[i]:=xl+d;
x2[i]:=xu-d;
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
xint:=xu-xl;
if f1[i]>f2[i] then
xl:=x2[i];
xopt:=x1[i];
fx:=f1[i];
else
xu:=x1[i];
xopt:=x2[i];
fx:=f2[i];
end if;
ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
break;
end if;
end for;
end Opt_Gold;
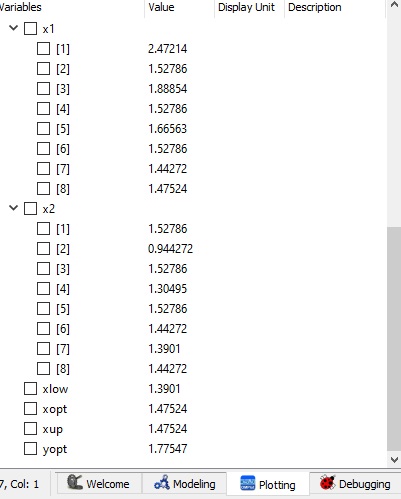
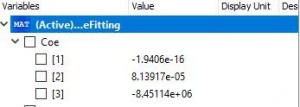
sehingga mendapatkan hasil running, seperti berikut:
dan dapat menentukan material yang paling optimal dengan hasil yang mendekati pada Xopt, yaitu pada material A36 dengan dimensi 40x40x4 mm
2. Area Lock
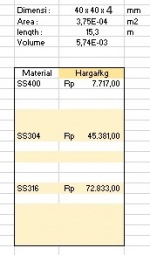
Area Lock merupakan pengambilan data dengan luas area yang sama dan memvariasikan materialnya. Pada area lock ini saya menggunakan material ASTM A36/SS400,SS304,SS316 yang berprofil siku dengan memberikan beberapa sample dengan variasi material dan harga, dimana data yang saya ambil sebagau berikut: .
Selanjutnya kita mencari harga, density dan yield memalui pengkodingan curve fitting untuk semua material.Sehingga didapatkan hasil curve fitting yang dituliskan pada excel sebagai berikut :
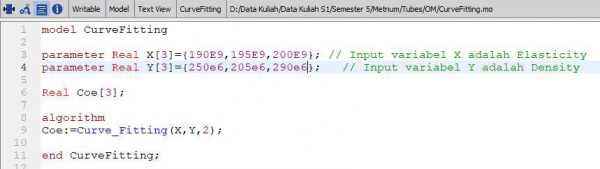
A. Koding curve
function
function Curve_Fitting input Real X[:]; input Real Y[size(X,1)]; input Integer order=2; output Real Coe[order+1]; protected Real Z[size(X,1),order+1]; Real ZTr[order+1,size(X,1)]; Real A[order+1,order+1]; Real B[order+1]; algorithm for i in 1:size(X,1) loop for j in 1:(order+1) loop Z[i,j]:=X[i]^(order+1-j); end for; end for; ZTr:=transpose(Z); A:=ZTr*Z; B:=ZTr*Y; Coe:=Modelica.Math.Matrices.solve(A,B); //Coe:=fill(2,size(Coe,1)); end Curve_Fitting; /* for i in 1:3 loop for j in 1:Points loop R[j]:=reaction[3*(j-1)+i]; end for; Sur[i]:=sum(R); end for; */
model_cost
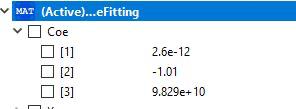
hasil model_cost
model_density
hasil model_density
model_yield
hasil model_yield
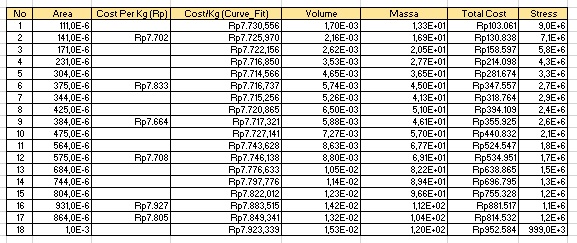
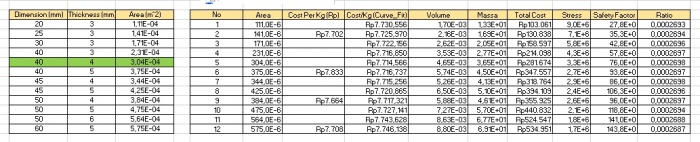
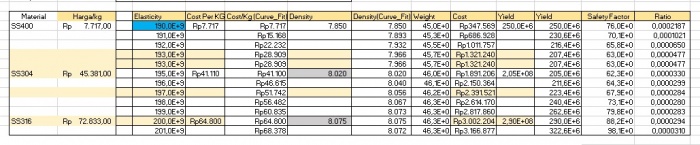
B.Hasil Excle
bisa kita lihat, akan terhitung secara otomatis harga di excel dengan menginput data hasil kodingan curve fitting.
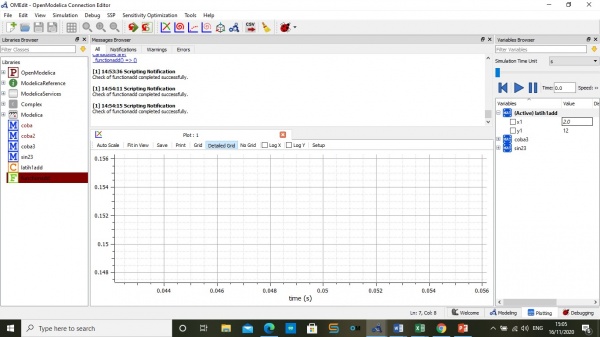
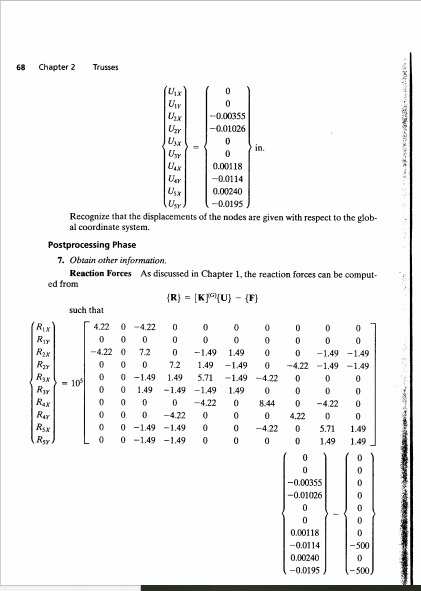
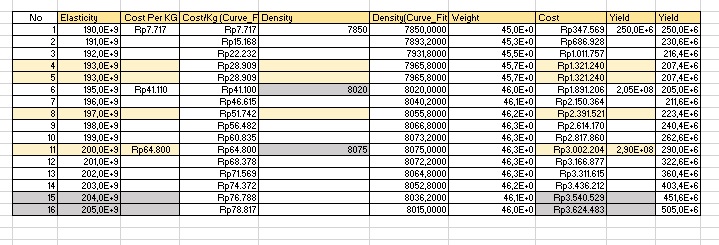
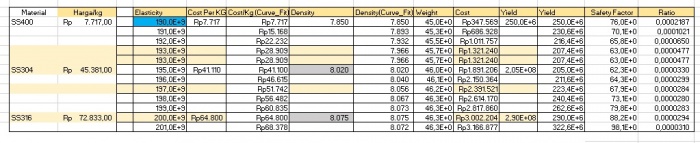
Menghitung safty factor dan rasio
kemudian,Memilih material yang paling optimal dengan menggunakan kodingan seperti berikut:
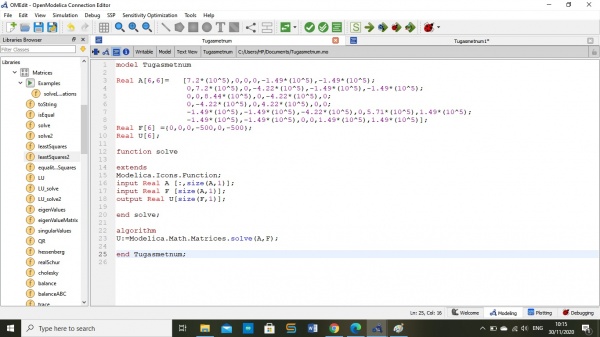
Opt.Gold
model Opt_Gold1
parameter Real xd[:]={1900E+9,1910E+9,1920E+9,1930E+9,1930E+9,1950E+9,1960E+9,1970E+9,1980E+9,1990E+9,2000E+9,2010E+9};
parameter Real yd[size(xd,1)]={0.0002697,0.0001259,0.0000802,0.0000589,0.0000589,0.0000406,0.0000369,0.0000350,0.0000345,0.0000349,0.0000362,0.0000382 };
parameter Real xlo=1900E+9;
parameter Real xhi=2010E+9;
parameter Integer N=100; // maximum iteration
parameter Real es=0.0001; // maximum error
Real f1[N], f2[N], x1[N], x2[N], ea[N], y[3];
Real xopt, fx;
protected
Real d, xl, xu, xint, R=(5^(1/2)-1)/2;
algorithm
xl := xlo;
xu := xhi;
y := curve_fitting(xd,yd);
for i in 1:N loop
d:= R*(xu-xl);
x1[i]:=xl+d;
x2[i]:=xu-d;
f1[i]:=y[1]*x1[i]^2+y[2]*x1[i]+y[3];
f2[i]:=y[1]*x2[i]^2+y[2]*x2[i]+y[3];
xint:=xu-xl;
if f1[i]>f2[i] then
xl:=x2[i];
xopt:=x1[i];
fx:=f1[i];
else
xu:=x1[i];
xopt:=x2[i];
fx:=f2[i];
end if;
ea[i]:=(1-R)*abs((xint)/xopt);
if ea[i]<es then
break;
end if;
end for;
end Opt_Gold1;
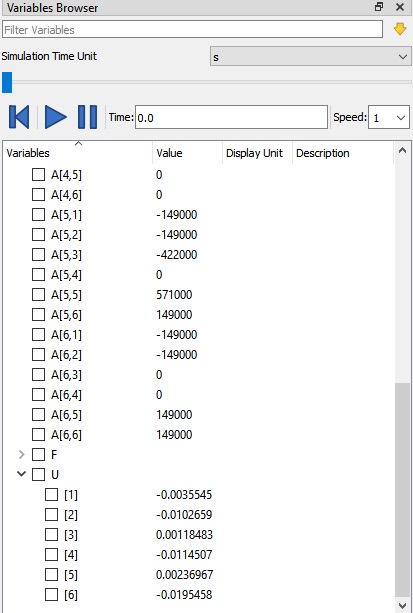
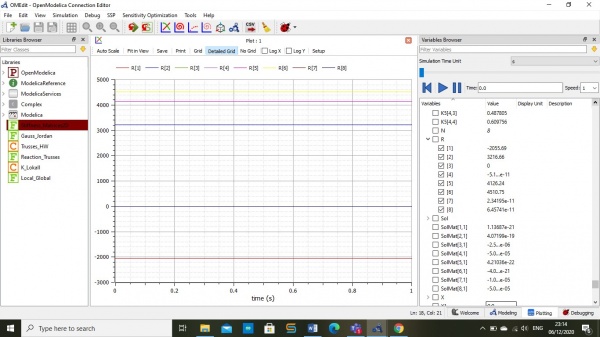
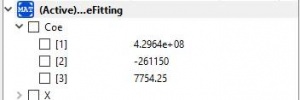
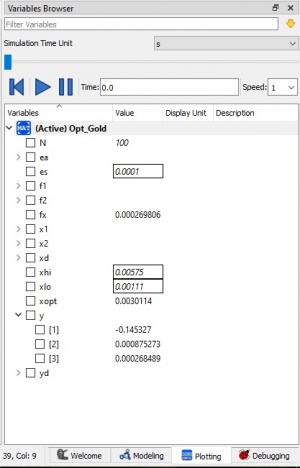
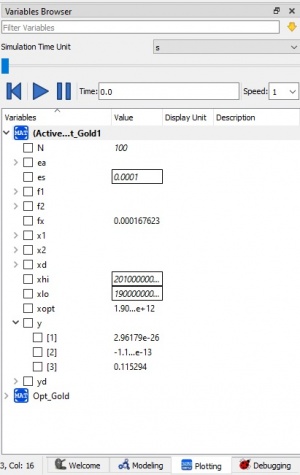
sehingga mendapatkan hasil running, seperti berikut:
dan dapat menentukan material yang paling optimal dengan hasil yang mendekati pada Xopt, yaitu pada material A36/SS400 dengan dimensi 40x40x4 mm
jadi dapat diambil kesimpulan,dari perhitungan yang di dapat dari optimasi maupun perhitungan, kita dapat menggunakan material SS400/A36 dengan dimensi 40x40x4