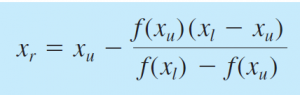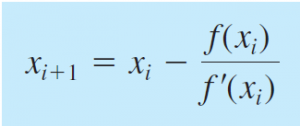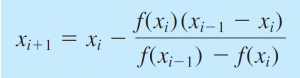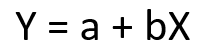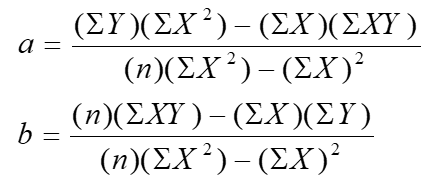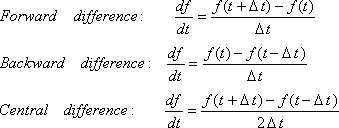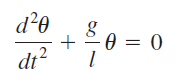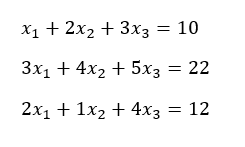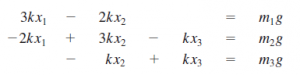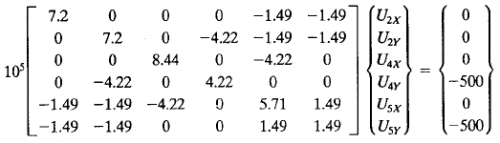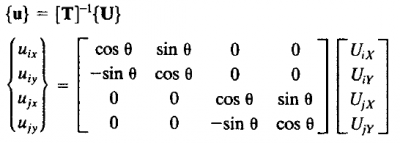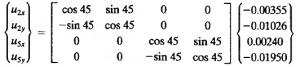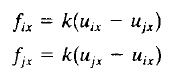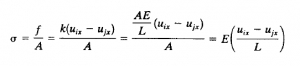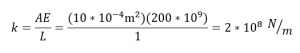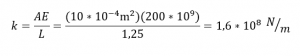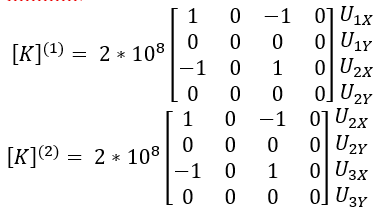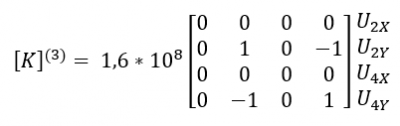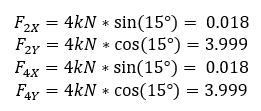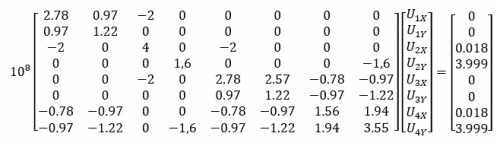Difference between revisions of "Metnum03 Edward Joshua Patrianus Mendrofa"

From ccitonlinewiki
Jump to: navigation, search
Line 158: Line 158:
  
 
[[File:example2-1.png|500px|center]]
 
[[File:example2-1.png|500px|center]]
 +
 +
'''Langkah Penyelesaian Example 2-1'''
  
 
{| class="mw-collapsible mw-collapsed wikitable"
 
{| class="mw-collapsible mw-collapsed wikitable"
−
! Langkah Penyelesaian Example 2-1 dapat dilihat dengan men-click "collapse"
+
! '''1. Mengubah problem menjadi node dan elemen'''
 
|-
 
|-
−
| '''1. Mengubah problem menjadi node dan elemen''' || [[File:Example2-1 table.png|400px|center]]
+
| [[File:Example2-1 table.png|400px|center]]
 +
|}
 +
 
 +
{| class="mw-collapsible mw-collapsed wikitable"
 +
! '''2. Menentukan nilai Konstanta kekakuan/stiffness constant dari elemen'''
 
|-
 
|-
−
| '''2. Menentukan nilai Konstanta kekakuan/stiffness constant dari elemen''' || - Elemen 1,3,4,6
+
| Elemen 1,3,4,6 || [[File:Stiffness-element1346.png|300px]]
 +
|-
 +
| Elemen 2,5 || [[File:Stiffness-element25.png|300px]]
 +
|}
  
−
[[File:Stiffness-element1346.png|300px]]
+
{| class="mw-collapsible mw-collapsed wikitable"
 +
! '''4. Menyusun dan menggabungkan matriks elemen-elemen'''
 +
|-
 +
| [[File:Kglobal-summary.png|400px]]  
 +
|}
  
−
- Elemen 2,5
+
{| class="mw-collapsible mw-collapsed wikitable"
−
 
+
! '''4. Menyusun dan menggabungkan matriks elemen-elemen'''
−
[[File:Stiffness-element25.png|300px]]
+
|-
 +
| [[File:Kglobal-summary.png|400px]]
 
|-
 
|-
−
| '''3. Membuat persamaan untuk elemen''' || ''Analisis Elemen 1,3,6''
+
| [[File:Kglobal-summary-simplified.png|400px]]
 +
|}
  
−
[[File:k1global.png|200px]] [[File:k3global.png|200px]] [[File:k6global.png|200px]]
+
{| class="mw-collapsible mw-collapsed wikitable"
−
 
+
! '''5. Menerapkan kondisi batas dan beban'''
−
''Analisis Elemen 4''
 
−
 
 
−
[[File:k4global.png|200px]]
 
−
 
 
−
''Analisis Elemen 2,5''
 
 
|-
 
|-
−
| '''4. Menyusun dan menggabungkan matriks elemen-elemen''' || [[File:Kglobal-summary.png|400px]]
+
| Kondisi batas untuk node 1 dan 3 adalah fixed || [[File:Boundary-condition-deflection-node13.png|400px]]
−
 
 
−
[[File:Kglobal-summary-simplified.png|400px]]
 
 
|-
 
|-
−
| '''5. Menerapkan kondisi batas dan beban''' || Diketahui:
+
| External force pada node 4 dan 5 || [[File:Externalforce-node45.png|400px]]
−
 
 
−
- Kondisi batas untuk node 1 dan 3 adalah fixed
 
−
 
 
−
[[File:Boundary-condition-deflection-node13.png|400px]]
 
−
 
 
−
- External force pada node 4 dan 5
 
−
 
 
−
[[File:Externalforce-node45.png|400px]]
 
−
 
 
−
Dengan menerapkan Hukum Hooke, F= k. x, maka dalam persamaan matrix menjadi [F]=[K].[U]. Didapat:
 
−
 
 
−
[[File:Deflection-matrix-simplified.png|500px|center]]
 
 
|-
 
|-
−
| '''6. Tahap pencarian solusi'''||
+
|Dengan menerapkan Hukum Hooke, F= k. x, maka dalam persamaan matrix menjadi [F]=[K].[U]. Didapat || [[File:Deflection-matrix-simplified.png|500px|center]]
−
 
 
−
[[File:k2global.png|200px]] [[File:k5global.png|200px]]
 
 
|}
 
|}
  
−
 
+
{| class="mw-collapsible mw-collapsed wikitable"
−
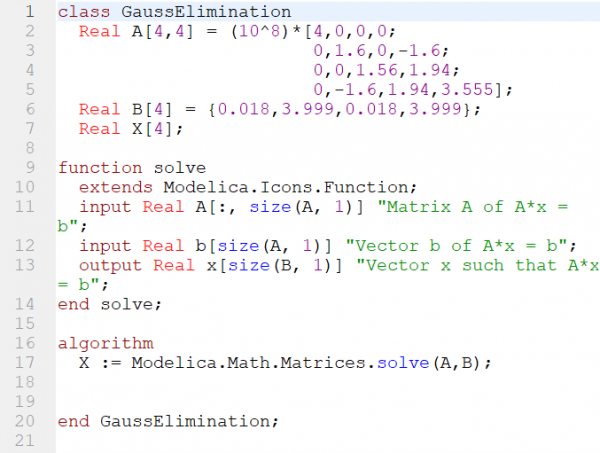
Persamaan matriks diatas dapat diselesaikan dengan OpenModelica, berikut adalah pemograman yang saya buat
+
! '''6. Tahap pencarian solusi'''
−
 
+
|-
−
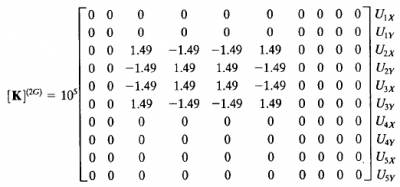
[[File:deflection-code.png|600px|center]]
+
| [[File:k2global.png|400px]]
−
 
+
|-
−
setelah melakukan pengecekan dan simulasi, saya melakukan plotting terhadap hasil simulasi. berikut hasilnya:
+
| [[File:k5global.png|400px]]
−
 
+
|-
 +
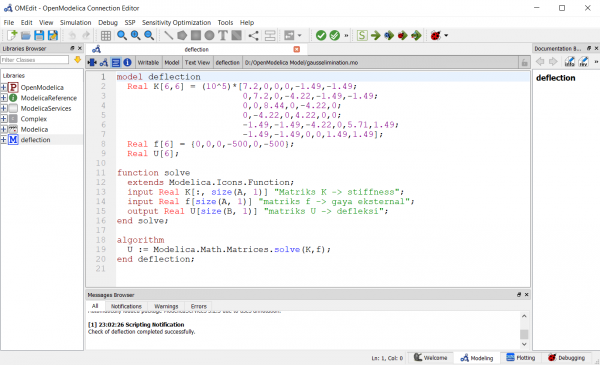
| Persamaan matriks diatas dapat diselesaikan dengan OpenModelica, berikut adalah pemograman yang saya buat || [[File:deflection-code.png|600px|center]]
 +
|-
 +
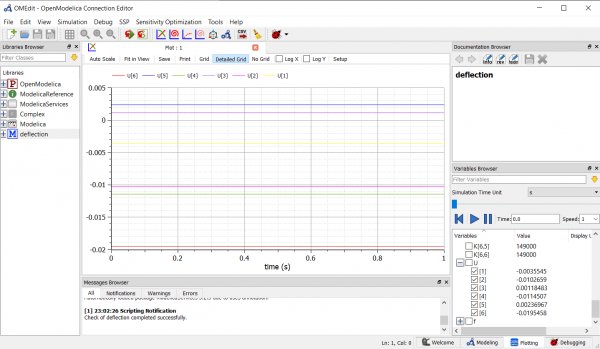
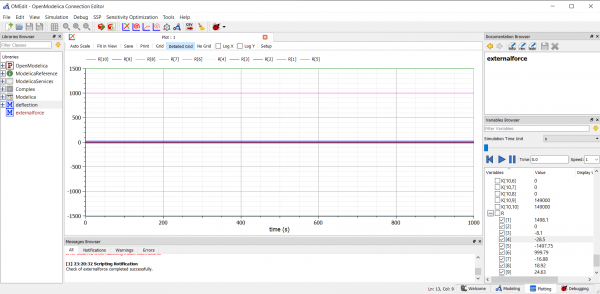
| setelah melakukan pengecekan dan simulasi, saya melakukan plotting terhadap hasil simulasi. berikut hasilnya: ||
 
[[File:Deflection-plot.png|600px|center]]
 
[[File:Deflection-plot.png|600px|center]]
 +
|}
  
−
'''Mendapatkan nilai gaya reaksi'''
+
{| class="mw-collapsible mw-collapsed wikitable"
 +
! '''7. Mendapatkan nilai gaya reaksi'''
 +
|-
 +
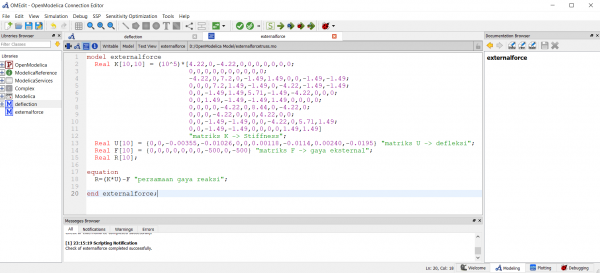
| Karena di soal ingin mencari gaya reaksi, maka perlu dilakukan perhitungan pada gaya reaksi dengan persamaan ||  '''{R} = [K] {U} - {F}'''
 +
|-
 +
| || [[File:Reaction-force-matrix.png|400px]]
 +
|-
 +
| Persamaan diatas dapat diselesaikan oleh OpenModelica, berikut adalah pemogramannya || [[File:Externalforce-code.png|600px|center]]
 +
|-
 +
| berikut hasil plottingnya || [[File:Externalforce-plot.png|600px|center]]
 +
|}
  
−
Karena di soal ingin mencari gaya reaksi, maka perlu dilakukan perhitungan pada gaya reaksi dengan persamaan
+
{| class="mw-collapsible mw-collapsed wikitable"
−
 
+
! '''8. Mendapatkan gaya Internal dan Normal Stress'''
−
'''{R} = [K] {U} - {F}'''
+
|-
−
 
+
| Untuk menghitung normal stress, perlu dilakukan transformasi dari hasil defleksi ditinjau dari koordinat global menjadi transformasi lokal, berikut adalah persamaan yang dapat digunakan || [[File:Global-to-local.png|400px]]
−
[[File:Reaction-force-matrix.png|400px]]
+
|-
−
 
+
|  || {u} -> koordinat local
−
Persamaan diatas dapat diselesaikan oleh OpenModelica, berikut adalah pemogramannya
 
−
 
 
−
[[File:Externalforce-code.png|600px|center]]
 
−
 
 
−
berikut hasil plottingnya
 
−
 
 
−
[[File:Externalforce-plot.png|600px|center]]
 
−
 
 
−
'''8. Mendapatkan gaya Internal dan Normal Stress'''
 
−
 
 
−
Untuk menghitung normal stress, perlu dilakukan transformasi dari hasil defleksi ditinjau dari koordinat global menjadi transformasi lokal, berikut adalah persamaan yang dapat digunakan
 
−
 
 
−
[[File:Global-to-local.png|400px]]
 
−
 
 
−
dimana:
 
−
 
 
−
  {u} -> koordinat local
 
  
 
  [U] -> koordinat global
 
  [U] -> koordinat global
  
 
  [T] -> matriks transformasi
 
  [T] -> matriks transformasi
 +
|-
 +
| Misalkan kita menganalisis stress pada elemen 5, maka node yang dianalisis adalah node 2 dan 5
 +
Sehingga persamaan matriks defleksi pada koordinat lokal menjadi || [[File:Global-to-local-element5.png|300px]]
 +
|-
 +
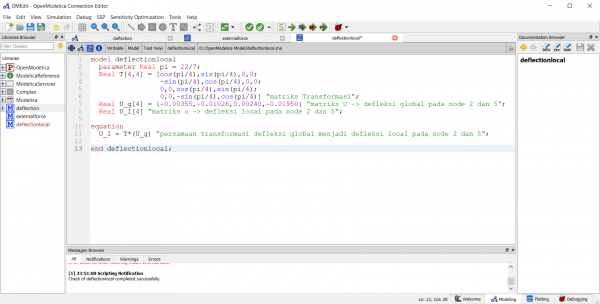
| Persamaan diatas dapat diselesaikan dengan OpenModelica, berikut adalah pemogramannya || [[File:Deflectionlocal-code.png|600px|center]]
 +
|-
 +
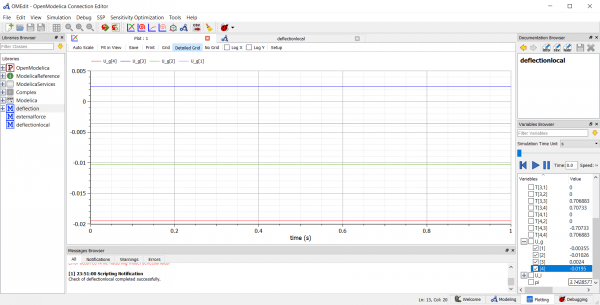
| berikut hasil plottingnya || [[File:Deflectionlocal-plot.png|600px|center]]
  
−
Misalkan kita menganalisis stress pada elemen 5, maka node yang dianalisis adalah node 2 dan 5
+
Didapatkan U2x=-0.00976 inch dan U6x=-0.01209 inch
−
Sehingga persamaan matriks defleksi pada koordinat lokal menjadi
+
|-
 +
| Internal force didapat dengan persamaan || [[File:Internal-force-equation.png|300px]]
  
−
[[File:Global-to-local-element5.png|300px]]
+
didapat internal force pada elemen 5 sebesar 696lb.
 +
|-
 +
| Normal stress didapat dengan persamaan || [[File:Normal-stress-equation.png|300px]]
  
−
Persamaan diatas dapat diselesaikan dengan OpenModelica, berikut adalah pemogramannya
+
didapat normal stress pada elemen 5 sebesar 87lb/in^2
 +
|}
  
−
[[File:Deflectionlocal-code.png|600px|center]]
+
=Pertemuan 4=
  
−
berikut hasil plottingnya
+
==Kuis==
  
−
[[File:Deflectionlocal-plot.png|600px|center]]
+
Membuat Flowchart untuk penyelesaian soal nomor 4 dan 8
  
−
Didapatkan U2x=-0.00976 inch dan U6x=-0.01209 inch
+
{|class="wikitable"
 +
| '''Soal No.4''' || [[File:Problem4-edo.png|800px]]
 +
|-
 +
| '''Soal No.8''' || [[File:Problem8-edo.png|800px]]
 +
|}
  
−
Internal force didapat dengan persamaan
+
Berikut adalah penyelesaian untuk soal diatas
  
−
[[File:Internal-force-equation.png|300px]]
+
{|class="wikitable"
 +
| '''Soal No.4''' ||
  
−
sehingga didapat internal force pada elemen 5 sebesar 696lb.
+
{| class="mw-collapsible mw-collapsed wikitable"
 +
! '''1. Mengubah problem menjadi node dan elemen'''
 +
|-
 +
| [[File:Element-Table-Problem4.png |400px|center]]
 +
|}
  
−
Normal stress didapat dengan persamaan
+
{| class="mw-collapsible mw-collapsed wikitable"
 +
! '''2. Menentukan nilai Konstanta kekakuan/stiffness constant dari elemen'''
 +
|-
 +
| Elemen 1,2 || [[File:Element12-problem4.png ‎|300px]]
 +
|-
 +
| Elemen 3 || [[File:Element3-problem4.png ‎|300px]]
 +
|-
 +
| Elemen 4,5 || [[File:Element45-problem4.png ‎|300px]]
 +
|}
  
−
[[File:Normal-stress-equation.png|300px]]
+
{| class="mw-collapsible mw-collapsed wikitable"
 +
! '''4. Menyusun dan menggabungkan matriks elemen-elemen'''
 +
|-
 +
| '''Elemen''' || '''Local Matrix''' || '''Global Matrix'''
 +
|-
 +
| Elemen 1,2 || [[File:Localmatrix-element12.png |400px]] || [[File:Globalmatrix-element12.png ‎ |400px]]
 +
|-
 +
| Elemen 3 || [[File:Localmatrix-element3.png ‎ |400px]] || [[File:Globalmatrix-element3.png ‎|400px]]
 +
|-
 +
| Elemen 4,5 || [[File:Localmatrix-element45.png |400px]] || [[File:Globalmatrix-element45.png ‎ |400px]] 
 +
|}
  
−
sehingga didapat normal stress pada elemen 5 sebesar 87lb/in^2
+
{| class="mw-collapsible mw-collapsed wikitable"
 +
! '''4. Menyusun dan menggabungkan matriks elemen-elemen'''
 +
|-
 +
| [[File:Matrixglobal-sum.png |400px]]
 +
|}
  
−
=Pertemuan 4=
+
{| class="mw-collapsible mw-collapsed wikitable"
 +
! '''5. Menerapkan kondisi batas dan beban'''
 +
|-
 +
| Kondisi batas untuk node 1, dan 3 adalah fixed
 +
|-
 +
| External force pada node 2 dan 4 || [[File:Externalforce-problem4.png|400px]]
 +
|-
 +
|Dengan menerapkan Hukum Hooke, F= k. x, maka dalam persamaan matrix menjadi [F]=[K].[U]. Didapat || [[File:Solving-equation-problem4.png|500px|center]]
 +
|}
  
−
==Kuis==
+
{| class="mw-collapsible mw-collapsed wikitable"
 +
! '''6. Tahap pencarian solusi'''
 +
|-
 +
| [[File:Solving-equation-simplified-problem4.png ‎ |500px|center]]
 +
|-
 +
| Persamaan matriks diatas dapat diselesaikan dengan OpenModelica, berikut adalah pemograman yang saya buat || [[File:Gauss-elimination-problem4.png|600px|center]]
 +
|-
 +
| setelah melakukan pengecekan dan simulasi, saya melakukan plotting terhadap hasil simulasi. berikut hasilnya: ||
 +
[[File:Plot-problem4.png|600px|center]]
 +
|}
  
−
Membuat Flowchart untuk penyelesaian soal nomor 4 dan 8
+
|}
−
 
 
−
'''Soal No.4'''
 
−
 
 
−
[[File:Problem4-edo.png|800px]]
 
−
 
 
−
'''Soal No.8'''
 
−
 
 
−
[[File:Problem8-edo.png|800px]]
 
  
 
=Pertemuan 5=
 
=Pertemuan 5=
Line 297: Line 339:
 
[[File:soal3.jpeg|thumb|example 3.3|center|300px]]
 
[[File:soal3.jpeg|thumb|example 3.3|center|300px]]
  
−
 
+
Berikut adalah langkah penyelesaian dari kuis nomor 5
  
  

Revision as of 14:13, 20 December 2020

Pertemuan Metode Numerik 03

Pertemuan 1

Metode Numerik adalah salah satu mata kuliah yang sangat banyak penerapannya dalam dunia keteknikan. Mata kuliah ini salah satu mata kuliah yang cukup menarik karena penerapannya sangat luas dan bermanfaat. Sejauh ini yang telah saya pelajari sebelum UTS mencakup 3 materi besar yaitu mencari akar-akar, regresi linier, dan turunan numerik.

1. Mencari Akar-Akar

Pada materi ini, saya mempelajari metode-metode untuk mencari akar secara numerik. Beberapa metode yang saya pelajari adalah metode pencarian akar menggunakan Closed methods (Bracketing Method) dan Open Methods.

Metode Closed Methods merupakan metode pencarian akar-akar dengan menggunakan batas atas dan batas bawah untuk mencari akar dan mengukur persentasi error yang didapat untuk mendapat tingkat akurasi dari iterasi. Metode yang saya pelajari ada 3 yaitu Graphical Methods, Bisection Methods, dan False-Position Methods.

Graphical Methods

Sebuah metode sederhana yang menggunakan grafik untuk memperkirakan akar-akar suatu fungsi. Metode ini dilakukan dengan melakukan plotting dari suatu fungsi ke dalam bentuk grafik.

Bisection Methods

Metode ini merupakan salah satu jenis metode incremental search method yang menggunakan batas atas dan batas bawah untuk mempersempit area pencarian akar-akar.

False-Position Methods

Rumus False Position Method

Metode ini sangat mirip dengan metode Bisection. Hal yang membedakan metode False-Position dengan Bisection adalah penentuan titik tengah dari batas-batas yang ditentukan. Penentuan titik tengah dari False-Position Method menggunakan persamaan berikut.

Metode Open Methods merupakan metode pencarian yang hanya menggunakan 1 titik untuk menemukan akar-akar. Metode ini dapat menggunakan turunan suatu fungsi untuk menentukan titik pengujian baru yang semakin dekat dengan nilai akar-akar yang diinginakn. Metode yang saya pelajari ada 3 yaitu Fixed-Point Iteration, Newton-Rapshon, dan Secant Method

Fixed-Point Iteration

Metode ini disebut juga metode iterasi sederhana, adalah metode yang memisahkan x dengan sebagian x yang lain sehingga diperoleh: x=g(x)

Newton-Raphson
Rumus Newton Rapshon

Metode ini menggunakan satu titik awal dan mendekatinya dengan memperhatikan slope atau gradien pada titik tersebut. Slop atau gradien didapatkan dengan melakukan turunan dari fungsi tersebut. Persamaan untuk Newton-Raphson adalah sebagai berikut:




Secant Method

Metode ini merupakan metode modifikasi Newton-Raphson dimana metode Newton-Raphson tidak digunakan (karena f'(x) sulit ditemukan atau tidak mungkin ditemukan). Persaman untuk metode Secant adalah sebagai berikut

Rumus Secant

2. Regresi Linier

regresi linear adalah sebuah pendekatan untuk memodelkan hubungan antara variable terikat Y dan satu atau lebih variable bebas yang disebut X. Salah satu kegunaan dari regresi linear adalah untuk melakukan prediksi berdasarkan data-data yang telah dimiliki sebelumnya. Hubungan di antara variable-variabel tersebut disebut sebagai model regresi linear.

Persamaan umum Regresi Linier adalah sebagai berikut:

Rumus-regresi-linier-umum.png

dimana:

Konstanta-regresi-linier.png

3. Turunan Numerik

Turunan Numerik adalah menentukan hampiran nilai turunan fungsi f yang diberikan dalam bentuk tabel. Terdapat 3 pendekatan dalam menghitung turunan numerik:

Numerical-difference-approx.png

Tugas Pertemuan 1: OpenModelica

Setelah pertemuan 1, pak Dai meminta kami untuk mempelajari OpenModelica

Untuk mempelajari OpenModelica, saya menggunakan referensi/tutorial dari YouTube dengan tautan berikut:

https://www.youtube.com/watch?v=SW5Eclf1tRs

https://www.youtube.com/watch?v=m0Ahs8fEN28&t=519s&ab_channel=NSTUFACE

Dari video-video tersebut saya diperkenalkan mengenai interface OpenModelica untuk pemula. Saya juga mempelajari bahwa OpenModelica menggunakan bahasa program Modelica untuk penggunaannya. Bahasa ini mirip dengan bahasa pemograman lain seperti python. Kelebihan yang saya lihat dari OpenModelica ini adalah program ini memiliki tools yang membantu mempermudah kita untuk membuat sistem dalam bentuk grafis atau skema. Model-model ini dapat kita aplikasikan dalam kehidupan nyata seperti membuat sistem elektrikal, magnetik, fluida, perpindahan panas, dsb.

Dalam konteks Metode Numerik, saya mempelajari bahwa OpenModelica dapat membantu kita dalam menyelesaikan permasalahan-permasalahan dalam mata kuliah Metode Numerik dan memvisualisasikan penyelesaian tersebut dalam bentuk grafik, salah satunya adalah penyelesaian Persamaan Diferensial Biasa atau ODE.

Contoh penyelesaian permasalahan ODE menggunakan OpenModelica adalah persamaan pendulum, yang didefinisikan sebagai berikut:

Persamaan-pendulum.png

Dengan menggunakan referensi dari tautan kedua, saya membuat bahasa pemograman untuk menyelesaikan persamaan pendulum tersebut. 

model pendulum
 Real y "variable state";
 Real x;
 parameter Real L=1 "pendulum length";
 constant Real g=9.80665;
initial equation
 y=9 "initial value";
equation
 x=der(y);
 der(x)+(g/L)*(y)=0 "differential equation";
annotation(experiment(StartTime = 0, StopTime = 100));
end pendulum;


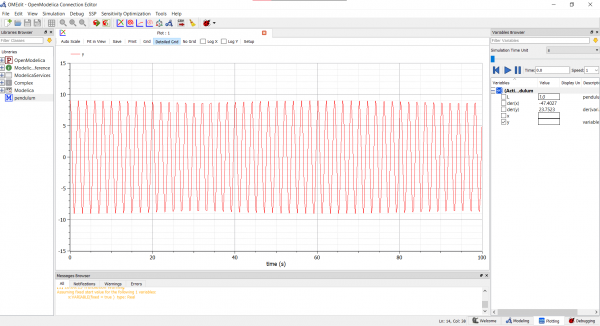
Penyelesaian dari persamaan tersebut digambarkan dalam bentuk grafik sebagai berikut

Hasil Plotting

Dari grafik tersebut dapat dilihat bahwa seiring berjalannya waktu, pendulum melakukan osilasi. Namun dapat dilihat bahwa pendulum tersebut tidak kembali ketitik semula seiring berjalannya waktu.

Dari pembelajaran ini, saya mempelajari bahwa OpenModelica merupakan tools yang berguna dalam pelajaran Metode Numerik.


Pertemuan 2

Pada pertemuan kedua ini, pak Dai mengevaluasi hasil belajar kami tentang yang sudah kami pelajari tentang Metode Numerik sebelum UTS, serta mempelajari penggunaan aplikasi OpenModelica. Kemudian kami diminta untuk membuat coding sederhana terkait nilai rata-rata 10 sample.

Setelah sesi belajar tatap muka berakhir, kami diberikan tugas oleh pak Dai untuk membuat model untuk menyelesaikan persamaan-persamaan aljabar simultan (seperti Gauss Elimination, Gauss-Seidel, dll.).

Untuk PR, saya menggunakan 3 persamaan aljabar sebagai berikut:

Fungsi-aljabar-simultan.png

Persamaan aljabar simultan tersebut dapat diselesaikan dengan metode konvensional seperti Naive Gauss Elimination, atau menggunakan metode lain sepertiGauss Elimination yang melibatkan matriks , atau Gauss Seidel. Pada kali ini, saya menggunakan metode Gauss Elimination untuk menyelesaikan persamaan tersebut.

Gauss Elimination adalah algoritme yang digunakan untuk menyelesaikan sistem persamaan linear. Metode ini melibatkan perubahan bentuk sistem persamaan menjadi bentuk matriks. Setelah mengubah sistem dalam bentuk matriks, lalu dilakukan pengurangan baris dengan mengganti posisi baris, dan/atau melakukan operasi penjumlahan dan pengurangan antar baris.

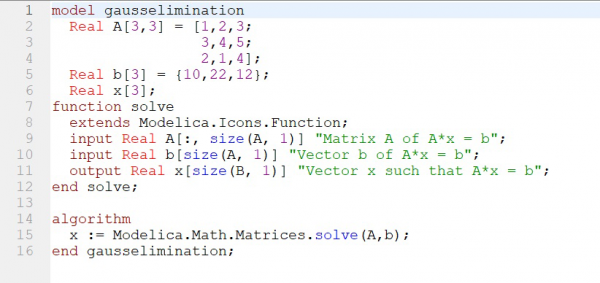
Modelica menyediakan model untuk menyelesaikan permasalahan aljabar simultan dengan menggunakan metode Gauss Elimination. Maka dari itu, saya mengubah sistem persamaan tersebut menjadi bentuk matriks. Berikut adalah model yang saya buat dengan OpenModelica:

Gauss-elimination.png

Saya menggunakan perintah dari library modelica yaitu "Modelica.Math.Matrices.solve(A,b)" untuk menyelesaikan sistem persamaan linier tersebut.

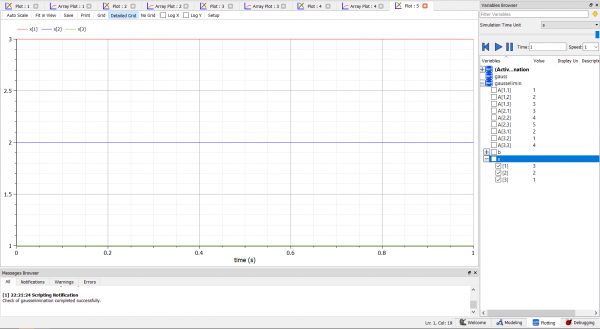
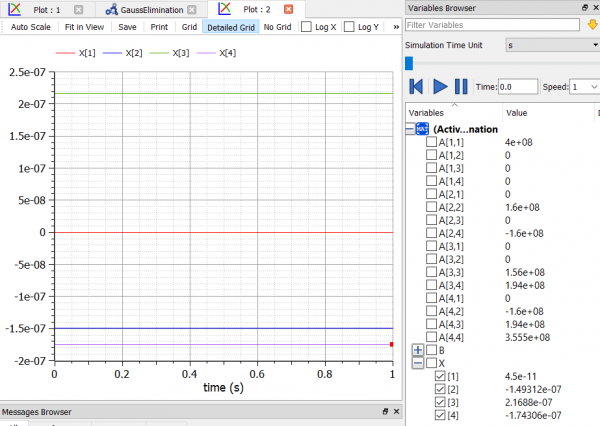
Setelah melakukan pengecekan dan melakukan simulasi terhadap model, saya melakukan plotting terhadap hasil simulasi tersebut. Berikut adalah hasil plotting tersebut:

Plotting-gauss-elimination.png

dapat dilihat bahwa hasil plotting tersebut menunjukkan penyelesaian dari permasalaha sistem persamaan yang telah ditunjukkan sebelumnya, yaitu x1=3, x2=2, x3=1.

Pertemuan 3

Pada pertemuan hari ini, Pak Dai menjelaskan mengenai aplikasi metode numerik pada permasalahan teknik. Salah satu permasalahan teknik yang dibahas adalah permasalahan sistem pegas-massa. Lalu pak Dai meminta kami untuk memahami permasalahan pada Figure 12.11 pada e-book Metode Numerik. Dengan mengubah sistem menjadi bentuk matrix, kita mendapatkan bentuk matrix dari sistem tersebut sebagai berikut:

Sistem-persamaan-aljabar-pegas-massa.png
Figure12 11.jpg

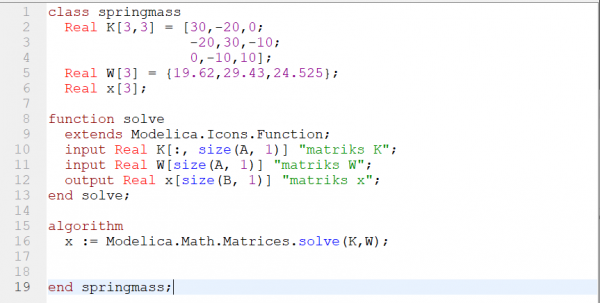
persamaan matrix tersebut dapat diselesaikan dengan metode eliminasi gauss. Lalu saya membuat coding di OpenModelica sebagai berikut:

Spring-mass-model.png

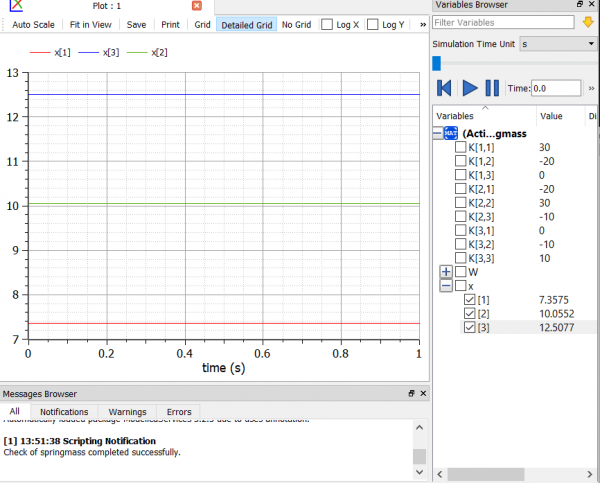
setelah melakukan melakukan pengecekan dan tidak ada masalah, saya melakukan simulasi untuk menemukan nilai x1,x2, dan x3 dari persamaan matriks tersebut. Setelah melakukan simulasi, saya melakukan plotting untuk melihat hasil yang ditemukan

Hasil-plotting-spring-mass.png

dapat dilihat bahwa nilai x1 = 7.3575; x2 = 10.0552; x3 = 12.5077, sesuai dengan hasil yang ada di buku Metode Numerik.

Tugas Pertemuan 3

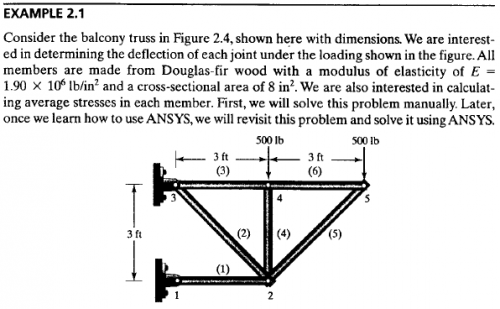
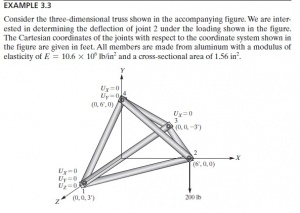
Setelah pertemuan ini, pak Dai memberikan PR untuk mengerjakan soal berikut:

Example2-1.png

Langkah Penyelesaian Example 2-1

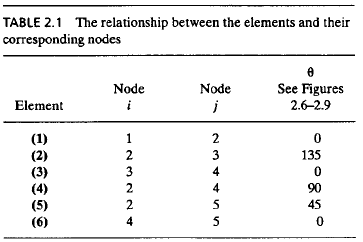
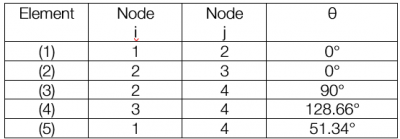
1. Mengubah problem menjadi node dan elemen
Example2-1 table.png
2. Menentukan nilai Konstanta kekakuan/stiffness constant dari elemen
Elemen 1,3,4,6 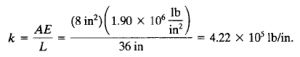Stiffness-element1346.png
Elemen 2,5 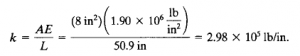Stiffness-element25.png
4. Menyusun dan menggabungkan matriks elemen-elemen
Kglobal-summary.png
4. Menyusun dan menggabungkan matriks elemen-elemen
Kglobal-summary.png
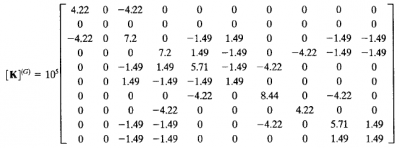
Kglobal-summary-simplified.png
5. Menerapkan kondisi batas dan beban
Kondisi batas untuk node 1 dan 3 adalah fixed Boundary-condition-deflection-node13.png
External force pada node 4 dan 5 Externalforce-node45.png
Dengan menerapkan Hukum Hooke, F= k. x, maka dalam persamaan matrix menjadi [F]=[K].[U]. Didapat
Deflection-matrix-simplified.png
6. Tahap pencarian solusi
K2global.png
K5global.png
Persamaan matriks diatas dapat diselesaikan dengan OpenModelica, berikut adalah pemograman yang saya buat
Deflection-code.png
setelah melakukan pengecekan dan simulasi, saya melakukan plotting terhadap hasil simulasi. berikut hasilnya:
Deflection-plot.png
7. Mendapatkan nilai gaya reaksi
Karena di soal ingin mencari gaya reaksi, maka perlu dilakukan perhitungan pada gaya reaksi dengan persamaan {R} = [K] {U} - {F}
Reaction-force-matrix.png
Persamaan diatas dapat diselesaikan oleh OpenModelica, berikut adalah pemogramannya
Externalforce-code.png
berikut hasil plottingnya
Externalforce-plot.png
8. Mendapatkan gaya Internal dan Normal Stress
Untuk menghitung normal stress, perlu dilakukan transformasi dari hasil defleksi ditinjau dari koordinat global menjadi transformasi lokal, berikut adalah persamaan yang dapat digunakan Global-to-local.png
{u} -> koordinat local 
[U] -> koordinat global

[T] -> matriks transformasi
Misalkan kita menganalisis stress pada elemen 5, maka node yang dianalisis adalah node 2 dan 5

Sehingga persamaan matriks defleksi pada koordinat lokal menjadi || Global-to-local-element5.png

Persamaan diatas dapat diselesaikan dengan OpenModelica, berikut adalah pemogramannya
Deflectionlocal-code.png
berikut hasil plottingnya
Deflectionlocal-plot.png

Didapatkan U2x=-0.00976 inch dan U6x=-0.01209 inch

Internal force didapat dengan persamaan Internal-force-equation.png

didapat internal force pada elemen 5 sebesar 696lb.

Normal stress didapat dengan persamaan Normal-stress-equation.png

didapat normal stress pada elemen 5 sebesar 87lb/in^2

Pertemuan 4

Kuis

Membuat Flowchart untuk penyelesaian soal nomor 4 dan 8

Soal No.4 Problem4-edo.png
Soal No.8 Problem8-edo.png

Berikut adalah penyelesaian untuk soal diatas

Soal No.4
1. Mengubah problem menjadi node dan elemen
Element-Table-Problem4.png
2. Menentukan nilai Konstanta kekakuan/stiffness constant dari elemen
Elemen 1,2 Element12-problem4.png
Elemen 3 Element3-problem4.png
Elemen 4,5 Element45-problem4.png
4. Menyusun dan menggabungkan matriks elemen-elemen
Elemen Local Matrix Global Matrix
Elemen 1,2 Localmatrix-element12.png Globalmatrix-element12.png
Elemen 3 Localmatrix-element3.png Globalmatrix-element3.png
Elemen 4,5 Localmatrix-element45.png Globalmatrix-element45.png
4. Menyusun dan menggabungkan matriks elemen-elemen
Matrixglobal-sum.png
5. Menerapkan kondisi batas dan beban
Kondisi batas untuk node 1, dan 3 adalah fixed
External force pada node 2 dan 4 Externalforce-problem4.png
Dengan menerapkan Hukum Hooke, F= k. x, maka dalam persamaan matrix menjadi [F]=[K].[U]. Didapat
Solving-equation-problem4.png
6. Tahap pencarian solusi
Solving-equation-simplified-problem4.png
Persamaan matriks diatas dapat diselesaikan dengan OpenModelica, berikut adalah pemograman yang saya buat
Gauss-elimination-problem4.png
setelah melakukan pengecekan dan simulasi, saya melakukan plotting terhadap hasil simulasi. berikut hasilnya:
Plot-problem4.png

Pertemuan 5

Pada pertemuan hari ini, kami diminta pak Dai untuk membahas tugas kuis yang sudah kami buat. Pak Dai meminta saya untuk menjelaskan tentang progress yang sudah saya buat. Namun, tugas yang saya kerjakan belum dalam bentuk coding. Kemudian saya menjelaskan mengenai ide besar coding untuk Tugas Kuis minggu lalu yang sudah dikerjakan oleh saudara Josiah Enrico. Secara garis besar, perlu dibuat fungsi panggil yang digunakan pada algoritme dalam model.

Setelah itu teman saya, Fahmi, menjelaskan mengenai coding yang ia buat untuk Tugas Kuis minggu lalu yaitu mengenai Plane Truss dan Space Truss.

Tugas Pertemuan 5

Setelah kelas, Pak Dai memberikan tugas 5 sebagai berikut:

example 3.3

Berikut adalah langkah penyelesaian dari kuis nomor 5


Pertemuan 6

Pada pertemuan hari ini, Pak Dai meminta kami untuk melakukan muhasabah terhadap hasil pembelajaran kami selama kelas Metode Numerik bersama Pak Dai. Berikut adalah muhasabah saya: 

Menurut saya, saya merasa sudah cukup paham untuk memahami dasar-dasar dari metode numerik yang sudah diajari sebelum UTS. Pemahaman ini menjadi dasar saya untuk menerapkan metode numerik dengan menggunakan pemorgraman seperti OpenModelica. Selain pemahaman numerik, saya juga sudah cukup memahami tentang fenomena fisika dan membuat model matematika dari fenomena fisika tersebut. Penyelesaian masalah dibantu dengan metode numerik akan sangat membantu kita dalam menyelesaikan masalah teknik. Namun karena saya belum memahami bahasa pemograman modelica, maka saya sedikit kesulitan untuk menterjemahkan flowchart dalam penyelesaian masalaha teknik menjadi bahasa program.
Retrieved from "http://air.eng.ui.ac.id/index.php?title=Metnum03_Edward_Joshua_Patrianus_Mendrofa&oldid=50044"