Difference between revisions of "Calvin rahmat pratama"
(→Pertemuan 16/12/2020) |
(→Pertemuan 16/12/2020) |
||
| Line 519: | Line 519: | ||
[[File:Golden_Ratio.png|200px|left]] | [[File:Golden_Ratio.png|200px|left]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Menentukan Global Maksimum dengan cara melakukan optimasi dengan nilai X untuk mendapatkan F(X) Maksimum | ||
| + | [[File:Golden_ratio_2.png|200px|left]] | ||
| + | 1. Menentukan batasan titik awal terendah (xL) dan tertinggi (xH) | ||
| + | |||
| + | 2. Mendapatkan nilai x1 dan x2 dari golden ratio (d) | ||
| + | |||
| + | 3. Menentukan xL dan xH berdasarkan nilai batasan maksimum dan minimal baru | ||
| + | |||
| + | 4. Mendapatkan nilai x1 dan x2 baru | ||
| + | |||
| + | |||
| + | |||
| + | [[File:Golden ratio 3.png|200px|left]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | f(x1)>f(x2) | ||
| + | |||
| + | domain x disebelah kiri x2 dapat dieliminasi | ||
| + | |||
| + | xL=x2 untuk iterasi berikutnya | ||
| + | |||
| + | xu=xu lama | ||
| + | |||
| + | f(x2)>f(x1) | ||
| + | |||
| + | Domain x disebelah kanan x1 dapat dieliminasi | ||
| + | |||
| + | xu=x1 untuk iterasi berikutnya | ||
| + | |||
| + | xL=xL lama | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Perhitungan Excel | ||
| + | [[File:Excel count.png|400px|left]] | ||
Revision as of 16:46, 16 December 2020
Biodata Diri
Nama: Calvin Rahmat Pratama
NPM: 1806200974
Tempat,tanggal lahir: Batam,14 Oktober 2000
Hobi: Gaming dan Golf
Saya adalah mahasiswa FTUI angkatan 2018 dari jurusan Teknik mesin dan saya adalah salah satu ciptaan terbaik dari Tuhan yang Maha Esa karena pada prinsipnya Tuhan yang Maha Esa itu mendesain manusia dengan sebaik baiknya makhluk.
Teknik Mesin merupakan program studi yang saya gemari dikarenakan ayah saya juga merupakan lulusan Teknik Mesin.
Contents
Tujuan Pembelajaran
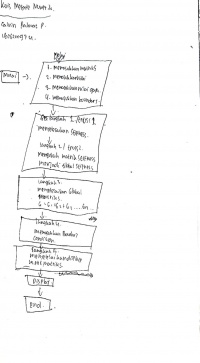
1. Memahami konsep dengan dengan baik tentang dasar-dasar metode numerik.
2. Mampu menerapkan pemahaman konsep tersebut didalam permodelan numerik.
3. Mampu menerapkan metode numerik dipersoalan keteknikan.
4. Sebagai nilai tambah bagi saya agar menjadi manusia yang beradab seperti pada Sila ke-2 Pancasila.
Metode Numerika
Sejauh ini yang dapat saya ketahui dalam metode numerika adalah metode numerika dapat menyelesaikan permasalahan yang tidak dapat diselesaikan oleh metoda analisis saya juga mempelajari cara menggunakan excel untuk menyelesaikan beberapa permasalahan metode numerika. Seperti menggunakan psuedocode dan metode newton rhapson.
Tugas Minggu 1
Review Minggu 1
Untuk pertemuan pertama saya mempelajari cara menggunakan OpenModelica dimulai dari persamaan yang cukup sederhana, OpenModelica sendiri merupakan aplikasi penghitungan permodelan yang lumayan kompleks, sehingga OpenModelica itu sendiri sangat membantu saat menyelesaikan permodelan masalah mulai dari yang cukup mudah sampai ke cukup kompleks
Review Minggu 2
Alasan mengapa menggunakan openmodelica dibanding aplikasi lainnya
- Secara penggunanaan lebih digunakan untuk permodelan bukan untuk programming
- Didalam melakukan perhitungan kode yang diinput di modelica itu di terjemahkan ke Bahasa C dan kemudian diterjemahkan lagi ke Bahasa permesinan sehingga bisa melakukan perhitungan permodelan
- Paling penting adalah openmodelica itu gratis
Pada pertemuan kedua saya juga mempelajari menggunakan modelica untuk "memanggil" fungsi. Pada pertemuan kedua juga mempelajari mengenai Fungsi tambah yang mana terlebih dahulu dari permodelan masalah di translasi kan terlebih dahulu ke dalam bahasa C++ yang nantinya akan di proses menjadi data-data perhitungan.
Tugas Minggu 2
Review Minggu 3
Pada minggu ke tiga ini saya mencoba untuk mempelajari kembali untuk membuat fungsi modelica 9x12 dengan metode gauss atau menggunakan metode lain, kemudian mencoba mengimplementasikan psuedocode pada Figure 9.4 di modelica yang mana nantinya akan di test coding dengan example 9.5.
Tugas Minggu 3
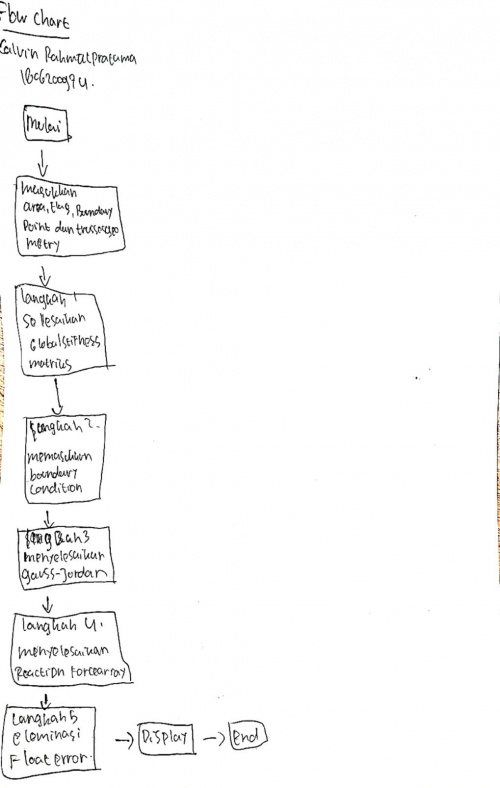
model Trusses
parameter Integer N=10; //Global matrice = 2*points connected
parameter Real A=8;
parameter Real E=1.9e6;
Real G[N,N]; //global
Real Ginitial[N,N]; //global
Real Sol[N]; //global dispplacement
Real X[N]={0,0,0,0,0,0,0,-500,0,-500};
Real R[N]; //global reaction force
Real SolMat[N,1];
Real XMat[N,1];
//boundary coundition
Integer b1=1; Integer b2=3;
//truss 1
parameter Real X1=0; //degree between truss Real k1=A*E/36; Real K1[4,4]; //stiffness matrice Integer p1a=1; Integer p1b=2; Real G1[N,N];
//truss 2
parameter Real X2=135; //degree between truss Real k2=A*E/50.912; Real K2[4,4]; //stiffness matrice Integer p2a=2; Integer p2b=3; Real G2[N,N];
//truss 3
parameter Real X3=0; //degree between truss Real k3=A*E/36; Real K3[4,4]; //stiffness matrice Integer p3a=3; Integer p3b=4; Real G3[N,N];
//truss 4
parameter Real X4=90; //degree between truss Real k4=A*E/36; Real K4[4,4]; //stiffness matrice Integer p4a=2; Integer p4b=4; Real G4[N,N];
//truss 5
parameter Real X5=45; //degree between truss Real k5=A*E/50.912; Real K5[4,4]; //stiffness matrice Integer p5a=2; Integer p5b=5; Real G5[N,N];
//truss 6
parameter Real X6=0; //degree between truss Real k6=A*E/36; Real K6[4,4]; //stiffness matrice Integer p6a=4; Integer p6b=5; Real G6[N,N];
/* for each truss, please ensure pXa is lower then pXb (X represents truss element number)
- /
algorithm
//creating global matrice
K1:=Matrices(X1); G1:=k1*GlobalMatrices(K1,N,p1a,p1b);
K2:=Matrices(X2); G2:=k2*GlobalMatrices(K2,N,p2a,p2b);
K3:=Matrices(X3); G3:=k3*GlobalMatrices(K3,N,p3a,p3b);
K4:=Matrices(X4); G4:=k4*GlobalMatrices(K4,N,p4a,p4b);
K5:=Matrices(X5); G5:=k5*GlobalMatrices(K5,N,p5a,p5b);
K6:=Matrices(X6); G6:=k6*GlobalMatrices(K6,N,p6a,p6b);
G:=G1+G2+G3+G4+G5+G6; Ginitial:=G;
//implementing boundary condition for i in 1:N loop
G[2*b1-1,i]:=0; G[2*b1,i]:=0; G[2*b2-1,i]:=0; G[2*b2,i]:=0;
end for;
G[2*b1-1,2*b1-1]:=1; G[2*b1,2*b1]:=1; G[2*b2-1,2*b2-1]:=1; G[2*b2,2*b2]:=1;
//solving displacement
Sol:=Gauss_Jordan(N,G,X);
//solving reaction force
SolMat:=matrix(Sol); XMat:=matrix(X); R:=Reaction_Matrices(N,Ginitial,SolMat,XMat);
end Trusses;
Fungsi Panggilan
Matriks
function Matrices input Real A; protected Real Y; public output Real X[4,4]; protected Real float_error = 10e-10; protected final constant Real pi=2*Modelica.Math.asin(1.0);
algorithm
Y:=A/180*pi; X:=[(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2;
-(Modelica.Math.cos(Y))^2,-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.cos(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y);
-Modelica.Math.cos(Y)*Modelica.Math.sin(Y),-(Modelica.Math.sin(Y))^2,Modelica.Math.cos(Y)*Modelica.Math.sin(Y),(Modelica.Math.sin(Y))^2];
for i in 1:4 loop for j in 1:4 loop if abs(X[i,j]) <= float_error then X[i,j] := 0; end if; end for; end for;
end Matrices;
Global Matriks
function GlobalMatrices
input Real Y[4,4]; input Integer B; input Integer p1; input Integer p2; output Real G[B,B];
algorithm
for i in 1:B loop for j in 1:B loop G[i,j]:=0; end for; end for;
G[2*p1,2*p1]:=Y[2,2]; G[2*p1-1,2*p1-1]:=Y[1,1]; G[2*p1,2*p1-1]:=Y[2,1]; G[2*p1-1,2*p1]:=Y[1,2];
G[2*p2,2*p2]:=Y[4,4]; G[2*p2-1,2*p2-1]:=Y[3,3]; G[2*p2,2*p2-1]:=Y[4,3]; G[2*p2-1,2*p2]:=Y[3,4];
G[2*p2,2*p1]:=Y[4,2]; G[2*p2-1,2*p1-1]:=Y[3,1]; G[2*p2,2*p1-1]:=Y[4,1]; G[2*p2-1,2*p1]:=Y[3,2];
G[2*p1,2*p2]:=Y[2,4]; G[2*p1-1,2*p2-1]:=Y[1,3]; G[2*p1,2*p2-1]:=Y[2,3]; G[2*p1-1,2*p2]:=Y[1,4];
end GlobalMatrices;
Reaction Matrices
function Reaction_Matrices
input Integer N; input Real A[N,N]; input Real B[N,1]; input Real C[N,1]; protected Real X[N,1]; public output Real Sol[N]; protected Real float_error = 10e-10;
algorithm
X:=A*B-C;
for i in 1:N loop
if abs(X[i,1]) <= float_error then X[i,1] := 0; end if;
end for;
for i in 1:N loop
Sol[i]:=X[i,1]; end for;
end Reaction_Matrices;
Gauss Jordan
input Integer N; input Real A[N,N]; input Real B[N]; output Real X[N]; Real float_error = 10e-10;
algorithm X:=Modelica.Math.Matrices.solve(A,B);
for i in 1:N loop
if abs(X[i]) <= float_error then X[i] := 0; end if;
end for;
end Gauss_Jordan;
|}
Kuis 1 Metode Numerik
Tugas 4
class truss_3d_try //define initial variable parameter Integer Points=4; //Number of Points parameter Integer Trusses=3; //Number of Trusses parameter Real Area=0.0015; //Area parameter Real Elas=70e9; //Elasticity
//define connection parameter Integer C[Trusses,2]=[1,2;
1,3;
1,4];
//define coordinates (please put orderly) parameter Real P[Points,3]=[2,0,0;
0,0,1.5;
0,0,-1.5;
0,1.5,0];
//define external force (please put orderly) parameter Real F[Points*3]={0,-5000,0,
0,0,0,
0,0,0,
0,0,0};
//define boundary parameter Integer b[:]={2,3,4};
//solution Real displacement[N], reaction[N];
protected parameter Integer N=3*Points; Integer boundary[3*size(b,1)]=cat(1,(3*b).-2,(3*b).-1,3*b); Real q1[3], q2[3], g[N,N], G[N,N], G_star[N,N], id[N,N]=identity(N), err=10e-10, cx, cy, cz, L, X[3,3];
algorithm //Creating Global Matrix G:=id; for i in 1:Trusses loop
for j in 1:3 loop
q1[j]:=P[C[i,1],j];
q2[j]:=P[C[i,2],j];
end for;
//Solving Matrix
L:=Modelica.Math.Vectors.length(q2-q1);
cx:=(q2[1]-q1[1])/L;
cy:=(q2[2]-q1[2])/L;
cz:=(q2[3]-q1[3])/L;
X:=(Area*Elas/L)*[cx^2,cx*cy,cx*cz;
cy*cx,cy^2,cy*cz;
cz*cx,cz*cy,cz^2];
//Transforming to global matrix
g:=zeros(N,N);
for m,n in 1:3 loop
g[3*(C[i,1]-1)+m,3*(C[i,1]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,2]-1)+n]:=X[m,n];
g[3*(C[i,2]-1)+m,3*(C[i,1]-1)+n]:=-X[m,n];
g[3*(C[i,1]-1)+m,3*(C[i,2]-1)+n]:=-X[m,n];
end for;
G_star:=G+g;
G:=G_star;
end for;
//Implementing boundary for i in boundary loop
for j in 1:N loop G[i,j]:=id[i,j]; end for;
end for;
//Solving displacement displacement:=Modelica.Math.Matrices.solve(G,F);
//Solving reaction reaction:=(G_star*displacement)-F;
//Eliminating float error for i in 1:N loop
reaction[i]:=if abs(reaction[i])<=err then 0 else reaction[i]; displacement[i]:=if abs(displacement[i])<=err then 0 else displacement[i];
end for; end truss_3d_try;
Pertemuan 16/12/2020
Aplikasi Metode Numerik Dalam Kasus Optimasi
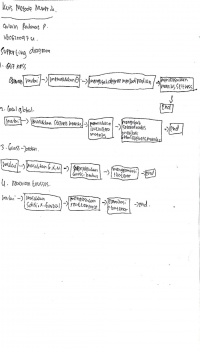
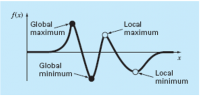
Bracket Optimization Using the Golden Ratio Ada Satu Grafik Fungsi Yang Memiliki Nilai F(X) Global Maksimum Dan Lokal Maksimum Serta F(X) Global Minimum Dan Lokal Minimum
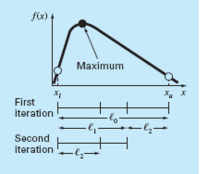
Menentukan Global Maksimum dengan cara melakukan optimasi dengan nilai X untuk mendapatkan F(X) Maksimum
1. Menentukan batasan titik awal terendah (xL) dan tertinggi (xH)
2. Mendapatkan nilai x1 dan x2 dari golden ratio (d)
3. Menentukan xL dan xH berdasarkan nilai batasan maksimum dan minimal baru
4. Mendapatkan nilai x1 dan x2 baru
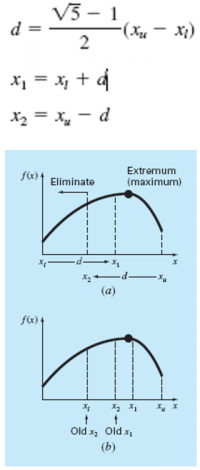
f(x1)>f(x2)
domain x disebelah kiri x2 dapat dieliminasi
xL=x2 untuk iterasi berikutnya
xu=xu lama
f(x2)>f(x1)
Domain x disebelah kanan x1 dapat dieliminasi
xu=x1 untuk iterasi berikutnya
xL=xL lama
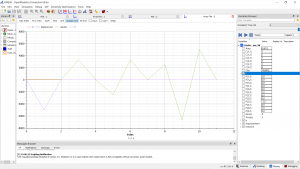
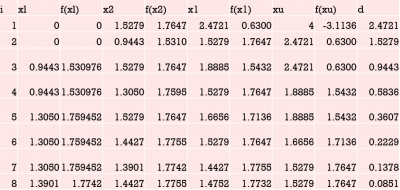
Perhitungan Excel